Operat losowania:

wykaz jednostek tworzących

badaną zbiorowość (populację)

1

Musi być:
- kompletny (bez brakujących elementów),
-aktualny (bez elementów, które nie należą obecnie do populacji),
- bez powtórzeń,
- gwarantujący identyfikowalność jednostek.

Zasady doboru próby

√√√√

Określenie populacji badanej.

√√√√

Określenie operatu losowania (jeśli istnieje)

√√√√

Określenie jednostki wyboru.

√√√√

Ustalenie wielkości próby.

√√√√

Wybór metody doboru jednostek:

Próba losowa:

Próba pseudo-losowa

:

Próba celowa

:

2

Próba losowa:

O trafieniu jednostki do próby

decyduje niezależny od

wybierającego mechanizm

wybory i można określić

prawdopodobieństwo trafienia

jednostki do próby

Próba pseudo-losowa

:

określamy proporcje osób,

które wezmą udział w badaniu

np. ze względu na wiek, płeć,

wykształcenie, miejsce

zamieszkania

(kwotowa)

Próba celowa

:

szukamy osób, które

należą do grupy

docelowej

Próba ma charakter losowy, gdy przyj

ę

te kryterium doboru

jednostek jest niezale

ż

ne od badanych cech i gdy ka

ż

da jednostka

zbiorowo

ś

ci ma ró

ż

ne od zera p-stwo znalezienia si

ę

w próbie.

Dobór celowy:

nie ma potrzeby dowodzenia reprezentatywności i

oceny precyzji

Dobór losowy:

3

Dobór losowy:

jest potrzeba zagwarantowania reprezentatywności i

oceny precyzji

Dobór celowy:

nie ma potrzeby dowodzenia reprezentatywności i

oceny precyzji

•

Dobór kwotowy:

gdy badane zjawiska, o których

nie ma żadnej informacji są silnie skorelowane z
cechami o znanych rozkładach (podstawa
ustalania kwot).

•

Dobór typowy

lub

przez eliminację

(warunki

4

•

Dobór typowy

lub

przez eliminację

(warunki

stosowania j.w.).

•

Dobór przypadkowy

: nie oczekuje się zgodności

jakichkolwiek struktur.

•

Dobór wg „

kuli śniegowej

”: badanie

środowiskowe o znacznej homogeniczności
populacji i trudnej dostępności jednostek

Zagrożenia w doborze celowym

•

Błędny osąd i intuicja badacza co do
prawidłowości występujących w populacji.

•

Nadmierna chęć uczestnictwa w badaniach jest

podyktowana specjalnymi predyspozycjami

5

podyktowana specjalnymi predyspozycjami
respondentów, które nie zawsze są zbieżne z
badanymi cechami populacji.

•

Brak uzasadnienia wiarygodności wyników dla
tego typu badań i łatwo argumentować przeciw
nim, jeśli są „niewygodne”.

Cechy doboru losowego:

•

W czasie losowania elementy populacji nie
przemieszczają się.

•

Dostęp do każdego elementu populacji jest
jednakowy.

•

Elementy populacji są dostatecznie wymieszane.

6

Próba ma charakter losowy, gdy przyj

ę

te

kryterium doboru jednostek jest niezale

ż

ne od

badanych cech i gdy ka

ż

da jednostka

zbiorowo

ś

ci ma ró

ż

ne od zera p-stwo

znalezienia si

ę

w próbie.

O zastosowaniu określonej metody doboru próby

decydują warunki,

w jakich będzie realizowane badanie.

1. Populacje mogą być skończone lub nieskończone.

2. Wiedza o populacji może być bardzo rozległa i opierać się na

dostępnych danych lub zweryfikowanych teoriach i hipotezach lub
też wiedza taka może w ogóle nie istnieć.

7

3. Skład populacji może być nieustannie lub okresowo weryfikowany

w postaci spisów i innych rejestrów, lub też nie ma możliwości
utworzenia imiennej listy jednostek tworzących populację.

Jeśli jest znana wielkość populacji i istnieje

możliwość nawiązania kontaktu z każdą jednostką,

to wystarczy, by zbudować próbę losową

Jak losować?

Prosto!!!

Próba losowa prosta:

10097

32533

76520

13586

34673

54876

80959

37542

04805

64894

74296

24805

24037

20636

08422

68953

19645

9303

23209

02560

15953

99019

02529

09376

70715

38311

31165

88676

8

99019

02529

09376

70715

38311

31165

88676

12807

99970

80157

36147

64032

36653

98951

66065

74717

34072

76850

36697

36170

65813

31060

10805

45571

82406

35303

42614

86799

85269

77602

02051

65692

68665

74818

73053

63573

32135

05325

47048

90553

57548

28468

73796

45753

03529

64778

35808

34282

60935

98520

17767

14905

68607

22109

40558

60970

11805

05431

39808

27732

50725

68248

29405

83452

99634

06288

98083

13746

70078

18475

88685

40200

86507

58401

36766

67951

90364

99594

67348

87517

64969

91826

8928

93785

Losowanie proste ze zwracaniem

lub bez (efektywniejsze)

Kiedy?

Brak jakichkolwiek informacji o populacji i populacje nie są

zbyt liczne.

Zalety:

Wady:

9

•

Próby wyważone
automatycznie.

•

Proste metody
obliczania precyzji

•

Łatwe!

•

Dogodny tylko dla
małych populacji.

•

Wymaga znajomości
operatu losowania.

Zalety:

Wady:

( )

( )

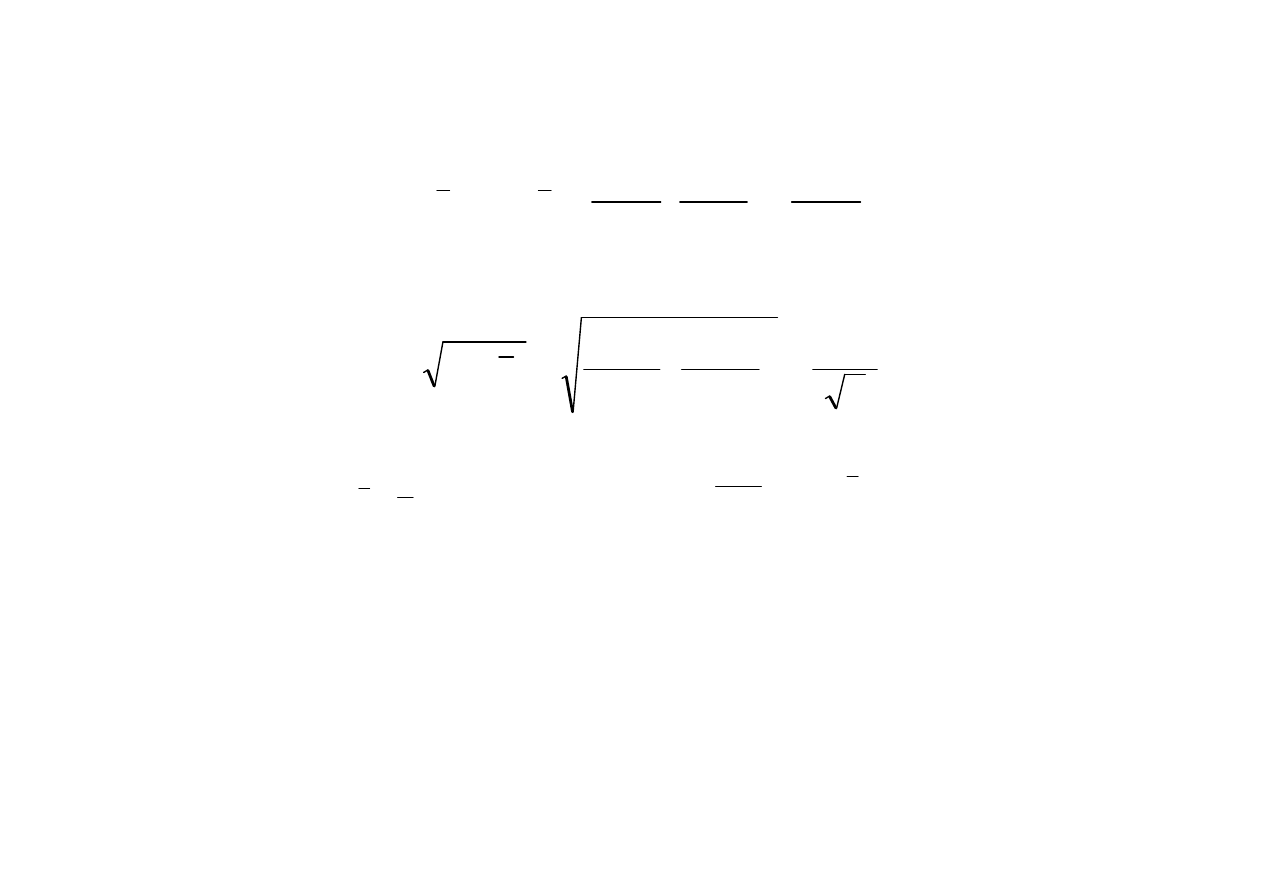
n

x

S

N

n

N

n

x

S

x

D

SE

)

(

ˆ

ˆ

2

2

≈













−

=

=

n

x

S

N

n

N

n

x

S

x

D

x

MSE

)

(

ˆ

)

(

ˆ

)

(

)

(

2

2

2

≈













−

=

=

Losowanie proste bez zwracania:

∑

=

=

n

i

i

x

n

x

1

1

( )

(

)

2

1

2

1

1

ˆ

∑

=

−

−

=

n

i

i

x

x

n

x

S

gdzie:

oraz

n – liczebno

ść

próby

N – liczebno

ść

populacji

Losowanie systematyczne

interwał losowania:

k = N/n

Kiedy?

Brak jakichkolwiek informacji o populacji i zawsze gdy

brak operatu losowania

Zalety:

Wady:

11

•

Próby wyważone
automatycznie.

•

Precyzja taka jak dla
próby prostej

•

Łatwe!

•

Ukryte
powarstwowanie
populacji

Zalety:

Wady:

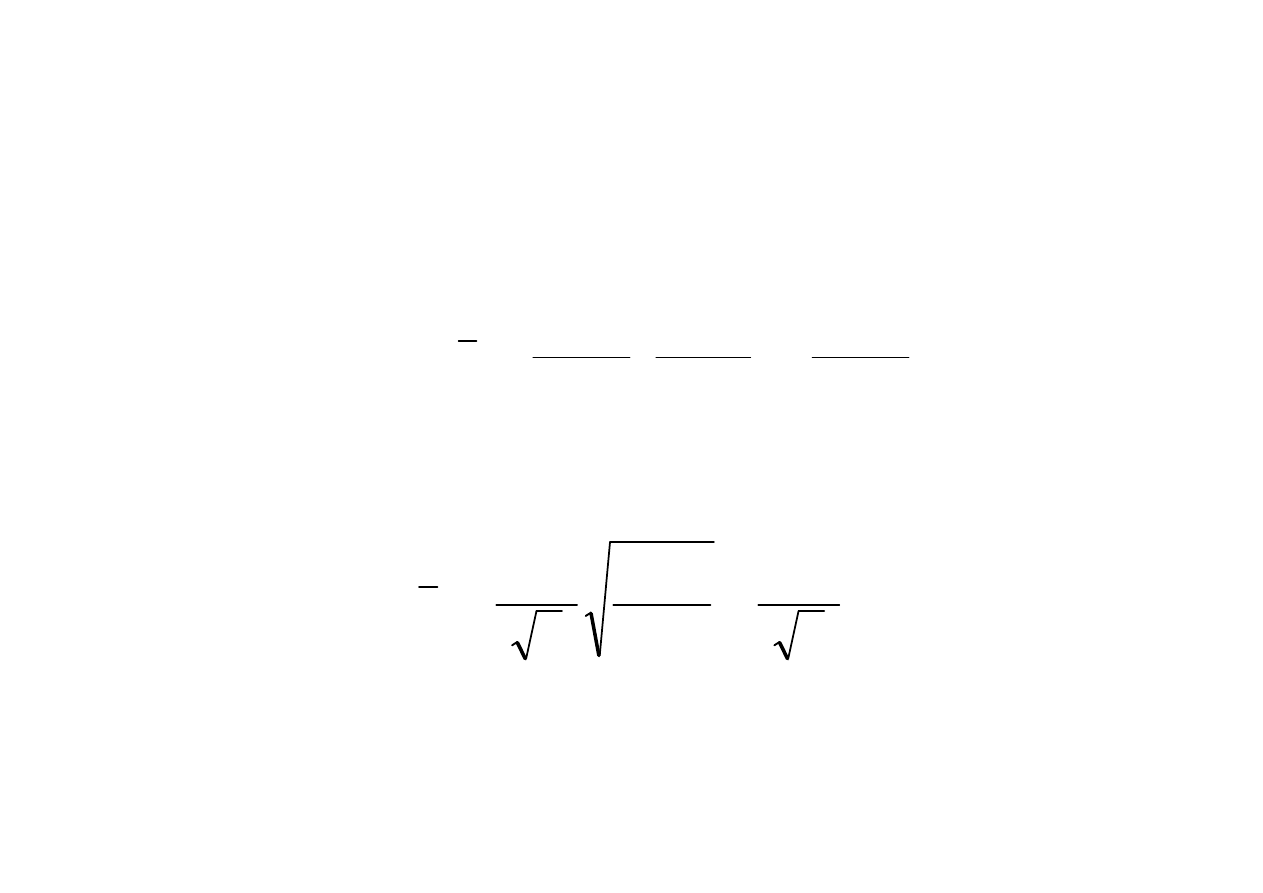
Losowanie systematyczne:

n

x

S

N

n

N

n

x

S

x

MSE

)

(

ˆ

)

(

ˆ

)

(

2

2

≈













−

≈

Je

ś

li jednostki populacji przed losowaniem zostały uporz

ą

dkowane w sposób losowy, to:

12

n

x

S

N

n

N

n

x

S

x

SE

)

(

ˆ

)

(

ˆ

)

(

≈

−

≈

Losowanie warstwowe

Kiedy?

Istnieją dodatkowe informacje o populacji i populacje są

bardzo liczne.

Zalety:

Wady:

13

•

Są bardziej efektywne, czyli
dostarczają bardziej precyzyjnych
informacji.

•

W każdej warstwie można
stosować inną technikę losowania.

•

Warstwowanie można
przeprowadzić po wylosowaniu
próby dostosowując się do
potrzeb

•

Wymaga znajomości struktur
populacji. Jest tym
efektywniejsze im mniejsze
jest zróżnicowanie warstw.

•

Pożądany operat losowania.

8

10

12

14

16

18

w

a

rt

o

śc

i

y

BSS

WSS

TSS

Równo

ść

wariancyjna

14

14

0

2

4

6

8

0

1

2

3

w

a

rt

o

śc

i

y

Nr grupy

BSS

WSS

WSS

BSS

TSS

+

=

przykład

nr jednostki

Liczba sprzedawców Obroty w tys. zł

1

2

15

2

2

21

3

2

27

4

2

29

5

2

14

6

2

16

7

3

21

8

3

25

9

3

29

10

3

34

11

3

34

12

3

19

13

3

36

14

3

36

15

4

22

16

4

25

17

4

27

18

4

34

WSS

BSS

TSS

+

=

∑ ∑

∑

=

=

=

−

=

−

=

k

1

i

n

1

j

2

i

ij

k

1

i

i

2

i

i

)

y

(y

n

*

)

y

y

(

WSS

BSS

18

4

34

19

4

34

20

5

36

21

5

36

22

5

36

23

5

36

24

5

37

25

5

31

26

5

40

27

5

38

28

5

36

29

5

37

30

6

42

31

6

35

32

6

39

33

6

39

34

6

41

35

6

43

36

6

35

Ź

ródło wariancji

SS

Pomi

ę

dzy grupami

1475,982

W obr

ę

bie grup

758,9905

Razem

2234,972

=

=

1

i

1

j

813

,

0

972

,

2234

982

,

1475

=

=

eta

Losowanie warstwowe:

∑

=

⋅

−

=

k

h

h

h

W

n

S

N

N

N

n

N

x

SE

1

2

ˆ

)

(

gdzie:

∑

=

⋅













−

=

=

k

h

h

h

W

W

n

S

N

N

N

n

N

x

D

x

MSE

1

2

2

ˆ

)

(

)

(

16

)

(

)

(

x

SE

x

SE

W

≤

( )

(

)

2

1

2

1

1

ˆ

∑

=

−

−

=

h

n

i

h

i

h

x

x

n

x

S

∑

=

=

n

i

i

x

n

x

1

1

gdzie:

oraz

∑

=

=

k

h

h

n

n

1

k – liczba warstw,

⇒

1

)

(

)

(

≤

=

x

SE

x

SE

Deft

W

Losowanie zespołowe

Kiedy?

Brak jakichkolwiek informacji o jednostkach populacji lecz

istnieją informacje o podgrupach (zespołach) oraz populacje

są bardzo liczne

Zalety:

Wady:

17

•

Ograniczenie operatu tylko do
listy zespołów.

•

Mało rozproszone terytorialnie
próby.

•

Efektywny! Ale przy dużej
liczbie zespołów o małych
rozmiarach w próbie

•

Złożony schemat losowania, na
ogół dwustopniowy: zespoły i
jednostki

Losowanie zespołowe:

∑

∑

=

=

−

−

⋅

−

=

=

k

j

Z

j

M

i

ij

Z

Z

M

x

M

x

k

K

k

K

k

x

D

x

MSE

j

1

2

2

1

2

)

(

)

1

(

1

1

)

(

)

(

18

∑

∑∑

=

=

=

=

=

m

h

h

k

h

n

j

hj

Z

x

k

x

n

x

1

1

1

1

1

0

k – liczba zespołów w próbie
K – liczba zespołów w populacji
M

j

– liczebność każdego zespołu

Techniki losowania:

Proporcjonalne, czyli z różnymi prawdopodobieństwami

wyboru zespołu

Kiedy?

Populacje są bardzo liczne. Istnieją zespoły o zdecydowanie

różnych rozmiarach

2

2

1

)

(

)

(

∑









−

⋅

=

=

k

j

j

x

x

M

p

x

D

x

MSE

19

1

2

1

)

(

)

(

∑

=















−

⋅

=

=

j

j

j

j

j

Z

Z

x

p

x

M

M

p

k

x

D

x

MSE

Gdzie:
k = liczba zespołów w próbie,
M

j

– rozmiar zespołu w populacji,

M – liczba jednostek całej populacji,
p

j

- prawdopodobie

ń

stwo wylosowania zespołu,

(

)

2

1

2

1

)

(

)

(

∑

=

−

=

=

k

j

j

j

Z

Z

x

x

p

k

x

D

x

MSE

Gdy: p

j

=M

j

/M

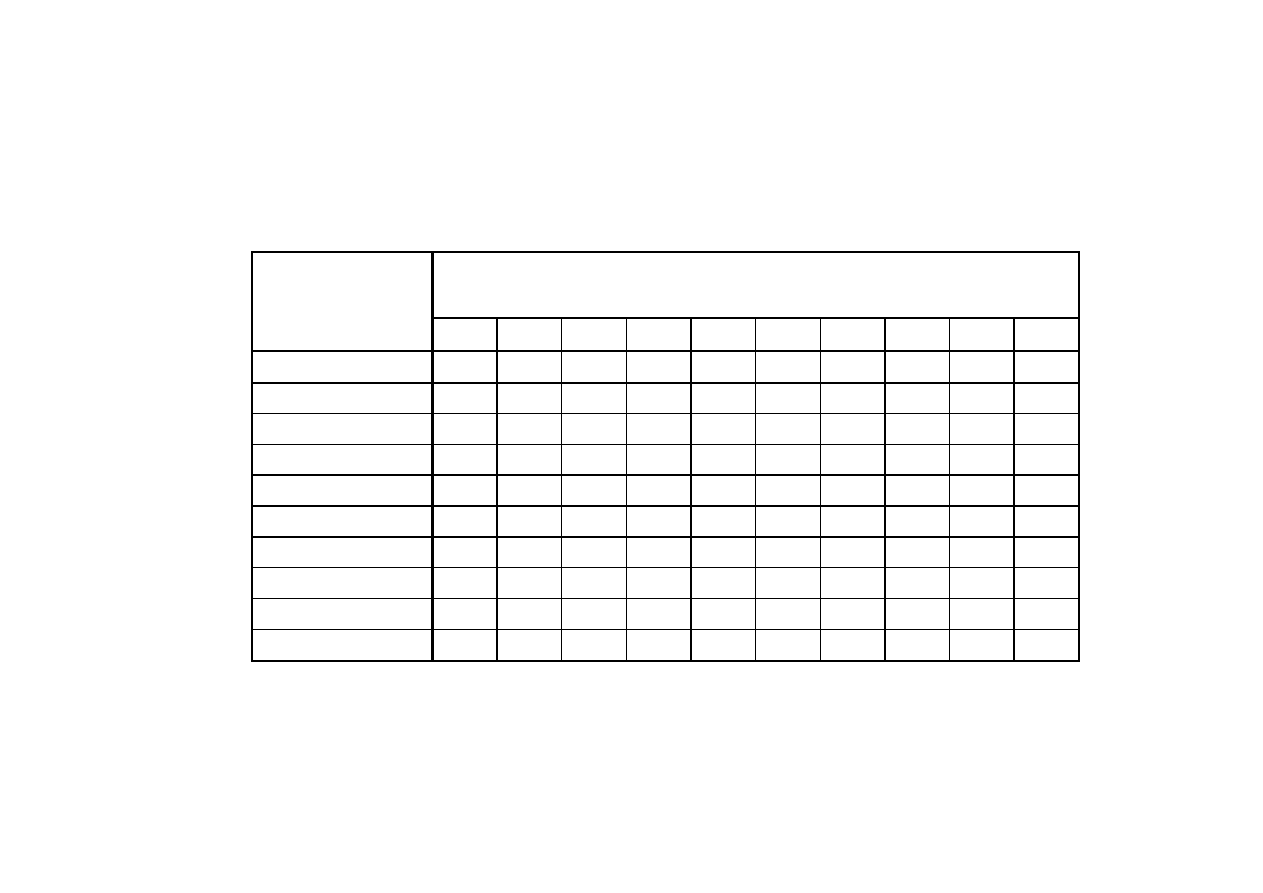
Tabela Kisha

liczba osób w

gospodarstwie

domowym

ostatnia cyfra numeru mieszkania (domu)

1

2

3

4

5

6

7

8

9

0

1

1

1

1

1

1

1

1

1

1

1

2

1

2

1

2

1

2

1

2

1

2

3

2

3

2

1

3

1

2

1

3

2

4

3

1

2

4

1

3

4

3

2

1

5

2

4

5

3

1

5

3

2

1

4

6

1

3

4

5

6

1

2

4

3

5

7

5

6

3

7

2

7

5

1

4

6

8

4

5

1

6

1

4

3

7

2

8

9

7

9

4

8

6

2

1

5

6

3

10 lub więcej

8

2

4

1

3

6

5

10

7

9

Losowanie dwustopniowe:

zespołowe i w zespołach proste bez zwracania

lub systematyczne

Kiedy?

Brak jakichkolwiek informacji o jednostkach populacji lecz

istnieją informacje o podgrupach (zespołach) oraz populacje

21

•

Ograniczenie operatu tylko do
listy zespołów.

•

Mało rozproszone terytorialnie
próby.

•

Efektywny! Ale przy dużej
liczbie zespołów o małych
rozmiarach w próbie

•

Złożony schemat losowania, na
ogół dwustopniowy: zespoły i
jednostki

istnieją informacje o podgrupach (zespołach) oraz populacje

są bardzo liczne

Zalety:

Wady:

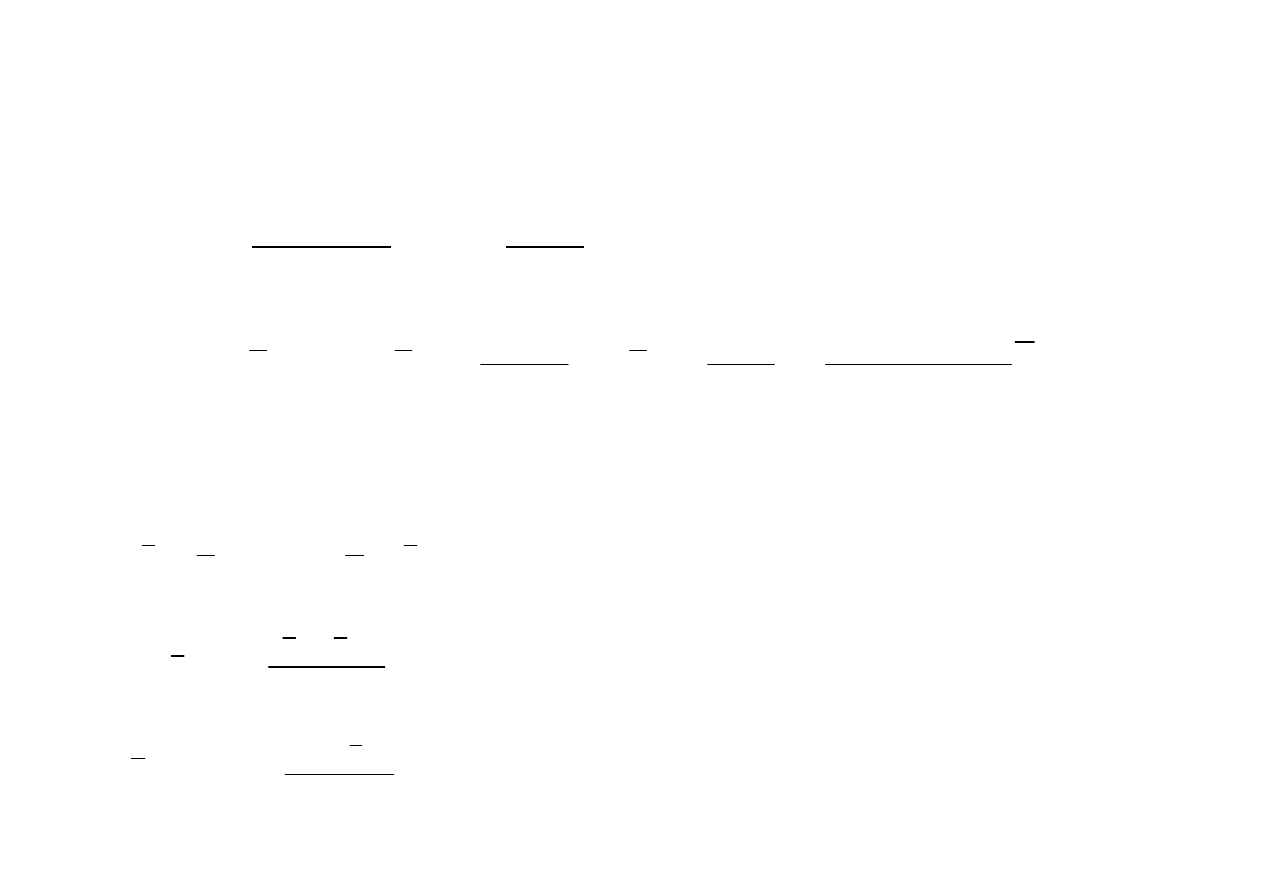
Dla zespołów ró

ż

nolicznych w populacji, równych liczebno

ś

ciach próby (n

0

) w ka

ż

dym zespole:

( )

)

(

)

(

)

(

)

(

2

1

0

0

2

2

2

x

S

n

n

N

N

kN

K

x

S

k

K

k

K

x

D

x

MSE

h

k

h

h

h

h

Z

Z

∑

=

−

+

⋅

−

=

=

Losowanie dwustopniowe: zespołowe i w zespołach proste bez zwracania:

∑

∑∑

=

=

=

=

=

k

h

h

k

h

n

j

hj

Z

x

k

x

n

x

1

1

1

1

1

0

∑

=

−

−

=

k

h

Z

h

h

k

x

x

x

S

1

2

2

1

)

(

)

(

∑∑

=

=

−

−

=

k

h

n

i

h

hj

h

k

n

x

x

x

S

1

1

2

2

0

)

(

)

(

to wariancja międzyzespołowa

to wariancja wewnątrzzespołowa

k – liczba zespołów w próbie
K – liczba zespołów w populacji
n

0

– liczebność każdej podpróby

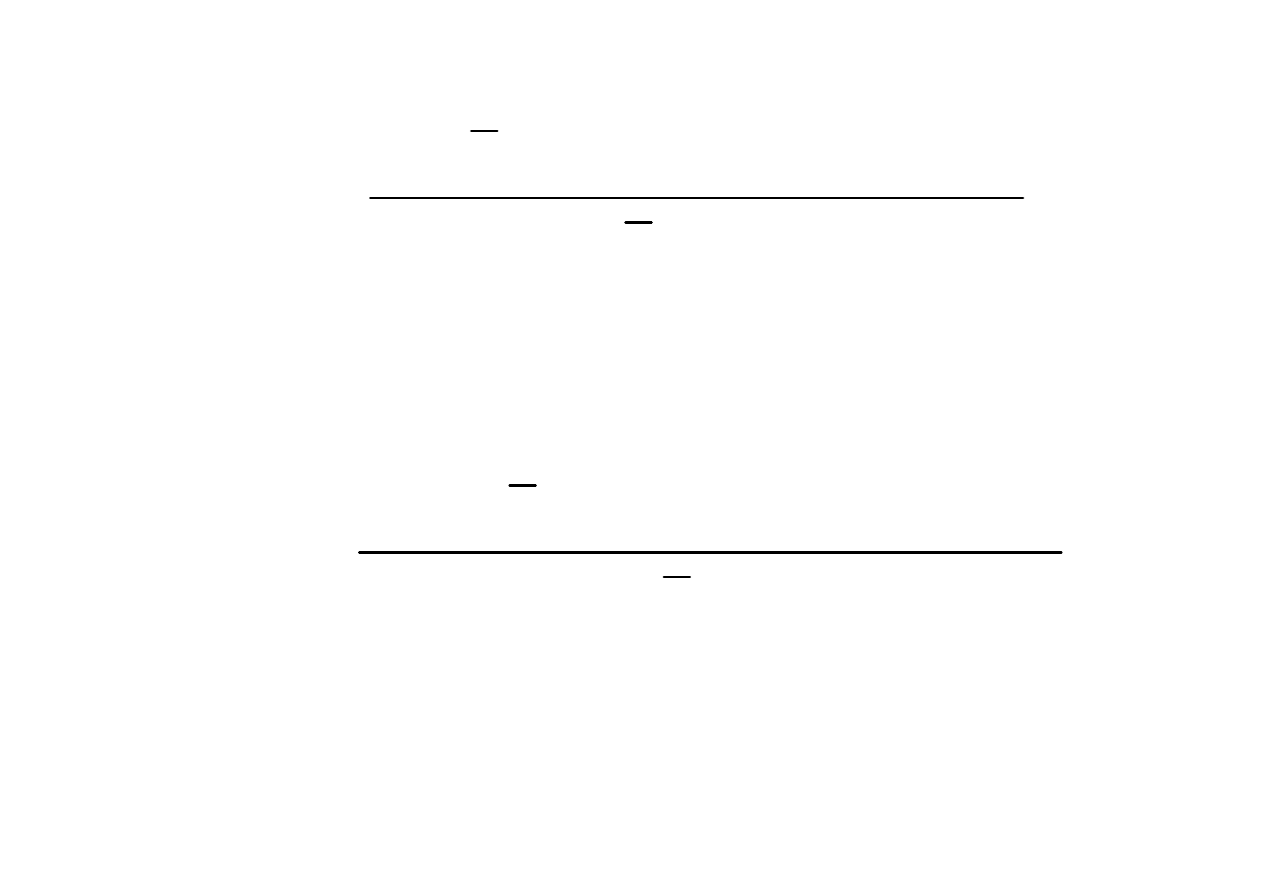
1

)

(

)

(

≤

=

prosta

próba

sposób

okreslony

wybrana w

próba

x

SE

x

SE

Deft

1

)

(

)

(

≤

=

prosta

próba

sposób

okreslony

wybrana w

próba

x

MSE

x

MSE

Deff

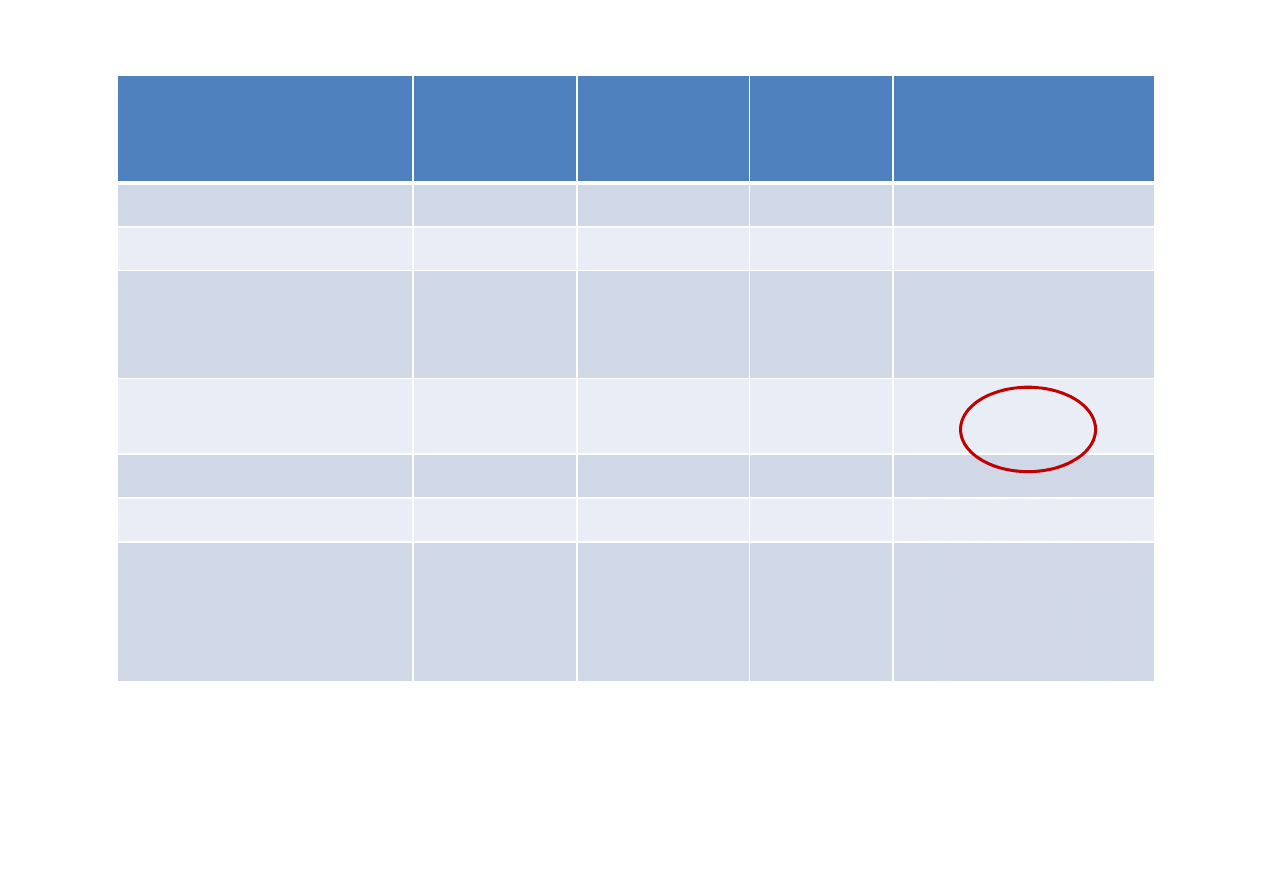
Typ losowania

Wartość
średnia w
próbie

Błąd
standardowy
(SE)

Błąd max

Deft =
SE

(próba)

/SE

(próba prosta)

Próba prosta

20,5

2,49

5,23

1

Próba systematyczna

29,6

2,81

6,349

1,12

Próba warstwowa o
jednakowych rozmiarach
z warstw

32,3

0,79

1,785

0,32

Próba warstwowa-
proporcjonalna

33,2

0,57

1,287

0,23

proporcjonalna

Próba zespołowa I

28,9

2,52

5,49

1,01

Próba zespołowa II

28,6

2,16

4,71

0,86

Zespołowa
proporcjonalna z
różnymi
prawdopodobieństwami

33,9

2,6

5,07

1,04

Zagrożenia w doborze losowym

• Ignorowanie konsekwencji wyboru techniki

losowania:

Sposób pobierania próby jest sprz

ęż

ony

ze sposobem estymacji wybranego parametru i
ocen

ą

bł

ę

du losowego. Dokonanie zmian w jednej ze

„stron” wywoływa

ć

musi zmian

ę

w drugiej.

25

•

Niedostosowana do rzeczywisto

ś

ci technika

losowania:

Otaczaj

ą

ca rzeczywisto

ść

ma zło

ż

on

ą

struktur

ę

i dlatego s

ą

potrzebne adekwatne do niej

schematy losowania.

• Ignorowanie sprawdzania losowo

ś

ci wylosowanej

próby

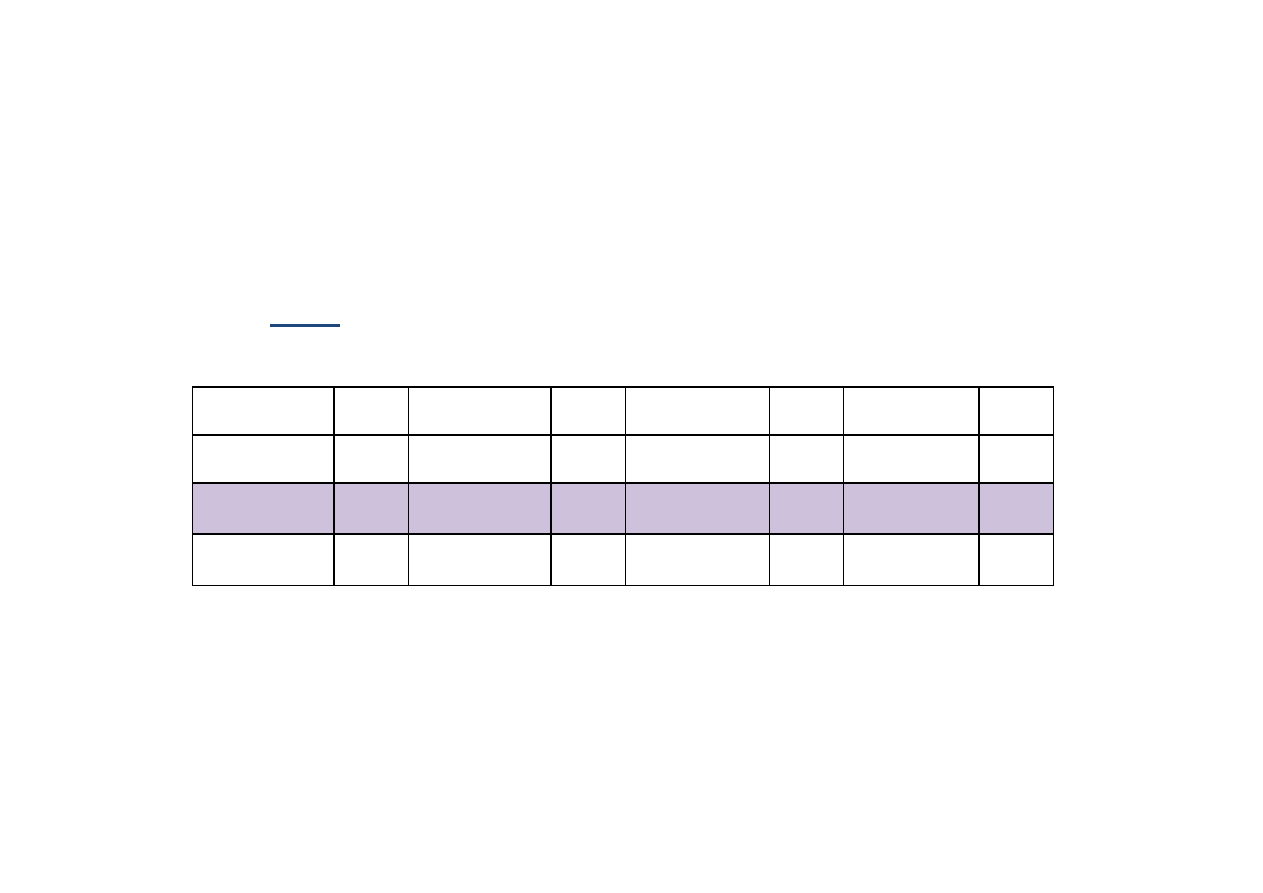
warstwowa I

wynik

warstwowa II

wynik

zespołowa I

wynik

zespołowa II

wynik

Ignorowanie konsekwencji wyboru techniki losowania:

Sposób pobierania próby jest sprz

ęż

ony ze sposobem estymacji wybranego

Parametru i ocen

ą

bł

ę

du losowego. Dokonanie zmian w jednej ze „stron”

wywoływa

ć

musi zmian

ę

w drugiej.

Ś

rednia

32,30

Ś

rednia

33,20

Ś

rednia

32,50

Ś

rednia

26,33

Bł

ą

d

standardowy

1,76

Bł

ą

d

standardowy

1,69

Bł

ą

d

standardowy

1,61

Bł

ą

d

standardowy

3,13

Wła

ś

ciwy

poziom SE

0,789

Wła

ś

ciwy

poziom SE

0,569

Wła

ś

ciwy

poziom SE

2,047

Wła

ś

ciwy

poziom SE

1,69

sprawdzania losowości

wylosowanej próby: test serii

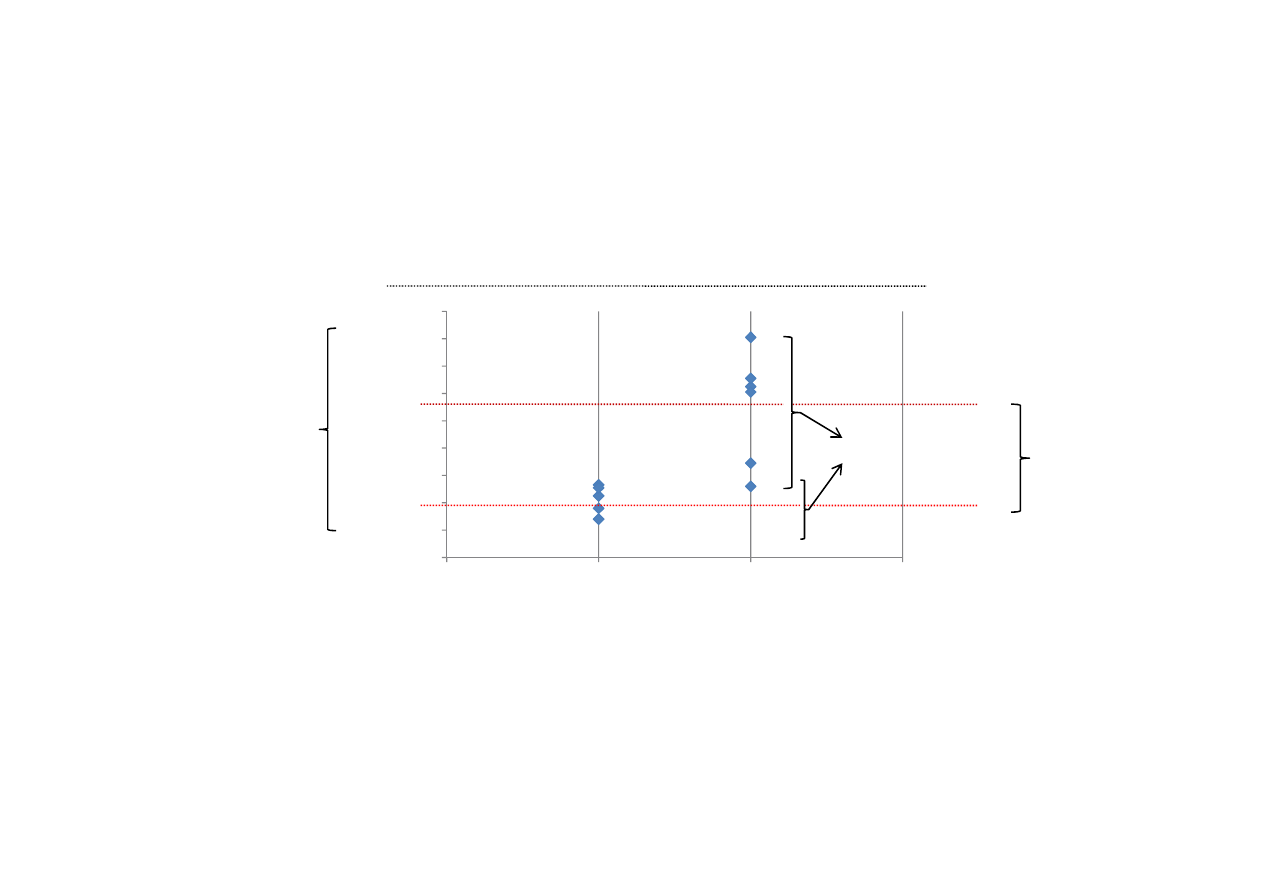
1. Wyznaczenie mediany dla cechy, według której losowo

ść

próby powinna by

ć

zachowana.
2. Oznaczenie symbolami:
np.

A

tych jednostek, których warto

ś

ci cechy s

ą

mniejsze od mediany,

symbolem

B

za

ś

warto

ś

ci, które s

ą

wi

ę

ksze od mediany.

symbolem

B

za

ś

warto

ś

ci, które s

ą

wi

ę

ksze od mediany.

W przypadku gdy jednostka posiada warto

ść

cechy identyczn

ą

z warto

ś

ci

ą

mediany,

nale

ż

y j

ą

pomin

ąć

.

3. Okre

ś

lenie liczby serii symboli A oraz B oraz liczby elementów A, tj. n

1

, i liczby

elementów B, tj. n

2

.

4. Odczytanie z tablic rozkładu serii warto

ś

ci krytycznych

k

1

i

k

2

, tzn. takich, które

wyznaczaj

ą

przedział warto

ś

ci (k

/2

, k

1-

α

/2

〉

, okre

ś

laj

ą

cych dopuszczalne liczby serii

obserwowane w próbie, z przyj

ę

tym ryzykiem bł

ę

du

α

(na ogół 5%).

Gdy rozmiar próby przekracza 40

elementów:

Wykorzystanie zbie

ż

no

ść

liczby serii do rozkładu normalnego.

H

0

: próba ma charakter losowy

H

1

: próba nie ma charakter ulosowego

Warto

ść

statystyki testuj

ą

cej okre

ś

la wzór:

k

k

u

−

=

)

(k

S

k

k

u

−

=

1

2

2

1

2

1

+

+

=

n

n

n

n

k

)

1

(

)

(

)

2

(

2

)

(

2

1

2

2

1

2

1

2

1

2

1

−

+

+

−

−

=

n

n

n

n

n

n

n

n

n

n

k

S

która ma rozkład N(0, 1).
Jeśli wartość statystyki u nie przekracza wartości 1,96, to nie ma podstaw do odrzucenia hipotezy zerowej,
czyli by podważać losowy charakter próby.

gdzie:

Techniki prowadzenia wywiadu

Zalety:

Wady:

1.

Niskie koszty.

2.

Brak wpływu ankietera na udzielane

odpowiedzi.

1.

Konieczność formułowania prostych pytań.

2.

Brak możliwości „sondowania” odpowiedzi.

Odpowiedzi są ostateczne.

Ankieta pocztowa:

odpowiedzi.

3.

Wysoki poziom anonimowości.

4.

Czas na przemyślenie odpowiedzi.

5.

Znaczna dostępność respondentów.

Odpowiedzi są ostateczne.

3.

Brak kontroli nad tym, kto w rzeczywistości

udziela odpowiedzi.

4.

Niski odsetek odpowiedzi.

Techniki prowadzenia wywiadu

Zalety:

Wady:

1.

Możliwość budowania pytań złożonych o

wyższym stopniu trudności.

2.

Możliwości „sondowania” odpowiedzi.

1.

Wysokie koszty.

2.

Wpływ ankietera na udzielane odpowiedzi.

3.

Brak wysokiego poziomu anonimowości.

Ankieta bezpo

ś

rednia (face-to-face):

3.

Możliwość bezpośredniego kodowania danych

(CATI).

4.

Kontrola nad tym, kto w rzeczywistości

udziela odpowiedzi.

5.

Wysoki odsetek odpowiedzi.

6.

Możliwość oceny warunków zbierania

informacji.

4.

Brak czasu na przemyślenie odpowiedzi.

Zasady prowadzenia wywiadu osobistego:

•Powiedz respondentowi, kim jeste

ś

i kogo reprezentujesz.

•Powiedz respondentowi, co robisz, w sposób wzbudzaj

ą

cy zainteresowanie.

•Powiedz respondentowi, w jak sposób został wybrany.

•Dostosuj post

ę

powanie do sytuacji.

•Dostosuj post

ę

powanie do sytuacji.

•Postaraj si

ę

wytworzy

ć

atmosfer

ę

zaufania i zrozumienia.

•Nie zadawaj pyta

ń

z pami

ę

ci.

•Nie interpretuj pyta

ń

.

•Nie zmieniaj kolejno

ś

ci i nie omijaj pyta

ń

.

Techniki prowadzenia wywiadu

Zalety:

Wady:

1.

Przeciętne koszty.

2.

Krótki czas realizacji.

3.

Duża liczba respondentów.

1.

Łatwość odmowy udziału w badaniu.

2.

Łatwość przerwania wywiadu.

3.

Brak wysokiego poziomu anonimowości.

Ankieta telfoniczna (TI):

4.

Wysoki odsetek odpowiedzi.

5.

Możliwość bezpośredniego kodowania danych

(CATI).

6.

Dotarcie do osób, które niechętnie uczestniczą w

badaniach pocztowych lub w wywiadach

osobistych.

7.

Możliwość kontroli zadawania pytań i rejestracji

danych.

8.

Możliwości „sondowania” odpowiedzi.

4.

Brak czasu na przemyślenie odpowiedzi.

5.

Brak kontroli nad tym, kto w rzeczywistości

udziela odpowiedzi.

Gdy respondent może mówić nieprawdę!

Technika odpowiedzi losowych

•

Reszka

– odpowiadamy na

pytanie 1

•

Orzeł

– odpowiadamy na

pytanie 2

•

Czy zdarzyło się, że w trakcie zakupów w
supermarkecie zjadła/zjadł Pani/Pan
batonik czekoladowy i nie
zapłaciła/zapłacił za niego?

•

Czy brała/brał Pani/Pan udział w
ostatnich wyborach parlamentarnych?

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

|

(

)

|

(

)

(

2

2

1

1

2

1

2

1

2

1

O

P

R

P

T

P

T

T

P

T

P

R

P

T

P

O

P

T

P

R

T

P

O

T

P

T

T

P

⋅

−

∪

=

⋅

+

⋅

=

+

=

∪

Estymacja frakcji odpowiedzi pozytywnych na pytanie 1:

Baza danych

Definiowanie zmiennych:

1. Nazwa
2. Typ
3. Liczba znaków

3. Liczba znaków
4. Liczba miejsc po przecinku
5. Etykieta
6. Wyodr

ę

bnione kategorie

7. Braki danych
8. Szeroko

ść

kolumny

9. Wyrównanie
10.Skala pomiaru

Badanie spójności bazy danych

1.

Wszystkie warto

ś

ci mieszcz

ą

si

ę

w ramach ustalonych przez zasady skalowania.

2.

Wyst

ę

puje zgodno

ść

w filtrach.

3.

Rozstrzygni

ę

ta kwestia obserwacji nietypowych.

4.

Wyst

ę

puje spójno

ść

logiczna danych.

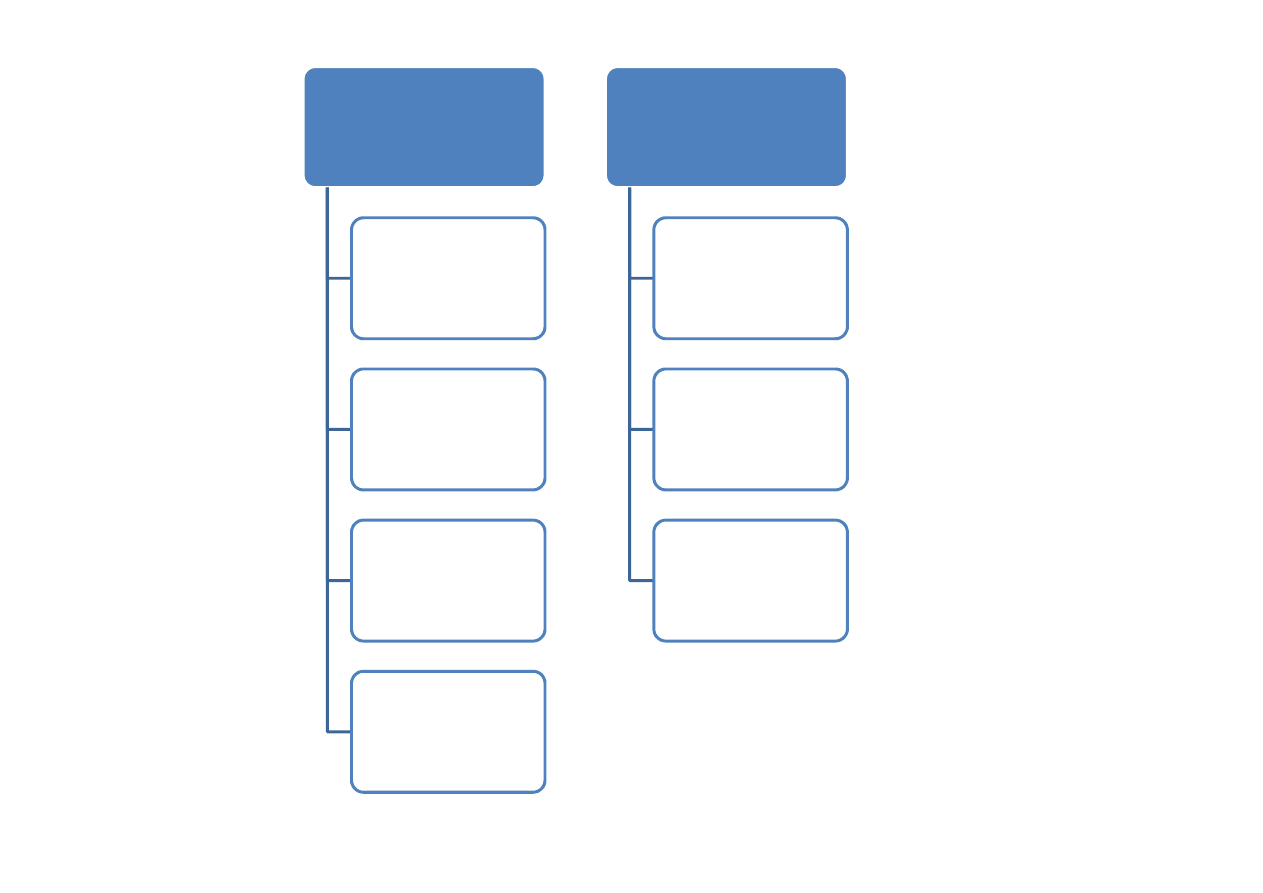
Błędy

pokrycia

Błąd

struktury

Błąd wybory i

braku reakcji

Błędy treści

Błąd pomiaru

Błąd analizy

braku reakcji

Błąd

zagubienia

Błąd

odrzucenia

Błąd

interpretacji

Metody redukcji

błędów

nielosowych

Imputacje

Ważenie danych

(poststratyfikacja)

Metody redukcji bł

ę

dów nielosowych

Imputacja - braki pojedynczych odpowiedzi

dedukcyjna

deterministyczna

stochastyczna

wprowadzenie wartości umownych

38

90

wprowadzenie wartości umownych

ś

rednie

cold-deck

hot-deck

z innych badań lub symulacji

podobieństwo obiektów

Uwzględnienie składnika losowego w imputacji deterministycznej

Dobór losowy:

jest potrzeba zagwarantowania reprezentatywności i

oceny precyzji

•

Dobór prosty ze zwracaniem lub bez zwracania.

•

Dobór warstwowy.

•

Dobór zespołowy.

•

Dobór wielostopniowy.

•

Dobór systematyczny.

Losowanie
ograniczone

39

•

Dobór systematyczny.

Losowanie z jednakowymi prawdopodobie

ń

stwami wyboru daje tzw. próby

samowa

żą

ce si

ę

Losowanie z ró

ż

nymi prawdopodobie

ń

stwami wyboru wymaga przewa

ż

enia wyników

Przyczyny ważenia danych:

•

Technika losowania.

•

Odmowy odpowiedzi.

40

•

Dostosowanie do reprezentatywności ze
względu na różne cechy (poststratyfikacja)

Ważenie:

•

Ważenie musi być stosowane jeśli próba nie jest
samoważąca się

⇒ losowanie proste,

systematyczne, proporcjonalne

41

•

W przypadku procedur ograniczonego doboru
losowego każda próba może być reprezentatywna dla
populacji, jeśli każdemu elementowi próby przypisze
się prawdopodobieństwo znalezienia się w próbie

poststratyfikacja

h

h

h

n

N

W

=

N

n

n

N

w

h

h

h

⋅

=

gdzie:
W

h

i w

h

– waga dla h-tej grupy wa

ż

enia;

n

h

– liczba jednostek z próby w h-tej grupie wa

ż

enia;

n

h

– liczba jednostek z próby w h-tej grupie wa

ż

enia;

N

h

– liczba jednostek z populacji w h-tej grupie wa

ż

enia;

– liczebno

ść

próby;

– liczebno

ść

populacji.

∑

=

=

k

h

h

n

n

1

∑

=

=

k

h

h

N

N

1