ZESTAW 7

Wydział: IMIR, I rok (A.Baczmański)

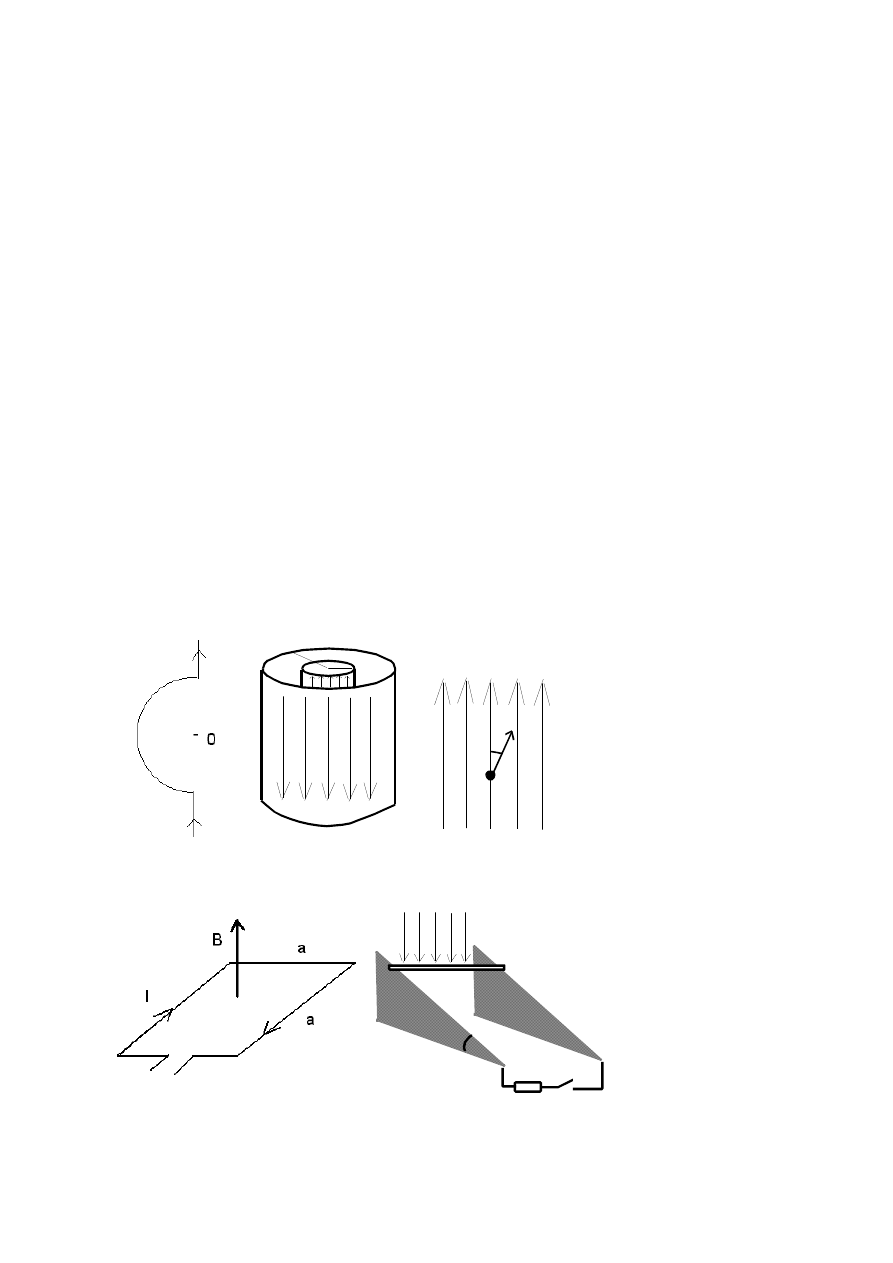
1. Wyznaczyć wektor indukcji pola magnetycznego w punkcie O na rys. 1 (przez drut płynie prąd o natężeniu I).

2. Korzystając z prava Ampere’a znaleźć wektor indukcji pola magnetycznego:
a) w odległości r od osi nieskończenie długiego prostoliniowego przewodnika walcowego o promieniu a, przez
który płynie prąd o stałej gęstości, i natężeniu I.
b) wewnątrz i na zewnątrz nieskończenie długiego solenoidu przez który płynie prąd o natężeniu I (promień
solenoidu wynosi R, a liczba zwojów na jednostkę długości równa jest n)

3. Przez dwa długie współosiowe cylindry przewodzące o promieniach R

1

i R

2

>R

1

płynie w przeciwnych

kierunkach prąd o natężeniu I (rys.2). Znaleźć i przedstawić graficznie wartość natężenia pola magnetycznego
wytworzonego w przestrzeni przez ten układ.

4. Obliczyć skok linii śrubowej, po której porusza się proton, wlatujący w stałe i jednorodne pole magnetyczne o
wektorze indukcji B z prędkością v skierowaną pod kątem

α

do linii sił pola (rys 3).

5. Kwadratową ramkę (o boku a ) z drutu umieszczono w jednorodnym polu magnetycznym o wektorze
indukcji B (rys. 4). Przez ramkę płynie prąd o natężeniu I. Oblicz moment siły obracającej ramkę oraz energię
potencjalną w zależności od kąta

θ

.

6. Pręt o długości l i masie m położono na dwóch równoległych szynach pod kątem

α

=30

o

do poziomu. Szyny

znajdują się w polu magnetycznym o wektorze indukcji B; linie tego pola są prostopadłe do poziomu (rys. 5).
Obliczyć maksymalną prędkość v

m

, jaką może uzyskać pręt, w przypadku gdy szyny nie są połączone oraz w

przypadku gdy są zwarte na jednych końcach opornikiem R. Przyjąć, że pręt może ślizgać się bez tarcia oraz
opór pręta i szyn można pominąć.

R

1

II

I

R

2

B

p

+

v

α

rys.1 rys. 2 rys.3

B

R

α

l

m

rys. 4 rys. 5