AiR II rok czwartek nieparzysty

Podstawy automatyki - ćwiczenia

Lista nr 2

1)

Wyznaczyć opis w przestrzeni stanu dla równań

a)

u

y

dt

dy

dt

y

d







3

2

2

2

b)

u

dt

du

dt

u

d

dt

u

d

y

dt

dy

dt

y

d

dt

y

d

3

3

5

4

2

3

2

2

3

3

2

2

3

3















2)

Dla przykładu z zadania 1a wyznaczyć macierz tranzycyjną:
a) metodą odwrotnego przekształcenia Laplace’a
b) metodą diagonalizacji macierzy

3)

Rozwiązać równania stanu z zadania 1a przy następujących założeniach:
a) u(t)=0, y’(0)=0, y(0)=1
b) u(t)=2*1(t), y’(0)=y(0)=0

4)

Wyznaczyć transmitancję operatorową dla równań stanu wyznaczonych w
zadaniu 1

OPIS UKŁADÓW DYNAMICZNYCH W PRZESTRZENI STANÓW

D

B

A

sI

C

s

G









1

]

[

)

(

Wyznaczanie równań stanu na podstawie równania różniczkowego

Metoda ogólna
W przypadku równania różniczkowego rzędu n-tego

d

n

y

dt

n

+ a

n-1

d

n-1

y

dt

n-1

+...+ a

1

dy

dt

+a

0

y= b

0

u

z prostym skladnikiem wymuszającym, jako zmienne stanu przyjmuje się

)

1

(

2

1

,

,

,











n

n

y

x

y

x

y

x



Wówczas otrzymujemy równania stanu































1

0

0

1

1

3

2

2

1

n

i

i

i

n

n

n

u

b

x

a

x

x

x

x

x

x

x



i równanie wyjścia

1

x

y



W przypadku równania różniczkowego rzędu n-tego z wymuszeniem zawierającym
pochodne

d

n

y

dt

n

+ a

n-1

d

n-1

y

dt

n-1

+...+ a

1

dy

dt

+a

0

y= b

m

d

m

u

dt

m

+ b

m-1

d

m-1

u

dt

m-1

+...+ b

1

du

dt

+b

0

u

wyznacza się opis metodą ogólną w postaci

u

c

c

c

x

x

x

x

a

a

a

a

x

x

x

x

n

n

n

n

n

n



















































































































































































2

1

1

2

1

1

2

1

0

1

2

1

1

0

0

0

0

1

0

0

0

0

1

0





u

c

x

x

x

y

n

0

2

1

0

0

1

































Następnie stosujemy podstawienie :

u

c

x

y

o





1

,

u

c

u

c

x

u

c

x

y

o

o











1

2

1

'

'

'

, .........

Powyższe wyrażenia należy podstawić do równania różniczkowego, porównać stronami i
wyliczyć współczynniki

,....

,

,

2

1

c

c

c

o

Rozwiązywanie równań stanu

Rozwiązanie równania

Bu

Ax

x







spełniające warunek początkowy

0

0

)

(

x

t

x



ma postać:











t

t

t

A

t

t

A

d

Bu

e

x

e

t

x

0

0

)

(

)

(

)

(

0

)

(







At

e

t





)

(

- macierz tranzycyjna

W przypadku gdy

0

)

(



t

u

rozwiązanie ma postać:

0

0

)

(

)

(

x

t

x

e

t

x

At







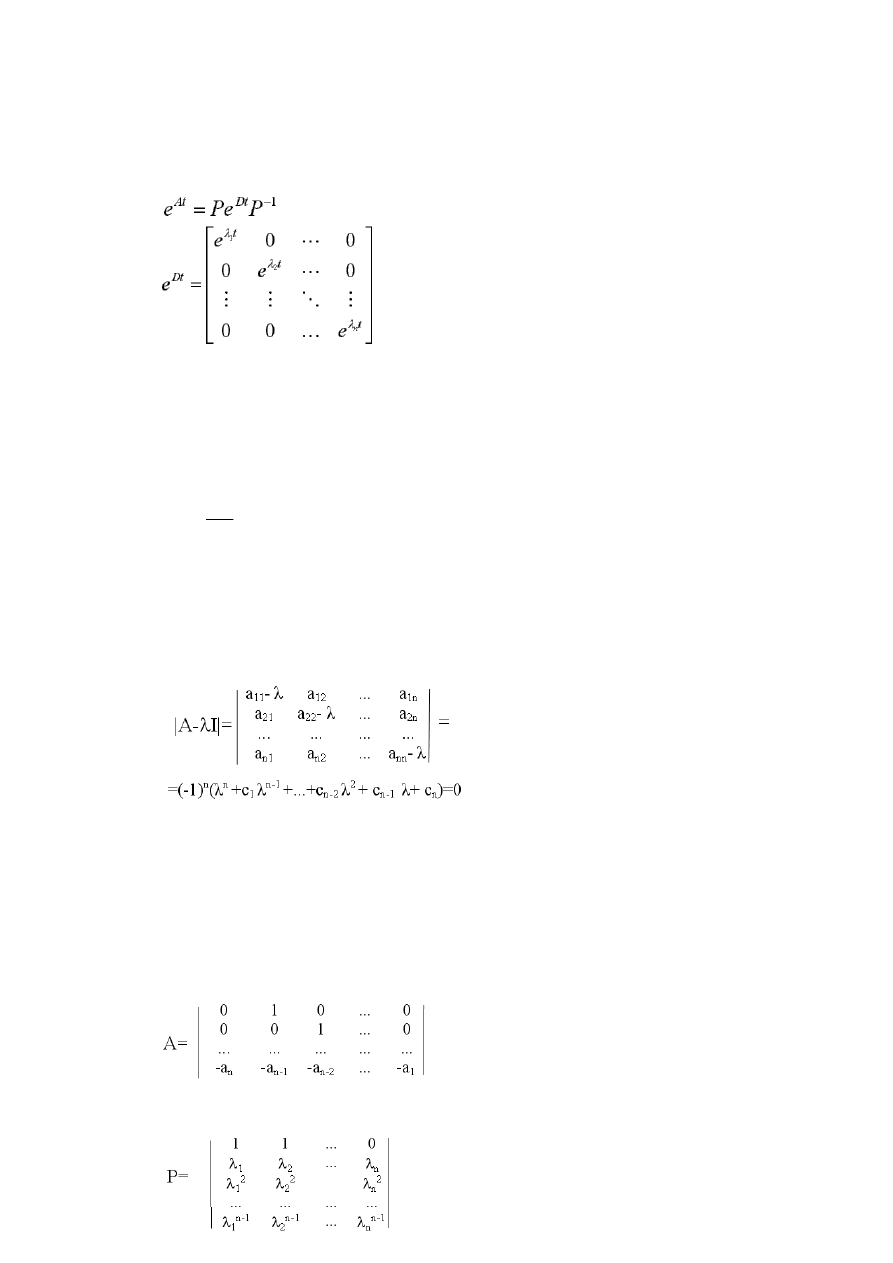
Wyznaczanie macierzy tranzycyjnej -metoda odwrotnego przekształcenia Laplaca

e

At

=L

-1

[(sI-A)

-1

]

Wyznaczanie macierzy tranzycyjnej -metoda diagonalizacji macierzy
Metoda ta oparta jest na następującej zależności

Minorem M

ij

nazywamy wyznacznik (n-1) - szego stopnia otrzymanego przez opuszczenie i-

tego wiersza i j-tej kolumny z wyznacznika n-tego stopnia
Dopełnienie algebraiczne D

ij

określa się z zależności D

ij

=(-1)

i+ j

M

ij

Macierz dołączoną macierzy kwadratowej A

d

otrzymuje się przez transpozycję macierzy,

w której każdy element A zastąpiono przez jego dopełnienie algebraiczne

A A

d

=A

d

A=|A| I

Macierz odwrotna A

-1

jest macierzą dołączoną podzieloną przez wyznacznik macierzy

|

A

|

A

A

d

1





A

-1

A=A A

-1

=I

Jeśli A jest macierzą o wymiarach n x n, to wyznacznik |A-



I| nazywa się wielomianem

charakterystycznym macierzy A
I - macierz jednostkowa, w której wszystkie elementy na przekątnej są równe 1
Równanie |A-



I|=0 nazywa się równaniem charakterystycznym

Pierwiastki równania charakterystycznego



1,



2,...,



n

stanowią wartości własne macierzy A

Wektor niezerowy V

i

który spełnia równanie AV

i

=



i

V

i

nazywa się wektorem własnym

macierzy A związanym z wartością własną



i

Wektory własne wyznacza się z następującego równania [A-



i

I ] V

i

=0

Jeśli



1,



2,...,



n

są pojedynczymi wartościami własnymi macierzy A, a wektory V

1

, V

2

,..., V

n

są wektorami własnymi macierzy A, to kolumny macierzy przekształcenia
diagonalizującego P stanowią wektory własne macierzy A

P=[V

1

, V

2

,..., V

n

]

Jeśli macierz A ma postac

i wartości własne macierzy A są pojedyncze



1,



2,...,



n,

to macierz diagonalizująca P ma

postac