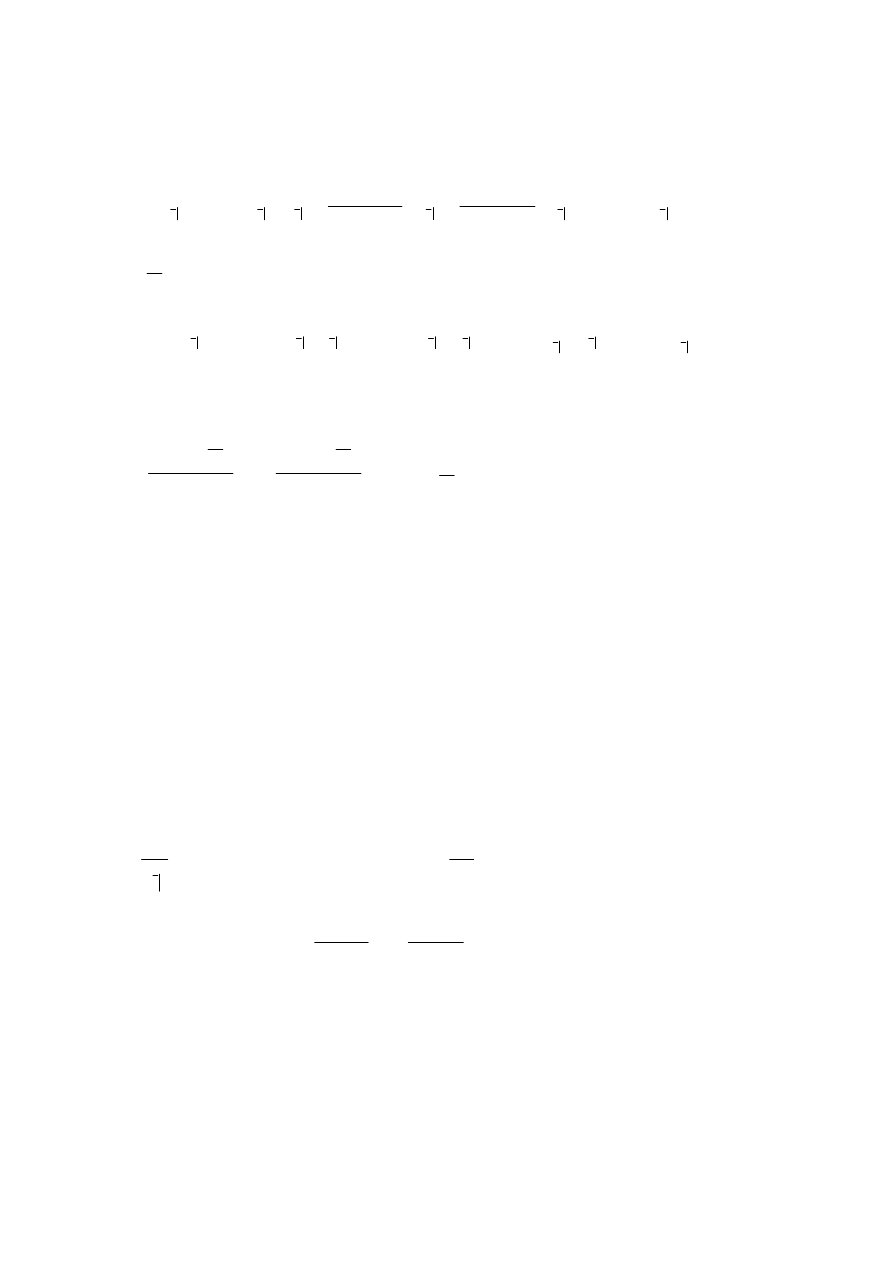
∑

=

−

+

⋅

=

n

1

j

j

j

i)

(1

R

P

,

∑

=

−

+

⋅

=

n

1

j

j

n

j

i)

(1

R

F

,

P

i)

(1

F

n

⋅

+

=

i

n

a

R

P

⋅

=

,

i

n

s

R

F

⋅

=

,

i

i)

(1

-

1

a

-n

i

n

+

=

,

i

1

i)

(1

s

n

i

n

−

+

=

,

i

n

n

i

n

a

i)

(1

s

⋅

+

=

i

R

P

=

∞

,

P

i)

(1

P

1)

(

⋅

+

=

+

,

F

i)

(1

F

1)

(

⋅

+

=

+

i

n

..

1)

(

a

R

P

⋅

=

+

,

i

n

..

1)

(

s

R

F

⋅

=

+

,

i

n

..

n

i

n

..

a

)

i

1

(

s

⋅

+

=

,

i

n

i

n

..

s

)

i

1

(

s

⋅

+

=

,

i

n

i

n

..

a

)

i

1

(

a

⋅

+

=

H

H)

(

i)

(1

P

P

−

−

+

⋅

=

,

F

F

H)

(

=

−

i)

ln(1

R

P

i

1

ln

n

+













⋅

−

−

=

,

i)

ln(1

R

F

i

1

ln

n

+













⋅

+

=

,

n

n

i|

1

n

i)

(1

R

a

R

P

−

−

+

⋅

+

⋅

=

j

n

1

j

j

0

i)

(1

R

K

−

=

+

⋅

=

∑

,

j

n

n

1

j

j

n

0

i)

(1

R

i)

(1

K

−

=

+

⋅

=

+

⋅

∑

j

j

j

U

I

R

+

=

,

i

K

I

1

j

j

⋅

=

−

,

j

1

j

j

j

1

j

j

U

K

R

I

K

K

−

=

−

+

=

−

−

m

j

j

1

m

m

j

0

j

i)

(1

R

i)

(1

K

K

−

=

+

⋅

−

+

⋅

=

∑

,

m

j

n

1

j

m

m

j

i)

(1

R

K

−

+

=

+

⋅

=

∑

∑

=

−

=

j

1

m

m

0

j

U

K

K

,

∑

+

=

=

n

1

j

m

m

j

U

K

,

∑

=

=

n

1

j

j

0

U

K

i

n

0

a

K

R

=

,

1

-

j

1

1

j

j

i)

(1

U

i)

(1

U

U

+

⋅

=

+

⋅

=

−

,

n

K

U

0

=

i)

(1

R

R

R

j

1

j

*

1

j

+

⋅

+

=

+

+

,

∑

∑

=

=

+

=

+

n

1

j

τ

j

m

1

i

t

i

j

i

r)

(1

B

r)

(1

A

,

r

1

i)

(1

k

+

=

+

∑

=

−

+

⋅

=

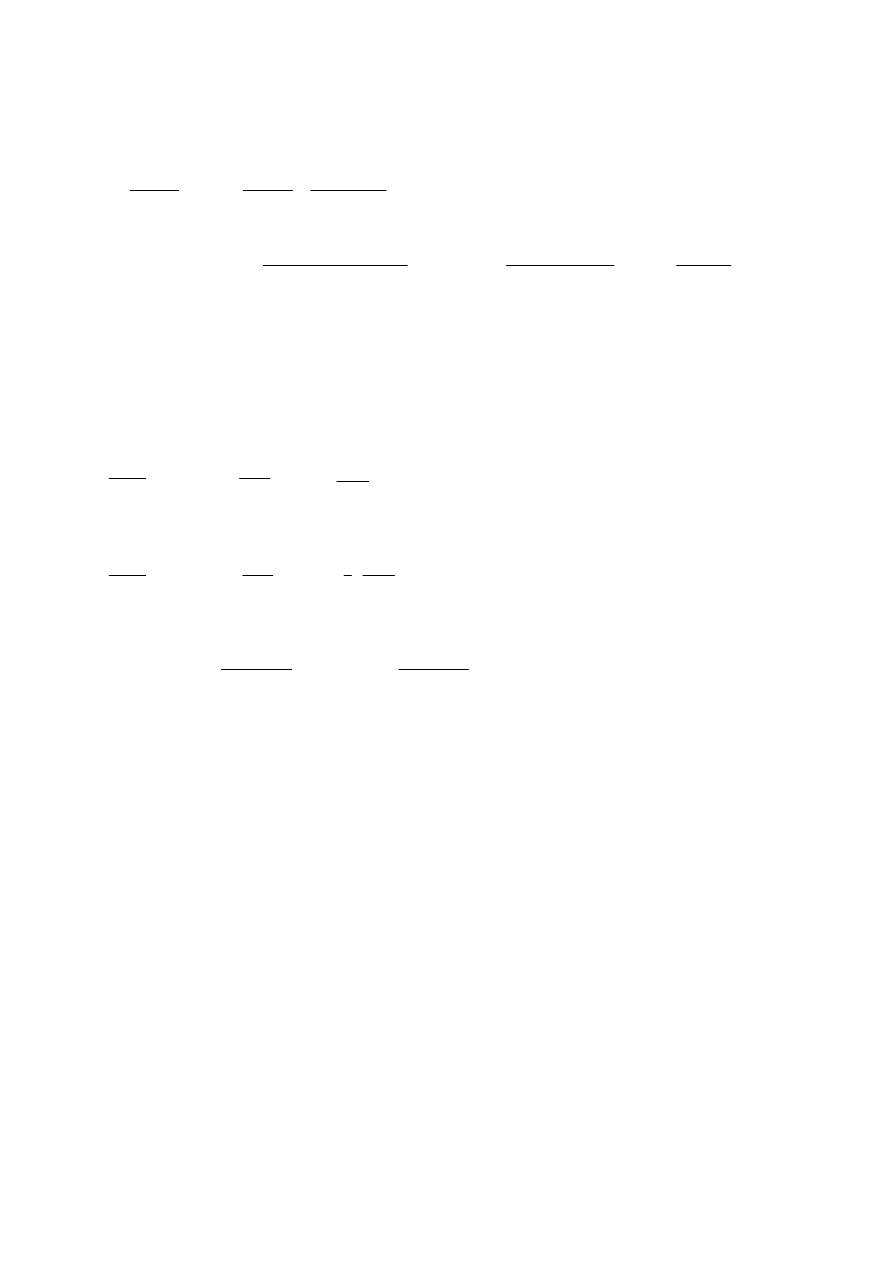
n

0

j

j

j

i)

(1

A

NPV

,

0

A

x

A

...

x

A

x

A

n

1

n

1

n

1

n

0

=

+

+

+

+

−

−

,

x

i

1

=

+

0

i)

(1

A

*

T

0

j

j

j

=

+

∑

=

,

0

i)

(1

x

A

i)

(1

A

x

[T*]

[T*]

0

j

j

j

1

[T*]

=

+

⋅

+

+

+

=

+

∑

,

x

[T*]

T*

+

=

,

1)

(0,

x

∈

∑

=

⋅

=

n

1

j

j

ω

j

D

,

∑

=

+

⋅

+

⋅

=

n

1

j

j

-

j

-j

j

j

IRR)

(1

A

IRR)

(1

A

ω

,

∑

=

−

+

⋅

⋅

=

n

1

j

0

-j

j

A

IRR)

(1

A

j

D

,

IRR

1

D

MD

+

=

PV

i)

(1

A

A

NPV

n

1

j

j

j

0

=

+

⋅

=

−

∑

=

−

,

0

A

IRR)

PV(i

−

=

=

,

D

IRR)

(i

E

i

1

|

PV

−

=

=

+

{

∆

IRR

PV

PV

IRR)

(i

PV

∆

PV

MD

'

0

⋅

≈

=

−

,

%

MD

%

100

01

,

0

MD

%

100

PV

∆

PV

−

=

⋅

⋅

−

≈

⋅

{

{

2

C

''

2

1

MD

'

0

∆

IRR

PV

PV

∆

IRR

PV

PV

IRR)

(i

PV

∆

PV

⋅

⋅

+

⋅

≈

=

−

∑

=

+

⋅

+

⋅

⋅

+

=

=

n

1

j

j

j

2

0

''

IRR)

(1

A

)

1

j

(

j

IRR)

1

(

1

IRR)

(i

PV