Instytut Automatyki
Zakład Teorii Sterowania
Podstawy automatyki i teoria sterowania
Krzysztof Marzjan
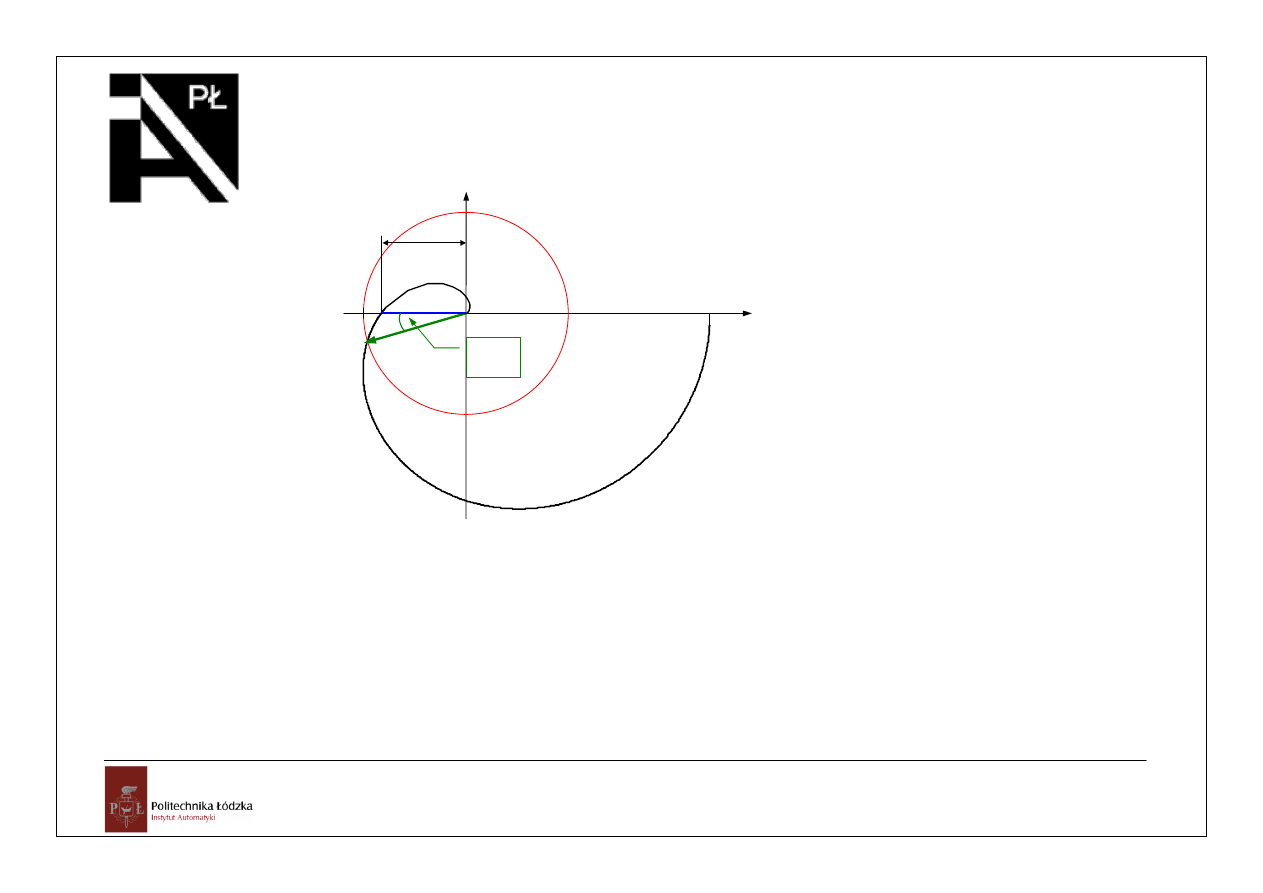
Re{G(jω)}
Im{G(jω)}
k
)
0
,
1
(
j
d
Δφ
2
asymptotyczne charakterystyki częstotliwościowe – przykłady
Asymptotyczne charakterystyki
częstotliwościowe – zastosowanie
1.
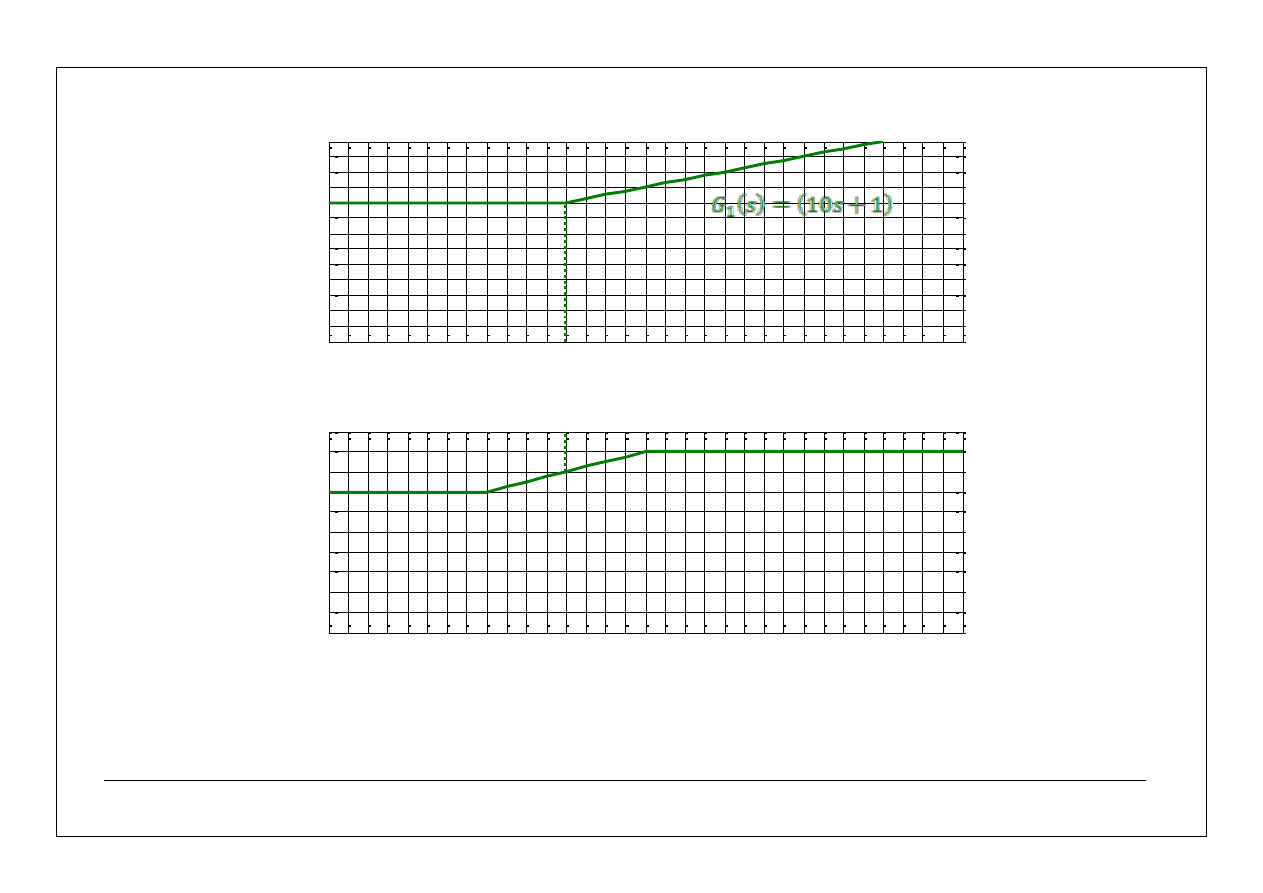
Element inercyjny I rzędu
1
)
(
Ts
k
s
G
.
10
-2
10
-1
10
0
10
1
10
2
-20
0
20
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
20logk
-20dB/dek
1/T
10
-2
10
-1
10
0
10
1
10
2
-90
-45
0
charakterystyka fazowo-częstotliwościowa
(
)
1/10T
10/T
1/T
rzeczywista
asymptotyczna
-2
-1
0
1
2
-30
-20
-10
0
10
20
30
log(
)
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
20logk
-20dB/dek
log(1/T)
-2
-1
0
1
2
-90
-45
0
charakterystyka fazowo-częstotliwościowa
log(
)
(
)
log(1/10T)
log(10/T)
log(1/T)
rzeczywista
asymptotyczna
3
asymptotyczne charakterystyki częstotliwościowe – przykłady
2. Regulator PD
)
1
(
)
(
s
T
k
s
G
D
p
.
10
-2
10
-1
10
0
10
1
10
2
-10
0
10
20
30
40
50
60
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
20logk
p
20dB/dek
1/T
D
10
-2
10
-1
10
0
10
1
10
2
0
45
90
charakterystyka fazowo-częstotliwościowa
(
)
1/10T
D
10/T
D
1/T
D
rzeczywista
asymptotyczna
-2
-1
0
1
2
-10
0
10
20
30
40
50
60
log(
)
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
20logk
p
20dB/dek
log(1/T
D
)
-2
-1
0
1
2
0
45
90
charakterystyka fazowo-częstotliwościowa
log(
)
(
)
log(1/10T
D
)
log(10/T
D
)
log(1/T
D
)
rzeczywista
asymptotyczna
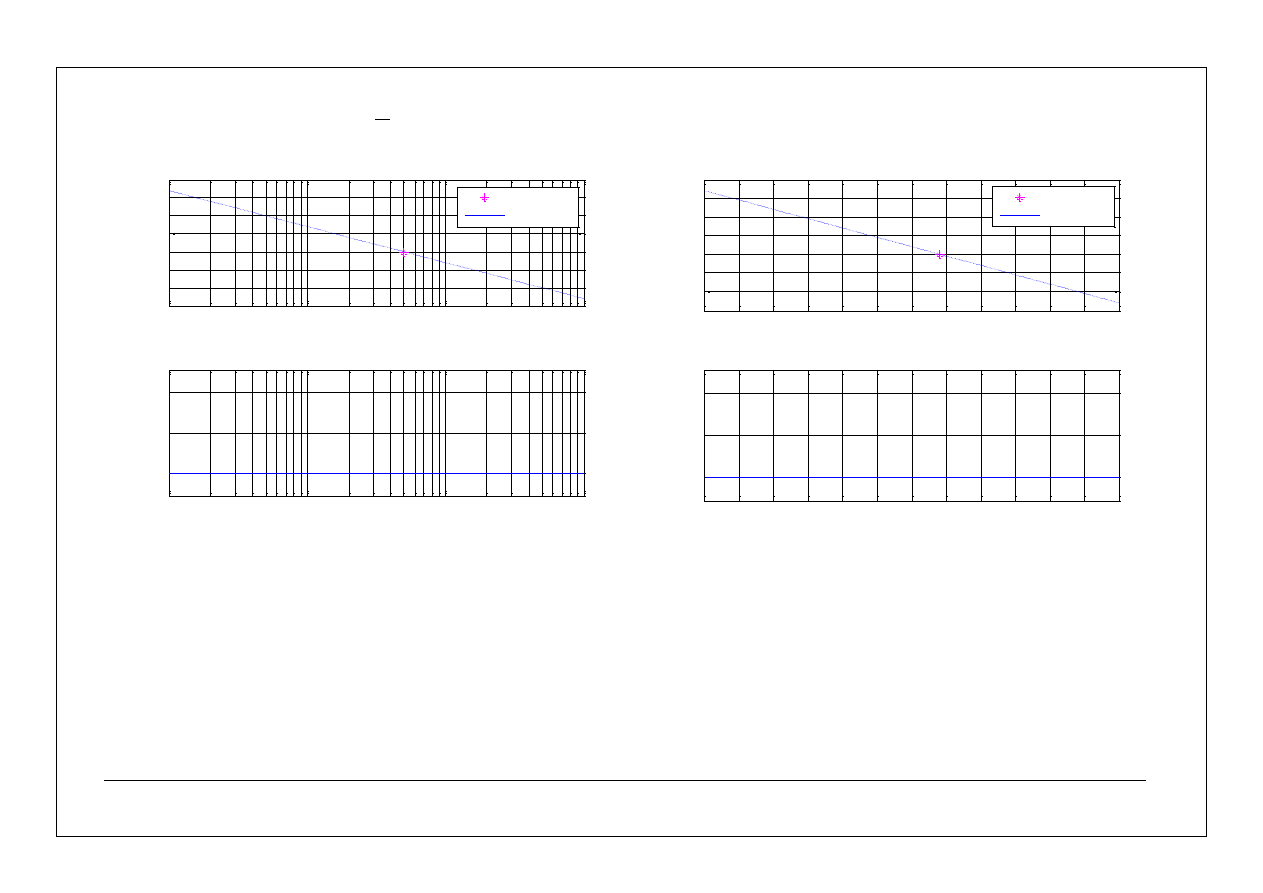
4
asymptotyczne charakterystyki częstotliwościowe – przykłady
3.
Element całkujący
s
k
s
G
)
(
.
10
-1
10
0
10
1
10
2
-30
-20
-10
0
10
20
30
40
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
-20dB/dek
k
k
rzeczywista
10
-1
10
0
10
1
10
2
-90
45
0
charakterystyka fazowo-częstotliwościowa
(
)
-1
0
1
2
-30
-20
-10
0
10
20
30
40
log(
)
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
-20dB/dek
log(k)
log(k)
rzeczywista
-1
0
1
2
-90
-45
0
charakterystyka fazowo-częstotliwościowa
log(
)
(
)
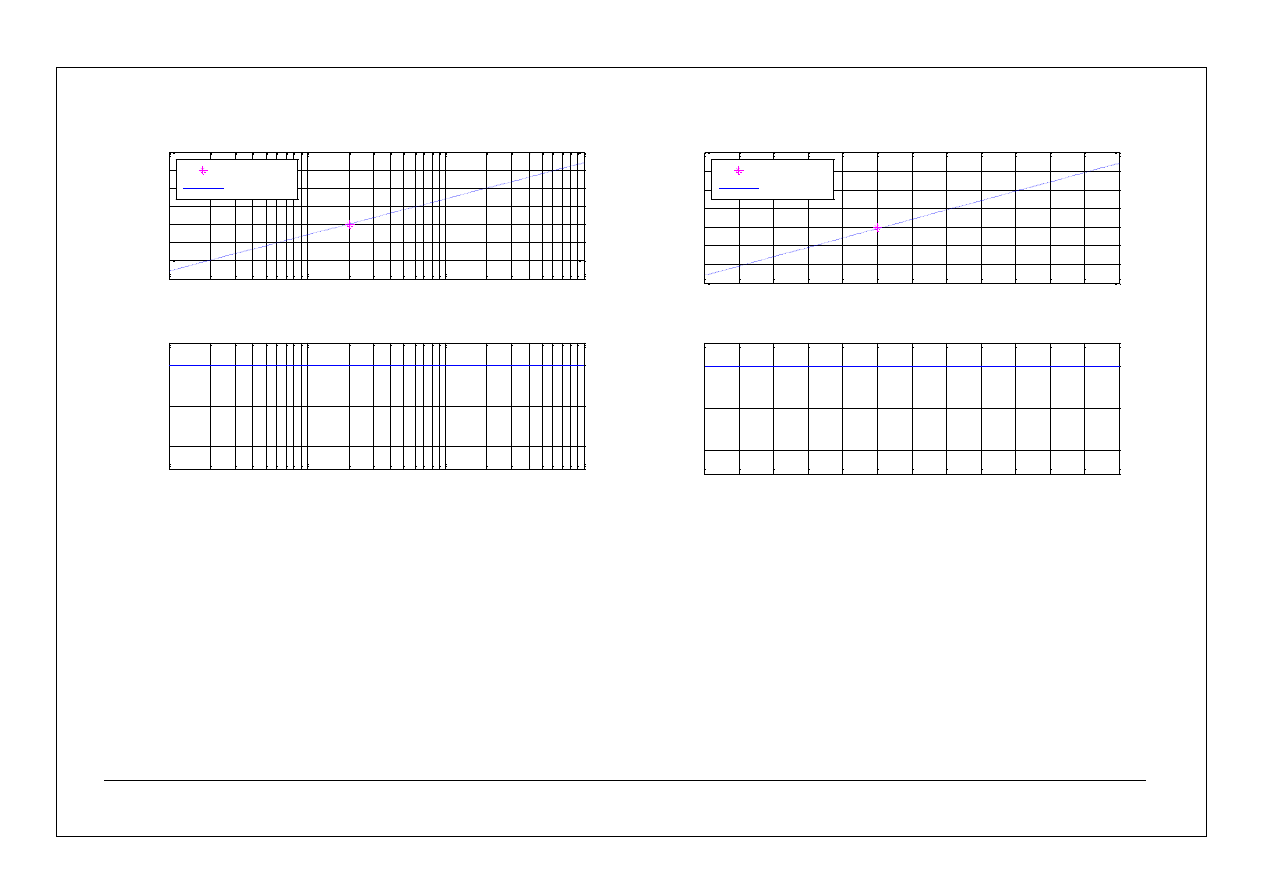
5
asymptotyczne charakterystyki częstotliwościowe – przykłady
4.
Element różniczkujący
Ts
s
G
)
(
.
10
-2
10
-1
10
0
10
1
-30
-20
-10
0
10
20
30
40
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
20dB/dek
1/T
1/T
rzeczywista
10
-2
10
-1
10
0
10
1
0
45
90
charakterystyka fazowo-częstotliwościowa
(
)
-2
-1
0
1
-30
-20
-10
0
10
20
30
40
log(
)
L(
)=
2
0
lo
g
[A
(
)]
charakterystyka amplitudowo-częstotliwościowa
20dB/dek
log(1/T)
log(1/T)
rzeczywista
-2
-1
0
1
0
45
90
charakterystyka fazowo-częstotliwościowa
log(
)
(
)
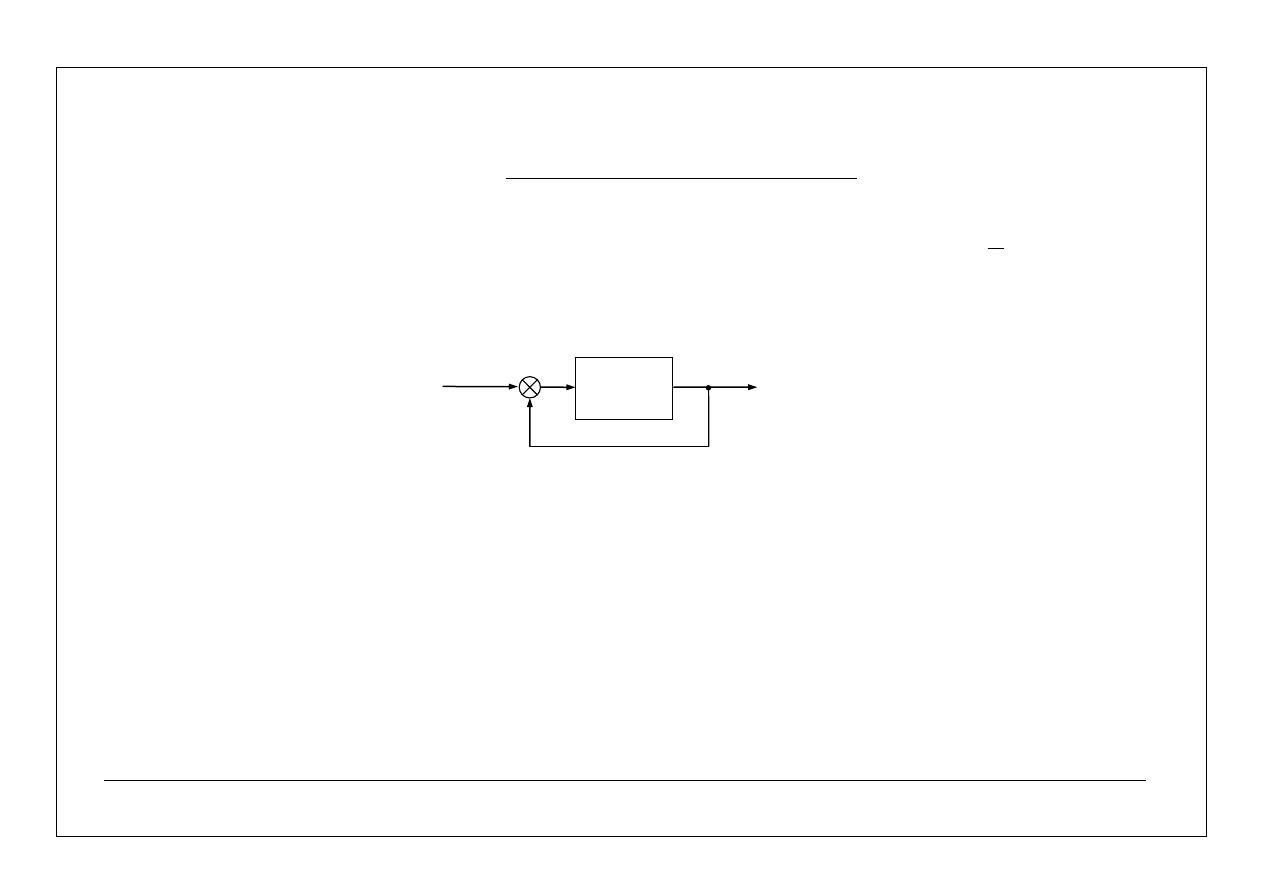
6
asymptotyczne charakterystyki częstotliwościowe – przykłady
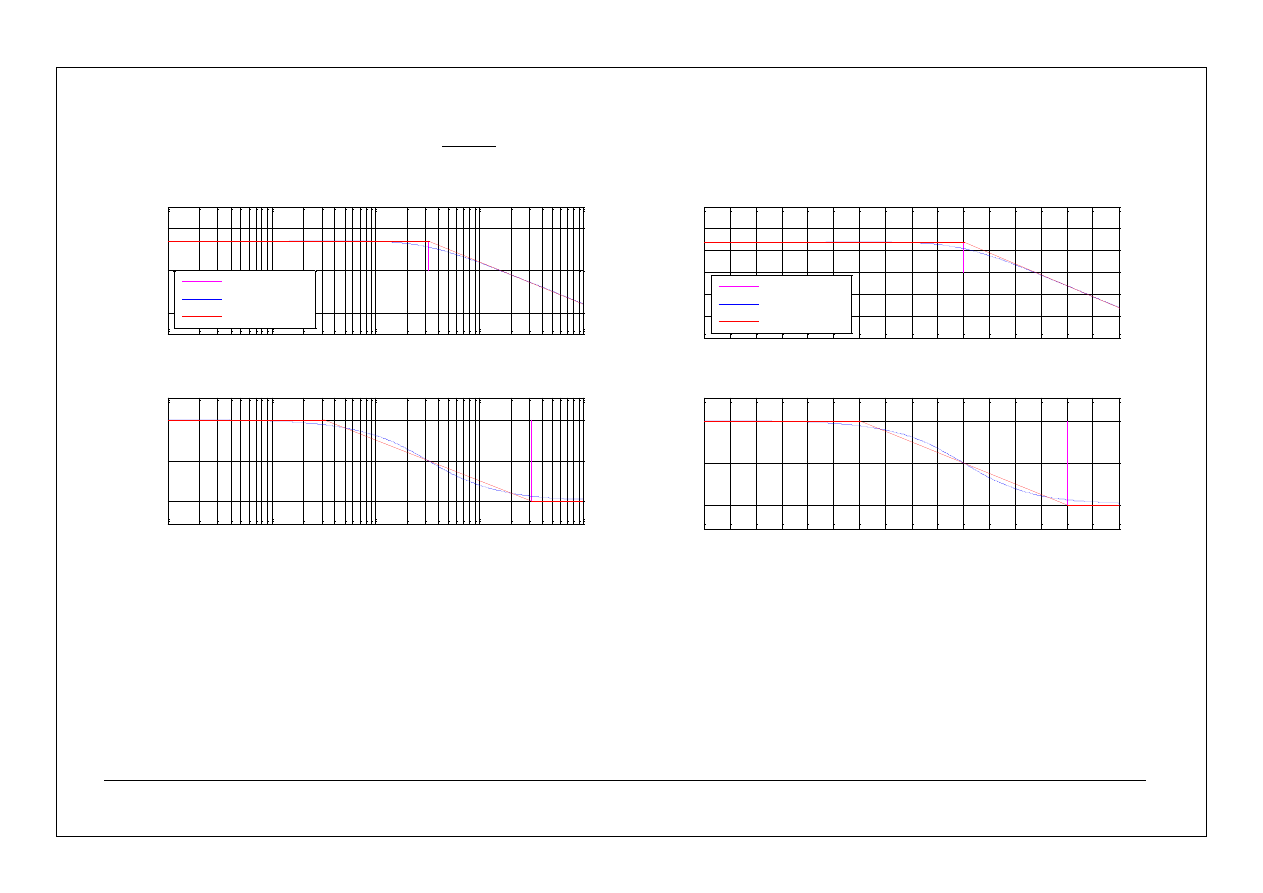
Przykład 1.
Transmitancja operatorowa układu otwartego ma postać:
)
1
01
,
0
(
)
1
1
,
0
(
)
1
100
(
)
1
10
(
)
(
0
s
s
s
s
s
k
s
G
Dla jakiej wartości statycznego współczynnika wzmocnienia k, układ zamknięty ma zapas fazy
8
.
Układ regulacji ma następującą strukturę:
)
(
0
s
G
+
_
y(s)
u(s)
7
asymptotyczne charakterystyki częstotliwościowe – przykłady
W pierwszej kolejności należy wyznaczyć zakres pulsacji dla którego będą rysowane charakterystyki:
100
max
T
2
10
1
max
min
T
(+ dwie dekady w lewo)
4
2
2
10
10
min
01
,
0
min
T
2
10
1
min
max
T
(+ dwie dekady w prawo)
4
2
2
10
10
max
2
log
min
(+ dwie dekady w lewo)
4
2
2
log
min
2
log
max
(+ dwie dekady w prawo)
4
2
2
log
max
Następnie należy zapisać transmitancję operatorową układu otwartego w postaci iloczynowej:
1
01
,
0
1
1
1
,
0
1
1
100
1
1
)
1
10
(
)
(
0
s
s
s
s
s
s
G
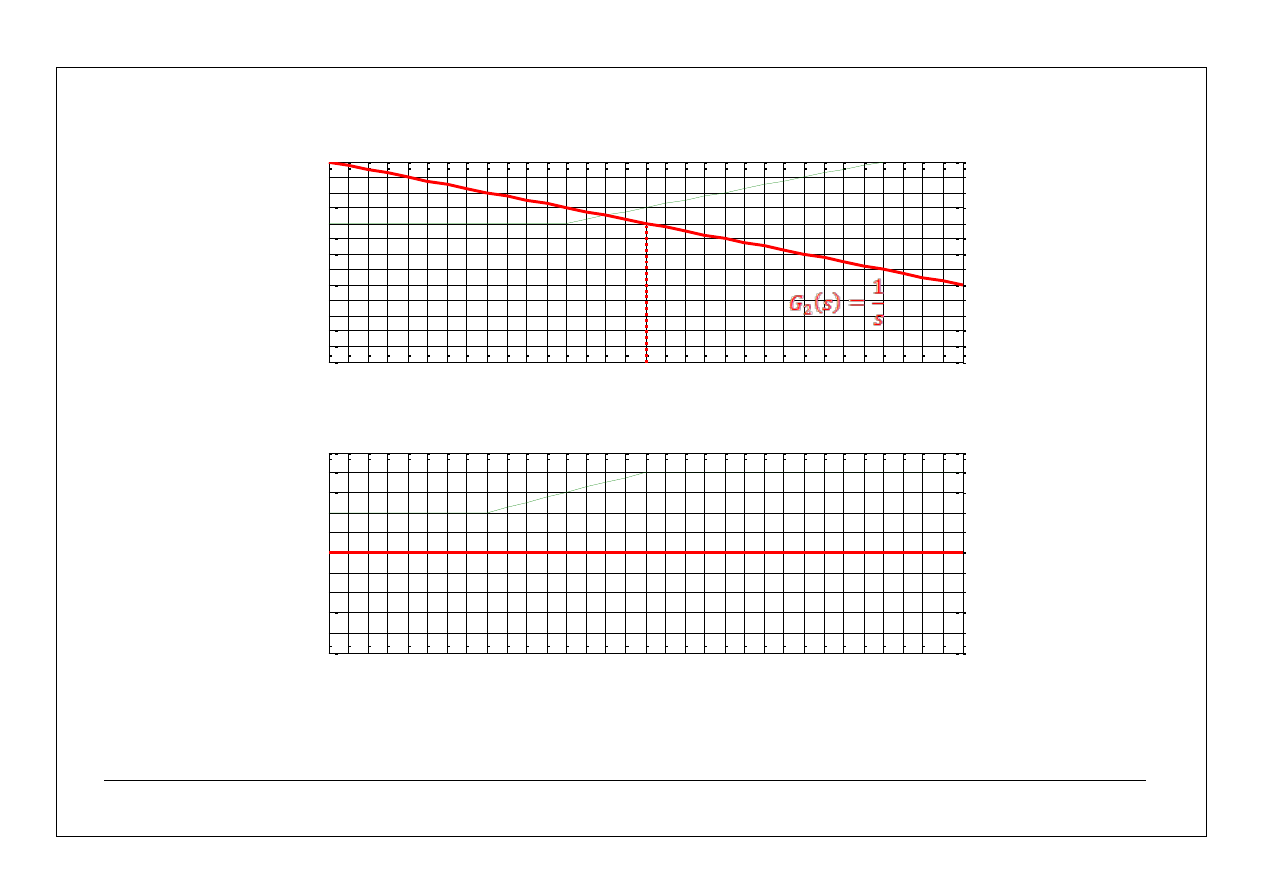
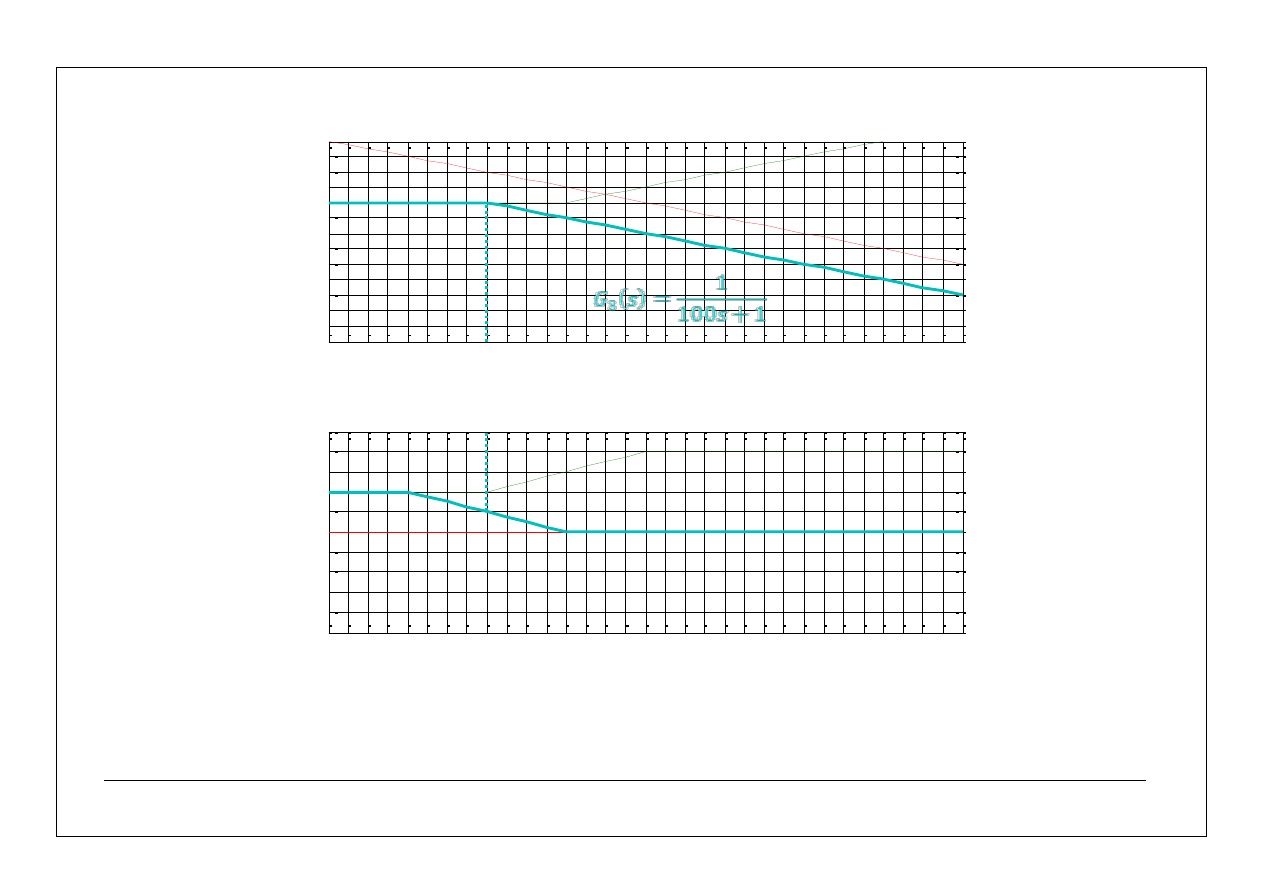
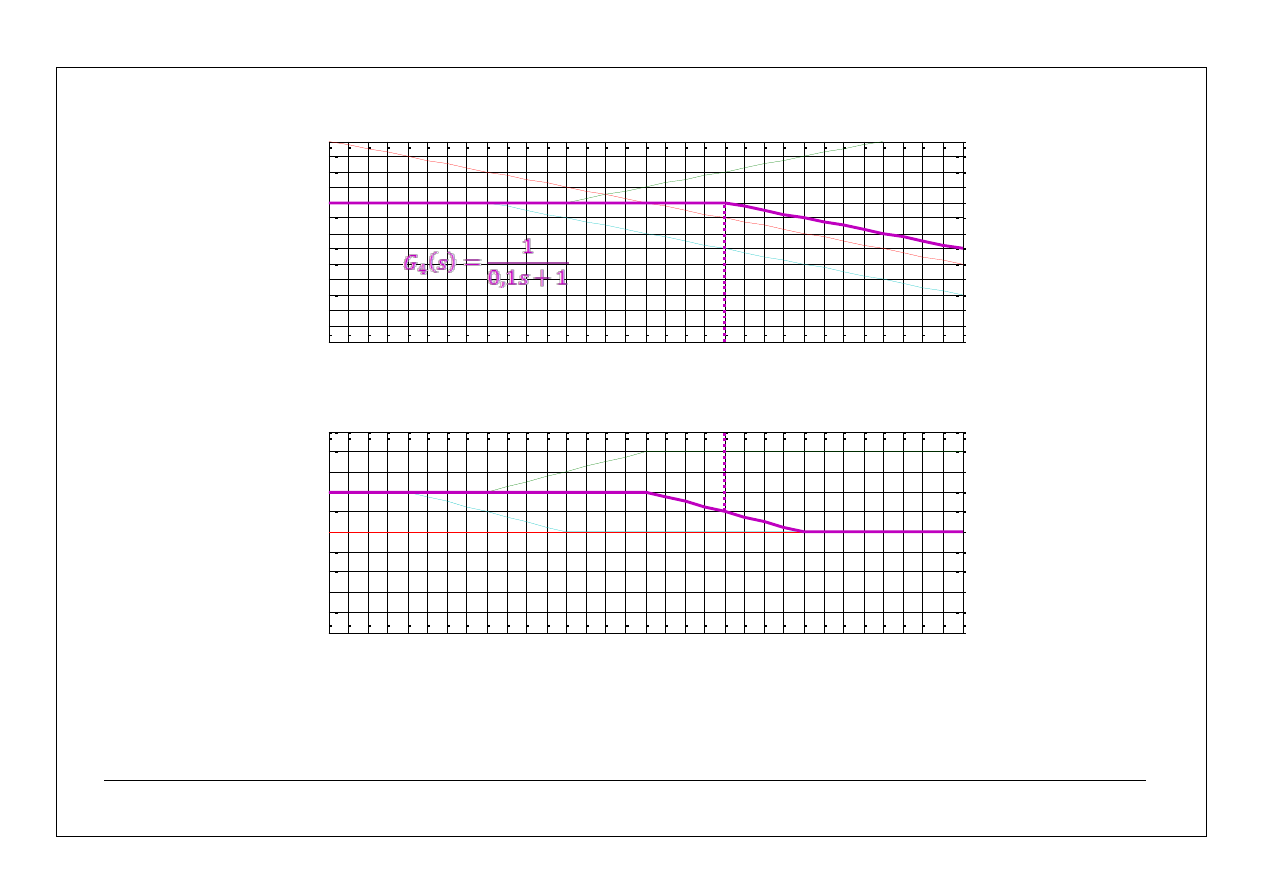
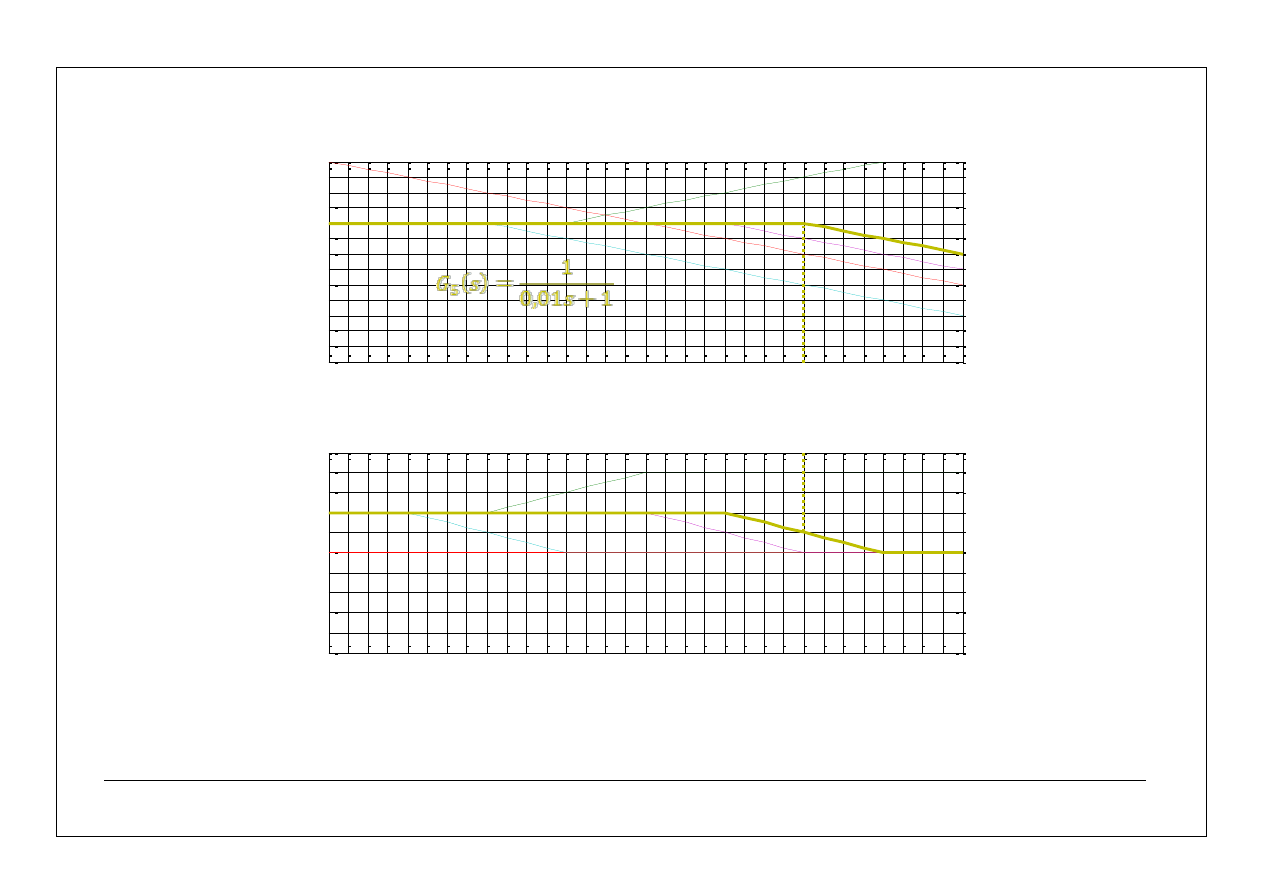
i po kolei narysować charakterystyki składowe:
8
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
log(
)=-1
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
9
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
log(k)=0
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
10
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
log(
)=-2
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
11
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
log(
)=1
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
12
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
log(
)=2
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
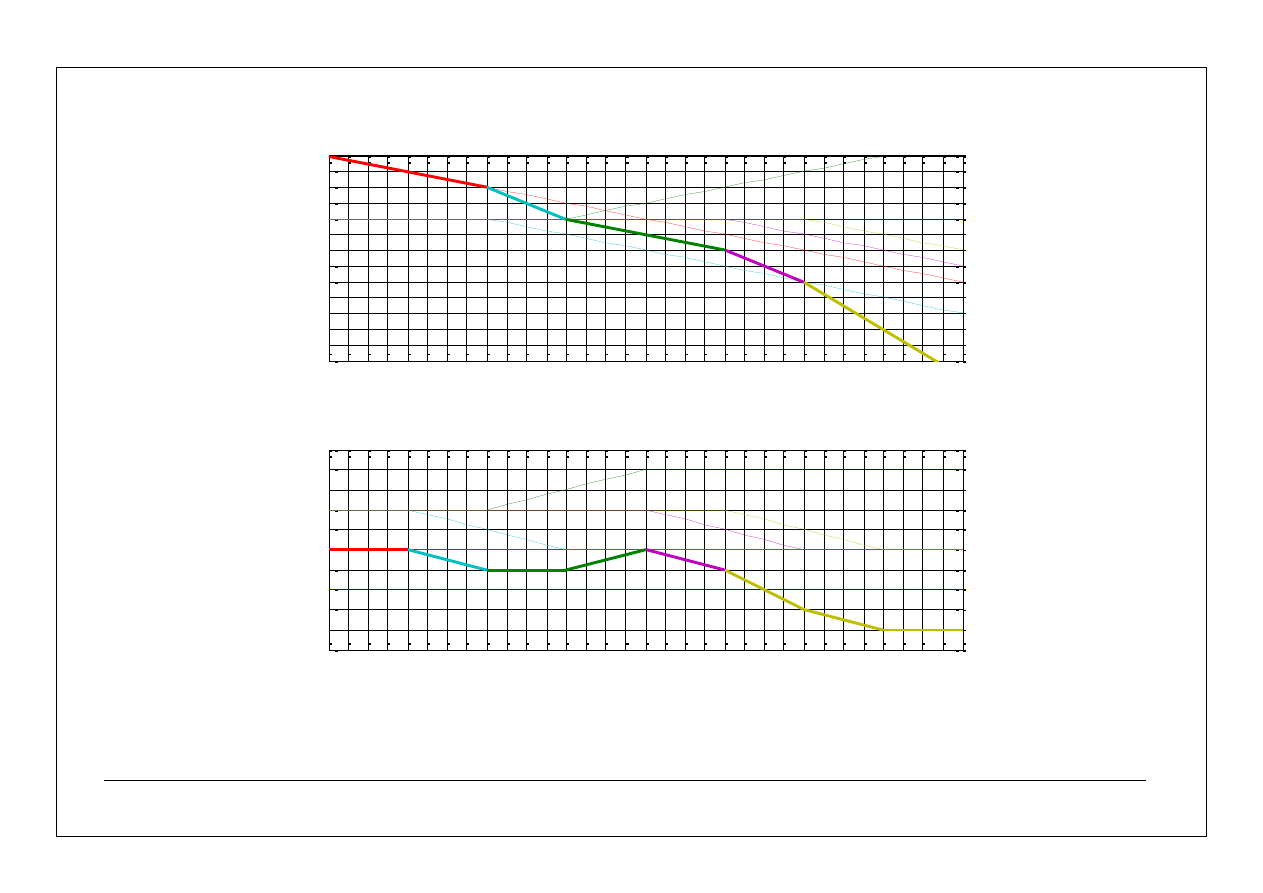
13
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
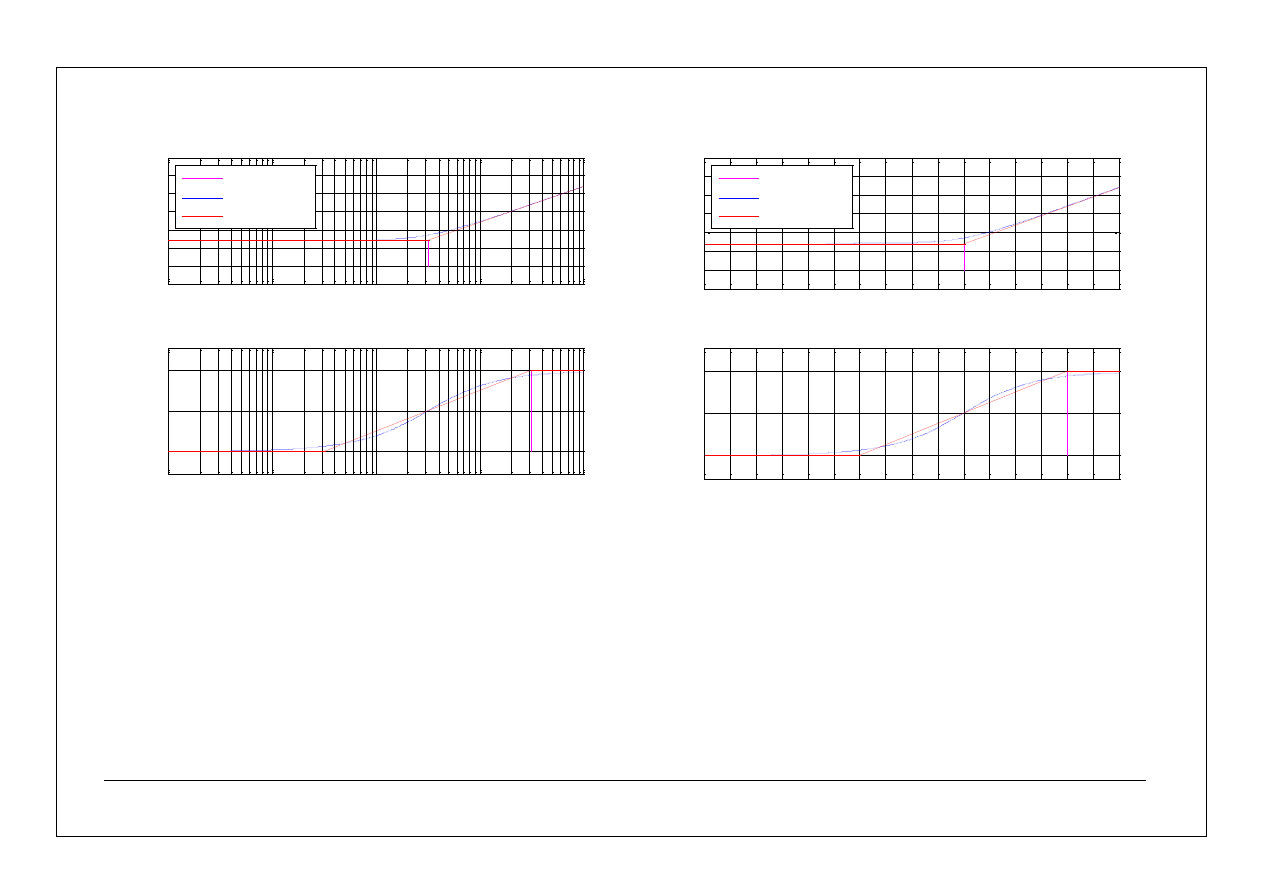
Po narysowaniu charakterystyk składowych dodajemy je.
14
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
L=60dB
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
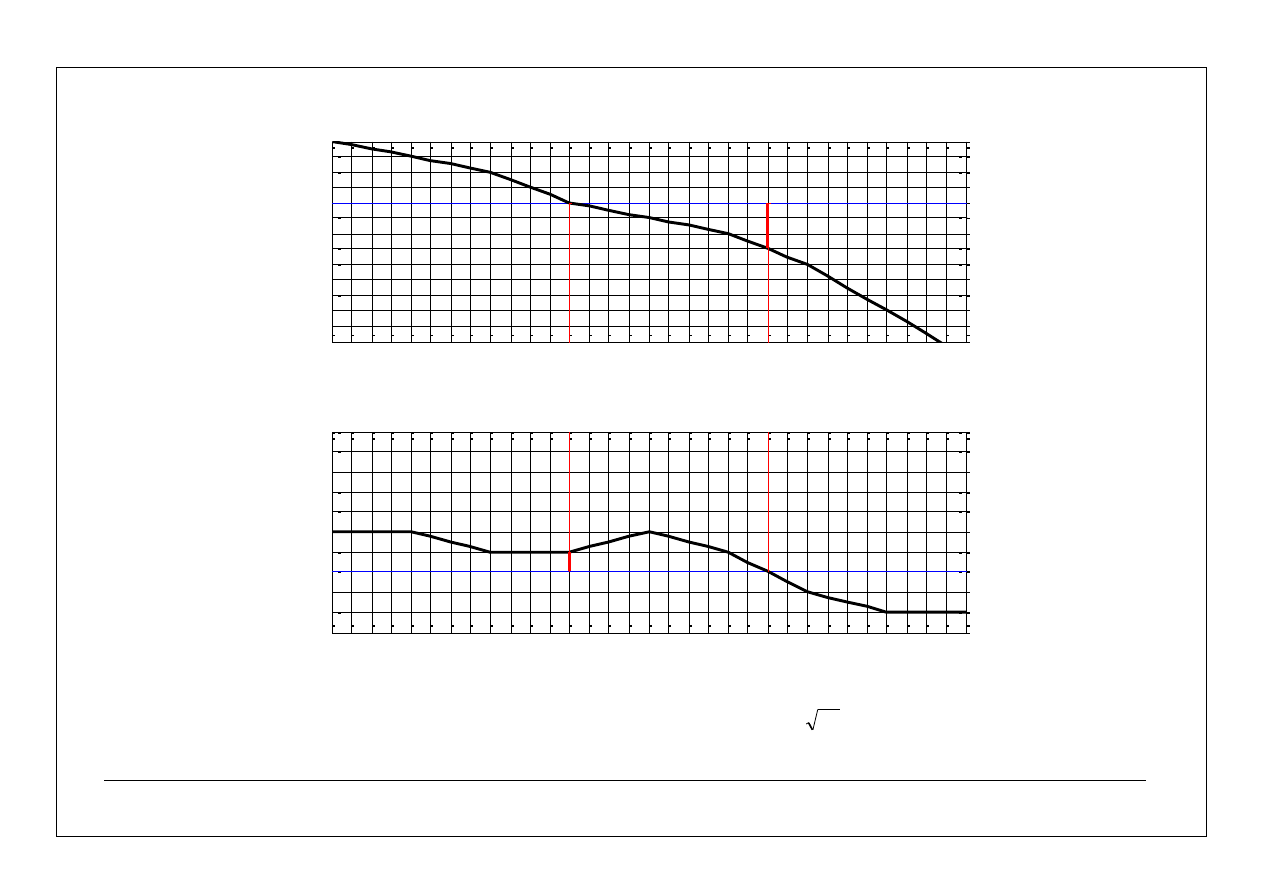
=45
o
Dla pulsacji odcięcia
1
,
0
1
odczytujemy zapas fazy
o
45
, dla pulsacji
10
10
odczytujemy zapas fazy
dB
L
60
15
asymptotyczne charakterystyki częstotliwościowe – przykłady
-4 -3 -2 -1 0 1 2 3 4
-180
-160
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
L=10dB
log(
)=5/4
50dB
-4 -3 -2 -1 0 1 2 3 4
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
=22,5
o
Dla pulsacji
4
5
10
zapas
fazy będzie równy
8
,
ponieważ wypadkowe
wzmocnienie układu dla tej
pulsacji jest równe
dB
j
G
50
)
(
log
20
0
, to
wypadkową charakterystykę
amplitudową należy przesunąć
do góry o 50dB, stąd
316
10
2
5
log
50
log
20
2
5
p
p
p
k
k
k
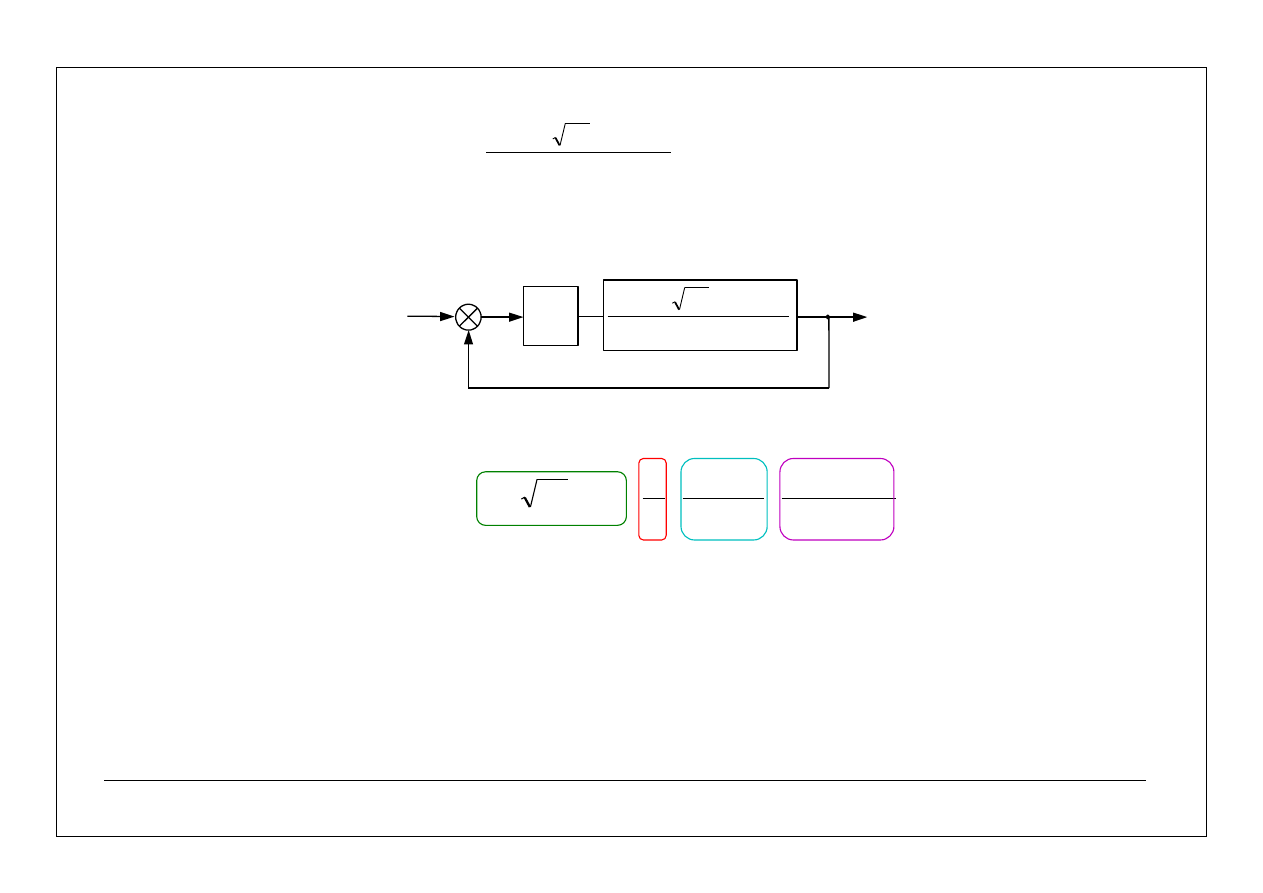
16
asymptotyczne charakterystyki częstotliwościowe – przykłady
Przykład 2.
Dany jest obiekt o transmitancji
2
)
1
1
,
0
(
)
1
10
(
)
1
10
(
10
)
(
s
s
s
s
s
G
OR
. Wyznacz krytyczną wartość współczynnika
wzmocnienia regulatora proporcjonalnego.
Układ regulacji ma następującą strukturę:
p
k
2
)
1
1
,
0
(
)
1
10
(
)
1
10
(
10
s
s
s
s
+
_
y(s)
u(s)
Krytyczna wartość współczynnika wzmocnienia będzie wyznaczona z asymptotycznych charakterystyk
częstotliwościowych.
2
)
1
1
,
0
(
1
1
10
1
1
)
1
10
(
10
)
(
s
s
s
s
s
G
OR
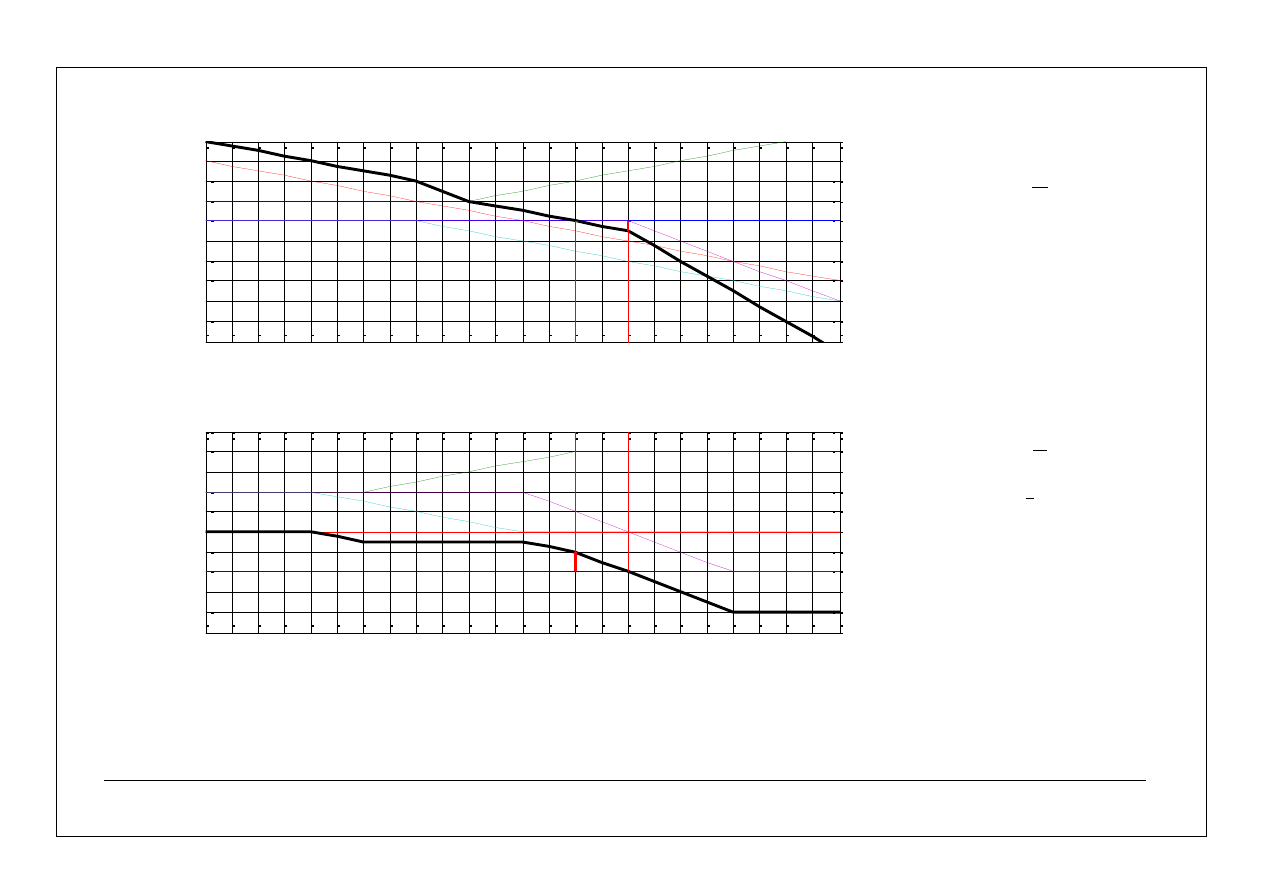
17
asymptotyczne charakterystyki częstotliwościowe – przykłady
-3
-2
-1
0
1
2
3
-120
-100
-80
-60
-40
-20
0
20
40
60
80
asymptotyczna charakterystyka amplitudowa
log
L(
)
L=10dB
-3
-2
-1
0
1
2
3
-315
-270
-225
-180
-135
-90
-45
0
45
90
135
asymptotyczna charakterystyka fazowa
log
(
)
=45
o
Zapas fazy dla tego układu
wynosi
4
, zapas
modułu
dB
L
10
. Aby
pulsacja odcięcia
1
była
równa pulsacji
,
wypadkową charakterystykę
amplitudową należy
przesunąć do góry o 10dB,
stąd
16
,
3
10
2
1
log
10
log
20
2
1
p
p
p
k
k
k
18
asymptotyczne charakterystyki częstotliwościowe – przykłady
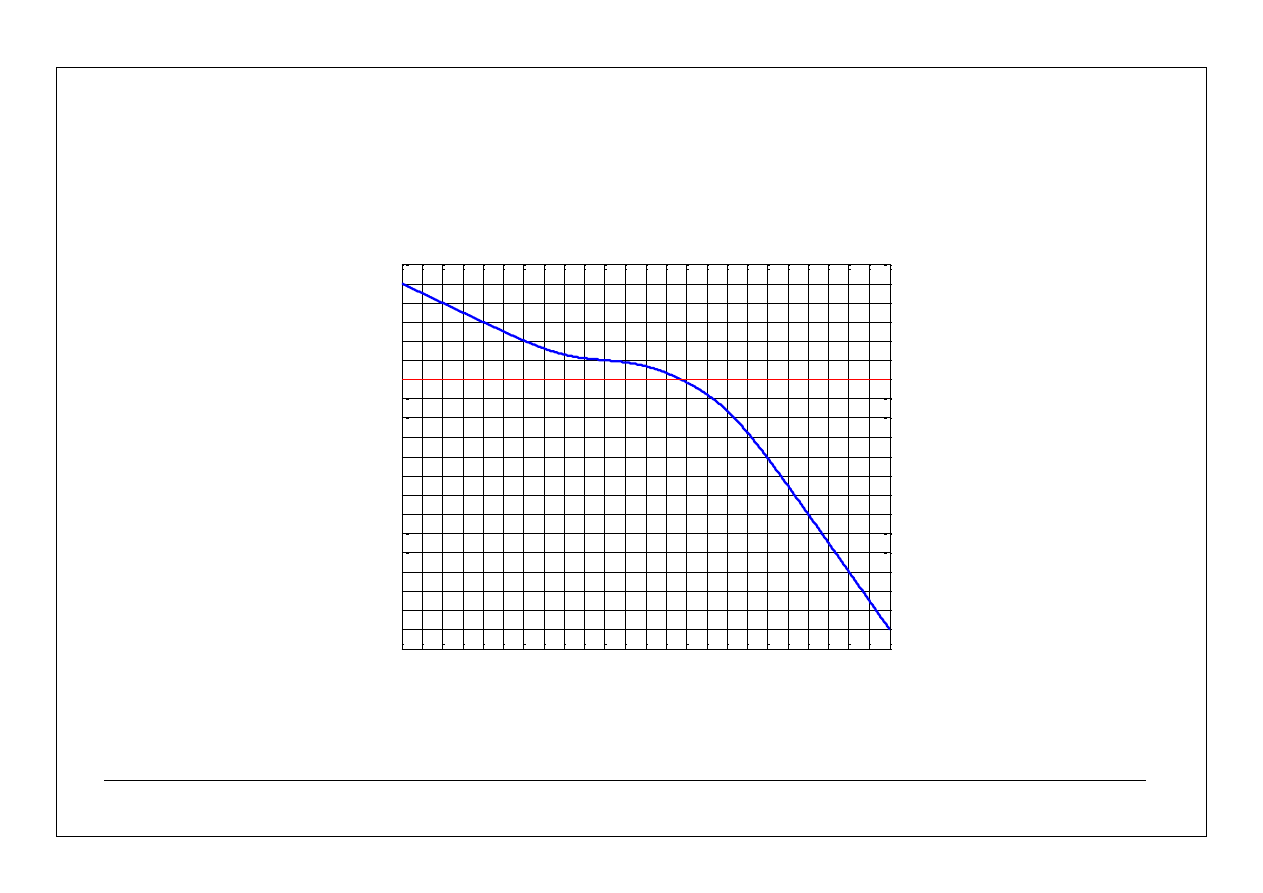
Przykład 3.
Na rysunku przedstawiono charakterystykę amplitudowo – częstotliwościową układu otwartego złożonego
z szeregowego połączenia członów minimalno – fazowych.
1.
Wyznacz transmitancję operatorową układu.
2. Narysuj asymptotyczne charakterystyki: amplitudowo
– częstotliwościową i fazowo – częstotliwościową.
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
19
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
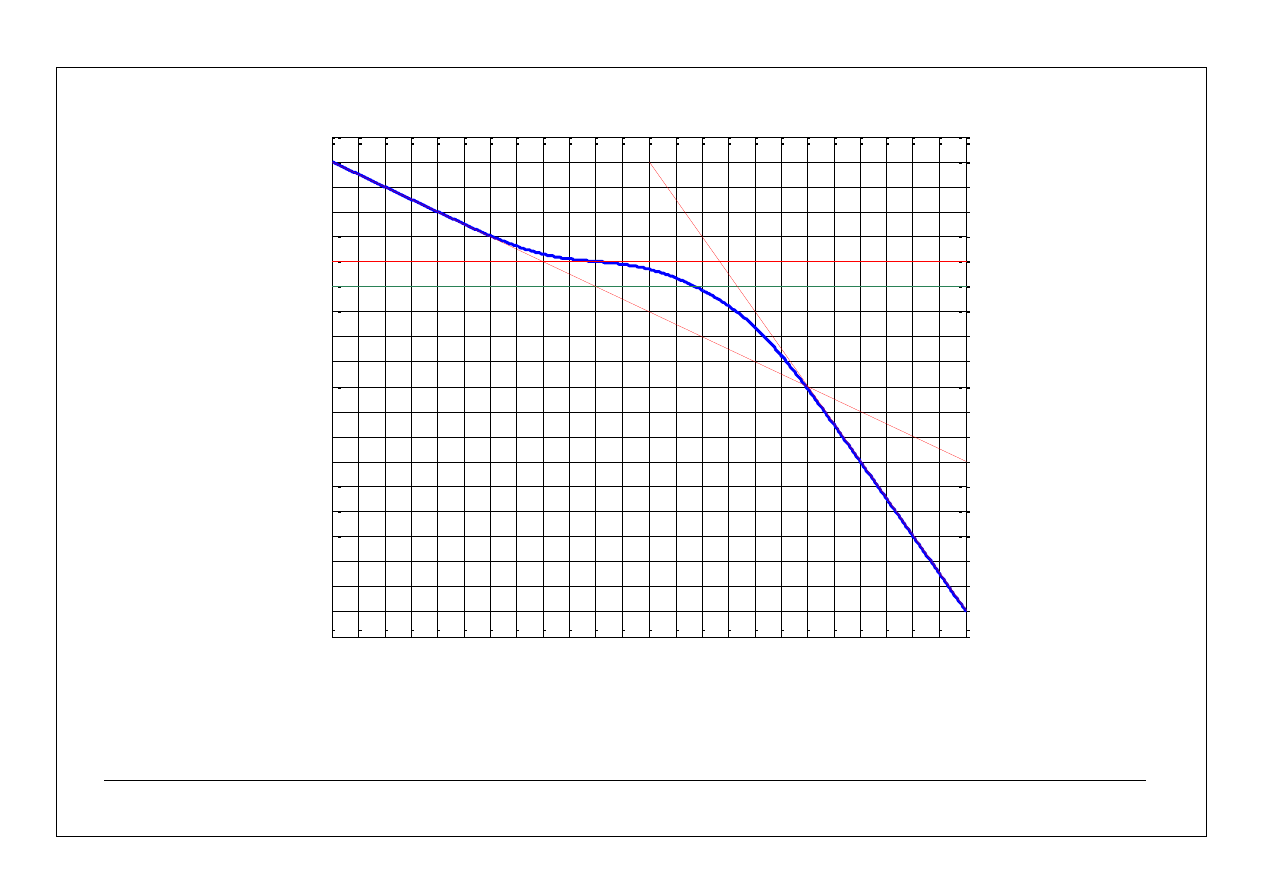
20
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(k)=1/2
log(
1
)=0
log(
2
)=5/3
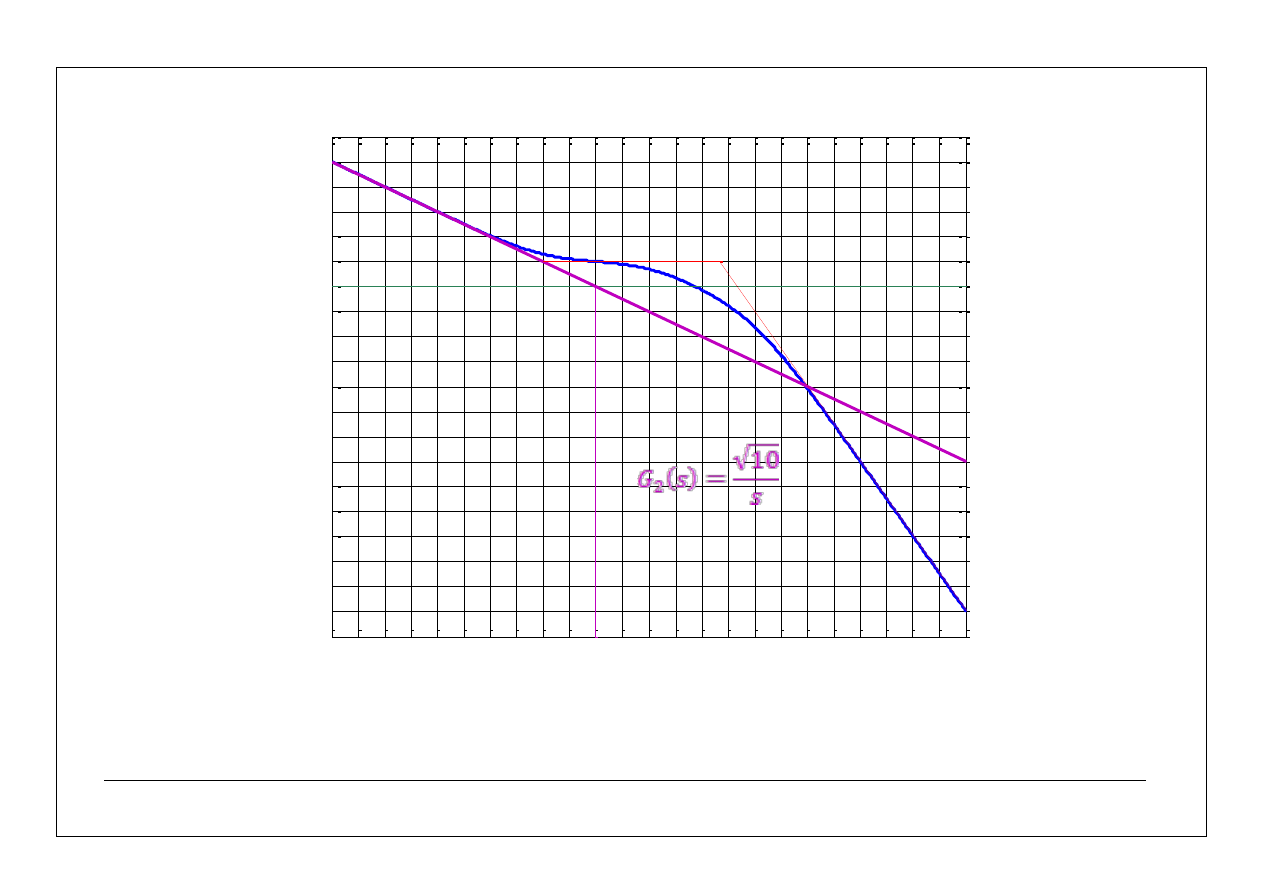
21
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(k)=1/2
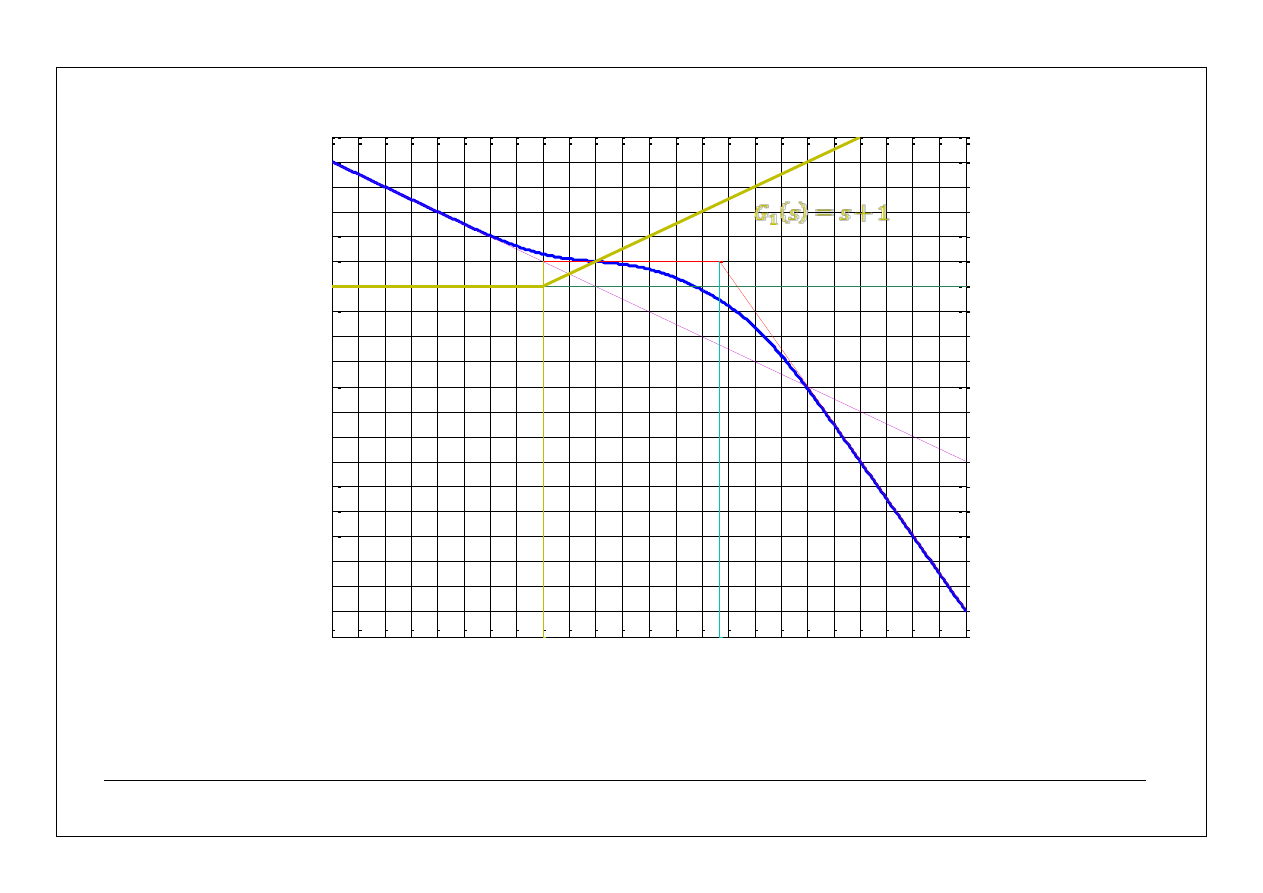
22
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(
1
)=0
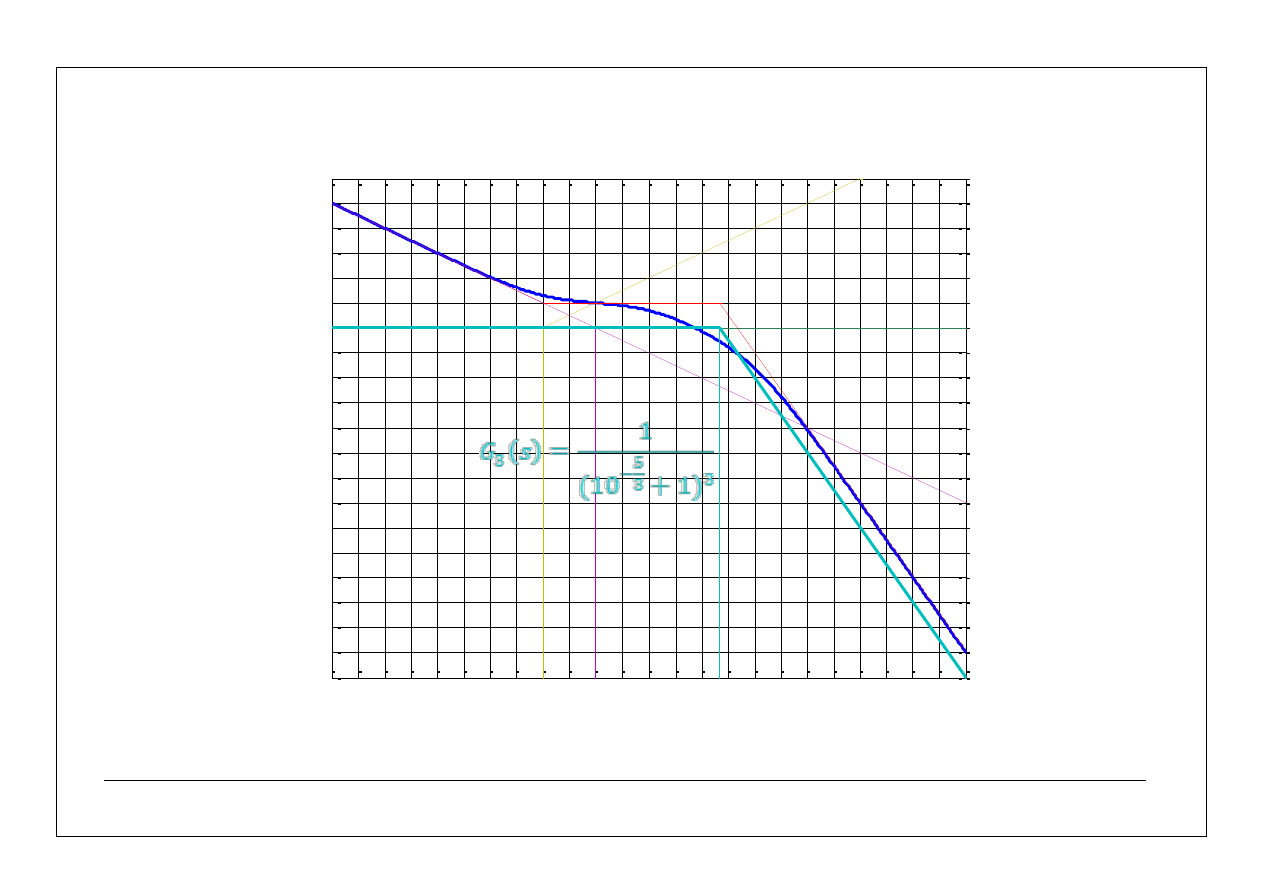
23
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(
2
)=5/3
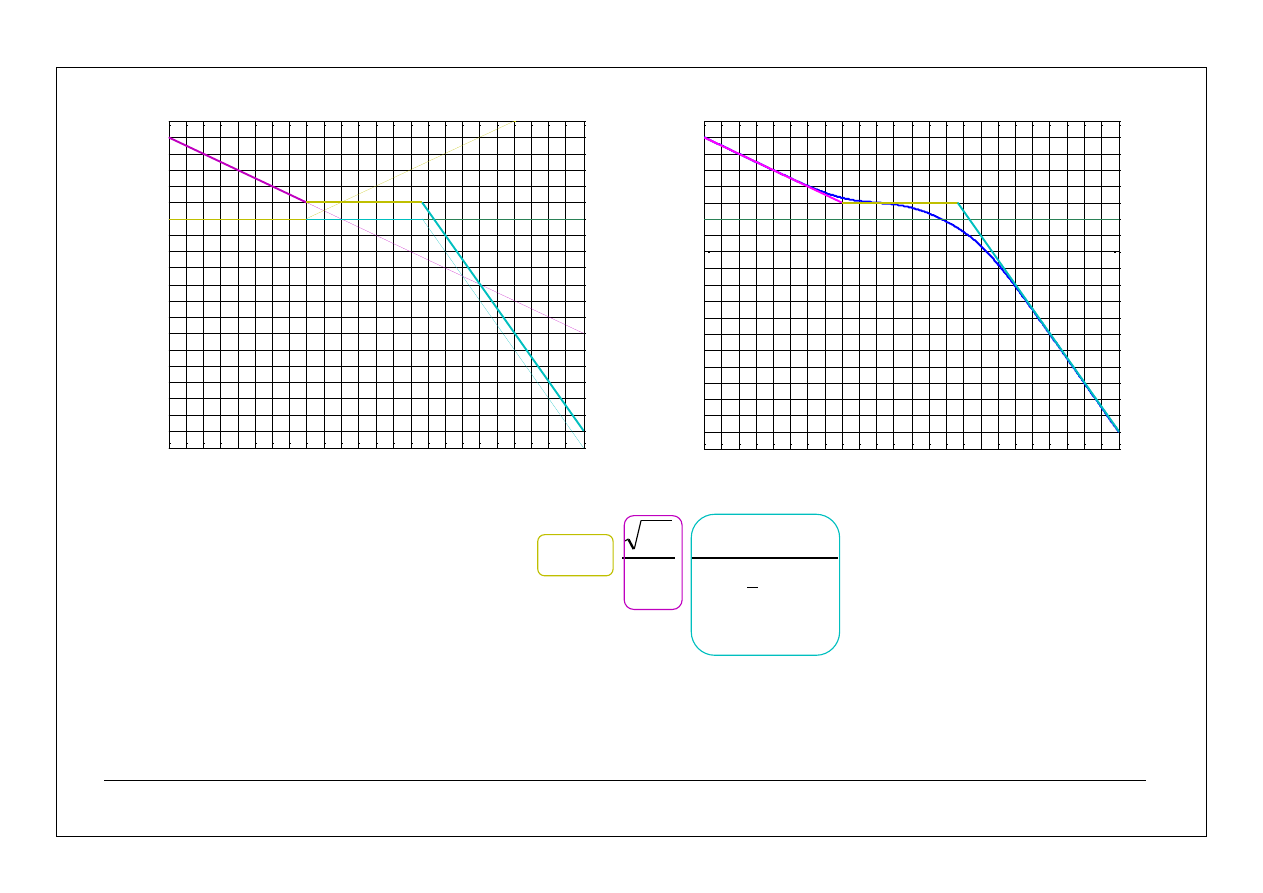
24
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
3
3
5
1
10
1
10
)
1
(
)
(
s
s
s
s
G
OR
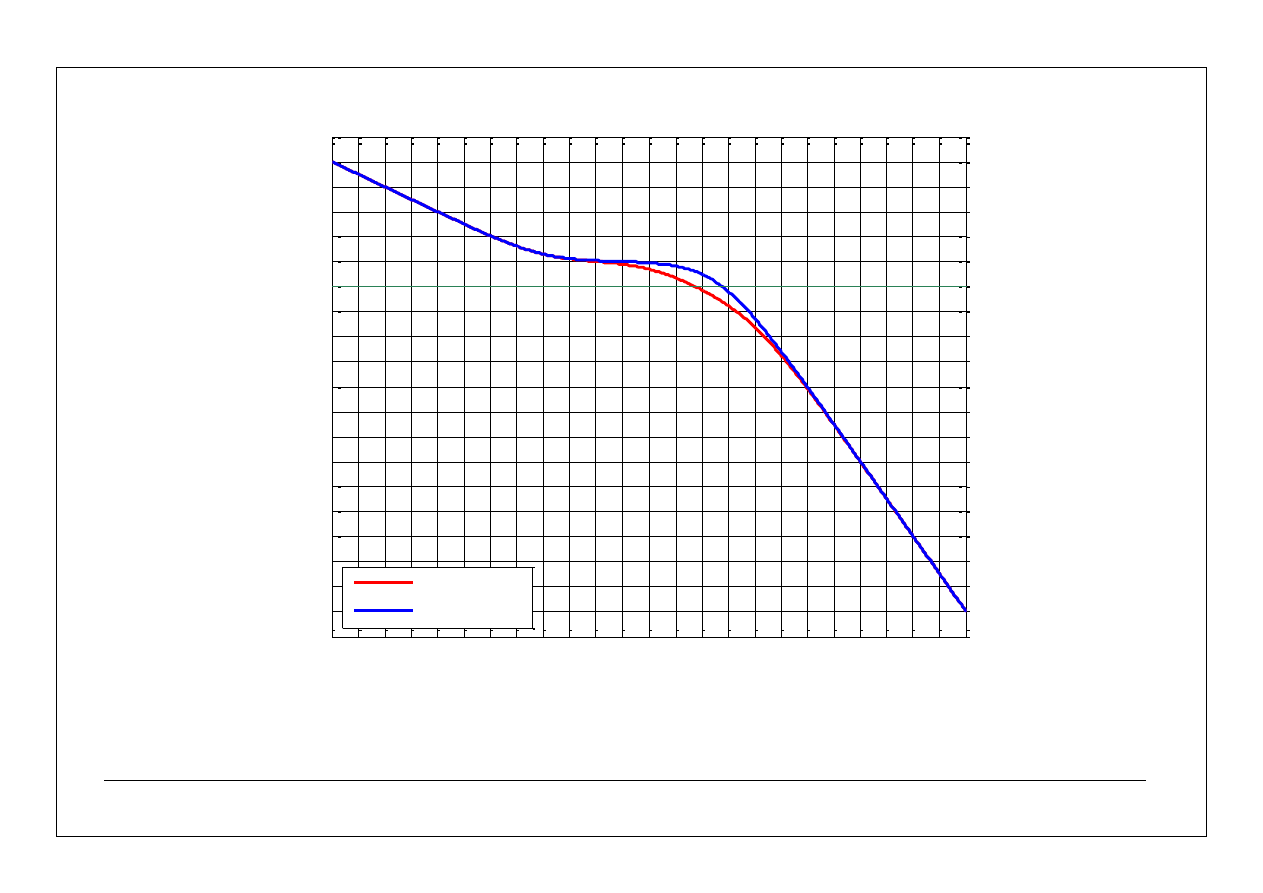
25
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
dana
wyznaczona
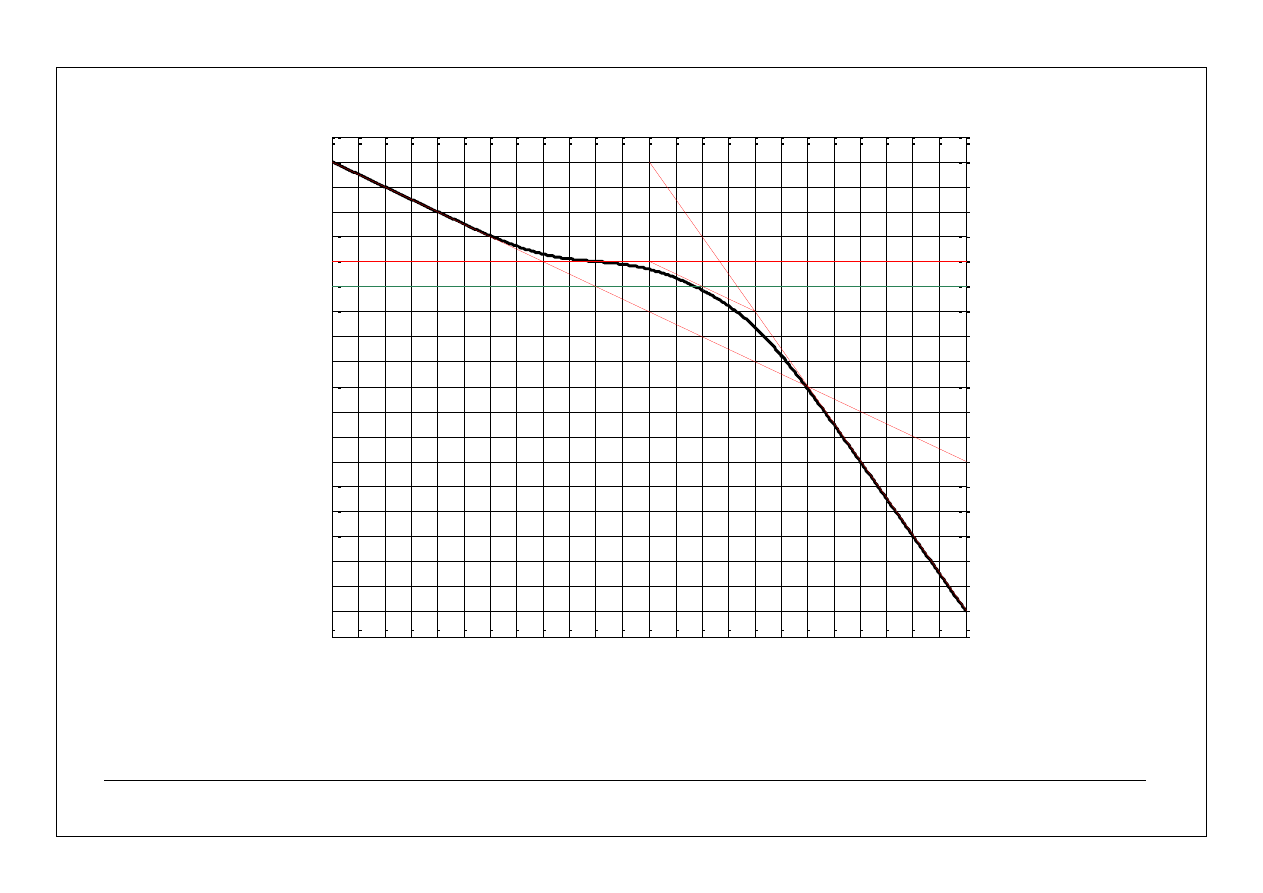
26
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
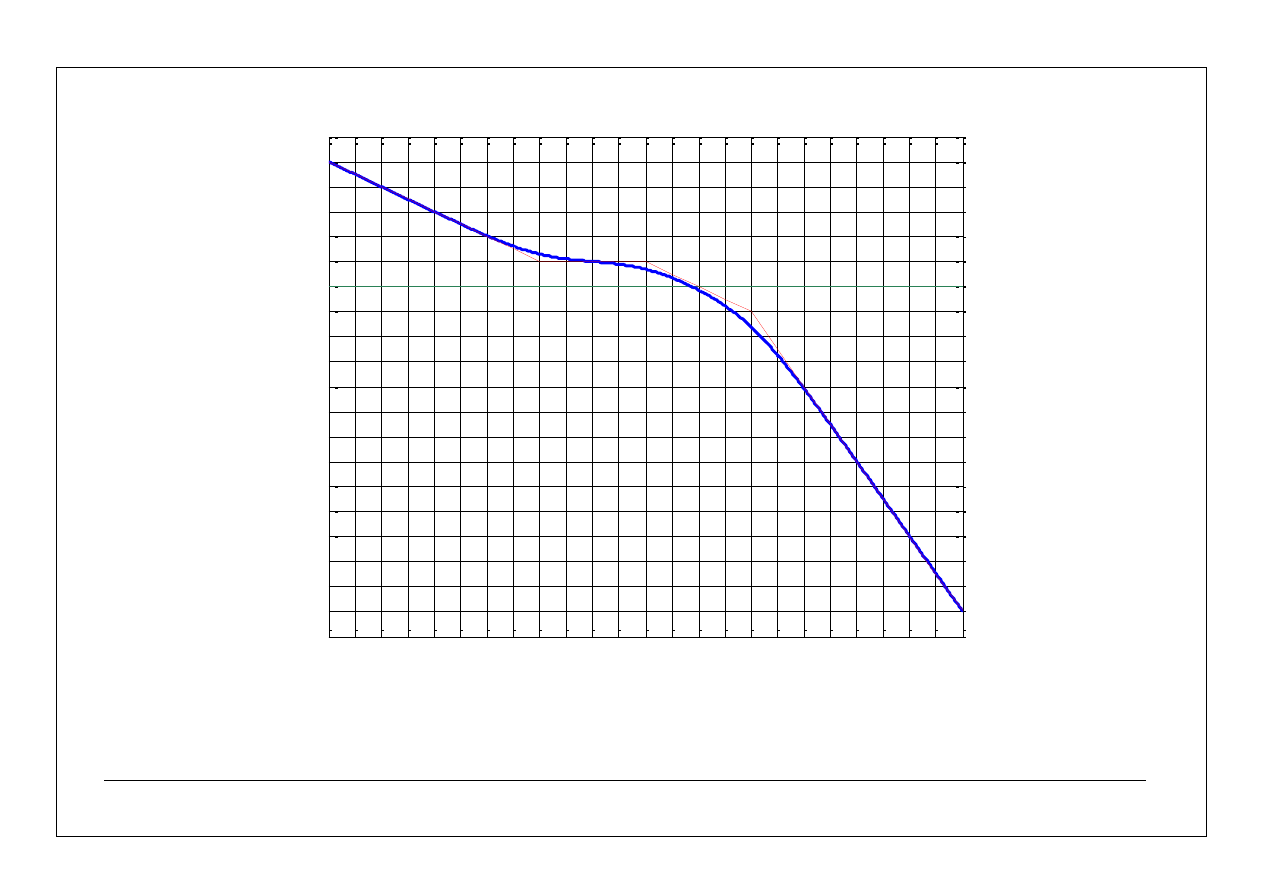
27
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
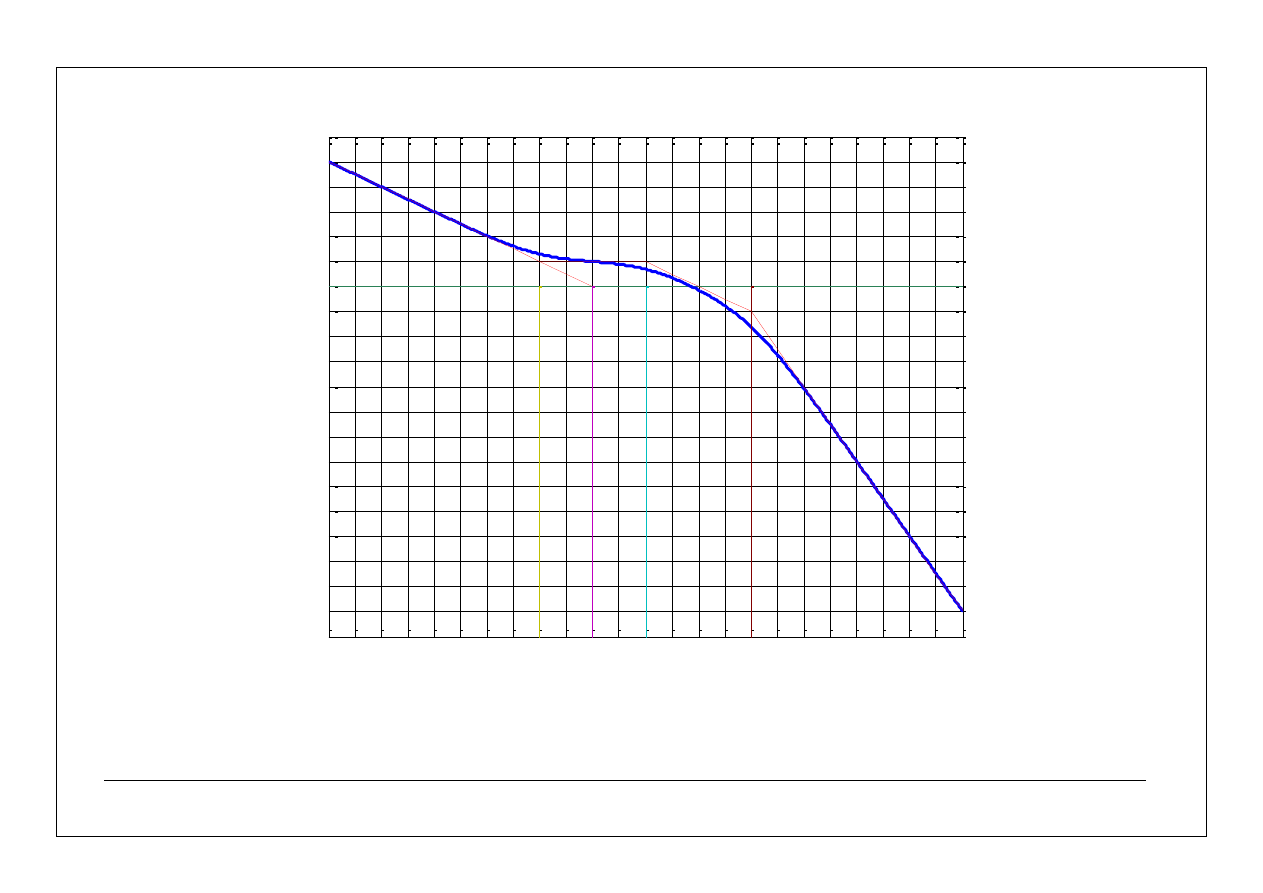
28
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
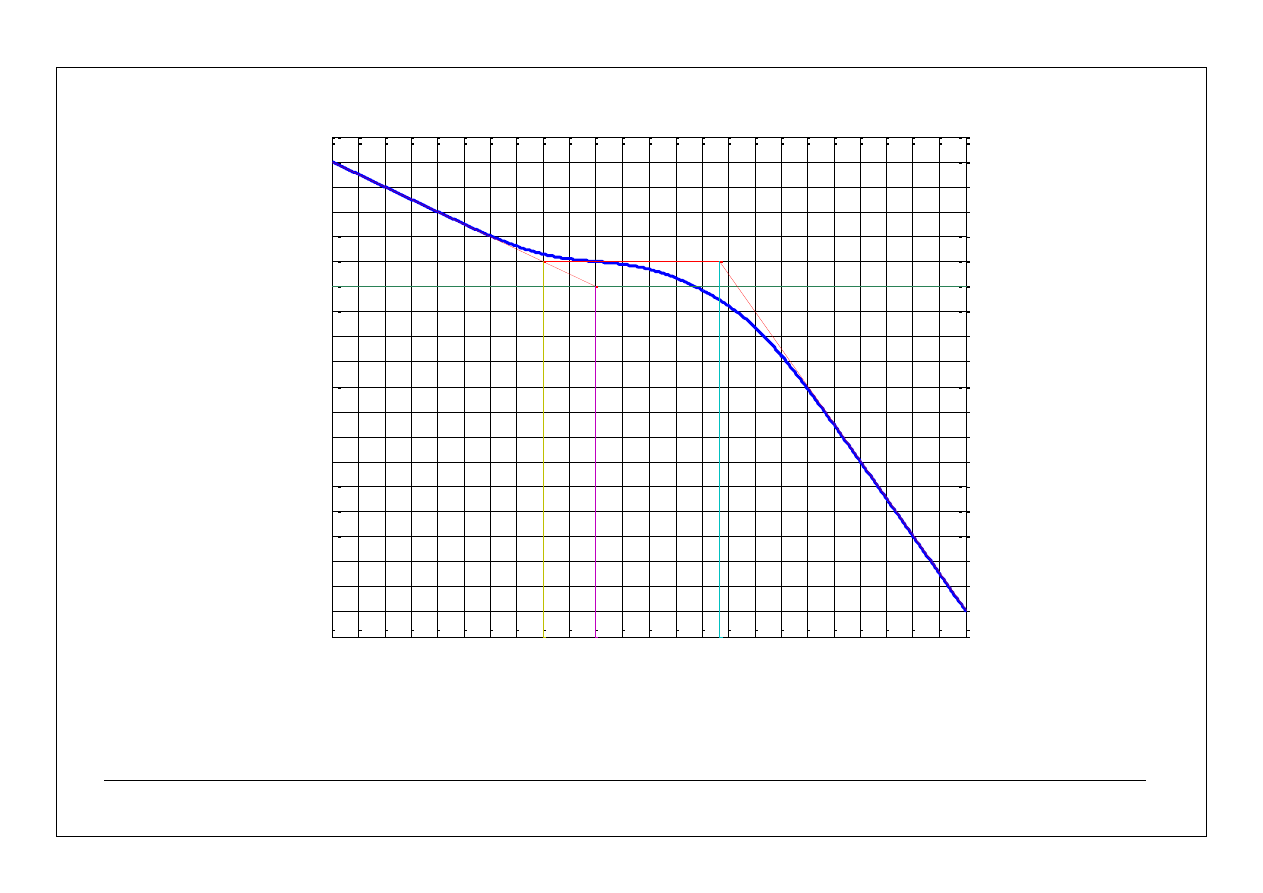
log(k)=1/2
log(
1
)=0
log(
2
)=1
log(
3
)=2
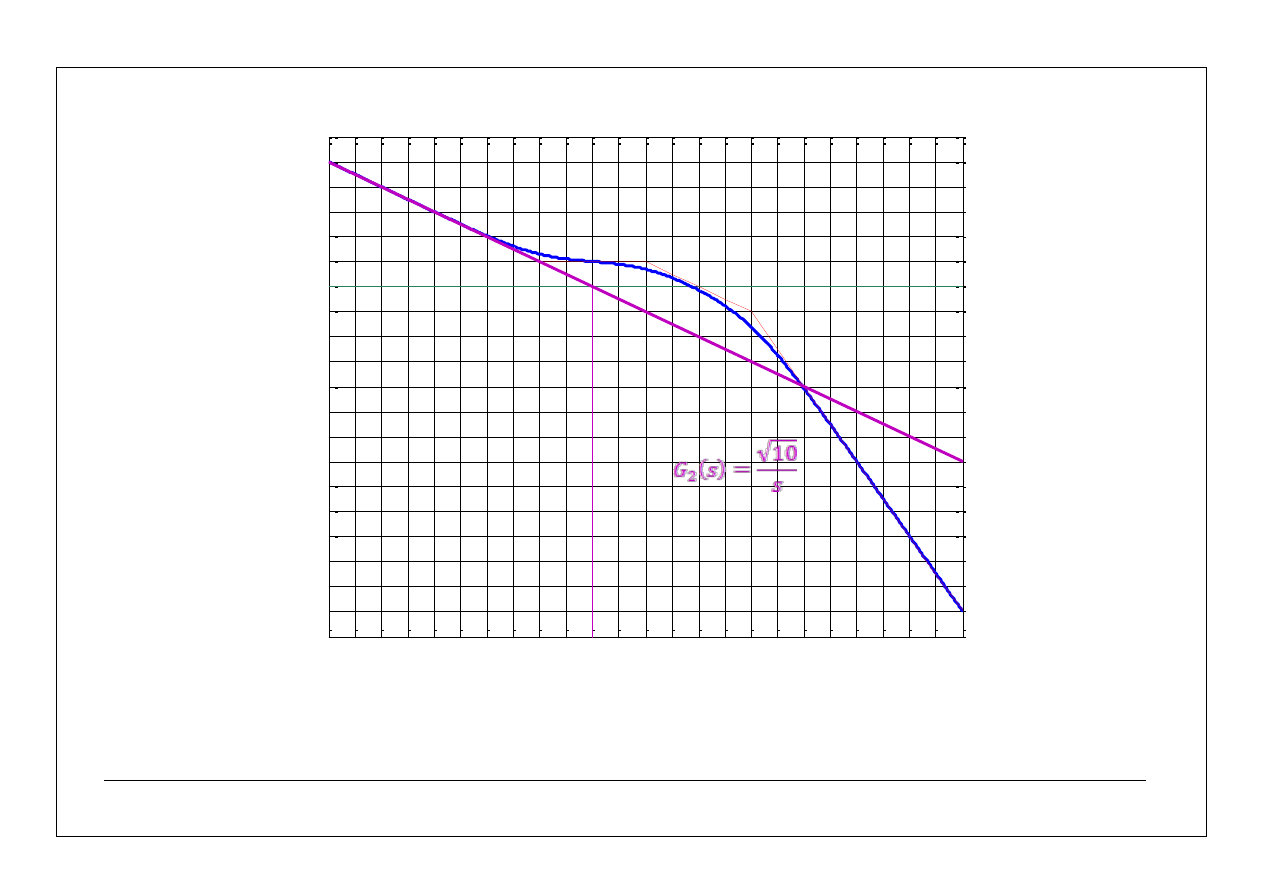
29
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(k)=1/2
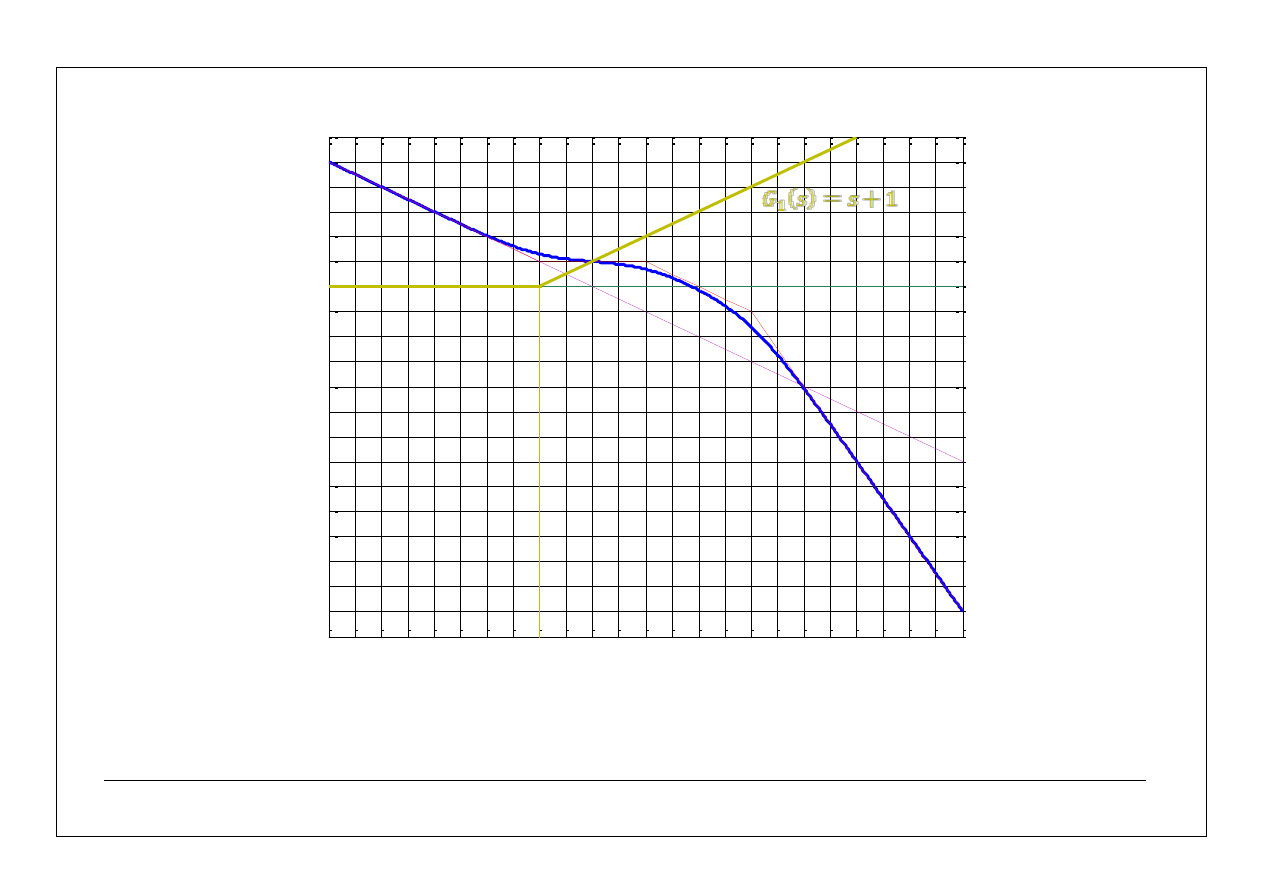
30
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(
1
)=0
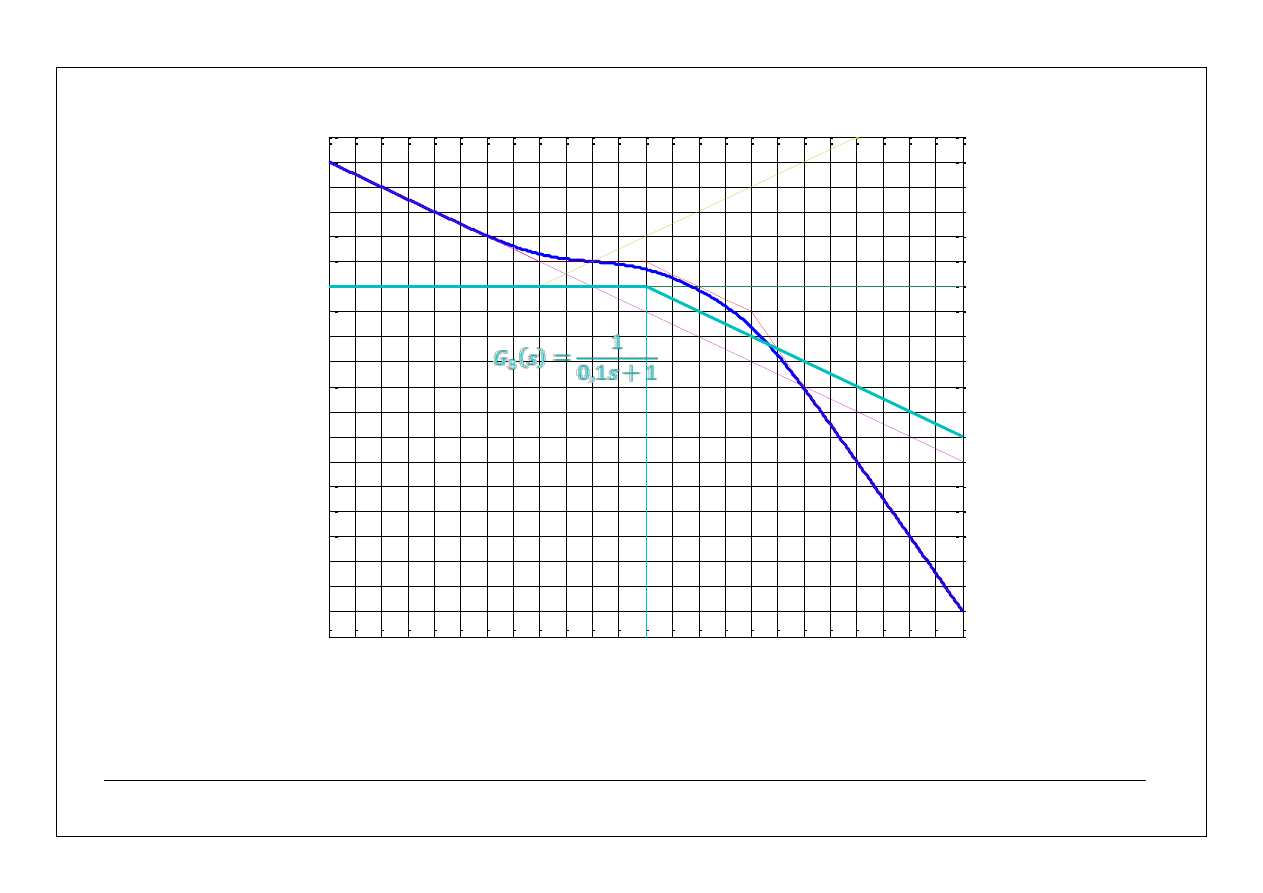
31
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(
2
)=1
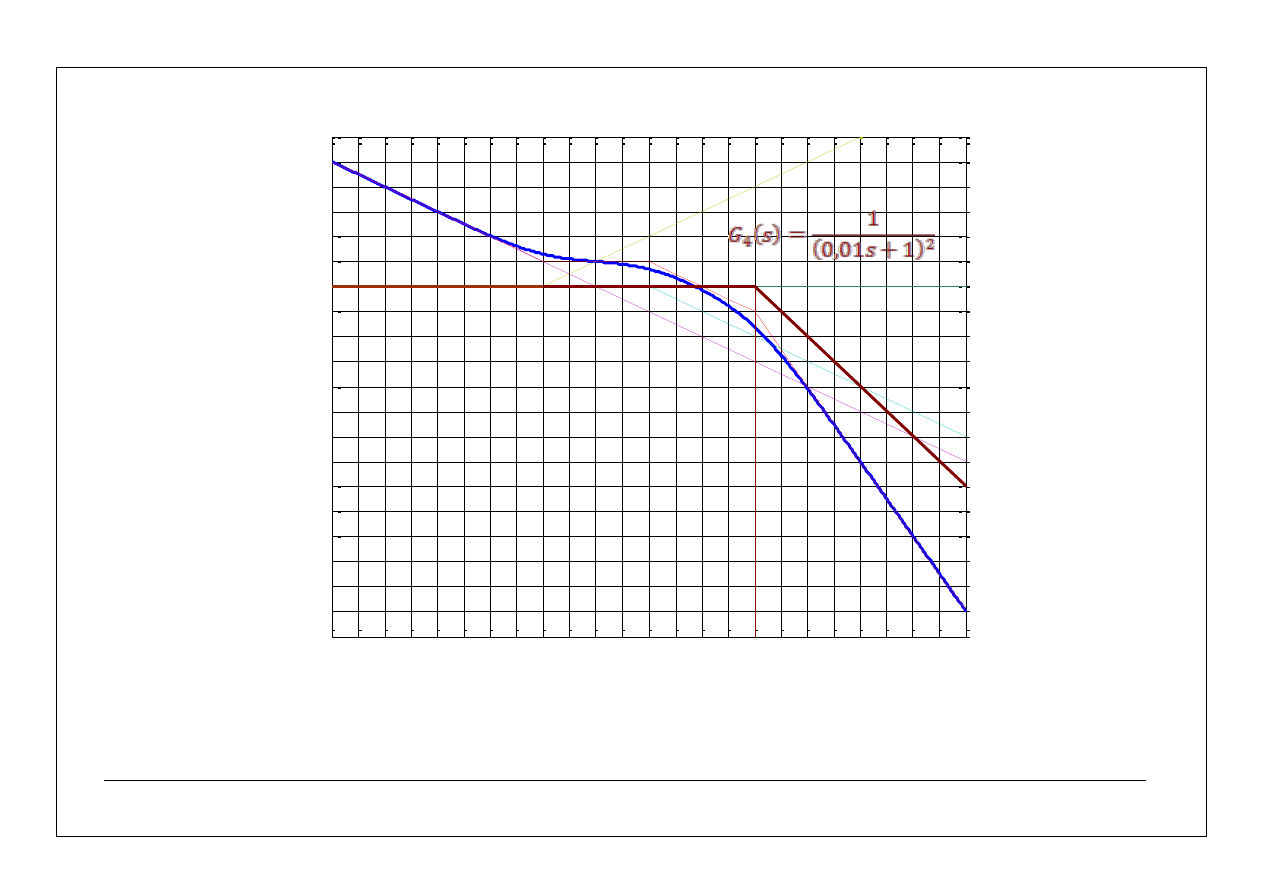
32
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
log(
3
)=2
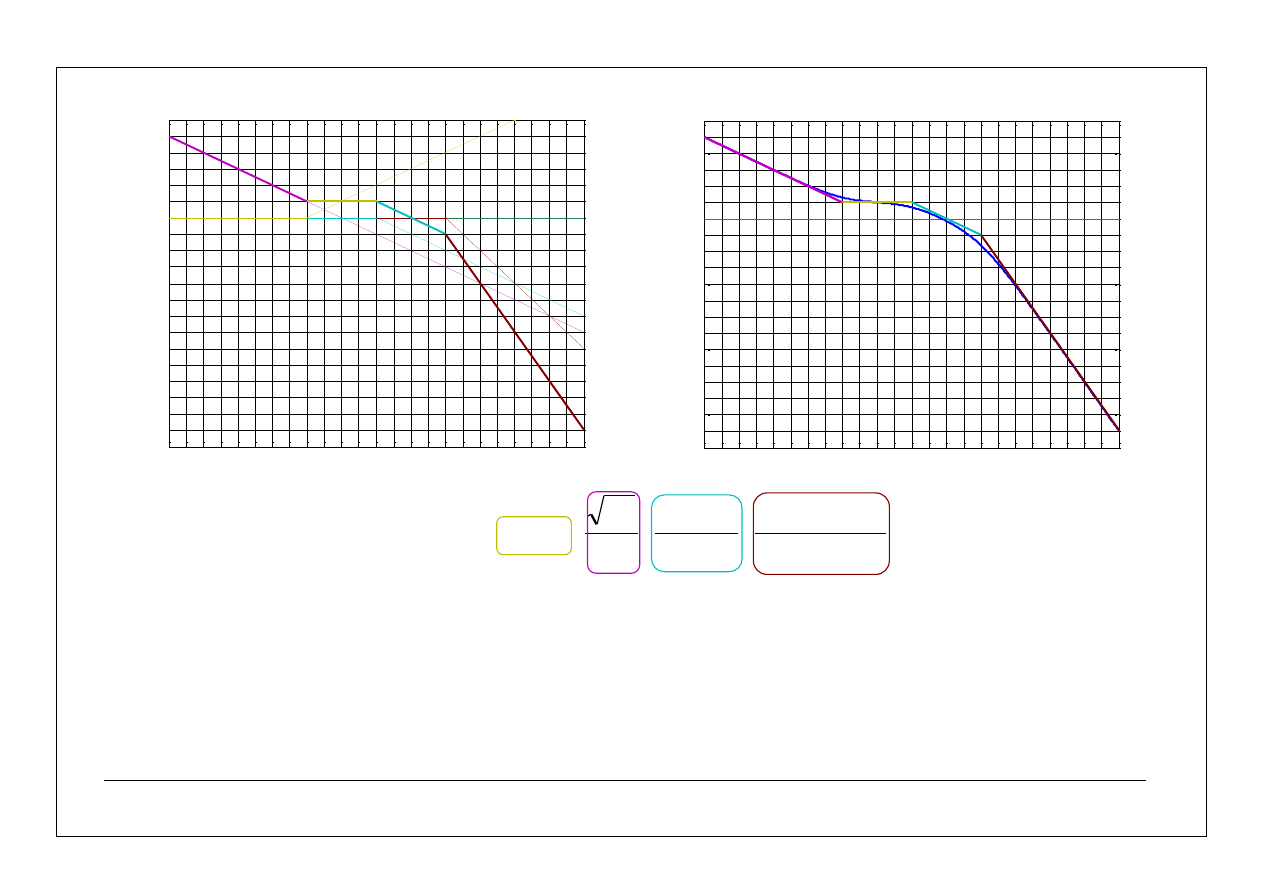
33
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
-2
-1
0
1
2
3
4
-140
-130
-120
-110
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
charakterystyka amplitudowa
log
L(
)
2
)
1
01
,
0
(
1
1
1
,
0
1
10
)
1
(
)
(
s
s
s
s
s
G
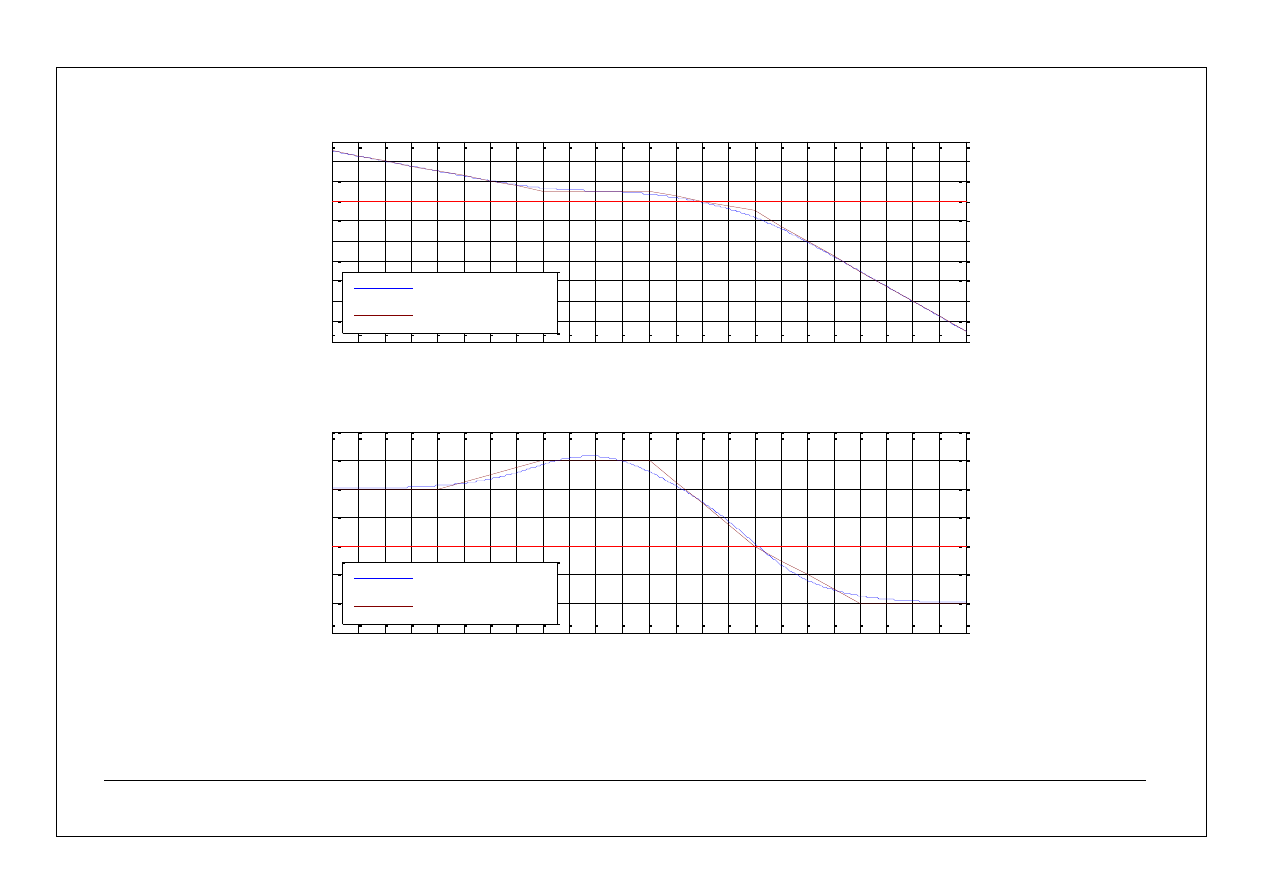
34
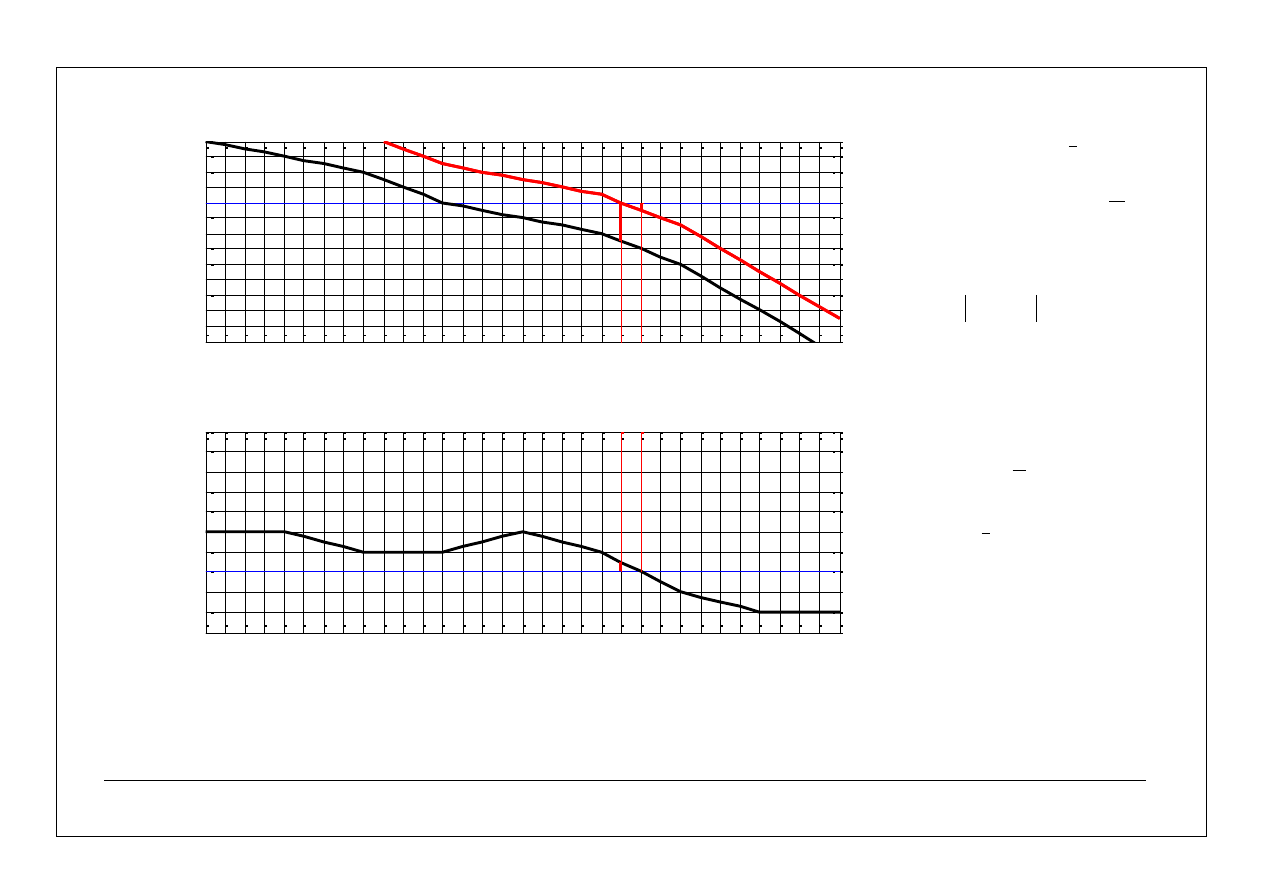
asymptotyczne charakterystyki częstotliwościowe – przykłady
-2
-1
0
1
2
3
4
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
charakterystyki amplitudowe: dokładna i asymptotyczna
log
L(
)
dokładna
asymptotyczna
-2
-1
0
1
2
3
4
-315
-270
-225
-180
-135
-90
-45
0
charakterystyki fazowe: dokładna i asymptotyczna
log
(
)
dokładna
asymptotyczna
Wyszukiwarka
Podobne podstrony:
cw PAiTS 05 id 122324 Nieznany
Matematyka III (Ćw) Lista 06 Ekstrema lokalne i globalne funkcji wielu zmiennych Zadania
socjologia kultury (ćw.) - syllabus (06-07), SOCJOLOGIA KULTURY
kolos automatyka cw PAiTS 03 id Nieznany
PNOP cw 2012 06 23
kolos automatyka cw PAiTS 03a i Nieznany
Matematyka II (Ćw) 2012 06 01
cw PAiTS 04 id 122323 Nieznany
postep.ad.cw.02.06, postępowanie administracyjne(8), cw
cw PAiTS 02
Matematyka cw z 2011 06 18(1)
cw PAiTS 09
cw PAiTS 08
Matematyka III (Ćw)-Lista 06-Ekstrema lokalne i globalne funkcji wielu zmiennych, Odpowiedzi 2
Biofizyka instrukcja do cw nr 06
cw PAiTS 01
Matematyka III (Ćw) - Lista 06 - Ekstrema lokalne i globalne funkcji wielu zmiennych, Zadania
cw PAiTS 07 id 122326 Nieznany
więcej podobnych podstron