
Dr inż. Tadeusz SALAMONOWICZ
PODSTAWY EKSPLOATACJI TECHNICZNEJ
Semestr 6
2 godz. wykładu + 1 godz. ćwiczeń audytoryjnych
Zakres przedmiotu:
1. Eksploatacja: pojęcia, zakres zagadnień. System
eksploatacji, proces eksploatacji.
2. Zmiany stanu technicznego obiektu: natura fizyczna, opis
losowy (statystyczny). Niezawodność obiektów.
3. Modele niezawodności obiektów nienaprawialnych.
Rodzaje uszkodzeń.
4. Struktury niezawodnościowe obiektów złożonych.
Rezerwowanie.
5. Modele niezawodności obiektów naprawialnych. Procesy
odnowy. Gotowość obiektów technicznych.
6. Rozpoznawanie stanu technicznego obiektu i jego
elementów. Podstawy diagnostyki technicznej.
7. Wielostanowe procesy eksploatacji. Opis i miary.
8. Utrzymanie obiektów w gotowości technicznej:
profilaktyka, wymiana, naprawa. Strategie
eksploatacyjne.
9. Badania eksploatacyjne.

Literatura uzupełniająca:
1. Bobrowski D. Modele i metody matematyczne teorii
niezawodności. WNT, Warszawa, 1985,
2. Dwiliński L. Wstęp do teorii eksploatacji obiektu
technicznego. Wydawnictwa Politechniki Warszawskiej.
Warszawa, 1991,
3. Kaźmierczak J. Eksploatacja systemów technicznych.
Wydawnictwo Politechniki Śląskiej. Gliwice, 2000,
4. Smalko Z. Podstawy eksploatacji technicznej pojazdów.
Wydawnictwa Politechniki Warszawskiej. Warszawa,
1998,
Zaliczenie przedmiotu:
Bez egzaminu,
2 kolokwia na ćwiczeniach – zadania,
2 kolokwia na wykładzie – materiał wykładowy.

Niezawodność obiektu – własność, która wyraża się
poprawnym wykonywaniem przez obiekt założonych zadań w
określonych warunkach i określonym czasie.
Inaczej
Niezawodność obiektu określa stopień zaufania, że
w rozpatrywanym przedziale czasu obiekt zachowa zdolność
do wypełniania swoich funkcji.
Formalnym (matematycznym) wyrażeniem tego zaufania jest
prawdopodobieństwo nieuszkodzenia obiektu.
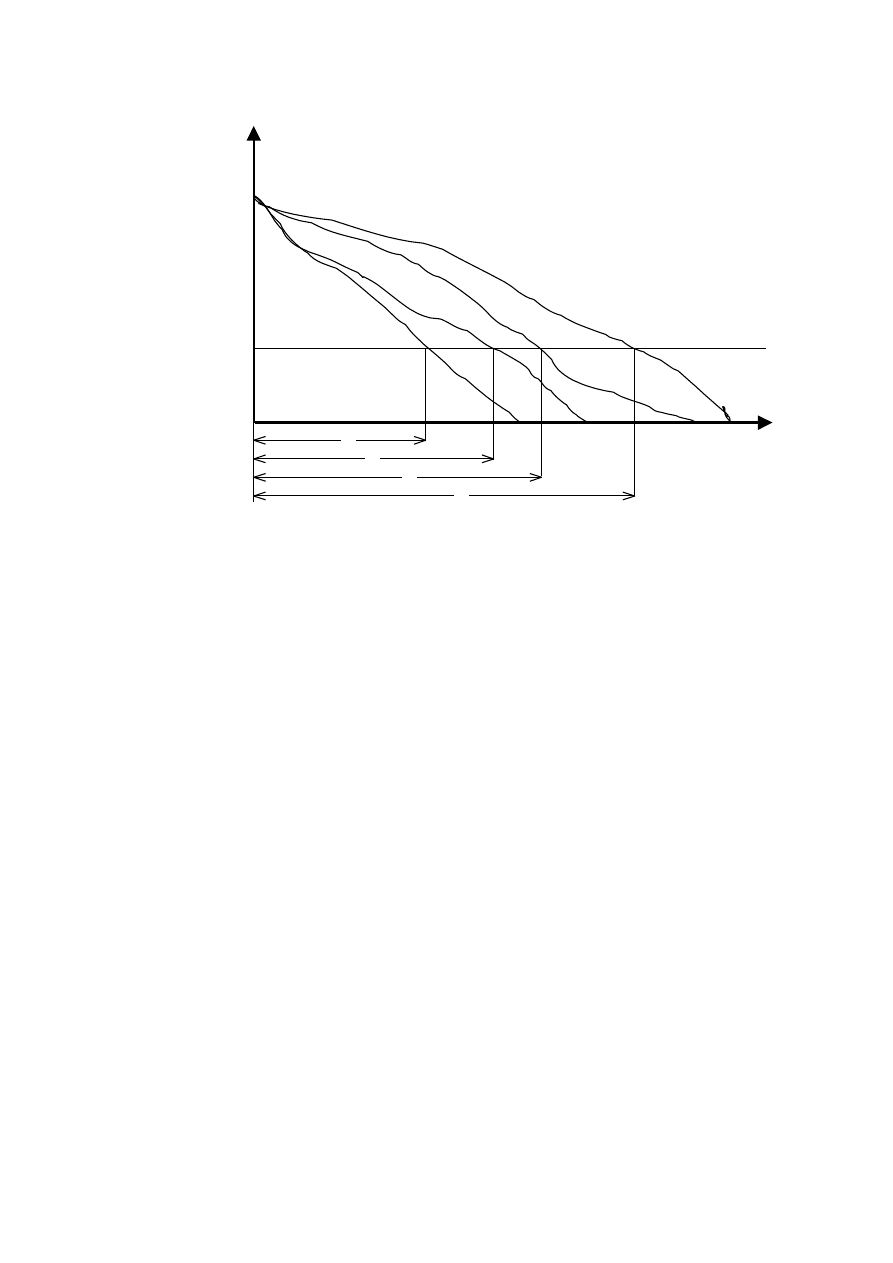
t
S(t)
T
T
T
T
S
gr
=const
S(0)
0

Zmienną losową T charakteryzują ciągłe względem czasu
funkcje określone dla
0
t
:
dystrybuanta
)
(t
F
,
gęstość prawdopodobieństwa uszkodzenia
)
(t
f
,
funkcja niezawodności
)
(t
R
,
intensywność uszkodzeń
)
(t
,
Dystrybuanta zmiennej losowej
T (funkcja zawodności) to
prawdopodobieństwo uszkodzenia obiektu do chwili t
)
(
)
(
t
T
P
t
F
, dla
0
t
przy czym
0
)
0
(
F
Funkcja niezawodności
)
(t
R
- prawdopodobieństwo, że do
chwili t nie nastąpi uszkodzenie.
)
(
)
(
t
T
P
t
R
, dla
0
t
Zakładając, że uszkodzenie obiektu (do chwili t , lub później)
jest zdarzeniem pewnym:
1
)
(
)
(
t
T
P
t
T
P
1
)
(
)
(
t
R
t
F
)
(
1
)
(
t
F
t
R
,
1
0
1
)
0
(
1
)
0
(
F
R
Gęstość prawdopodobieństwa uszkodzenia
)
(t
f
jest
pochodną dystrybuanty
)
(t
F
dt
t
dF
t
f
)
(
)
(
dla
0
t
dt
t
dR
t
R
dt
d
t
f
)
(
))
(
1
(
)
(

Intensywność uszkodzeń
)
(t
definiuje się jako:
)
(
)
(
'
)
(
1
)
(
)
(
t
R
t
R
t
F
t
f
t
; dla
0
t
Oznaczamy:
)
,
(
t
t
t
P
- prawdopodobieństwo warunkowe, że nie nastąpi
uszkodzenie w przedziale
)
,
(
t
t
t
pod warunkiem, że nie
nastąpiło w przedziale
)
,
0
( t .
Zgodnie z twierdzeniem Bayesa na prawdopodobieństwo
warunkowe można zapisać:
)
(
)
(
)
,
(
t
R
t
t
R
t
t
t
P
)
,
(
t
t
t
Q
- prawdopodobieństwo warunkowe, że nastąpi
uszkodzenie w przedziale
)
,
(
t
t
t
pod warunkiem, że nie
nastąpiło w przedziale
)
,
0
( t .
)
(
)
(
)
(
)
(
)
(
1
)
,
(
1
)
,
(
t
R
t
t
R
t
R
t
R
t
t
R
t
t
t
P
t
t
t
Q
)
(
1
)
(
)
(
)
,
(
t
R
t
t
t
R
t
R
t
t
t
t
Q
)
(
1
)
(
)
(
lim
)
,
(
lim
0
0
t
R
t
t
t
R
t
R
t
t
t
t
Q
t
t
)
(
)
(
'
)
(
)
(
lim
)
(
1
0
t
R
t
R
t
t
R
t
t
R
t
R
t

Otrzymana granica jest lokalną (w chwili t ) funkcją
zawodności będącą warunkową gęstością
prawdopodobieństwa powstania uszkodzenia w chwili t , pod
warunkiem, że do chwili t uszkodzenie nie nastąpiło.
Oznaczamy ją
)
(t
i nazywamy intensywnością uszkodzeń.
)
(
1
)
(
)
(
ln
)
(
)
(
'
)
(
t
F
t
f
t
R
dt
d
t
R
t
R
t

Każda z czterech zdefiniowanych funkcji
)
(t
F
,
)
(t
f
,
)
(t
R
,
)
(t
w sposób jednoznaczny określa zmianę losową
T ,
determinując tym samym postać pozostałych funkcji.
Poprzez dystrybuantę
)
(t
F
wyrazić je można jako:
)
(
'
)
(
t
F
t
f
)
(
1
)
(
t
F
t
R
)
(
1
)
(
'
)
(
t
F
t
F
t
Poprzez gęstość
)
(t
f
wyrazić je można jako:
t
dx
x
f
t
F
0
)
(
)
(
t
t
dx
x
f
dx
x
f
t
R
)
(
)
(
1
)
(
0
t
t
dx
x
f
t
f
dx
x
f
t
f
t
)
(
)
(
)
(
1
)
(
)
(
0
Poprzez funkcję niezawodności
)
(t
R
wyrazić je można jako:
)
(
1
)
(
t
R
t
F
)
(
'
)
(
t
R
t
f
)
(
)
(
'
)
(
t
R
t
R
t

Znając funkcję intensywności uszkodzeń
)
(t
, w celu
wyznaczenia pozostałych funkcji rozwiązujemy równanie
różniczkowe:
)
(
)
(
'
)
(
t
R
t
R
t
o warunku początkowym
1
)
0
(
R
Równanie całkujemy obustronnie w granicach od 0 do t
)
(
1
)
(
)
(
x
R
dx
x
R
d
x
t
t
x
R
x
dR
dx
x
0
0
)
(
)
(
)
(
)
(
ln
1
ln
)
(
ln
)
0
(
ln
)
(
ln
)
(
ln
)
(
0
0
t
R
t
R
R
t
R
x
R
dx
x
t
t
t
dx
x
t
R
0
)
(
exp
)
(
t
dx
x
t
F
0
)
(
exp
1
)
(
t
dx
x
t
t
R
t
t
F
t
t
f
0
)
(
exp
)
(
)
(
)
(
)
(
1
)
(
)
(

Wielkości
znane
Wielkości
szukane
F(t)
f(t)
R(t)
(t)
F(t)
---
t
dx
x
f
0
t
R
1
t
dx
x
0
exp
1
f(t)
t
F '
---
t
R'
t
dx
x
t
0
exp
R(t)
t
F
1
t
dx
x
f
---
t
dx
x
0
exp
(t)
t
F
t
F
1
'
t
dx
x
f
t
f
t
R
t
R'
---

Wskaźniki liczbowe niezawodności
wartość oczekiwana
)
(T
E
0
)
(
)
(
dt
t
f
t
T
E
def
;
0
)
(
)
(
t
dF
t
T
E
0
)
(
dt
t
f
t
całkujemy przez części wg:
du
v
uv
dv
u
t
u
,
dt
du
,
)
(
dt
t
f
dv
)
(
)
(
'
)
(
'
)
(
t
R
dt
t
R
dt
t
F
dt
t
f
v
0
0
0
0
)
(
)
(
)
(
)
(
dt
t
R
dt
t
R
t
R
t
dt
t
f
t
0
)
(
)
(
dt
t
R
T
E
wariancja
)
(
2
T
D
2
0
2
2
2
2
)
(
)
(
)
(
)
(
)
(
T
E
dt
t
f
t
T
E
T
E
T
D
po scałkowaniu przez części otrzymujemy:
2
0
2
2
)
(
)
(
2
)
(
T
E
dt
t
R
t
T
D
,
)
(
2
T
D
Wielkość
)
(T
E
oznacza średni czas życia obiektu,
a
przeciętne odchylenie czasu życia obiektów od
oczekiwanego
)
(T
E
.
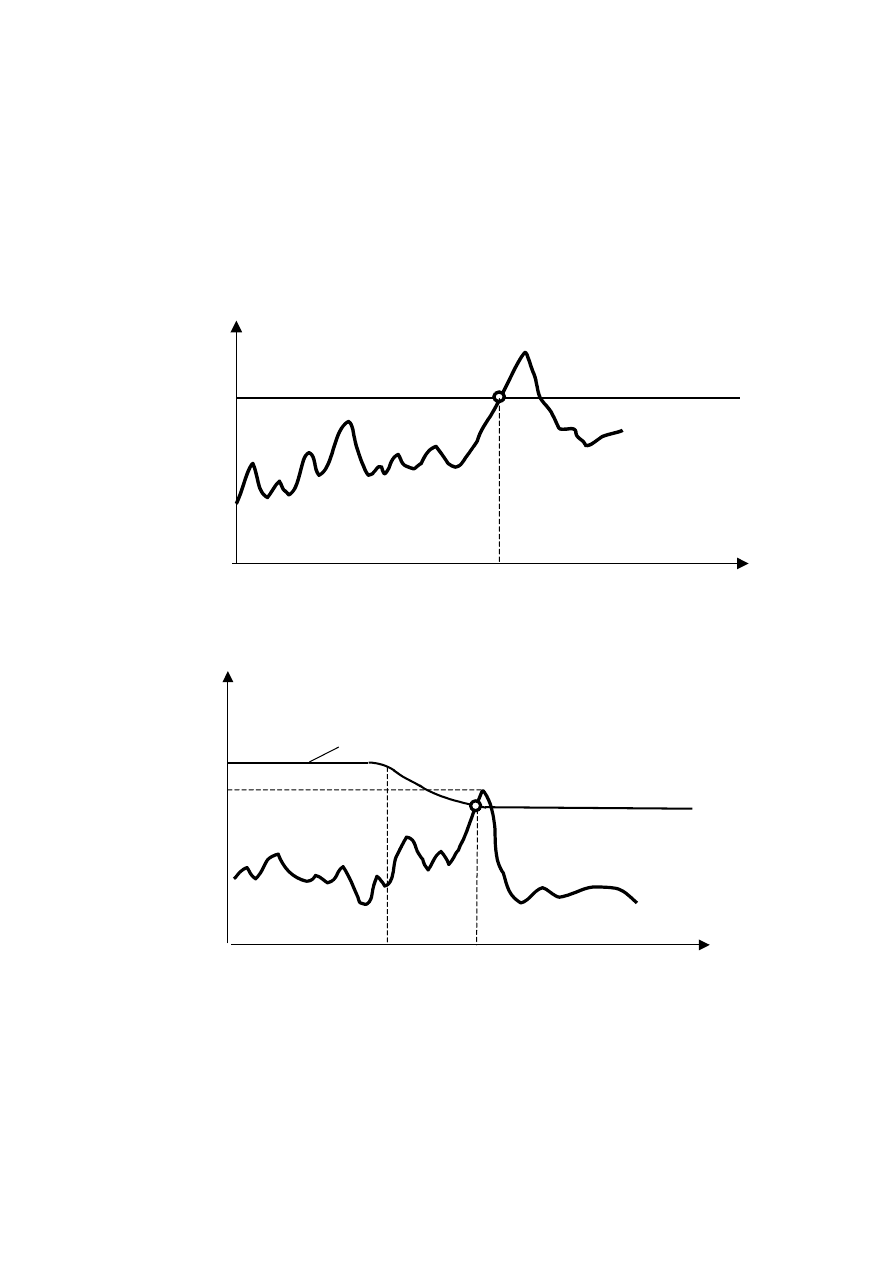
Zmiany stanu technicznego spowodowane wymuszeniami
skokowymi:
S(t)
S
dop
t
o
t
a)
S(t)
S
dop
(t)
S
max
t
o
t
b)

a)
stała wartość dopuszczalna
b) zmienna wartość dopuszczalna
Przy dowolnym wymuszeniu zmiana stanu technicznego
obiektu (przekroczenie wartości granicznej, uszkodzenie)
może nastąpić z prawdopodobieństwem q
i nie nastąpić z prawdopodobieństwem
q
1
.
Jakie jest prawdopodobieństwo, że uszkodzenie nastąpi
przy
tym
k
wymuszeniu?
Niech:
A
- zdarzenie polegające na wystąpieniu uszkodzenia
A
- zdarzenie polegające na niewystąpieniu uszkodzenia
Wystąpienie uszkodzenia przy
tym
k
wymuszeniu oznacza
wystąpienie k wymuszeń, przy czym przy
1
k
uszkodzenie
nie nastąpiło a przy
tym
k
nastąpiło.
k
B
- zdarzenie łączne odpowiadające sytuacji, że
uszkodzenie nastąpiło przy
tym
k
wymuszeniu
)
(
)
(
.
).........
(
)
(
)
(
1
2
1
k
k
k
A
P
A
P
A
P
A
P
B
P
gdzie:
)
(
i
A
P
- prawdopodobieństwo zmiany przy
tym
i
wymuszeniu
)
1
(
)
(
k
T
P
B
P
k

gdzie:
T - czas pozostawania w wymaganym stanie (stanie
zdatności) mierzony liczbą wymuszeń
Ponieważ:
q
A
P
A
P
A
P
k
1
)
(
.........
)
(
)
(
1
2
1
stąd
q
q
k
T
P
k 1
)
1
(
)
1
(
rozkład geometryczny
1
1
1
2
1
1
)
1
(
..
)
(
)
(
)
(
..
)
(
)
(
k
k
k
k
k
T
P
B
P
B
P
B
P
B
P
B
P
)
1
(
k
T
P
+
)
1
(
k
t
P
=1
)
1
(
)
2
(
.....
)
1
(
)
0
(
)
1
(
k
T
P
k
T
P
T
P
T
P
k
T
P
q
T
P
)
0
(
)
1
(
)
1
(
q
q
T
P
2
)
1
(
)
2
(
q
q
T
P
............................................
2
)
1
(
)
2
(
k
q
q
k
T
P
1
)
1
(
)
1
(
k
q
q
k
T
P
k
i
i
i
k
i
q
q
q
q
k
T
P
1
1
1
0
)
1
(
)
1
(
)
1
(

q
q
q
q
q
k
k
k
i
i
)
1
(
1
)
1
(
1
)
1
(
1
)
1
(
1
1
k
q
k
T
P
)
1
(
1
)
1
(
k
q
k
T
P
)
1
(
)
1
(

1
)
1
(
)
1
(
k
q
q
k
T
P
t
- czas trwania wymuszenia,
Uszkodzenie przy k-tym wymuszeniu jest równoważne
uszkodzeniu w przedziale
)
,
(
t
t
t
gdzie
,
)
1
(
t
k
t
t
q
1
k
t
t
1
k
t
q
prawdopodobieństwo wystąpienia uszkodzenia w przedziale
)
,
(
t
t
t
wynosi
t
k
t
k
T
P
p
k
t
1
)
1
1
(
)
1
(
~
dt
e
p
p
t
t
t
k
~
lim
Jeżeli zmienna losowa jest ciągła, to:
dt
t
f
t
t
T
t
P
p
t
)
(
)
(
t
e
t
f
)
(
- gęstość prawdopodobieństwa uszkodzenia
dla rozkładu wykładniczego
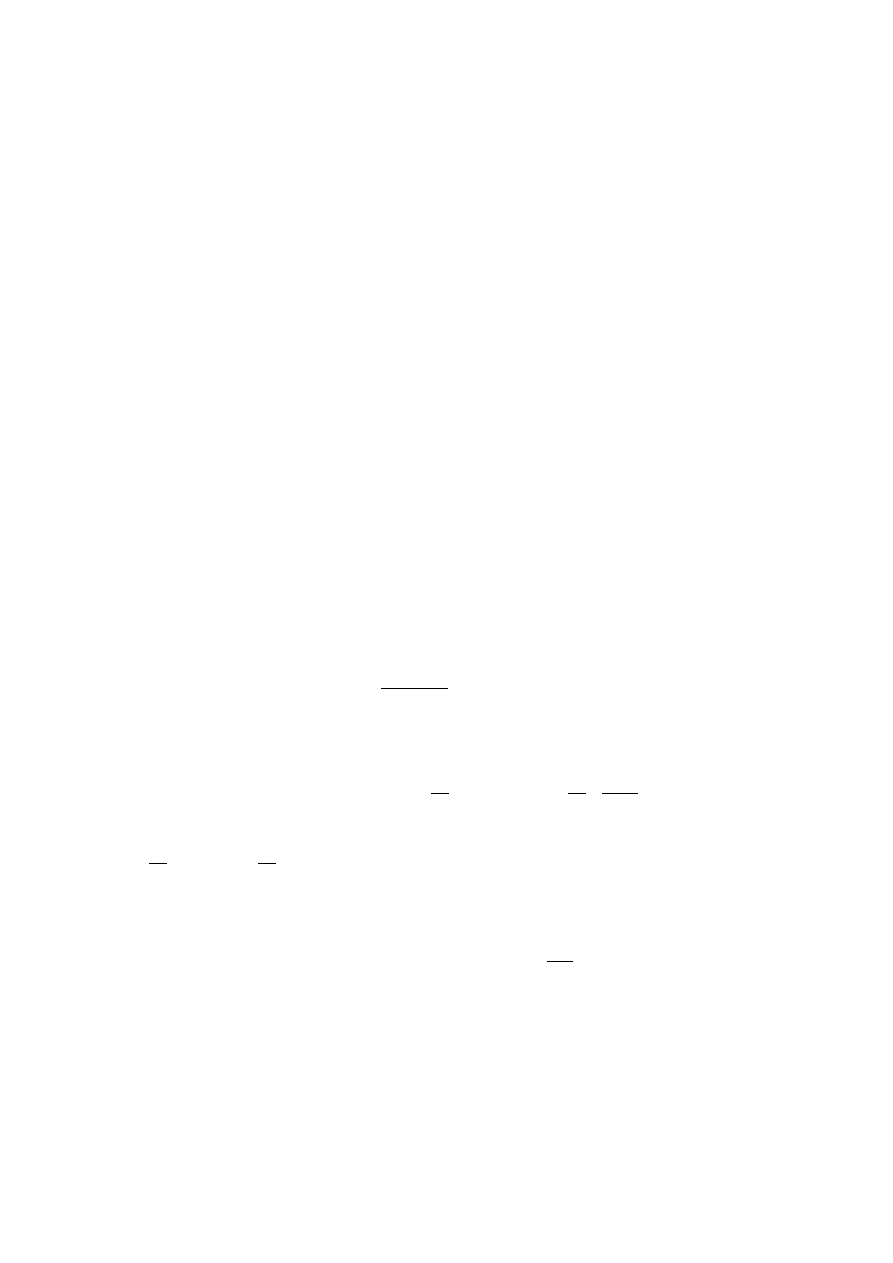
Niezawodność typu wykładniczego
Wówczas, gdy czas życia obiektu jest zmienną losową T
o rozkładzie wykładniczym z parametrem
0
, a więc:
t
e
t
f
)
(
dla
0
t
t
e
t
F
1
)
(
dla
0
t
t
e
t
R
)
(
ostatnia równość zwana jest
wykładniczym prawem niezawodności
.
)
(
const
e
e
t
t
t
0
0
0
0
1
1
1
)
(
)
(
t
t
t
e
e
dt
e
dt
t
R
T
E
1
1
0
1
0
2
2
1
2
)
(
dt
e
t
T
D
t
0
dt
e
t
t
t
u
dt
du
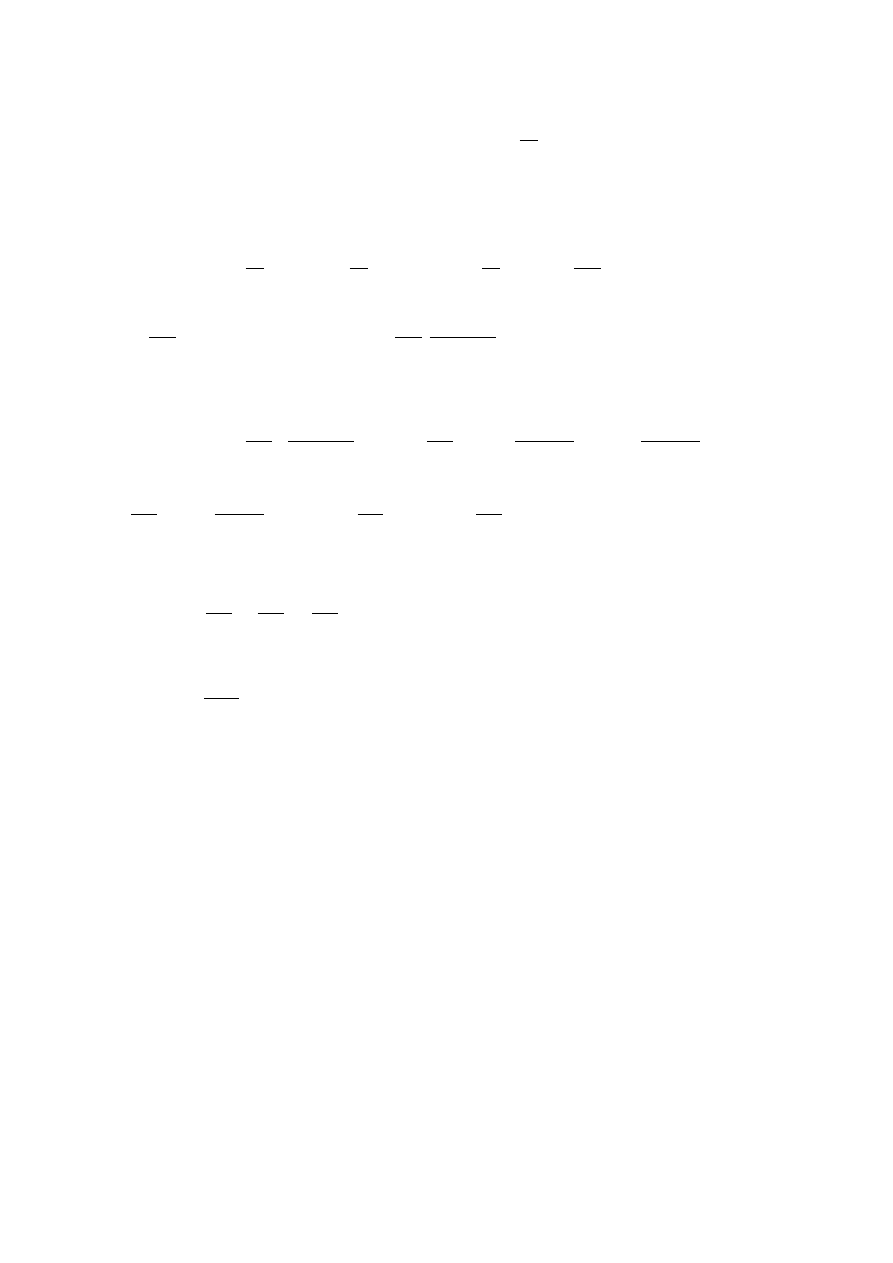
dt
e
dv
t
,
t
e
v
1
t
t
t
t
t
e
e
t
dt
e
e
t
dt
e
t
2
1
1
t
t
t
e
t
e
e
t
1
1
)
(
1
2
2
t
t
t
t
t
t
e
t
e
t
e
t
dt
e
t
1
lim
1
lim
1
1
1
0
2
0
0
2
2
2
2
1
1
0
1
1
lim
1
t
t
e
2
2
2
2
1
1
2
)
(
T
D
)
(
)
(
T
E
t
e
t
R
wykładnicze prawo niezawodności
Wykładniczemu prawu niezawodności podlegają obiekty, dla
których
.
)
(
const
t
, tzn. takie, których odporność na
bodźce wymuszające uszkodzenia nie maleje z upływem
czasu.
Omawiane prawo ma jeszcze jedną charakterystyczną
własność: warunkowe prawdopodobieństwo poprawnej pracy
obiektu w przedziale
)
,
(
t
t
t
pod warunkiem
nieuszkodzenia w czasie
)
,
0
( t
, zależy jedynie od długości
przedziału t
, nie zależy zaś od długości czasu t
wcześniejszej pracy obiektu.

)
(
)
(
)
(
)
(
)
/
(
t
R
t
t
R
t
T
P
t
t
T
P
t
T
t
t
T
P
t
t
t
t
t
t
t
e
e
e
e
e
e
)
(

Rozkład jednostajny
b
t
b
t
a
a
b
a
t
t
f
,
0
,
1
,
0
)
(
dla
0
a
b
t
f
1
)
(
t
t
b
t
dx
b
dx
x
f
t
F
0
0
1
)
(
)
(
b
t
b
b
t
t
R
1
)
(
t
b
t
R
t
f
t
1
)
(
)
(
)
(
f(t)
a
b
0
1/(b-a)
t
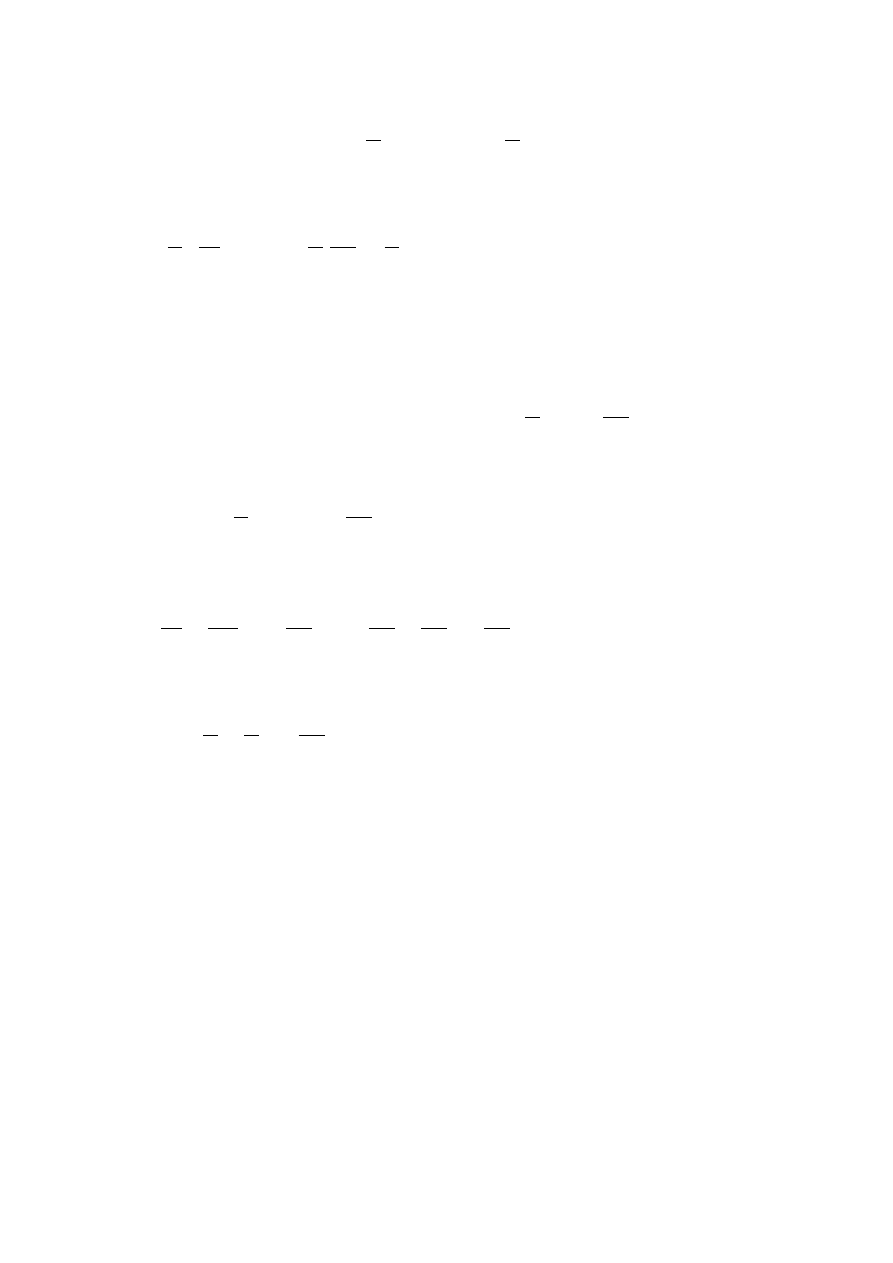
b
b
b
b
dt
t
b
dt
dt
b
t
dt
t
R
T
E
0
0
0
0
1
)
1
(
)
(
)
(
2
2
1
2
1
2
0
2
b
b
b
b
t
b
b
b
4
)
1
(
2
)
(
)
(
2
)
(
2
0
0
2
2
b
dt
b
t
t
T
E
dt
t
R
t
T
D
b
b
4
1
2
2
0
0
2
b
dt
t
b
dt
t
b
b
4
3
2
2
4
3
2
2
2
2
2
2
0
3
2
b
b
b
b
b
t
t
b
12
4
1
3
2
1
2
2
b
b

System o strukturze szeregowej
1
2
k
n-1
n
...
...
0
...
...
,
...
,
,
min
1
2
1
2
1
2
1
t
dla
t
R
t
R
t
R
t
R
t
R
t
R
t
T
P
t
T
P
t
T
P
t
T
P
T
T
T
T
n
k
k
n
n
n

Jeżeli
)
(t
R
k
wyrazimy przez
)
(t
k
jako:
t
k
k
dx
x
t
R
0
)
(
exp
)
(
to:
t
n
k
k
n
k
n
k
t
k
k
dx
x
dx
x
t
R
t
R
0
1
1
1
0
)
(
exp
)
(
exp
)
(
)
(
t
n
k
k
t
dx
x
dx
x
0
1
0
)
(
exp
)
(
exp
n
k
k
t
t
1
)
(
)
(
n
k
n
k
k
k
t
F
t
R
t
F
1
1
)
(
1
1
)
(
1
)
(
Wartości
)
(T
E
i
)
(
2
T
D
wyznacza się ze wzorów
definicyjnych. W ogólnym przypadku t.j. dla zmiennych
losowych
k
T
o dowolnym rozkładzie prawdopodobieństwa
nie można podać bezpośredniej zależności między
)
(T
E
i
)
(
k
T
E

Przypadki szczególne
1) Niech zmienne losowe
k
T
T
T
,....,
,
2
1
mają taki sam rozkład
prawdopodobieństwa
)
(
)
(
1
t
F
t
F
k
dla
n
k
,....,
2
,
1
,
0
t
Wszystkie elementy mają więc również jednakowe
)
(
)
(
1
t
t
k
dla
n
k
,....,
2
,
1
,
0
t
stąd
)
(
)
(
)
(
1
1
t
n
t
t
n
k
k
Intuicyjnie zrozumiała interpretacja:
połączenie szeregowe
n
identycznych elementów zwiększa
n
krotnie prawdopodobieństwo uszkodzenia w danej chwili
t
dt
t
n
t
R
0
1
)
(
exp
)
(
)
(
)
(
1
t
R
t
R
n

2) Niech zmienne losowe
n
T
T
T
,....,
,
2
1
mają rozkład
wykładniczy o parametrach odpowiednio
2
1
, ....,
n
,
czyli:
t
k
k
k
e
t
f
)
(
const
t
k
k
)
(
const
t
n
k
k
1
)
(
t
e
t
R
)
(
n
k
k
n
k
k
T
E
T
E
1
1
)
(
1
1
1
1
)
(
3) Niech zmienne losowe
n
T
T
T
,....,
,
2
1
mają rozkład
wykładniczy o tym samym parametrze
1
1
)
(
n
t
t
n
e
t
R
1
)
(
n
T
E
n
T
E
)
(
1
)
(
1
1
System o strukturze równoległej
1
2
k
n
n
k
k
n
k
k
n
n
n
t
R
t
R
t
dla
t
F
t
F
t
F
t
F
t
F
t
F
t
T
P
t
T
P
t
T
P
t
T
P
T
T
T
T
1
1
2
1
2
1
2
1
1
1
0
...
...
,
...
,
,
max

Przypadki szczególne
1) Niech zmienne losowe
n
T
T
T
,....,
,
2
1
mają jednakowy
rozkład prawdopodobieństwa o dystrybuancie
)
(
1
t
F
,
wówczas:
)
(
)
(
1
t
F
t
F
n
n
t
R
t
R
)
(
1
1
)
(
1
2) Niech zmienne losowe
n
T
T
T
,....,
,
2
1
maja rozkład
wykładniczy o parametrach odpowiednio
2
1
, ....
n
,
wówczas:
n
k
t
k
e
t
R
1
)
1
(
1
)
(
korzystając z rozwinięcia funkcji
t
k
e
w szereg
Maclaruina można przyjąć, że
t
e
k
t
k
1
,
czyli
n
n
n
k
k
t
t
t
R
....
1
1
)
(
...
2
1
1

3) Niech zmienne losowe
n
T
T
T
,....,
,
2
1
maja wykładniczy
rozkład prawdopodobieństwa o jednakowym parametrze
1
,
wówczas:
n
n
t
t
e
t
F
)
(
)
1
(
)
(
1
1
n
t
t
R
)
(
1
)
(
1
Wyznaczamy dla tego przypadku
)
(T
E
dt
e
dt
t
R
T
E
n
t
0
0
)
1
(
1
)
(
)
(
1
podstawiamy:
z
e
t
1
1
z
t
1
1
ln
1
1
,
)
1
(
1
z
dz
dt
1
0
1
1
1
0
1
)
.....
1
(
1
1
1
1
)
(
dz
z
z
dz
z
z
T
E
n
n
=
)
1
.....
2
1
1
(
1
1
n
)
1
......
2
1
1
(
)
(
)
1
........
2
1
1
(
1
)
(
1
1
n
T
E
n
T
E
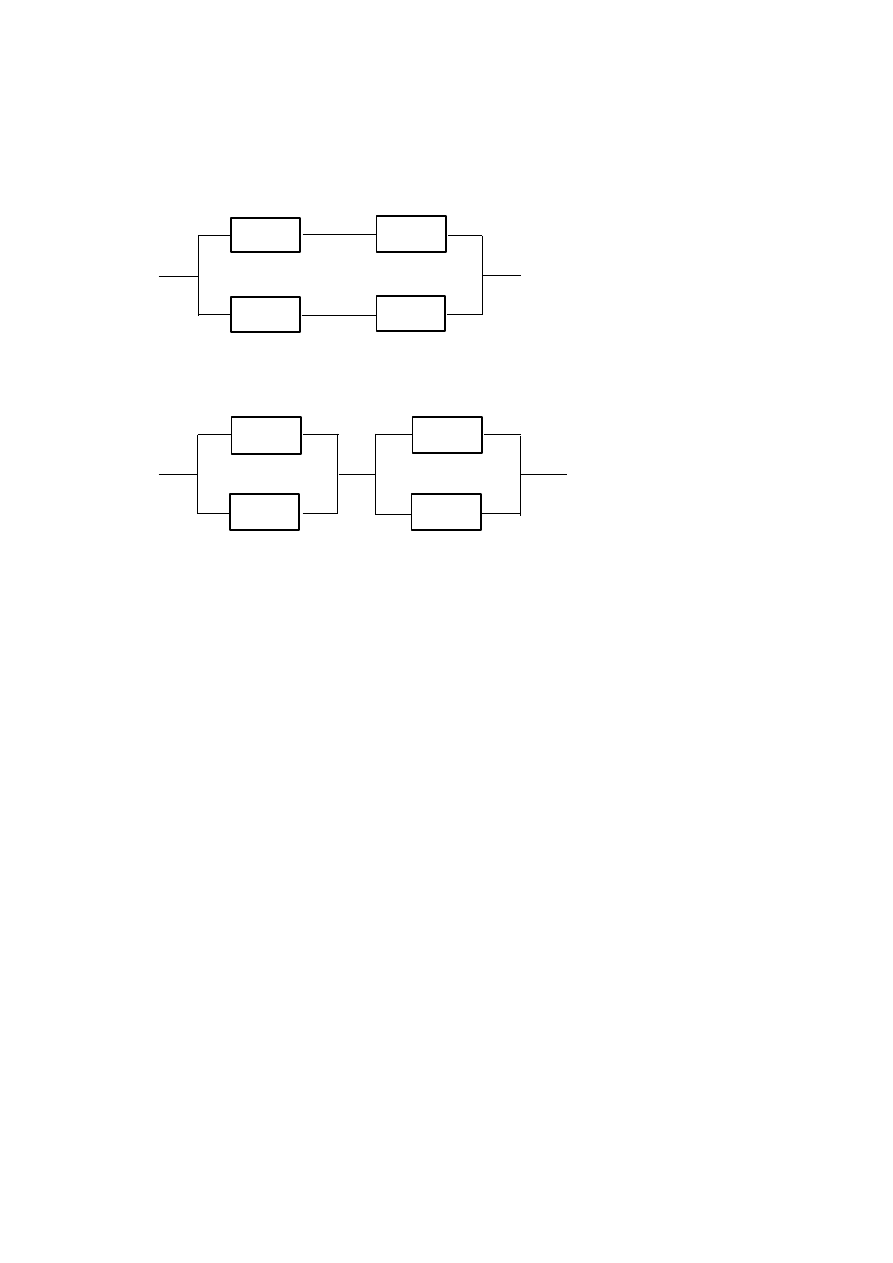
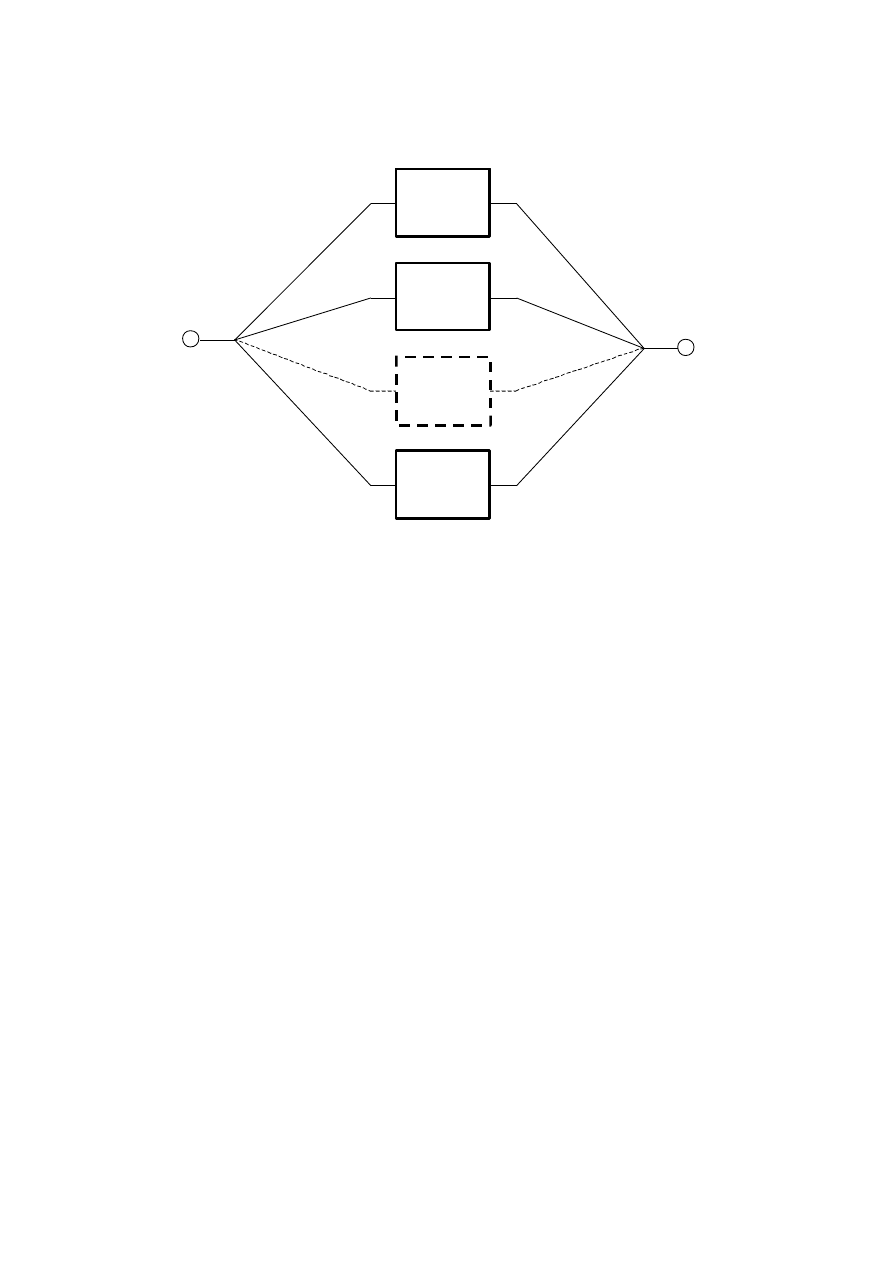
Który wariant jest korzystniejszy?
)
2
(
)
1
(
1
2
2
2
2
R
R
R
R
a
2
2
2
2
)
2
(
)
1
(
1
R
R
R
R
b
)
2
4
4
(
)
2
(
)
2
(
2
2
2
2
2
2
2
R
R
R
R
R
R
R
R
R
R
a
b
0
)
1
(
2
)
2
1
(
2
)
2
4
2
(
2
2
2
2
2
2
R
R
R
R
R
R
R
R
a
b
R
R
a)
b)
R
R
R
R
R
R
R
R
Krotność rezerwowania
n
m
u
R
R
)
1
(
1
n
u
m
R
R
1
1
)
1
(
)
1
(
log
)
1
(
log
1
n
u
R
R
m
)
1
(
log
)
1
(
log
1
R
R
m
n
u
dla
1
n
)
1
(
log
)
1
(
log
R
R
m
u
12
22
1n
2n
mn
m2
11
21
m1

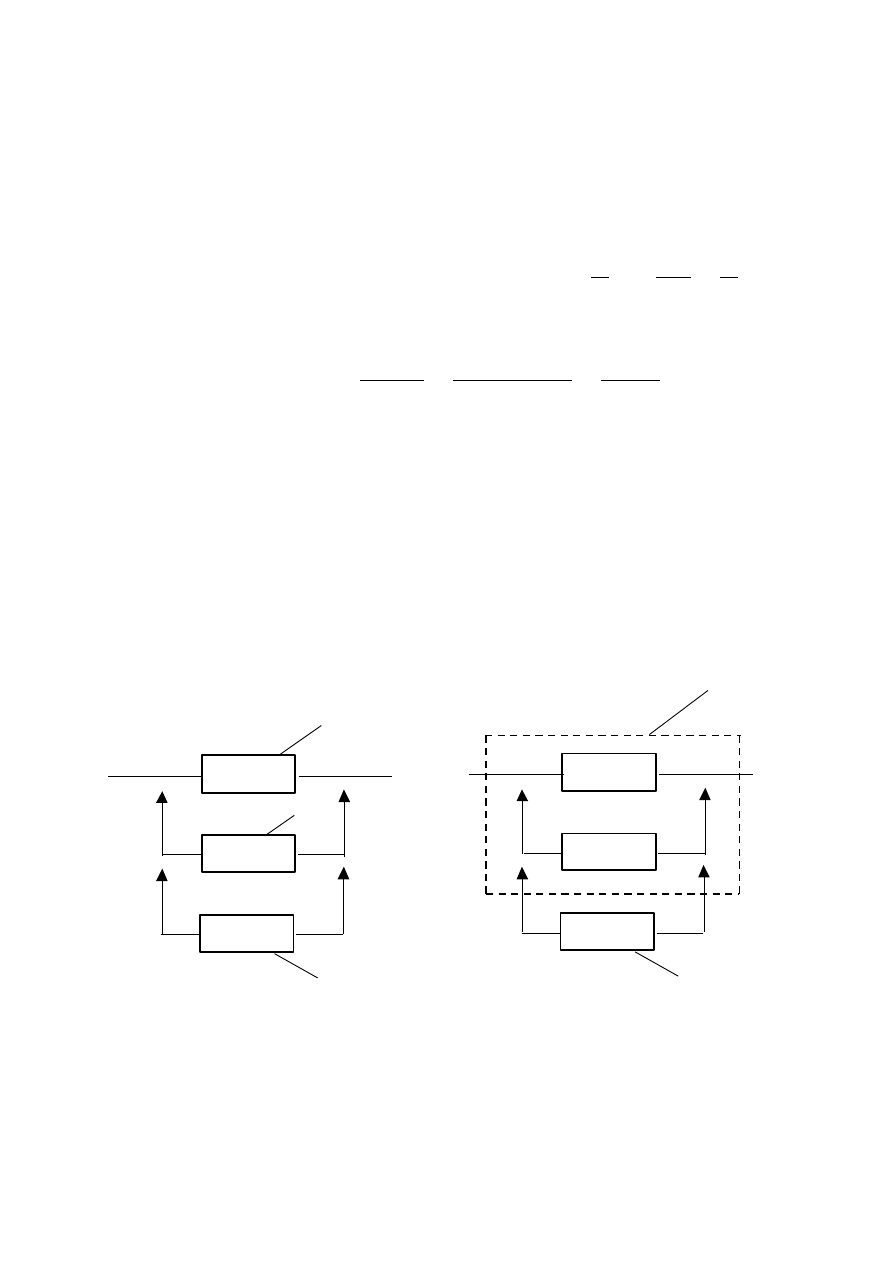
Rezerwa nieobciążona (zimna)
2
1
1
)
(
)
(
)
(
2
1
T
E
T
E
T
E
u
ale
)
(
1
)
(
t
T
E
u
u
W jakich sytuacjach układ będzie zdatny w chwili t ?
1) element podstawowy (1) nie uszkodzi się do chwili t :
t
e
t
R
P
)
(
1
1
2) element podstawowy (1) uszkodzi się w pewnej chwili
t
, element rezerwowy (2) nie uszkodzi się w
przedziale
)
,
( t
:
d
t
R
f
P
t
)
,
(
)
(
0
2
e
f
)
(
)
(
)
,
(
t
e
t
R
(1)
(2)
t
e
t
P
2
t
t
t
u
e
t
te
e
P
P
t
R
)
1
(
)
(
2
1
2
1
1
)
1
(
)
(
)
(
2
0
0
dt
e
t
dt
t
R
T
E
t
u
u
t
t
e
t
te
t
R
t
R
t
t
t
u
u
u
1
)
1
(
)
(
)
(
'
)
(
2
2
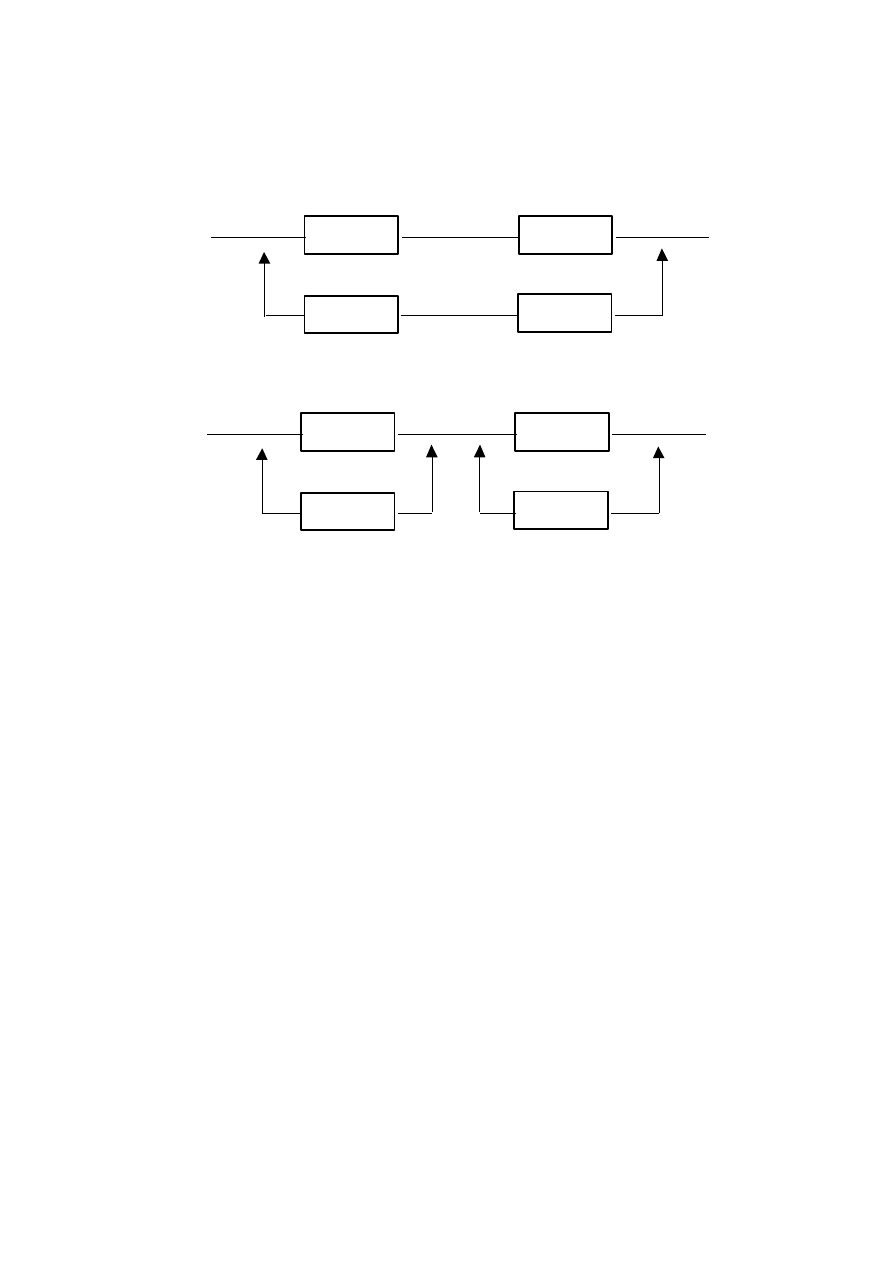
Jeżeli będą dwa elementy rezerwowe, to pojawi się trzecia
sytuacja, w której układ zachowa zdatność do chwili t :
3) element podstawowy (1) i element rezerwowy (2)
uszkodzą się do pewnej chwili
t
, element rezerwowy (3)
nie uszkodzi się w przedziale
)
,
( t
d
t
R
f
P
t
)
,
(
)
(
0
3
e
f
2
)
(
(1)
(2)
(3)
(1)
(2)

)
(
)
,
(
t
e
t
R
.
t
e
t
P
2
2
3
2
1
t
u
e
t
t
P
P
P
t
R
)
2
1
1
(
)
(
2
2
3
2
1

Zwiększając liczbę elementów rezerwowych możemy
wyznaczyć kolejno:
t
e
t
P
3
3
4
6
1
t
e
t
P
4
4
5
24
1
t
k
k
e
k
t
P
!
)
(
t
m
k
k
m
k
k
u
e
k
t
P
t
R
0
0
!
)
(
)
(
Który wariant jest korzystniejszy?
t
a
e
t
t
R
2
)
2
1
(
)
(
t
t
b
e
t
e
t
t
R
2
2
2
)
1
(
1
)
(
t
t
e
t
R
t
R
t
a
b
2
1
1
)
(
)
(
2
2
0
2
1
2
1
2
2
2
2
2
2
t
t
e
t
t
t
t
e
)
(
)
(
t
R
t
R
a
b
a)
b)

Rezerwa częściowo obciążona (chłodna)
1
0
2
do chwili uszkodzenia elementu (1)
2
po chwili uszkodzenia elementu (1)
1) element podstawowy (1) nie uszkodzi się do chwili t :
t
e
P
1
2) element podstawowy (1) uszkodzi się w pewnej chwili
t
, element rezerwowy (2) nie uszkodzi się do chwili
t :
d
t
R
R
f
P
t
)
,
(
)
(
)
(
0
2
2
1
2
e
f
)
(
1
0
)
(
2
e
R
)
(
2
)
,
(
t
e
t
R
t
t
e
e
P
0
1
0
2
1
2
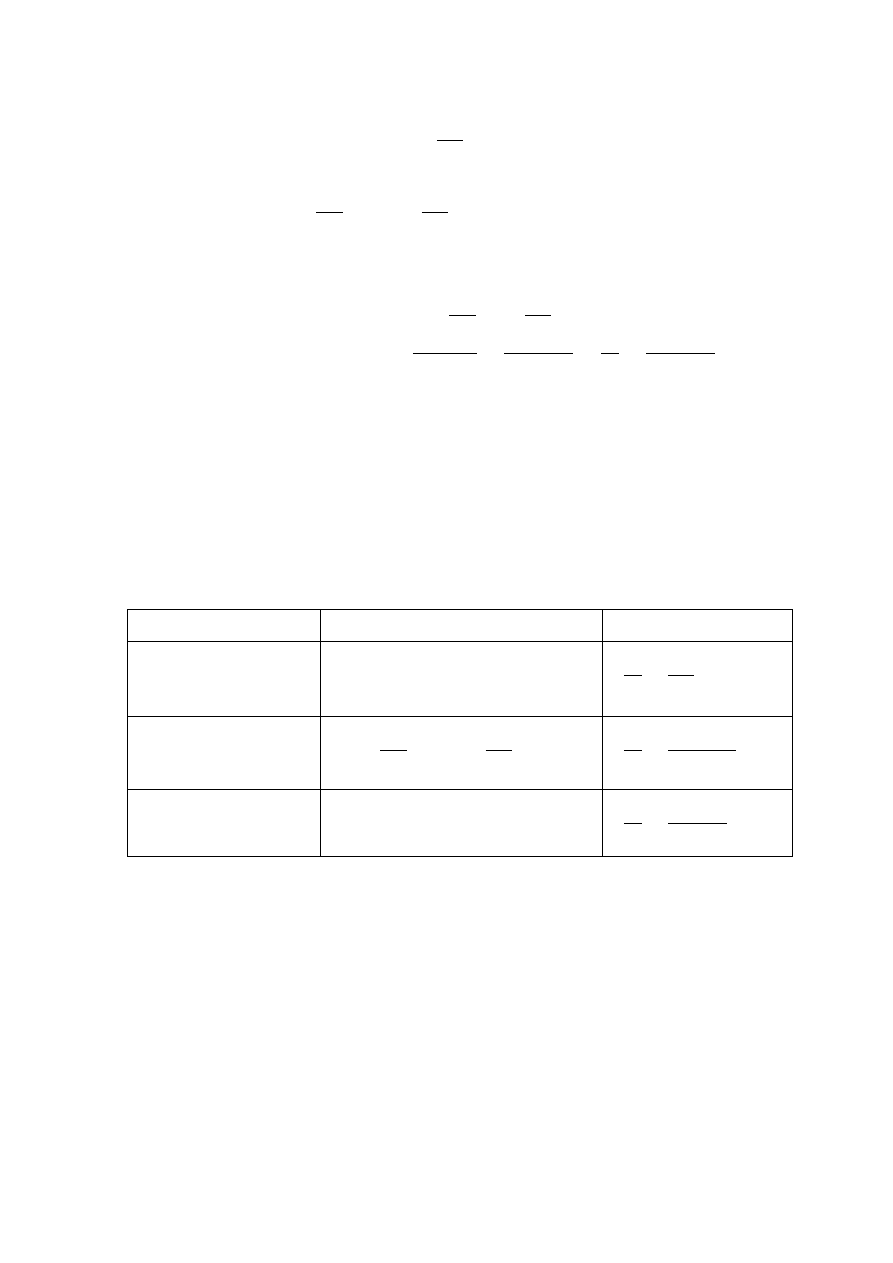
)
1
(
)
(
0
0
2
1
t
t
t
u
e
e
e
P
P
t
R
t
t
e
e
)
(
0
0
0
)
1
(
0
0
0
0
0
1
1
1
)
(
)
(
dt
t
R
T
E
u
u
Porównanie rodzajów rezerwowania dla układów z jednym
elementem rezerwowym
rezerwa
)
(t
R
)
(T
E
nieobciążona
t
e
t
)
1
(
1
1
częściowo
obciążona
t
t
e
e
)
(
0
0
0
)
1
(
0
1
1
obciążona
)
2
(
t
t
e
e
1
1
niech
b
t
t
R
t
R
t
R
m
1
)
(
.......
)
(
)
(
2
1
2
)
(
.......
)
(
)
(
2
1
b
T
E
T
E
T
E
m
m
u
b
t
t
R
1
)
(
b
m
m
b
m
b
m
b
u
u
m
t
b
b
dt
t
b
dt
dt
t
R
T
E
0
1
0
0
0
1
1
1
)
(
)
(
1
1
m
m
b
m
b
b
m
1
2
3
4
5
)
(
u
T
E
1/2 b 2/3 b 3/4 b 4/5 b 5/6 b
b
1
2
m

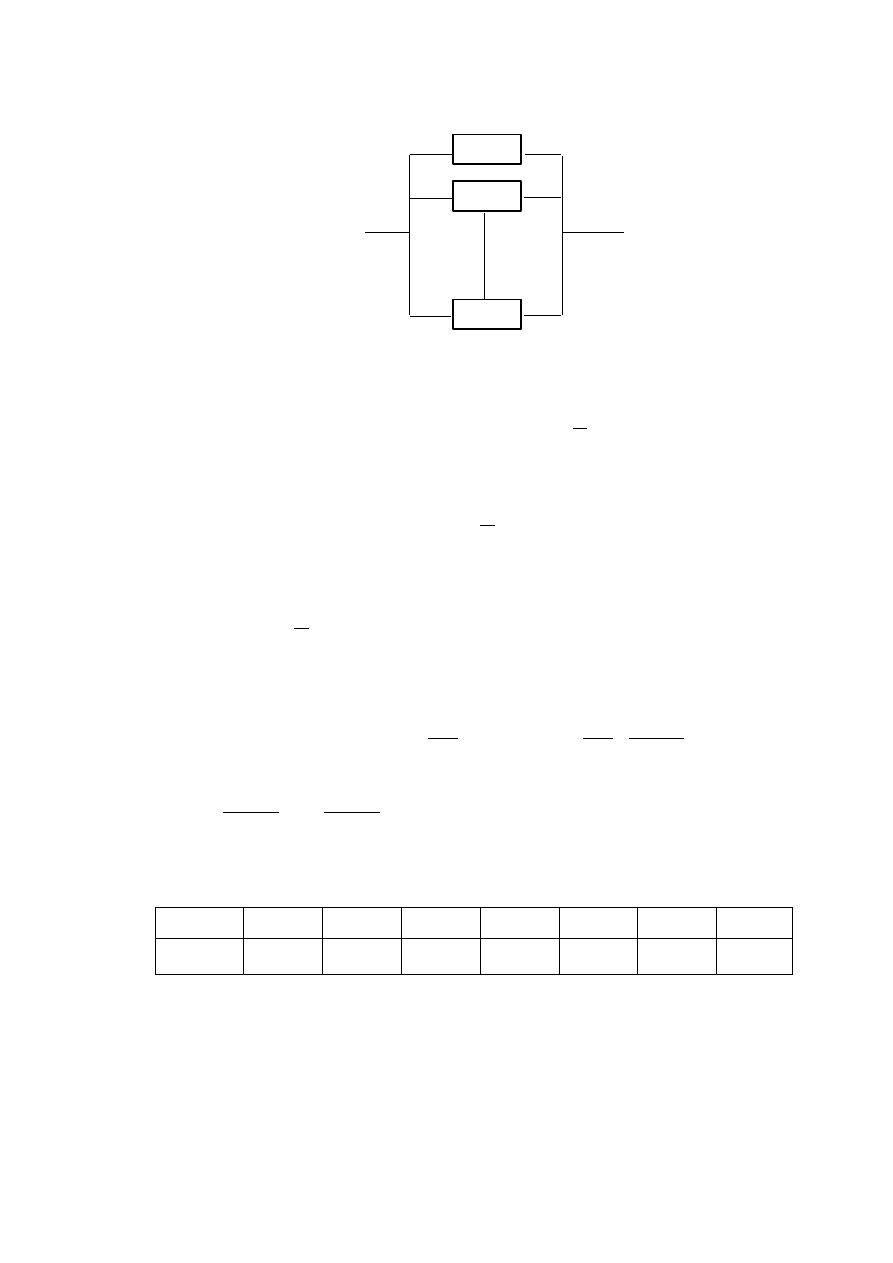
Zależne uszkodzenia elementów
2
1
gdy jeden z elementów uszkodzi się to intensywność
uszkodzeń elementu pozostającego w stanie zdatności wzrasta
do
1
1) ani jeden element nie uszkodzi się do chwili t :
t
e
P
2
1
2) element (1) uszkodzi się w pewnej chwili
t
,
element (2) nie uszkodzi się do chwili t :
d
t
R
R
f
P
t
)
,
(
)
(
)
(
0
2
e
f
)
(
,
e
R )
(
,
)
(
1
)
,
(
t
e
t
R
d
e
e
d
e
e
e
P
t
t
t
t
)
2
(
0
)
(
0
2
1
1
1
1
2
2
)
2
(
1
0
1
)
2
(
1
1
1
1
t
t
t
t
e
e
e
e
1
2

3) element (2) uszkodzi się w pewnej chwili
t
,
element (1) nie uszkodzi się do chwili t :
2
3
P
P
2
1
3
2
1
2
)
(
P
P
P
P
P
t
R
u
1
2
2
)
(
)
2
(
1
2
1
1
t
t
t
u
e
e
e
t
R
t
t
t
e
e
e
1
2
2
2
2
1
2
1
2
t
t
e
e
1
2
2
2
1
2
1
1
dt
e
2
2
e
2
dt
)
t
(
R
)
T
(
E
0
t
1
0
t
2
1
1
0
u
u
1
1
1
2
2
1
1
1
1
1
2
)
2
(
4
1
2
2
2
1
2
1
1
1
1
2
1
2
2

1
)
(
)
(
2
1
t
P
t
P
1
)
(
)
(
2
1
t
t
P
t
t
P
jeżeli
:
.
)
(
const
t
;
.
)
(
const
t
)
(
1
1
T
E
;
)
(
1
2
T
E
t
t
P
t
t
P
t
t
P
)
(
1
)
(
)
(
2
1
1
)
(
)
(
)
(
)
(
2
1
1
1
t
P
t
P
t
t
P
t
t
P
)
(
)
(
)
(
'
2
1
1
t
P
t
P
t
P
,
1
)
0
(
1
P
t
t
t+
t
0
t
1
2
(t)
(t)

)
(
)
(
)
(
1
t
k
e
t
P
g
t
0
t
;
1
1
P
t
;
g
k
P
1
e
z
z
nz
z
g
T
T
T
T
T
T
E
T
E
T
E
T
E
T
E
T
E
k
)
(
)
(
)
(
)
(
1
)
(
1
)
(
1
1
2
1
2
1
2
0
t
1
0
P
1
(t)

e
T
-
całkowity czas eksploatacji
u
T - całkowity czas użytkowania,
u
T
i
i
o
T
- całkowity czas obsługiwania,
o
T
=
i
i
i liczba przejść obiektu do danego stanu
W dwustanowym modelu procesu eksploatacji:
u
z
T
T
,
o
nz
T
T
g
k
nz
z
z
e
z
T
T
T
T
T
o
u
u
T
T
T

W trójstanowym modelu procesu eksploatacji
ou
T - całkowity czas oczekiwania na użytkowanie,
i
i
ou
T
oo
T - całkowity czas oczekiwania na obsługiwanie,
i
i
oo
T
'
Przypadek 1 Przypadek 2
o
ou
u
e
T
T
T
T
oo
o
u
e
T
T
T
T
ou
u
z
T
T
T
u
z
T
T
o
nz
T
T
oo
o
nz
T
T
T
e
z
g
T
T
k
o
ou
u
ou
u
g
T
T
T
T
T
k
oo
o
u
u
g
T
T
T
T
k
z
u
w
T
T
k
w
k
- wskaźnik wykorzystania obiektu zdatnego
ou
u
u
w
T
T
T
k
<1
1
u
u
w
T
T
k
nz
o
e
T
T
k
e
k
- wskaźnik efektywności obsługiwania obiektu niezdatnego
1
o
o
e
T
T
k
oo
o
o
e
T
T
T
k
<1

W czterostanowym modelu procesu eksploatacji
:
oo
o
ou
u
e
T
T
T
T
T
oo
o
ou
u
ou
u
g
T
T
T
T
T
T
k
jeżeli:
ou
u
u
w
T
T
T
k
;
oo
o
o
e
T
T
T
k
o
w
u
e
u
e
g
T
k
T
k
T
k
k
e
e
T
L
-
intensywność eksploatacji
u
z
T
L
-
intensywność użytkowania
e
u
V
T
L
-
prędkość eksploatacyjna
t
j
V
T
L
-
prędkość techniczna
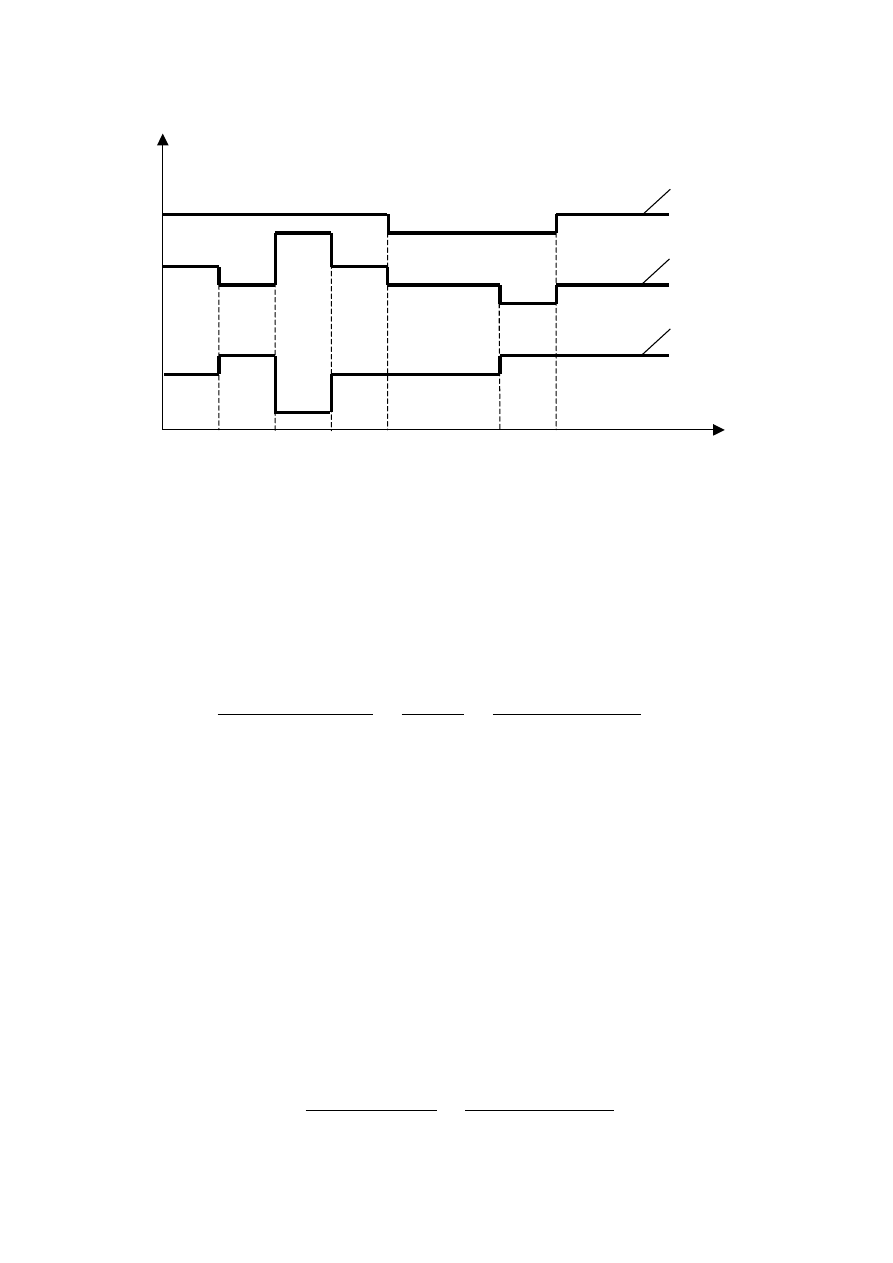
T
j
T
p
T
u
T
ou
T
e
T
o
T
oo
T
z
T
nz
)
(t
N
u
- liczba urządzeń użytkowanych w chwili t
)
(t
N
o
- liczba urządzeń obsługiwanych w chwili t
)
(
)
(
t
N
t
N
z
e
)
(t
N
nz
;
)
(
)
(
t
N
t
N
u
z
;
)
(
)
(
t
N
t
N
o
nz
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
t
N
t
N
t
N
t
N
t
N
t
N
t
N
t
N
t
k
o
u
u
e
u
nz
z
z
g
)
(t
k
g
- chwilowy wskaźnik gotowości technicznej
W przypadku jednorodnej grupy urządzeń eksploatowanych
w ustalonych warunkach, można potraktować historię
eksploatacji grupy w krótkim przedziale jako ekwiwalentną
historii eksploatacji pojedynczego urządzenia tej grupy, ale
w dłuższym przedziale.
)
(
)
(
)
(
)
(
)
(
)
(
t
N
t
N
t
N
t
T
t
T
t
T
o
u
u
o
u
u
N(t)
N
e
(t)
N
u
(t)
N
o
(t)
t

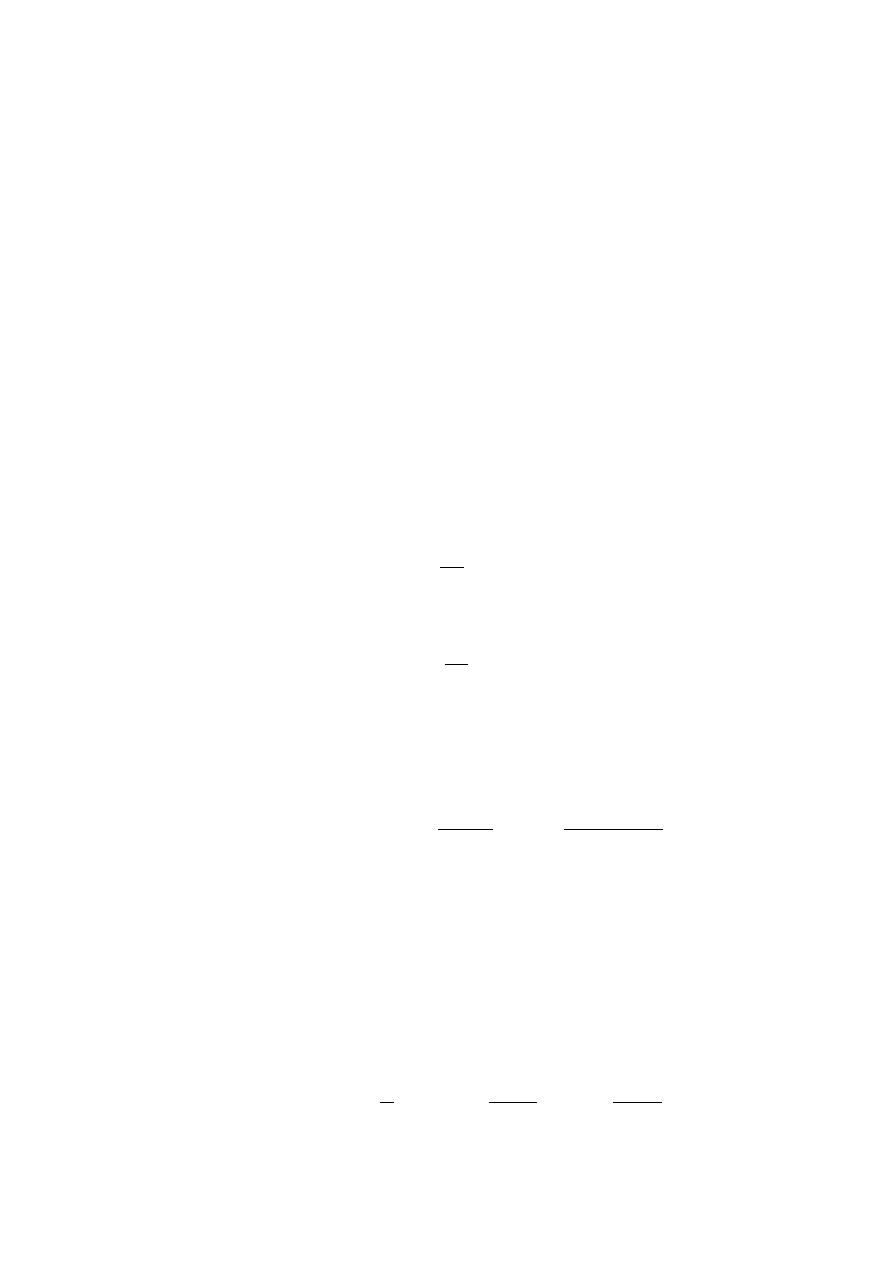
Funkcja wiodąca (skumulowana intensywność uszkodzeń)
dx
x
t
t
0
)
(
)
(
Można ją interpretować jako miarę wyczerpywania się
„zapasu niezawodności obiektu”.
Ponieważ
t
dx
x
e
t
R
0
)
(
)
(
to
)
(
)
(
t
e
t
R
)
(
1
)
(
t
e
t
F
)
(
)
(
t
e
dt
d
t
f
)
(
)
(
t
dt
d
t
)
(
1
ln
)
(
ln
)
(
t
F
t
R
t
t
x
t
t
du
u
f
dx
x
f
dx
x
R
x
f
dx
x
t
0
0
0
)
(
)
(
)
(
)
(
)
(
)
(
dla rozkładu wykładniczego:
t
t
)
(
dla rozkładu jednostajnego w przedziale od 0 do b:
t
b
b
b
t
b
b
t
t
ln
ln
1
ln
)
(

Oczekiwany pozostały czas zdatności
)
/
(
)
(
t
T
t
T
E
t
r
jest to warunkowa wartość oczekiwana pozostałego czasu
zdatności
t
T
pod warunkiem, że w chwili t obiekt jest
zdatny.
Warunkowa dystrybuanta pozostałego czasu zdatności
wynosi:
)
(
)
(
)
(
)
(
)
(
)
/
(
)
,
(
t
R
t
F
x
t
F
t
T
P
x
t
T
t
P
t
T
x
t
T
P
x
t
F
)
(
)
(
)
,
(
)
,
(
t
R
x
t
f
x
t
F
x
x
t
f
0
0
)
(
)
(
1
)
,
(
)
/
(
)
(
dx
x
t
f
x
t
R
dx
x
t
f
x
t
T
t
T
E
t
r
podstawiamy:
z
x
t
stąd:
t
z
x
;
dz
dx
t
dz
z
f
t
z
t
R
t
r
)
(
)
(
)
(
1
)
(
dz
du
t
z
u
0
t
t+x
t

)
(
)
(
z
R
v
dz
z
f
dv
t
t
t
dz
z
R
t
R
dz
z
R
z
R
t
z
t
R
t
r
)
(
)
(
1
)
(
)
(
)
(
)
(
1
)
(
t
dx
x
R
t
R
t
r
)
(
)
(
1
)
(
)
(
)
(
)
0
(
1
)
0
(
0
T
E
dx
x
R
R
r
Możemy za pomocą oczekiwanego pozostałego czasu
zdatności
)
(t
r
wyrazić poznane uprzednio charakterystyki
funkcyjne niezawodności:
dt
t
dr
t
r
t
)
(
1
)
(
1
)
(
)
(
)
0
(
ln
)
(
)
(
0
t
r
r
x
r
dx
t
t
t
x
r
dx
t
r
r
t
R
0
)
(
exp
)
(
)
0
(
)
(
t
x
r
dx
t
r
r
t
F
0
)
(
exp
)
(
)
0
(
1
)
(
t
x
r
dx
dt
t
dr
t
r
r
t
f
0
2
)
(
exp
)
(
1
)
(
)
0
(
)
(
Dla odpowiednio dużych wartości argumentu t wartość
funkcji
)
(t
r
ulega niewielkim zmianom i dąży do:
)
(
1
lim
)
(
)
(
lim
)
(
)
(
lim
)
(
lim
t
t
f
t
R
t
R
dx
x
R
t
r
t
t
t
t
t
Dla rozkładu wykładniczego:
dx
e
e
dx
x
R
t
R
t
r
t
x
t
t
1
)
(
)
(
1
)
(
1
1
1
t
t
t
x
t
e
e
e
e
Dla rozkładu jednostajnego w przedziale od 0 do b:
b
t
b
t
b
x
x
t
b
b
dx
b
x
b
t
t
r
2
)
1
(
1
1
)
(
2
)
2
2
2
2
(
)
2
(
)
2
(
2
2
2
2
2
b
t
bt
b
b
b
t
b
b
b
t
t
b
b
b
t
b
b
2
)
(
2
)
(
)
2
(
2
1
2
2
2
t
b
t
b
t
b
t
bt
b
b
t
b
b

Podobnie możemy wyznaczyć oczekiwany czas zdatności
obiektu jeżeli wiadomo, że uszkodził się do chwili t :
)
/
(
t
T
T
E
)
(
)
(
)
(
)
(
)
/
(
)
,
(
t
F
x
F
t
T
P
x
T
P
t
T
x
T
P
x
t
F
)
(
)
(
)
,
(
)
,
(
t
F
x
f
x
t
F
x
x
t
f
t
t
dx
x
f
x
t
F
dx
x
t
f
x
t
T
T
E
0
0
)
(
)
(
1
)
,
(
)
/
(
t
t
t
t
dx
x
R
t
tR
dx
x
R
x
R
x
dx
x
f
x
0
0
0
0
)
(
)
(
)
(
)
(
)
(
t
t
tR
dx
x
R
t
F
t
T
T
E
0
)
(
)
(
)
(
1
)
/
(
)
(
)
(
)
(
)
/
(
)
0
(
t
R
t
r
t
t
F
t
T
T
E
r
t
t
t
R
t
r
dx
x
R
t
R
t
r
t
R
t
t
tR
dx
x
R
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
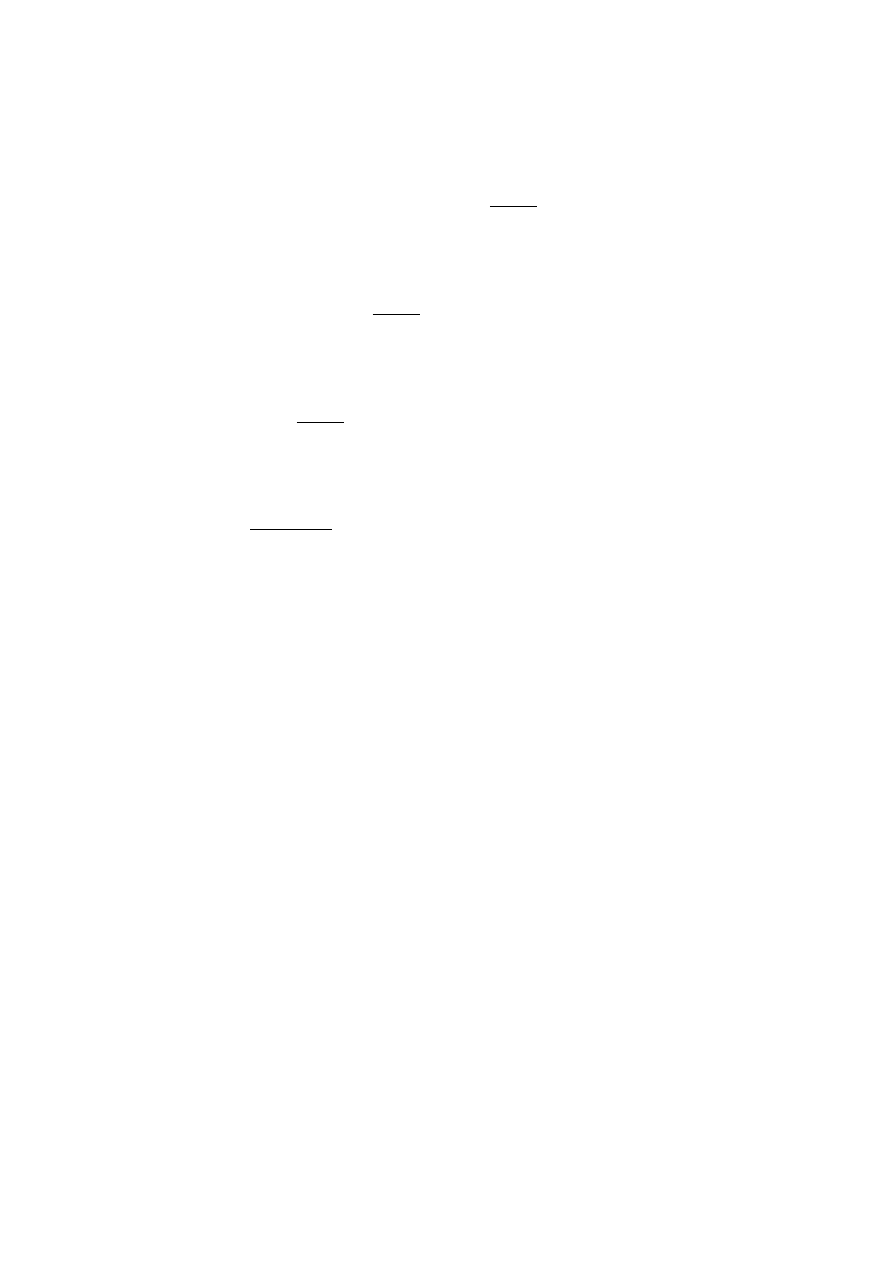
inaczej:
t
dx
x
R
t
R
dx
x
R
t
r
r
)
(
)
(
1
)
(
)
(
)
0
(
0
t
t
t
dx
x
R
t
R
dx
x
R
dx
x
R
)
(
)
(
1
)
(
)
(
0
t
t
dx
x
R
t
R
dx
x
R
0
)
(
)
(
1
1
)
(
t
t
t
t
r
t
F
dx
x
R
dx
x
R
t
R
t
R
dx
x
R
0
0
)
(
)
(
)
(
)
(
)
(
1
)
(
)
(
t
t
t
R
t
r
dx
x
R
t
r
t
F
t
r
dx
x
R
r
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
0
(
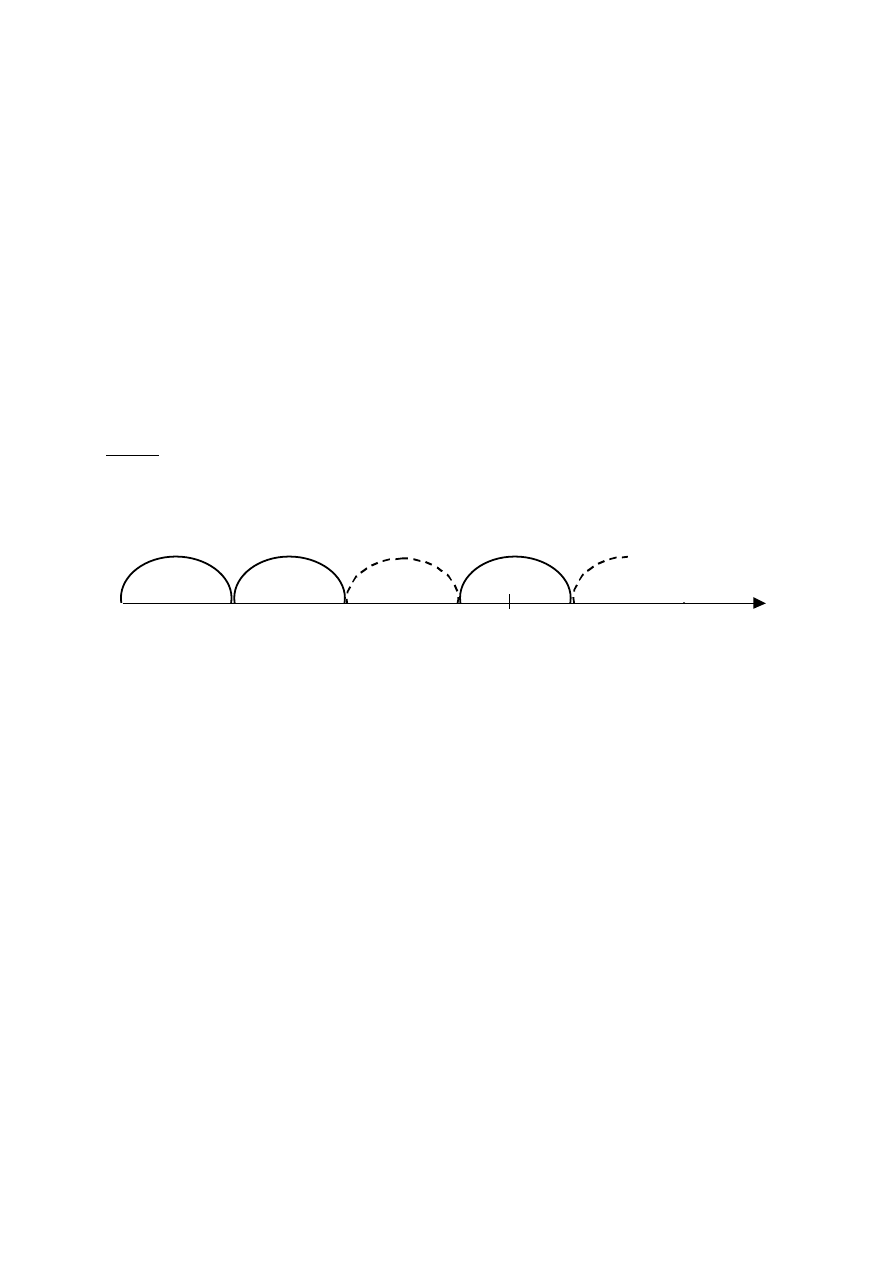
Niezawodność obiektów naprawialnych
(odnawialnych)
Rozpatrzmy dwa przypadki:
1) czas naprawy (odnowy) jest bardzo mały w stosunku do
czasu życia elementu. Mówimy wówczas, że odnowa jest
natychmiastowa (czas jej trwania
0
)
2) czas naprawy (odnowy) posiada pewną skończoną
wartość i nie jest pomijalny.
ad. 1.
Chwile uszkodzeń (odnowień) obiektu są następujące:
1
1
T
t
2
1
2
T
T
t
3
2
1
3
T
T
T
t
...............................
n
n
T
T
T
t
........
2
1
1
2
1
1
.........
n
n
n
T
T
T
T
t
......................................................
Chwile uszkodzeń (odnowień) przedstawiają strumień losowy,
który nazywamy strumieniem odnowy.
T
1
T
2
T
n+1
t
1
t
2
t
n
t
n+1
0
t
t

Zakładamy, że:
1) proces taki powtarza się nieograniczenie,
2)
.....
,
,
2
1
T
T
są zmiennymi losowymi niezależnymi o takim
samym rozkładzie prawdopodobieństwa określonym
dystrybuantą
)
(
)
(
t
T
P
t
F
n
,
)
(T
E
i
)
(
2
T
D
dla
wszystkich
n
T są jednakowe i wynoszą:
dt
t
F
T
E
0
)
(
1
)
(
,
2
0
2
)
(
)
(
1
2
)
(
T
E
dt
t
F
t
T
D
Niech
)
(t
N
będzie zmienną losową określającą liczbę
uszkodzeń (odnowień) powstałych do chwili t .
Zdarzenie
n
t
N
)
(
jest równoważne zdarzeniu
t
t
n
)
(
)
......
(
)
(
)
(
2
1
t
F
t
T
T
T
P
t
t
P
n
t
N
P
n
n
n
Dystrybuantę
)
(t
F
n
można wyznaczyć dla dowolnego
n
:
n=2
t
dF
t
T
P
T
t
T
P
t
T
T
P
t
F
0
1
2
1
2
1
2
)
(
)
(
)
(
)
(
)
(
t
dF
t
F
0
1
)
(
)
(
n=3
)
(
)
(
)
(
3
2
1
3
2
1
3
T
t
T
T
P
t
T
T
T
P
t
F
t
t
dF
t
F
dF
t
T
T
P
0
2
0
2
1
)
(
)
(
)
(
)
(

uogólniając
t
n
n
dF
t
F
t
F
0
1
)
(
)
(
)
(
,.........
)
(
)
(
1
t
F
t
F
Wyznaczamy
n
t
N
P
)
(
P
1
)
(
)
(
)
(
n
t
N
n
t
N
P
n
t
N
zdarzenie
n
t
N
)
(
jest równoważne
t
t
n
zdarzenie
1
)
(
n
t
N
jest równoważne
t
t
n
1
)
(
)
(
)
(
)
(
1
1
t
t
t
t
P
t
t
P
t
t
P
n
t
N
P
n
n
n
n
)
(t
F
n
+
)
(
1
1
t
F
n
1
)
(
)
(
)
(
1
t
F
t
F
n
t
N
P
n
n
Nie wystarczy wiedzieć jakie jest prawdopodobieństwo
wystąpienia
n
uszkodzeń (odnowień). Równie ważną
informacją jest oczekiwana liczba tych zdarzeń
)
(t
N
E
.
Wielkość ta jest funkcją czasu określoną dla
0
t
oznaczaną
)
(t
H
i nazywaną funkcją odnowy (naprawy).
1
1
1
)
(
)
(
)
(
)
(
)
(
n
n
n
n
t
F
t
F
n
n
t
N
P
n
t
N
E
t
H
)
(
)
1
(
)
(
)
(
)
(
2
1
1
1
1
t
F
n
t
F
n
t
F
n
t
F
n
n
n
n
n
n
n
n
n
1
2
2
2
1
)
(
)
(
)
(
)
(
)
(
n
n
n
n
n
n
n
n
t
F
t
F
t
F
n
t
F
n
t
F

)
(
)
(
1
t
F
t
H
n
n
W praktyce często posługujemy się pochodna funkcji odnowy
i nazywamy ja gęstością odnowy.
1
1
1
)
(
)
(
)
(
)
(
)
(
n
n
n
n
n
n
t
f
dt
t
dF
t
F
dt
d
dt
t
dH
t
h
Funkcję odnowy można wyznaczyć inaczej:
1
1
1
1
)
(
)
(
)
(
)
(
n
n
n
n
t
F
t
F
t
F
t
H
ale
)
(
)
(
1
t
F
t
F
i
)
(
)
(
)
(
0
1
dF
t
F
t
F
t
n
n
1
0
1 0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
n
n
t
n
t
n
dF
t
F
t
F
dF
t
F
t
F
t
H
)
(
)
(
1
)
(
)
(
)
(
0
0
dF
t
H
dF
t
H
t
F
t
t
)
(t
H
spełnia powyższe równanie całkowe. Równanie to nosi
nazwę równania odnowy (odnowienia).
Funkcję
)
(t
H
wykorzystuje się do wyznaczenia oczekiwanej
liczby uszkodzeń w dowolnym przedziale czasu
2
1
t
,
t
,
wynosi ona
)
(
)
(
1
2
t
H
t
H
.
Przy pomocy
)
(t
H
można wyznaczyć wariancję liczby
uszkodzeń (odnów) w przedziale
t
,
0
t
t
H
t
H
dF
t
H
t
N
D
0
2
2
)
(
)
(
)
(
)
(
2
)
(

Badając proces odnowy przy
t
korzysta się z
następujących twierdzeń:
Twierdzenie 1 (elementarne twierdzenie odnowy).
Jeżeli czas życia obiektu jest zmienną losową o dystrybuancie
)
(t
F
i skończonej wartości oczekiwanej
)
(T
E
, to
)
(
1
)
(
lim
T
E
t
t
H
t
Oznacza to, że oczekiwana liczba odnowień w jednostce czasu
dąży do odwrotności średniego czasu życia obiektu, czyli
średni odstęp miedzy uszkodzeniami jest równy średniemu
czasowi życia obiektu.
Twierdzenie 2 (Blackwella)
Jeśli czas życia obiektu jest zmienną losowa typu ciągłego
o skończonej wartości oczekiwanej
)
(T
E
to dla
0
zachodzi:
)
(
)
(
)
(
lim
T
E
t
H
t
H
t
Oznacza to, ze po upływie długiego czasu liczba uszkodzeń
w przedziale o długości
zależy tylko od długości przedziału
i średniego czasu życia obiektu.

Twierdzenie 3 (Smitha)
Jeżeli czas życia obiektu jest zmienną losową o skończonej
wartości oczekiwanej
)
(T
E
oraz wariancji
)
(
2
T
D
, to
2
1
)
(
2
)
(
)
(
)
(
lim
2
2
T
E
T
D
T
E
t
t
H
t
stąd wzór przybliżony:
2
1
)
T
(
E
2
)
T
(
D
)
T
(
E
t
)
t
(
H
2
2
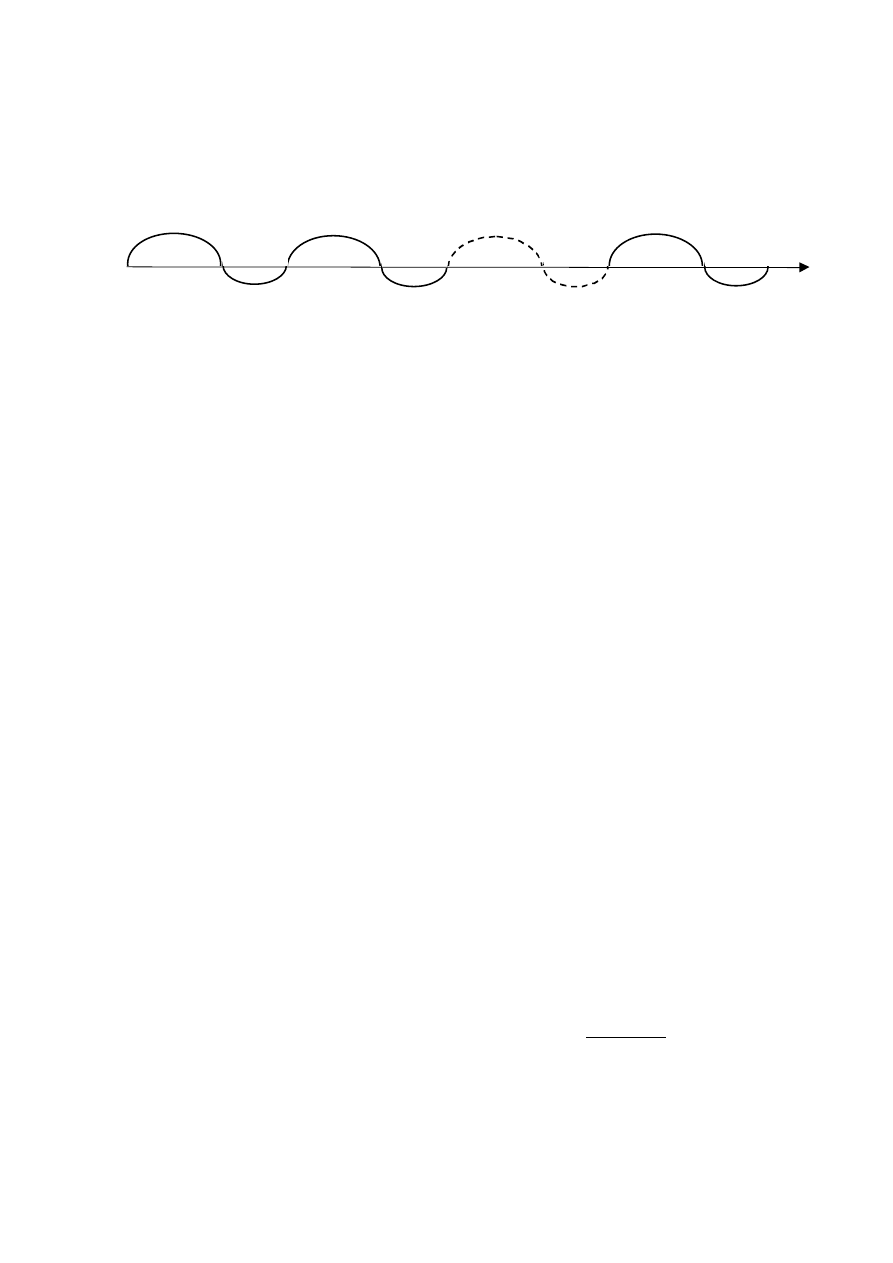
Proces odnowy o skończonym czasie odnowy (naprawy)
Zmienne
,
,
2
1
T
T
......oraz
,
,
2
1
U
U
..... są zmiennymi losowymi
niezależnymi o rozkładach odpowiednio:
)
(
)
(
t
T
P
t
F
n
)
(
)
(
t
U
P
t
G
n
Utwórzmy zmienną losową
1
1
n
n
n
U
T
T
, gdzie:
n
n
T
T
T
T
.....
2
1
1
,
n
n
U
U
U
U
.....
2
1
1
t
n
n
n
dF
t
F
t
F
t
T
P
0
1
1
)
(
)
(
)
(
)
(
,
)
(
)
(
1
t
F
t
F
t
n
n
n
dG
t
G
t
G
t
U
P
0
1
1
)
(
)
(
)
(
)
(
,
)
(
)
(
1
t
G
t
G
t
n
n
n
n
dG
t
F
t
t
T
P
0
)
(
)
(
)
(
)
(
1
1 0
)
(
)
(
)
(
)
(
n
n
t
n
n
n
dG
t
F
t
t
H
1
)
(
)
(
n
n
t
t
h
, gdzie:
dt
t
d
t
n
n
)
(
)
(
T
1
T
2
T
n
U
1
U
2
U
n
0
t

WYMIANA W USTALONYM WIEKU
)
(
)
(
)
(
nw
t
R
w
R
t
P
n
w
;
w
n
t
nw
)
1
(
gdzie:
)
(t
P
w
- prawdopodobieństwo, że obiekt wymieniany
profilaktycznie w ustalonym czasie (co stały okres
w) nie uszkodzi się do chwili t,
)
(w
R
n
- prawdopodobieństwo, że obiekt nie uszkodzi się
w kolejnych przedziałach czasu o długości w,
)
(
nw
t
R
- prawdopodobieństwo, że obiekt nie uszkodzi
się
w przedziale
)
,
(
t
nw
;
w
n
t
)
1
(
0
0
)
(
)
(
)
(
)
(
dt
nw
t
R
w
R
dt
t
P
T
E
n
w
w
)
(
w
T
E
- oczekiwany czas do uszkodzenia obiektu;
w
w
w
w
w
n
dt
w
t
R
w
R
dt
w
t
R
w
R
dt
t
R
dt
nw
t
R
w
R
2
3
2
2
0
0
)
2
(
)
(
)
(
)
(
)
(
)
(
)
(
0
)
1
(
)
(
)
(
)
(
)
(
..........
n
w
n
nw
n
nw
n
dt
nw
t
R
w
R
dt
nw
t
R
w
R
podstawiamy: t - nw = x
dt = dx
dla t = nw→x = 0
0
nw
w
(n+1)w
2w
t
t
3w

t = (n+1)w→x = w
0
0 0
)
1
(
)
(
)
(
)
(
)
(
n
n
w
n
n
w
n
nw
dx
x
R
w
R
dt
nw
t
R
w
R
)
(
)
(
)
(
)
(
0
0
0
0
w
R
dx
x
R
dx
x
R
w
R
w
w
n
n
n
n
w
w
R
dx
x
R
0
)
(
1
1
)
(
gdyż:
x
x
n
n
1
1
0
dla x<1
w
w
dx
x
R
w
R
T
E
0
)
(
)
(
1
1
)
(

)
(
)
(
)
(
)
(
u
T
E
w
F
b
w
R
a
w
C
C(w) – jednostkowy koszt utrzymania obiektu
a – koszt wymiany profilaktycznej
b – koszt naprawy
Zakładamy, że a < b
E(T
u
) – oczekiwany czas użytkowania obiektu (do
uszkodzenia
lub wymiany)
)
(
)
/
(
)
(
)
(
w
F
w
T
T
E
w
R
w
T
E
u
w
w
dx
x
f
x
w
F
dx
w
F
x
f
x
w
T
T
E
0
0
)
(
)
(
1
)
(
)
(
)
/
(
w
w
u
dx
x
R
dx
x
f
x
w
R
w
T
E
0
0
)
(
)
(
)
(
)
(
w
w
dx
x
R
b
w
R
b
a
dx
x
R
w
F
b
w
R
a
w
C
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
)
(
)
(
)
(
)
(
)
(
)
(
'
)
(
)
(
2
0
0
w
w
dx
x
R
w
R
b
w
R
b
a
dx
x
R
w
R
b
a
dw
w
dC
)
(
)
(
)
(
)
(
)
(
'
)
(
0
w
R
b
w
R
b
a
dx
x
R
w
R
b
a
w
w
b
w
R
b
a
dx
x
R
w
R
w
R
a
b
0
)
(
)
(
)
(
)
(
)
(
'
)
(

w
a
b
b
w
R
dx
x
R
w
0
)
(
)
(
)
(
w
a
b
b
w
R
dx
x
R
w
0
)
(
)
(
)
(
a
b
b
w
R
dx
x
R
dx
x
R
w
w
)
(
)
(
)
(
)
(
0

1. Rozpatrzmy obiekt techniczny składający się z n
elementów składowych.
2. Załóżmy, że elementy są jednakowe w sensie ich
niezawodności
3. Struktura niezawodnościowa obiektu jest szeregowa.
Funkcja niezawodności obiektu do chwili wykonania
naprawy
)
(
1
x
R
jest opisana zależnością:
n
e
x
R
x
R
1
gdzie:
)
(x
R
e
- funkcja niezawodności elementu
Jeżeli naprawa wykonana w chwili t polegała na wymianie k
spośród n elementów składowych to funkcja niezawodności
obiektu po naprawie
)
(
2
x
R
wynosi:
k
n
e
e
k
e
t
R
x
t
R
x
R
x
R
2

Z wzoru określającego
)
(
1
x
R
wynikają następujące
zależności:
n
e
x
R
x
R
1
1
,
n
k
k
e
x
R
x
R
1
n
k
k
n
e
x
t
R
x
t
R
1
1
n
k
k
n
e
t
R
t
R
1
1
Po podstawieniu do zależności wyrażającej
)
(
2
x
R
otrzymujemy:
n
k
n
k
t
R
x
t
R
x
R
x
R
1
1
1
1
2
Jeżeli stosunek
n
k
potraktujemy jako stopień odnowienia
obiektu (stopień naprawy), to:
1
1
1
1
2
t
R
x
t
R
x
R
x
R

Logarytmując i następnie różniczkując stronami otrzymujemy:
x
t
R
dx
d
α)
(1
x
R
dx
d
α
x
R
dx
d
1
1
2
ln
ln
ln
i podstawiając
x
x
R
dx
d
)
(
ln
otrzymujemy zależność
wyrażająca związek między funkcjami intensywności
uszkodzeń
x
2
i
x
1
:
x
t
x
x
1
1
2
)
1
(
czyli
x
x
t
x
x
t
1
1
2
1
Można też współczynnik
przedstawić z wykorzystaniem
funkcji wiodących rozkładów
x
t
x
t
x
t
x
t
1
1
1
2
1
1
)
(
)
(
gdzie:
x
du
u
x
0
)
(
)
(
Wyszukiwarka
Podobne podstrony:
PET, PETy, wyklad - kolos 1, DRUK, Niezawodność typu wykładniczego
konspekt wykladu PET id 245738 Nieznany
PET notki do kolosa I na podstawie materiałów do wykładu
PET, 0 konspekt wykladu PET, Niezawodność typu wykładniczego
Wyklad PET zaliczewnie final 01 2012
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
geriatria p pokarmowy wyklad materialy
ostre stany w alergologii wyklad 2003
WYKŁAD VII
Wykład 1, WPŁYW ŻYWIENIA NA ZDROWIE W RÓŻNYCH ETAPACH ŻYCIA CZŁOWIEKA
Zaburzenia nerwicowe wyklad
Szkol Wykład do Or
więcej podobnych podstron