
mjr mgr inż. Robert CZAPLA
Katedra Płatowca i Silnika
Pok. 21
Tel. 51-77-31
GRAFIKA INŻYNIERSKA
I ZAPIS KONSTRUKCJI CAD CAM

Założenia i cele przedmiotu
W wyniku realizacji zajęć z przedmiotu student powinien:
znać:
metody geometrycznego odwzorowania obiektów
przestrzennych na płaszczyźnie
podstawowe zasady zapisu konstrukcji
ogólną wiedzę z dziedziny CAD/CAM/CAE
funkcje i możliwości systemów komputerowego wspomagania
projektowania, wytwarzania i analizy inżynierskiej
umieć:
dokonywać analizy przestrzennych własności figur
rozwiązywać zadania konstrukcyjne wymagające wyobraźni
przestrzennej
posługiwać się wybranym systemem CAD w zakresie
konstruowania środków technicznych

Literatura
Lewandowski Z., Geometria wykreślna, PWN, Warszawa 1989.
Paprocki K., Zasady zapisu konstrukcji, OWPW, Warszawa 2000.
Dobrzański T., Rysunek techniczny maszynowy, WNT, Warszawa
2002.
Kazimierczak G., SOLID EDGE. Komputerowe wspomaganie
projektowania, Helion 2004.
Bieliński A., Grafika inżynierska. Cześć I. Geometria wykreślna,
WAT, Warszawa
OTTO F., OTTO E., Podręcznik geometrii wykreślnej, PWN,
Warszawa 1994.
http://fluid.itcmp.pwr.wroc.pl/~eichler/program.html
(CAD w grafice inżynierskiej)

Forma zaliczenia przedmiotu
pozytywne oceny z kolokwiów na ćwiczeniach
pozytywna ocena z projektu

TEMAT 1:
ELEMENTY PRZESTRZENNE
I ZASADY ICH
ODWZOROWANIA

Elementy podstawowe przestrzeni
Punkty. Proste. Płaszczyzny.
Punkty oznaczamy dużymi literami alfabetu łacińskiego A,
B, C, ... lub cyframi arabskimi 1, 2, 3, ...
Proste - małymi literami alfabetu łacińskiego a, b, c, ...
Płaszczyzny – małymi literami alfabetu greckiego
,
,
, ...
Wszystkie elementy opisujemy na rysunkach pismem technicznym.
Obowiązuje poziomy kierunek pisma.
Elementy występujące na rysunkach w geometrii wykreślnej dzielimy
na 3 grupy: dane, pomocnicze, wynikowe.
Grubość linii danych wynosi zwykle 0,2-0,4 mm.
Linie wynikowe są w przybliżeniu dwa razy grubsze od linii
danych,
a linie pomocnicze dwa razy cieńsze.

Oznaczenia
Prosta m określona przez punkty A i B:
m=AB
Prosta m określona dwoma płaszczyznami
i :
m=
x
Odcinek o końcach A i B:
AB
Długość odcinka o końcach A i B:
(AB)
Płaszczyzna
określona punktami lub liniami: =ABC,
=mA, =mn
Punkt A określony liniami lub płaszczyznami: A=m x n , A=
m x
,
A=
x x
Prosta a równoległa / prostopadła do b:
a ba b
Prosta a nierównoległa / nieprostopadła do b: a b
a b

Podstawowe definicje
Wiązką prostych nazywamy zbiór prostych przechodzących
przez dany punkt W, zwany wierzchołkiem wiązki prostych.
Wiązką płaszczyzn nazywamy zbiór płaszczyzn przechodzących
przez dany punkt W, zwany wierzchołkiem wiązki płaszczyzn.
Pękiem płaszczyzn nazywamy zbiór płaszczyzn przechodzących
przez jedną prostą.
Pękiem prostych nazywamy zbiór prostych leżących na jednej
płaszczyźnie i przechodzących przez jeden punkt.
Układem płaskim nazywamy zbiór punktów i prostych leżących
na jednej płaszczyźnie.
Tworami geometrycznymi (figurami geometrycznymi) nazywamy
wszystkie zbiory utworzone z elementów podstawowych
przestrzeni i oznaczamy je dużymi literami alfabetu greckiego
,
,
, ... Przykłady figur: wielokąty, wielościany, linie krzywe,
powierzchnie.

Definicja i cel geometrii
wykreślnej
GEOMETRIA WYKREŚLNA to nauka o metodach odwzorowań,
które figurom w przestrzeni przyporządkowują odpowiedniki
na płaszczyźnie zwane obrazami w taki sposób, aby była
możliwość odtworzenia ich kształtu i położenia w przestrzeni.
Jest ona podstawą zapisu konstrukcji przy projektowaniu i
konstruowaniu środków technicznych.
Celem nauczania geometrii wykreślnej jest poprawne kształtowanie
wyobraźni przestrzennej oraz opanowanie podstawowych metod
wzajemnie jednoznacznego odwzorowania przestrzeni na
płaszczyznę.
Geometria wykreślna opiera się na geometrii elementarnej
(euklidesowej), którą dzielimy na planimetrię i stereometrię.
Rysunek techniczny – wywodzi się z geometrii wykreślnej; konwencja
graficznego przedstawiania maszyn, urządzeń, mechanizmów,
konstrukcji, itp., dostarczająca pełnej informacji o działaniu,
wykonaniu elementów oraz montażu przedstawianego obiektu.

Podstawowe metody odwzorowań w
geometrii
Rzut środkowy
Rzut równoległy
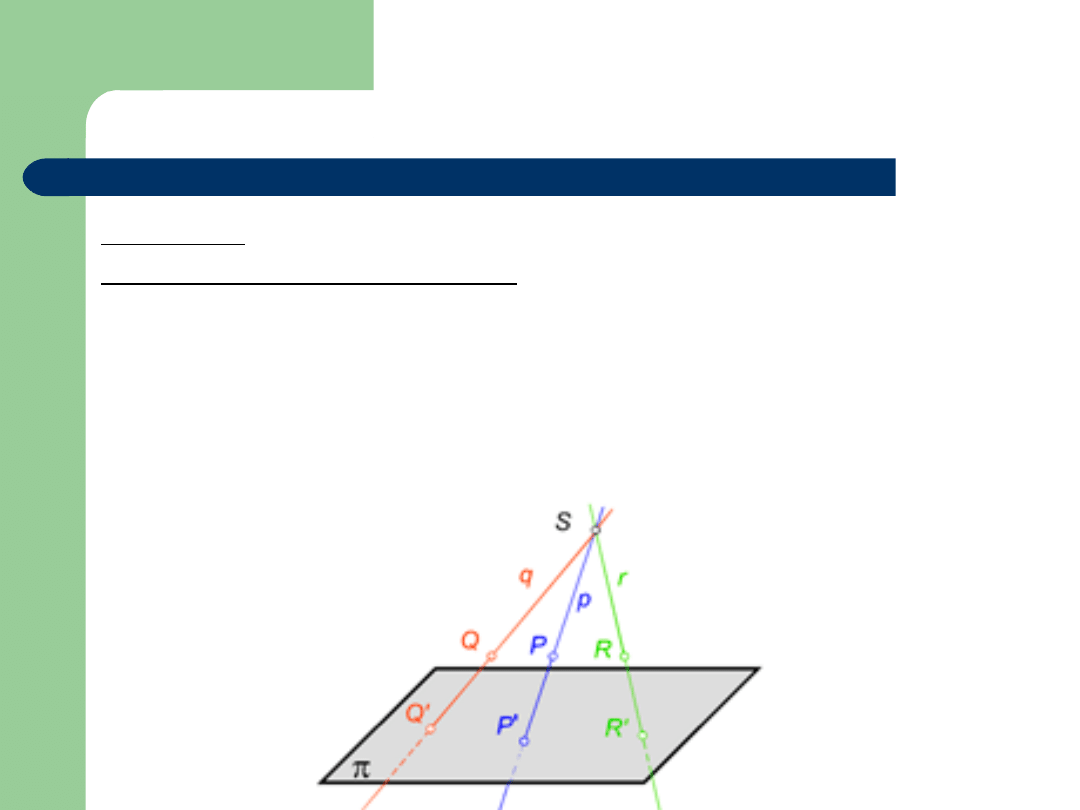
Rzut środkowy
Definicja 1
Rzutem środkowym punktu P na rzutnię
nazywamy
punkt P’, w którym prosta rzutująca p, przechodząca
przez punkty S i P, przebija rzutnię
.
gdzie:
rzutnia
– płaszczyzna, na którą rzutujemy;
punkt S – środek rzutowania;
proste rzutujące – wiązka prostych o wierzchołku S.
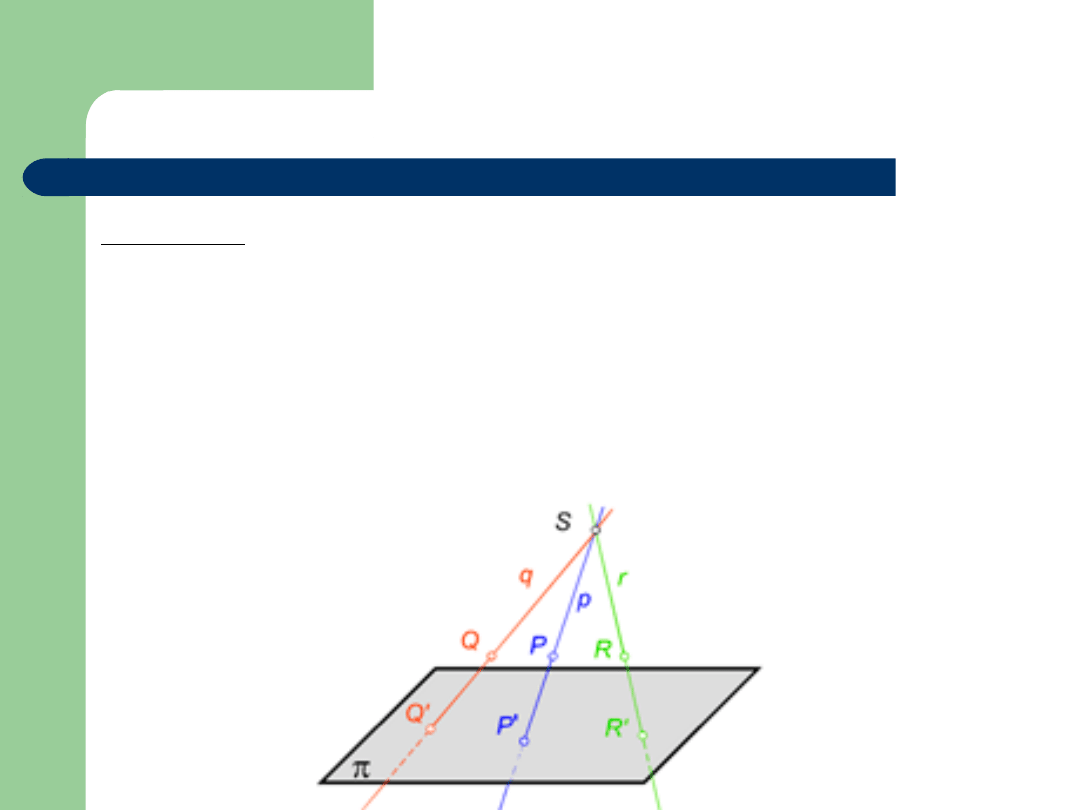
Rzut środkowy
Definicja 2
Każdemu punktowi P przestrzeni, nie leżącemu na
płaszczyźnie zniknienia
, przyporządkowany jest na
rzutni
jeden i tylko jeden punkt P’.
gdzie:
płaszczyzna zniknienia
- płaszczyzna równoległa do rzutni, do
której należy środek rzutowania.
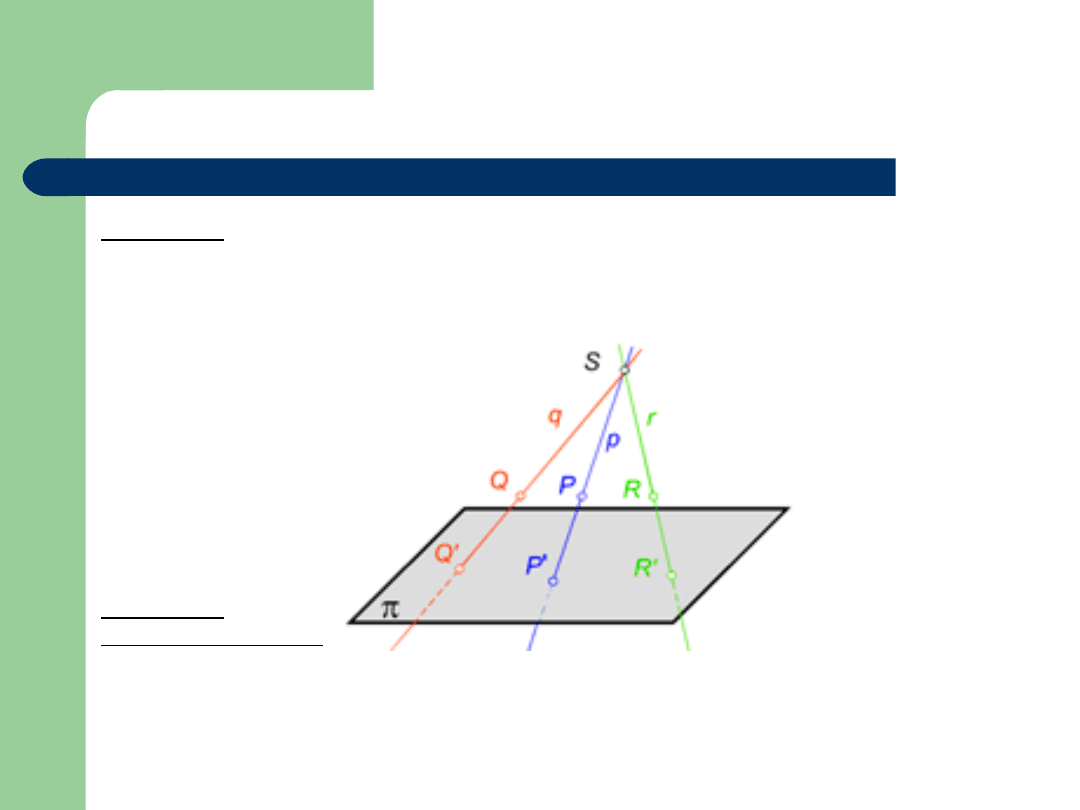
Rzut środkowy
Definicja 3
Każdy punkt P’ rzutni
może być uważany za rzut środkowy
dowolnego punktu P prostej rzutującej p przechodzącej przez punkt
P’.
Definicja 4
Rzutem środkowym figury
nazywamy figurę
’ będącą zbiorem
rzutów środkowych wszystkich tych punktów figury
, które nie
leżą na płaszczyźnie zniknienia
.

Przykłady rzutu środkowego
Aparat fotograficzny (matryca, środek optyczny
obiektywu, promienie światła)
Cień rzucany na ścianę od lampy
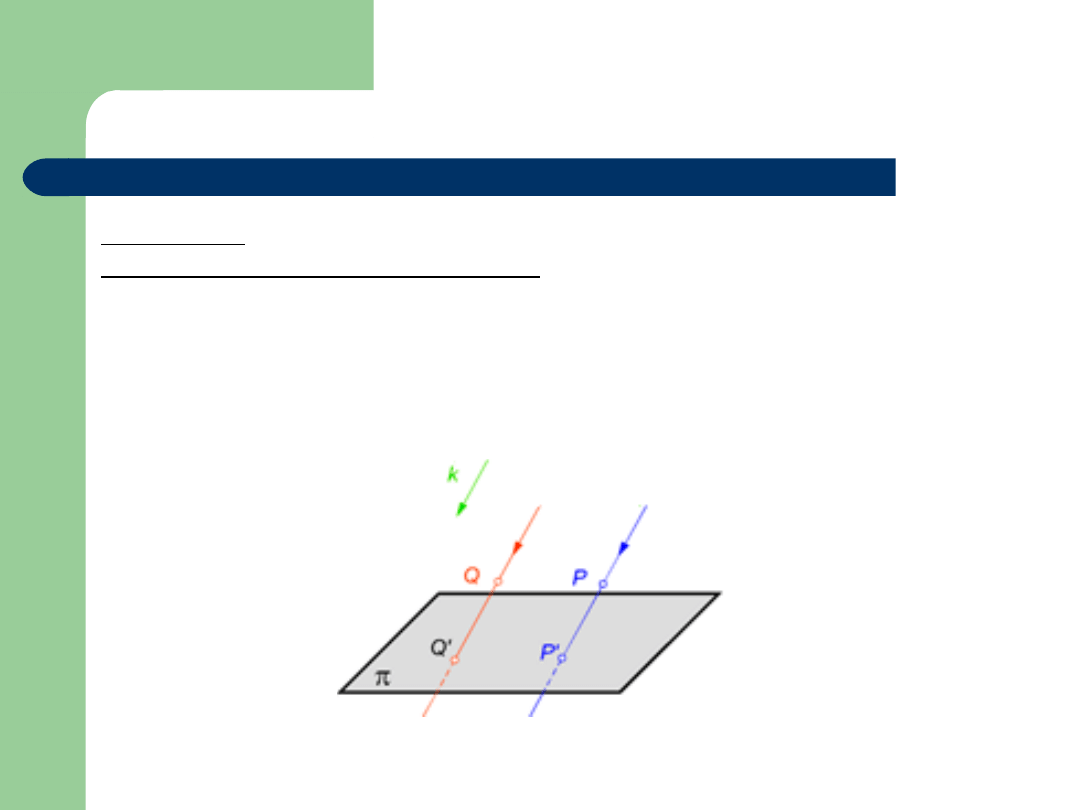
Rzut równoległy
Definicja 5
Rzutem równoległym punktu P na rzutnię
nazywamy
punkt P’, w którym prosta rzutująca p, przechodząca
przez punkt P, przebija rzutnię
.
gdzie:
proste rzutujące – zbiór prostych równoległych do kierunku
rzutowania k;
kierunek rzutowania k – dowolna prosta k nie leżąca na rzutni i
nie równoległa do niej.

Rzut równoległy
Definicja 6
Rzutem równoległym figury
nazywamy figurę
’, będącą zbiorem
rzutów równoległych wszystkich punktów figury
.
Definicja 7
Rzutem równoległym ukośnokątnym nazywamy rzut równoległy, w
którym kierunek rzutowania k nie jest prostopadły do rzutni
.
Definicja 8
Rzutem równoległym prostokątnym (rzutem prostokątnym)
nazywamy rzut równoległy, w którym kierunek rzutowania k jest
prostopadły do rzutni
.
Twierdzenie 1
Jeżeli przynajmniej jedna z dwu prostych prostopadłych jest
równoległa do rzutni (lub leży na rzutni), a druga nie jest prostą
rzutującą, to rzutem prostokątnym takich prostych, na te rzutnię,
są dwie proste prostopadłe
.

Niezmienniki rzutowania
równoległego
N1. współliniowość punktów (rzuty punktów leżących na prostej będą leżały na rzucie tej
prostej),
N2. przynależności elementów (jeżeli punkt leży np. na prostej, to rzut tego punktu leży
na rzucie tej prostej),
N3. równoległość prostych (rzutami prostych równoległych są proste równoległe lub
punkty),
N4. stosunek długości odcinków równoległych do siebie, nierównoległych do
kierunku rzutowania, (jeżeli długości odcinków równoległych pozostają w określonym
stosunku do siebie to długości ich rzutów pozostają w stosunku ident.)
N5. stosunek podziału odcinka (jeżeli punkt A dzieli odcinek w określonym stosunku, to
rzut punktu A' dzieli rzut tego odcinka w takim samym stosunku),
N6. długość odcinków równoległych do rzutni (długość odcinka równoległego do rzutni
jest taka sama jak długość rzutu tego odcinka),
N7. kąt o obu ramionach równoległych do rzutni (wielkość kąta, którego obydwa
ramiona są równoległe do rzutni jest taka sama jak wielkość rzutu tego kąta),
N8. związki miarowe w płaszczyźnie równoległej do rzutni (długości odcinków, kąty,
wielkości figur leżących na płaszczyźnie równoległej do rzutni zachowują się).

Przybory rysunkowe
2 ekierki, linijka;
cyrkiel;
2 ołówki:
- twardy 2H, 4H (do rysowania linii pomocniczych,
- średni HB (do wyciągania linii);
gumka;
papier A4 (nie w kratkę!).
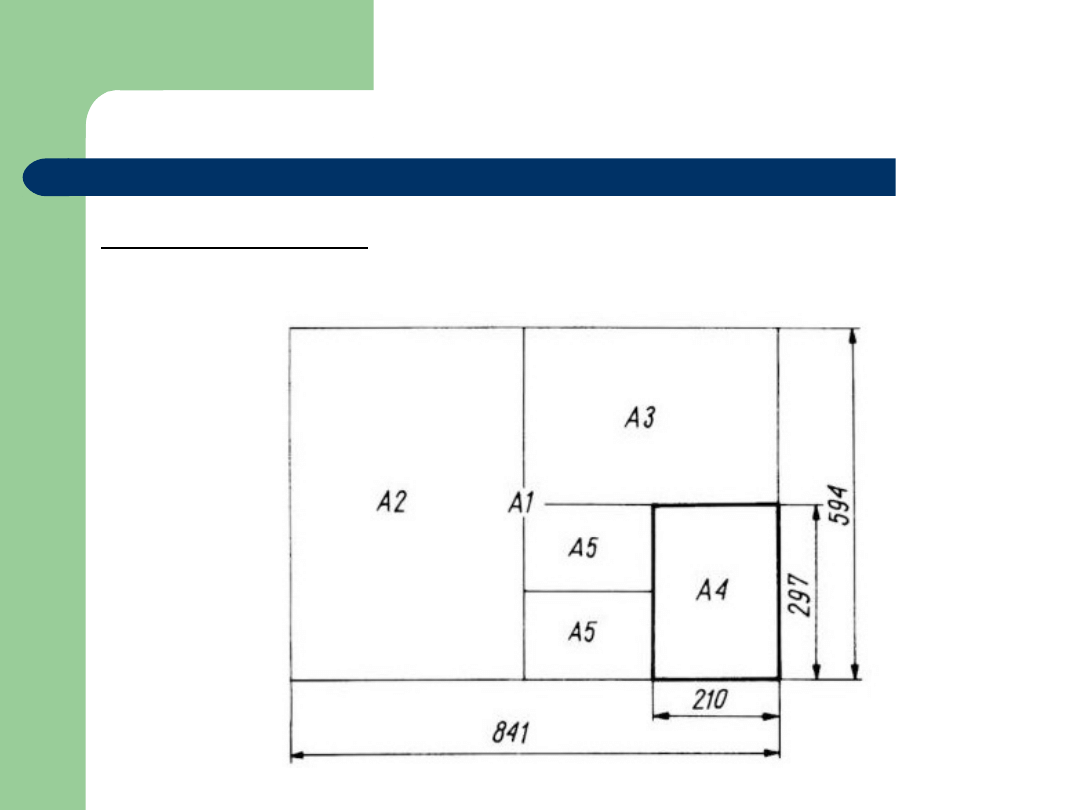
Arkusze rysunkowe
Formaty zwykłe
(A4 – format podstawowy)
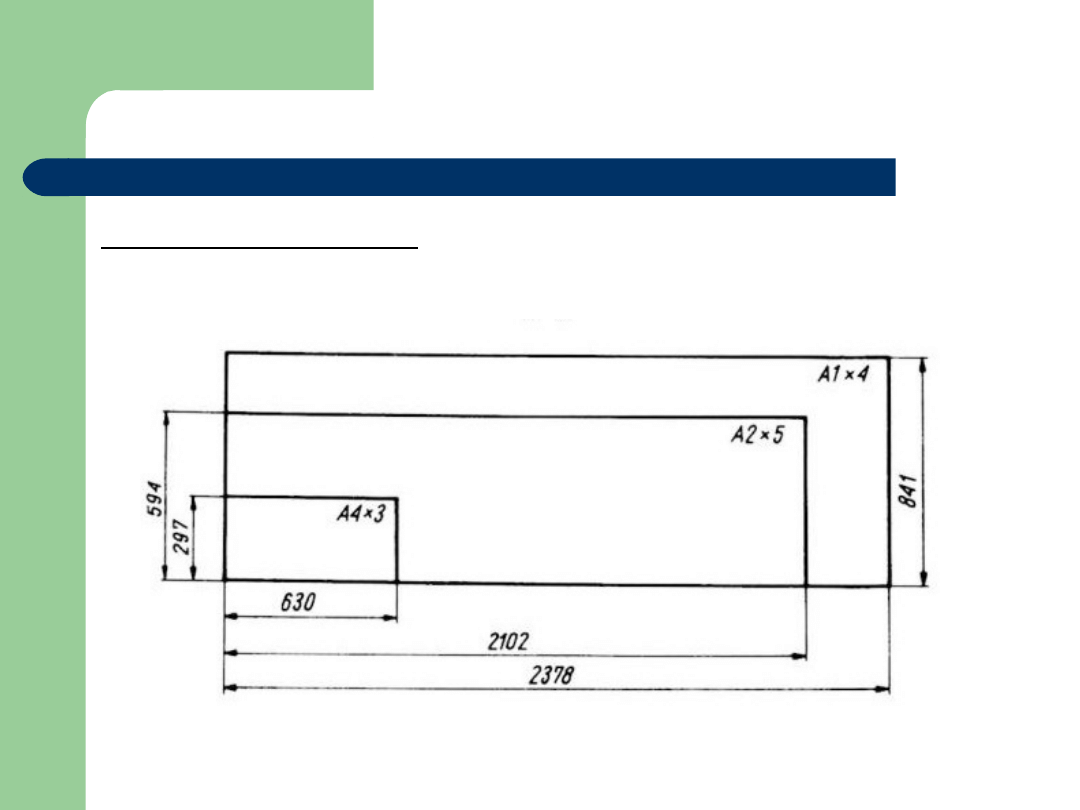
Arkusze rysunkowe
Formaty pochodne
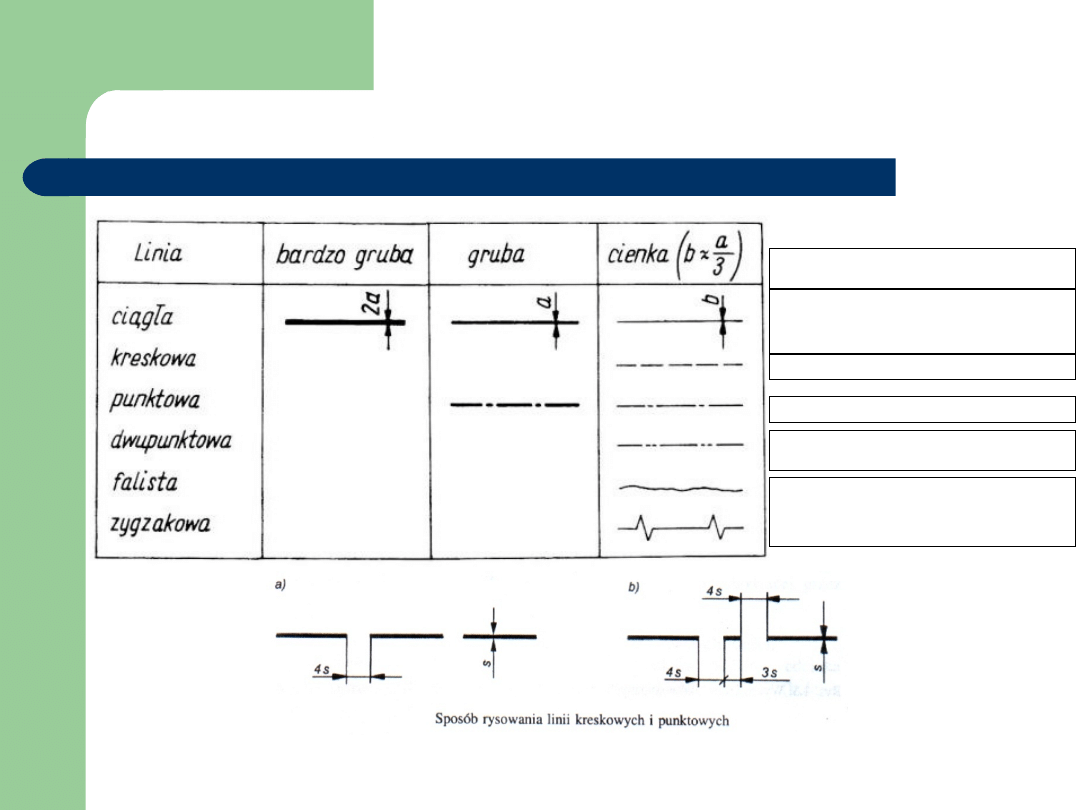
Rodzaje linii rysunkowych
Zarysy kładów miejscowych, oznaczenia
gwintów, linie wymiarowe i pomocnicze
linie wymiarowe, linie odniesienia, linie
kreskowania
Zarysy widoczne widoków i przekrojów,
kłady przesunięte, obramowanie rysunku
Urwania rzutów obiektów
Linie wyobrażalne, np. osie symetrii
Zarysy niewidoczne
Skrajne położenie części ruchomych,
zarysy obiektu przed obróbką
Dla A4 i A3 a=0,5mm, dla A2 i A1 a=0,7mm

Pismo techniczne
Wysokość pisma zależy od formatu opisywanego arkusza.
Dla formatów A4 i A3 stosuje się najczęściej pismo
wysokości 7 mm lub 5 mm dla napisów głównych i 3,5
mm lub 2,5mm dla n. pomocniczych.
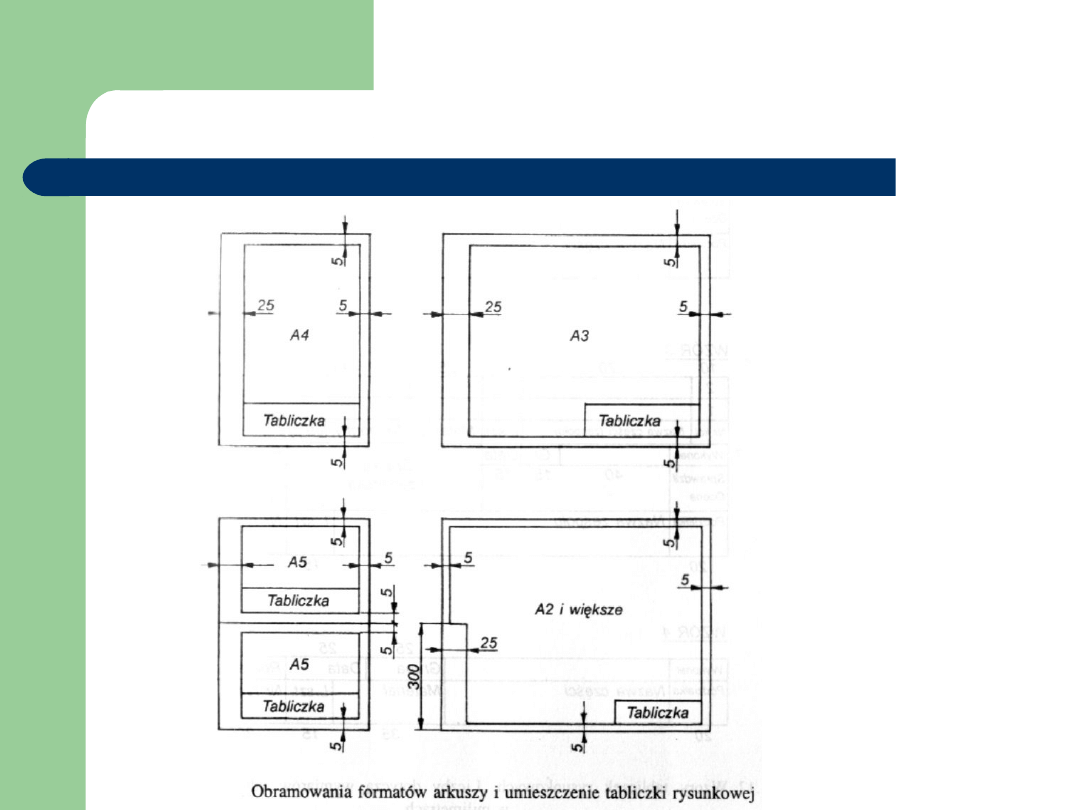
Obramowanie rysunku i tabliczki
rysunkowe
Format A4 jest
formatem
stojącym,
A3 – leżącym,
A2 i
A1dowolnym!!!!
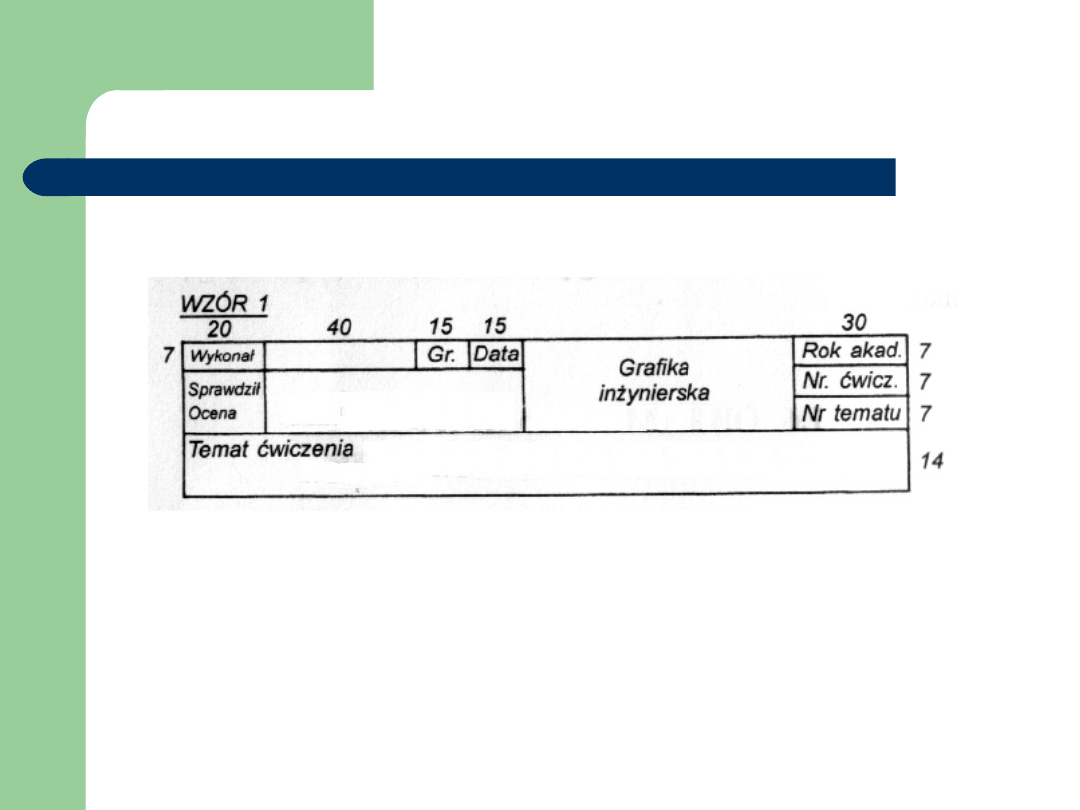
Tabliczki rysunkowe

Technika wykonywania rysunku (w
ołówku)
przygotowanie odpowiedniego arkusza;
wykreślenie ołówkiem średnim ramki i tabliczki
rysunkowej;
odpowiednie usytuowanie rysunku;
wykreślenie ołówkiem twardym liniami cienkimi
- linii osiowych, linii pomocniczych
- zarysów brył
- kreskowanie przekrojów
- linii wymiarowych;
wykreślenie liniami grubymi zarysów rzutów i opisanie
rysunku (zwymiarowanie, wypełnienie tabliczki i
wpisanie dodatkowych oznaczeń).

Podstawowe twierdzenia ze
stereometrii
Dwa różne punkty wyznaczają dokładnie jedną prostą,
do której należą.
Płaszczyznę wyznaczają:
–
trzy punkty, które nie leżą na prostej
–
dwie niepokrywające się proste równoległe
–
dwie proste przecinające się
–
prosta i nieleżący na niej punkt
Dwie proste nie leżące w jednej płaszczyźnie
nazywamy prostymi skośnymi
Odległością punktu od płaszczyzny nazywamy długość
odcinka o jednym końcu w tym punkcie drugim końcu
na płaszczyźnie i prostopadłego do tej płaszczyzny.
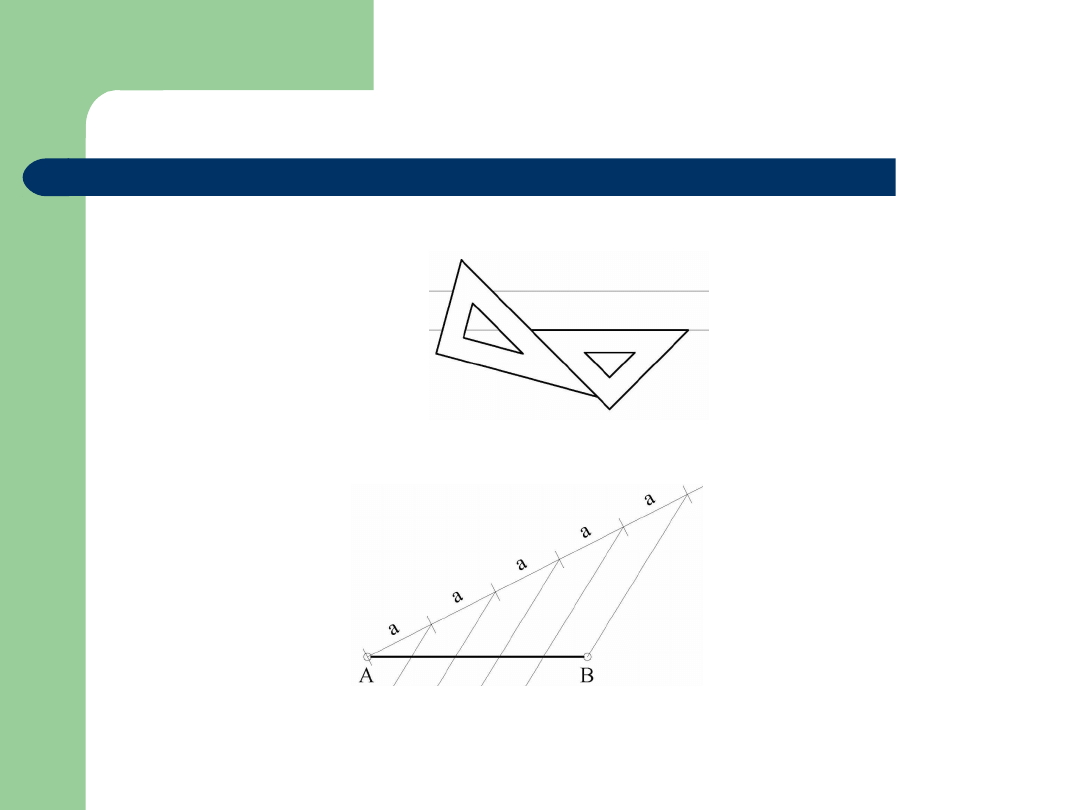
Konstrukcje linii
Proste równoległe i prostopadłe
Podział odcinka na n częsci
Rysowanie prostokątów, równoległoboków, trójkątów,
symetralnej odcinka, itp.
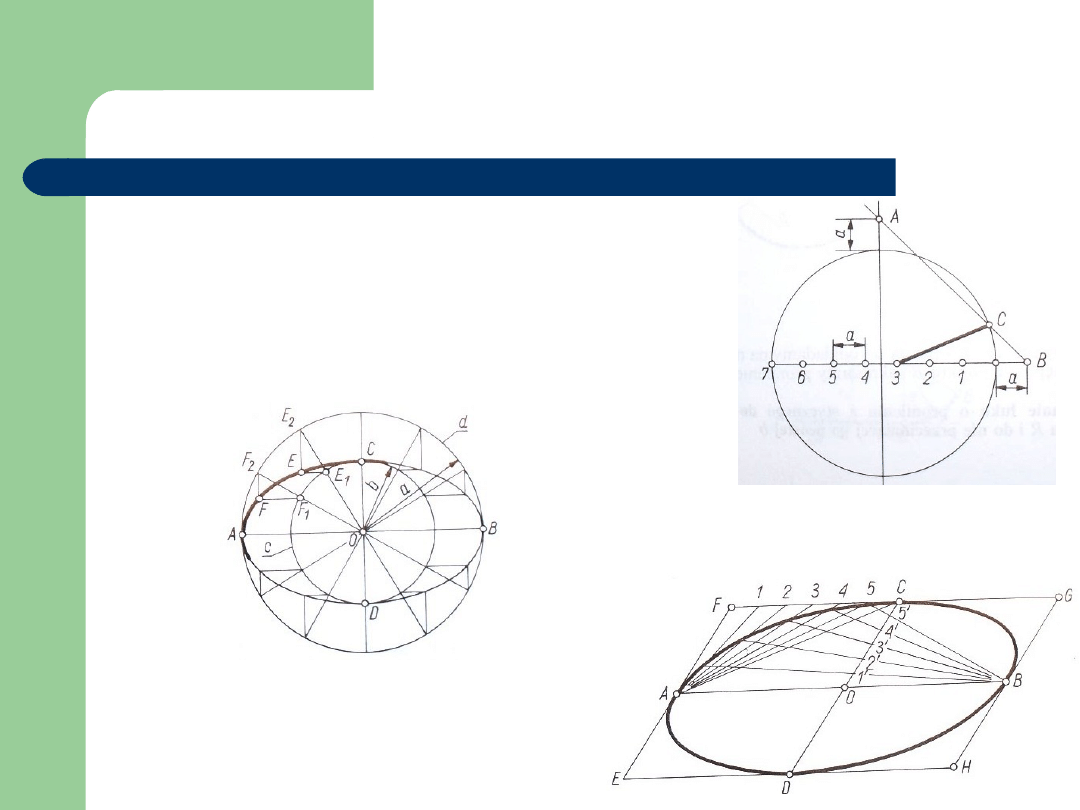
Konstrukcje linii
Wykreślanie wielokąta foremnego o n bokach
(Dobrzański,RTM R.III).
Wykreślanie elipsy zadanej osiami
Wykreślanie elipsy zadanej średnicami
sprzężonymi
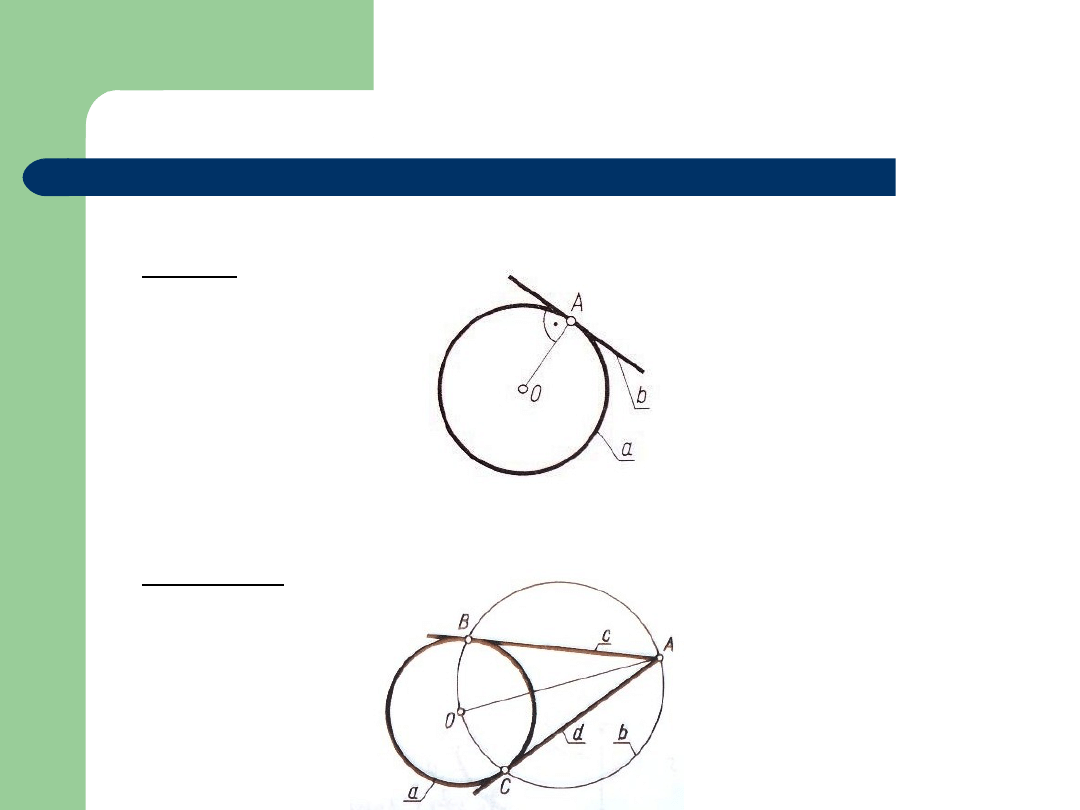
Konstrukcje linii
Wykreślanie stycznej do okręgu przechodzącej przez
leżący na nim punkt A
Wykreślanie stycznej do okręgu przechodzącej przez
nieleżący na nim punkt A

DZIĘKUJĘ...
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
Wyszukiwarka
Podobne podstrony:
Algebra i Analiza Matematyczna, Elementy geometrii analitycznej w przestrzeni, ROZDZIAŁ VI
prawo przestepstwo i jego elementy(z kolumnami)
Glowne elementy kompozycji przestrzennej
Przestrzeń zdarzeń elementarnych
A Zoll Karalnosc i karygodnosc czynu jako odrebne elementy struktury przestepstwa
PRZEST~1, PRZEST~1, METODY OPISU WŁAŚCIWOŚCI DYNAMICZNYCH ELEMENTÓW AUTOMATYKI
Zorganizowana przestępczość jako element zagrożenia funkcjonowania społeczeństwa
Hamarnik Diana Socjolekt więzienny jako element podkultury przestępczej
Diana Hamarnik Socjolekt więzienny jako element podkultury przestępczej
Model prętowy i przestrzenny stalowego elementu obetonowanego w świetle wyników eksperymentu
POJĘCIE PRZESTĘPSTWA I JEGO ELEMENTY
POJĘCIE PRZESTĘPSTWA I JEGO ELEMENTY
Adobe Photoshop Elements 10 Tworzenie przestrzennej fotografii
Przestępczość
więcej podobnych podstron