Prądy i napięcia

sinusoidalnie zmienne

-0,005

0,000

0,005

0,010

0,015

0,020

-1,5

-1,0

-0,5

0,0

0,5

1,0

1,5

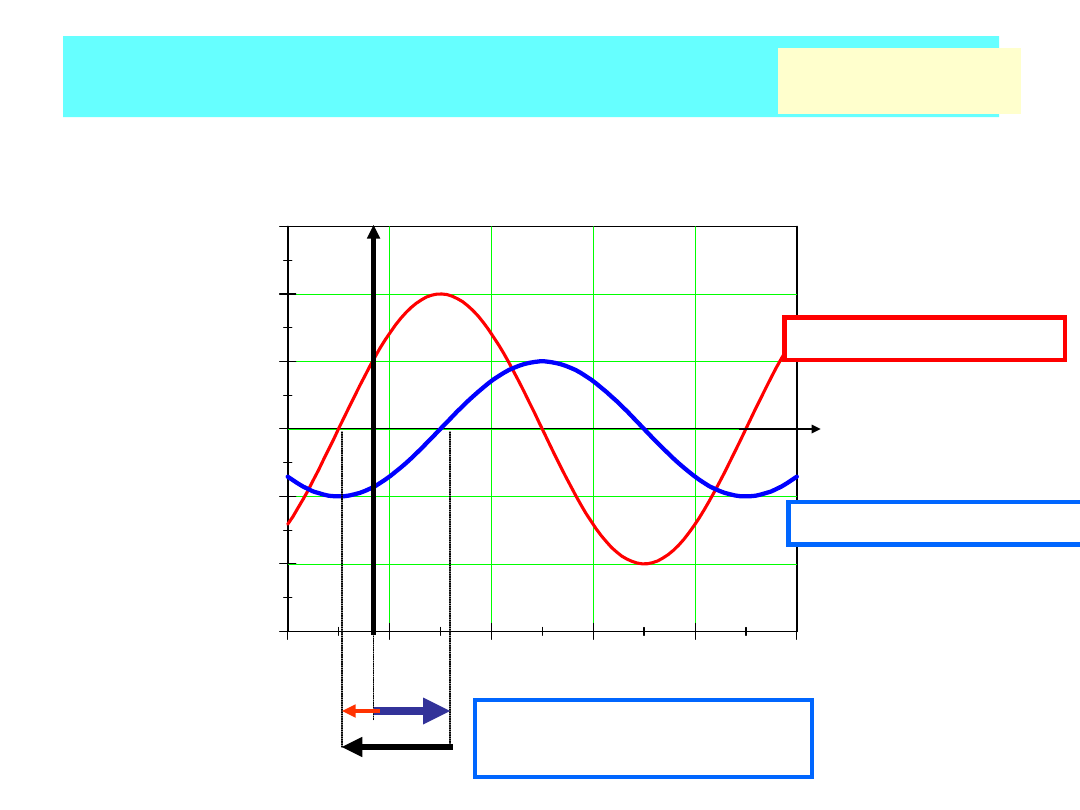
Przebiegi przesunięte o kąt:





1

1

1

sin

)

(









t

X

t

x

m





2

2

2

sin

)

(









t

X

t

x

m

x

1

(t),x

2

(t)

t

2

1











2



1



0

2

1













0

1





0

2





-0,005

0,000

0,005

0,010

0,015

0,020

-1,5

-1,0

-0,5

0,0

0,5

1,0

1,5

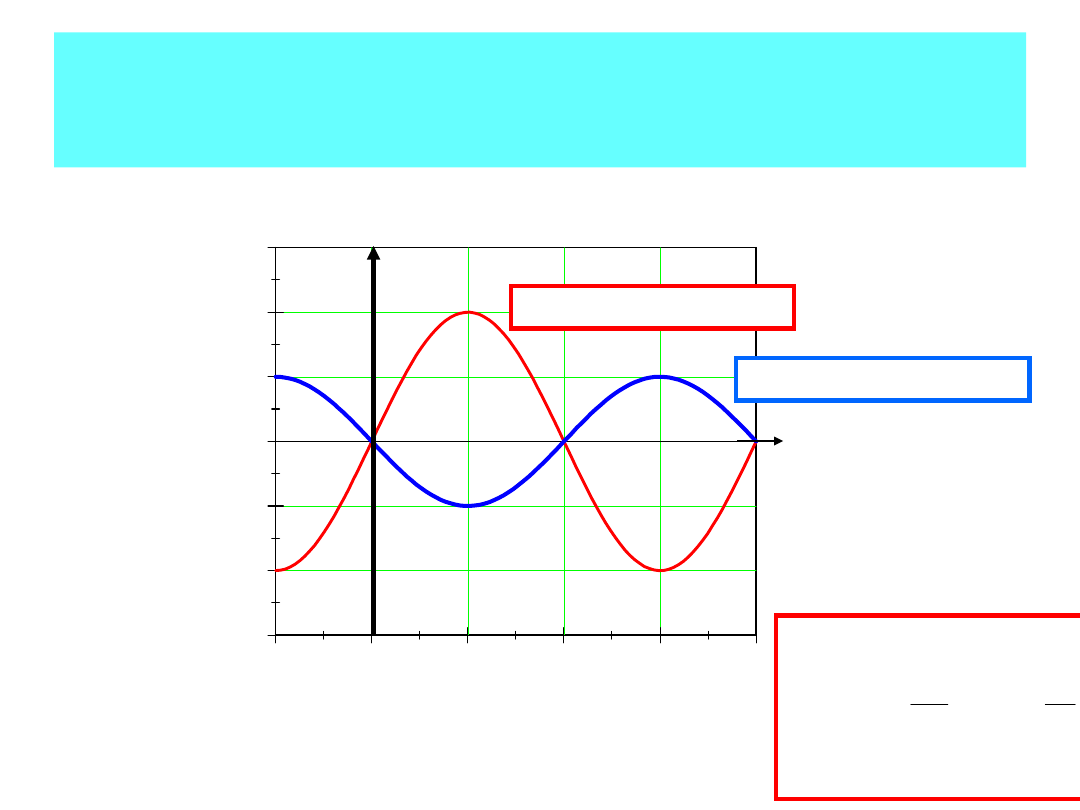
W przeciwfazie





1

1

1

sin

)

(









t

X

t

x

m





2

2

2

sin

)

(









t

X

t

x

m

x

1

(t),x

2

(t)

t



180

10

2

2

02

.

0

2

1

2































s

rd

T

f

s

T

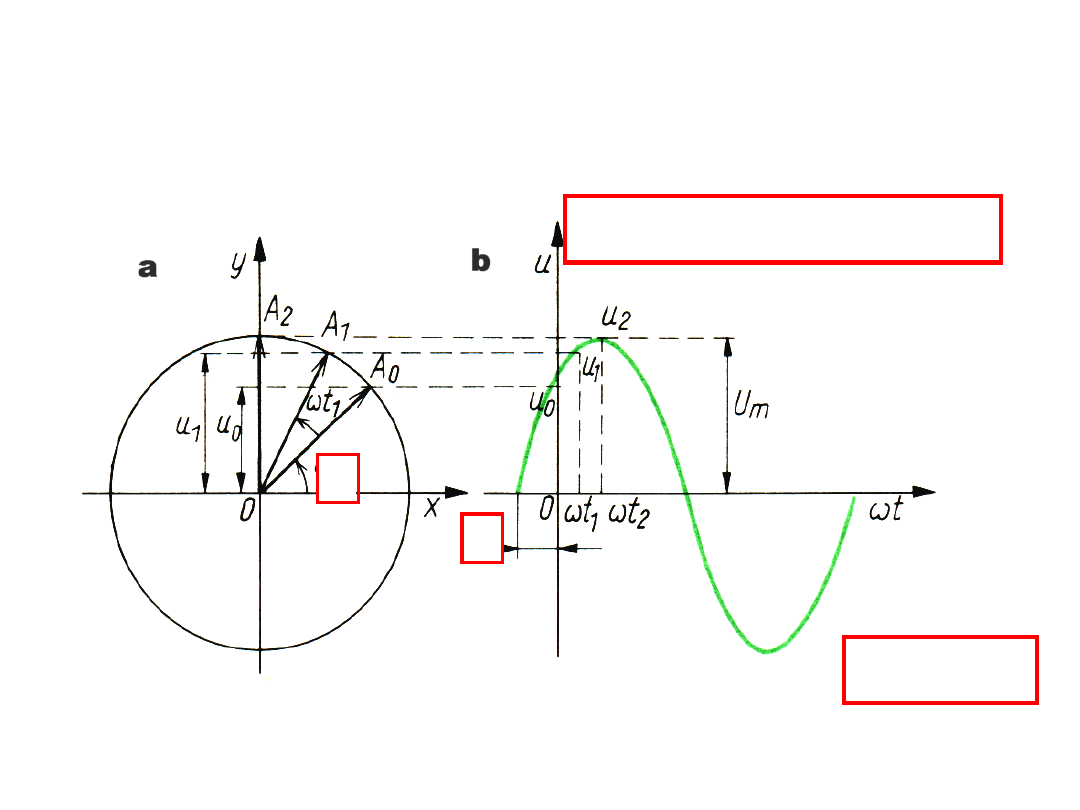
Wektory a sinusoida

u



u



)

sin(

)

(

u

m

t

U

t

u









o

o

u

t

u



)

(

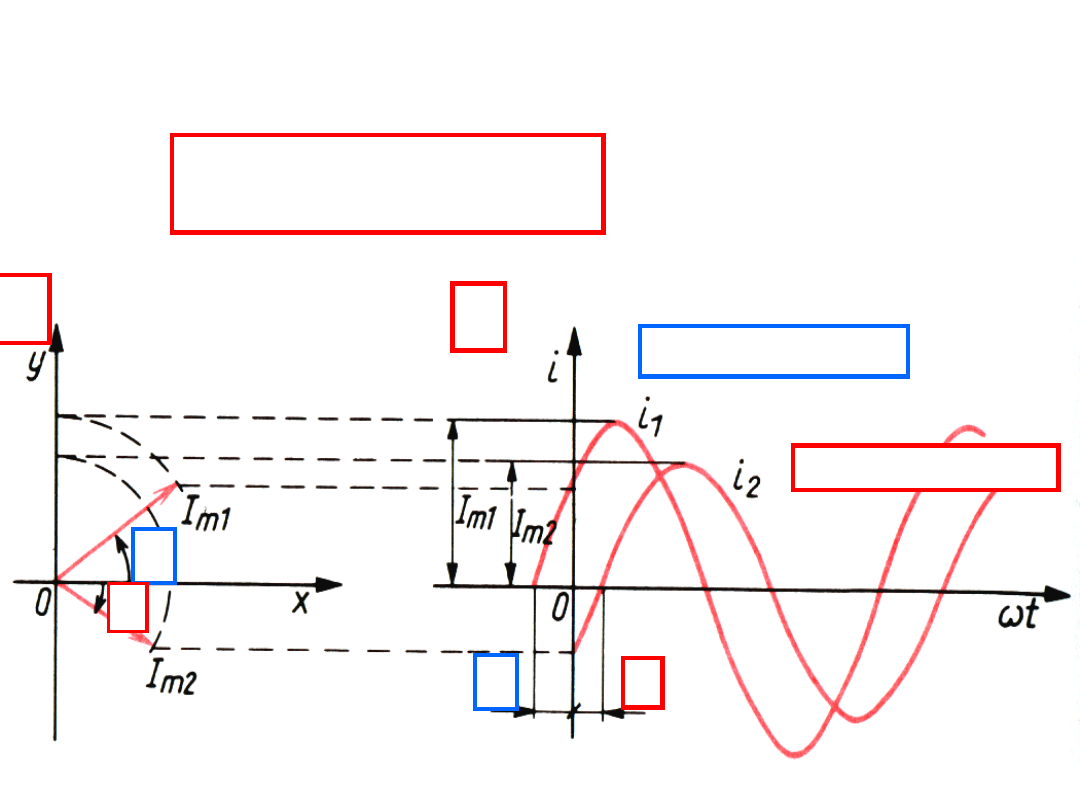
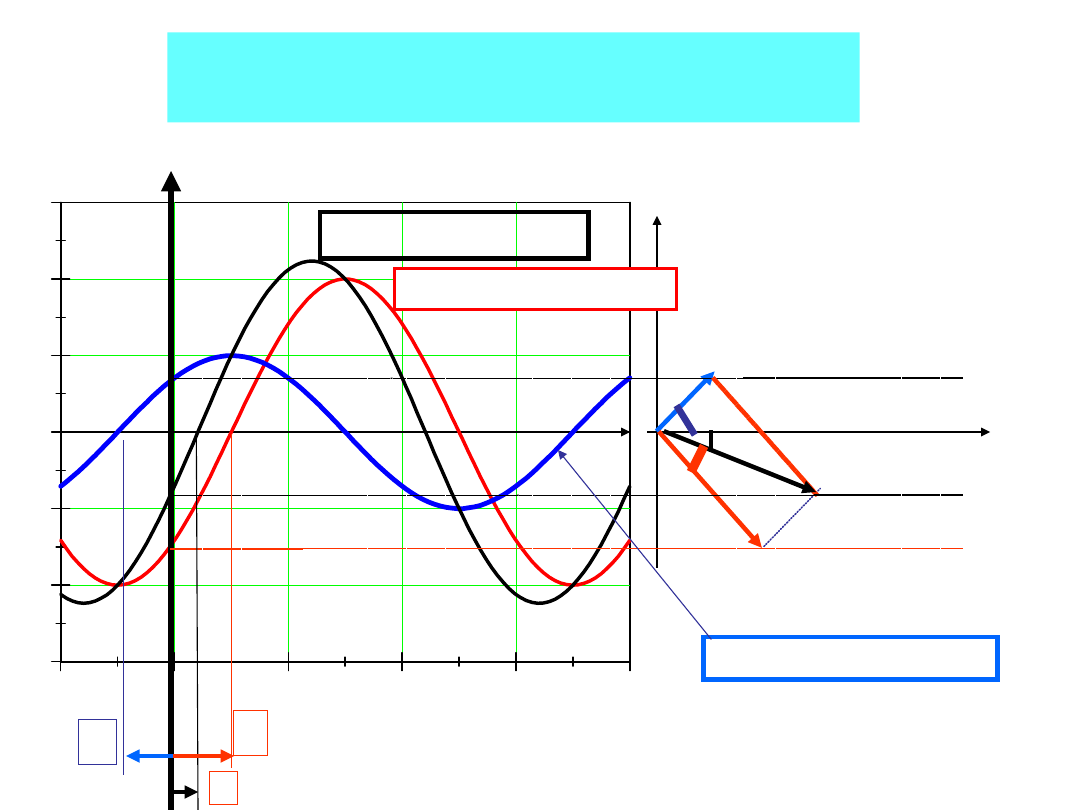
Związek między wykresem wektorowym a

czasowym

1

i



2

i



1

i



2

i



A

B

)

sin(

)

(

1

1

1

i

m

t

I

t

i









)

sin(

)

(

2

2

2

i

m

t

I

t

i









A – wykres wektorowy
B – wykres czasowy

-0,005

0,000

0,005

0,010

0,015

0,020

-1,5

-1,0

-0,5

0,0

0,5

1,0

1,5

1



2





x(t),x

1

(t),x

2

(t)

t

z

y





1

1

1

sin

)

(









t

X

t

x

m

X

m1

X

m

X

m2













t

X

t

x

m

sin

)

(





2

2

2

sin

)

(









t

X

t

x

m

x

1

(t=0)

x(t=0)

x

2

(t=0)

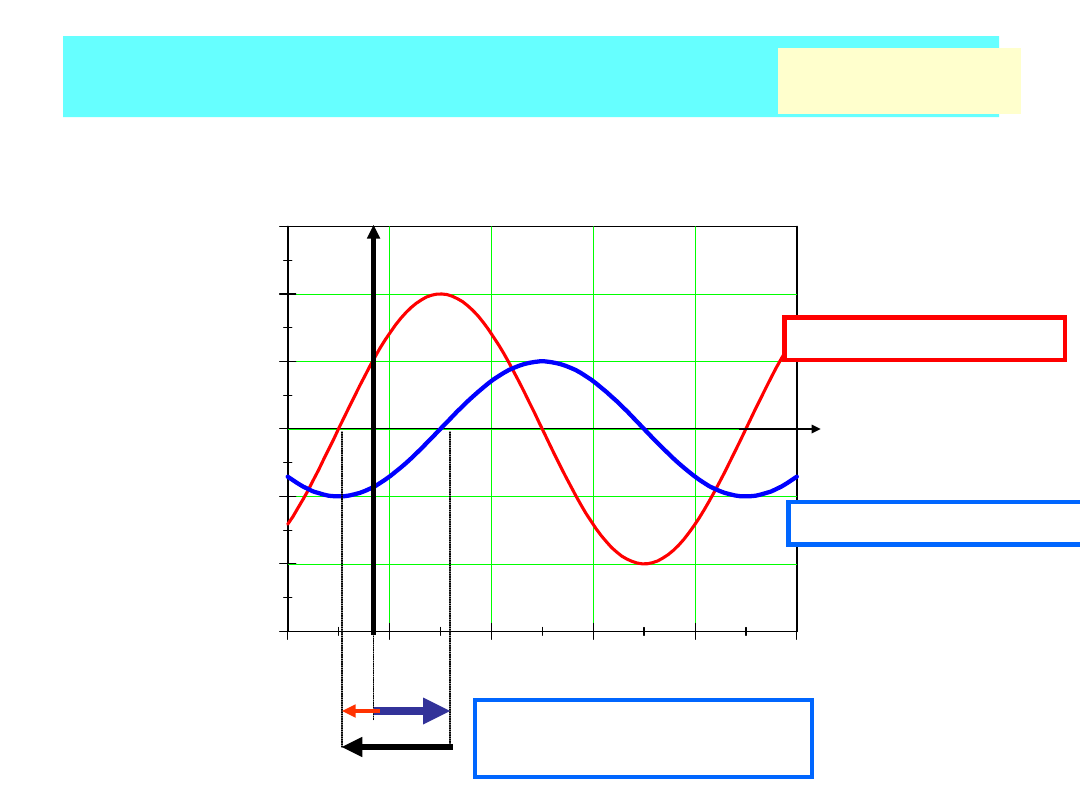
Dodawanie sinusoid

-0,005

0,000

0,005

0,010

0,015

0,020

-1,5

-1,0

-0,5

0,0

0,5

1,0

1,5

Przebiegi przesunięte o kąt:





1

1

1

sin

)

(









t

X

t

x

m





2

2

2

sin

)

(









t

X

t

x

m

x

1

(t),x

2

(t)

t

2

1











2



1



0

2

1













0

1





0

2





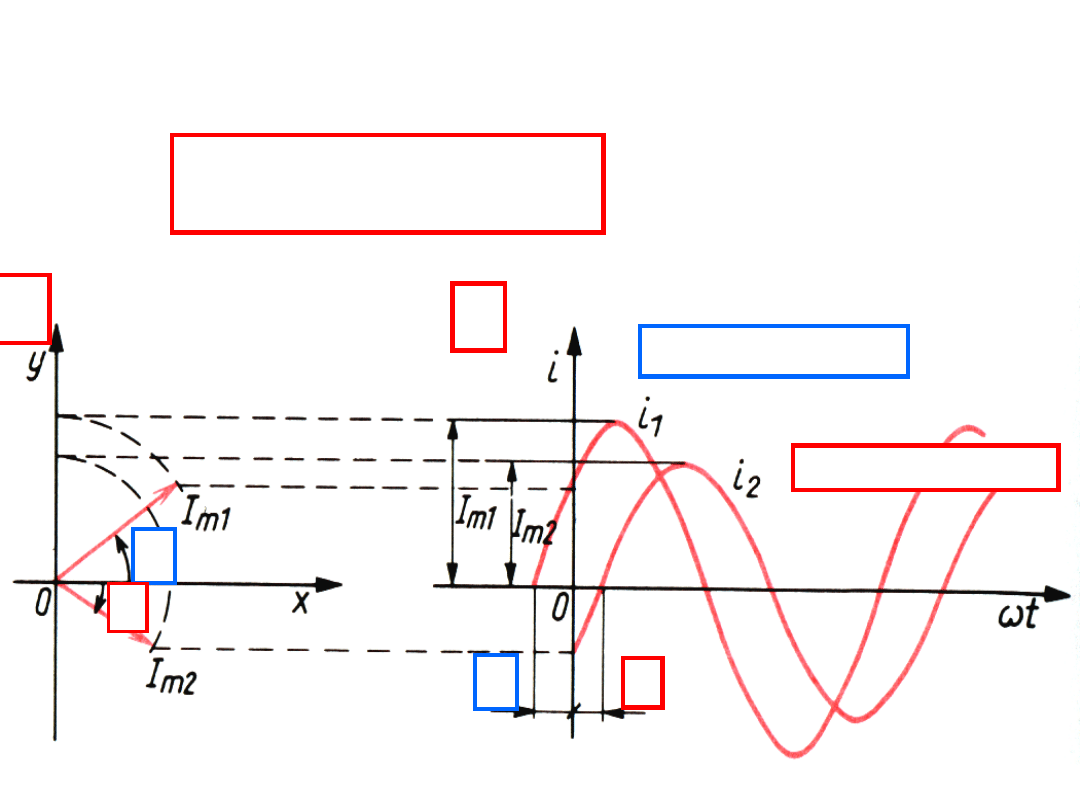
Związek między wykresem wektorowym a

czasowym

1

i



2

i



1

i



2

i



A

B

)

sin(

)

(

1

1

1

i

m

t

I

t

i









)

sin(

)

(

2

2

2

i

m

t

I

t

i









A – wykres wektorowy
B – wykres czasowy

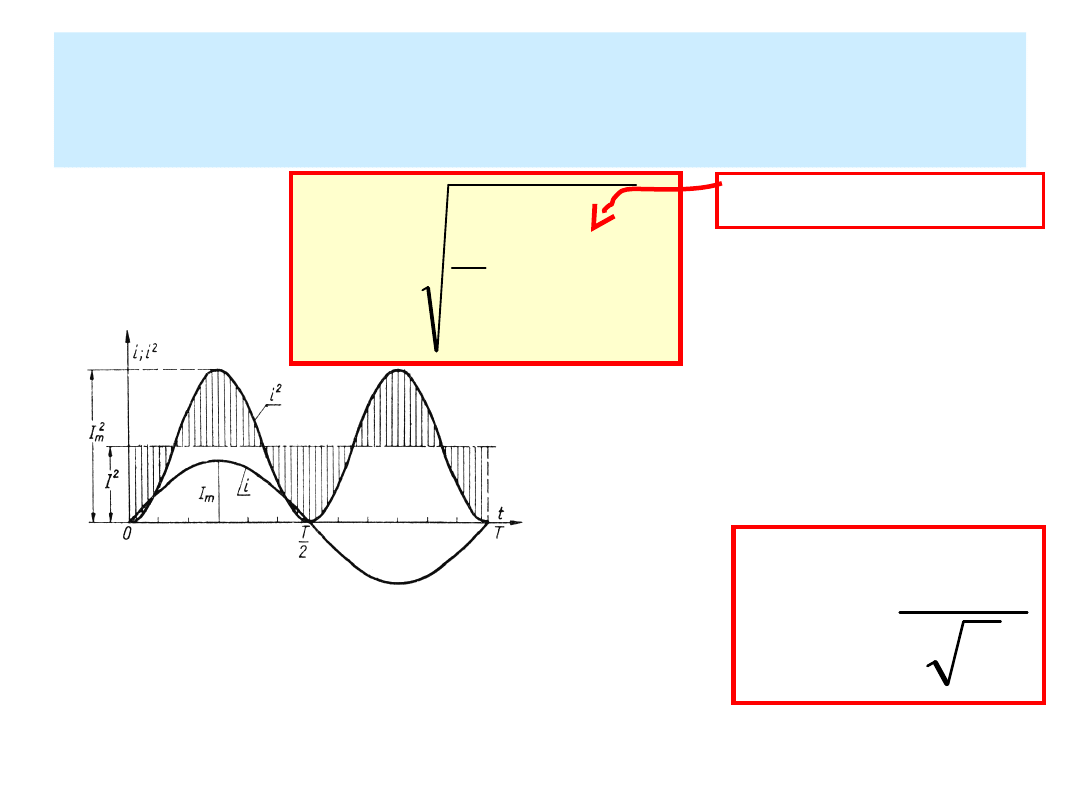
Wartość skuteczna

2

max

X

X

sk



 

dt

t

x

T

X

T

t

t

sk







0

0

2

1

Dla funkcji sinus
zachodzi:

 





x

t

X

t

x









sin

max

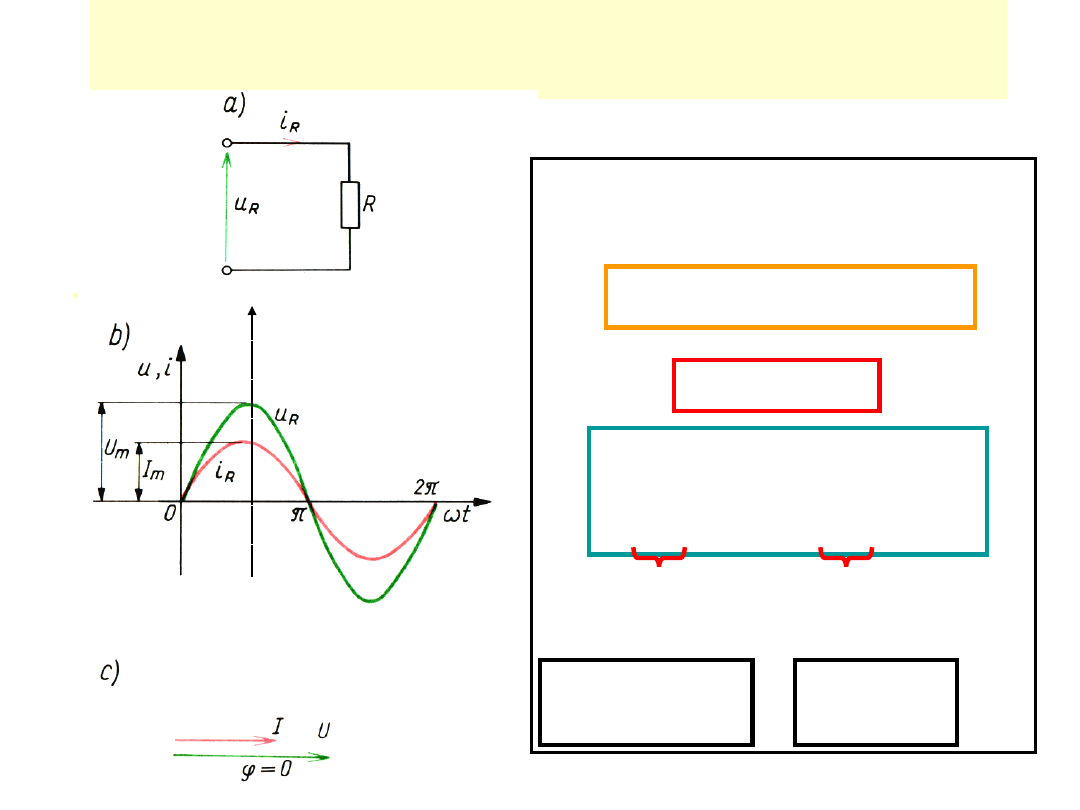
REZYSTOR

idealny(liniowy)

• Zależności

podstawowe:

• stąd:

)

sin(

)

sin(

)

(

i

m

u

m

t

RI

t

U

t

u



















)

sin(

)

(

i

m

t

I

t

i









R

)

t

(

i

)

t

(

u



i

u

m

m

RI

U









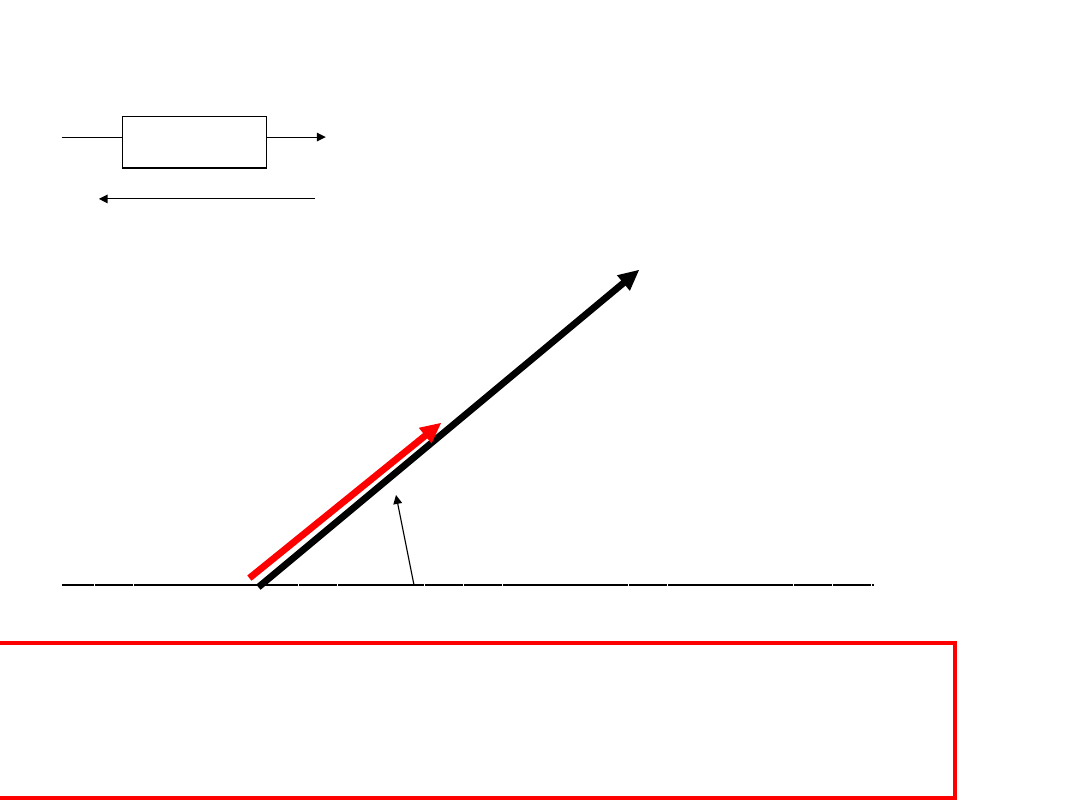
U

I

i

u







I

U

R

UWAGA:
Prąd i napięcie opornika są w fazie,
tzn. nie ma przesunięcia fazowego między nimi !!!!!!!!!!!!

)

2

sin(

)

cos(

)

(

























i

m

i

m

t

U

t

I

L

t

u

dt

di

L

u

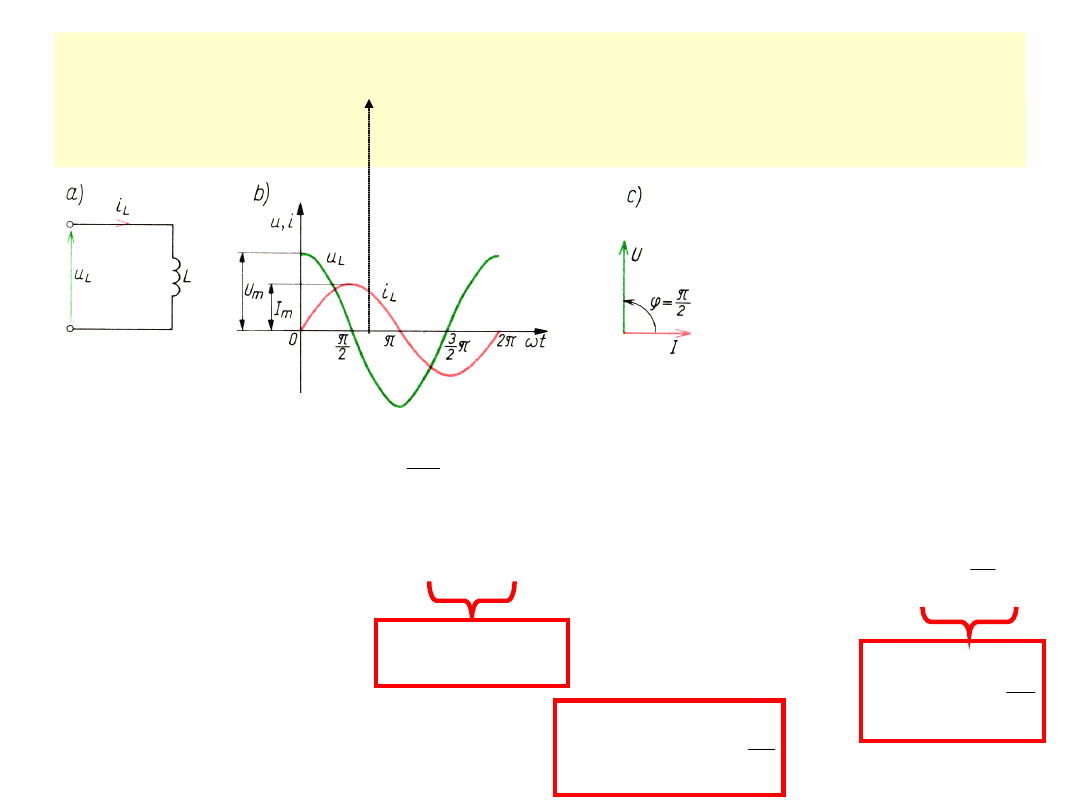
CEWKA idealna (liniowa)

m

m

LI

U





)

sin(

)

(

i

m

t

I

t

i









2















i

u

2











i

u

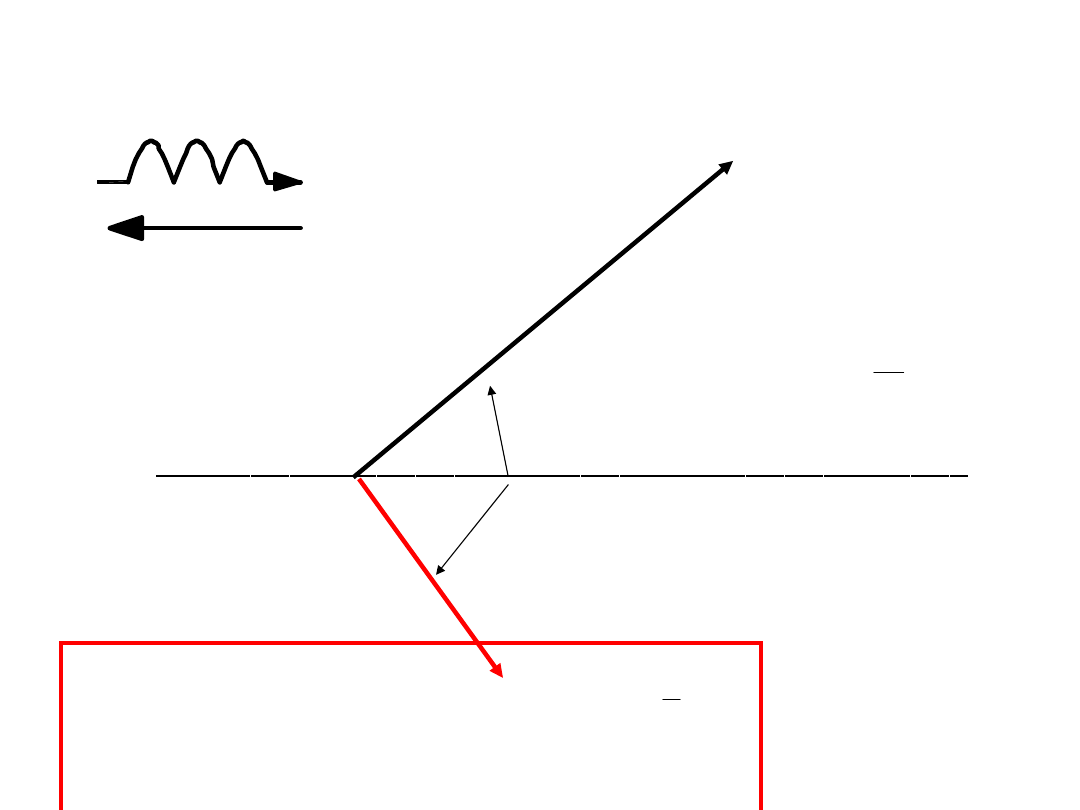
U

I

u



i



2















i

u

L

I

U

UWAGA:
Prąd cewki opóźnia się względem
napięcia o
!!!!!!!!!!!!

2



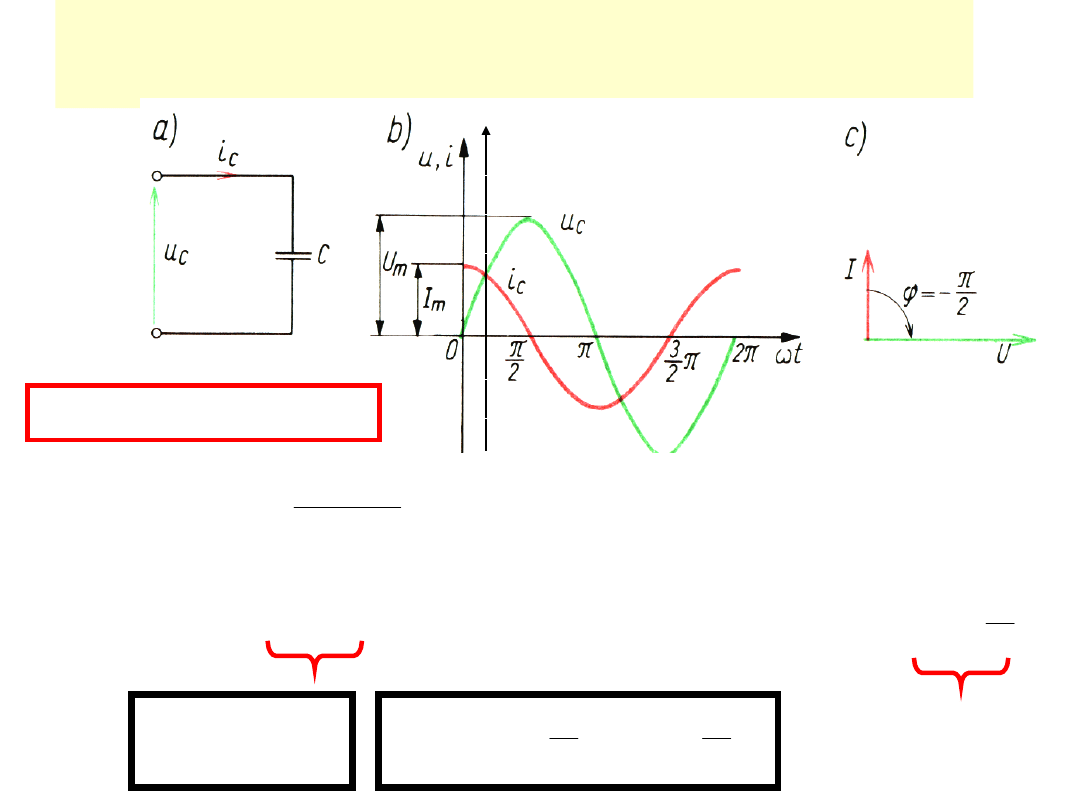
Kondensator idealny liniowy

2

2

)

2

sin(

)

cos(

)

(

)

(

)

(

















































u

i

m

m

u

m

u

m

c

c

c

CU

I

t

U

C

t

U

C

t

i

dt

t

du

C

t

i

)

sin(

)

(

u

m

t

U

t

u









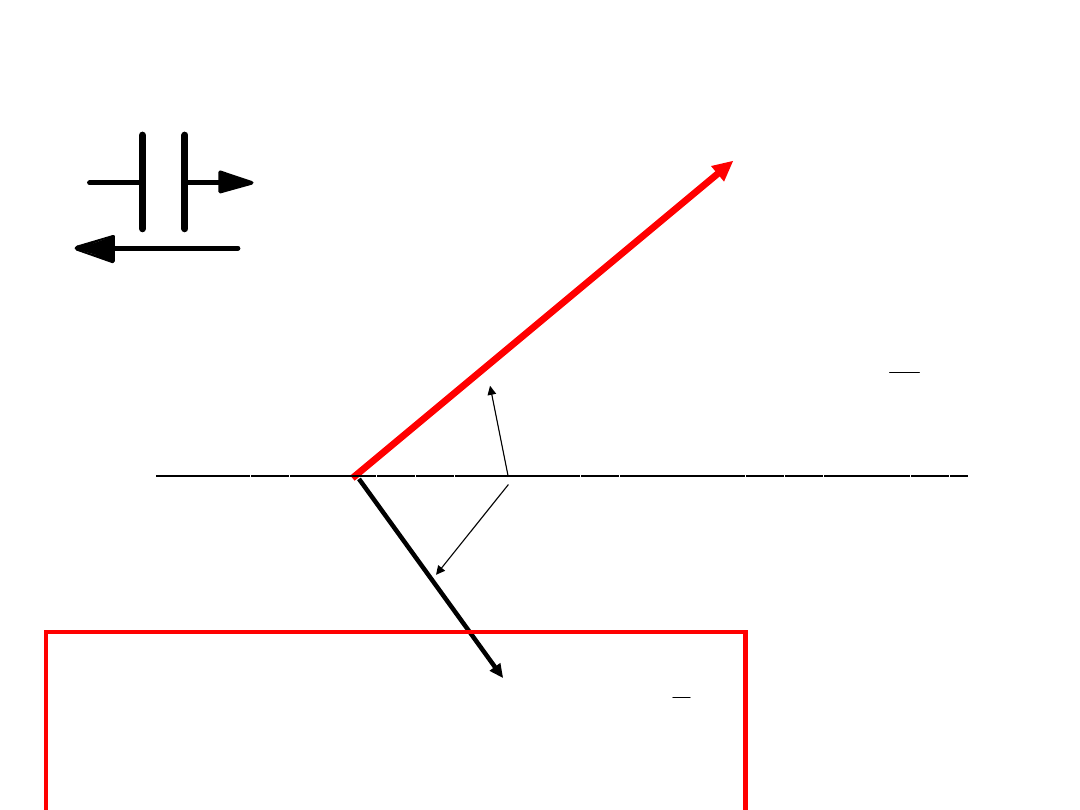
I

u



i



2

















i

u

C

I

U

U

UWAGA:
Prąd kondensatora wyprzedza napięcie
o kąt
!!!!!!!!!!!!

2



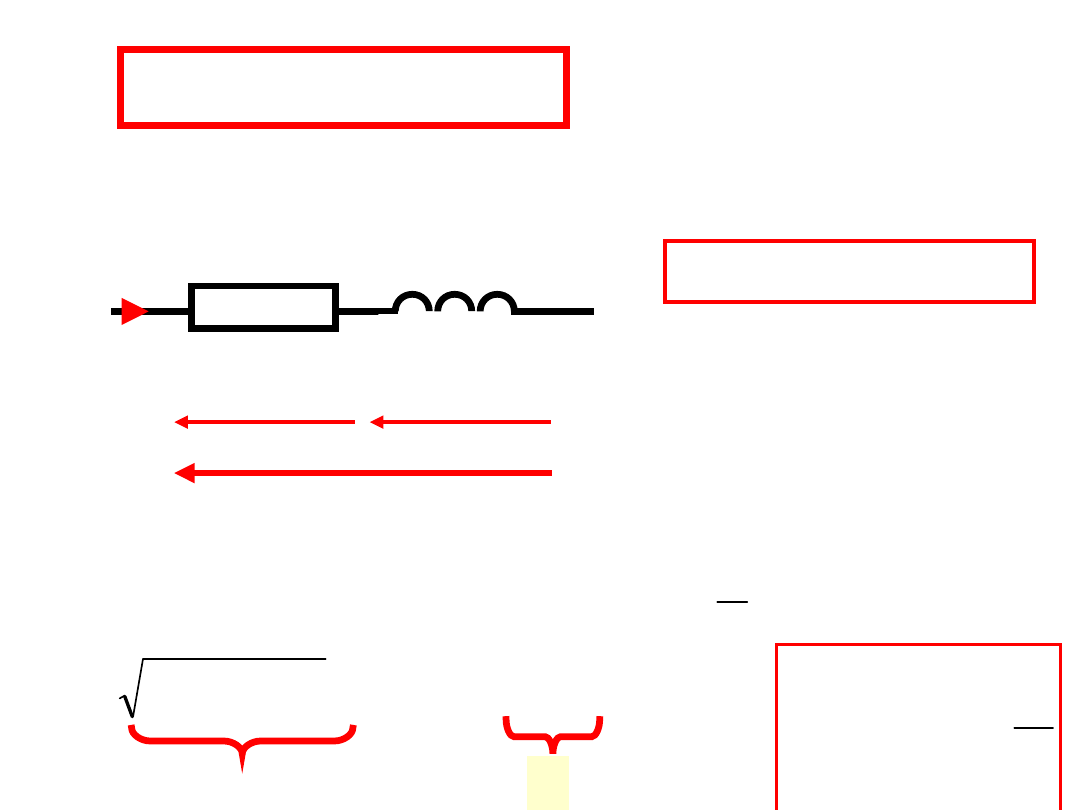
Połączenie RL

R

L

u

R

u

L

i

 



















)

2

sin(

)

sin(













i

m

i

m

L

R

t

LI

t

I

R

u

u

t

u

)

sin(

)

(

i

m

t

I

t

i









 

)

sin(

2

2

















i

m

t

I

L

R

R

L

tg

arc

gdzie

i

u















U

m

u



u

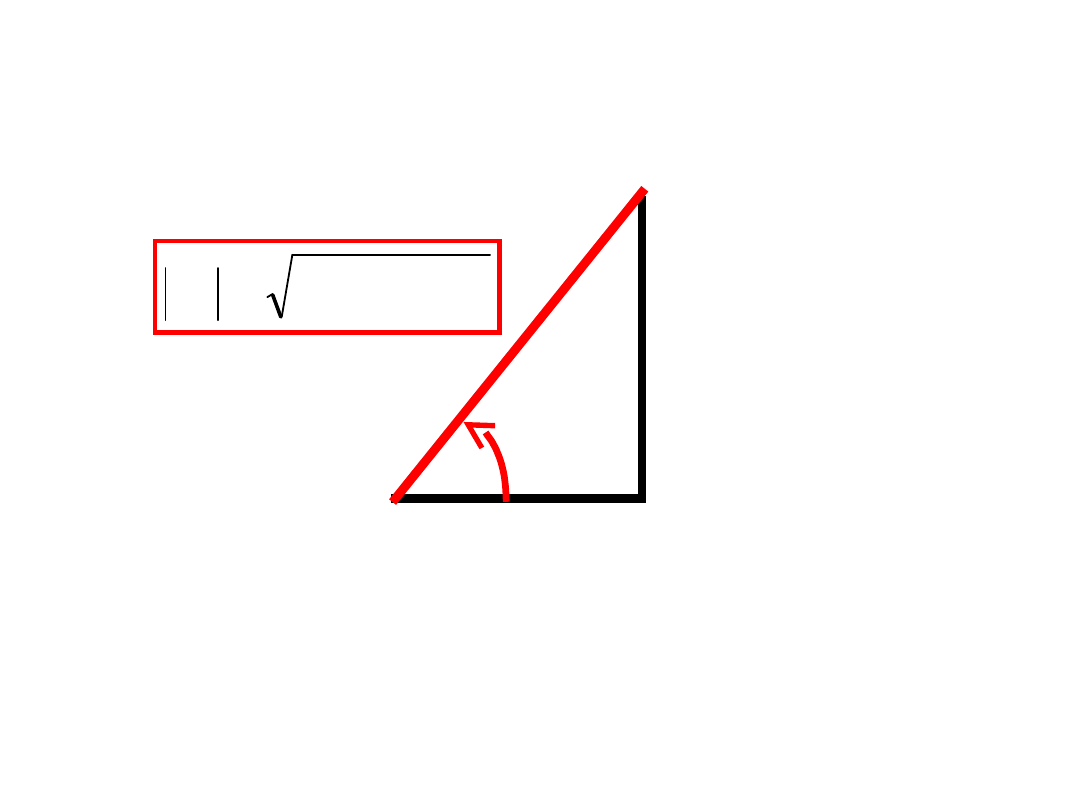
Takiemu połączeniu odpowiada trójkąt impedancji:

R

L

X





 

2

2

L

R

Z







R - rezystancja
X – reaktancja indukcyjna
Z – impedancja (moduł impedancji)



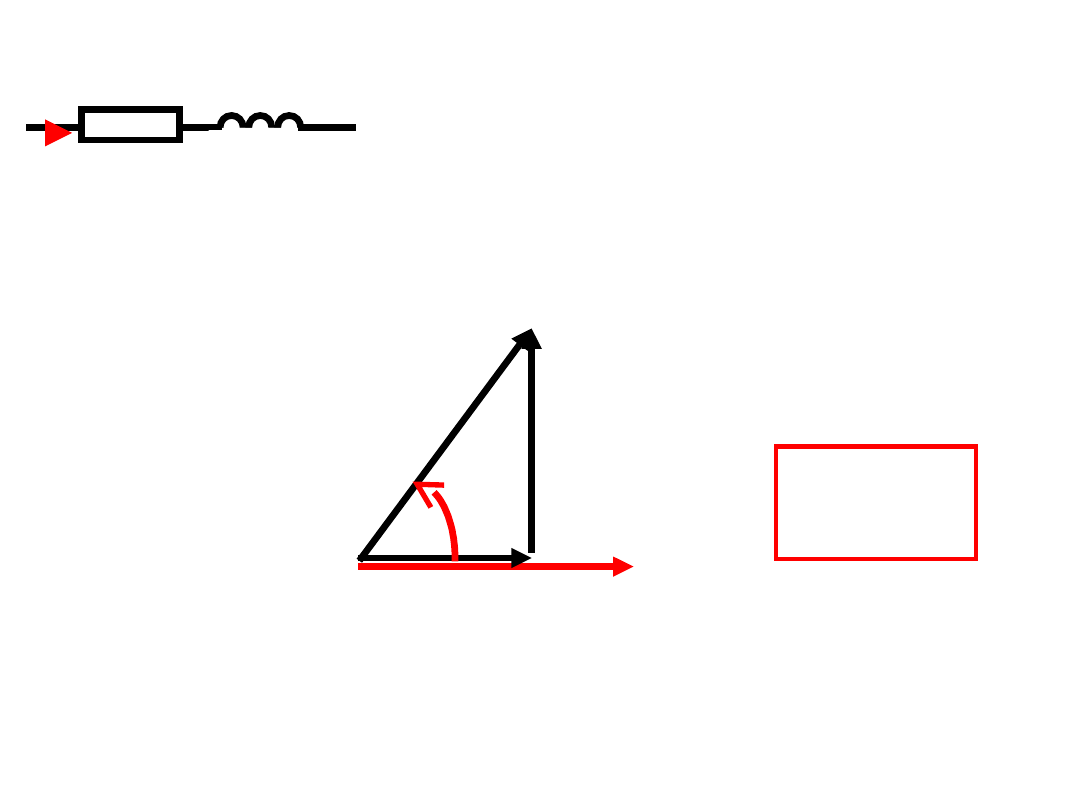
Takiemu połączeniu odpowiada wykres wskazowy:

R

L

i

i

U

R

U

L

U

0





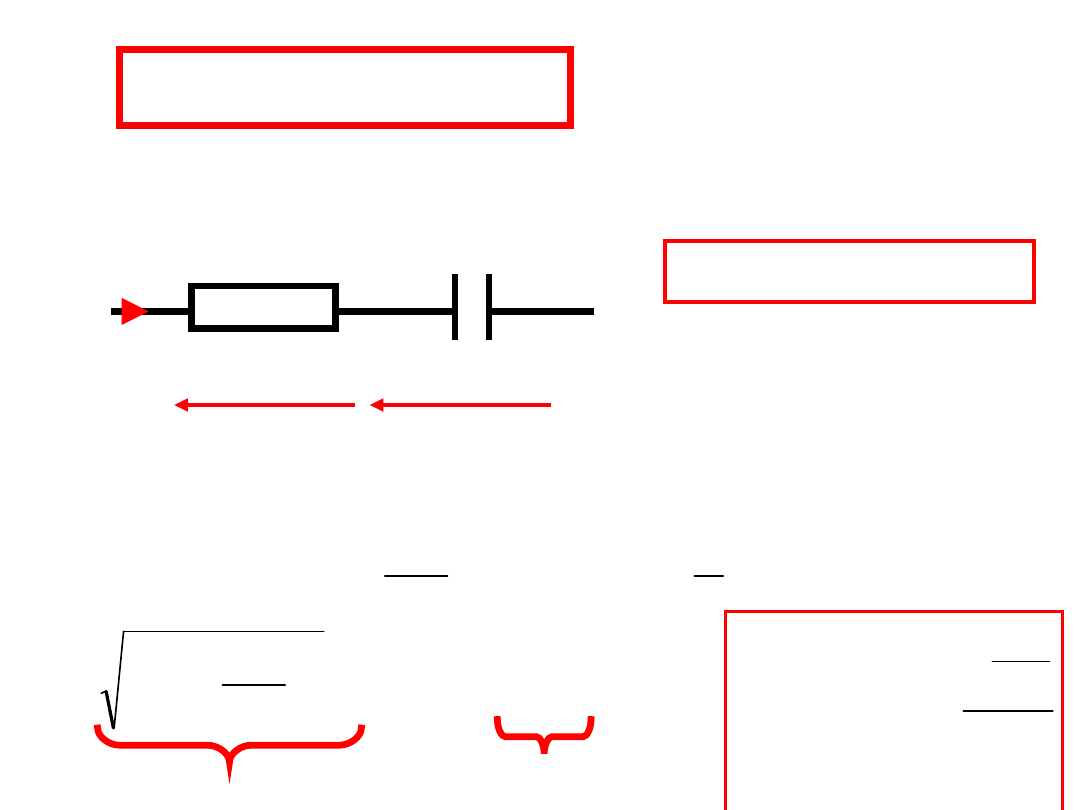
Połączenie RC

u

R

u

C

 































































i

m

i

m

i

m

C

R

t

I

C

R

t

I

C

t

I

R

u

u

t

u

sin

1

)

2

sin(

1

)

sin(

2

2

)

sin(

)

(

i

m

t

I

t

i









R

C

tg

arc

gdzie





1





U

m

u



R

C

i

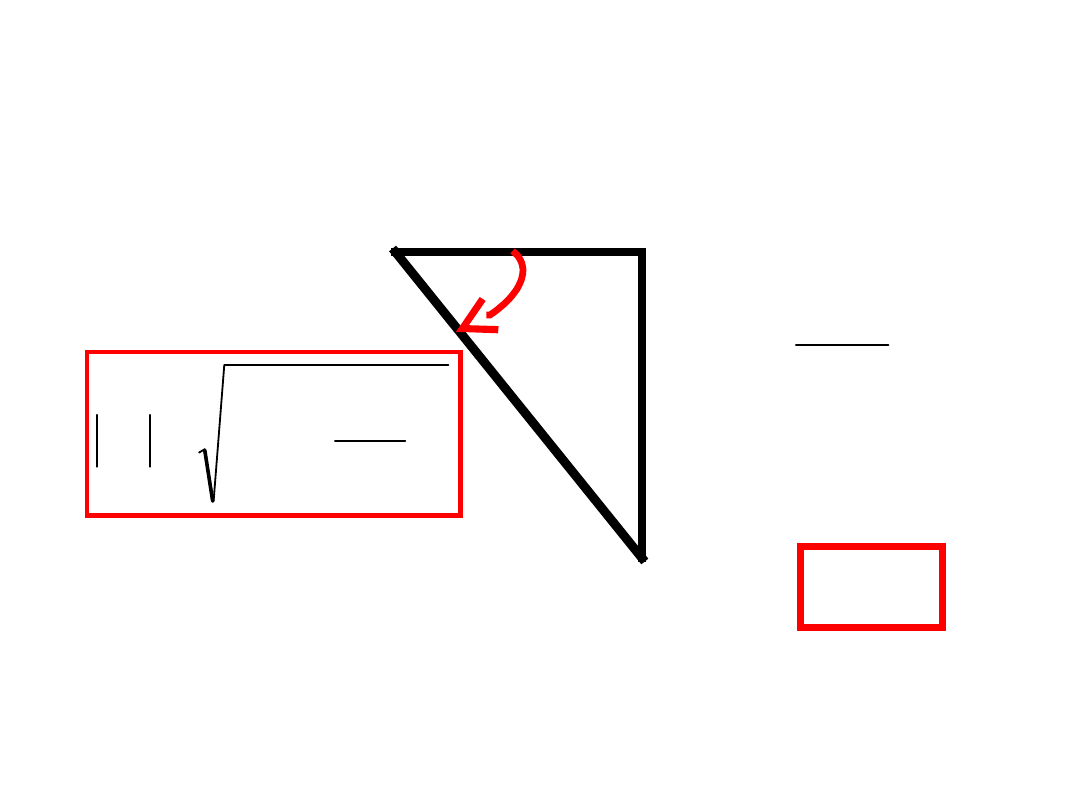
Takiemu połączeniu odpowiada trójkąt impedancji:

R

C

X



1





R - rezystancja
X – reaktancja pojemnościowa
Z – impedancja (moduł impedancji)



0





2

2

1

















C

R

Z



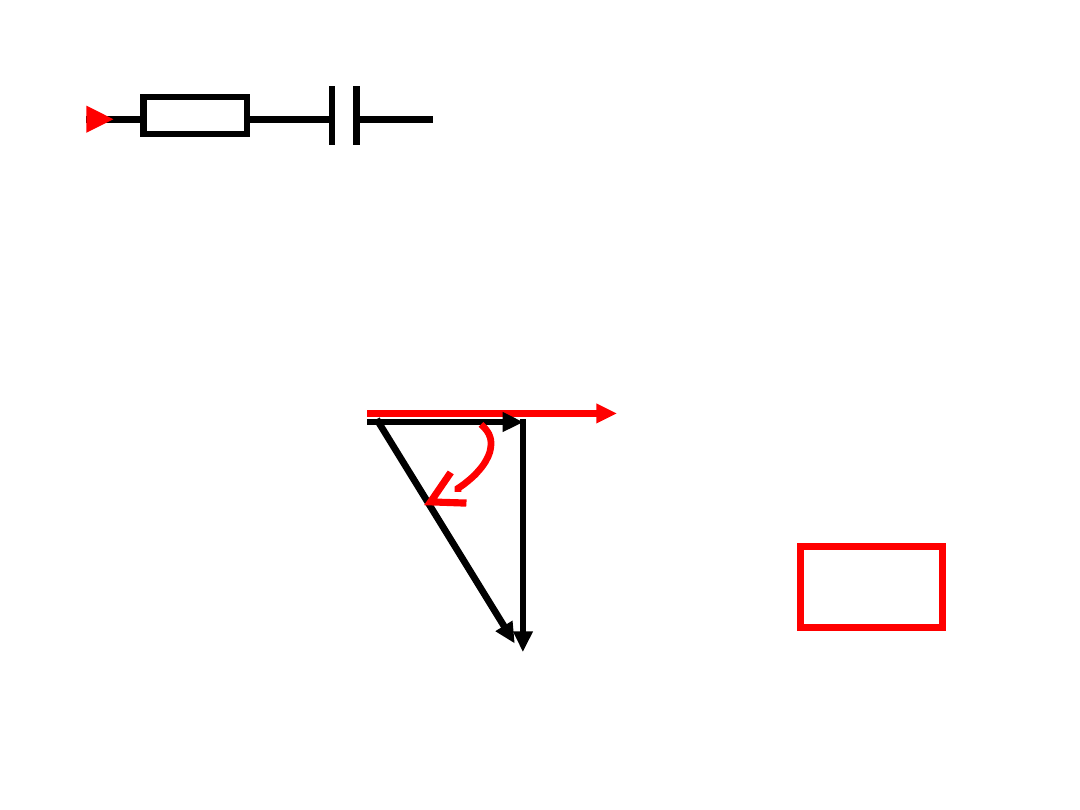
Takiemu połączeniu odpowiada wykres wskazowy:

R

C

i

i

u

R

u

C

u

0





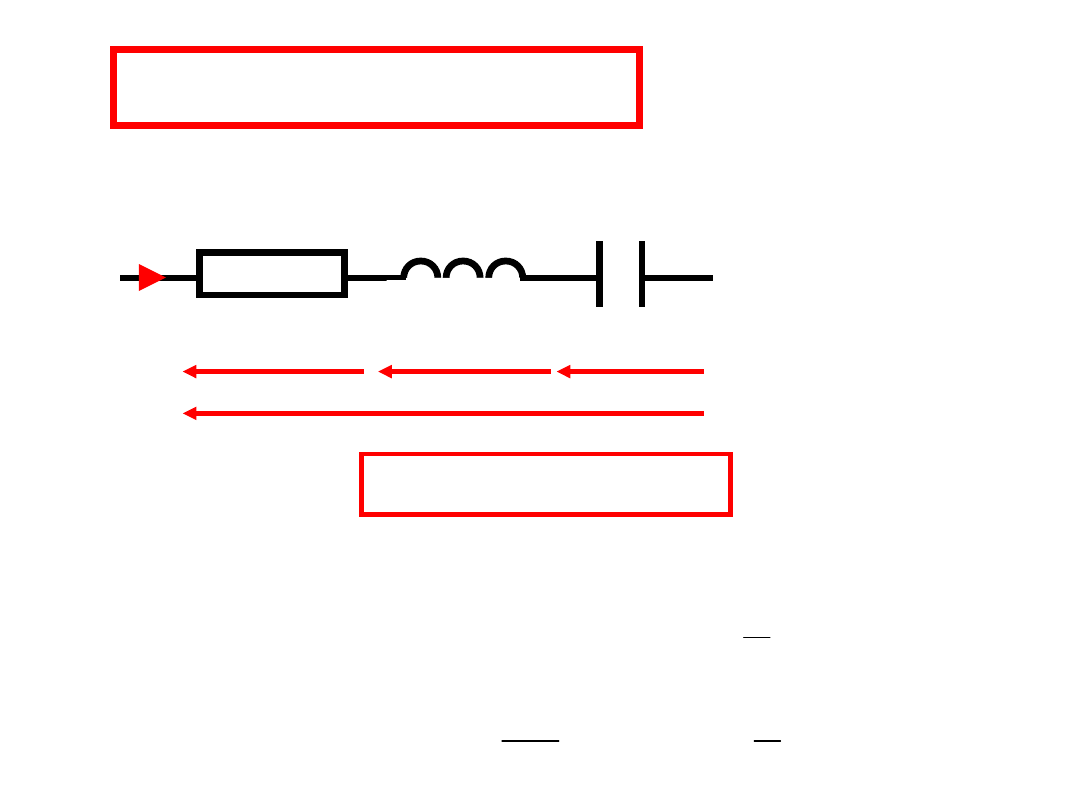
Połączenie R L C

R

L

C

u

R

u

L

u

C

u

i

)

sin(

)

(

i

m

t

I

t

i









Przyjmijmy, że













































2

sin

1

2

sin

sin





















i

m

C

i

m

L

i

m

R

t

C

I

u

t

L

I

u

t

R

I

u













































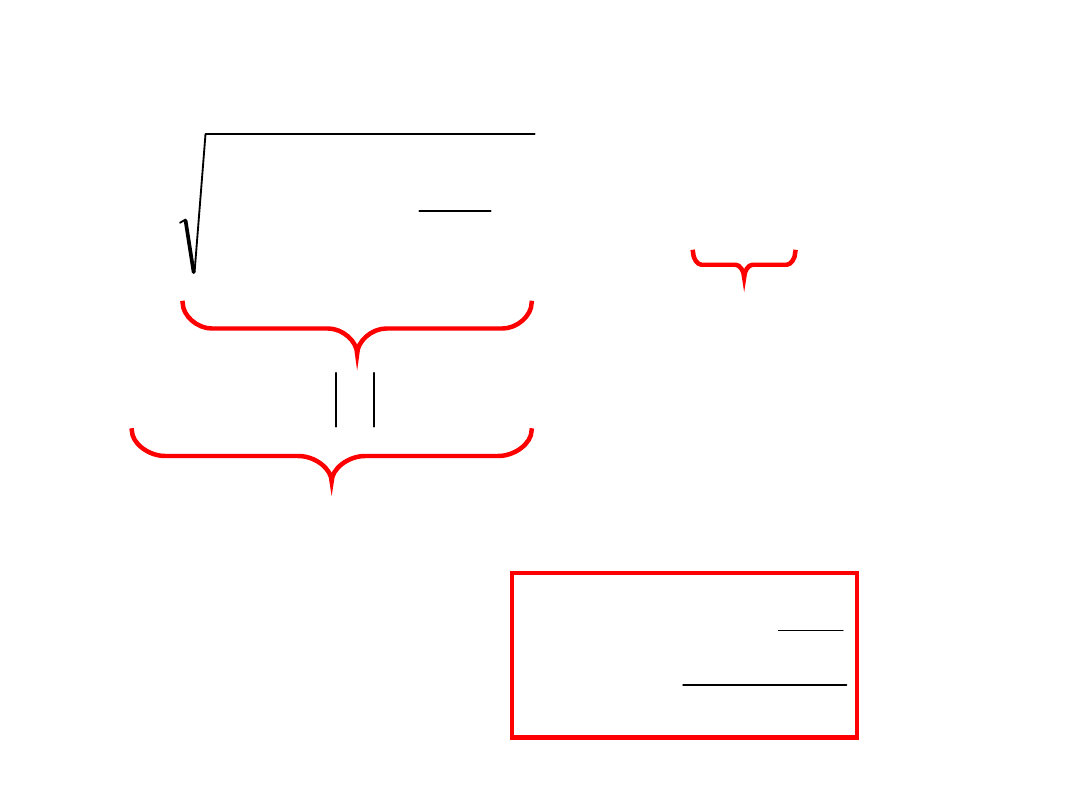
i

m

C

L

R

t

C

L

R

I

u

u

u

u

sin

1

2

2

Z

U

m

u



R

C

L

tg

arc







1





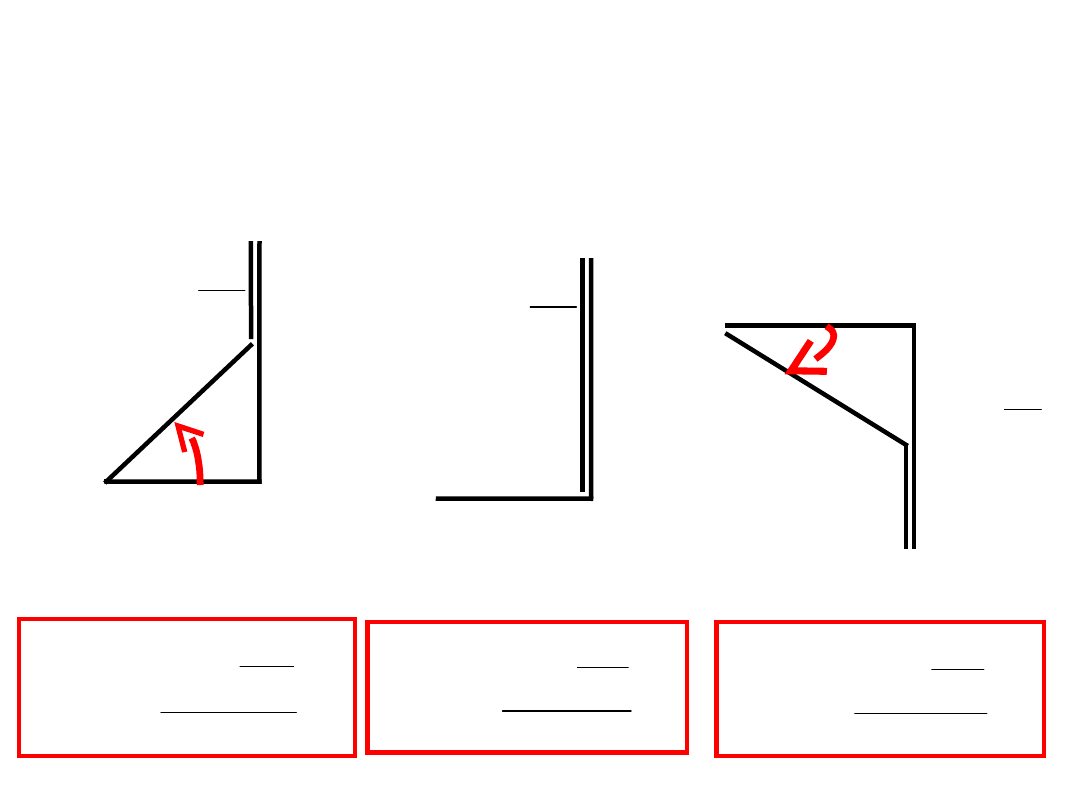
Takiemu połączeniu odpowiada trójkąt impedancji:

0

1







R

C

L

tg

arc







0

1







R

C

L

tg

arc







0

1







R

C

L

tg

arc







R

C

X

C



1





L

X

L





R

C

X

C



1





L

X

L





R

C

X

C



1





L

X

L





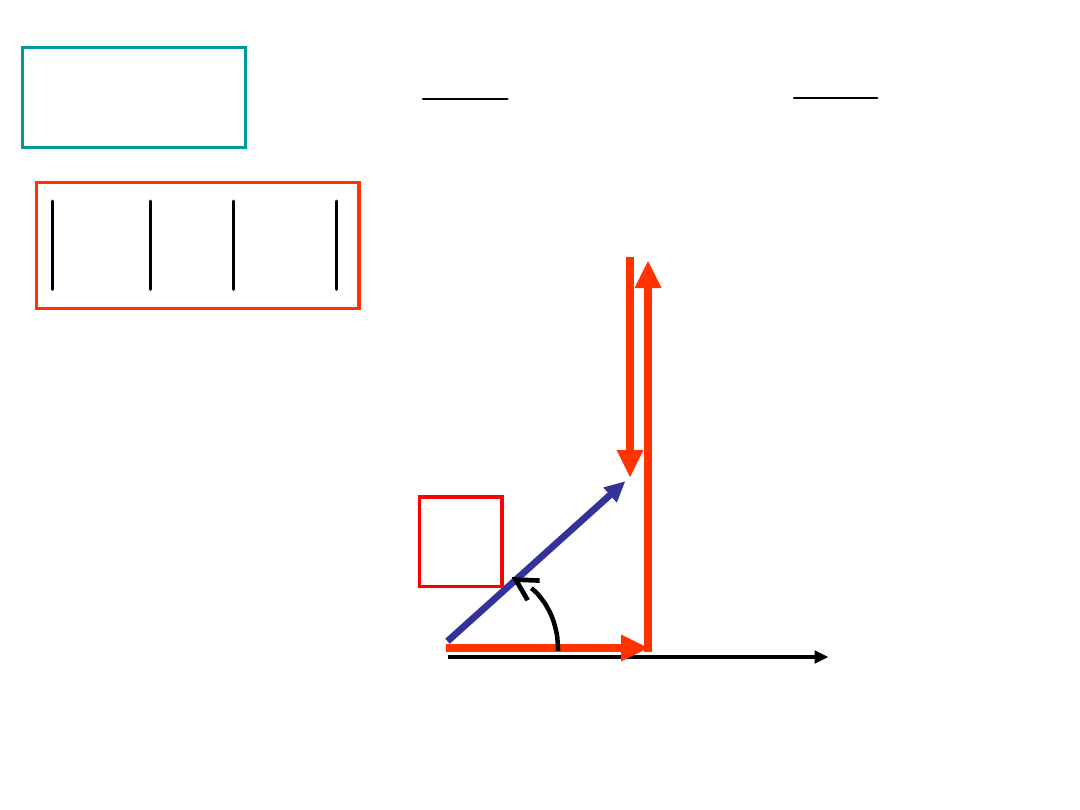
0



X

0

1





C

L





C

L





1



C

L

U

U 

I

RI

U

R



L

U

C

U

U



0





OBWÓD O CHARAKTERZE INDUKCYJNYM

OBWÓD O CHARAKTERZE INDUKCYJNYM

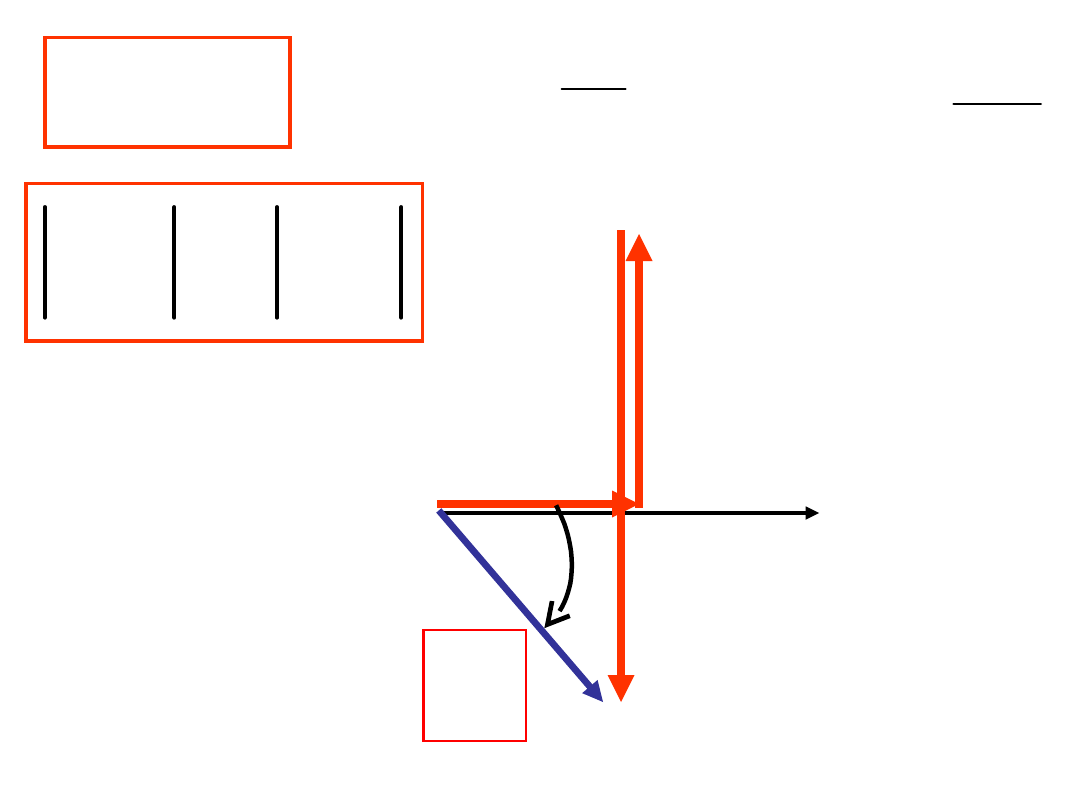
0



X

0

1





C

L





C

L





1



L

C

U

U 

I

RI

U

R



L

U

C

U

U



0





OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

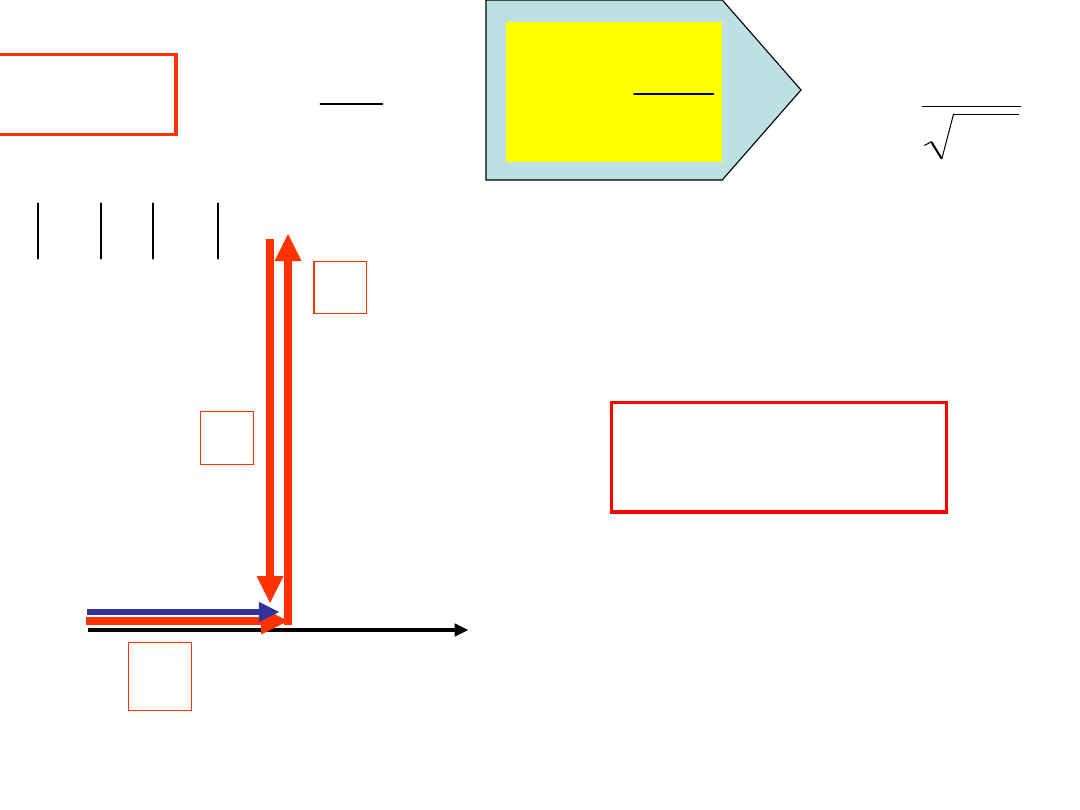
0



X

0

1





C

L





C

L





1



C

L

U

U 

I

U

L

U

C

U

R

U



0





OBWÓD O CHARAKTERZE REZYSTANCYJNYM

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

LC

1

r





0

)

(



r

X



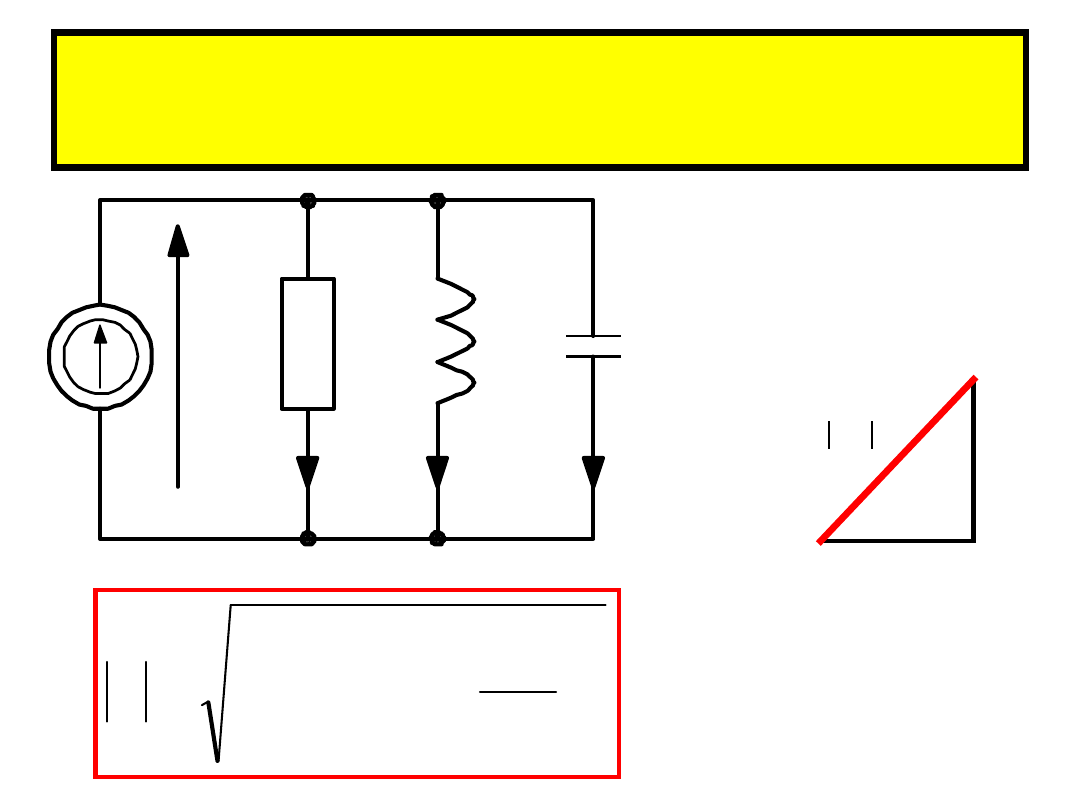
Połączenie równoległe RLC

I

L

I

C

I

R

I

U

G

L

C

2

2

1



















L

C

G

Y





G

B

Y

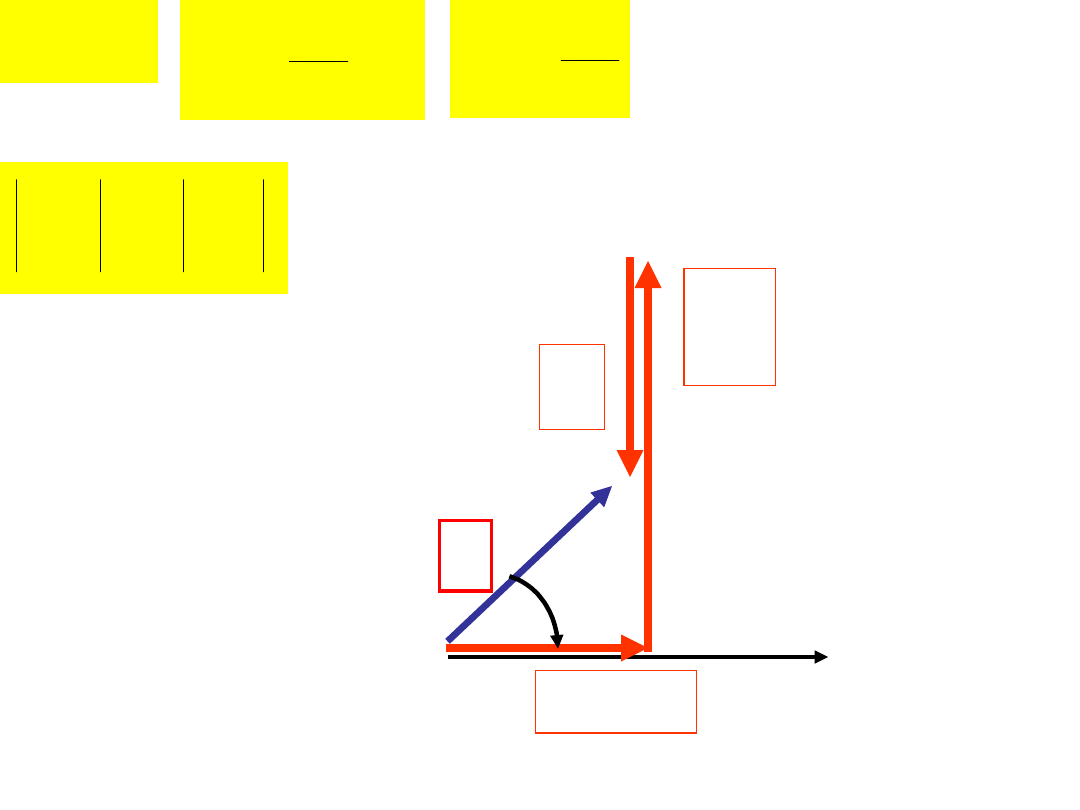
0



B

0

1





L

C





L

C





1



L

C

I

I 

U

GU

I

R



C

I

L

I

I



0





OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

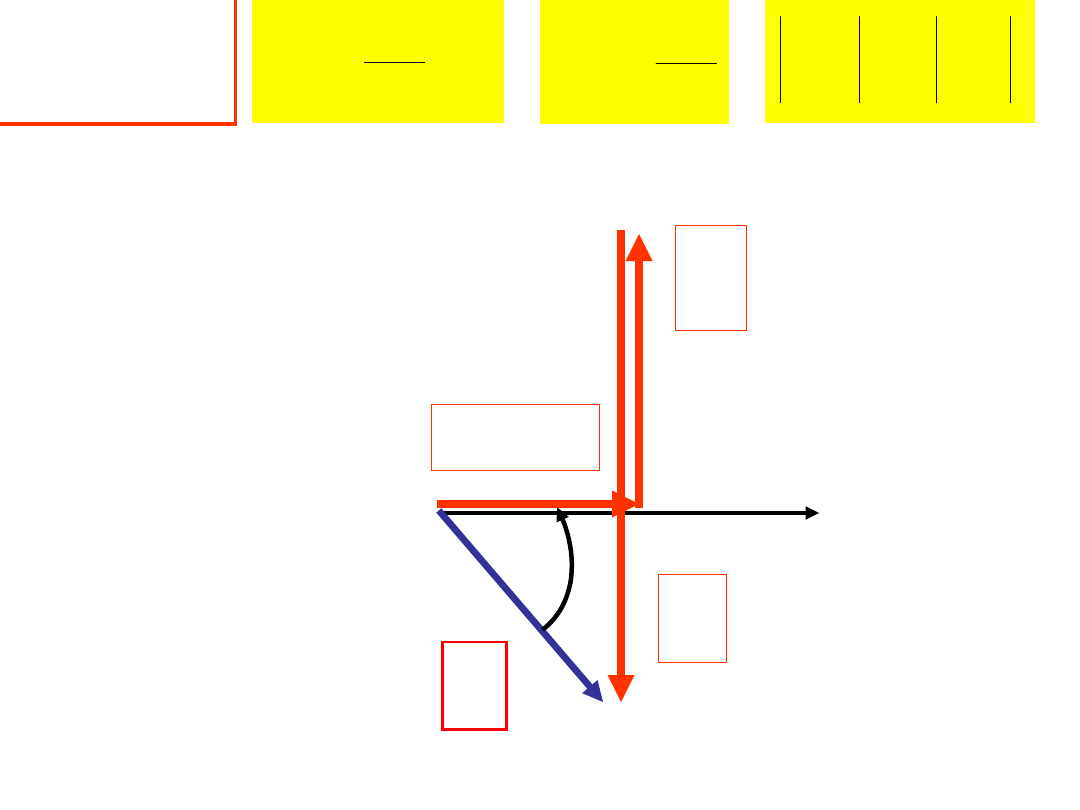
0



B

0

1





L

C





L

C





1



L

C

I

I 

U

GU

I

R



c

I

L

I

I



0





OBWÓD O CHARAKTERZE INDUKCYJNYM

OBWÓD O CHARAKTERZE INDUKCYJNYM

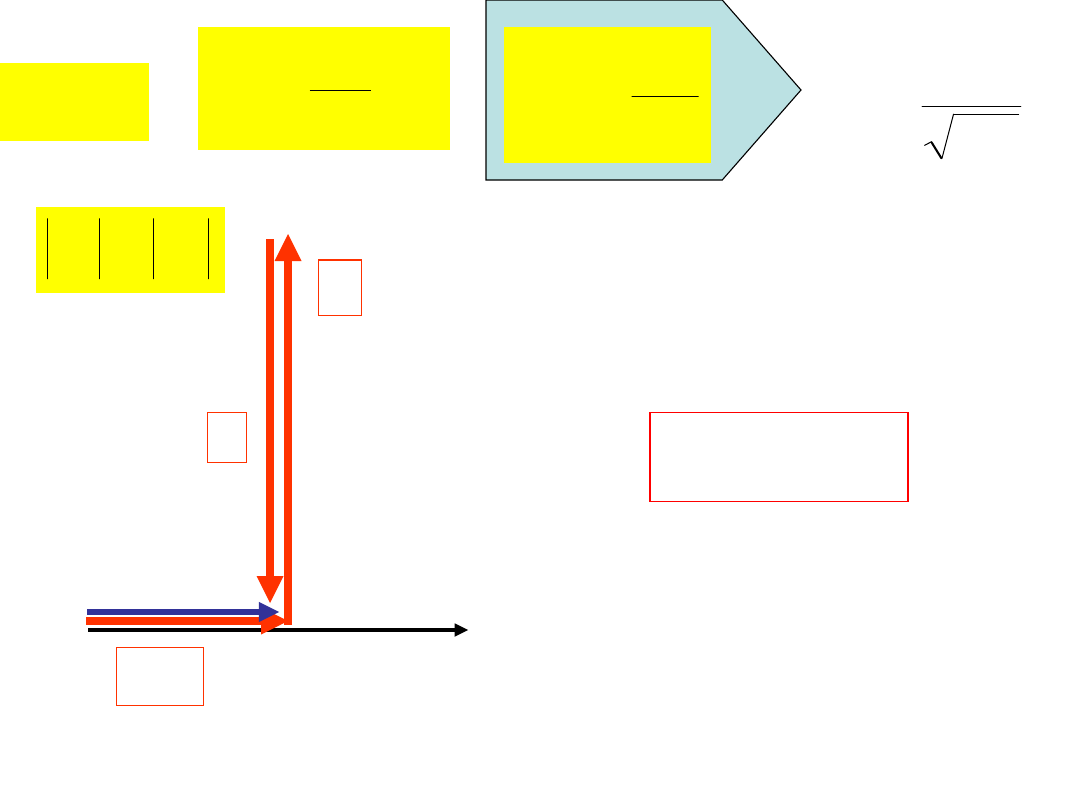
0



B

0

1





L

C





L

C





1



C

L

I

I 

U

GU

C

I

L

I

R

I

I 



0





OBWÓD O CHARAKTERZE REZYSTANCYJNYM

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

LC

1

r





0



)

(

B

r



Moce

w obwodach prądu sinusoidalnie zmiennego

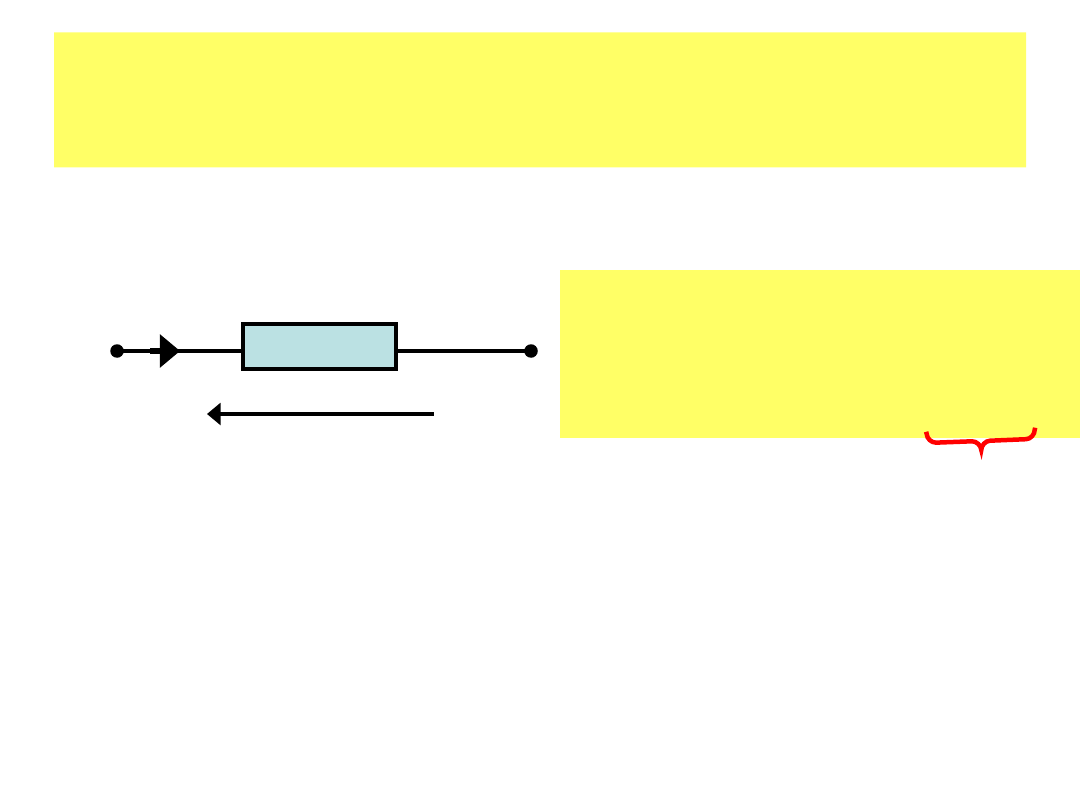
Moc chwilowa, czynna i

bierna

i

u

Mocą chwilową dwójnika nazywamy iloczyn wartości
chwilowych prądu

i

i napięcia

u

.





























i

m

i

m

t

U

u

t

I

i

sin

sin



 























i

i

m

m

t

t

I

U

ui

p

sin

sin

u



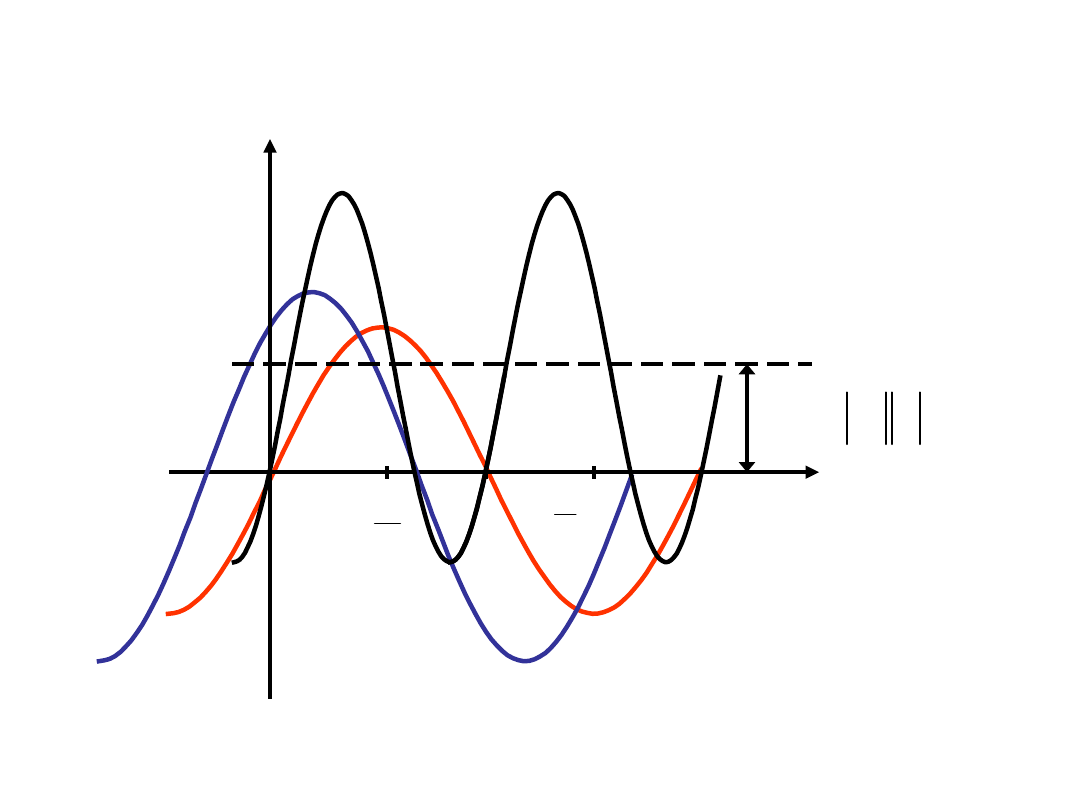
u,i,p



cos

I

U

P 

p

i

u



2

3

2





0



2

t



D E FIN IC J A

M ocą cz ynną P dw ójnika ( u,i są w ielkościam i okresow y m i)

nazyw am y w artość średnią za okres m ocy chw ilow ej:







T

pdt

T

p

P

0

1

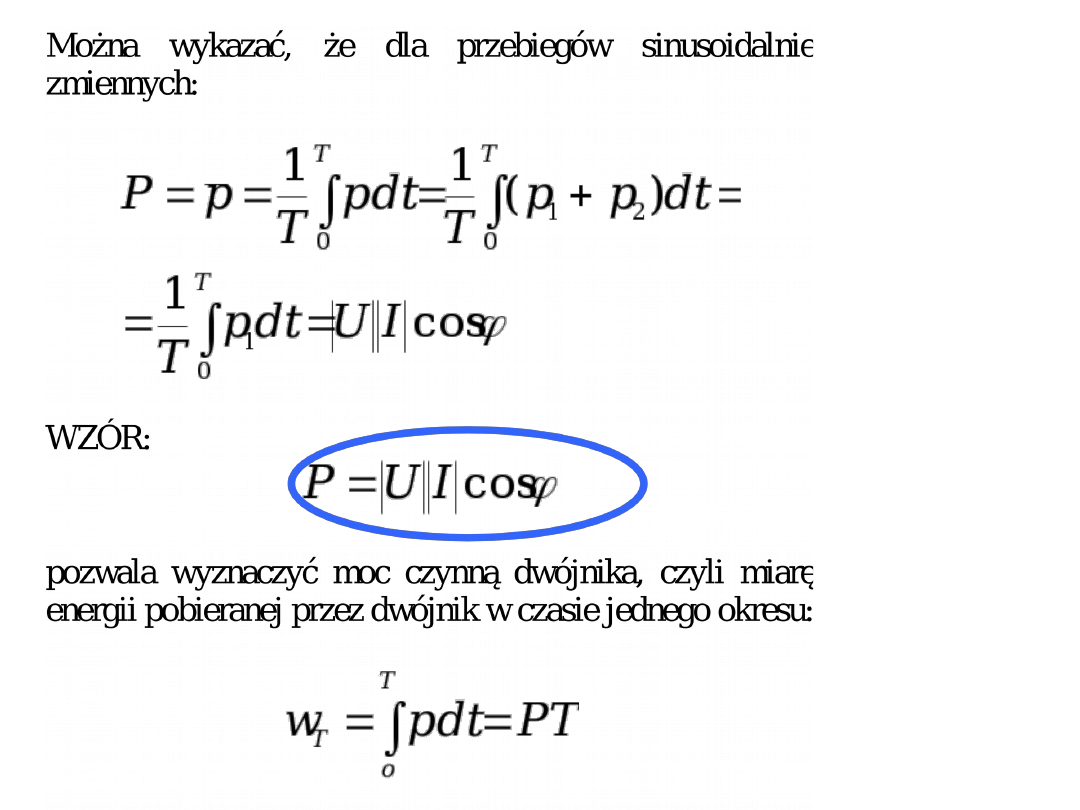
t



0

2





p

,

p

1

,

p

2

p

p

1

p

2

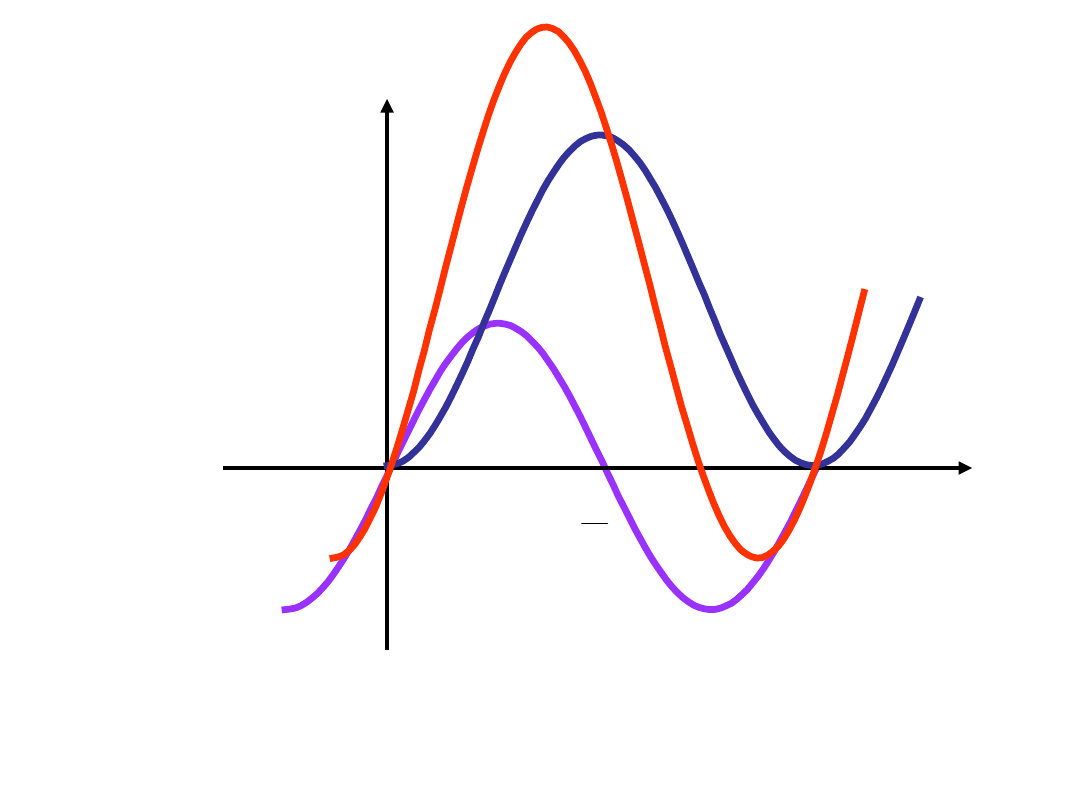
Rozkład mocy chwilowej na moc tętniącą i moc przemienną

p

1

p

2

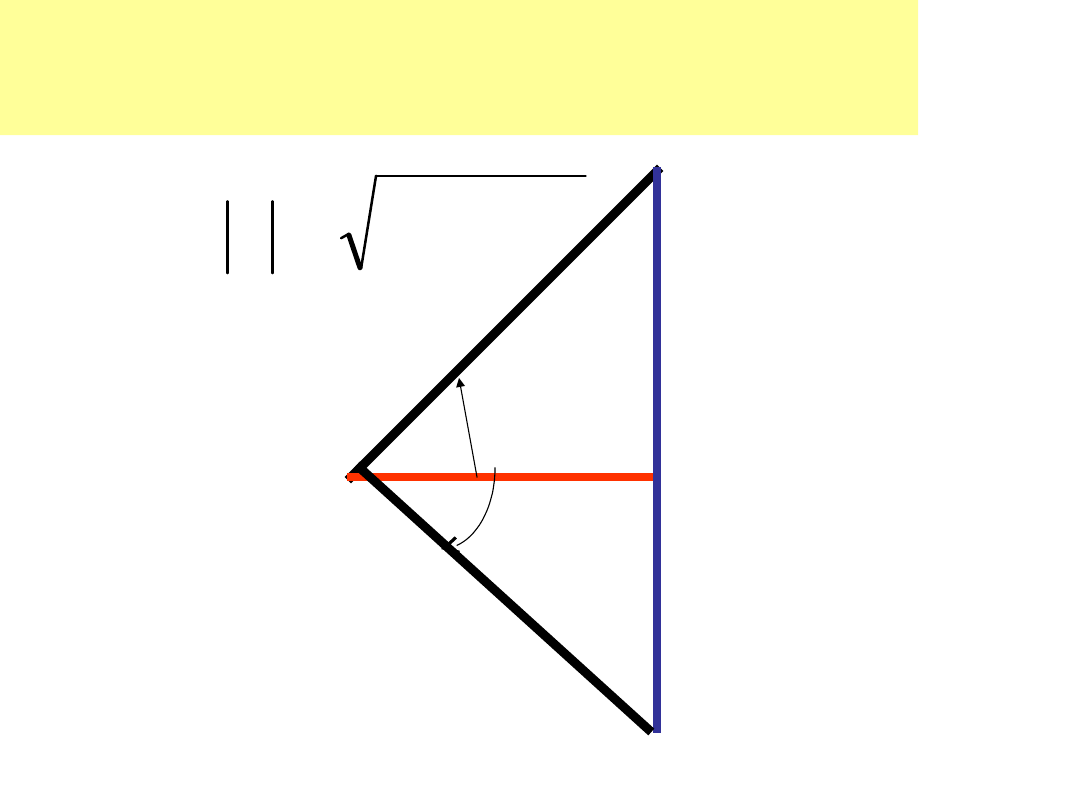
Trójkąt mocy

Q>0

P

2

2

Q

P

S







Q<0