Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody
Elektryczne I

Obwody
Elektryczne I

Zakład Układów i Systemów Nieliniowych

dr Marek Korzybski

email:

[e-mail]

godz. konsultacji: wtorek 12-13

tel. [phone]

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

2

Literatura

Literatura

1.

Michał Tadeusiewicz -

Teoria

Obwodów,

część I, Wydawnictwo PŁ,

Łódź 2003

2.

Jerzy Osiowski, Jerzy Szabatin -

Podstawy Teorii Obwodów,

tom I,

WNT, Warszawa 1992

3.

Teoria Obwodów - zadania

pod

redakcją M. Tadeusiewicza,
Wydawnictwo PŁ

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

3

Wiadomości
elementarne

Wiadomości
elementarne

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

4

Wiadomości elementarne

Wiadomości elementarne

•

Prąd elektryczny to zjawisko fizyczne polegające na
uporządkowanym ruchu ładunków elektrycznych
wywołanym działaniem pola elektrycznego. Kierunkiem
prądu jest kierunek ruchu ładunków dodatnich, tzn. od
punktu o wyższym do punktu o niższym potencjale.
Określenia prąd elektryczny używa się także jako skrótu
terminu natężenie prądu elektrycznego, który
oznacza granicę stosunku ładunku elektrycznego Δq
przepły-wającego w ciągu pewnego czasu Δt przez
poprzeczny przekrój przestrzeni do rozpatrywanego
czasu, gdy czas dąży do zera

dt

dq

t

q

lim

i

t













0

Jednostka prądu
to amper - 1A

Jednostka prądu
to amper - 1A

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

5

Wiadomości elementarne

Wiadomości elementarne

• Napięcie jest wielkością skalarną charakteryzującą

potencjalne pole elektryczne i wyraża się
stosunkiem pracy potrzebnej do przesunięcia
dodatniego ładunku z punktu B do A, do wartości
tego ładunku. Jednostka napięcia to wolt – 1V.
Napięcie między punktami A oraz B jest różnicą
potencjałów tych punktów. Napięcie oznaczamy
literą

u

oraz strzałką z grotem skierowanym do

punktu o wyższym potencjale, tzn. punktu, którego
potencjał występuje we wzorze określającym
napięcie między punktami A i B jako odjemna.

B

A

AB

V

V

u





Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

6

Wiadomości elementarne

Wiadomości elementarne

• Obwód elektryczny to połączenie elementów

elektrycznych umożliwiające przepływ prądu
elektrycznego.

• Schemat obwodu to jego graficzne odwzorowanie.

Schemat zawiera informacje o elementach tworzących
obwód przedstawionych za pomocą symboli oraz o
sposobie ich połączenia.

• Elementy obwodu elektrycznego są połączone

przewodami. Najczęściej zakłada się, że są one idealnie
przewodzące. Oznacza to, że przy przepływie prądu
elektrycznego napięcie między końcami przewodu jest
zawsze równe 0.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

7

Wiadomości elementarne

Wiadomości elementarne

• Gałąź obwodu elektrycznego to jego część posiadająca

dwa końce określane jako węzły. Jest ona związana z
elementem obwodu.

• Węzeł obwodu to punkt połączenia dwóch lub większej

liczby gałęzi.

• Celem analizy obwodu elektrycznego jest zwykle

wyznaczenie prądów płynących w gałęziach obwodu oraz
napięć pomiędzy jego węzłami

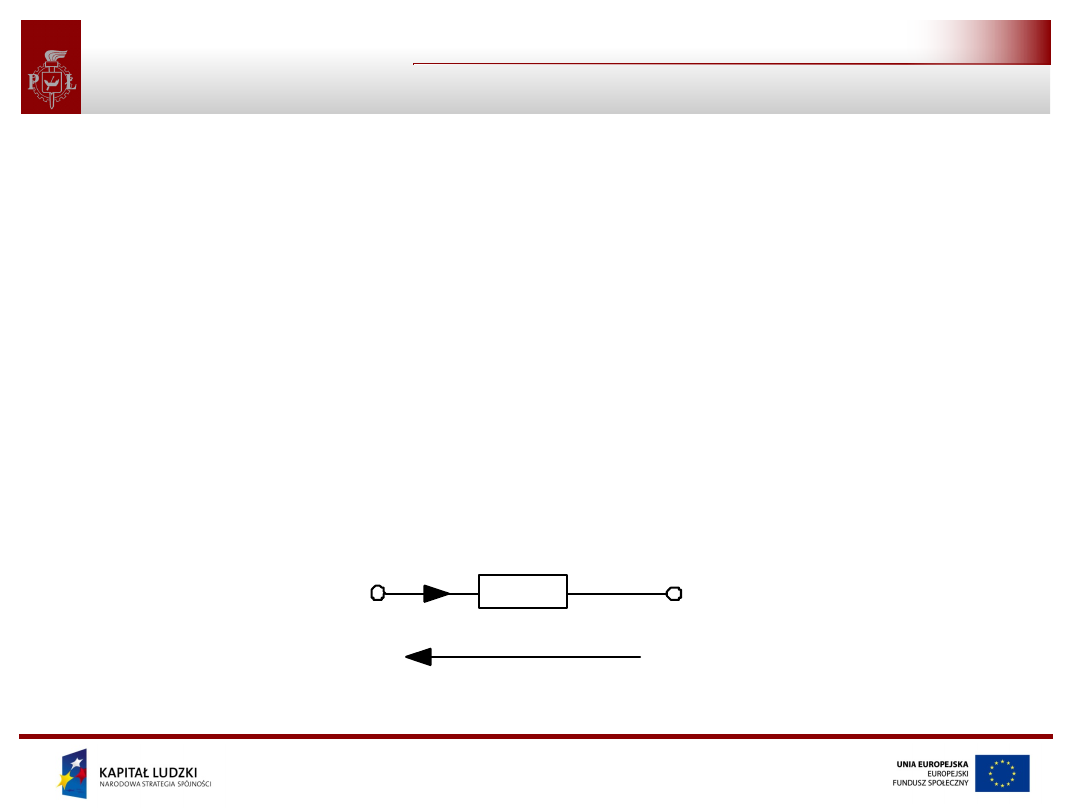
• Strzałki umieszczane na schematach związane z prądami i

napięciami wyznaczają kierunki odniesienia tych
wielkości. Rzeczywiste kierunki to te, które wynikają z
uwzględnienia kierunku strzałki (kierunku odniesienia) oraz
wartości liczbowej związanej z tym kierunkiem.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

8

Wiadomości elementarne

Wiadomości elementarne

• Ustalono, że kierunkiem przepływu prądu elektrycznego

jest kierunek ruchu ładunków dodatnich, tzn. od punktu
o wyższym do punktu o niższym potencjale. Strzałka
napięcia wskazuje punkt o wyższym potencjale. Jeżeli
napięcie i prąd pewnego elementu (gałęzi) mają mieć
jednocześnie wartości dodatnie lub jednocześnie
ujemne to kierunki odniesienia prądu i napięcia muszą
być przeciwne (jak na rysunku poniżej). Kierunki takie
określa się jako stowarzyszone kierunki odniesienia
napięcia i prądu.

i(t)

1

2

u(t)

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

9

Elementy obwodów
elektrycznych

Elementy obwodów
elektrycznych

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

10

Elementy obwodów elektrycznych

Elementy obwodów elektrycznych

• Element obwodu elektrycznego to jego część

niepodzielna pod względem funkcjonalnym na danym
poziomie dokładności rozważań.

• Z elementami obwodu są związane trzy rodzaje

procesów energetycznych:

- wytwarzanie energii elektrycznej,
- akumulacja energii,
- rozpraszanie energii.
• W schematach obwodu umieszczane są zwykle

elementy idealne, tzn. takie, które są związane
wyłącznie z jednym rodzajem procesu energetycznego.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

11

Elementy obwodów elektrycznych

Elementy obwodów elektrycznych

• Rozpatrywane będą obwody o parametrach skupionych. Ich

wymiary są znacznie mniejsze od długości fali
elektromagnetycznej. Mogą być przedstawione za pomocą
elementów skupiających przypisane im właściwości w
określonych punktach przestrzeni. Elementy są połączone
bezoporowymi przewodami.

• Klasyfikacja elementów w zależności od liczby końcówek
- elementy dwukońcówkowe, dwójniki
- elementy wielokońcówkowe, wśród których bardzo ważne

to trójniki (elementy o trzech końcówkach) oraz czwórniki
(elementy o dwóch parach końcówek).

• Rozpatrywane będą obwody stacjonarne. Elementy takiego

obwodu i jego sposób połączeń nie są funkcją czasu.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

12

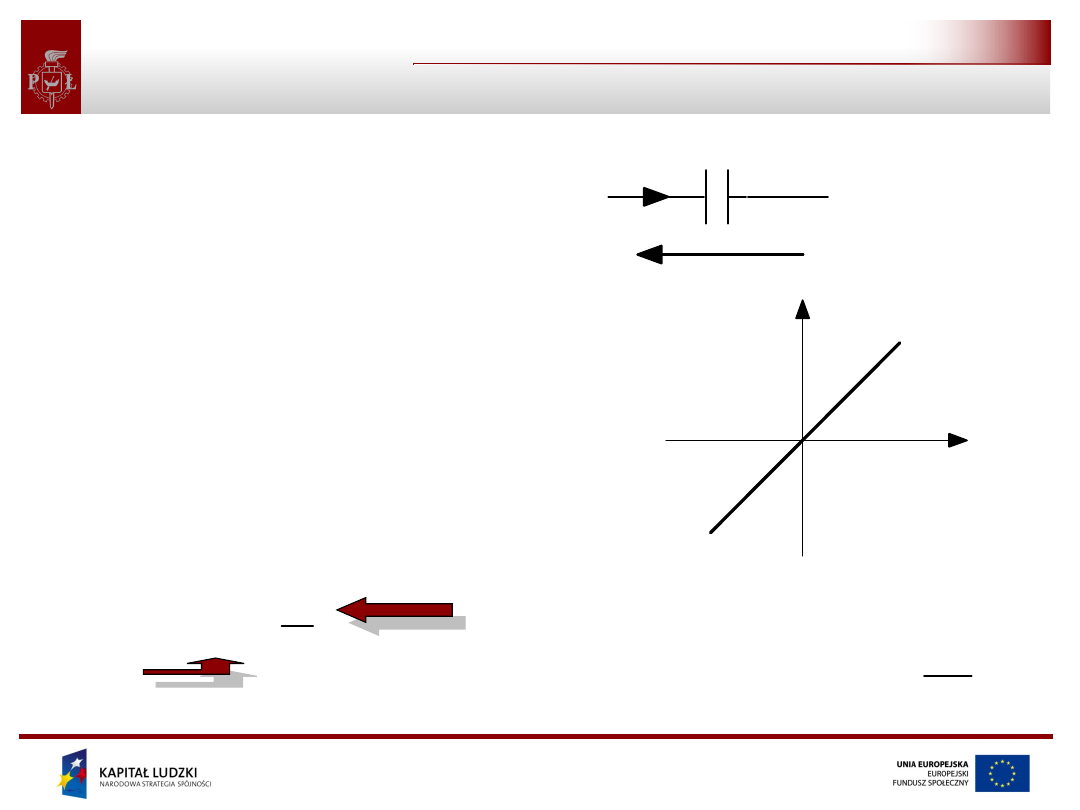
Opornik liniowy

Opornik liniowy

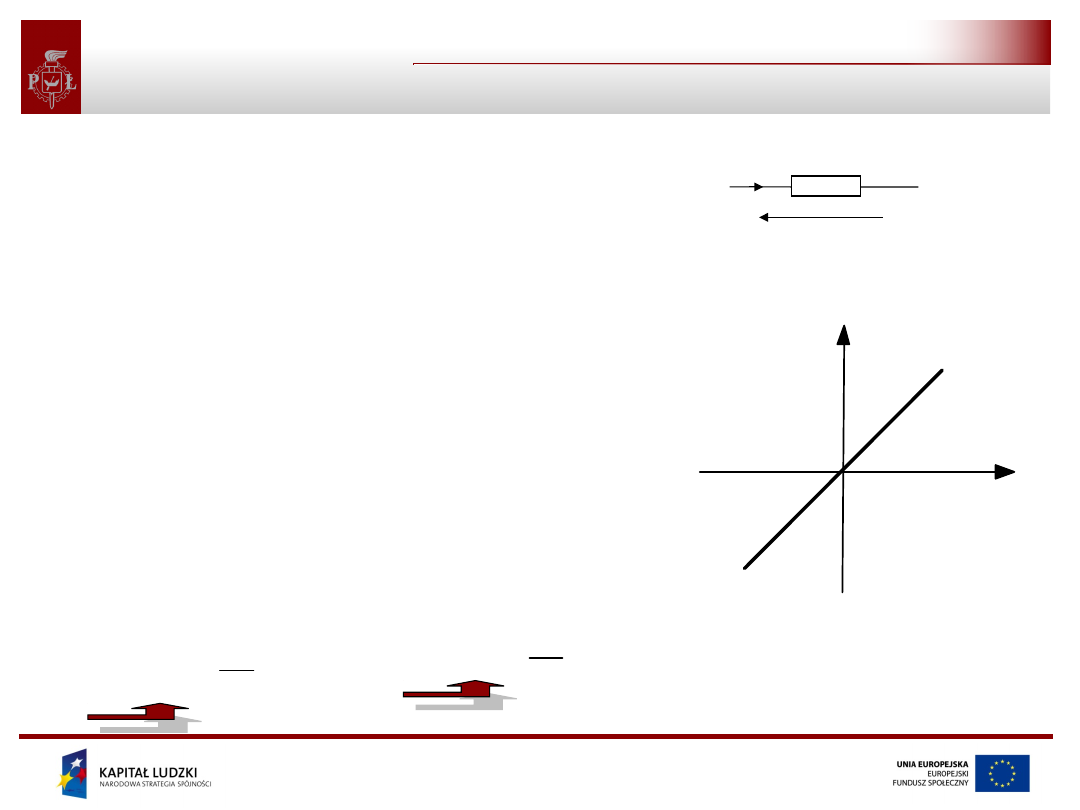
• Idealny opornik jest elementem,

którego jedyną własnością jest
rozpraszanie pobieranej z obwodu
energii.

• Opornik liniowy to taki, którego

charakterystyka napięciowo-
prądowa (wykres zależności
napięcia w funkcji prądu) jest linią
prostą przechodzącą przez początek
układu współrzędnych.

• Dla opornika liniowego obowiązuje

prawo Ohma

i

R

u 

Gu

i 

u(t)

i(t)

symbol opornika liniowego

symbol opornika liniowego

i

u

charakterystyka napięciowo-
prądowa opornika liniowego

charakterystyka napięciowo-
prądowa opornika liniowego

lub

lub

R - rezystancja
(opór elektryczny)

R - rezystancja
(opór elektryczny)

G - konduktancja
(przewodność)

G - konduktancja
(przewodność)

A

V

1

1 



A

V

1

S

1 

o
m

o
m

simens

simens

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

13

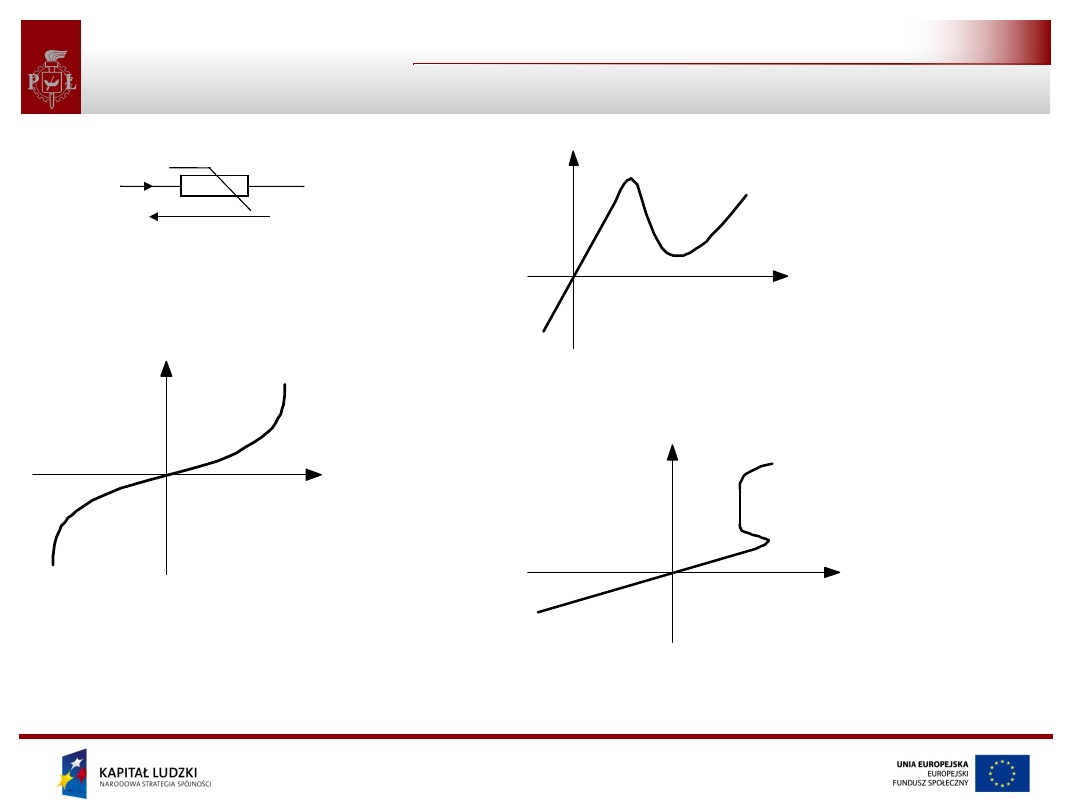
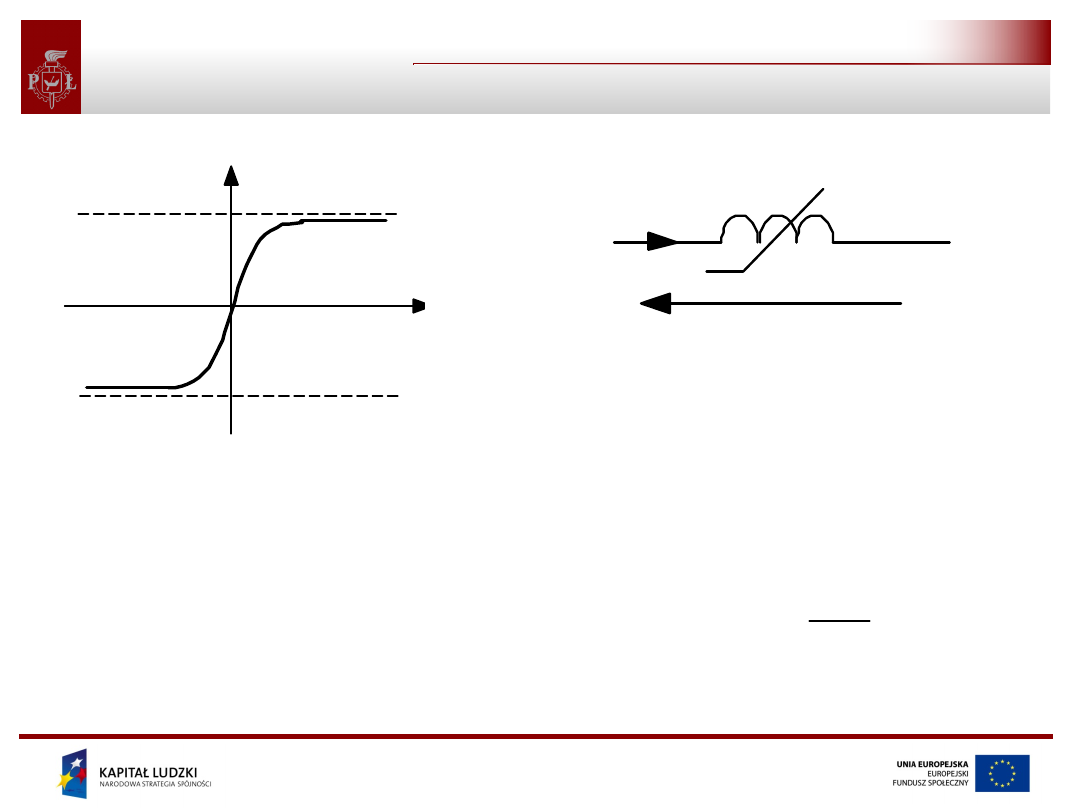
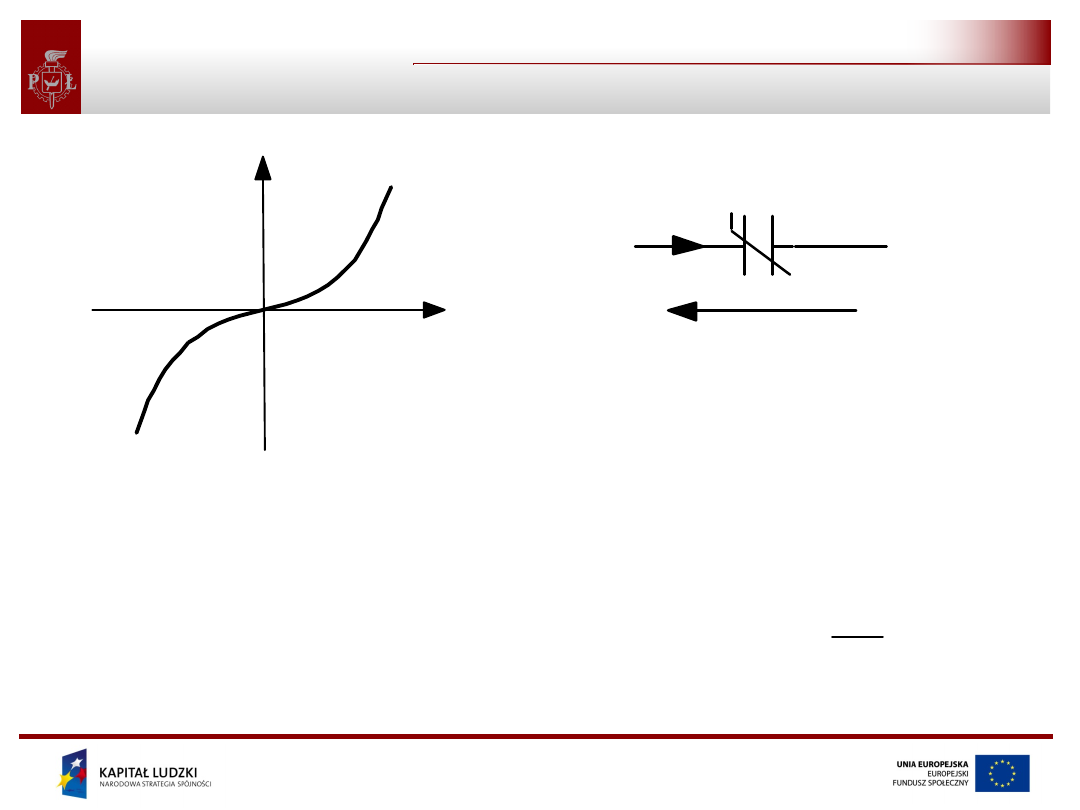
Opornik nieliniowy

Opornik nieliniowy

i

u

i

u

i

u

u(t)

i(t)

symbol opornika
nieliniowego

symbol opornika
nieliniowego

charakterystyka opornika
nieliniowego – opornik
nieuzależniony

charakterystyka opornika
nieliniowego – opornik
nieuzależniony

charakterystyka opornika nieliniowego
– opornik zależniony prądowo

charakterystyka opornika nieliniowego
– opornik zależniony prądowo

charakterystyka opornika nieliniowego
– opornik uzależniony napięciowo

charakterystyka opornika nieliniowego
– opornik uzależniony napięciowo

 

 

i

f

u

u

f

i

R

G





 

 

u

f

i

i

f

u

G

R





 

 

i

f

u

u

f

i

1







Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

14

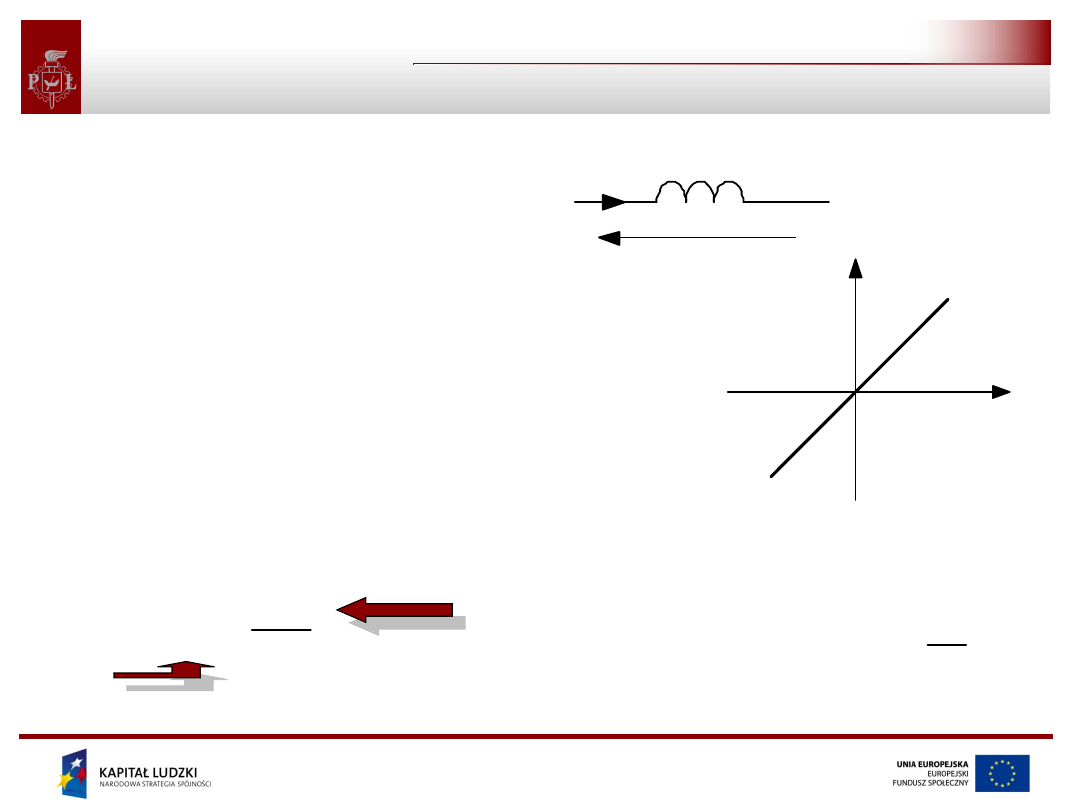
Cewka liniowa

Cewka liniowa

• Idealna cewka to element,

którego jedyną własnością jest
gromadzenie energii pobieranej z
obwodu w polu magnetycznym.

• Cewka liniowa to taka, której

strumień magnetyczny skojarzony
jest proporcjonalny do prądu
płynącego przez cewkę

• Dla cewki liniowej obowiązuje

zależność:

Li





L – indukcyjność cewki

L – indukcyjność cewki

A

Wb

1

H 

1

L

i

u

i

y

Ψ

i

charakterystyka cewki liniowej

charakterystyka cewki liniowej

napięcie cewki
liniowej

napięcie cewki
liniowej

t

i

L

u

d

d



symbol cewki
liniowej

symbol cewki
liniowej

henr

henr

weber

weber

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

15

Cewka nieliniowa

Cewka nieliniowa

 

nieliniowa

funkcja

f

i

f







przykładowa charakterystyka
cewki nieliniowej

przykładowa charakterystyka
cewki nieliniowej

symbol cewki nieliniowej

symbol cewki nieliniowej

t

u

d

d



napięcie panujące na zaciskach
cewki nieliniowej

napięcie panujące na zaciskach
cewki nieliniowej

y

i

Ψ

i

i

u

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

16

Kondensator liniowy

Kondensator liniowy

• Idealny kondensator to

element, którego jedyną
własnością jest gromadzenie
energii pobieranej z obwodu w
polu elektrycznym.

• Kondensator liniowy to taki, w

którym napięcie u między
okładkami jest proporcjonalne do
gromadzonego na okładkach
ładunku q.

• Dla kondensatora liniowego

obowiązuje zależność:

u

C

q 

C – pojemność kondensatora

C – pojemność kondensatora

V

C

1

F 

1

farad

farad

kulomb

kulomb

i

q

q

u

charakterystyka kondensatora liniowego

charakterystyka kondensatora liniowego

t

u

C

i

d

d



prąd kondensatora
liniowego

prąd kondensatora
liniowego

C

i

u

symbol
kondensatora

symbol
kondensatora

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

17

Kondensator nieliniowy

Kondensator nieliniowy

u

q

i

u

 

nieliniowa

funkcja





f

q

f

u

przykładowa charakterystyka
kondensatora nieliniowego

przykładowa charakterystyka
kondensatora nieliniowego

symbol kondensatora
nieliniowego

symbol kondensatora
nieliniowego

t

q

i

d

d



prąd płynący przez kondensator
nieliniowy

prąd płynący przez kondensator
nieliniowy

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

18

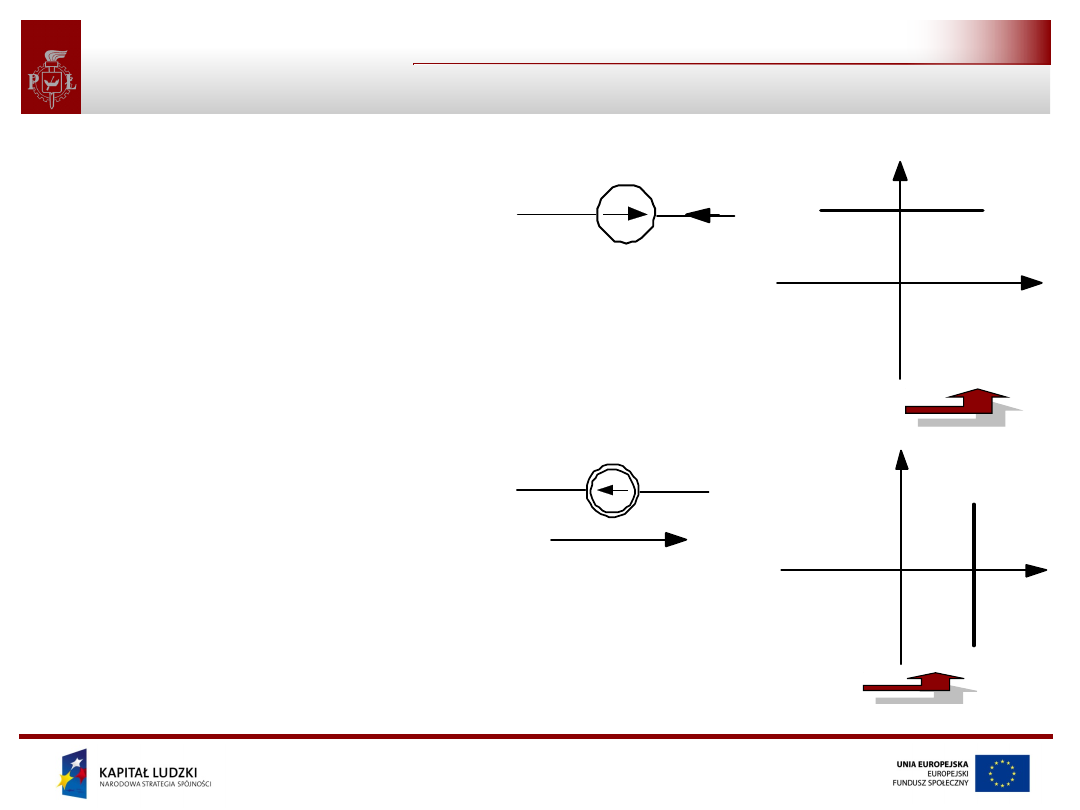
Źródła niezależne

Źródła niezależne

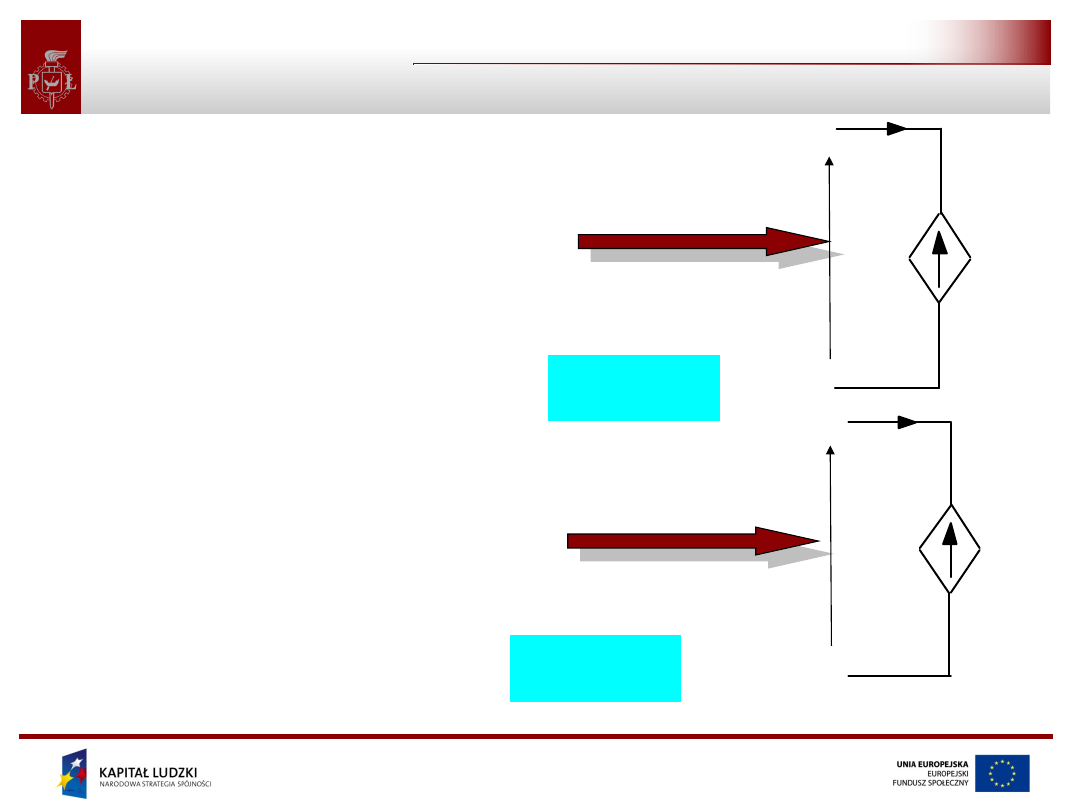
• Idealne źródło napięcia jest

takim elementem, na
zaciskach którego panuje
napięcie niezalażne od
płynącego przez źródło prądu
(może być tylko funkcją
czasu).

• Idealne źródło prądu jest

takim elementem, przez
którey płynie prąd niezalażny
od napięcia panującego na
zaciskach źródła (może być
tylko funkcją czasu).

i

u

z

u

i

i

z

u

u

i

symbol idealnego
źródła napięcia

symbol idealnego
źródła napięcia

symbol idealnego
źródła prądu

symbol idealnego
źródła prądu

charakterystyka idealnego źródła napięciowego

charakterystyka idealnego źródła napięciowego

charakterystyka idealnego źródła prądowego

charakterystyka idealnego źródła prądowego

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

u

Obwody Elektryczne I

19

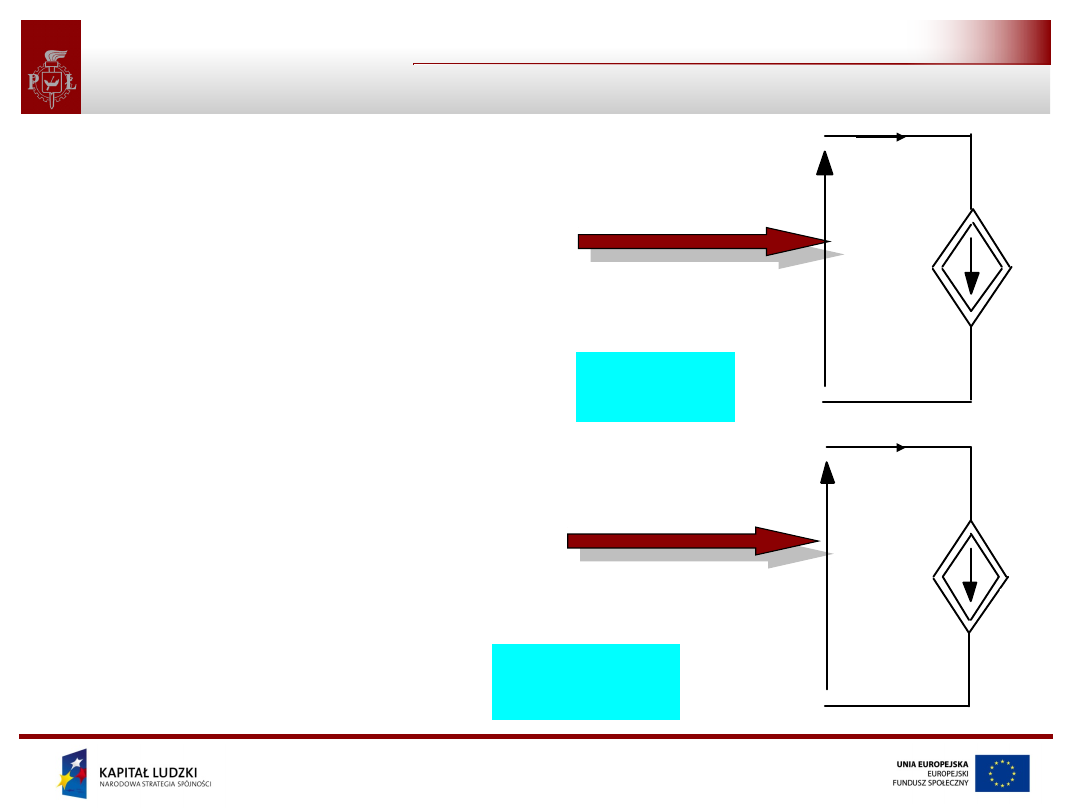
Źródła napięciowe sterowane

Źródła napięciowe sterowane

• Źródło napięciowe

sterowane napięciowo

• Źródło napięciowe

sterowane prądowo

i

u=f (u )

x

i

u=r(i )

x

u

symbol źródła

symbol źródła

symbol źródła

symbol źródła

dla źródła nieliniowego

dla źródła nieliniowego

dla źródła liniowego

dla źródła liniowego

dla źródła liniowego

dla źródła liniowego

dla źródła nieliniowego

dla źródła nieliniowego

x

u

k

u

1



 

x

u

f

u

1



 

x

i

f

u

2



x

i

k

u

2



Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

i

Obwody Elektryczne I

20

Źródła prądowe sterowane

Źródła prądowe sterowane

• Źródło prądowe

sterowane napięciowo

• Źródło prądowe

sterowane prądowo

i

symbol źródła

symbol źródła

symbol źródła

symbol źródła

dla źródła nieliniowego

dla źródła nieliniowego

dla źródła liniowego

dla źródła liniowego

dla źródła liniowego

dla źródła liniowego

dla źródła nieliniowego

dla źródła nieliniowego

i=g(u )

x

u

i=h(i )

x

u

 

x

u

f

i

3



x

u

k

i

3



 

x

i

f

i

4



x

i

k

i

4



Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

21

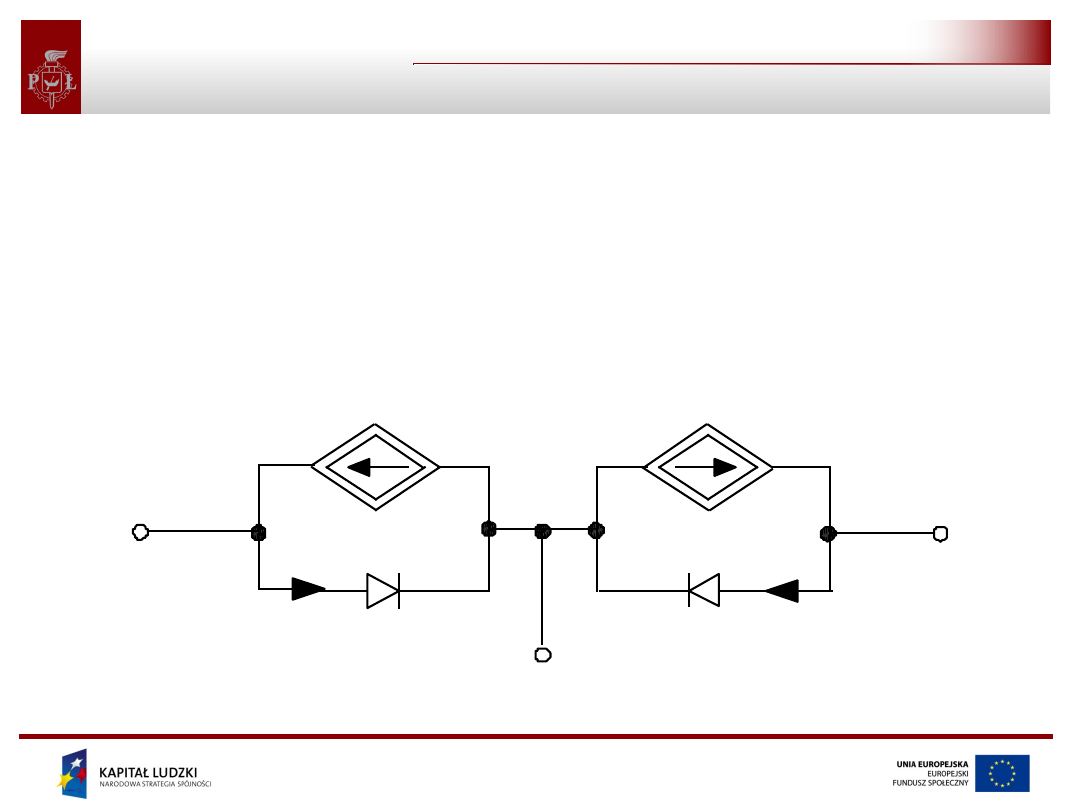
Przykład zastosowania źródel
sterowanych

Przykład zastosowania źródel
sterowanych

Przedstawiony poniżej układ zawiera dwa źródła prądowe sterowane
prądowo. Jest to schemat zastępczy tranzystora bipolarnego
nazywany modelem Ebersa – Molla. Jest przykładem praktycznego
zastosowania źródeł sterowanych.

Przedstawiony poniżej układ zawiera dwa źródła prądowe sterowane
prądowo. Jest to schemat zastępczy tranzystora bipolarnego
nazywany modelem Ebersa – Molla. Jest przykładem praktycznego
zastosowania źródeł sterowanych.

E

ˆ i

r r

ˆ i

f

f

C

i

r

i

f

B

α

f

i

f

α

r

i

r

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

22

Proste połączenia
rezystorów

Proste połączenia
rezystorów

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

23

Połączenie szeregowe

Połączenie szeregowe





i

R

R

i

R

i

R

u

u

u

2

1

2

1

2

1













2

1

R

R

i

u

R

z







2

1

R

R

R

z





n

z

R

...

R

R

R









2

1

u

R

1

R

2

u

2

u

1

i

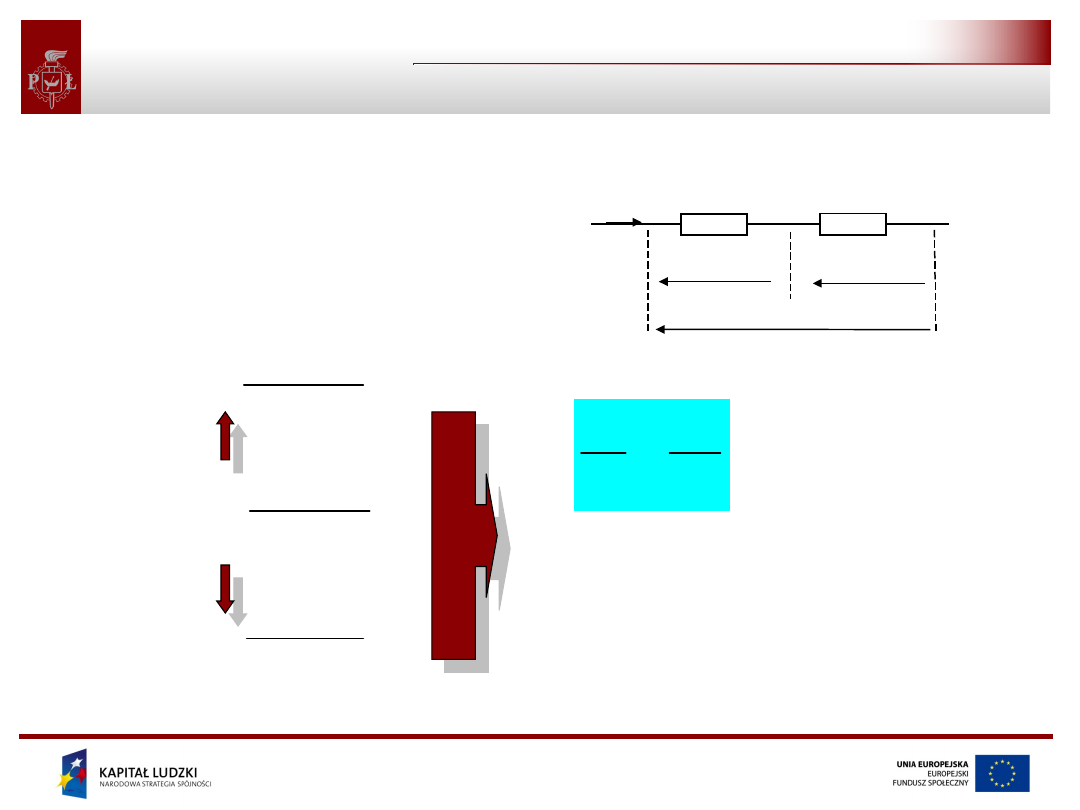
Połączenie szeregowe to takie, w którym
przez połączone elementy płynie ten sam
prąd.
Wyznaczamy rezystancję zastępczą
połączenia szeregowego.

Połączenie szeregowe to takie, w którym
przez połączone elementy płynie ten sam
prąd.
Wyznaczamy rezystancję zastępczą
połączenia szeregowego.

prawo Ohma

prawo Ohma

dla dwóch oporników
połączonych szeregowo

dla dwóch oporników
połączonych szeregowo

dla wielu oporników
połączonych szeregowo

dla wielu oporników
połączonych szeregowo

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

24

Połączenie szeregowe – dzielnik napięcia

Połączenie szeregowe – dzielnik napięcia

2

1

R

R

u

i





u

R

R

R

i

R

u

2

1

2

2

2







2

1

2

1

R

R

u

u



u

R

1

R

2

u

2

u

1

i

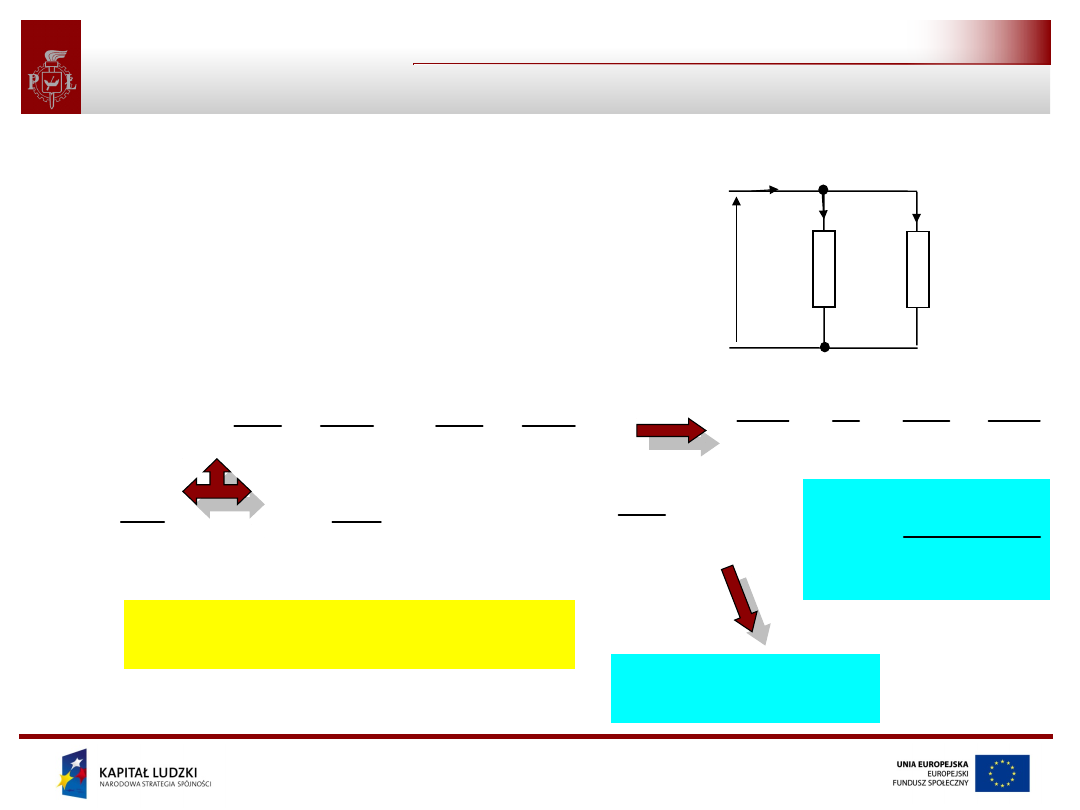
Połączenie szeregowe jest
dzielnikiem napięcia dołączonego
do zacisków zewnętrznych połączenia

Połączenie szeregowe jest
dzielnikiem napięcia dołączonego
do zacisków zewnętrznych połączenia

u

R

R

R

i

R

u

2

1

1

1

1







Napięcie przyłożone do zacisków
połączenia szeregowego ulega
podziałowi na napięcia połączonych
szeregowo elementów wprost propor-
cjonalnie do ich rezystancji.

Napięcie przyłożone do zacisków
połączenia szeregowego ulega
podziałowi na napięcia połączonych
szeregowo elementów wprost propor-
cjonalnie do ich rezystancji.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

25

Połączenie równoległe

Połączenie równoległe

u

R

R

R

u

R

u

i

i

i

























2

1

2

1

2

1

1

1

,

R

u

i

,

R

u

i

2

2

1

1





2

1

1

1

1

R

R

u

i

R

z







2

1

G

G

G

z





2

1

2

1

R

R

R

R

R

z





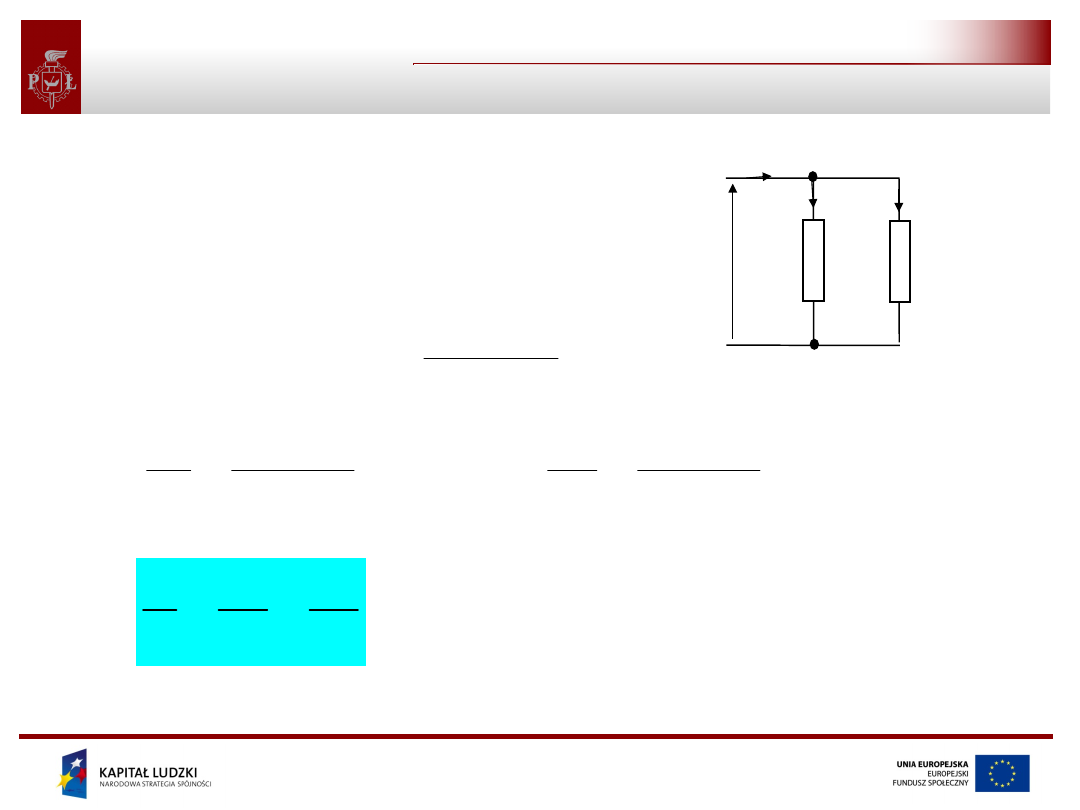
Połączenie równoległe to takie, w którym
na połączonych elementach panuje to
samo sam napięcie.
Wyznaczamy rezystancję zastępczą
połączenia równoległego.

Połączenie równoległe to takie, w którym
na połączonych elementach panuje to
samo sam napięcie.
Wyznaczamy rezystancję zastępczą
połączenia równoległego.

i

i

1

i

2

u

R

1

R

2

i

i

G

R



1

n

z

G

G

G

G











2

1

dla dwóch
oporników

dla dwóch
oporników

dla wielu oporników

dla wielu oporników

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

26

Połączenie równoległe – dzielnik prądu

Połączenie równoległe – dzielnik prądu

i

R

R

R

R

i

R

u

z

2

1

2

1







i

R

R

R

R

u

i

i

R

R

R

R

u

i

2

1

1

2

2

1

2

1

1













2

,

2

1

1

2

2

1

G

G

R

R

i

i





i

i

1

i

2

u

R

1

R

2

Połączenie równoległe jest
dzielnikiem prądu dopływającego
do zacisków zewnętrznych połączenia

Połączenie równoległe jest
dzielnikiem prądu dopływającego
do zacisków zewnętrznych połączenia

Prąd dopływający do połączenia równoległego
ulega podziałowi na prądy płynące przez
elementy połączone równolegle wprost propor-
cjonalnie do ich przewodności (odwrotnie
proporcjonalnie do ich rezystancji).

Prąd dopływający do połączenia równoległego
ulega podziałowi na prądy płynące przez
elementy połączone równolegle wprost propor-
cjonalnie do ich przewodności (odwrotnie
proporcjonalnie do ich rezystancji).

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

27

Moc i energia

Moc i energia

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

28

Moc i energia

Moc i energia

• Moc chwilowa dwójnika, przez

który płynie prąd i(t) i na którego
zaciskach panuje napięcie u(t)
wynosi:

jednostką mocy jest 1wat: 1W=1V

1A

• Energia dostarczona do dwójnika w

czasie od do t określona jest
zależnością:

jednostką energii jest 1dżul=1W 1s

• Związek między mocą chwilową

i energią określa zależność:

Wynika z niej, że moc chwilowa

jest prędkością zmiany energii.

 

   

t

i

t

u

t

p 

0

t

 

 

   

τ

d

τ

i

τ

u

τ

d

τ

p

t

,

t

w

t

t

t

t









0

0

0

 

 

dt

t

dw

t

p 

dwójnik

i(t)

u(t)

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

29

Moc i energia opornika

Moc i energia opornika

 

   

 

 

 

 

 

 

2

2

2

1

t

u

G

t

u

R

t

i

R

t

i

t

u

t

p









 

 

t

Ri

t

u



 

 

t

u

R

t

i

1



Dla opornika obowiązują następujące
zależności:

Dla opornika obowiązują następujące
zależności:

i(t)

u(t)

R

R

G

1



Z powyższych zależności wynika, że moc chwilowa opornika jest
zawsze nieujemna. Oznacza to, że opornik nigdy nie przekazuje
energii do obwodu.

Z powyższych zależności wynika, że moc chwilowa opornika jest
zawsze nieujemna. Oznacza to, że opornik nigdy nie przekazuje
energii do obwodu.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

30

Podstawowe pojęcia
topologiczne

Podstawowe pojęcia
topologiczne

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

31

Podstawowe pojęcia topologiczne

Podstawowe pojęcia topologiczne

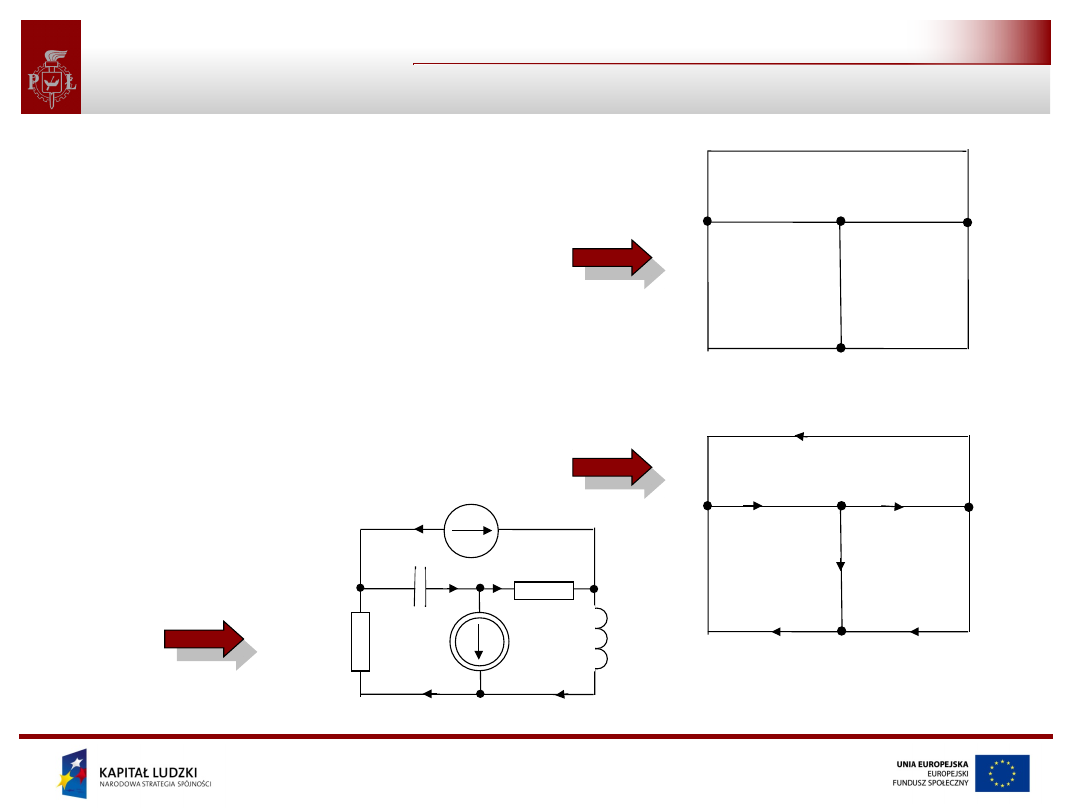
• Graf obwodu to graficzne

przedstawienie struktury połączeń
obwodu nie zawierające informacji o
elementach. Graf składa się z gałęzi
łączących węzły obwodu.

• Graf skierowany to taki, który

zawiera informacje o kierunkach
wszystkich gałęzi obwodu (kierunek
gałęzi jest zgodny z kierunkiem
płynącego w niej prądu).

6

5

4

3

1

2

6

5

4

3

1

2

schemat obwodu

schemat obwodu

L

3

i

6

i

5

i

4

i

1

E

6

R

5

C

4

J

2

R

1

i

3

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

32

Podstawowe pojęcia topologiczne

Podstawowe pojęcia topologiczne

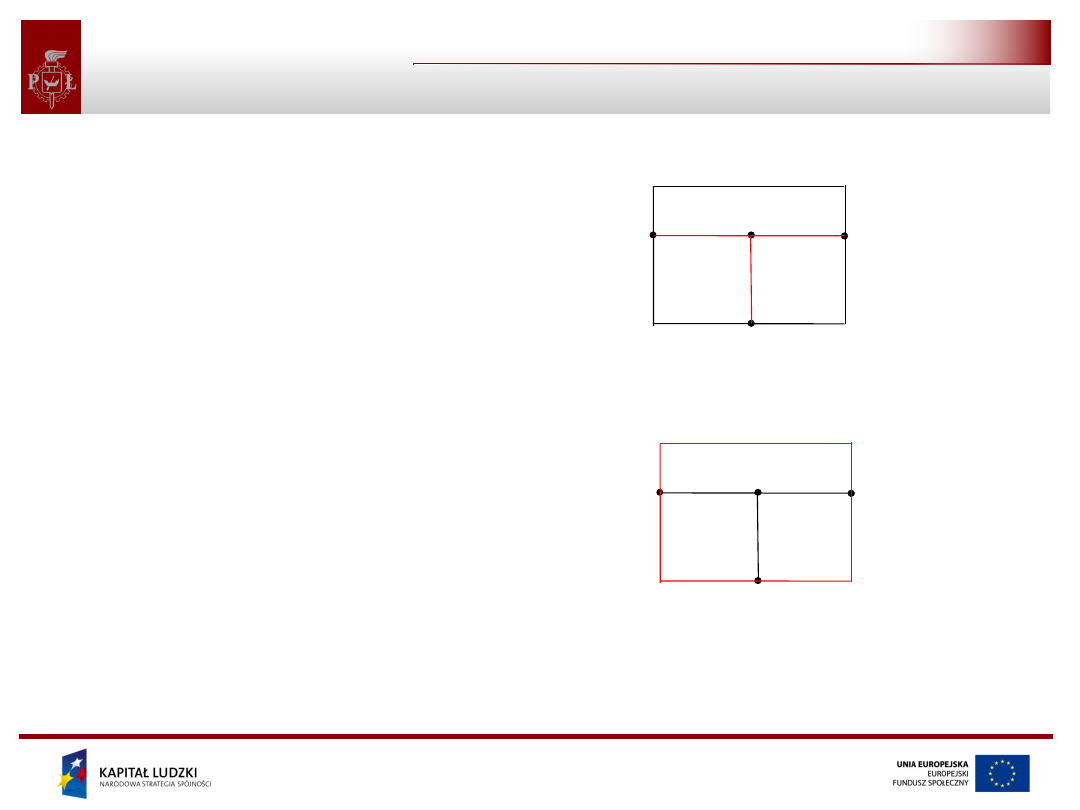
• Droga między węzłami k oraz

l to zbiór gałęzi, wśród których
kolejne gałęzie mają wspólny
węzeł i w każdym węźle łączą się
nie więcej niż dwie gałęzie. Z
węzłami końcowymi łączy się
jedna gałąź.

• Graf jest spójny, jeżeli istnieje

droga między dowolnymi jego
węzłami.

• Podgraf to część grafu.
• Pętla grafu to spójny podgraf, w

którym w każdym węźle łączą się
dokładnie dwie gałęzie.

6

5

4

3

1

2

6

5

4

3

1

2

zbiór gałęzi 2, 4, 5 nie jest pętlą

zbiór gałęzi 2, 4, 5 nie jest pętlą

zbiór gałęzi 1, 3, 6 jest pętlą

zbiór gałęzi 1, 3, 6 jest pętlą

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

33

Podstawowe pojęcia topologiczne

Podstawowe pojęcia topologiczne

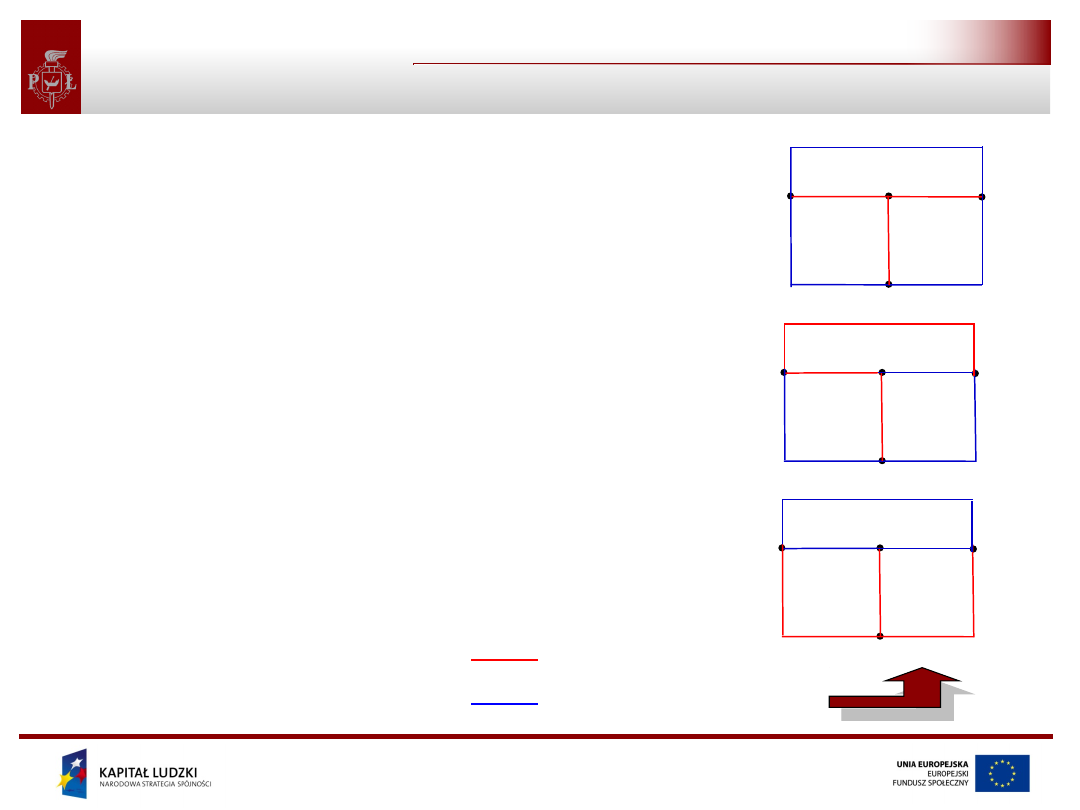
• Drzewo grafu spójnego to spójny podgraf

obejmujący wszystkie węzły grafu i nie
zawierający żadnej pętli.

• Dopełnienie to zbiór pozostałych gałęzi

grafu.

• W dowolnym grafie można najczęściej

utworzyć wiele drzew i odpowiadających
im dopełnień. Obok pokazane są trzy różne
drzewa utworzone dla tego samego grafu
oraz odpowiadajace im dopełnienia.

• Można wykazać, że drzewo grafu spójnego,

który składa się z n węzłów i b gałęzi,
zawiera (n-1) gałęzi. Wynika z tego, że
dopełnienie tego grafu składa się z (b-n+1)
gałęzi

6

5

4

3

1

2

6

5

4

3

1

2

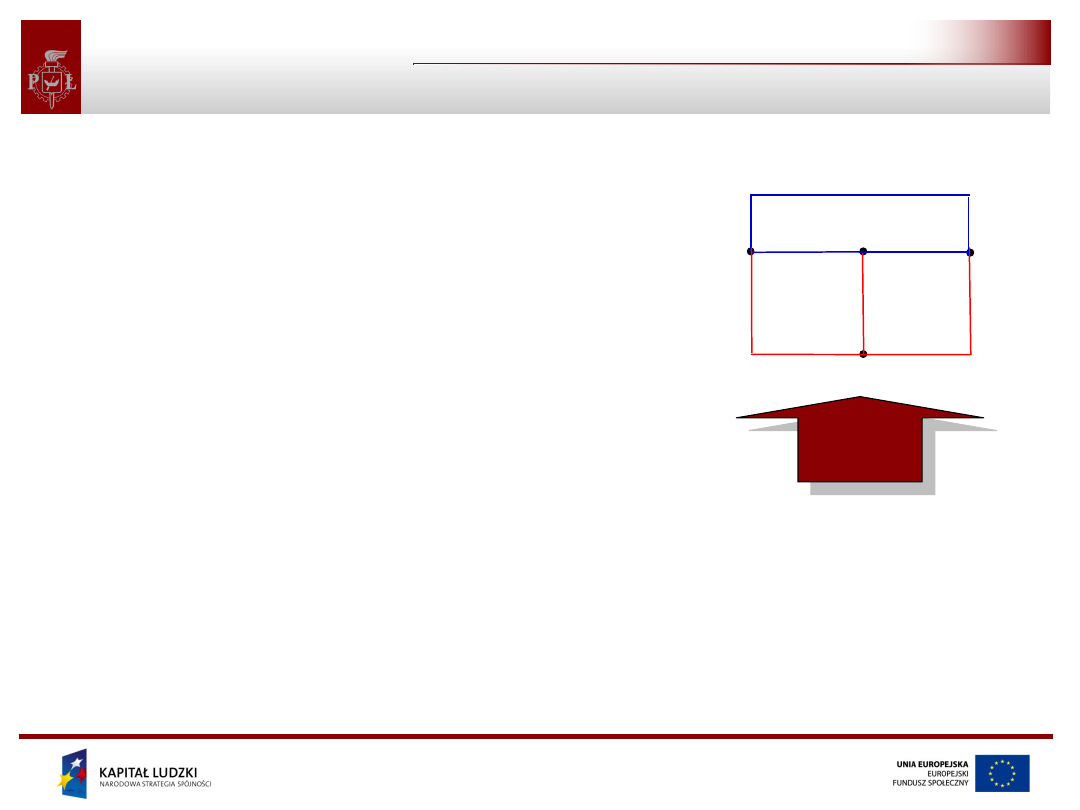
drzewo grafu

drzewo grafu

dopełnienie grafu

dopełnienie grafu

6

5

4

3

1

2

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

34

Podstawowe pojęcia topologiczne

Podstawowe pojęcia topologiczne

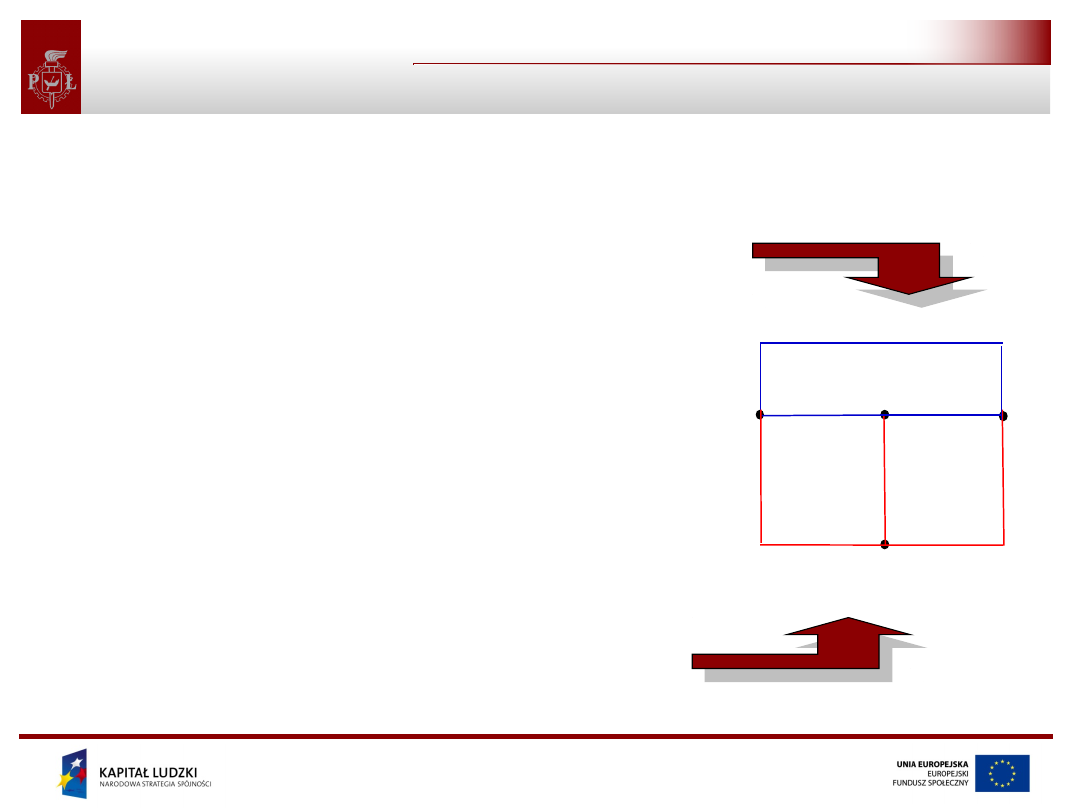
• Przekrój grafu spójnego to najmniej

liczny zbiór takich gałęzi, których
usunięcie z obwodu, jednocześnie
wszystkich bez węzłów końcowych,
powoduje podział grafu na dwa podgrafy.

• Przekrój fundamentalny zawiera jedną

gałąź drzewa i pozostałe gałęzie
dopełnienia.

• Liczba fundamentalnych przekrojów w

obwodzie to (n-1).

• Pętla fundamentalna jest utworzona z

dokładnie jednej gałęzi dopełnienia i
gałęzi drzewa.

• Liczba fundamentalnych pętli w obwodzie

dla określonego drzewa to (b-n+1).

przekroje to np.1,4,6;
3,5,6; 1,2,3; 1,4,5,3;
trzy ostatnie to
przekroje
fundamentalne

przekroje to np.1,4,6;
3,5,6; 1,2,3; 1,4,5,3;
trzy ostatnie to
przekroje
fundamentalne

6

5

4

3

1

2

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

35

Podstawowe pojęcia topologiczne

Podstawowe pojęcia topologiczne

• Dla wybranego drzewa składającego się z

gałęzi 1,2,3 są w obwodzie trzy
fundamentalne pętle bo tyle gałęzi ma
dopełnienie zawierające gałęzie: 4,5,6.
Pętle fundamentalne składają się z gałęzi:
1,2,4; 2,3,5; 1,3,6.

• Grafy planarne to takie, które można

narysować na płaszczyźnie w taki sposób,
że gałęzie grafu przecinają się tylko w
węzłach.

• Oczko to pętla grafu planarnego, która nie

zawiera wewnątrz żadnej gałęzi.

• Graf planarny zawiera dokładnie (b-n+1)

oczek.

• Oczka w przykładowym obwodzie to: 1,2,4;

2,3,5; 4,5,6.

6

5

4

3

1

2

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

36

Fundamentalne
prawa
teorii obwodów

Fundamentalne
prawa
teorii obwodów

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

37

Prądowe Prawo Kirchhoffa

Prądowe Prawo Kirchhoffa

• Najbardziej znana postać prądowego prawa Kirchhoffa (PPK) to:
W dowolnym obwodzie elektrycznym, dla dowolnego węzła

tego obwodu, w dowolnej chwili czasu algebraiczna suma

wszystkich prądów dopływających do węzła jest równa zero.

sumowanie dotyczy wszystkich gałęzi
łączących się z rozważanym węzłem
Określenie suma algebraiczna oznacza, że prądy posiadające różne

zwroty względem węzła mają w tej sumie różne znaki. W dalszej

części rozważań prądom odpływającym będzie przypisywany znak:

„+” a prądom dopływającym znak: „-”.

• Prądowe prawo Kirchhoffa obowiązuje również dla dowolnego

przekroju obwodu elektrycznego:

W dowolnym obwodzie elektrycznym suma algebraiczna

prądów wszystkich gałęzi należących do przekroju jest w

każdej chwili równa zero.

 

0





t

i

α

α

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

38

Prądowe Prawo Kirchhoffa

Prądowe Prawo Kirchhoffa

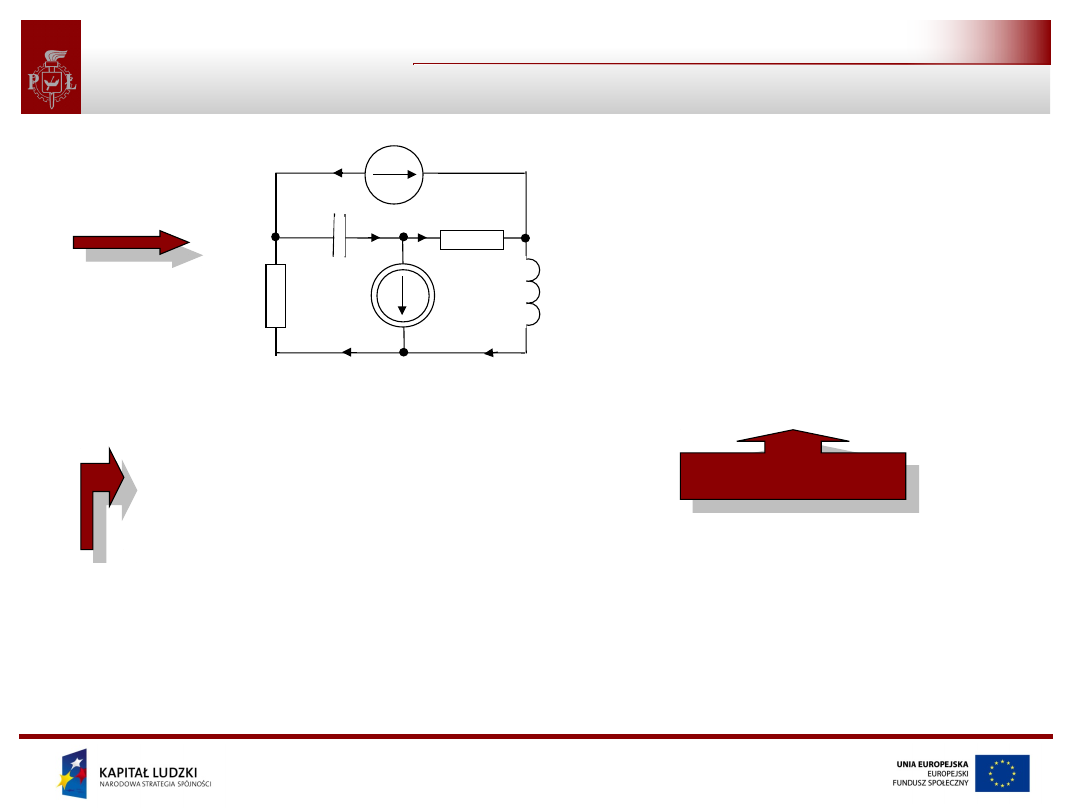
Dla analizy obwodów elektrycznych istotne jest twierdzenie

związane z przytoczonymi wcześniej pojęciami topologicznymi.

Twierdzenie
Maksymalna liczba równań liniowo niezależnych

otrzymanych na podstawie prądowego prawa Kirchhoffa w

obwodzie o n węzłach wynosi (n-1). Równania te mogą być

sformułowane przez zastosowanie PPK do:

1. (n-1) węzłów obwodu (wszystkich węzłów obwodu z

wyjątkiem jednego, dowolnie wybranego),

2. (n-1) fundamentalnych przekrojów (wszystkich

fundamentalnych przekrojów dla wybranego drzewa

obwodu).

Równania te rozważane samodzielnie nie pozwalają na

wyznaczenie prądów w obwodzie gdyż ich liczba jest mniejsza niż

liczba gałęzi i nie zawierają one informacji o elementach

występujących w obwodzie.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

39

Prądowe Prawo Kirchhoffa - przykład

Prądowe Prawo Kirchhoffa - przykład

0

0

0

0

3

2

1

6

5

3

5

4

2

6

4

1



























i

J

i

.

D

i

i

i

.

C

i

i

J

.

B

i

i

i

.

A

L

3

i

6

i

5

i

4

i

1

E

6

R

5

C

4

J

2

R

1

i

3

A

A

B

B

D

D

C

C

równania dla wszystkich węzłów
przykładowego obwodu; układ
niezależny tworzą trzy dowolnie
wybrane spośród
przedstawionych czterech

równania dla wszystkich węzłów
przykładowego obwodu; układ
niezależny tworzą trzy dowolnie
wybrane spośród
przedstawionych czterech

równania dla fundamentalnych
przekrojów wynikających z
wybranego drzewa obwodu
składającego się
z gałęzi 1,2,3

równania dla fundamentalnych
przekrojów wynikających z
wybranego drzewa obwodu
składającego się
z gałęzi 1,2,3

przykładowy
obwód

przykładowy
obwód

0

0

0

6

5

3

5

4

2

6

4

1





















i

i

i

i

i

J

i

i

i

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

40

Napięciowe Prawo Kirchhoffa

Napięciowe Prawo Kirchhoffa

• Najbardziej znana postać napięciowego prawa Kirchhoffa (NPK) to:
W dowolnym obwodzie elektrycznym, dla dowolnej pętli tego

obwodu, w dowolnej chwili czasu algebraiczna suma napięć
wszystkich elementów znajdujących się w gałęziach tej pętli
jest równa zero.

sumowanie dotyczy wszystkich elementów
znajdujących się w gałęziach tworzących

pętlę

Określenie suma algebraiczna oznacza, że napięcia posiadające różne

zwroty względem przyjętego kierunku obiegu pętli mają w tej sumie
różne znaki. W dalszej części rozważań napięciom o kierunkach
zgodnych z przyjętym kierunkiem obiegu pętli będzie przypisywany
znak: „+”, o kierunku przeciwnym znak: „-”.

• Dwa problemy powstające przy analizie obwodu to: jaka jest

maksymalna liczba równań sformułowanych na podstawie NPK
tworzących niezależny układ i w jaki sposób należy je formułować.

 

0





t

u

β

β

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

41

Napięciowe Prawo Kirchhoffa

Napięciowe Prawo Kirchhoffa

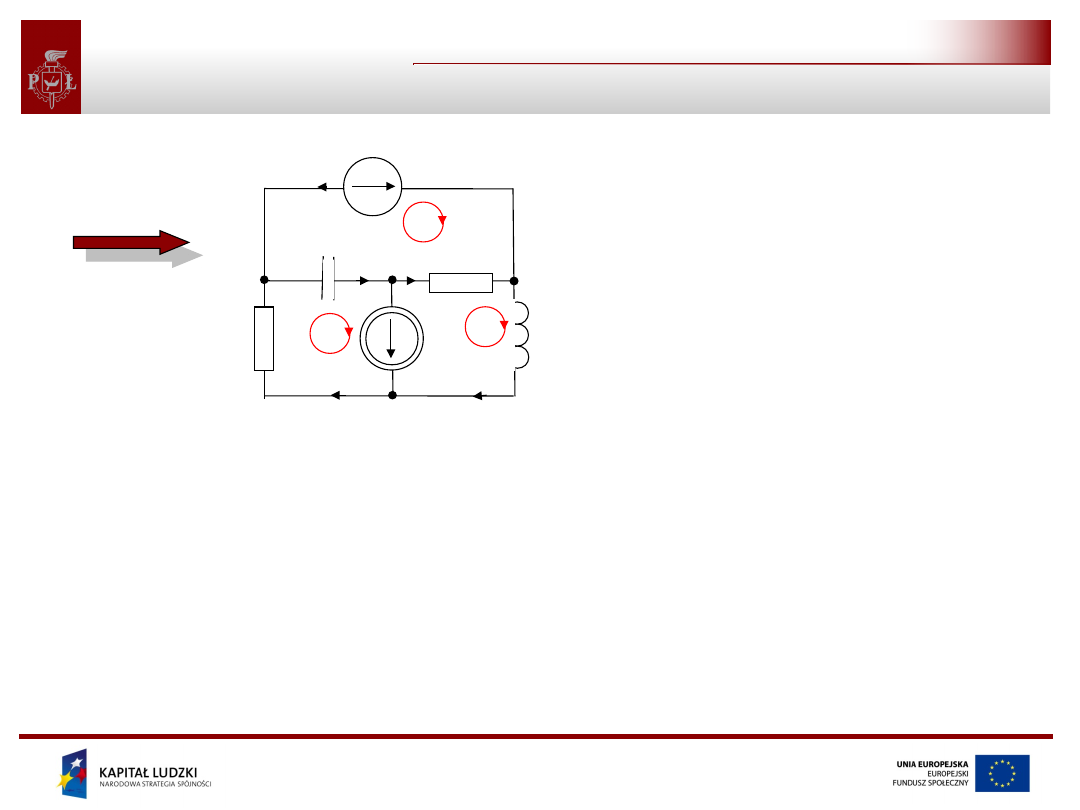
Dla analizy obwodów elektrycznych istotne jest twierdzenie

zawierające rozwiązanie dwóch przedstawionych problemów:

Twierdzenie
Maksymalna liczba równań liniowo niezależnych otrzymanych

na podstawie napięciowego prawa Kirchhoffa w obwodzie o b

gałęziach i n węzłach wynosi (b- n+1). Równania te mogą być

sformułowane przez zastosowanie NPK do:

1. (b-n+1) fundamentalnych pętli obwodu (wszystkich

fundamentalnych pętli obwodu ),

2. (b-n+1) oczek obwodu (wszystkich oczek obwodu).
Równania te rozważane samodzielnie nie pozwalają na wyznaczenie

prądów w obwodzie gdyż ich liczba jest mniejsza niż liczba gałęzi.

Łącznie z równaniami sformułowanymi na podstawie PPK mogą

tworzyć układ równań niezależnych. Liczba niewiadomych będzie

równa liczbie równań po uzależnieniu napięć na elementach od

płynących przez nie prądów.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

42

Napięciowe Prawo Kirchhoffa - przykład

Napięciowe Prawo Kirchhoffa - przykład

0

0

0

3

6

1

3

5

4

1

























u

E

u

u

u

u

u

u

u

J

J

III

II

I

i

3

L

3

i

6

i

5

i

4

i

1

E

6

R

5

C

4

J

2

R

1

A

A

B

B

D

D

C

C

drzewo: 1,2,3
dopełnienie: 4,5,6

drzewo: 1,2,3
dopełnienie: 4,5,6

0

0

0

3

5

5

6

4

4

1























J

J

u

u

u

.

III

u

E

u

.

II

u

u

u

.

I

przykładowy
obwód

przykładowy
obwód

równania dla wszystkich oczek
przykładowego obwodu

równania dla wszystkich oczek
przykładowego obwodu

równania dla fundamentalnych pętli:
1,4,2; 2,5,3; 1,6,3; kierunek obiegu
zgodny z ruchem wskazówek zegara

równania dla fundamentalnych pętli:
1,4,2; 2,5,3; 1,6,3; kierunek obiegu
zgodny z ruchem wskazówek zegara

kierunki napięć występujących
w obu układach równań są
stowarzyszone z kierunkami
prądów płynących przez elementy

kierunki napięć występujących
w obu układach równań są
stowarzyszone z kierunkami
prądów płynących przez elementy

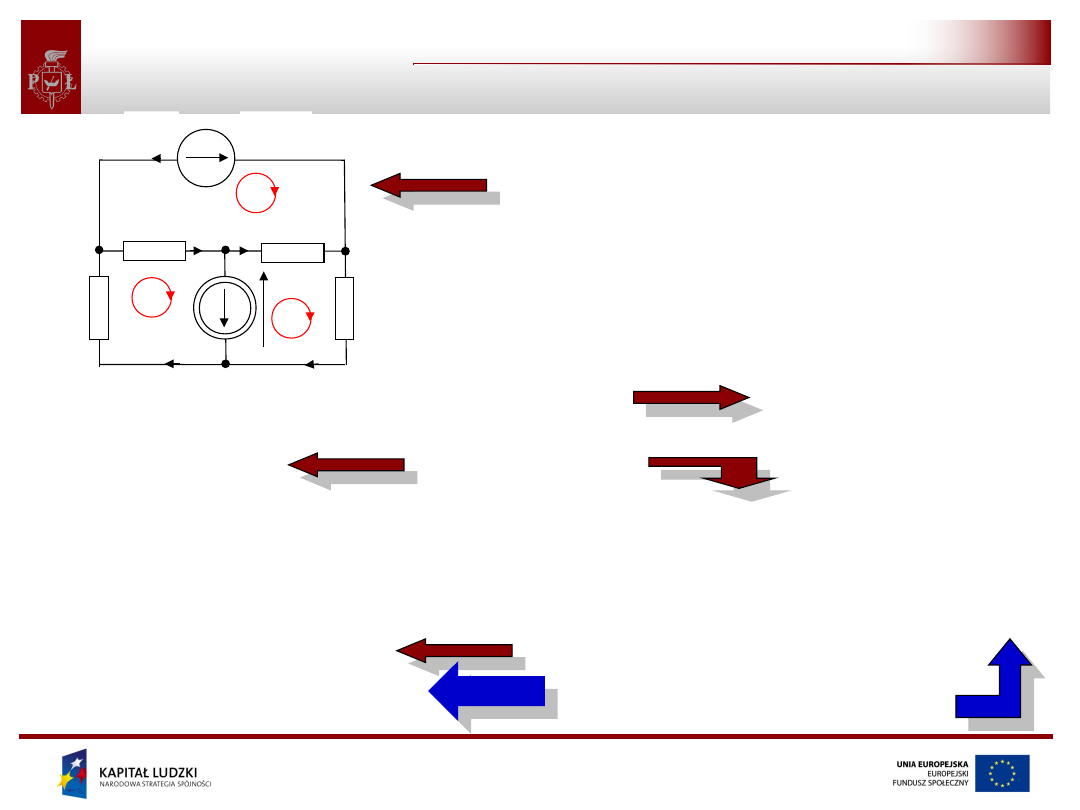
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

43

PPK i NPK – przykład zastosowania

PPK i NPK – przykład zastosowania

0

0

0

3

3

6

1

1

3

3

5

5

4

4

1

1

























R

i

E

R

i

u

R

i

R

i

u

R

i

R

i

J

J

0

0

0

3

2

1

6

5

3

5

4

2



















i

J

i

.

D

i

i

i

.

C

i

i

J

.

B

0

0

0

6

5

3

5

4

2

6

4

1





















i

i

i

i

i

J

i

i

i

u

J

II

i

3

R

3

i

6

i

5

i

4

i

1

E

6

R

5

R

4

J

2

R

1

A

A

B

B

D

D

C

C

III

I

przykładowy obwód
zawierający źródła i oporniki

przykładowy obwód
zawierający źródła i oporniki

drzewo: 1,2,3; dopełnienie: 4,5,6

drzewo: 1,2,3; dopełnienie: 4,5,6

0

0

0

3

3

5

5

5

5

6

4

4

4

4

1

1























J

J

u

R

i

R

i

.

III

R

i

E

R

i

.

II

u

R

i

R

i

.

I

w równaniach napięcia na opornikach zostały
zastąpione zgodnie z prawem Ohma iloczynami
wartości oporu i prądu opornika

w równaniach napięcia na opornikach zostały
zastąpione zgodnie z prawem Ohma iloczynami
wartości oporu i prądu opornika

PPK dla węzłów

PPK dla węzłów

NPK dla oczek

NPK dla oczek

PPK dla przekrojów
fundamentalnych

PPK dla przekrojów
fundamentalnych

NPK dla pętli
fundamentalnych

NPK dla pętli
fundamentalnych

układy równań z PPK i NPK

układy równań z PPK i NPK

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

44

Twierdzenie Tellegena

Twierdzenie Tellegena

m

i

m

u

Twierdzenie Tellegena
Jeżeli prądy gałęziowe spełniają PPK w każdym węźle
grafu mającego b gałęzi oraz napięcia gałęziowe
spełniają NPK w każdej pętli tego grafu to:

Twierdzenie Tellegena
Jeżeli prądy gałęziowe spełniają PPK w każdym węźle
grafu mającego b gałęzi oraz napięcia gałęziowe
spełniają NPK w każdej pętli tego grafu to:









b

m

m

m

m

o

i

u

1

- napięcia gałęziowe

- napięcia gałęziowe

- prądy gałęziowe

- prądy gałęziowe

Prądy gałęziowe i napięcia gałęziowe dotyczą tego samego grafu lecz
nie muszą dotyczyć tego samego obwodu. Jeżeli dotyczą tego samego
obwodu to iloczyny w przedstawionym wzorze są mocami chwilowymi
a równanie będące tezą twierdzenia przedstawia bilans mocy obwodu.

Prądy gałęziowe i napięcia gałęziowe dotyczą tego samego grafu lecz
nie muszą dotyczyć tego samego obwodu. Jeżeli dotyczą tego samego
obwodu to iloczyny w przedstawionym wzorze są mocami chwilowymi
a równanie będące tezą twierdzenia przedstawia bilans mocy obwodu.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

45

Analiza obwodów
stałoprądowych

Analiza obwodów
stałoprądowych

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

46

Metoda potencjałów węzłowych

Metoda potencjałów węzłowych

• Metoda potencjałów węzłowych jest jedną z najbardziej efektywnych

oraz najpopularniejszych metod analizy obwodów elektrycznych.

• Niewiadomymi w równaniach metody są potencjały węzłów obwodu

względem węzła odniesienia dowolnie wybranego.

• Punktem wyjścia są równania sformułowane na podstawie prądowego

prawa Kirchhoffa. W równaniach tych dokonuje się transformacji
zmiennych zamieniając prądy tam, gdzie jest to możliwe, na
wyrażenia uzależniające je od potencjałów węzłów obwodu.

• Metoda potencjałów węzłowych umożliwia przeprowadzenie analizy

obwodu poprzez rozwiązanie układu równań najczęściej o mniejszej
liczbie niż w przypadku innych metod ( np. metody praw Kirchhoffa).

• Znane są różne sposoby formułowania równań węzłowych. Niektóre

pozwalają na implementację komputerową powodując, że metoda
węzłowa jest często wykorzystywana w najbardziej znanych
programach analizy obwodów elektrycznych (np. SPICE).

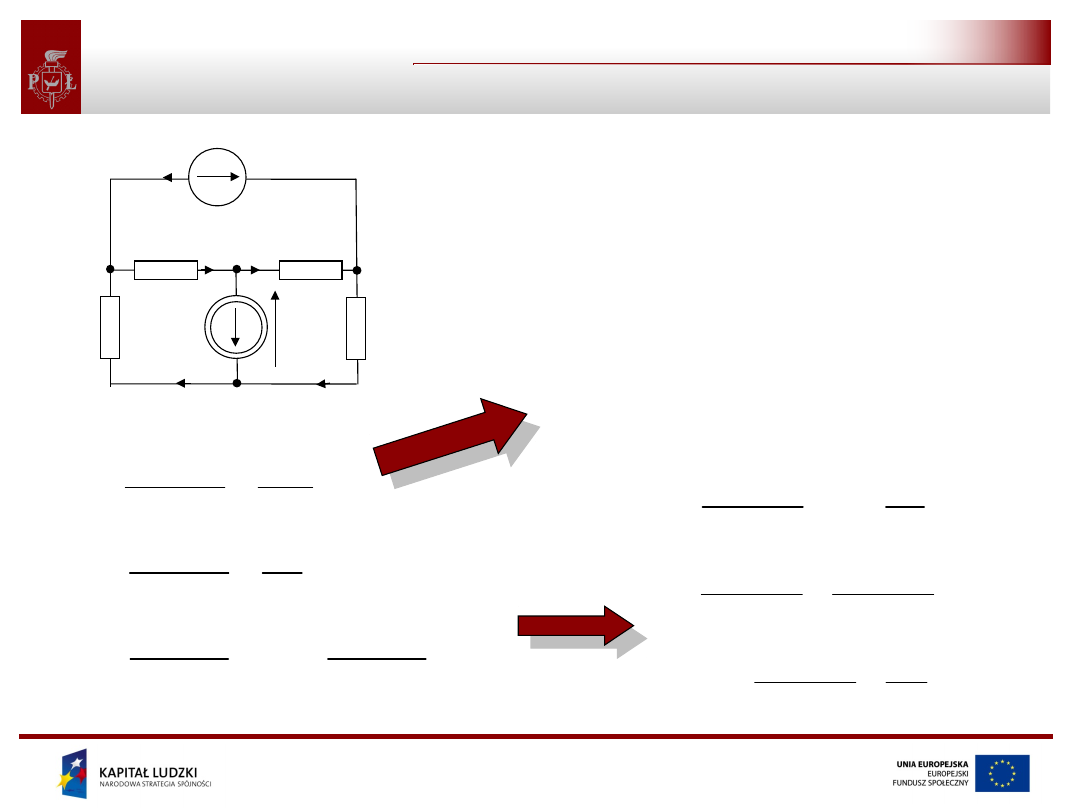
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

47

Metoda potencjałów węzłowych - przykład

Metoda potencjałów węzłowych - przykład

0

0

0

3

5

6

2

4

5

1

6

4



















i

i

i

.

C

J

i

i

.

B

i

i

i

.

A

5

5

4

4

3

3

3

1

1

1

R

V

V

i

;

R

V

V

i

R

V

R

V

V

i

;

R

V

R

V

V

i

C

B

B

A

C

D

C

A

A

D























Formułowanie równań
węzłowych do
podanego obwodu.
Obieramy węzeł D węzłem
odniesienia.
Równania PPK dla pozostałych
węzłów:

Formułowanie równań
węzłowych do
podanego obwodu.
Obieramy węzeł D węzłem
odniesienia.
Równania PPK dla pozostałych
węzłów:

0

0

0

3

5

6

2

4

5

1

6

4



























R

V

R

V

V

i

.

C

J

R

V

V

R

V

V

.

B

R

V

i

R

V

V

.

A

C

B

C

A

B

C

B

A

B

A

trzy równania, cztery
niewiadome

trzy równania, cztery
niewiadome

u

J

i

3

R

3

i

6

i

5

i

4

i

1

E

6

R

5

R

4

J

2

R

1

A

A

B

B

D

D

C

C

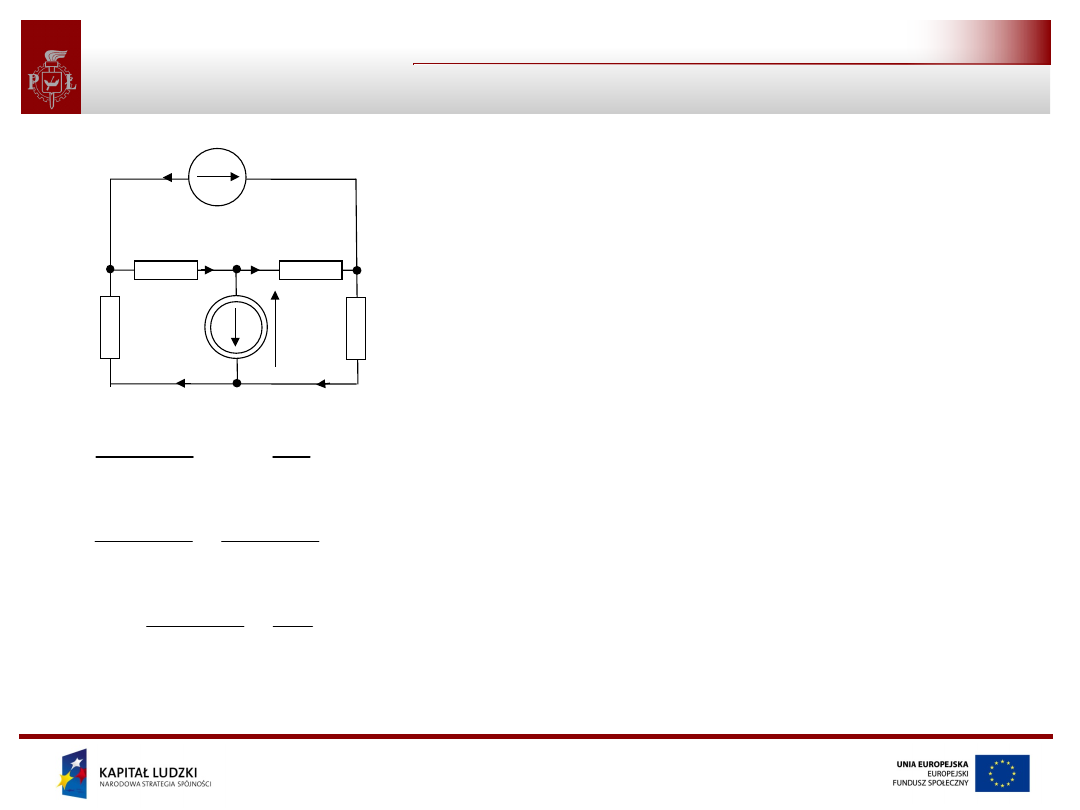
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

48

Metoda potencjałów węzłowych - przykład

Metoda potencjałów węzłowych - przykład

0

0

0

3

5

6

2

4

5

1

6

4



























R

V

R

V

V

i

.

C

J

R

V

V

R

V

V

.

B

R

V

i

R

V

V

.

A

C

B

C

A

B

C

B

A

B

A

u

J

i

3

R

3

i

6

i

5

i

4

i

1

E

6

R

5

R

4

J

2

R

1

A

A

B

B

D

D

C

C

Równanie uzupełniające otrzymany układ
równań

Równanie uzupełniające otrzymany układ
równań

6

E

V

V

A

C





Dodanie stronami równań dla węzłów A i
C, jedynych zawierających prąd źródła
napięciowego, skraca układ o jedno
równanie
eliminując z układu jedną niewiadomą.

Dodanie stronami równań dla węzłów A i
C, jedynych zawierających prąd źródła
napięciowego, skraca układ o jedno
równanie
eliminując z układu jedną niewiadomą.

Pozostają wtedy trzy równania z trzema
niewiadomymi, którymi są potencjały
węzłów A, B oraz C względem wyróżnionego.
Po rozwiązaniu układu prądy w obwodzie
wyznacza się z równań umieszczonych na
poprzedniej stronie. Prąd źródła napięciowego
wyznacza się z jednego z równań: A lub C
(równań poprzednio dodanych stronami)

Pozostają wtedy trzy równania z trzema
niewiadomymi, którymi są potencjały
węzłów A, B oraz C względem wyróżnionego.
Po rozwiązaniu układu prądy w obwodzie
wyznacza się z równań umieszczonych na
poprzedniej stronie. Prąd źródła napięciowego
wyznacza się z jednego z równań: A lub C
(równań poprzednio dodanych stronami)

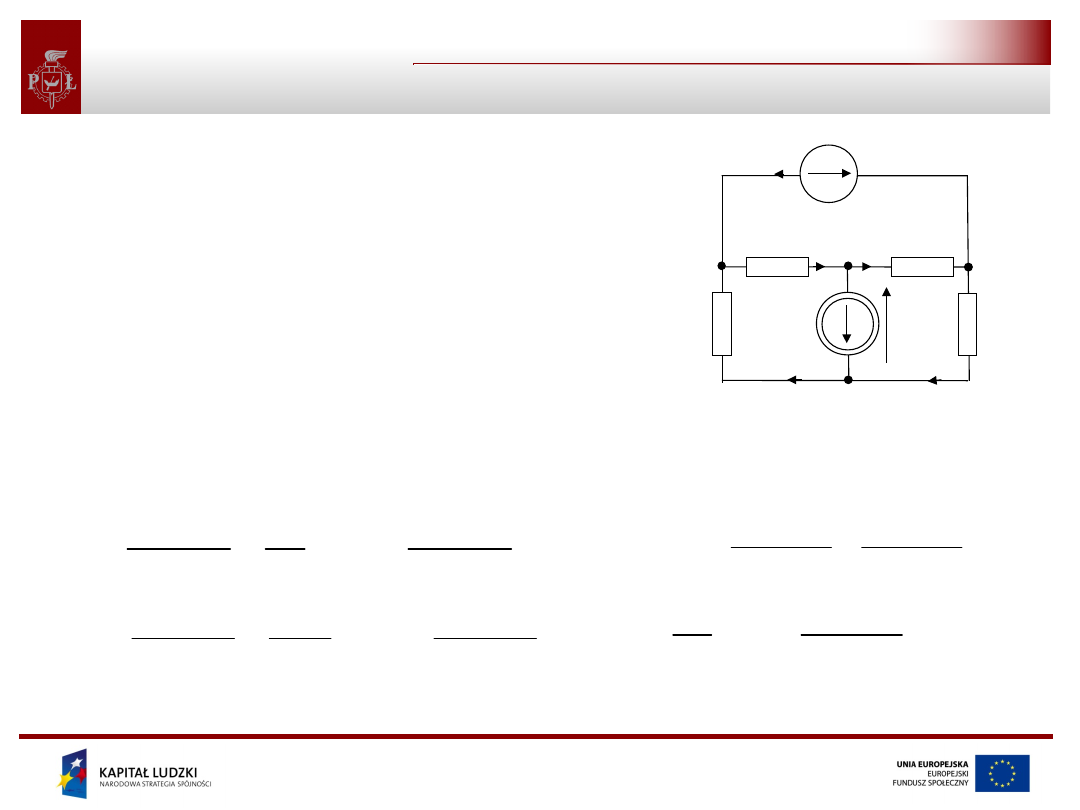
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

49

Metoda potencjałów węzłowych - przykład

Metoda potencjałów węzłowych - przykład

0

0

3

2

1

5

4

2













i

J

i

.

D

i

i

J

.

B

6

3

2

1

5

4

2

0

0

E

V

R

V

V

J

R

V

.

D

R

V

V

R

V

V

J

.

B

C

C

D

D

C

B

A

B





















Przy innym wyborze węzła
odniesienia,
takim, w którym będzie nim jeden z
końców źródła napięciowego, np.
węzeł A,
można otrzymać układ równań w
nieco krótszy sposób formułując PPK
dla węzłów B i D:

Przy innym wyborze węzła
odniesienia,
takim, w którym będzie nim jeden z
końców źródła napięciowego, np.
węzeł A,
można otrzymać układ równań w
nieco krótszy sposób formułując PPK
dla węzłów B i D:

u

J

i

3

R

3

i

6

i

5

i

4

i

1

E

6

R

5

R

4

J

2

R

1

A

A

B

B

D

D

C

C

5

5

4

4

4

3

3

1

1

1

R

V

V

i

;

R

V

R

V

V

i

R

V

V

i

;

R

V

R

V

V

i

C

B

B

B

A

D

C

D

A

D























Uwzględnienie równań uzależniających prądy od potencjałów węzłów
oraz dodanie równania określającego potencjał węzła C prowadzi do układu

Uwzględnienie równań uzależniających prądy od potencjałów węzłów
oraz dodanie równania określającego potencjał węzła C prowadzi do układu

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

50

Metoda potencjałów węzłowych

Metoda potencjałów węzłowych

Algorytm formułowania równań węzłowych:

1.

Wybór węzła odniesienia.

2.

Sformułowanie dla wszystkich węzłów obwodu z wyłączeniem

węzła odniesienia równań na podstawie prądowego prawa

Kirchhoffa.

3.

Transformacja zmiennych polegająca na zastąpieniu w

równaniach prądów gałęzi zawierających oporniki wyrażeniami

uzależniającymi je od potencjałów węzłów i elementów obwodu

oraz zastąpienie wszystkich napięć sterujących źródeł

sterowanych różnicami odpowiednich potencjałów.

4.

Uzupełnienie układu równań o równania wiążące potencjały

końców niezależnych i sterowanych źródeł napięciowych z ich

napięciami źródłowymi.

Otrzymany układ równań będzie zawierał o jedno równanie

mniej niż liczba węzłów w obwodzie (punkt 2) uzupełnionych

tyloma równaniami ile jest w obwodzie niezależnych i

sterowanych źródeł napięciowych (punkt 4).

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

51

Zasada superpozycji

Zasada superpozycji

• Zasada superpozycji obowiązuje w układach liniowych.
• Bardzo ogólne sformułowanie zasady superpozycji to:
Skutek pochodzący od wielu przyczyn jest sumą

skutków pochodzących od każdej z tych przyczyn
oddzielnie.

• W liniowych obwodach elektrycznych skutkami są napięcia i

prądy w obwodzie, wymuszeniami napięcia źródłowe
niezależnych źródeł napięciowych oraz prądy źródłowe
niezależnych źródeł prądowych.

• Każdy prąd oraz każde napięcie w obwodzie liniowym

(wielkość obwodowa – WO) zawierającym k niezależnych
źródeł napięciowych oraz m niezależnych źródeł prądowych
jest liniowo zależne od tych wielkości a więc jest funkcją
postaci:

















k

r

r

m

s

s

s

s

r

r

j

b

e

a

WO

1

1

s

r

b

,

a

- współczynniki zależne wyłącznie od wartości
elementów obwodu z wyłączeniem źródeł
niezależnych

- współczynniki zależne wyłącznie od wartości
elementów obwodu z wyłączeniem źródeł
niezależnych

s

r

j

,

e

- napięcia i prądy
źródłowe

- napięcia i prądy
źródłowe

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

52

Zasada superpozycji

Zasada superpozycji

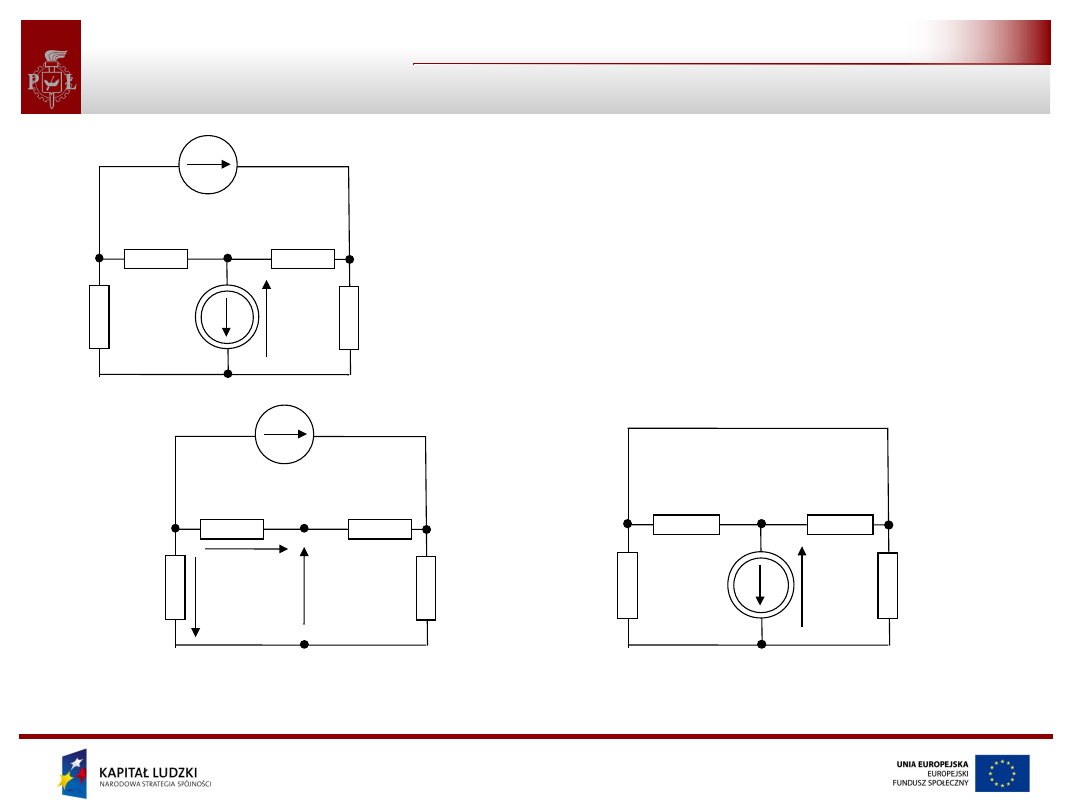
• Na mocy zasady superpozycji dowolne napięcie (prąd) w obwodzie

liniowym może być obliczone jako algebraiczna suma wartości
tego napięcia (prądu) w obwodach powstałych z obwodu
analizowanego przez usunięcie części źródeł niezależnych. W
analizowanych obwodach każde z niezależnych źródeł musi
być obecne dokładnie jeden raz.

• Po usunięciu niezależnego źródła napięciowego jego zaciski

zostają zwarte, następstwem usunięcia niezależnego źródła
prądowego z obwodu jest pozostawienie jego zacisków
rozwartych.

• Szczególnym przypadkiem jest analiza tylu obwodów powstałych z

obwodu wyjściowego ile zawiera on źródeł niezależnych. Każdy z
tych obwodów zawiera dokładnie jedno wymuszenie (źródło
niezależne), każdy inne.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

53

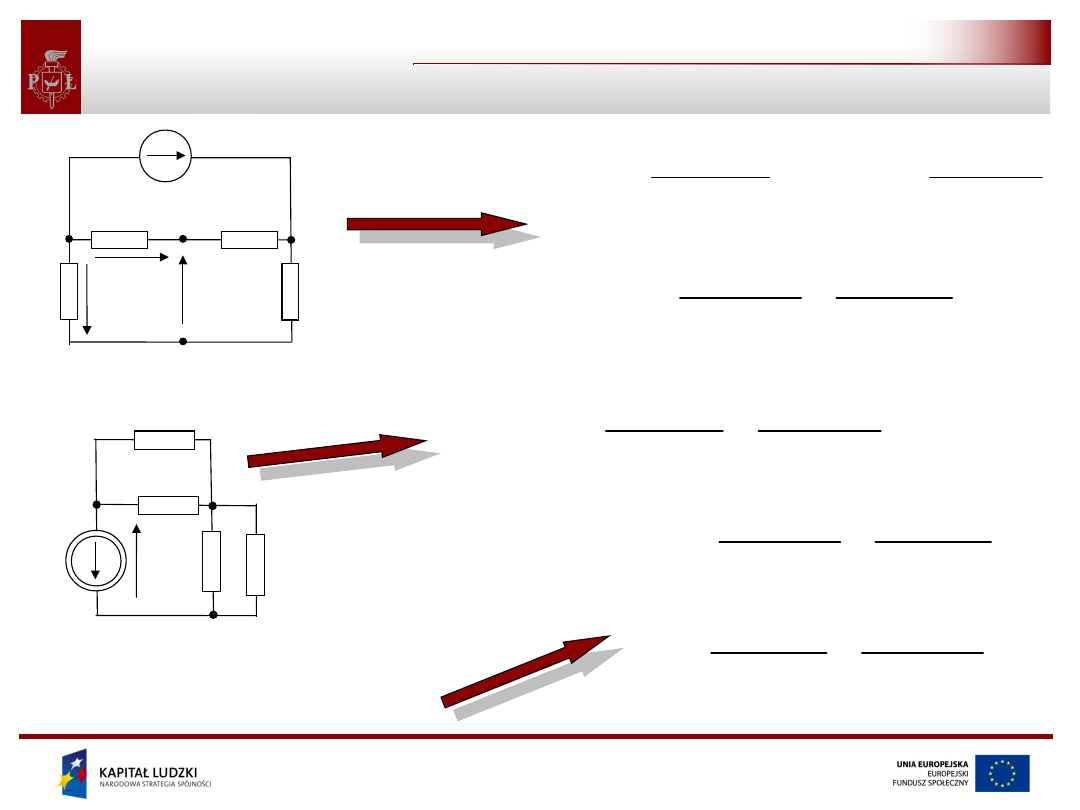
Zasada superpozycji - przykład

Zasada superpozycji - przykład

Przykładem wykorzystania zasady
superpozycji do przeprowadzenia
analizy obwodu jest obliczenie
napięcia na źródle prądowym w
przedstawionym obok obwodzie.
Zasada superpozycji prowadzi do
analizy przedstawionych poniżej
dwóch obwodów:

Przykładem wykorzystania zasady
superpozycji do przeprowadzenia
analizy obwodu jest obliczenie
napięcia na źródle prądowym w
przedstawionym obok obwodzie.
Zasada superpozycji prowadzi do
analizy przedstawionych poniżej
dwóch obwodów:

u

J

R

3

E

6

R

5

R

4

J

2

R

1

u

J

’

R

3

u

4

’

u

1

’

E

6

R

5

R

4

R

1

Obwód I

Obwód I

Obwód II

Obwód II

u

J

’’

R

3

R

5

R

4

J

2

R

1

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

54

Zasada superpozycji - przykład

Zasada superpozycji - przykład

3

1

1

6

1

5

4

4

6

4

R

R

R

E

u

;

R

R

R

E

u











































3

1

1

5

4

4

6

1

4

R

R

R

R

R

R

E

u

u

u

J

u

J

’

R

3

u

4

’

u

1

’

E

6

R

5

R

4

R

1

u

J

’’

R

3

R

5

R

4

J

2

R

1

Obwód I

Obwód I

Obwód II

Obwód II



























5

4

5

4

3

1

3

1

2

R

R

R

R

R

R

R

R

J

u

J





















































5

4

5

4

3

1

3

1

2

3

1

1

5

4

4

6

R

R

R

R

R

R

R

R

J

R

R

R

R

R

R

E

u

u

u

J

J

J

z dzielnika
napięciowego

z dzielnika
napięciowego

rozwiązanie
końcowe

rozwiązanie
końcowe

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

55

Układy równoważne

Układy równoważne

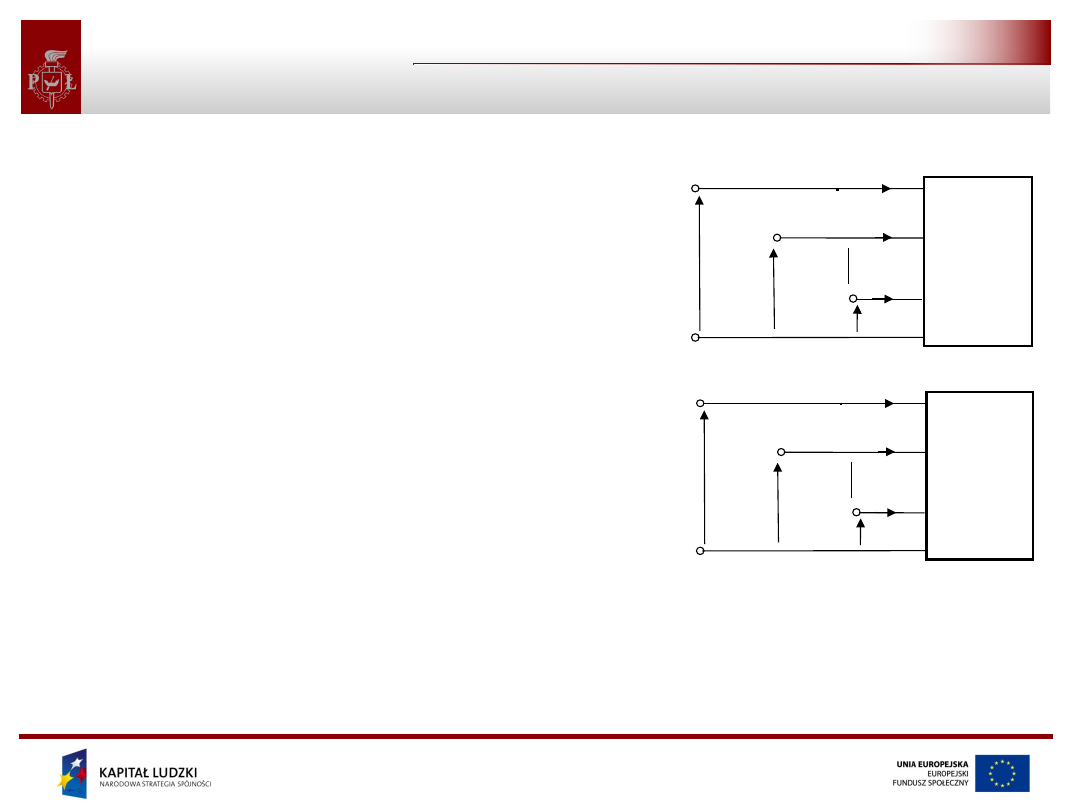
• Układy A i B nazywamy równoważnymi,

jeżeli ich opis matematyczny jest taki
sam.

• Oznacza to, że opis matematyczny

otrzymany w wyniku zamiany
występujących w opisie obwodu A
napięć i prądów na odpowiadające im
napięcia i prądy obwodu B będzie
prawdziwy dla obwodu B i odwrotnie.

• Fizyczna interpretacja równoważności

układów jest następująca: po dołączeniu
do dowolnego obwodu w miejsce układu
A układu B (układy równoważne muszą
mieć tą samą liczbę końcówek) w
obwodzie, do którego układ B został
dołączony żadne wielkości obwodowe nie
ulegną zmianie.

i

A,r-1

i

A,2

i

A,1

układ

A

u

A,2

u

A,1

u

A,r-1

i

A,2

i

B,r-1

i

A,2

i

B,1

układ

B

u

B,2

u

B,1

u

B,r-1

i

B,2









1

2

1







r

,

,

,

k

i

,

u

f

i

,

u

f

k

,

B

k

,

B

k

k

,

A

k

,

A

k



Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

56

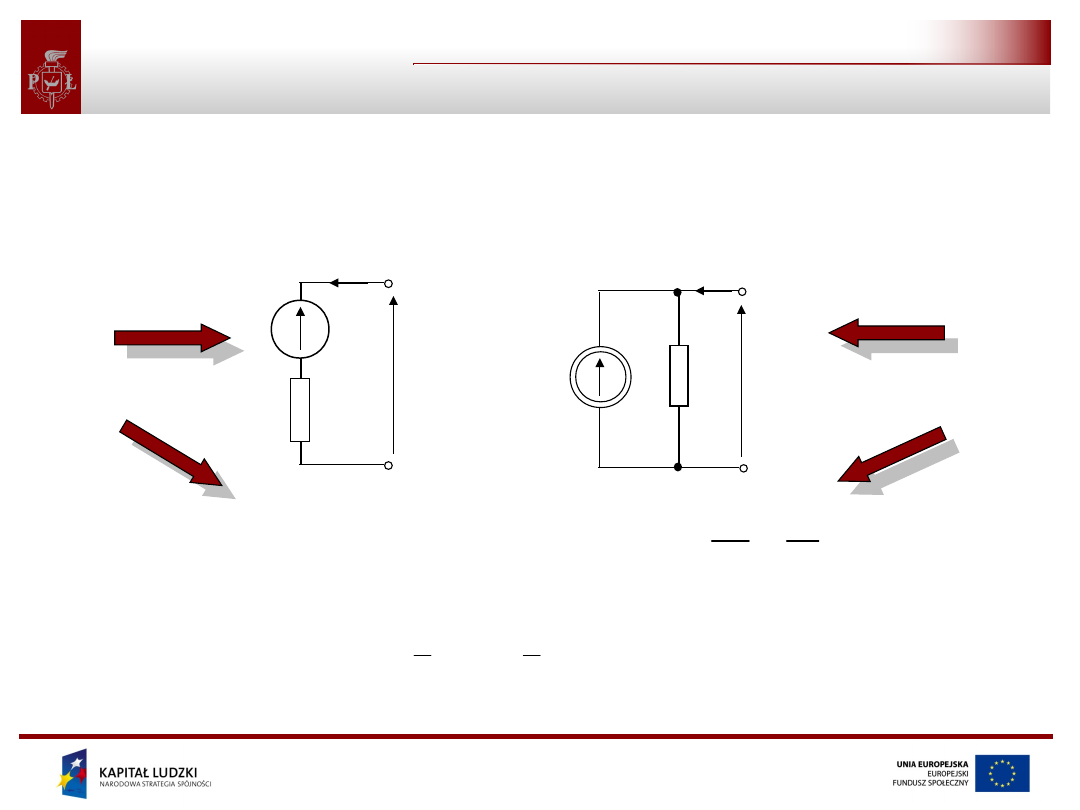
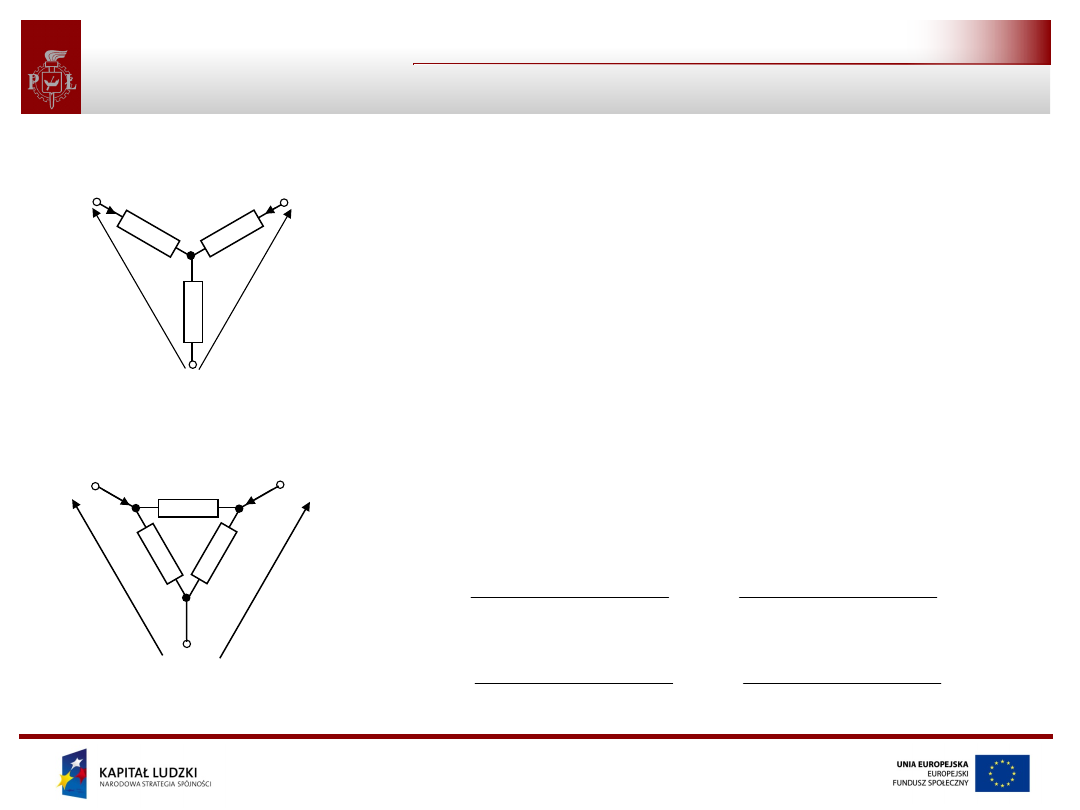
Układy równoważne – źródła rzeczywiste

Układy równoważne – źródła rzeczywiste

e

Ri

u

A

A





R

e

i

A

u

A

i

B

j

G

u

B

G

j

G

i

u

B

B





najprostszy model
rzeczywistego źródła napięciowego

najprostszy model
rzeczywistego źródła napięciowego

najprostszy model
rzeczywistego źródła prądowego

najprostszy model
rzeczywistego źródła prądowego

obwód A

obwód A

obwód B

obwód B

opis obwodu A

opis obwodu A

opis obwodu B

opis obwodu B

warunki równoważności obwodów A i B
są następujące:

warunki równoważności obwodów A i B
są następujące:

R

e

j

;

R

G





1

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

57

Układy równoważne – transfiguracja gwiazda -
trójkąt

Układy równoważne – transfiguracja gwiazda -
trójkąt

















3

2

2

3

1

3

2

1

2

2

2

3

2

3

1

1

3

2

1

1

1

1

R

R

i

R

i

R

i

i

R

i

u

R

i

R

R

i

R

i

i

R

i

u

A

A

A

A

A

A

A

A

A

A

A

A

























R

2

i

A1

i

A2

R

1

R

3

3

1

2

u

A1

u

A2

R

12

R

31

R

23

1

2

3

i

B1

i

B2

u

B1

u

B2

układ A – połączenie gwiazdowe trzech oporników (połączenie w gwiazdę)

układ A – połączenie gwiazdowe trzech oporników (połączenie w gwiazdę)

układ B – połączenie trójkątowe trzech oporników (połączenie w trójkąt)

układ B – połączenie trójkątowe trzech oporników (połączenie w trójkąt)









31

12

23

31

12

23

2

23

12

31

23

31

1

2

31

12

23

31

23

2

23

12

31

23

12

31

1

1

R

R

R

R

R

R

i

R

R

R

R

R

i

u

R

R

R

R

R

i

R

R

R

R

R

R

i

u

B

B

B

B

B

B





























na podstawie praw Kirchhoffa można napisać
równania:

na podstawie praw Kirchhoffa można napisać
równania:

traktując prądy płynące przez zaciski 1 i 2 jako prądy
źródeł prądowych oraz stosując zasadę superpozycji
i zależności dzielnika prądowego otrzymuje się:

traktując prądy płynące przez zaciski 1 i 2 jako prądy
źródeł prądowych oraz stosując zasadę superpozycji
i zależności dzielnika prądowego otrzymuje się:

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

58

Układy równoważne – transfiguracja gwiazda
- trójkąt

Układy równoważne – transfiguracja gwiazda
- trójkąt









3

2

2

3

1

2

3

2

3

1

1

1

R

R

i

R

i

u

R

i

R

R

i

u

A

A

A

A

A

A













31

23

12

31

23

23

12

2

31

23

12

31

23

1

2

31

23

12

31

23

2

31

23

12

31

23

31

12

1

1

R

R

R

R

R

R

R

i

R

R

R

R

R

i

u

R

R

R

R

R

i

R

R

R

R

R

R

R

i

u

B

B

B

B

B

B





























31

23

12

31

23

3

31

23

12

23

12

2

31

23

12

31

12

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R



















Otrzymane wzory dla połączenia gwiazdowego i trójkątowego
są następujące

Otrzymane wzory dla połączenia gwiazdowego i trójkątowego
są następujące

Można stwierdzić, że układ gwiazdowy (układ A) jest równoważny
układowi trójkątowemu (układowi B) jeżeli jego oporniki spełniają warunki

Można stwierdzić, że układ gwiazdowy (układ A) jest równoważny
układowi trójkątowemu (układowi B) jeżeli jego oporniki spełniają warunki

Są to zależności umożliwiające wyznaczenie
wartości rezystorów gwiazdy przy zamianie
trójkąta na gwiazdę.

Są to zależności umożliwiające wyznaczenie
wartości rezystorów gwiazdy przy zamianie
trójkąta na gwiazdę.

Przy układach symetrycznych:

Przy układach symetrycznych:

tr

gw

R

R

3

1



Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

59

Układy równoważne – transfiguracja gwiazda
- trójkąt

Układy równoważne – transfiguracja gwiazda
- trójkąt

2

1

3

1

3

31

1

3

2

3

2

23

3

2

1

2

1

12

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R



















Wyznaczając z przedstawionych na poprzedniej stronie zależności
rezystancje trójkąta jako funkcje rezystancji gwiazdy otrzymuje się
następujące zależności:

Wyznaczając z przedstawionych na poprzedniej stronie zależności
rezystancje trójkąta jako funkcje rezystancji gwiazdy otrzymuje się
następujące zależności:

Są to zależności umożliwiające
wyznaczenie wartości rezystorów
trójkąta przy zamianie gwiazdy
na trójkąt.

Są to zależności umożliwiające
wyznaczenie wartości rezystorów
trójkąta przy zamianie gwiazdy
na trójkąt.

Przy zamianie symetrycznej gwiazdy na trójkąt:

Przy zamianie symetrycznej gwiazdy na trójkąt:

gw

tr

R

R

3



Wzory na wyznaczanie rezystorów równoważnej gwiazdy oraz
równoważnego trójkąta można łatwo zapamiętać zauważając, że
kolejną zależność można otrzymać z poprzedniej przez cykliczną zamianę
indeksów, tzn. zamieniając w indeksach 1 na 2, 2 na 3 oraz 3 na 1.

Wzory na wyznaczanie rezystorów równoważnej gwiazdy oraz
równoważnego trójkąta można łatwo zapamiętać zauważając, że
kolejną zależność można otrzymać z poprzedniej przez cykliczną zamianę
indeksów, tzn. zamieniając w indeksach 1 na 2, 2 na 3 oraz 3 na 1.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

60

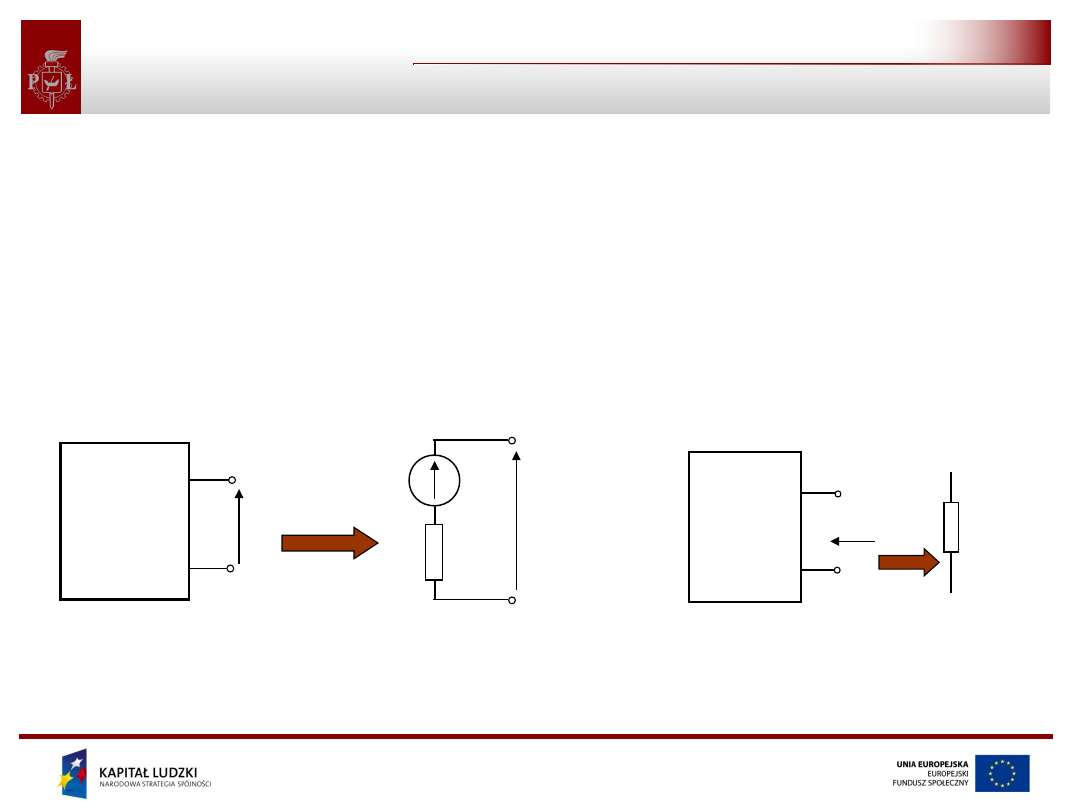
Twierdzenie Thevenina

Twierdzenie Thevenina

Twierdzenie Thevenina:
Obwód liniowy rozpatrywany od strony dowolnie wybranych

dwóch punktów tego obwodu można zastąpić szeregowym

połączeniem źródła napięciowego o napięciu źródłowym

równym napięciu między wybranymi punktami obwodu oraz

rezystancji równej rezystancji obwodu widzianej z wybranych

punktów po usunięciu wszystkich źródeł niezależnych, tzn,

zwarciu zacisków źródeł napięciowych oraz rozwarciu zacisków

źródeł prądowych.

układ
liniow
y
bez
źródeł

A

B

R

z

R

z

układ
liniowy

e

z

u

AB

A

B

B

A

u

AB

=e

z

R

z

równoważność układu liniowego
i dwójnika Thevenina

równoważność układu liniowego
i dwójnika Thevenina

sposób wyznaczania rezystancji
dwójnika Thevenina

sposób wyznaczania rezystancji
dwójnika Thevenina

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

61

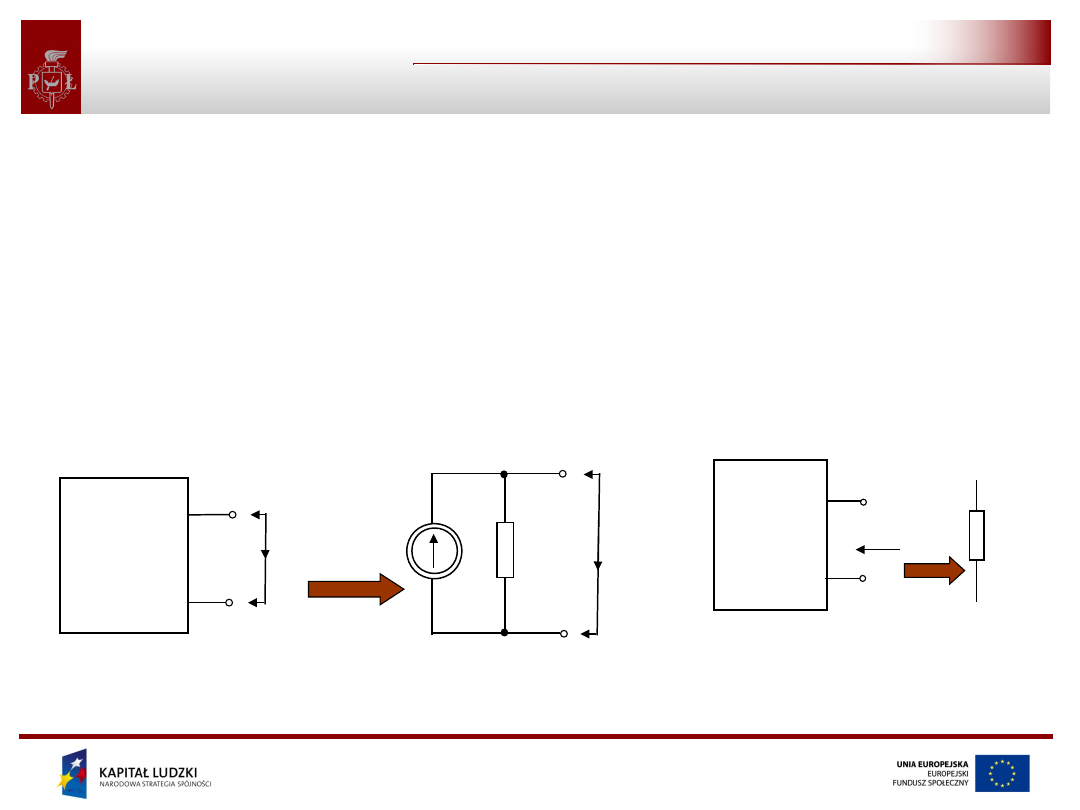
Twierdzenie Nortona

Twierdzenie Nortona

A

j

z

G

z

B

układ
liniowy

A

B

j

AB

=j

z

j

AB

=j

z

Twierdzenie Nortona:
Obwód liniowy rozpatrywany od strony dowolnie

wybranych dwóch punktów tego obwodu można zastąpić

równoległym połączeniem źródła prądowego o prądzie

źródłowym równym prądowi płynącemu w bezoporowej

zworze łączącej wybrane punkty obwodu oraz

konduktancji równej konduktancji obwodu widzianej z

wybranych punktów po usunięciu wszystkich źródeł

niezależnych, tzn, zwarciu zacisków źródeł napięciowych

oraz rozwarciu zacisków źródeł prądowych.

układ
liniow
y
bez
źródeł

A

B

G

z

G

z

równoważność układu liniowego
i dwójnika Nortona

równoważność układu liniowego
i dwójnika Nortona

sposób wyznaczania konduktancji
dwójnika Nortona

sposób wyznaczania konduktancji
dwójnika Nortona

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

62

Twierdzenia Thevenina - przykład

Twierdzenia Thevenina - przykład

z

AB

E

E

E

R

R

R

U









2

U

AB

B

A

R

E

R

R

R

AB

=R

z

B

A

R

R

R

B

A

R

E

R

R

R

z

B

A

E

z

Kolorem czerwonym
oznaczony jest
rozważany układ
liniowy, A i B to wybrane
punkty

Kolorem czerwonym
oznaczony jest
rozważany układ
liniowy, A i B to wybrane
punkty

z

AB

R

R

R

R

R

R

R

R

R















2

3

2

2

dwójnik Thevenina,
zastępcze źródło
rzeczywiste
napięciowe

dwójnik Thevenina,
zastępcze źródło
rzeczywiste
napięciowe

parametry zastępczego
źródła

parametry zastępczego
źródła

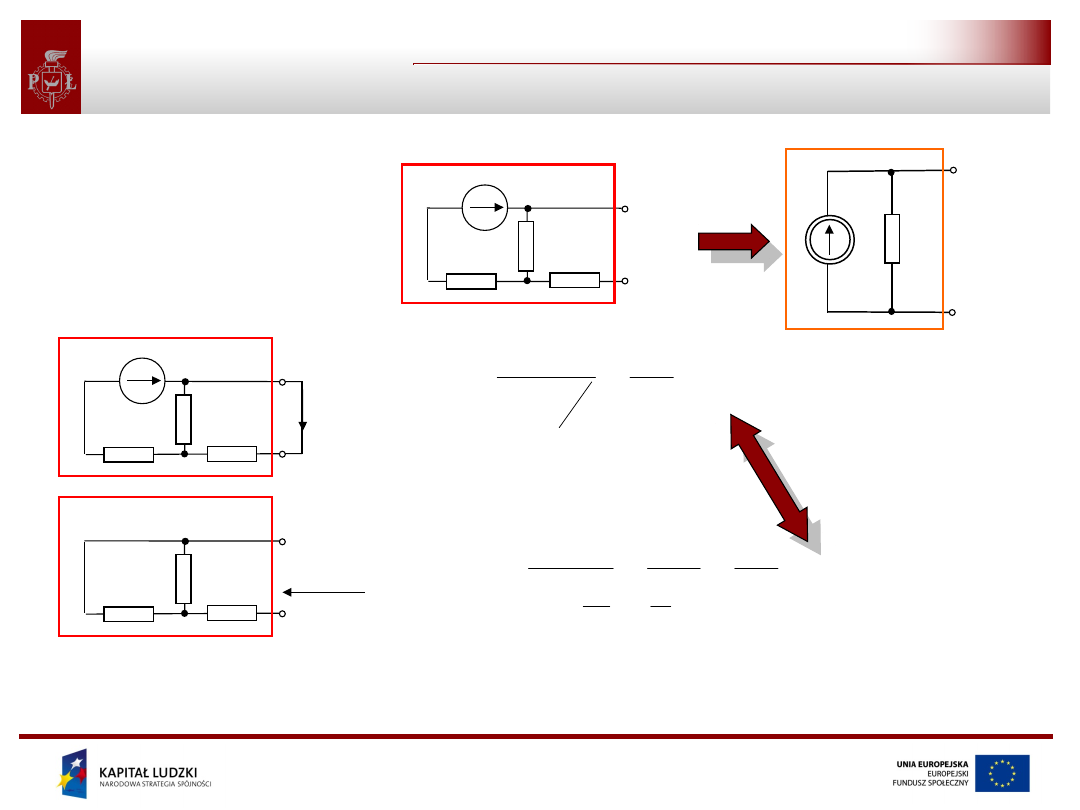
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

63

Twierdzenie Nortona - przykład

Twierdzenie Nortona - przykład

z

AB

J

R

E

R

R

E

,

I









3

2

5

0

I

AB

B

A

R

E

R

R

B

A

R

E

R

R

A

J

z

G

z

B

Kolorem czerwonym
oznaczony jest
rozważany układ
liniowy, A i B to wybrane
punkty

Kolorem czerwonym
oznaczony jest
rozważany układ
liniowy, A i B to wybrane
punkty

dwójnik Nortona,
zastępcze źródło
rzeczywiste
prądowe

dwójnik Nortona,
zastępcze źródło
rzeczywiste
prądowe

G

AB

=G

z

B

A

R

R

R

z

AB

G

R

R

R

R

G











3

2

2

3

1

2

1

parametry zastępczego
źródła

parametry zastępczego
źródła

Parametry zastępczego źródła prądowego można otrzymać również przez
zamianę zastępczego źródła napięciowego na równoważne źródło prądowe

Parametry zastępczego źródła prądowego można otrzymać również przez
zamianę zastępczego źródła napięciowego na równoważne źródło prądowe

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

64

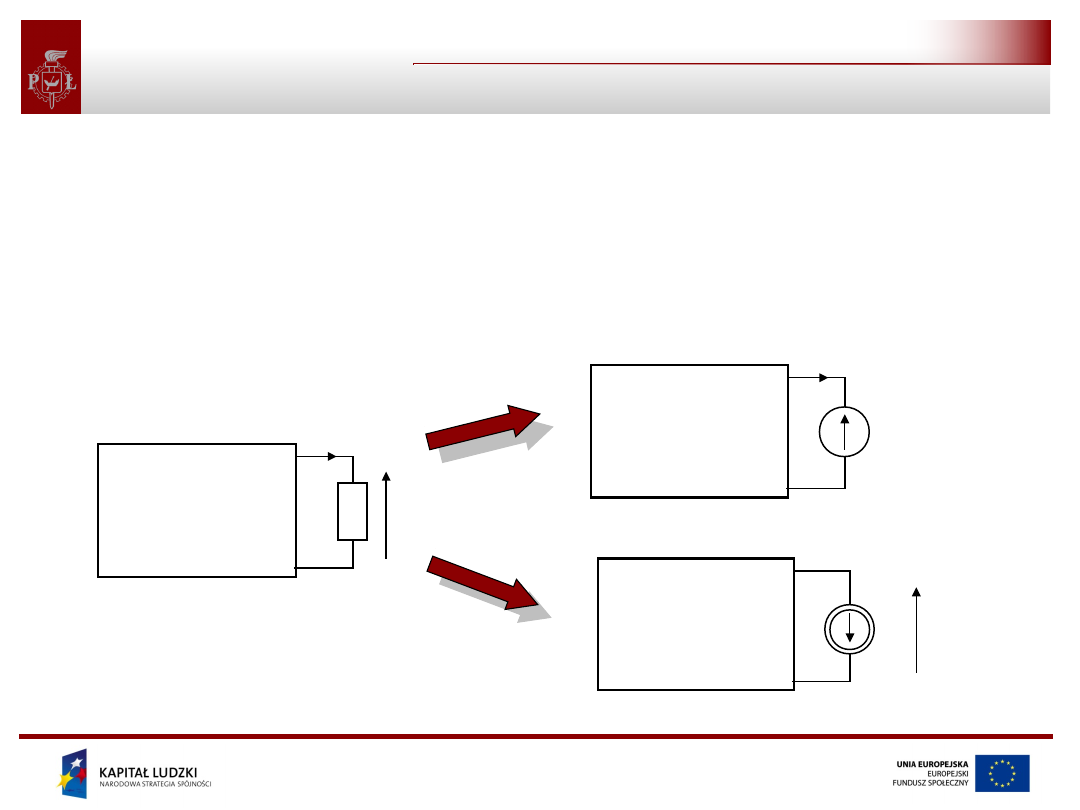
Zastępowanie elementu źródłem napięcia lub
prądu

Zastępowanie elementu źródłem napięcia lub
prądu

Dowolny element obwodu (liniowego lub nieliniowego), na zaciskach

którego panuje napięcie u oraz przez który płynie prąd i można
zastąpić idealnym źródłem napięcia o napięciu źródłowym równym
napięciu u panującym na elemencie lub idealnym źródłem prądu o
prądzie źródłowym równym prądowi i płynącemu przez element.

układ
nieliniowy
lub liniowy

u

i

układ
nieliniowy
lub liniowy

e=u

i

układ
nieliniowy
lub
liniowy

u

j=i

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

65

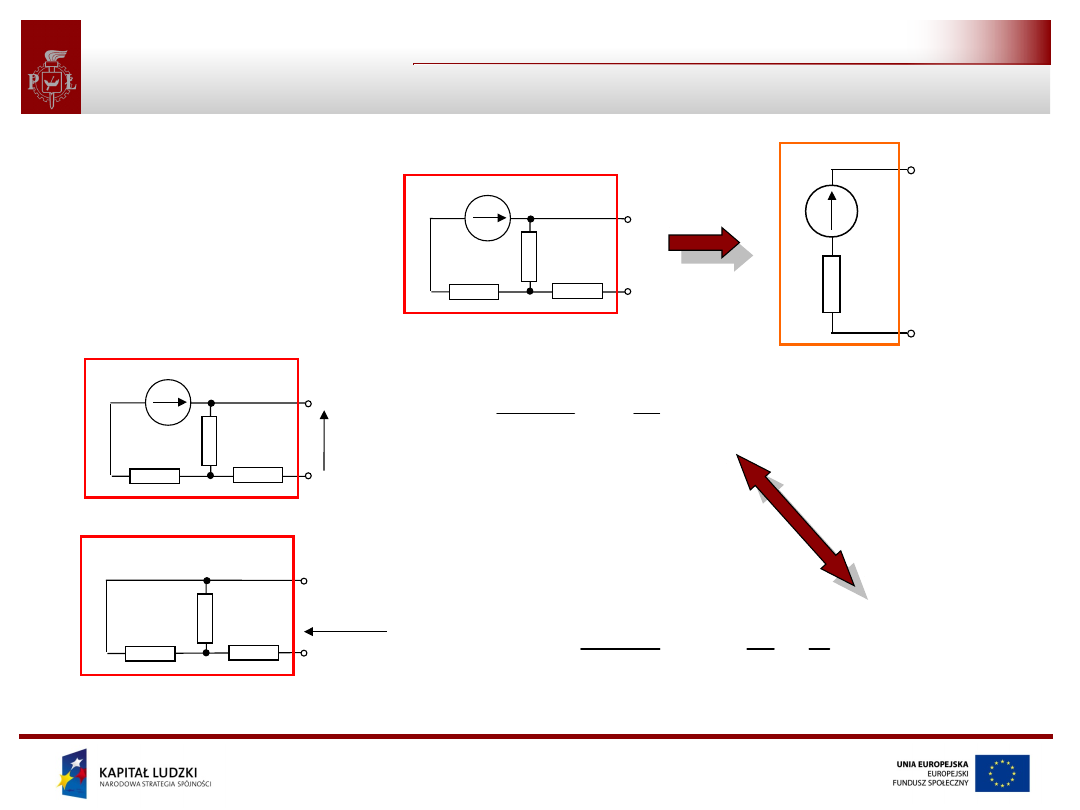
Włączanie i przenoszenie źródeł

Włączanie i przenoszenie źródeł

Twierdzenie1
Jeżeli do każdej ze zbiegających się w dowolnym węźle układu

gałęzi zostanie włączone idealne źródło napięciowe o tej samej
wartości napięcia źródłowego oraz tej samej orientacji względem
węzła to rozpływ prądów w tym obwodzie nie zmieni się.

Twierdzenie2
Jeżeli między każde dwa węzły dowolnie wybranej pętli obwodu

zostanie włączone idealne źródło prądowe o tej samej wartości
prądu źródłowego oraz tej samej orientacji względem pętli to
rozkład napięć w tym obwodzie nie zmieni się.

• Przedstawione powyżej dwa twierdzenia pozwalają na włączanie

do obwodu w określony sposób źródeł napięciowych i prądowych
oraz realizowanie przenoszenia źródeł obecnych w obwodzie
przez odpowiednie włączanie nowych źródeł.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

66

Wprowadzenie do analizy
obwodów prądu
sinusoidalnego

Wprowadzenie do analizy
obwodów prądu
sinusoidalnego

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

67

Wiadomości podstawowe

Wiadomości podstawowe

• Rozważany będzie stan ustalony obwodów liniowych, w których

napięcia źródłowe niezależnych źródeł napięciowych i prądy

źródłowe niezależnych źródeł prądowych są sinusoidalnie

zmiennymi funkcjami czasu o tym samym okresie T.

• Elementami obwodów będą oprócz źródeł niezależnych oporniki,

cewki, kondensatory oraz wszystkie rodzaje źródeł sterowanych.

Prądy i napięcia w takich obwodach są tak, jak wielkości

charakteryzujące źródła, sinusoidalnymi funkcjami czasu.

• Argumentem funkcji sinusoidalnie zmiennych jest wielkość ωt

(wymiar tej wielkości to radian), gdzie ω nosi nazwę pulsacji. Jej

jednostką jest radian na sekundę (rad/s). Pulsacja jest związana z

okresem T oraz częstotliwością f w następujący sposób:

• Wprowadzenie wielkości ωt jako argumentu funkcji sinusoidalnej

pozwala na sprowadzenie okresu sinusoidalnie zmiennych funkcji

dla różnych częstotliwości do wartości

2Π.

T

f

ω









2

2

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

68

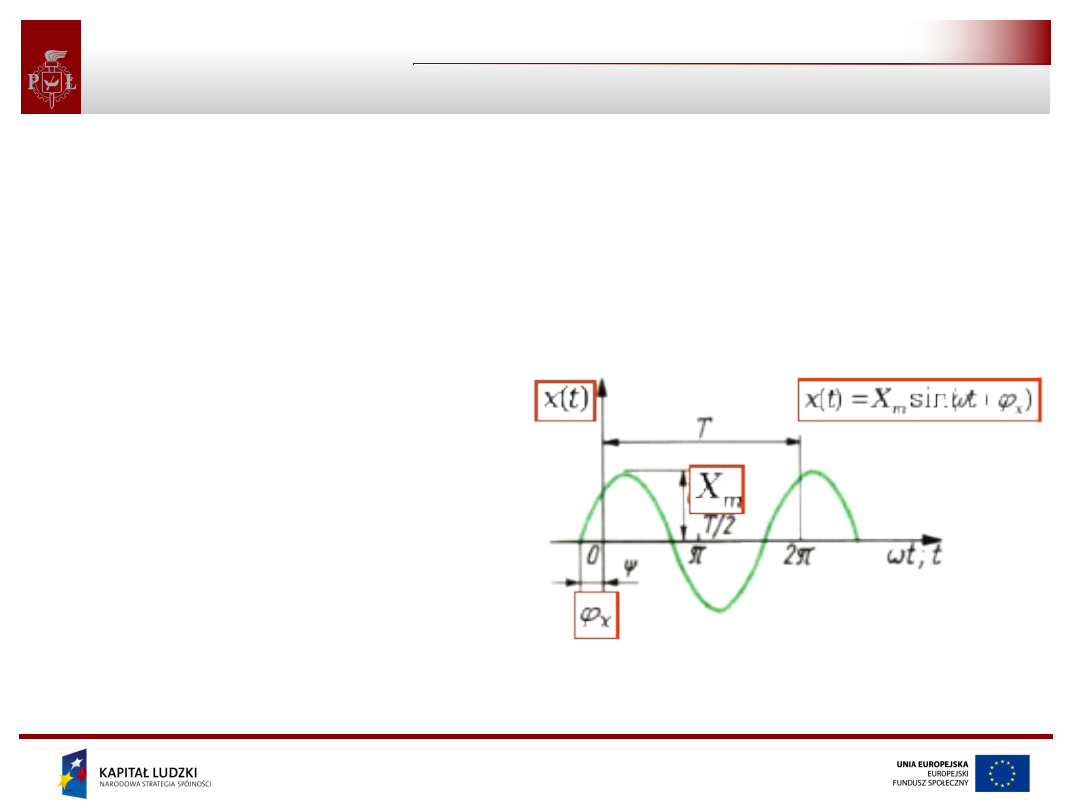
Wiadomości podstawowe

Wiadomości podstawowe

m

X

– amplituda

ω – pulsacja

– faza początkowa,

czyli przesunięcie fazowe

dla t=0

T – okres funkcji równy 2Π

f – częstotliwość

– amplituda

ω – pulsacja

– faza początkowa,

czyli przesunięcie fazowe

dla t=0

T – okres funkcji równy 2Π

f – częstotliwość

Poniżej przedstawiona jest funkcja sinusoidalnie zmienna x(t).
Jej zapis matematyczny oraz wielkości jednoznacznie określające
tę funkcję znajdują się w czerwonych ramkach. Dla określonej pulsacji,
która w każdym z rozważanych obwodów jest wspólna dla wszystkich
prądów i napięć, dwie wielkości jednoznacznie określają każdą
sinusoidalnie zmienną funkcję: wartość maksymalna oraz faza
początkowa.

Poniżej przedstawiona jest funkcja sinusoidalnie zmienna x(t).
Jej zapis matematyczny oraz wielkości jednoznacznie określające
tę funkcję znajdują się w czerwonych ramkach. Dla określonej pulsacji,
która w każdym z rozważanych obwodów jest wspólna dla wszystkich
prądów i napięć, dwie wielkości jednoznacznie określają każdą
sinusoidalnie zmienną funkcję: wartość maksymalna oraz faza
początkowa.

x

φ

W dalszej części przedstawione zostały prądy i napięcia w postaci
wykresów oraz zależności analitycznych elementów oraz ich połączeń.

W dalszej części przedstawione zostały prądy i napięcia w postaci
wykresów oraz zależności analitycznych elementów oraz ich połączeń.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

69

Wartość skuteczna

Wartość skuteczna

 

 







T

t

t

sk

dt

t

x

T

X

0

0

2

1

X

;

X

sk

 





x

m

φ

t

ω

sin

X

t

x





Wartość skuteczna jest wielkością powszechnie stosowaną do
charakteryzowania wielkości okresowych, w tym także
zmiennych
sinusoidalnie. Wartość skuteczną dowolnej okresowej
wielkości x(t)
definiuje się jako pierwiastek z wartości średniej za okres
kwadratu
wartości chwilowej:

Wartość skuteczna jest wielkością powszechnie stosowaną do
charakteryzowania wielkości okresowych, w tym także
zmiennych
sinusoidalnie. Wartość skuteczną dowolnej okresowej
wielkości x(t)
definiuje się jako pierwiastek z wartości średniej za okres
kwadratu
wartości chwilowej:

Stosowane oznaczenia wartości skutecznej to:

Stosowane oznaczenia wartości skutecznej to:

Można wykazać, że wartość skuteczna dowolnej sinusoidalnie zmiennej

wielkości x(t):

Można wykazać, że wartość skuteczna dowolnej sinusoidalnie zmiennej

wielkości x(t):

jest równa:

jest równa:

2

m

X

X 

 





 





i

u

φ

t

ω

sin

I

t

i

;

φ

t

ω

sin

U

t

u









2

2

Duże znaczenie wartości skutecznych wielkości sinusoidalnie zmiennych
powoduje, że wartości chwilowe napięć i prądów są często zapisywane
jako:

Duże znaczenie wartości skutecznych wielkości sinusoidalnie zmiennych
powoduje, że wartości chwilowe napięć i prądów są często zapisywane
jako:

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

70

Opornik

Opornik

 





i

φ

t

ω

sin

I

t

i

Rm

R





 

 





 





u

Rm

R

i

Rm

R

R

φ

t

ω

sin

U

t

u

φ

t

ω

sin

RI

t

Ri

t

u











R

u

R

(t)

i

R

(t)

0









i

u

i

u

φ

φ

φ

φ

φ

symbol opornika liniowego

symbol opornika liniowego

Niech prąd opornika będzie określony przez:

Niech prąd opornika będzie określony przez:

Przez porównanie obu powyższych
zależności otrzymuje się związki:

Przez porównanie obu powyższych
zależności otrzymuje się związki:

Prawo Ohma dla wartości
maksymalnych i skutecznych

Prawo Ohma dla wartości
maksymalnych i skutecznych

kąt przesunięcia
fazowego

kąt przesunięcia
fazowego

R

R

Rm

Rm

I

R

U

RI

U





Napięcie na jego zaciskach wynosi zatem (na podstawie
prawa Ohma):

Napięcie na jego zaciskach wynosi zatem (na podstawie
prawa Ohma):

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

71

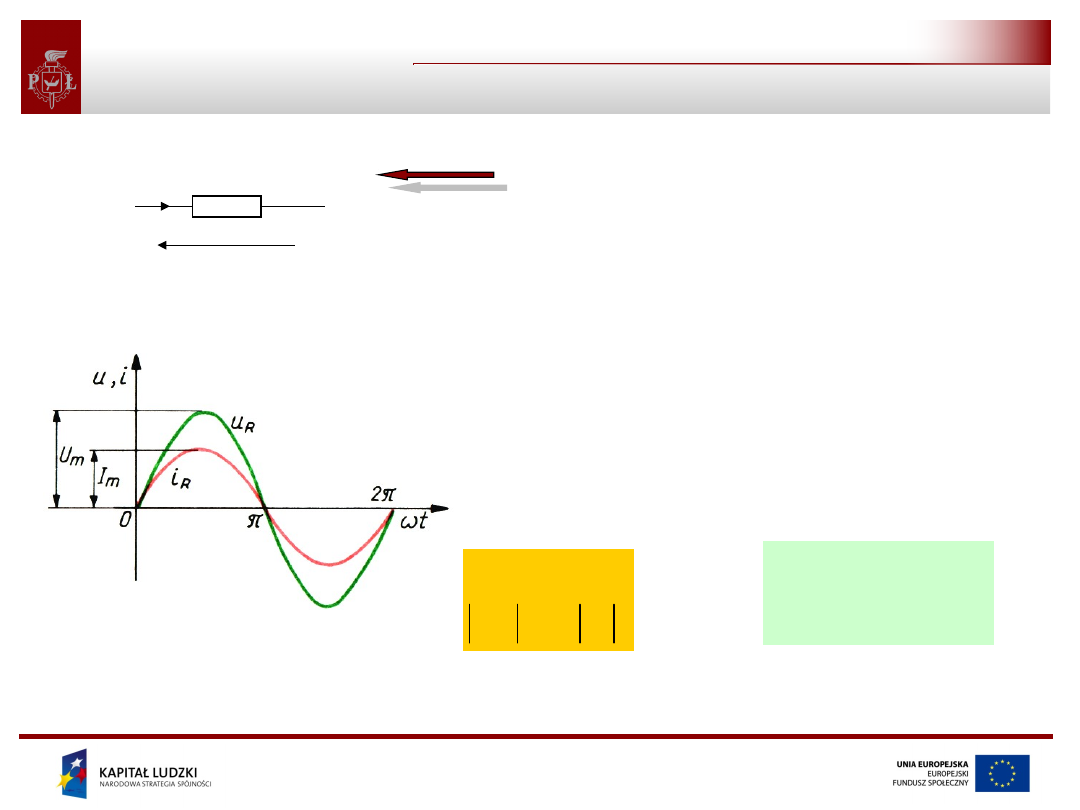
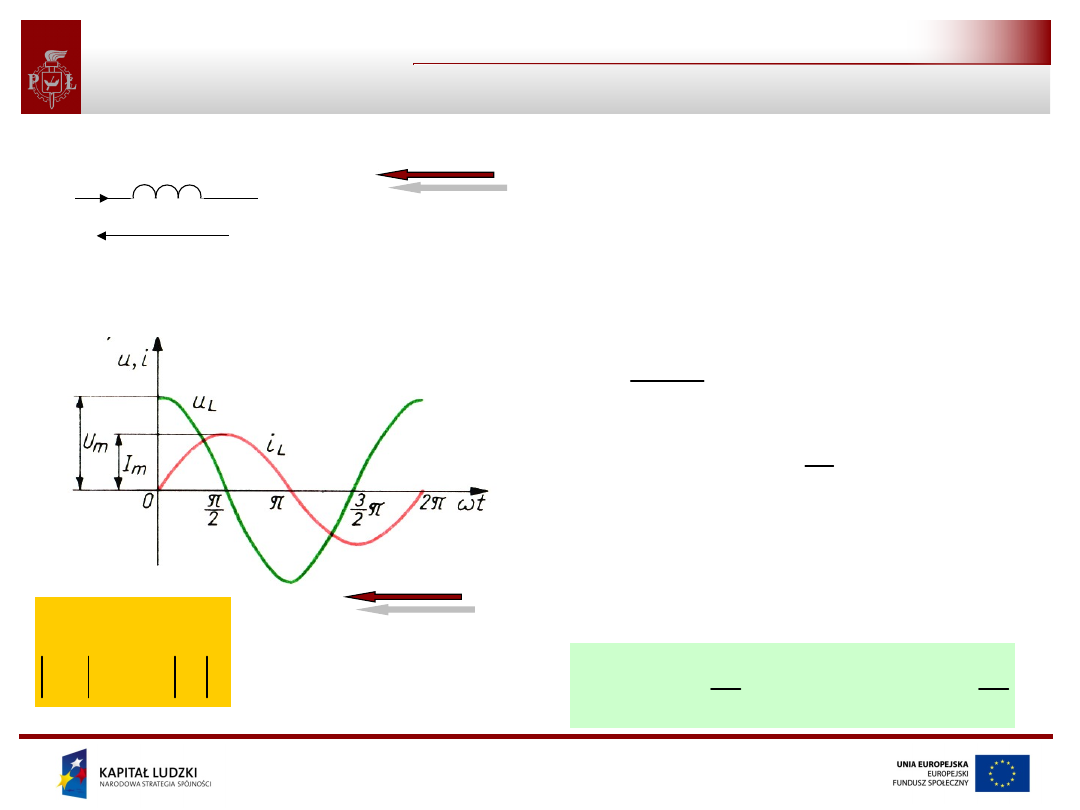
Cewka

Cewka

 





i

φ

t

ω

sin

I

t

i

Lm

L





 

 





 





u

Lm

L

i

Lm

i

Lm

L

L

φ

t

ω

sin

U

t

u

φ

t

ω

sin

LI

ω

φ

t

ω

cos

LI

ω

dt

t

di

L

t

u

































2

L

u

L

(t)

i

L

(t)

L

L

Lm

Lm

I

L

ω

U

LI

ω

U





2

2















i

u

i

u

φ

φ

φ

;

φ

φ

symbol opornika liniowego

symbol opornika liniowego

Niech prąd opornika będzie określony przez:

Niech prąd opornika będzie określony przez:

Napięcie na jego zaciskach wynosi zatem (na podstawie
prawa Ohma):

Napięcie na jego zaciskach wynosi zatem (na podstawie
prawa Ohma):

Przez porównanie obu powyższych
zależności otrzymuje się związki:

Przez porównanie obu powyższych
zależności otrzymuje się związki:

Prawo Ohma dla
wartości
maksymalnych
i skutecznych

Prawo Ohma dla
wartości
maksymalnych
i skutecznych

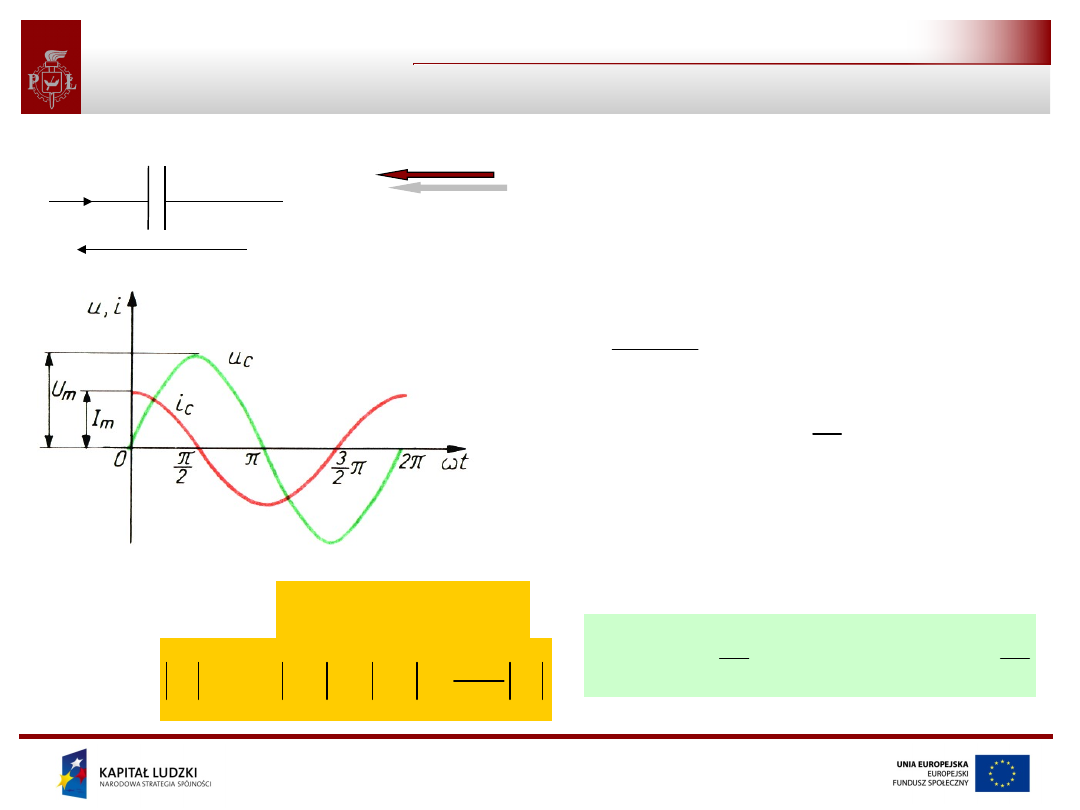
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

72

Kondensator

Kondensator

 





u

φ

t

ω

sin

U

t

u

Cm

C





 

 





 





i

Cm

C

u

Cm

u

Cm

C

C

φ

t

ω

sin

I

t

i

φ

t

ω

sin

CU

ω

φ

t

ω

cos

CU

ω

dt

t

du

C

t

i

































2

;

CU

ω

I

Cm

Cm



2

2

















i

u

u

i

φ

φ

φ

;

φ

φ

u

C

(t)

C

i

C

(t)

symbol kondensatora liniowego

symbol kondensatora liniowego

Niech napięcie kondensatora będzie określone przez:

Niech napięcie kondensatora będzie określone przez:

Prąd płynący przez kondensator wynosi zatem:

Prąd płynący przez kondensator wynosi zatem:

Przez porównanie obu powyższych
zależności otrzymuje się związki:

Przez porównanie obu powyższych
zależności otrzymuje się związki:

C

C

C

C

I

C

ω

U

;

U

C

ω

I

1





Prawo Ohma dla
wartości
maksymalnych
i skutecznych

Prawo Ohma dla
wartości
maksymalnych
i skutecznych

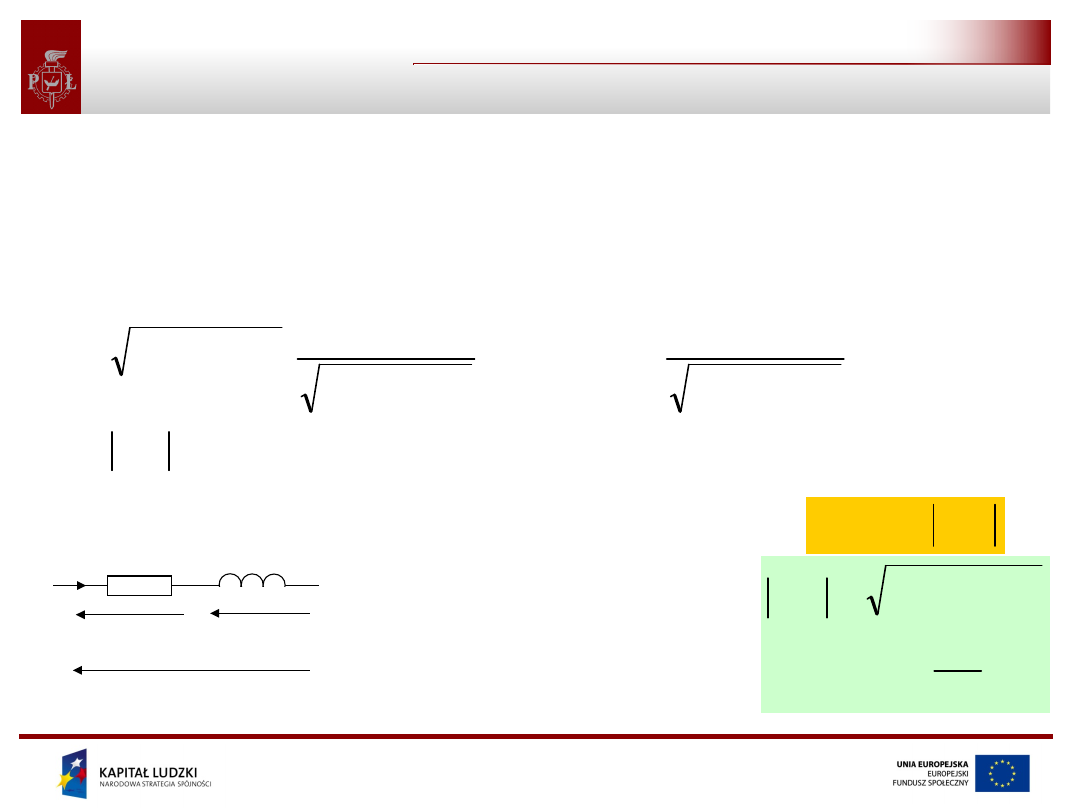
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

73

Szeregowe połączenie RL

Szeregowe połączenie RL









 

 





 





















RL

i

m

i

RL

i

RL

RL

m

i

i

m

i

m

i

m

L

R

φ

φ

t

ω

sin

U

φ

t

ω

cos

φ

sin

φ

t

ω

sin

φ

cos

Z

I

φ

t

ω

cos

L

ω

R

L

ω

φ

t

ω

sin

L

ω

R

R

L

ω

R

I

φ

t

ω

cos

LI

ω

φ

t

ω

sin

RI

u

u

u





























































2

2

2

2

2

2

 

R

L

ω

arctg

φ

L

ω

R

Z

RL

RL







2

2

 





i

φ

t

ω

sin

I

t

i

m





R

u

R

(t)

i(t)

L

u

L

(t)

u(t)

Niech prąd połączenia wynosi:

Niech prąd połączenia wynosi:

Napięcie na połączeniu na podstawie NPK oraz poprzednich rozważań to:

Napięcie na połączeniu na podstawie NPK oraz poprzednich rozważań to:

moduł impedancji

moduł impedancji

kąt przesunięcia fazowego
między napięciem i prądem

kąt przesunięcia fazowego
między napięciem i prądem

RL

m

m

Z

I

U 

prawo Ohma

prawo Ohma

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

74

Szeregowe połączenie RC

Szeregowe połączenie RC

 





i

φ

t

ω

sin

I

t

i

m





































RC

i

m

i

RC

i

RC

RC

m

i

i

m

i

m

i

m

C

R

φ

φ

t

ω

sin

U

φ

t

ω

cos

φ

sin

φ

t

ω

sin

φ

cos

Z

I

φ

t

ω

cos

C

ω

R

C

ω

φ

t

ω

sin

C

ω

R

R

C

ω

R

I

φ

t

ω

cos

I

C

ω

φ

t

ω

sin

RI

u

u

u

















































































































2

2

2

2

2

2

1

1

1

1

1

R

u

R

(t)

i(t)

C

u

C

(t)

u(t)

CR

ω

arctg

φ

;

C

ω

R

Z

RC

RC

1

1

2

2





















Niech prąd połączenia wynosi:

Niech prąd połączenia wynosi:

Napięcie na połączeniu na podstawie NPK oraz poprzednich rozważań to:

Napięcie na połączeniu na podstawie NPK oraz poprzednich rozważań to:

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

75

Szeregowe połączenie RLC

Szeregowe połączenie RLC

 





i

φ

t

ω

sin

I

t

i

m









































RLC

i

m

i

RLC

i

RLC

RLC

m

i

RLC

i

RLC

RLC

m

i

m

i

m

i

m

C

L

R

φ

φ

t

ω

sin

U

φ

t

ω

cos

φ

sin

φ

t

ω

sin

φ

cos

Z

I

φ

t

ω

cos

Z

C

ω

L

ω

φ

t

ω

sin

Z

R

Z

I

φ

t

ω

cos

I

C

ω

φ

t

ω

cos

LI

ω

φ

t

ω

sin

RI

u

u

u

u









































































1

1

C

u

C

(t)

R

u

R

(t)

i(t)

L

u

L

(t)

u(t)

Niech prąd połączenia wynosi:

Niech prąd połączenia wynosi:

Napięcie na połączeniu na podstawie NPK oraz poprzednich rozważań to:

Napięcie na połączeniu na podstawie NPK oraz poprzednich rozważań to:

gdzie to moduł impedancji połączenia

gdzie to moduł impedancji połączenia

RLC

Z

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

76

Szeregowe połączenie RLC

Szeregowe połączenie RLC

R

C

ω

L

ω

arctg

φ

;

C

ω

L

ω

R

Z

RLC

RLC

1

1

2

2























Wielkość występująca w wyprowadzonej zależności:

Wielkość występująca w wyprowadzonej zależności:

nazywana jest reaktancją połączenia. Jej znak określa charakter połączenia.
Dodatnia wartość reaktancji oznacza indukcyjny charakter połączenia; kąt
przesunięcia fazowego jest też dodatni, co oznacza, że napięcie wyprzedza
prąd. Ujemna wartość reaktancji oznacza pojemnościowy charakter
połączenia; kąt przesunięcia fazowego jest wówczas ujemny, co oznacza,
że napięcie jest opóźnione względem prądu. Przy zerowej wartości
reaktancji połączenia napięcie jest w fazie z prądem; połączenie ma
charakter rezystancyjny.

nazywana jest reaktancją połączenia. Jej znak określa charakter połączenia.
Dodatnia wartość reaktancji oznacza indukcyjny charakter połączenia; kąt
przesunięcia fazowego jest też dodatni, co oznacza, że napięcie wyprzedza
prąd. Ujemna wartość reaktancji oznacza pojemnościowy charakter
połączenia; kąt przesunięcia fazowego jest wówczas ujemny, co oznacza,
że napięcie jest opóźnione względem prądu. Przy zerowej wartości
reaktancji połączenia napięcie jest w fazie z prądem; połączenie ma
charakter rezystancyjny.

C

ω

L

ω

X

1





W wyprowadzonej zależności wprowadzone zostały następujące
oznaczenia:

W wyprowadzonej zależności wprowadzone zostały następujące
oznaczenia:

moduł impedancji

moduł impedancji

kąt przesunięcia fazowego połaczenia

kąt przesunięcia fazowego połaczenia

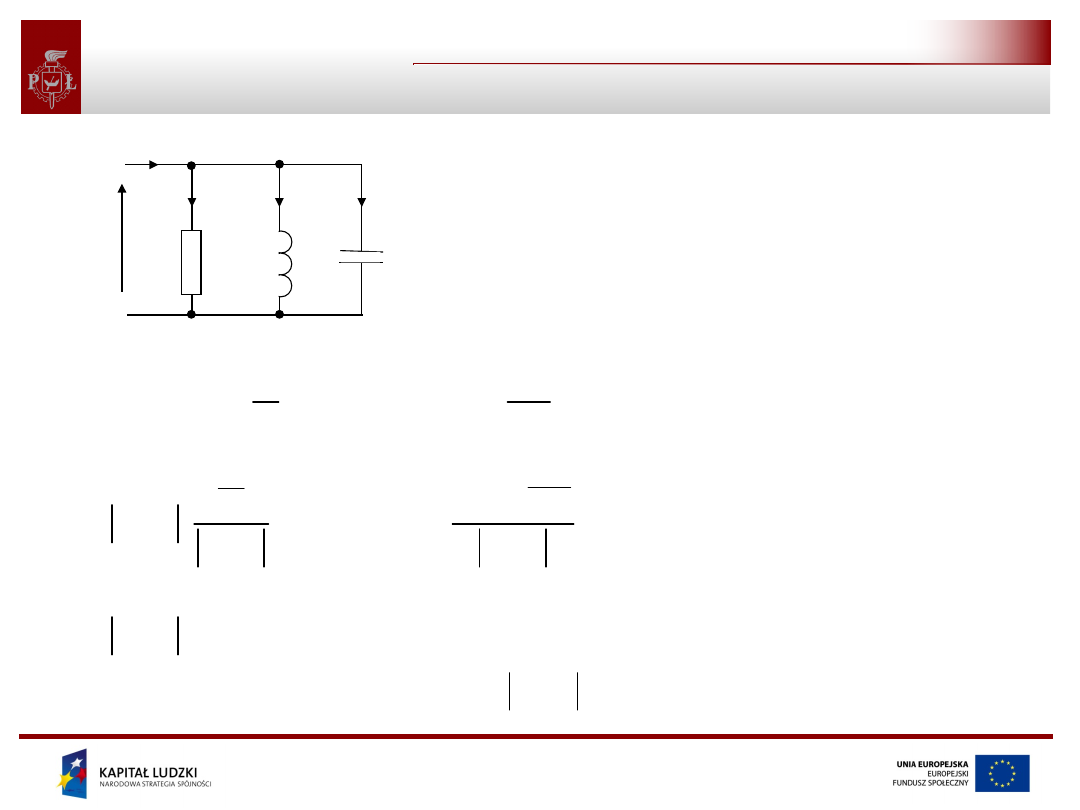
Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

77

Równoległe połączenie RLC

Równoległe połączenie RLC

 





u

φ

t

ω

sin

U

t

u

m























































































































RLC

u

m

u

RLC

u

RLC

RLC

m

u

RLC

u

RLC

RLC

m

u

m

u

m

u

m

C

L

R

φ

φ

t

ω

sin

I

φ

t

ω

cos

φ

sin

φ

t

ω

sin

φ

cos

Y

U

φ

t

ω

cos

Y

L

ω

C

ω

φ

t

ω

sin

Y

R

Y

U

φ

t

ω

cos

CU

ω

φ

t

ω

cos

U

L

ω

φ

t

ω

sin

U

R

i

i

i

i

1

1

1

1

RLC

Y

C

i

C

(t)

R

i

R

(t)

i(t)

L

i

L

(t)

u(t)

Niech napięcie na połączeniu wynosi:

Niech napięcie na połączeniu wynosi:

Prąd połączenia na podstawie PPK oraz poprzednich rozważań to:

Prąd połączenia na podstawie PPK oraz poprzednich rozważań to:

gdzie to moduł admitancji
połączenia

gdzie to moduł admitancji
połączenia

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

78

Szeregowe połączenie RLC

Szeregowe połączenie RLC

L

ω

C

ω

B

1





φ

G

L

ω

C

ω

arctg

φ

;

L

ω

C

ω

G

Y

RLC

RLC





























1

1

2

2

Wielkość występująca w wyprowadzonej zależności:

Wielkość występująca w wyprowadzonej zależności:

nazywana jest susceptancją połączenia. Jej znak określa charakter
połączenia. Dodatnia wartość susceptancji oznacza pojemnościowy
charakter połączenia; kąt przesunięcia fazowego jest wtedy ujemny, co
oznacza, że napięcie jest opóźnione względem prądu. Ujemna wartość
susceptancji oznacza indukcyjny charakter połączenia; kąt przesunięcia
fazowego jest wówczas dodatni, co oznacza, że napięcie wyprzedza
prąd. Przy zerowej wartości susceptancji połączenia napięcie jest w fazie
z prądem; połączenie ma charakter rezystancyjny.

nazywana jest susceptancją połączenia. Jej znak określa charakter
połączenia. Dodatnia wartość susceptancji oznacza pojemnościowy
charakter połączenia; kąt przesunięcia fazowego jest wtedy ujemny, co
oznacza, że napięcie jest opóźnione względem prądu. Ujemna wartość
susceptancji oznacza indukcyjny charakter połączenia; kąt przesunięcia
fazowego jest wówczas dodatni, co oznacza, że napięcie wyprzedza
prąd. Przy zerowej wartości susceptancji połączenia napięcie jest w fazie
z prądem; połączenie ma charakter rezystancyjny.

W wyprowadzonej zależności wprowadzone zostały następujące
oznaczenia:

W wyprowadzonej zależności wprowadzone zostały następujące
oznaczenia:

moduł impedancji

moduł impedancji

kąt przesunięcia fazowego połaczenia

kąt przesunięcia fazowego połaczenia

R

G

1



Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

Obwody Elektryczne I

79

Analiza prostych połączeń

Analiza prostych połączeń

• Analiza obwodów prądu sinusoidalnie zmiennego może być

prowadzona w oparciu o wyprowadzone zależności pomiędzy

napięciami i prądami w elementach tych obwodów oraz ich

podstawowych połączeniach. Połączenia złożone są

przekształcane w prostsze struktury, których napięcia i prądy są

wyznaczane w sposób przedstawiony na poprzednich stronach.

Ten sposób obliczania obwodów prądu sinusoidalnie zmiennego

nazywany jest analizą czasową.

• Prowadzenie analizy obwodów prądu sinusoidalnie zmiennego w

dziedzinie czasu prowadzi do stosunkowo pracochłonnych obliczeń

już w przypadku niezbyt skomplikowanych struktur. Jej praktyczne

zastosowanie jest ograniczone do prostych połączeń. Przykłady

takich analiz wraz ze szczegółowymi wyjaśnieniami przedstawione

zostały w materiałach pomocniczych do przedmiotu Obwody

Elektryczne I.

• Do analizy stanów ustalonych dowolnie skomplikowanych

obwodów elektrycznych prądu sinusoidalnie zmiennego

najbardziej efektywna jest metoda symboliczna oraz jej odmiany

(np. metoda amplitud zespolonych). Wykorzystuje ona rachunek

liczb zespolonych. Szczegółowe omówienie tej metody jest

zawarte w programie przedmiotu Obwody Elektryczne II.

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

„ Obwody Elektryczne I”

Prezentacja jest współfinansowana przez

Unię Europejską w ramach

Europejskiego Funduszu Społecznego w projekcie

pt.

„Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki

Łódzkiej - zarządzanie Uczelnią, nowoczesna oferta edukacyjna i

wzmacniania zdolności do zatrudniania osób niepełnosprawnych”

Prezentacja dystrybuowana jest bezpłatnie

„ Obwody Elektryczne I”

Prezentacja jest współfinansowana przez

Unię Europejską w ramach

Europejskiego Funduszu Społecznego w projekcie

pt.

„Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki

Łódzkiej - zarządzanie Uczelnią, nowoczesna oferta edukacyjna i

wzmacniania zdolności do zatrudniania osób niepełnosprawnych”

Prezentacja dystrybuowana jest bezpłatnie

Politechnika Łódzka, ul. Żeromskiego 116, 90-924 Łódź, tel. (042) 631

28 83

www.kapitalludzki.p.lodz.pl