Zdania kategoryczne:

S a P

Każde S jest P

S e P

Żadne S nie jest P

S i P

Niektóre S są P

S o P

Niektóre S nie są P

S a P

=

df

Λ

x

[S(x)

 P(x)]

S e P

=

df

Λ

x

[S(x)

 ~P(x)]

S i P

=

df

V

x

[S(x)

 P(x)]

S o P

=

df

V

x

[S(x)

 ~P(x)]



V

x

S(x)



V

x

S(x)  P(x)

S a P

S a P

S e P

S e P

S i P

S i P

S o P

S o P

Zdania

twierdzące

Zdania

przeczące

Zdania

ogólne

Zdania

szczegółowe

S a P

S e P

S i P

S o P

przeciwieństwo

podprzeciwieństwo

p

o

d

p

o

rz

ą

d

k

o

w

a

n

ie

p

o

d

p

o

rz

ą

d

k

o

w

a

n

ie

/

v





sp

rze

cz

n

oś

ć

sp

rz

ec

z

n

oś

ć

v

S a P

S e P

S i P

S o P

/

v





v

Prawa kwadratu logicznego

p

p

q

q

p

p

/

/

q

q

1

1

1

1

0

0

1

1

0

0

1

1

0

0

1

1

1

1

0

0

0

0

1

1

S a P  ~ S

e P

S e P  ~ S

a P

S a P  S i P
S e P  S o P
~ S i P  ~ S a
P
~ S o P  ~ S
e P

p

p

q

q

p

p





q

q

1

1

1

1

1

1

1

1

0

0

0

0

0

0

1

1

1

1

0

0

0

0

1

1

p

p

q

q

p

p





q

q

1

1

1

1

1

1

1

1

0

0

1

1

0

0

1

1

1

1

0

0

0

0

0

0

~ S i P  S o P
~ S o P  S i P

p

p

q

q

p

p





q

q

1

1

1

1

0

0

1

1

0

0

1

1

0

0

1

1

1

1

0

0

0

0

0

0

S a P  ~ S o
P
~ S o P  S a
P

S a P ↔ ~ S o P
S e P ↔ ~ S i P
S i P ↔ ~ S e P
S o P ↔ ~ S a P

Konwersja (odwrócenie) –

przekształcenie zdań kategorycznych

polegające na zamianie miejscami

podmiotu z orzecznikiem.

Prawa konwersji

prostej

S e P ↔ P e S

S i P ↔ P i S

Prawa konwersji

ograniczonej

S a P → P i S

S e P → P o S

Obwersja – przekształcenie

zdania kategorycznego

polegające na zmianie jego

„jakości” (bez zmiany „ilości”)

z równoczesnym

zanegowaniem orzecznika.

S a P ↔ S e P’ (S e nie-

P)

S e P ↔ S a P’ (S a

nie-P)

S i P ↔ S o P’ (S o nie-

P)

S o P ↔ S i P’ (S i nie-

P)

Każdy student jest sympatyczny.

S a P

S a P → S i P

Niektórzy studenci są

sympatyczni.

S a P → ~ S e P Nieprawda, że żaden student

nie jest sympatyczny.

S a P → ~ S o P Nieprawda, że niektórzy
studenci

nie są

sympatyczni.

S a P → P i S

Niektóre sympatyczne

osoby

są studentami.

S a P → S e P’

Żaden student nie jest nie-

sympatyczny.

S a P

S a P → S i
P

S a P → ~ S
e P

S a P → ~ S
o P

S a P → P i
S

S a P → S e
P’

S e P

S e P → S o P

S e P → ~ S a
P

S e P → ~ S i
P

S e P → P e S

S e P → P o S

S e P → S a
P’

S i P

S i P → ~ S e
P

S i P → P i S

S i P → S o P’

S o P

S o P → ~ S a
P

S o P → S i P’

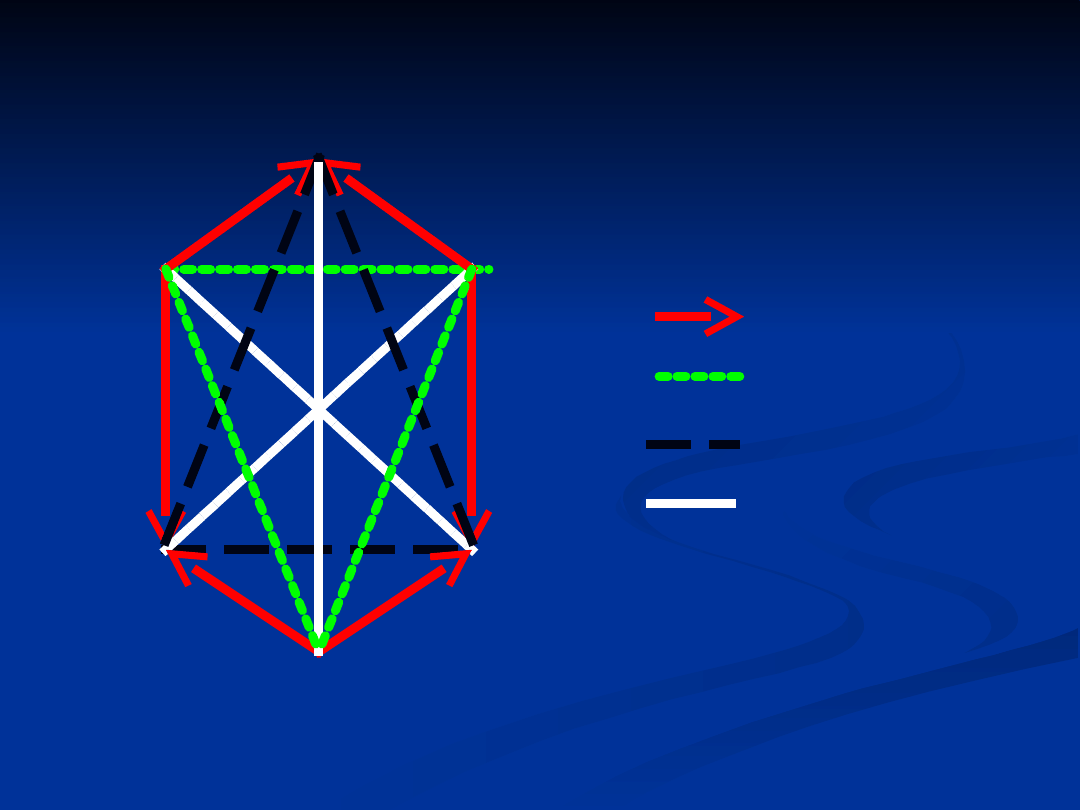
Nncx

Zncx

Dncx

Fncx

Oncx

Incx

wynikanie

przeciwieństw
o

podprzeciwień
stwo

sprzeczność

Nncx

Nncx → Oncx

Nncx → Dncx

Nncx → ~
Zncx

Nncx → ~
Fncx

Nncx → ~
Incx

Zncx

Zncx → Oncx

Zncx → Fncx

Zncx → ~
Nncx

Zncx → ~
Dncx

Zncx → ~
Incx

Incx

Incx → Dncx

Incx → Fncx

Incx → ~
Nncx

Incx → ~
Zncx

Incx → ~
Oncx