Filozoficzne implikacje

sylogistyki modalnej



Pogląd, że zdania analityczne, przypisujące przedmiotom

cechy istotne są prawdziwe z konieczności stało się
podstawą dla długotrwałego procesu prowadzącego do
podziału nauk na dwie grupy:



nauki aprioryczne, złożone z twierdzeń apodyktycznych, jak
np. logika czy matematyka;



nauki aposterioryczne / empiryczne, złożone ze zdań
asertorycznych bazujących na doświadczeniu.



Dopiero J. Łukasiewicz wykazał, że nie istnieją prawdziwe

zdania apodyktyczne i z punktu widzenia logiki, pomiędzy
prawdą matematyczną a empiryczną nie ma różnicy.

Uwagi wstępne



Sylogistyka zdań asertorycznych jest jasna i

bezbłędna; podczas gdy sylogistyka modalna
zawiera liczne błędy i sprzeczności co sprawia,
że jest niemal niezrozumiała.



Modalnością zajmował się Arystoteles w

Hermeneutyce, ale sylogistykę modalną
wyłożył w Analitykach pierwszych (księga I
rozdz. 3 oraz 8 – 22).



Idąc za niemieckim badaczem logiki Stagiryty

Paulem Gohlke (Die Entstehung der
Aristotelischen Logik, Berlin 1936) który
utrzymywał, że

Uwagi wstępne

rozdziały o których mowa są późniejszymi
dodatkami, a rozdział 23 był wcześniej kontynuacją
rozdziału 7; można przyjąć, iż



Sylogistyka modalna była ostatnim dziełem

logicznym Arystotelesa. Stanowi ona pierwszą,
niedopracowaną wersję rachunku.



Takie stanowisko pozwala wyjaśnić błędy systemu

i poprawki Teofrasta oraz Eudemosa poczynione
być może pod wpływem uwag Stagiryty.



System modalny kierujący się wskazówkami

samego Arystotelesa zbudował J. Łukasiewicz (A
System of Modal Logik, „The Journal of Computing
system” t. I, 1953, s. 111-149

Uwagi wstępne

przekład polski L. Borkowskiego ukazał się w

zbiorze Z zagadnień logiki i filozofii).



Stagiryta, jak się wydaje, nie zdawał sobie

sprawy, że logika modalna nazw zakłada logikę
modalną zdań. W ujęciu filozofa logika modalna
jest logika nazw.



Mówienie o Arystotelesowskiej logice modalnej

zdań jest jednak możliwe, gdyż niektóre jego
twierdzenia są tak ogólne, że zawierają wszystkie
rodzaje zdań; są także takie twierdzenia, które
Stagiryta formułuje używając zmiennych
zdaniowych.

Uwagi wstępne



Ponieważ logika modalna zdań jest

ważniejsza od sylogistyki modalnej nazw,
tak z logicznego jak i z filozoficznego
punktu widzenia, od niej rozpoczniemy
wywód.

Funktory modalne



Arystoteles używa następujących terminów

modalnych:



konieczne (anagkaion)



możliwe (dynaton)



niemożliwe (adynaton)



kontyngentne (endechomenon)



Grecki termin ἐνδεχόμενον nastręcza wiele

trudności. K. Leśniak przekłada go raz na
„przypadkowe” (np. tytuł r. 13 An.pr.), innym
razem na „możliwe” czy „dopuszczalne”.

Funktory modalne



T. Czeżowski (Arystotelesa teoria zdań modalnych,

„Przegląd Filozoficzny”, t. XXXIX, 1936, s. 232-241)
przekłada ten termin na zwrot „to, co zdarza się” i
wywodzi, że w myśl ontologicznych założeń filozofii
A. „możliwe” (dynaton) i „to, co się zdarza” mają
takie same znaczenia. Podobnie argumentuje Jaakko
Hintikka (Aristole on Modality and Determinism,
„Acta Philosophica Fennica, t. XXIX, nr 1)



Łukasiewicz, za Rossem, posługuje się terminem

„kontyngentne” (ang. contingent = przypadkowe,
ewentualne, możliwe, nieprzewidywalne, warunkowe,
…) co pozwala mu zachować różnicę miedzy
„możliwym” (dynaton, ang. possible).

Funktory modalne

Należy jednak zaznaczyć, że Łukasiewicz w pracy

Uwagi filozoficzne o wielowartościowych
systemach rachunku zdań, przekłada grecki
termin na „możliwość obustronna”.



Najczęściej używanym polskim odpowiednikiem

greckiego terminu (przekładanego za
Boecjuszem? na łac. contingens) jest
„przygodność” rozumiana w sposób przyjęty w
teologii np. „przygodność bytu ludzkiego” .



„Kontyngencja” znaczy niemal to samo co

„przygodność” ale nie kojarzy się z teologią i jest
terminem bardziej technicznym i bardziej
ogólnym od „przygodności”

Funktory modalne



Arystoteles uważa, że konieczne, możliwe,

niemożliwe czy kontyngentne mogą być tylko
zdania.



W „Zdanie »p« jest konieczne”, »p« jest nazwą

zdania. Powyższe zamienimy na „Jest konieczne,
że p” gdzie p jest zdaniem.
Przykład:

„Zdanie »Człowiek jest zwierzęciem« jest

konieczne” = „jest konieczne, aby człowiek był
zwierzęciem”



„Jest konieczne, że p” oznaczymy: □ p

Funktory modalne



„Jest możliwe, że p” oznaczymy ◊ p



□ p oraz ◊ p to funkcje modalne, zaś



□ - „jest konieczne” oraz ◊ - „jest możliwe” to

funktory modalne;



p jest argumentem funktora modalnego



Ponieważ wszystkie funkcje modalne są zdaniami,

funktory modalne są funktorami zdaniotwórczymi od
jednego argumentu zdaniowego.



Zdania rozpoczynające się od □ lub ich równoważniki

nazywane są zdaniami apodyktycznymi.

Funktory modalne



Zdania rozpoczynające się od ◊ oraz ich

równoważniki nazywane są zdaniami
problematycznymi.



Terminy modalne „konieczne” i „możliwe” (dziś:

logika aletyczna) oraz wzajemne związki między
nimi mają dla nas znaczenie podstawowe.



W Hermeneutyce (13, 22 a 15) Stagiryta pisze:

Z „może być” wynika „jest dopuszczalne” (i na

odwrót, to drugie z pierwszego), a także „nie może

być” i „nie musi być”

Funktory modalne



Twierdzenie, że możliwość implikuje nie-

konieczność tj.

(1) jeśli jest możliwe, że p, to nie jest konieczne, że p

◊ p → ~□ p



Następnie Arystoteles dostrzega błędność tego

sformułowania i uznaje, że konieczność implikuje
możliwość, czyli:
(2) Jeżeli jest konieczne, że p, to jest możliwe, że p

□ p → ◊ p

Funktory modalne



Z (2) i (1) można zbudować sylogizmy hipotetyczny

zgodnie z którym

(3) Jeżeli jest konieczne, że p, to nie jest konieczne,

że p

(□ p → ◊ p)

^

(◊ p → ~□ p)

→ (□ p → ~□ p)

co jest absurdalne:

Bo to co musi być, również może być […] Atoli ze

zdania „może być” wynika, że to nie jest możliwe, a

z tego znów wynika, że to nie jest konieczne; w

rezultacie to, co musi być konieczne, nie musi być –

co jest znów absurdem. (Herm. 22 b 11)

Funktory modalne



Następnie Arystoteles stwierdza, iż:

(4) Jeżeli jest możliwe, że p, to nie jest konieczne,

że nie p

◊ p → ~□ ~ p

Pozostaje więc dla zdania „Nie musi nie być”

wynikanie ze zdania „Może być”. (Herm. 22 b 22)

•

Poprawkę wcześniejszej pomyłki odnajdujemy
jednak w Analitykach pierwszych (I 13, 32 a 25),
nie zaś w Hermeneutyce.

Funktory modalne



Poprawka o której mowa ma postać

równoważności:
(I) Jest możliwe, że p – wtw, gdy nie jest
konieczne, że nie p.

◊ p ≡ ~□ ~ p

„Jest możliwe żeby przysługiwało”, „Nie jest

niemożliwe, żeby przysługiwało” i „Nie musi nie

przysługiwać” albo są identyczne, albo

nawzajem z siebie wynikają” (An. pr. I 13, 32 a

25)

Funktory modalne



Można zatem przyjąć, iż relacja konieczności

do możliwości przedstawiona w
Hermeneutyce w formie implikacji (4) także
powinna mieć kształt równoważności,
mianowicie

(II) □ p ≡ ~ ◊ ~ p



Formuły (I) i (II) stanowią podstawę każdego

systemu logiki modalnej.

Podstawowa logika modalna



Stagiryta znał dwie podstawowe zasady logiki modalnej

znane w scholastycznej formie:



Ab oportere ad esse valet consequentia, co w przyjętej tu
symbolice wyraża się:

(III) □ p → p, czyli Jeśli jest konieczne, że p, to p



Ab esse ad posse valet consequentia, co można zapisać:

(IV) p → ◊ p, tj. Jeżeli p, to jest możliwe, że p

•

Arystoteles wie, że z asertorycznego wniosku
przeczącego „Nie p” wynika wniosek
problematyczny „Jest możliwe, że nie p”.
Implikacja o której mowa ma następującą postać:

Podstawowa logika modalna

~ p → ◊ ~ p

Okazuje się zatem, że można utworzyć sylogizm

przecząco problematyczny, skoro już mamy sylogizm

przecząco asertoryczny.

(An. pr. I 16, 36 a 15)



Aleksander w swoim komentarzu przywołanego

fragmentu podaje ogólną regułę:

Istnienie implikuje możliwość p → ◊ p,
ale nie odwrotnie, tj.
(V*) jeżeli jest możliwe, że p, to p - należy odrzucić.

◊ p → p

Podstawowa logika modalna



Aleksander podaje także odpowiednie reguły dla

konieczności – konieczność implikuje istnienie, ale
nie odwrotnie, należy zatem odrzucić:
(VI*) Jeżeli p, to jest konieczne, że p

p → □ p



Formuły I – VI są uznawane przez wszystkich

współczesnych logików, są też uznawane na
gruncie logiki tradycyjnej.



Nie wystarczają one jednak dla charakterystyki ◊ p

oraz □ p jako funkcji modalnych, gdyż wszystkie
one będą spełnione wówczas gdy zinterpretujemy

Podstawowa logika modalna



◊ p jako zawsze prawdziwe (verum od p)



□ p jako zawsze fałszywe (falsum od p)



Przy takiej interpretacji system zbudowany na

formułach I – VI przestałby być logika
modalną. Nie można przyjąć, że wszystkie
zdania problematyczne są prawdziwe (nie
można uznać ◊ p) lub że wszystkie zdania
problematyczne są fałszywe (nie można uznać
~□ p). Obydwa wyrażenia należy odrzucić.



Dwie kolejne odrzucone formuły to:

Podstawowa logika modalna

(VII*) Jest możliwe, że p

◊ p

(VIII*) Nie jest konieczne, że p

~□ p



Za Łukasiewiczem system nazywać będziemy

„podstawową logiką modalną” wtedy i tylko
wtedy, gdy spełnia formuły I – VIII. Badacz
wykazał również, że podstawową logikę
modalną można zaksjomatyzować na gruncie
klasycznego rachunku zdań (System logiki
modalnej)

Podstawowa logika modalna



Spośród dwóch terminów modalnych, za

pierwotny uznamy „jest możliwe” (◊)



Definicją terminu „jest konieczne” jest formuła

(II), czyli

□ p = ~ ◊ ~ p



W ten sposób otrzymujemy podstawowy zbiór

aksjomatów logiki modalnej:
(IV) p → ◊ p; (V*) ◊ p → p; (VII*) ◊ p;
(IX) ◊ p ≡ ◊ ~~ p (definicyjnie równoważna I, tj.
◊ p → ~□ p)

Podstawowa logika modalna



Inny zbiór aksjomatów otrzymamy przyjmując

za funktor pierwotny „jest konieczne” (□) i
formułę (I) jako definicję „jest możliwe”, tj.

◊ p = ~ □ ~ p



Zbiór ten wygląda następująco:

(III) □ p → p; (VI*) p → □ p; (VIII*) ~ □

p;
(X) □ p ≡ □ ~ ~ p (dedukcyjnie równoważna
II, ze względu na def. 1 i klasyczny rachunek
zdań)

Podstawowa logika modalna



Podstawowa logika modalna stanowi bazę dla

każdego systemu logiki modalnej, każdy taki
system musi ją więc zawierać.



Formuły I – VIII odpowiadają intuicjom

Arystotelesa i leżą u podłoża naszych pojęć
„konieczności” i „możliwości”, chociaż nie
wyczerpują dziedziny uznawanych praw
modalnych.



Jesteśmy przekonani, iż jeśli możliwa jest

koniunkcja, to każdy jej element powinien być
możliwy, czyli

Podstawowa logika modalna

(XI)

◊ (p

^

q) → ◊ p; (XII) ◊ (p

^

q) → ◊ q



Jeśli koniunkcja jest konieczna, każdy z jej

elementów jest konieczny, czyli:

(XIII) □ (p

^

q) → □ p; (XIV) □ (p

^

q) → □ q

•

Żadnej z formuł XI – XIV nie można wyprowadzić
praw I – VIII.

•

Podstawowa logika formalna jest więc modalnym
systemem niezupełnym wymagającym
dołączenia kilku aksjomatów.

Kwadrat modalny

Podstawowe relacje zachodzące między

funkcjami:

□ p; □ ~ p; ◊ p; ◊ ~ p; p; ~ p;

□ p

□ ~ p

p

~ p

◊ p ◊ ~ p

Związki konieczne pomiędzy

zdaniami



Prawa ekstensjonalności dla konieczności i

możliwości sformułował Arystoteles w An. pr. (34
a 22)

Jeżeli zatem ktoś oznacza przesłanki przez A, a

wniosek przez B, to z tego wyniknie nie tylko to, że

jeżeli A jest konieczne, to i B jest także konieczne,

lecz również i to, że jeżeli A jest możliwe, to i B jest

możliwe.



Arystoteles twierdzi, że pomiędzy przesłankami α

poprawnego sylogizmu a jego wnioskiem β
zachodzi związek konieczny

Prawa ekstensjonalności



Prawa (1) i (3) powinny, jak się wydaje,

zawierać w poprzednikach konieczność



Dla konieczności

(1) (α → β) → (□ α → □ β)
(2) □ (α → β) → (□ α → □ β)



Dla możliwości

(3) (α → β) → (◊ α → ◊ β)
(4) ◊ (α → β) → (◊ α → ◊ β)

Prawa ekstensjonalności



Ogólne prawa mają następującą postać:



dla konieczności

(5) □ (p → q) → (□ p → □ q)



dla możliwości

(6)

◊ (p → q) → (◊ p → ◊ q)



Formuły (5) i (6) są słabsze niż odpowiadające

im formuły o poprzednikach asertorycznych i
można je wyprowadzić ze zdań asertorycznych
według aksjomatu (III), czyli □ p → p i prawa
sylogizmu hipotetycznego

Prawa ekstensjonalności



Trudność I:

W rachunku zdań powszechnie przyjęta jest implikacja
materialna, tymczasem implikacja „ścisła”: „Jest
konieczne, że jeżeli p, to q” czyli □ (p → q) jest konieczną
implikacją materialną, którą do logiki wprowadził C.I.
Lewis. Jak należy traktować poprzednik prawa
ekstensjonalności dla konieczności?
Arystoteles nie był świadom różnicy między tymi dwoma
interpretacjami; nie mógł znać definicji Filona (implikacja
materialna).
Należy się uważnie przyjrzeć zdaniom koniecznym
Arystotelesa

Komentarz Aleksandra

Aleksander komentując tekst „Jeżeli (jeżeli jest
α, to musi być i β), to (jeżeli α jest możliwe, to
możliwe musi być i β)”
podkreślał konieczny charakter przesłanek
„jeżeli jest α, to musi być i β”
Ujęcie implikacji ścisłej Aleksandra różni się od
ujęcia Lewisa
Według Aleksandra (176. 2)w implikacji
koniecznej następnik zawsze musi wynikać z
poprzednika:

Komentarz Aleksandra

Konieczne danie warunkowe nie ma charakteru

czasowego. Wyrażenie „dana przesłanka wynika z”

jest zawsze równoznaczne z wyrażeniem „dana
przesłanka jest następnikiem”. Nie jest bowiem

prawdziwe połączenie: „Jeżeli istnieje Aleksander, to

mówi się o Aleksandrze” lub „Jeżeli Aleksander

istnieje, to ma tyle a tyle lat”. Nawet gdyby

rzeczywiście miał tyle właśnie lat, kiedy owa

przesłanka jest wypowiadana.

Aby drugie z podanych przez Aleksandra zdań było
prawdziwe należy uzupełnić je o kwalifikacje
czasowe, aby mogło być zawsze prawdziwe, zatem
przywołany komentarz jest zgodny z interpretacją
mocną – nie pomaga w rozwiązaniu problemu.

Zdania analityczne

Prawdziwa implikacja materialna musi być
prawdziwa dla wszystkich wartości zmiennych,
zatem komentarz Aleksandra nie rozwiązuje
problemu.
Stagiryta uznaje zdanie (An. pr. I 9, 30a 30)

jest konieczne aby człowiek był zwierzęciem

Stwierdza zatem konieczne połączenie między
terminami – podmiotem i orzecznikiem. Zdanie:

„Każdy człowiek jest zwierzęciem”

jest zdaniem apodyktycznym, gdyż definiuje termin
„człowiek” i „zwierzę” tak, aby orzecznik (zwierzę)
zawierał się w podmiocie (człowiek)

Zdania analityczne



Zdanie w którym orzecznik zawiera się

w podmiocie, nazywa Arystoteles,
zdaniem analitycznym.



Wszystkie zdania analityczne oparte na

definicjach są zdaniami apodyktycznymi,
gdyż atrybuty istotne (wynikające z
definicji) przysługują swym podmiotom
w sposób konieczny (An. wt. I 6, 74 b 6).



W Hermeneutyce (9, 19 a) czytamy:

Zasada konieczności

To co jest, jest konieczne, gdy jest, a tego czego

nie ma, koniecznie nie ma, gdy go nie ma.

dodaje, że nie znaczy to, iż wszystko co jest,
jest konieczne; a wszystko czego nie ma jest
niemożliwe; bo powiedzieć, że wszystko co jest
jest konieczne gdy jest; nie jest tym samym co
powiedzieć, że to jest konieczne po prostu.
Przywołany

fragment

nie

zawiera

warunkowego „jeżeli” ale czasowe „gdy”.
Cóż znaczy przywołana zasada?

Zasada konieczności



Przywołana zasada może mieć następujące

znaczenia:

(1)

Stagiryta mówi tu o „konieczności hipotetycznej”

Aleksander mówi, że Arystoteles odnosił się tu do
zdań pojedynczych mówiących o wydarzeniach
przyszłych.
Konieczność hipotetyczna polega na polega na
koniecznym połączeniu zdań

„Jest konieczne, aby bitwa morska była, gdy jest” =
„Jest konieczne, aby bitwa morska odbyła się jutro,

jeśli jutro się odbędzie”

„Jest konieczne, że jeśli jutro odbędzie się bitwa

morska, to jutro się odbędzie” □ (p → p)

Zasada konieczności



Ta konieczność hipotetyczna nie różni się

od konieczności warunkowej tyle, że nie
odnosi się do sylogizmów ale do
jednostkowych zdań mówiących o
zdarzeniach, czyli takich które zawierają
kwalifikację czasową.



Jeśli włączymy ją w treść zdania możemy

zastąpić spójnik czasowy („gdy”)
spójnikiem warunkowym („jeżeli”)

Zasada konieczności

(2) Konieczność odnosi się do terminów, konieczne

jest połączenie terminów. W Hermeneutyce (9,
18 a) czytamy:

Jeżeli można zgodnie z prawdą powiedzieć, że coś

jest białe albo niebiałe, to z konieczności to coś

musi być białe albo niebiałe.

Zdanie stwierdza konieczne połączenie między
„rzeczą” jako podmiotem oraz „bielą” jako
orzecznikiem.
Przyjmijmy, że „coś jest białe” – p

„Jeżeli prawdą jest, że p, to jest konieczne, że p”

Zasada konieczności



W logice dwuwartościowej każde zdanie jest

albo prawdziwe, albo fałszywe.



„Prawdą jest, że p” ≡ „p”



„Jeżeli prawdą jest, że p, to konieczne, że p” ≡

„jeżeli p, to jest konieczne, że p”;
symbolicznie:

p → □ p

ale jak formułę tę należy odrzucić, gdyż jej

uznanie spowoduje załamanie się logiki
modalnej zdań.

Kontyngencja



Arystoteles podaje definicję kontyngencji w

An. pr. (I 13, 32 a)

Przez „kontyngentne” rozumiem coś, co nie jest

konieczne, a czego założenie nie pociąga za

sobą niczego niemożliwego.

Co, po przekształceniach ma postać:

 p ≡ ~ □ p

^

~ □ ~ p

„Coś jest kontyngentne wtedy i tylko wtedy, gdy

nie jest konieczne i nie jest niemożliwe”

gdzie  symbolizuje funktor kontyngencji.

Kontyngencja



Aleksander mówi:

Kontyngentne nie jest konieczne i nie jest niemożliwe



Korzystając z definicji (I)

◊ p ≡ ~ □ ~ p możemy

przekształcić

~ □ p ≡ ◊ ~ p

otrzymamy inną definicję kontyngencji:

 p ≡ ◊ p

^

◊ ~ p

Konsekwencje tej definicji oraz inne twierdzenia A.

o kontyngencji prowadzą do trudności II.

Kontyngencja

 Trudność II:

Arystoteles zakłada, że rzeczy, które nie zawsze
są w akcie mają zarówno możność bycia jak i
niebycia. Bitwa morska może odbyć się jutro ale
w równej mierze może się nie odbyć.

Z dwóch zdań sprzecznych o takich rzeczach jedno

musi być prawdziwe a drugie fałszywe, ale nie to

czy tamto, lecz to, które może zajść, jedno z nich

może być bardziej prawdziwe niż drugie, ale

żadne z nich nie jest jeszcze prawdziwe czy

fałszywe (Herm. 9, 19 a)

Kontyngencja



Załóżmy, że dzisiaj w sprawie bitwy morskiej nie

została podjęta żadna decyzja (dzisiaj nie ma nic,
co mogłoby być przyczyną dla jutrzejszej bitwy
morskiej; ani nic, co mogłoby być przyczyną, dla
której się ona nie odbędzie).



Jeśli prawda jest zgodnością myśli z rzeczywistością

zdanie „Bitwa morska odbędzie się jutro” nie jest
dzisiaj ani prawdziwe, ani fałszywe.



Jeśli więc słowa Arystotelesa „ nie jest jeszcze

prawdziwe czy fałszywe” tak rozumiemy, wszystko
jest w porządku.

Kontyngencja



Jeśli jednak to, że dziś nie jest ono ani prawdziwe ani

fałszywe prowadzi do wniosku, że nie jest ani
konieczne ani niemożliwe, że jutro odbędzie się bitwa
morska, wówczas obydwa zdania:

„Jest możliwe, że jutro odbędzie się bitwa morska”

„Jest możliwe, że jutro nie odbędzie się bitwa morska”

są dzisiaj prawdziwe, a przyszłe wydarzenie jest

kontyngentne, co w konsekwencji prowadzi tego, że
jeśli uznamy jakieś zdanie kontyngentne za
prawdzie, musimy uznać dowolne zdanie, które jest
możliwe. To z kolei spowodowałoby upadek logiki
modalnej.

Kontyngencja



Trudność I wiązała się z faktem, że Arystoteles

uznawał prawdziwe zdania apodyktyczne.



Trudność II wiązała się z faktem, że uznawał

prawdziwe zdania kontyngentne.



Obydwie trudności pojawią się w sylogistyce

modalnej.



Pierwszą odnajdujemy w teorii sylogizmów o

jednej przesłance asertorycznej a drugiej
apodyktycznej; drugą zaś w teorii sylogizmów
kontyngentnych.

Tryby

o dwóch przesłankach

apodyktycznych



Podobnie jak w sylogistyce asertorycznej

Arystoteles dzieli sylogizmy na figury i tryby.



Za tryby doskonałe uznaje tryby figury I.



Tryby niedoskonałe dowodzone są za

pomocą konwersji i redukcji do absurdu lub
przez ektezę.



Tryby niepoprawne są odrzucane poprzez

wskazanie ich interpretacji za pomocą
terminów konkretnych.



Stagiryta niemal nie korzysta z własnych

twierdzeń logiki zdań modalnych.

Prawa konwersji



Prawa konwersji dla zdań apodyktycznych są

analogiczne do praw konwersji dla zdań
asertorycznych.

1. □ S e P → □

P e S

2.

□ S a P → □ P i S

3. □ S i P → □ P i S

Sylogizmy apodyktyczne



Sylogizmy apodyktyczne są identyczne jak

asertoryczne; do przesłanek i wniosku tych
ostatnich należy dodać funktor konieczności.



Sylogizm Barbara ma postać:

□ (M a P)

^

□ (S a M) → □ (S a P)

Celarent:

□ (M e P)

^

□ (S a M) → □ (S e P)

Darii:

□ (M a P)

^

□ (S i M) → □ (S i P)

Ferio:

□ (M e P)

^

□ (S i M) → □ (S o P)



Wniosek wynikający z przesłanek według figury I zależy

od tego która przesłanka (większa czy mniejsza) jest
zdaniem apodyktycznym.



Jeśli przesłanka większa jest zdaniem apodyktycznym a

mniejsza asertorycznym, wniosek jest apodyktyczny, np.

□ (M a P)

^

(S a M) → □ (S a P)

•

Jeśli przesłanka większa jest zdaniem asertorycznym,
a mniejsza apodyktycznym, możemy otrzymać tylko
wniosek asertoryczny, np.

(M a P)

^

□ (S a M) → (S a P)



Arystoteles zaniedbuje tryby o przesłankach

możliwych na rzecz trybów i przesłankach
kontyngentnych.



Wnioski konkluzywnych trybów sylogizmów figury I i

III, których przesłanki są zdaniami kontyngentnymi
także są zdaniami kontyngentnymi.



Nie wiemy ile jest konkluzywnych trybów dla figury I,

Arystoteles podał jedynie ogólna formułę ich
otrzymywania a 8 opracował szczegółowo.



Za tryby doskonałe, podobnie jak w dwóch

wcześniejszych grupach, uznał tryby figury I, czyli:
Barbara, Celarent, Darii oraz Ferio.
 M a P  M e P

 M a P

 M e P

 S a M  S a M

 S i M

 S i M

 S a P

 S e P

 S i P

 S o P



Tryby sylogistyczne w których większa przesłanka

jest zdaniem problematycznym mniejsza zaś
asertorycznym mają wniosek kontyngenty albo
możliwy w takim sensie, że przez „możliwe”
rozumiemy „to, co jest konieczne jest także
możliwe”. Wniosek otrzymujemy w jednym trybie
figury II (Camestres) oraz w dwóch trybach figury
III (Disamis i Bocardo).



Rolę aksjomatów pełnią analogony cztery

pierwsze tryby figury I, mianowicie:
 M a P  M e P  M i P  M e P

S a M S a M S a M S i M
 S a P  S e P  S i P

 S o P



Szósta grupa sylogizmów, tj. sylogizmy w

których większa przesłanka jest zdaniem
asertorycznym, mniejsza zaś kontyngentnym,
nie zawiera trybów doskonałych.



Wnioski analogonów dwóch trybów figury III

(Disamis i Disemis) są zdaniami
kontyngentnymi.



Arystoteles rozważa dwa możliwe połączenia takich

przesłanek.



Gdy przesłanka większa jest zdaniem

kontyngentnym, mniejsza zaś apodyktycznym;
wówczas wniosek jest:



zdaniem kontyngentnym w analogonach trybów

figury I (Barbra, Celarent, Darii, Ferio)oraz w
analogonach trybów figury III (Darapti, Felapton,
Datisi, Ferison);



zdaniem asertorycznym w analogonie trybu

Camestres figury II;



zdaniem możliwym w analogonie trybu Disamis figury

III.



Rolę aksjomatów pełnią analogony czterech

pierwszych tryby figury I, czyli:

 M a P

 M e P

 M a P

 M e P

□ S a M

□ S a M □ S i M □ S a M

 S a P

 S e P

 S i P

 S o P



Wśród trybów w których przesłanka większa jest

zdaniem apodyktycznym, a mniejsza
kontyngentnym, nie ma trybów doskonałych.



Wnioski 22 konkluzywnych trybów tej grupy są

zdaniami:



asertorycznymi w analogonach trybów figury I

(Celarent, Celerent, Ferio, Feroo), figury II (Cesare,
Cesere) oraz III (Festino, Festono, Felapton, Felepton,
Ferison, Feroson);



kontyngentnymi w analogonach dwóch trybów figury

III (Disamis, Disemis);



możliwymi w analogonach czterech trybów figury I

(Barbara, Barbera, Darii, Daroi) i czterech figury III
(Darapti, Darepti, Datisi, Datosi).

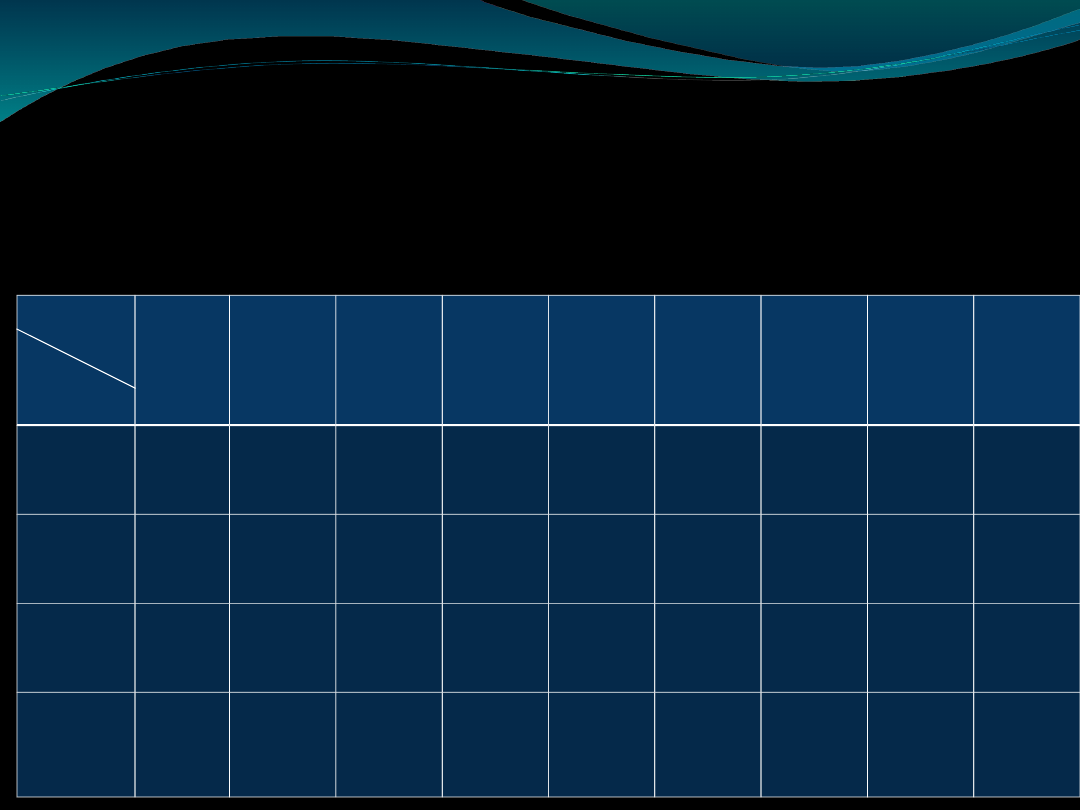
Konkluzywne sylogizmy

modalne (ilość)

Przesł.

figura

I

□

□

II

□

as.

III

as.

□

IV

 

V



as.

VI

as.



VII

 □

VIII

 □

Suma

I

4

4

4

8

?

4

8

4

8

44

II

4

4

4

-

1

4

1

4

22

III

6

6

6

10

6

10

5

10

59

Suma

14

14

14

18

11

22

10

22 125

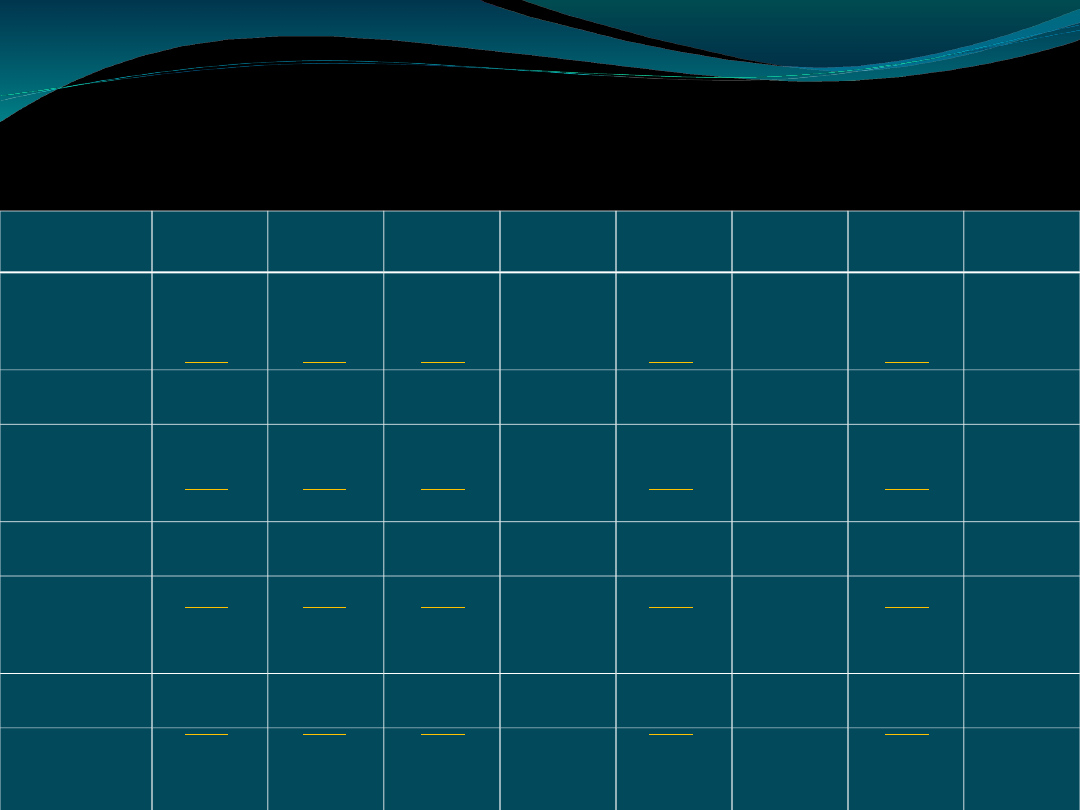
Tryby modalne (doskonałe i

niedoskonałe) figury I

Nazwa

analogonu

I

II

III

IV

V

VI

VII

VIII

Barbara

□

d.

□

d.

As.
d.

 d.

 d.

∆

 d.

∆

Barbera



∆

∆

Celarent

□

d.

□

d.

As.

d.

 d.

 d.

∆

 d.

As.

Celerent



∆

As.

Darii

□

d.

□

d.

As.

d.

 d.

 d.

∆

 d.

∆

Daroi



∆

∆

Ferio

□

d.

□

d.

As.

d.

 d.

 d.

∆

 d.

As.

Feroo



∆

As.

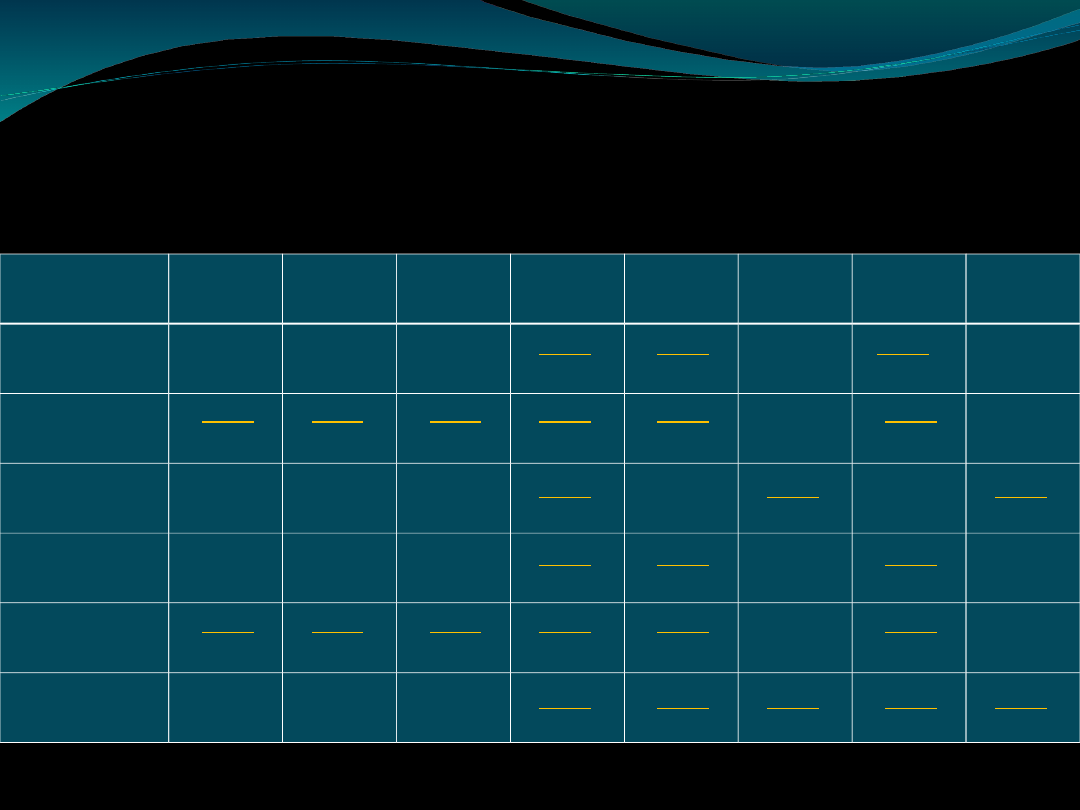
Tryby modalne (doskonałe i

niedoskonałe) figury II

Nazwa

analogonu

I

II

III

IV

V

VI

VII

VIII

Cesare

□

□

As.

∆

As.

Cesere

∆

As.

Camestres

□

As.

□

∆

As.

Festino

□

□

As.

∆

As.

Festono

∆

As.

Baroco

□

As.

?

As.

?

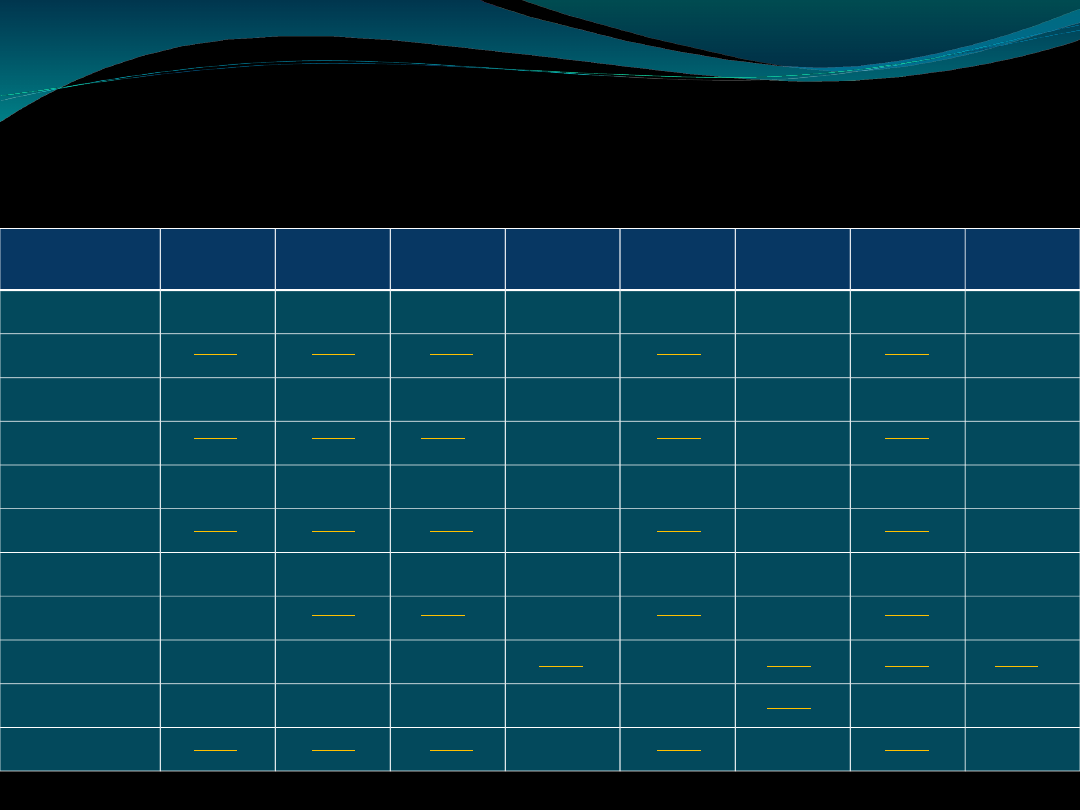
Tryby modalne (doskonałe i

niedoskonałe) figury III

Nazwa

Analogonu

I

II

III

IV

V

VI

VII

VIII

Darapti

□

□

As.





∆



∆

Darepti



∆

∆

Felapton

□

□

As.





∆



As.

Felepton



∆

As.

Disamis

□

As.

□



∆



∆



Disemis







Datisi

□

□

As.





∆



∆

Datosi



∆

∆

Bocardo

□

As.

As.

?

∆

Ferison

□

□

□







As.

Feroson



∆

As.

Ocena



Dla logików współczesnych sylogistyka modalna

Arystotelesa przedstawia się jako mało interesujący
i słabo opracowany fragment systemu.



Jednak ze stanowiska historycznego jest to jedno z

największych dzieł jakiego dokonano w dziedzinie
logiki. Należy pamiętać, że Stagiryta nie miał
poprzedników i nie dysponował nawet
dwuwartościową teorią dedukcji, a zbudował
system modalny, który w głównych zarysach jest
sprawny.

Ocena



System sylogistyki modalnej stanowi z jednej

strony podstawę dla wszelkich spekulacji
dotyczących modalności aż do Ockhama, z
drugiej natomiast zawiera tylko jedną z
możliwych koncepcji modalnych, której zaraz
po śmierci Arystotelesa przeciwstawiono inną.



Ze stanowiska systematycznego najlepiej

scharakteryzować sylogistykę zdań modalnych
za pomocą dwóch ocen:



wszystkie przesłanki są rozłączne;



„możliwy” ma w przesłankach zawsze znaczenie

„kontyngentny”

Ocena



Z faktu, że przesłanki są rozłączne wynika m.in.

to, że wniosek nie zawsze „idzie za słabszą
przesłanką” ale, że mamy w tym systemie tryby
w których: przesłanki to zdania apodyktyczne i
asertoryczne a wniosek jest zdaniem
apodyktycznym lub przesłanki to zdania
apodyktyczne i kontyngentne, a wniosek jest
zdaniem asertorycznym, itp. podczas, gdy tryby o
przesłankach apodyktycznej i kontyngentnej (VIII)
czy asertorycznej i kontyngentnej (VI) wszystkie
są niedoskonałe i muszą być dowodzone za
pomocą skomplikowanych metod.

Ocena



Faktu, że ◊ ma w przesłankach znaczenie „jeżeli

jest możliwe, że coś zajdzie, to jest możliwe, że
nie zajdzie” (= kontyngentny ), nigdy zaś „jeśli
coś jest konieczne, to jest także możliwe” (=
możliwy ∆) pociąga za sobą odwracalność
wszystkich przesłanek kontyngentnych i
niesprawność konwersji zdań kontyngentnych
ogólnoprzeczących, co z kolei daje z jednej strony
szereg sylogizmów o dwóch przesłankach
przeczących, z drugiej natomiast brak wielu
analogonów sprawnych trybów asertorycznych,
głównie w figurze II.

Ocena



Należy pamiętać, że Arystoteles nie pojmował

swego systemu w taki sposób - stosowanie
przesłanek w sensie rozłącznym jest mu obce.
Także z tego powodu system zawiera tyle
błędów i niekonsekwencji.

Filozoficzne implikacje logiki

modalnej Arystotelesa



Zdania analityczne przypisujące przedmiotom

cechy istotne są według Stagiryty faktycznie i z
konieczności prawdziwe.



To wyróżnienie stało się podstawą dla

późniejszego podziału nauk na dwie grupy:



nauki aprioryczne / dedukcyjne np. takie jak logika
czy matematyka, złożone z twierdzeń
apodyktycznych;



nauki aposterioryczne / empiryczne złożone przede
wszystkim ze zdań asertorycznych bazujących na
doświadczeniu.

Filozoficzne implikacje logiki

modalnej Arystotelesa



Jak wykazał J. Łukasiewicz, z punktu widzenia

logiki, pomiędzy prawdą matematyczną a
empiryczną nie ma żadnej różnicy.



Arystotelesowskie a priori opiera się na

definicjach i jest analityczne.



Definicje występują w każdej nauce bez względu

na jej charakter. Każda bowiem musi dysponować
ścisłym językiem, a do tego niezbędne są definicje
wyjaśniające znaczenie terminów.



Jednak żadna definicja nie zastąpi doświadczenia.

Filozoficzne implikacje logiki

modalnej Arystotelesa



Zdanie analityczne „człowiek jest zwierzęciem”

(„zwierzę” przysługuje istocie człowieka) nie niesie ze
sobą żadnej informacji w odróżnieniu od zdania
„Urodziłem się 21 grudnia 1878 roku.”



Istotę odkrywamy poprzez badanie osobników

ludzkich korzystając z osiągnięć, anatomii, fizjologii
… a to zadanie wydaje się nie mieć końca. Istota
zatem, jeśli istnieje, nie polega na znaczeniu słów.



Także w odniesieniu do nauk apriorycznych, nie

możemy opierać się na definicjach jako podstawach.

Filozoficzne implikacje logiki

modalnej Arystotelesa



Każda definicja zakłada jakieś terminy pierwotne ,

które są wyjaśniane poprzez przykłady, aksjomaty albo
reguły bazujące na doświadczeniu.



Prawda a priori zawsze jest syntetyczna i osiągana

jest dzięki doświadczeniom, które można powtarzać, a
nie dzięki jakiejś tajemniczej zdolności umysłu.



Wyobraźmy sobie urnę zawierającą kule białe i czarne.

Jeśli ktoś wylosował z nie dwie kule, można a priori
przepowiedzieć, że możliwe są cztery kombinacje:
biała-biała, biała-czarna, czarna-biała, czarna-czarna.

Filozoficzne implikacje logiki

modalnej Arystotelesa



Aksjomaty logiki i matematyki bazują – zdaniem

Łukasiewicza – na takich właśnie doświadczeniach,
stąd nie ma żadnej fundamentalnej różnicy między
naukami apriorycznymi a aposteriorycznymi.
Dlatego logik ten uznał Arystotelesowską teorię
konieczności za błędną.



Eksponował natomiast doniosłość i owocność idei

kontyngencji (użytej do obalenia determinizmu).



Jeśli za teorię deterministyczną uznamy teorię,

która stwierdza, że

Filozoficzne implikacje logiki

modalnej Arystotelesa



Jeśli w danej chwili t zachodzi zdarzenie X, to w dowolnej

chwili wcześniejszej od t prawdą jest, że X zachodzi w
chwili t.



Najsilniejsze uzasadnienie determinizmu bazuje na prawie

przyczynowości, które głosi, że każde zdarzenie ma swoją
przyczynę w jakimś zdarzeniu wcześniejszym.



Zgonie z powyższym, wszystkie przyszłe wydarzenia mają

swoje przyczyny, które istnieją dzisiaj i istniały
odwiecznie, zatem są predeterminowane.



Nawet jeśli uznamy, że prawo przyczynowości, które ma

charakter hipotezy, jest ogólnie prawdziwe; możemy

Filozoficzne implikacje logiki

modalnej Arystotelesa



Łańcuch przyczyn powodujący przyszłe wydarzenia,

choć nieskończony nie musi sięgać chwili teraźniejszej;
tj. możemy przyjąć, że bitwa morska chociaż będzie
miała swoją przyczynę, a ta przyczyna swoją przyczynę
itd. , nie ma jednak przyczyny w dniu dzisiejszym.



Analogicznie możemy przyjąć, że dzisiaj nie istniej nic,

co mogłoby zapobiec jutrzejszej bitwie morskiej.



Skoro prawda jest zgodnością myśli z rzeczywistością,

to w dniu dzisiejszym prawdziwe są zdania zgodne z
rzeczywistością dzisiejszą lub przyszłą, o ile ta ostatnia
jest zdeterminowana istniejącymi dziś przyczynami.

Filozoficzne implikacje logiki

modalnej Arystotelesa



Ponieważ jednak jutrzejsza bitwa morska dzisiaj nie

istnieje, a jej przyszłe istnienie bądź nieistnienie nie
dziś rzeczywistej przyczyny, zatem zdanie „Jutro
odbędzie się bitwa morska” dzisiaj nie ma żadnej
wartości logicznej.



Możemy powiedzieć: „Jutro może się odbyć bitwa

morska” i „Jutro może się nie odbyć bitwa morska”.
Jutrzejsza bitwa morska jest zdarzeniem
kontyngentnym.



Jeżeli istnieją wydarzenia kontyngentne, to nie istnieje

determinizm.