Nazwy i definicje

Logika. Wykład 5

dr Tomasz Kowalski

Slajd

2/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Wprowadzenie do sylogistyki

Klasyczny rachunek zdań nie jest narzędziem
uniwersalnym nadającym się do analizy
wszelkich rozumowań.

Slajd

3/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Wprowadzenie do

sylogistyki

Rozważmy następujące rozumowanie:

Każdy jamnik jest psem.

Każdy pies jest ssakiem.

Zatem: Każdy jamnik jest ssakiem.

Rozumowanie to
wydaje się
intuicyjnie
poprawne.

Reguła, na której
wnioskowanie to jest
oparte, wygląda
następująco:

p, q

––––

r

Reguła ta, z punktu widzenia
klasycznego rachunku zdań, nie jest
jednak dedukcyjna.

Slajd

4/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Sylogistyka – rachunek

nazw

Do analizy tego typu rozumowań służy system
nazywany sylogistyką (teorią sylogizmów) lub
rachunkiem nazw.

Sylogistyka to najstarszy system logiczny –
opracowany w IV w p.n.e przez greckiego
filozofa Arystotelesa.

Slajd

5/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwa – podstawowe pojęcie

sylogistyki

Nazwa jest to wyraz lub wyrażenie, któremu w
zdaniu przypisuje się rolę podmiotu lub orzecznika.

Jan jest artystą.

podmiot

orzeczenie

imienne

orzecznik

Slajd

6/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady nazw

- człowiek,

- Polak,

- czarny kot,

- ten, kto mówi cicho,

- krasnoludek.

Slajd

7/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwy mogą być:

- rzeczownikami,

- wyrażeniami złożonymi.

- przymiotnikami,

- liczebnikami,

- zaimkami,

- pewnymi formami czasowników,

- pewnymi przysłówkami przymiotnikami,

Slajd

8/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Desygnat nazwy

Desygnatem danej nazwy nazywamy
dowolny obiekt (rzecz, przedmiot, osobę,
itp.), do którego nazwę tę można odnieść;
obiekt, który nazwą tą można nazwać,
określić.

Slajd

9/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Desygnat nazwy -

przykłady

Desygnatem nazwy sala wykładowa jest
pomieszczenie, w którym aktualnie się
znajdujemy.

Desygnatem nazwy pies jest każde zwierzę
będące psem.

Slajd

10/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zakres (denotacja) nazwy

Zakres (denotacja) nazwy jest to zbiór
jej wszystkich desygnatów.

Zakres (denotację) nazwy A symbolicznie
będziemy oznaczać D(A).

Slajd

11/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zakres nazwy - przykłady

Zakres nazwy „człowiek” to zbiór wszystkich ludzi.

Zakres nazwy „ludzkość” to jednoelementowy zbiór
zawierający zbiór wszystkich ludzi.

Zakres nazwy „wysoki mężczyzna” to
zbiór wszystkich wysokich mężczyzn.

Slajd

12/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Rodzaje nazw

• Podział ze względu na ilość wyrazów

określających: proste i złożone.

• Podział ze względu na sposób istnienia

desygnatów: konkretne i abstrakcyjne.

• Podział ze względu na sposób wskazywania

desygnatów: indywidualne i generalne.

• Podział ze względu na ilość desygnatów:

ogólne, jednostkowe i puste.

• Podział ze względu na jednoznaczność

(ostrość) zakresu: ostre i nieostre.

Slajd

13/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwy: prosta - złożona

Nazwa prosta to

nazwa składająca się

z jednego wyrazu.

1. książka,

2.
samochód,

3. Ziemia,

4. zwierzę,

5.
przyjaźń,

6.
wypadek.

Nazwa złożona to nazwa
składająca się z co
najmniej dwóch
wyrazów.

1. ciekawa książka,

2. samochód marki
„Fiat”,

3. planeta w Układzie
Słonecznym,

4. zwierzę domowe,

5. dozgonna
przyjaźń,

6. nieszczęśliwy
wypadek.

Slajd

14/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwy: konkretna -

abstrakcyjna

Nazwa konkretna to

nazwa, której

desygnatami są rzeczy

lub osoby, istniejące lub

fikcyjne.

1. student,

2. stół,

3. ciekawa
książka,

4. Sierotka
Marysia,

5.
Atlantyda.

Nazwa abstrakcyjna to

nazwa, której

desygnatem jest cecha

lub zdarzenie lub

zjawisko lub stosunek lub

relacja, itp.

1. biel (nazwa cechy),

2. sprawiedliwość (nazwa
własności),

3. wypadek (nazwa
zdarzenia),

4. zamarzanie (nazwa
zjawiska),

5. miłość (nazwa
relacji).

Slajd

15/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwy: indywidualna -

generalna

Nazwa indywidualna to
nazwa stosowana do
oznaczania obiektów
(indywiduów, rzeczy,
osób, itp.) bez względu
na ich cechy
charakterystyczne;
inaczej: nazwa imienna,
nazwa własna.

Nazwa generalna to
nazwa posiadająca
znaczenie, utworzona ze
względu na
charakterystyczny
zestaw cech
przysługujący jej
desygnatom.

1. Adam
Mickiewicz,

2. Koszalin,

3. Wisła,

4.
Atlantyda.

1. autor
„Dziadów”,

2. miasto,

3. najdłuższa rzeka
Polski,

4. student,

5. chłopiec o imieniu
Jan.

Slajd

16/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwy: ogólna – jednostkowa

- pusta

Nazwa ogólna

to nazwa

posiadająca co

najmniej dwa

desygnaty.

1. człowiek,

2. miasto,

3. rzeka,

4. student,

5. mieszkaniec
Koszalina.

Nazwa

jednostkowa to

nazwa

posiadająca

dokładnie jeden

desygnat.

1. Koszalin,

2. Polska,

3. najdłuższa rzeka
świata,

4. aktualny prezydent
RP.

Nazwa pusta to

nazwa nie

posiadająca

desygnatów.

1. kwadratowe
koło,

2. płytka głębina,

3. sucha
woda.

Slajd

17/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwy: ostra - nieostra

Nazwa ostra to
nazwa, w
przypadku której
daje się
jednoznacznie
określić jej zakres,
czyli oddzielić jej
desygnaty od
pozostałych
przedmiotów.

1. człowiek,

2. miasto wojewódzkie,

3.
Polska,

4. student,

5. pierwiastek
chemiczny.

Nazwa nieostra to nazwa,
dla której nie istnieje
jednoznaczna, obiektywna
granica oddzielająca
przedmioty będące jej
desygnatami od
przedmiotów desygnatami
takimi nie będących.

1. piękna
kobieta,

2. ciekawa książka,

3. tłum,

4. łysy człowiek,

5. pornografia.

Slajd

18/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Cwiczenie – klasyfikowanie

nazw

Sklasyfikować nazwę:

Jest to nazwa:

student
.

prosta (składa się z jednego

wyrazu),

konkretna (desygnaty nazwy są obiektami
fizycznymi),

generalna (nazwa podaje pewną cechę
desygnatu),

ogólna (istnieje więcej niż jeden
student),

ostra (istnieje jednoznaczna granica
oddzielająca studentów i nie-studentów).

prosta - złożona
konkretna -

abstrakcyjna
indywidualna -

generalna
ogólna - jednostkowa -

pusta
ostra - nieostra

Slajd

19/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Cwiczenie – klasyfikowanie

nazw

Sklasyfikować nazwę:

Jest to nazwa:

obecna stolica Rosji.

złożona (składa się z trzech wyrazów),

konkretna (desygnat nazwy jest obiektem
fizycznym),

generalna (nazwa podaje pewną cechę
desygnatu),

jednostkowa,

ostra.

prosta - złożona
konkretna -

abstrakcyjna
indywidualna -

generalna
ogólna - jednostkowa -

pusta
ostra - nieostra

Slajd

20/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Cwiczenie – klasyfikowanie

nazw

Sklasyfikować nazwę:

Jest to nazwa:

wielka miłość.

złożona (składa się z dwóch wyrazów),

abstrakcyjna (desygnat nazwy nie jest obiektem
fizycznym),

generalna (nazwa podaje pewną cechę
desygnatu),

???

nieostra (nie istnieje ścisła granica oddzielająca
to, co jest wielką miłością, od tego, co nią nie
jest).

prosta - złożona
konkretna -

abstrakcyjna
indywidualna -

generalna
ogólna - jednostkowa -

pusta
ostra - nieostra

Slajd

21/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Uwagi

W przypadku nazwy wielka miłość, podobnie jak
przy innych nazwach abstrakcyjnych, mogą powstać
wątpliwości odnośnie ilości desygnatów.

Dla pesymisty nazwa wielka miłość jest pusta.

Dla filozofa jest to nazwa jednostkowa (bo istnieje
tylko jedna idea Wielkiej Miłości).

Dla „kochliwych” nazwa ta jest ogólna (bo
przeżywają kolejne wielkie miłości średnio co
miesiąc).

Slajd

22/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Cwiczenie – klasyfikowanie

nazw

Sklasyfikować nazwę:

Jest to nazwa:

król Polski.

złożona (składa się z dwóch wyrazów),

konkretna (desygnaty nazwy są obiektami
fizycznymi),

generalna (nazwa podaje pewną cechę
desygnatu),

ogólna (było wielu królów Polski)

ostra.

prosta - złożona
konkretna -

abstrakcyjna
indywidualna -

generalna
ogólna - jednostkowa -

pusta
ostra - nieostra

Slajd

23/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Uwagi

Pewną trudność w klasyfikacji nazw sprawić może
fakt, że niektóre nazwy są wieloznaczne.

Na przykład nazwa Mars może być:

jednostkowa w znaczeniu planety,

pusta w znaczeniu mitologicznego boga
wojny,

ogólna w znaczeniu popularnego
batonika.

Slajd

24/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zależności między zakresami

nazw

Dowolne dwie nazwy mogą znajdować się względem
siebie w różnych zależnościach wynikających z
ich zakresów (denotacji).

Slajd

25/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zależności między zakresami

nazw

D (A) = D (B)

(zakresy nazw są identyczne).

Mówimy wtedy, że

nazwy A i B są równoważne

(zakresy tych nazw pozostają w stosunku
zamienności).

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

A

B

Slajd

26/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zależności między zakresami

nazw

D (A) = D (B).

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

Inne przykłady:

A- dom

B- budynek

mieszkalny

A – Wisła

,

A – C

2

H

5

OH

,

B – najdłuższa rzeka w
Polsce

B – alkohol etylowy

.

Slajd

27/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

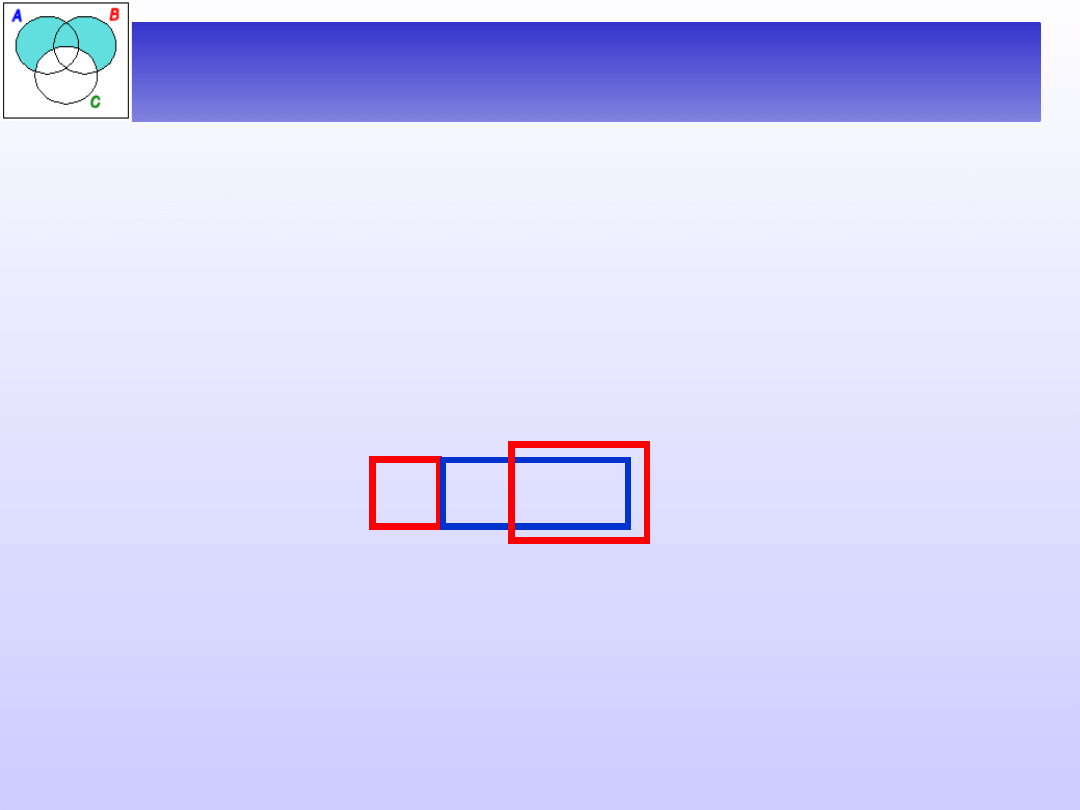
Zależności między zakresami

nazw

D (A)  D (B)

(zakres nazwy A zawiera się w zakresie nazwy

B).

Mówimy wtedy, że

nazwa A jest podrzędna względem nazwy B,

lub, że

nazwa B jest nadrzędna względem A.

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

A

B

Slajd

28/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

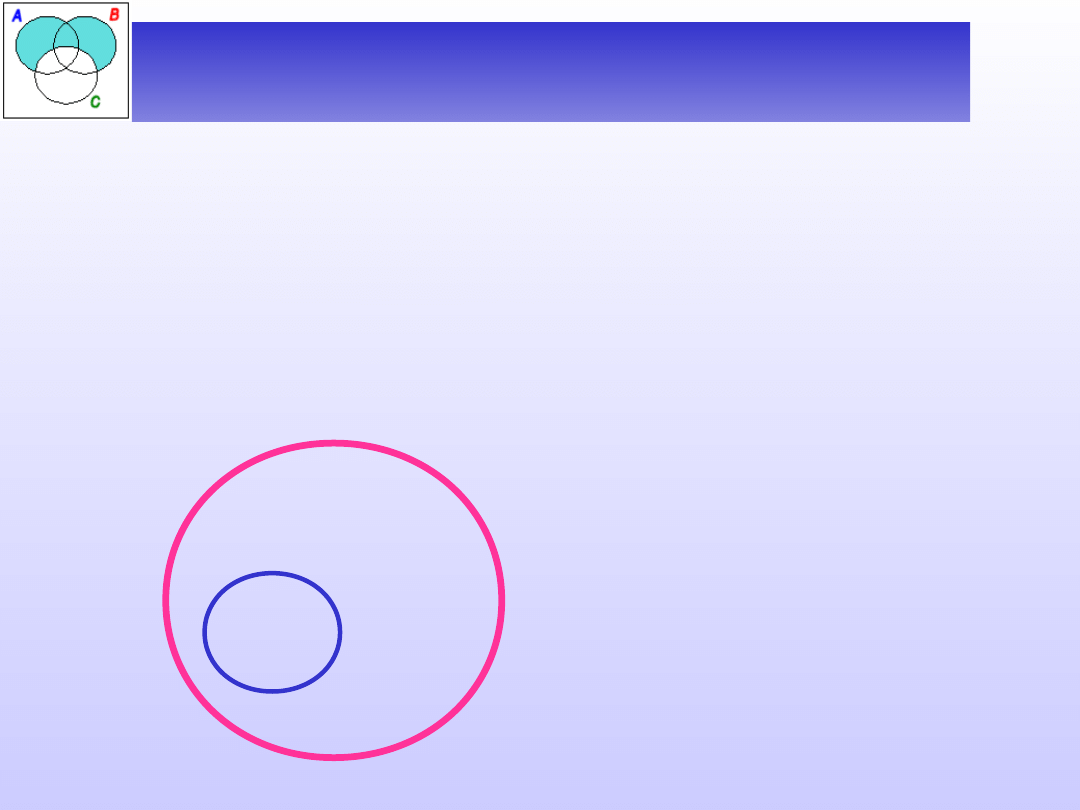
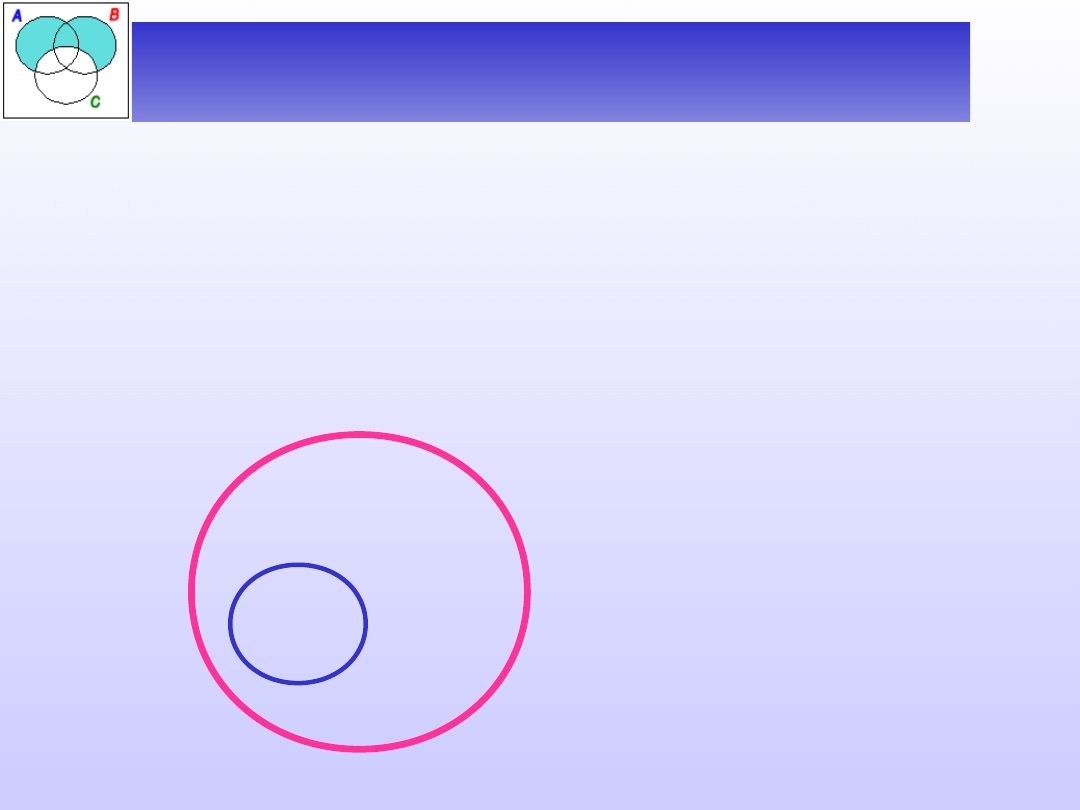
Zależności między zakresami

nazw

D (A)  D (B)

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

A-

koń

B -

zwierzę

Inne przykłady:

A – dzięcioł

,

A – zdolny student

,

B – ptak

B – student

.

Slajd

29/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

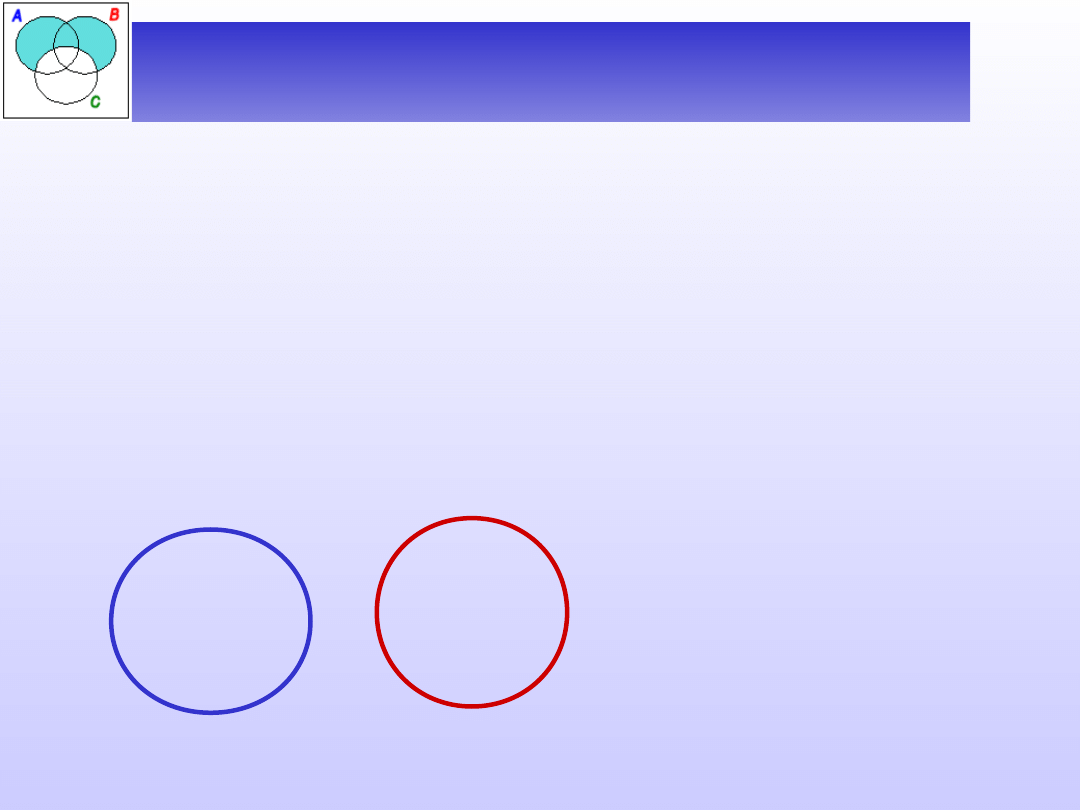
Zależności między zakresami

nazw

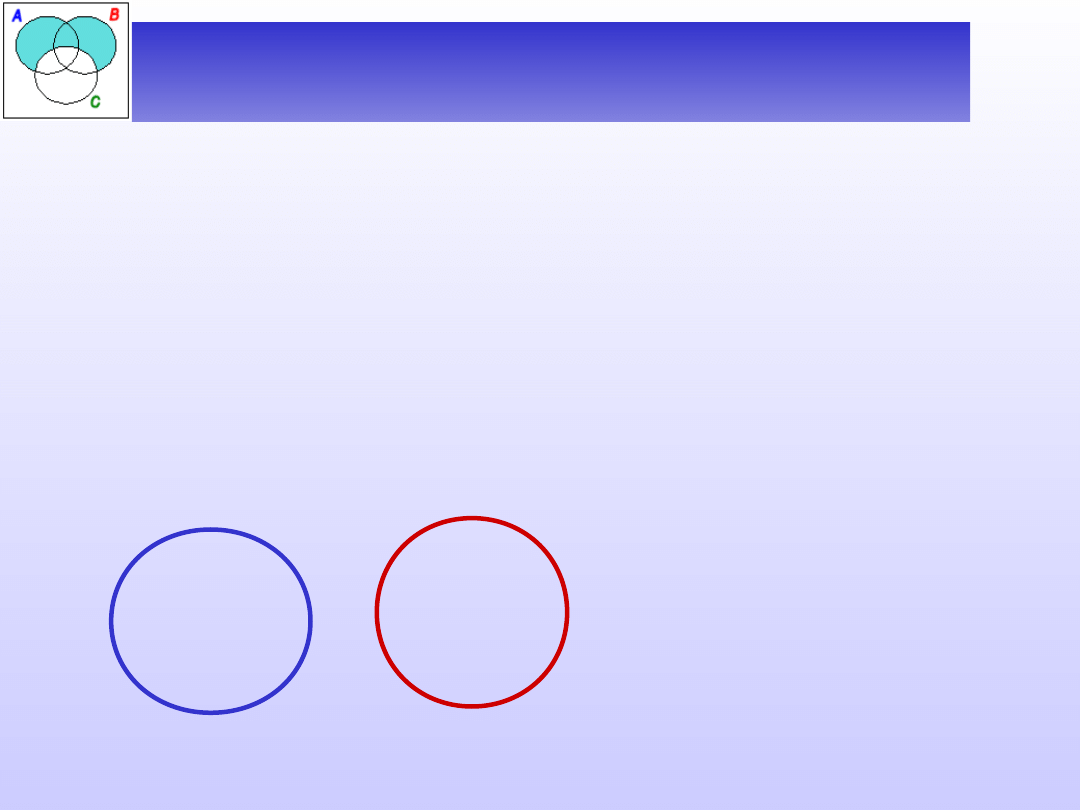
D (A) )( D (B)

(zakresy nazw A i B są rozłączne).

Mówimy wtedy, że

nazwy A i B się wykluczają.

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

A

B

Slajd

30/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zależności między zakresami

nazw

D (A) )( D (B).

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

Inne przykłady:

A - student

B- ołówek

A – słoń

,

A – człowiek uczciwy

,

B – mrówka

B – złodziej

.

Slajd

31/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zależności między zakresami

nazw

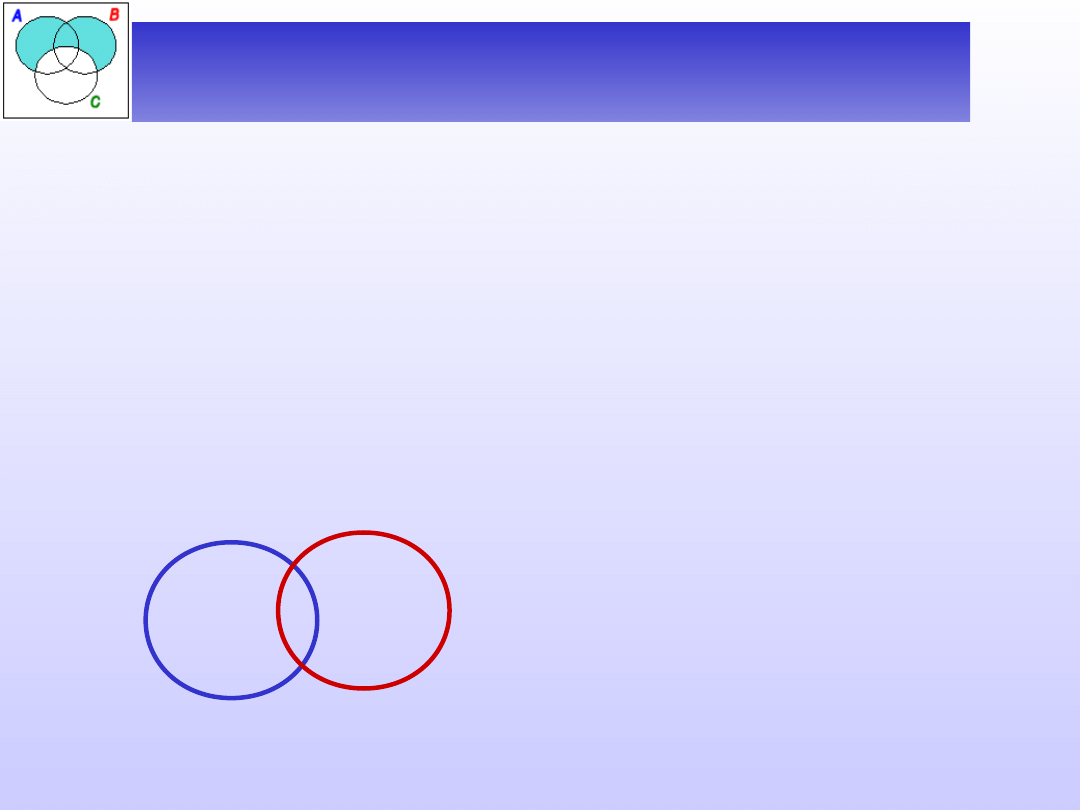
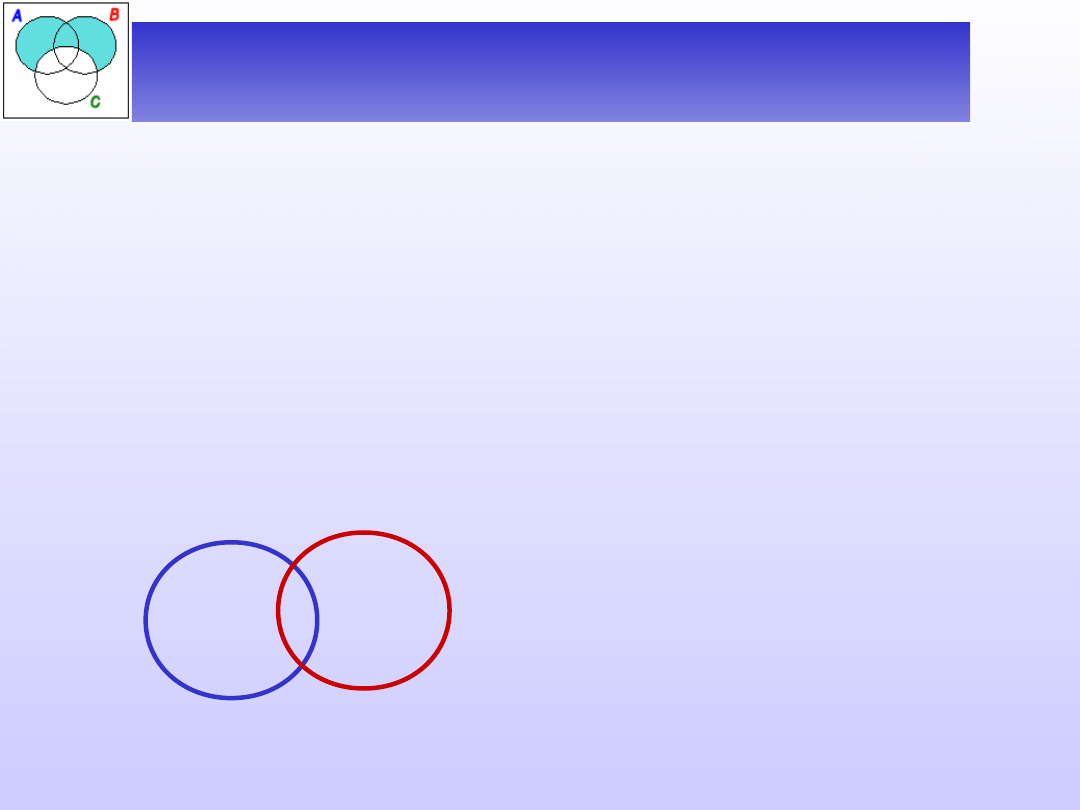
D (A) # D (B)

(zakresy nazw się krzyżują).

Mówimy wówczas, że

nazwy A i B się krzyżują (lub że są niezależne).

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

A

B

Zbiory krzyżują się, jeżeli
mają jakieś elementy
wspólne, ale oprócz tego
każdy ma też takie, które
nie są elementami
drugiego zbioru.

Slajd

32/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zależności między zakresami

nazw

D (A) # D (B)

Zależności między nazwami to stosunki zachodzące
między ich zakresami. Mogą być one następujące:

Inne przykłady:

słoń

afrykańsk

ie

zwierzę

A – człowiek bogaty

,

A – blondynka

,

B – człowiek
inteligentny.

B – studentka

.

Slajd

33/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Nazwa negatywna

Nazwę postaci nie-A nazywamy nazwą negatywną

do nazwy A.

Nazwa nie-pies jest nazwą negatywną do

nazwy pies.

Zakresem nazwy negatywnej nie-A jest zbiór
wszystkich obiektów nie będących w zakresie
nazwy A.

Desygnatem nazwy negatywnej nie-A jest dowolny
obiekt (rzecz, przedmiot, osoba, itp.), który nie jest
desygnatem nazwy A.

Slajd

34/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Sprawdzanie zależności między

nazwami

W prostych przypadkach zadania takie można
rozwiązać bez uciekania się do jakichkolwiek
wyrafinowanych sposobów.

W przypadku niewielkich wątpliwości można
spróbować określić zależności między nazwami
drogą eliminacji.

Slajd

35/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

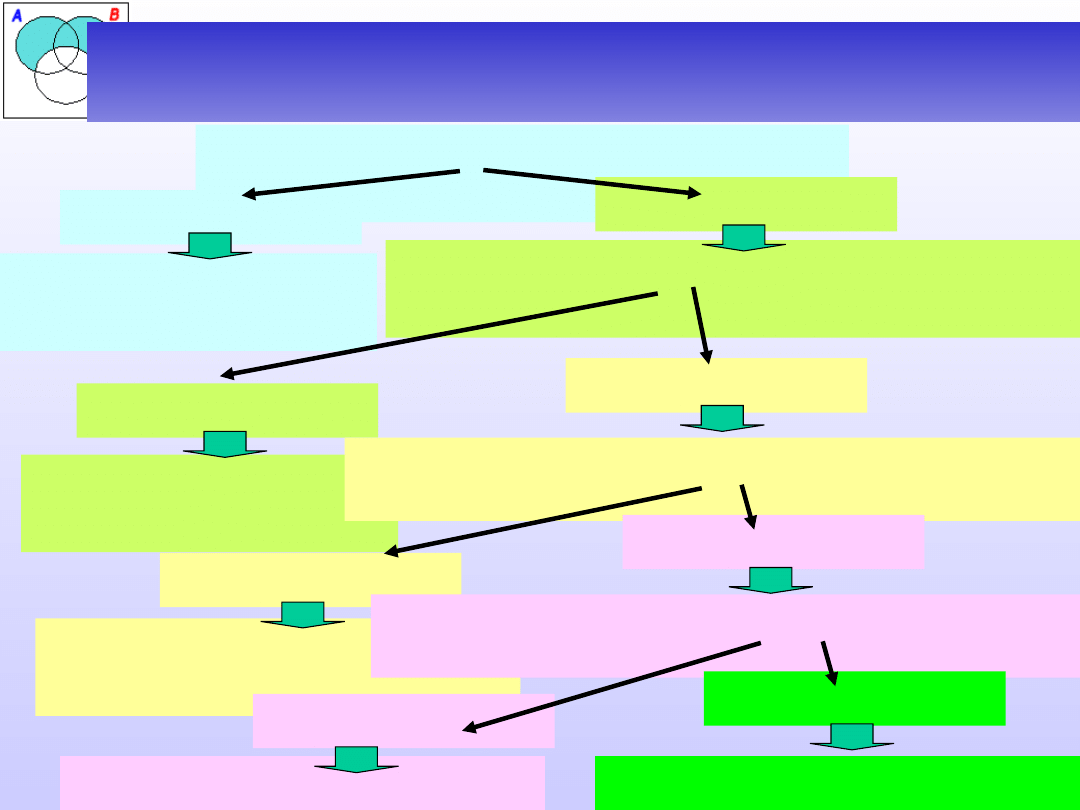
Procedura sprawdzania zależności

między nazwami:

1. Czy nazwy mają takie same
zakresy?

Nazwy są

równoważne.

TAK

NIE

2. Czy nazwy mają jakieś wspólne
desygnaty?

NIE

Nazwy wykluczają

się.

TAK

3. Czy każdy desygnat nazwy A jest
desygnatem nazwy B?

TAK

Nazwy A jest podrzędna

do B.

NIE

4. Czy każdy desygnat nazwy B jest
desygnatem nazwy A?

TAK

Nazwa B jest podrzędna

do A.

NIE

Nazwy krzyżują się.

Slajd

36/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie 1 – zależności między

nazwami

Zbadać zależność między nazwami:

A – piernik, B – wiatrak.

Nazwy piernik i wiatrak mają różne zakresy.

1. Czy nazwy mają te same zakresy?

TAK –

równoważność

.

2. Czy nazwy mają wspólne desygnaty?

NIE –

wykluczanie się

.

3. Czy każde A jest B? TAK –

A jest podrzędna

względem B

.

4. Czy każde B jest A? TAK –

A jest nadrzędna

względem B

.

5.

Krzyżowanie się!

Nie mają one wspólnych desygnatów. (Nie istnieje
coś, co byłoby jednocześnie piernikiem i
wiatrakiem.)

Badane nazwy się
wykluczają.

Slajd

37/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie 1 – zależności między

nazwami

Zbadać zależność między nazwami:

A – karp, B – ryba.

Nazwy karp i ryba mają różne zakresy.

1. Czy nazwy mają te same zakresy?

TAK –

równoważność

.

2. Czy nazwy mają wspólne desygnaty?

NIE –

wykluczanie się

.

3. Czy każde A jest B? TAK –

A jest podrzędna

względem B

.

4. Czy każde B jest A? TAK –

A jest nadrzędna

względem B

.

5.

Krzyżowanie się!

Mają one wspólne desygnaty.

Nazwa karp jest podrzędna względem nazwy
ryba (lub nazwa ryba nadrzędna względem
nazwy karp).

Każdy karp jest rybą , czyli D(A)  D(B).

Slajd

38/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie 1 – zależności między

nazwami

Zbadać zależność między nazwami:

A – student, B –
ojciec.

Nazwy student i ojciec mają różne zakresy.

1. Czy nazwy mają te same zakresy?

TAK –

równoważność

.

2. Czy nazwy mają wspólne desygnaty?

NIE –

wykluczanie się

.

3. Czy każde A jest B? TAK –

A jest podrzędna

względem B

.

4. Czy każde B jest A? TAK –

A jest nadrzędna

względem B

.

5.

Krzyżowanie się!

Mają one wspólne desygnaty.

Badane nazwy krzyżują
się.

Nie każdy student jest ojcem.

Nie każdy ojciec jest studentem.

Slajd

39/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie 1 – zależności między

nazwami

Zbadać zależność między nazwami:

A – dłoń, B – palec.

Nazwy dłoń i palec mają różne zakresy.

1. Czy nazwy mają te same zakresy?

TAK –

równoważność

.

2. Czy nazwy mają wspólne desygnaty?

NIE –

wykluczanie się

.

3. Czy każde A jest B? TAK –

A jest podrzędna

względem B

.

4. Czy każde B jest A? TAK –

A jest nadrzędna

względem B

.

5.

Krzyżowanie się!

Nie mają one wspólnych desygnatów. (Nie istnieje
coś, co byłoby jednocześnie dłonią i palcem.)

Badane nazwy wykluczają
się.

Slajd

40/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Uwagi

Zależność między dwiema nazwami nie zawsze
da się odkryć w tak prosty sposób, jak w
powyższych przykładach.

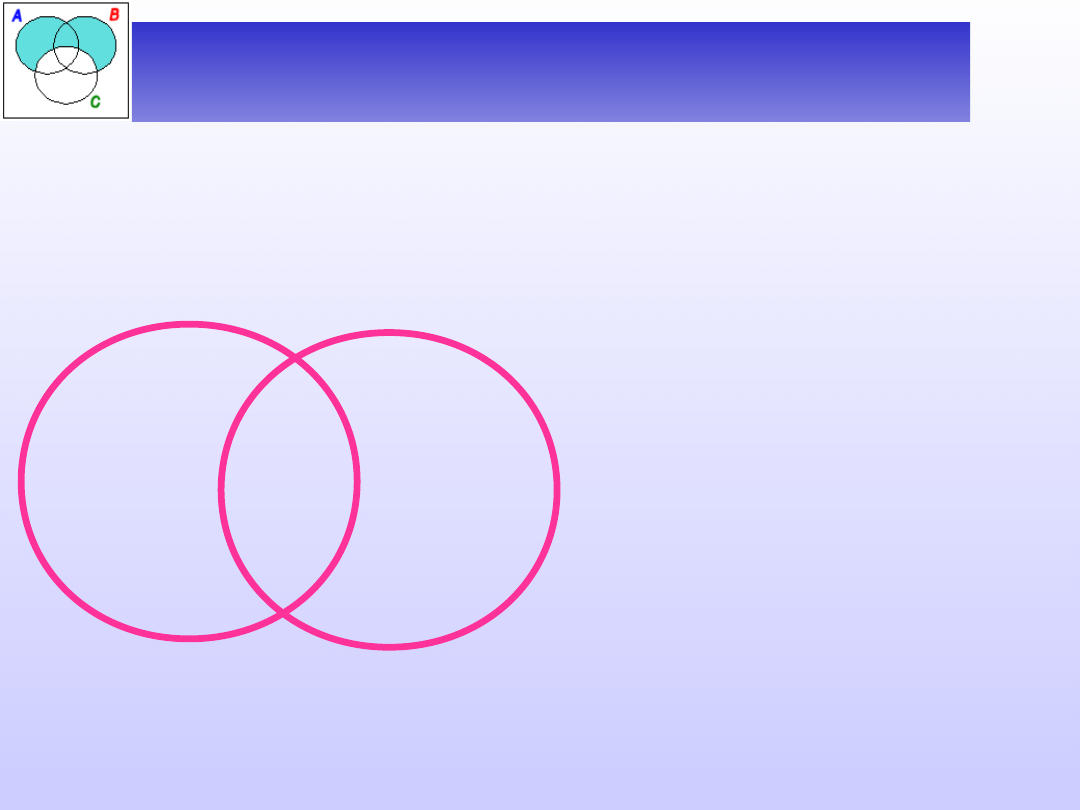
W niektórych przypadkach, szczególnie gdy mamy
do czynienia z nazwami złożonymi, dobrze jest się
posłużyć bardziej wyrafinowanym sposobem –
metodą diagramów Venna.

Slajd

41/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

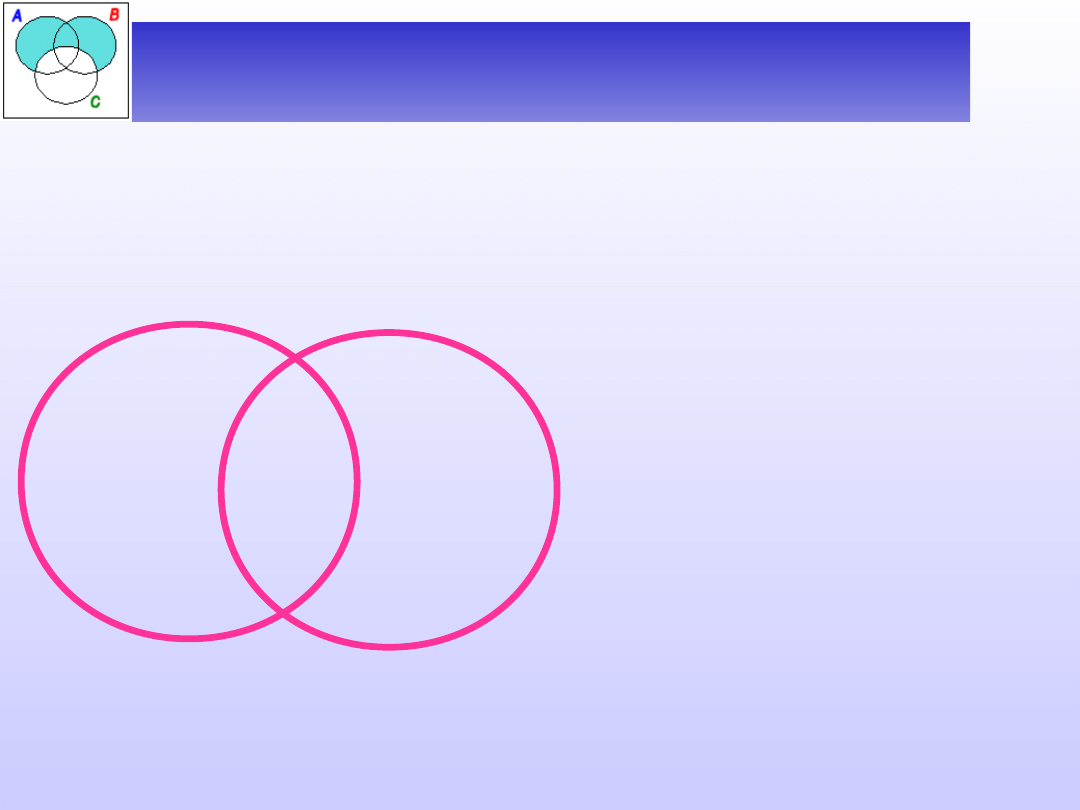
Zastosowanie diagramów

Venna

Badanie zależności między dwiema nazwami A i B przy
pomocy diagramów Venna rozpoczynamy od narysowania
dwóch kół symbolizujących zakresy rozważanych nazw:

D(A)

D(B)

Diagram taki składa się z
trzech obszarów.

I

II

III

W obszary te wpisujemy
znaki „+” lub „–” w
zależności od tego, czy
coś się w nich znajduje,
czy też są one puste.

Slajd

42/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zastosowanie diagramów

Venna

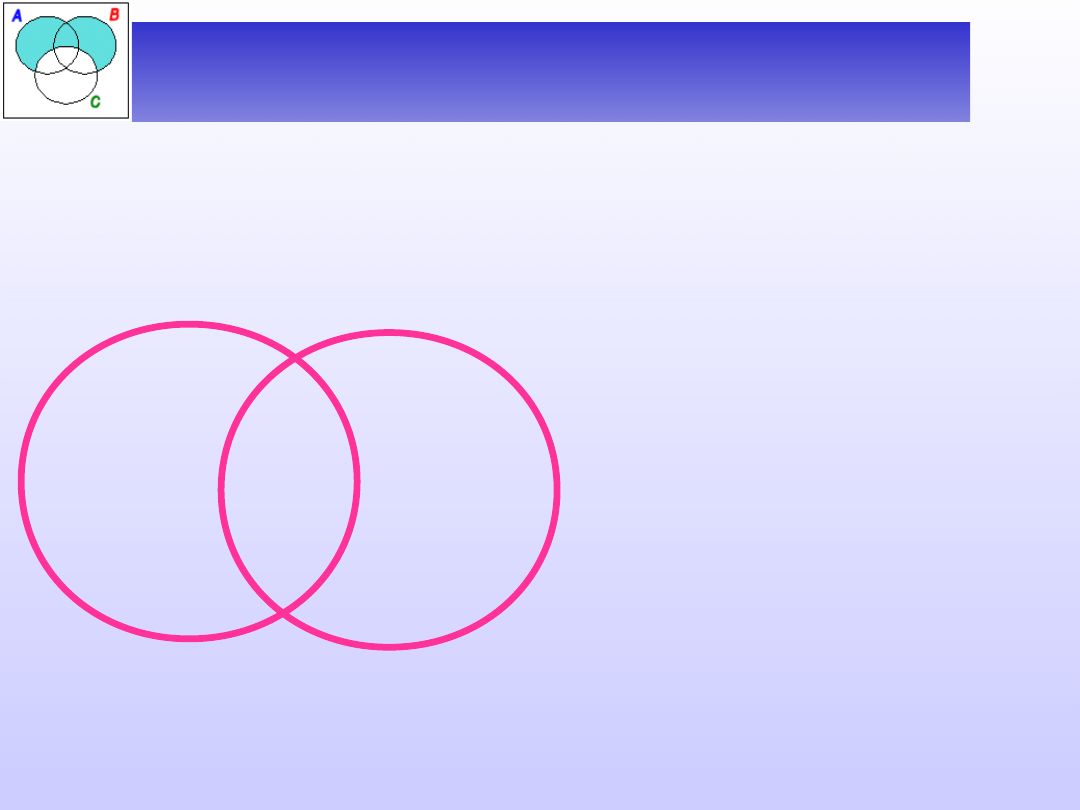
To, czy w danych obszarach diagramu znajdują się jakieś
elementy zaznaczamy odpowiadając na trzy pytania:

D(A)

D(B)

I – czy istnieje A, które nie
jest B?

I

II

III

II – czy istnieje A, które
jest B?

III– czy istnieje B, które nie
jest A?

Slajd

43/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zastosowanie diagramów

Venna

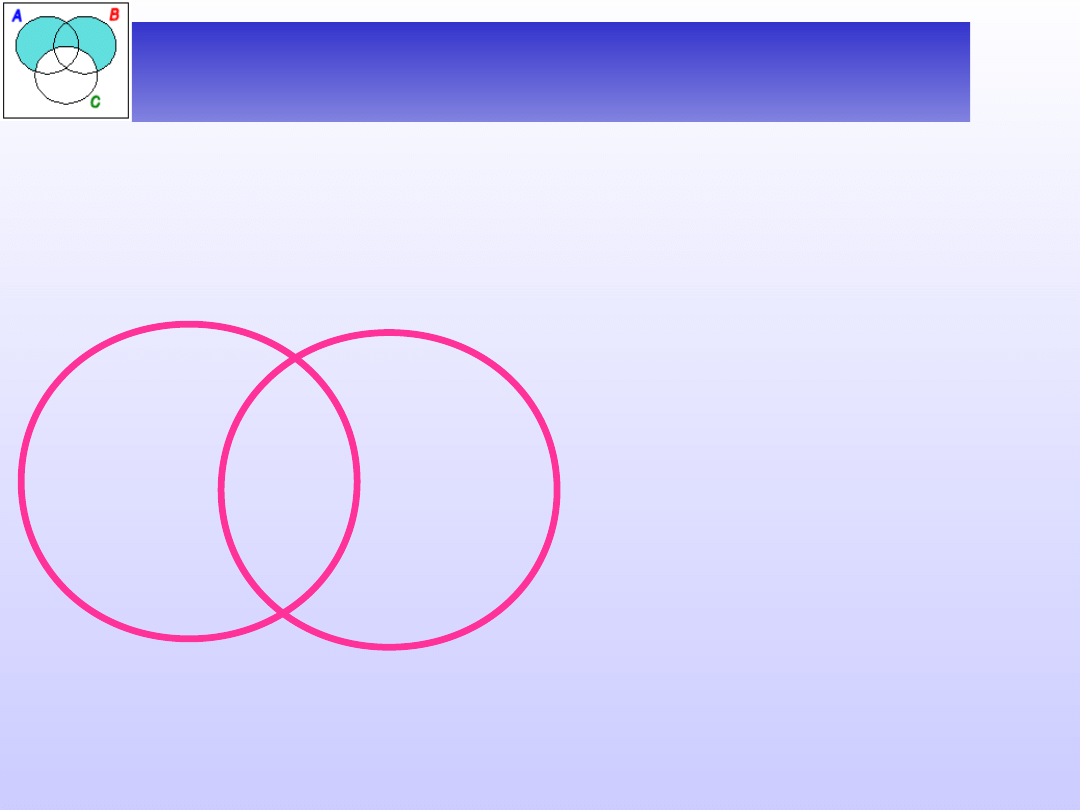
Przy założeniu, że żadna z nazw nie jest nazwą pustą,
możemy otrzymać jeden z następujących rysunków:

D(A)

D(B)

_

+

_

Nazwy A i B są równoważne
(zamienne).

Slajd

44/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zastosowanie diagramów

Venna

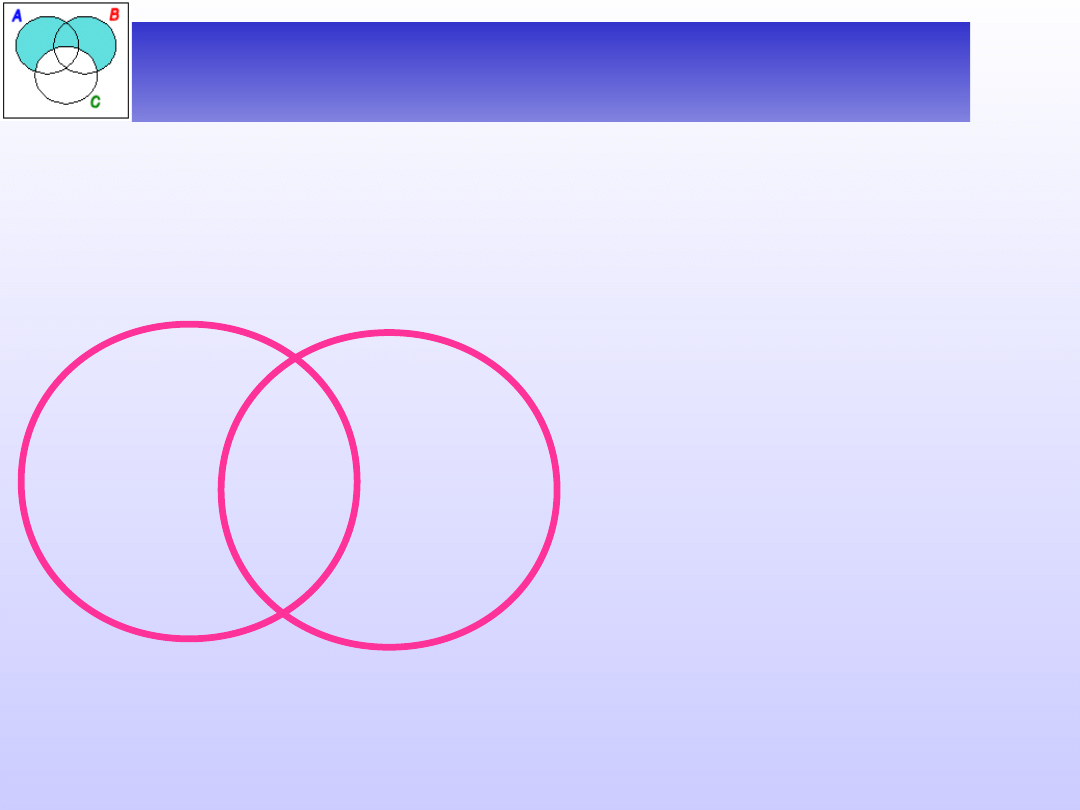
Przy założeniu, że żadna z nazw nie jest nazwą pustą,
możemy otrzymać jeden z następujących rysunków:

D(A)

D(B)

_

+

+

Nazwy A i B wykluczają się.

Slajd

45/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zastosowanie diagramów

Venna

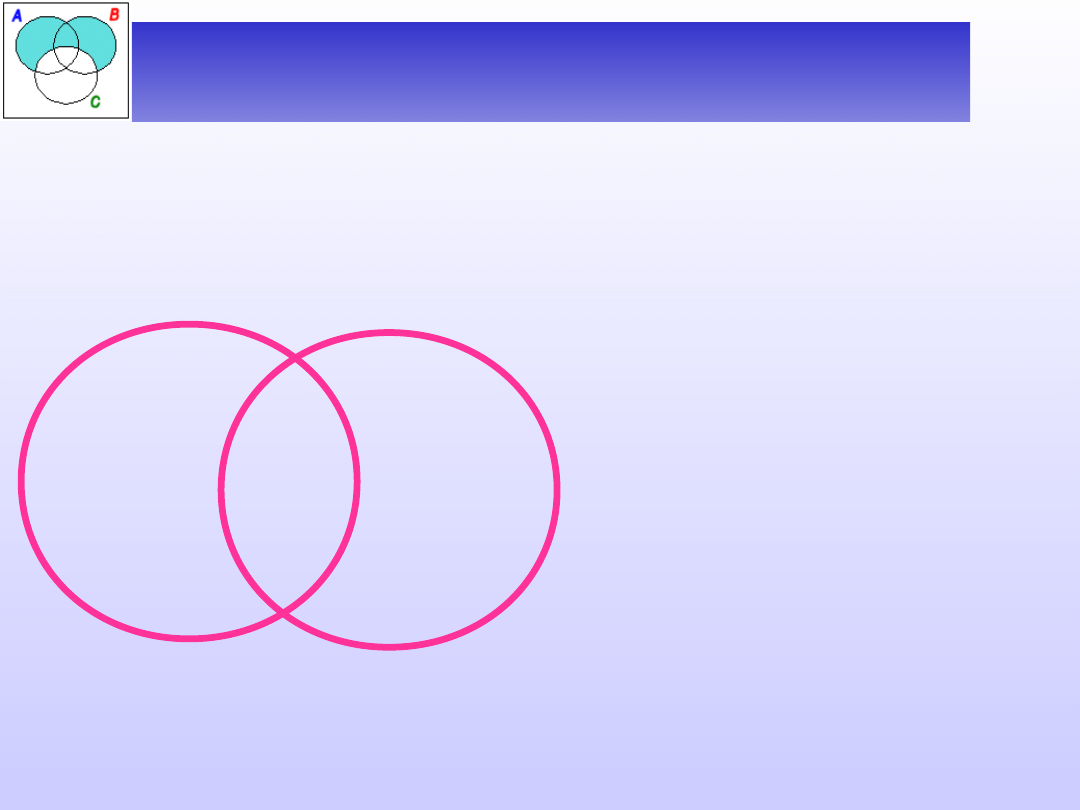
Przy założeniu, że żadna z nazw nie jest nazwą pustą,
możemy otrzymać jeden z następujących rysunków:

D(A)

D(B)

_

+

+

Nazwa A jest nadrzędna względem
B.

Slajd

46/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zastosowanie diagramów

Venna

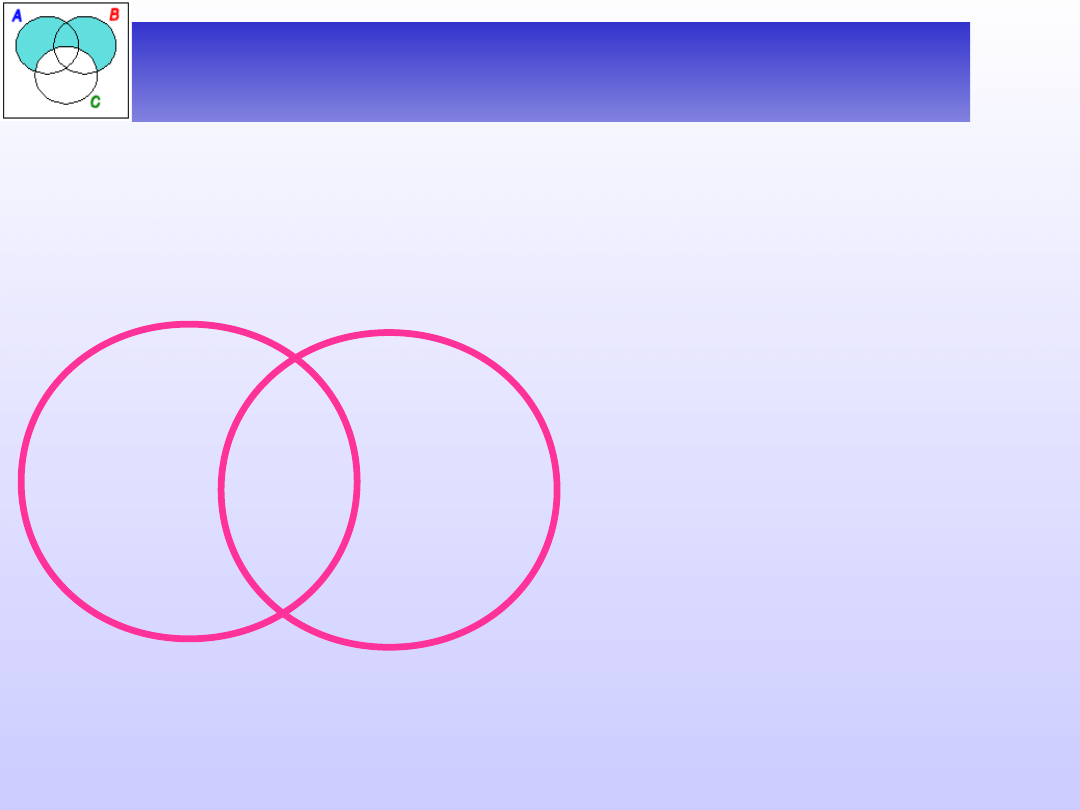
Przy założeniu, że żadna z nazw nie jest nazwą pustą,
możemy otrzymać jeden z następujących rysunków:

D(A)

D(B)

_

+

+

Nazwa A jest podrzędna względem
B.

Slajd

47/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Zastosowanie diagramów

Venna

Przy założeniu, że żadna z nazw nie jest nazwą pustą,
możemy otrzymać jeden z następujących rysunków:

D(A)

D(B)

+

+

+

Nazwy A i B krzyżują się.

Slajd

48/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Uwaga

Każda nazwa pusta jest podrzędna względem
dowolnej nazwy niepustej, natomiast dwie nazwy
puste są sobie zawsze równoważne.

Slajd

49/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

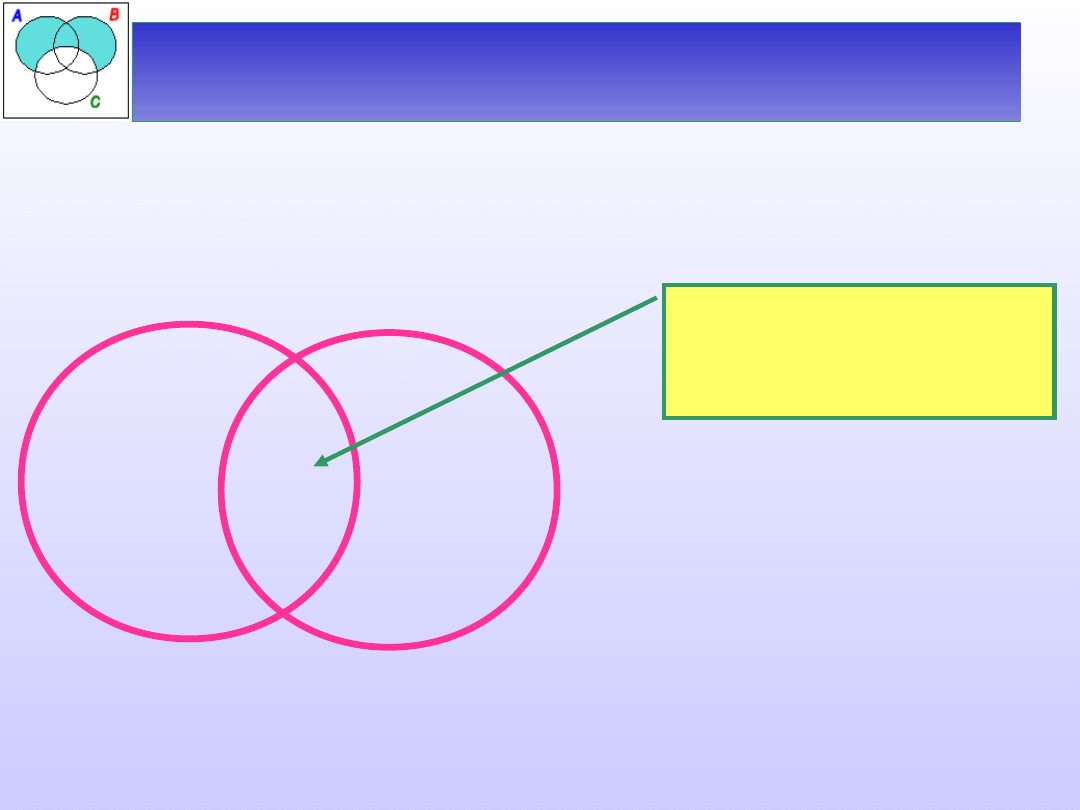
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

+

A – kot, B – pies.

Czy istnieje kot,
który nie jest psem?

Slajd

50/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

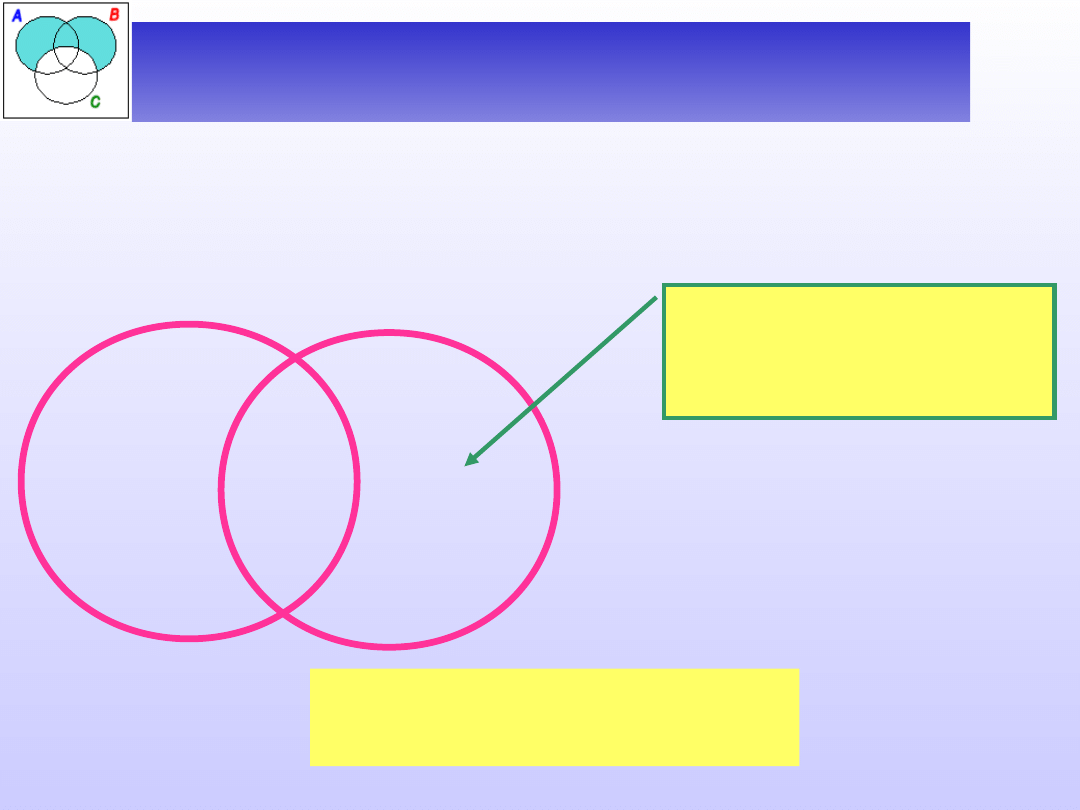
Zbadać zależność między nazwami:

D(A)

D(B)

+

_

A – kot, B – pies.

Czy istnieje kot,
który jest
jednocześnie psem?

Ćwiczenie 2 – zależności między

nazwami

Slajd

51/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

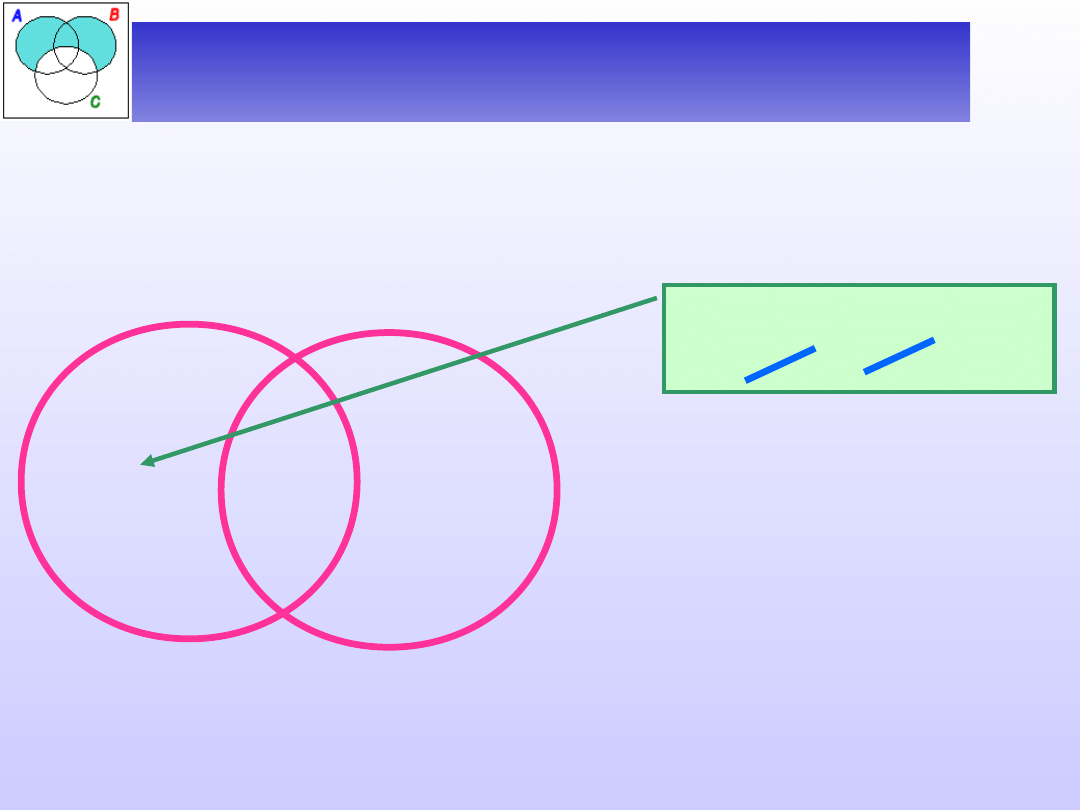
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

+

+

_

Nazwy A i B wykluczają
się.

A – kot, B – pies.

Czy istnieje pies,
który nie jest
kotem?

Slajd

52/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

+

A – nie-pies, B – nie-wydra.

Czy istnieje nie-
pies, który nie jest
nie-wydrą?

Slajd

53/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

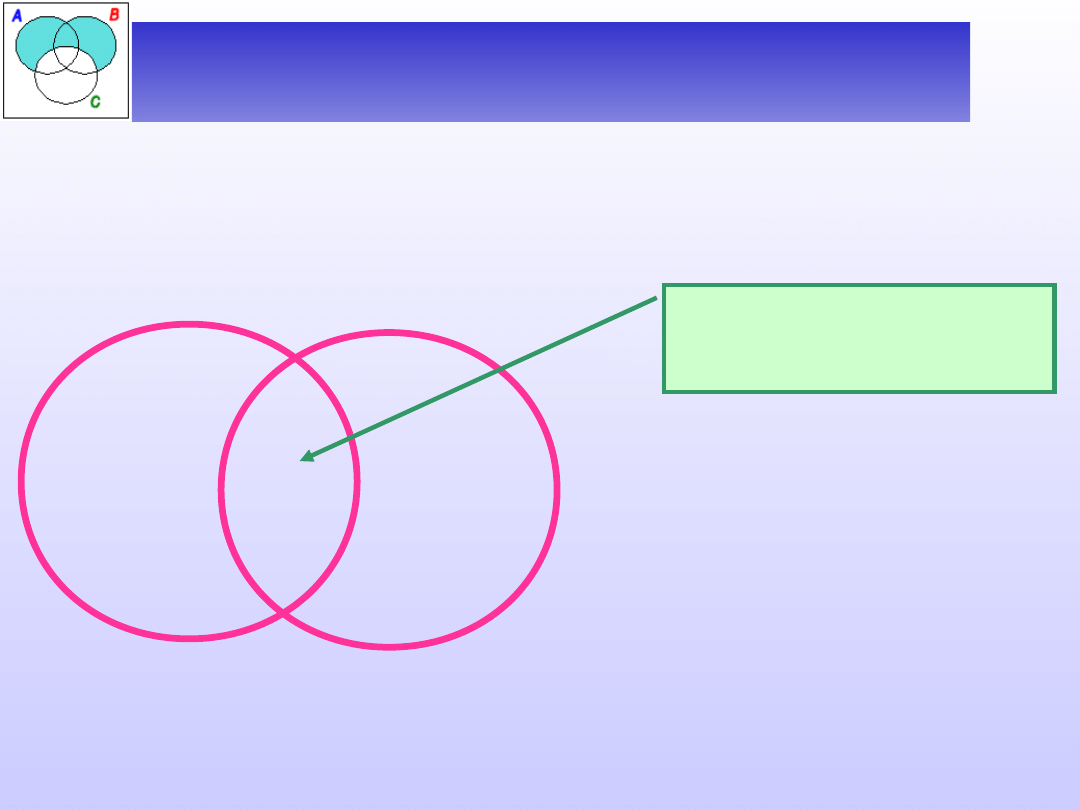
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

+

A – nie-pies, B – nie-wydra.

Czy istnieje nie-
pies, który jest nie-
wydrą?

+

Slajd

54/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

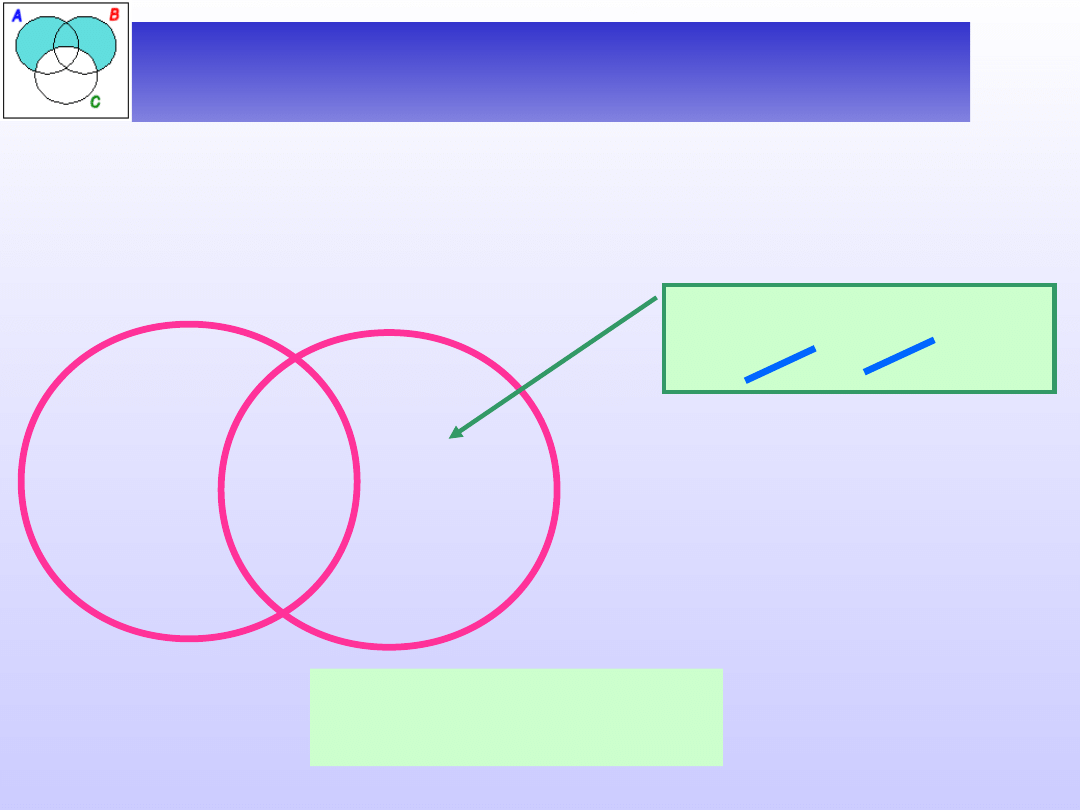
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

+

A – nie-pies, B – nie-wydra.

Czy istnieje nie-
wydra, która nie
jest nie-psem?

+

+

Nazwy A i B krzyżują
się.

Slajd

55/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

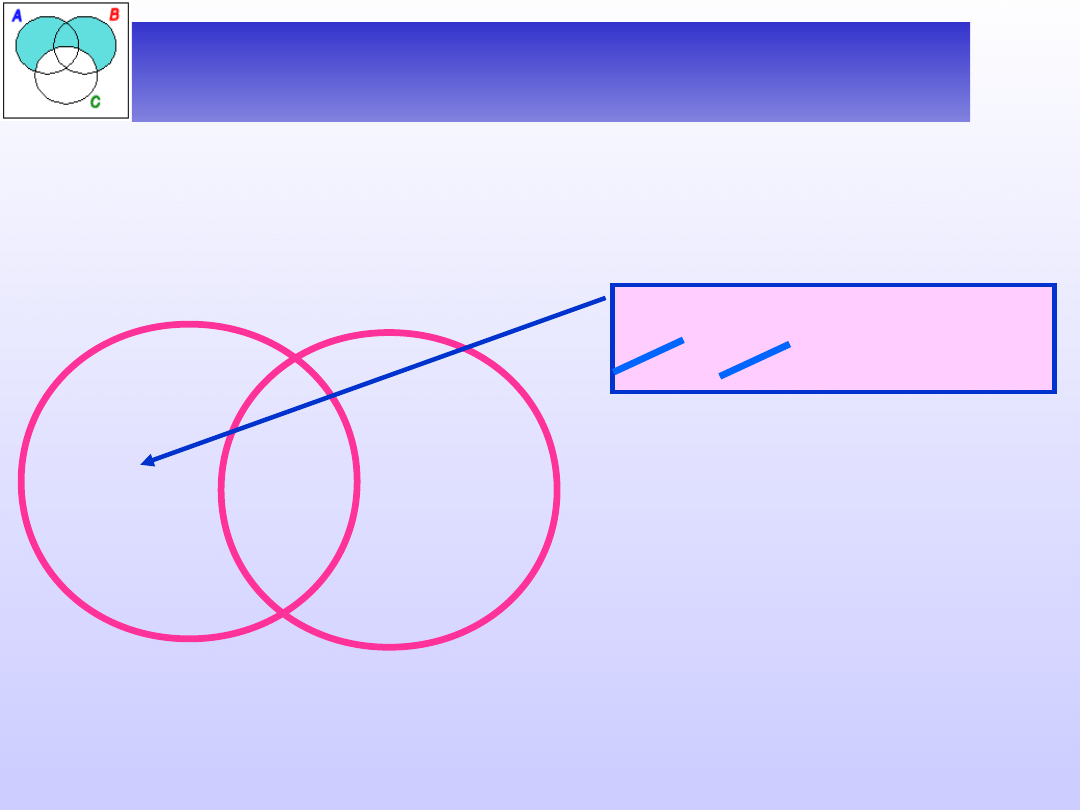
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

_

A – nie-ojciec, B – nie-dziadek.

Czy istnieje nie-ojciec,
który nie jest nie-
dziadkiem?

Slajd

56/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

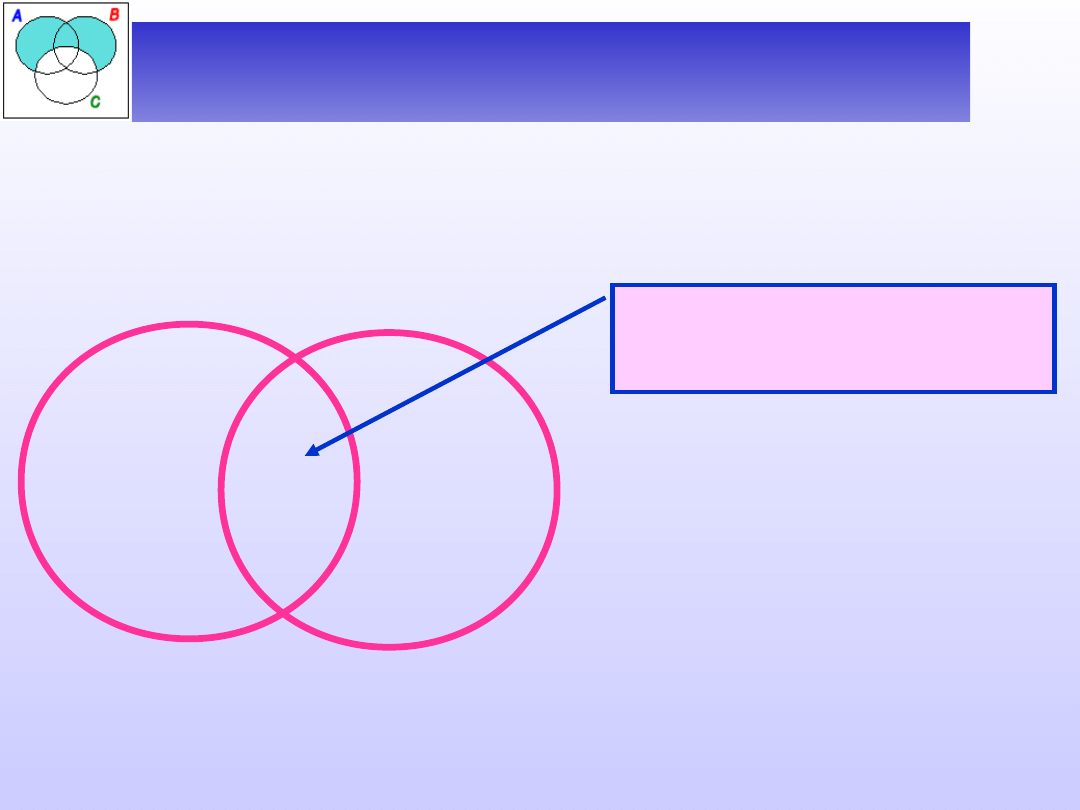
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

_

A – nie-ojciec, B – nie-dziadek.

Czy istnieje nie-ojciec,
który jest nie-
dziadkiem?

+

Slajd

57/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

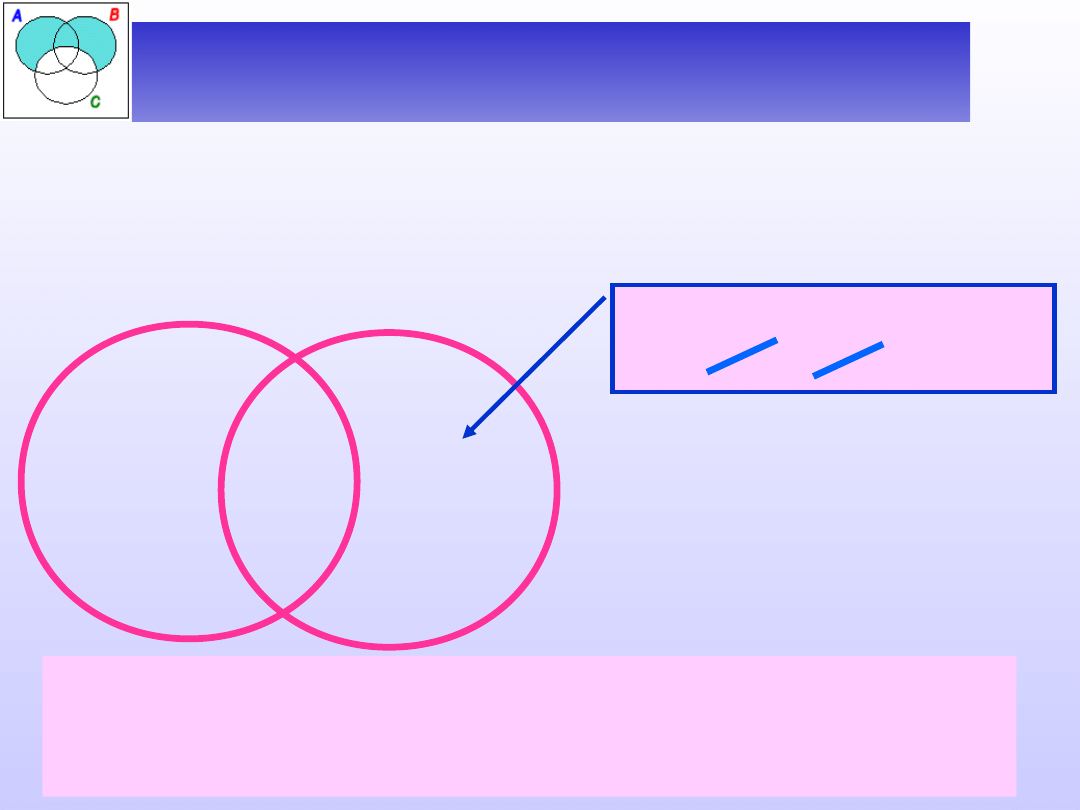
Ćwiczenie 2 – zależności między

nazwami

Zbadać zależność między nazwami:

D(A)

D(B)

_

A – nie-ojciec, B – nie-dziadek.

Czy istnieje nie-
dziadek, który nie jest
nie-ojcem?

+

+

Nazwa nie-ojciec jest podrzędna względem nazwy
nie-dziadek (nazwa nie-dziadek jest nadrzędna do
nie-ojciec).

Slajd

58/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Dobrać nazwę nadrzędną w stosunku do nazwy A –
słoń.

Ćwiczenie 3– zależności między

nazwami

Nazwa nadrzędna do A to posiadająca szerszy
zakres niż nazwa A.

Ponieważ każdy słoń jest ssakiem (ale nie na
odwrót), to nazwą nadrzędną do nazwy słoń może
być ssak.

słoń

ssa

k

Slajd

59/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Dobrać nazwę podrzędną w stosunku do nazwy A –
słoń.

Ćwiczenie 3– zależności między

nazwami

Nazwa podrzędna do A to taka, która posiada
węższy zakres.

Najprostszym sposobem utworzenia nazwy
podrzędnej jest dodanie do nazwy wyjściowej
jakiegoś przymiotnika zawężającego jej zakres.

W przypadku nazwy słoń zawężeniem zakresu
może być słoń afrykański (każdy słoń afrykański
jest słoniem, ale nie na odwrót).

słoń

afrykańsk

i

słoń

Slajd

60/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Dobrać nazwę wykluczającą się w stosunku do nazwy
A – słoń.

Ćwiczenie 3– zależności między

nazwami

W naszym przypadku może być to mysz.

Nazwa wykluczająca się z A to taka, która posiada
rozłączny zakres.

Nazwę wykluczającą można też zawsze utworzyć
przez zaprzeczenie nazwy A – na przykład nie-słoń.

słoń

mysz

Slajd

61/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Dobrać nazwę krzyżującą w stosunku do nazwy A –
słoń.

Ćwiczenie 3– zależności między

nazwami

Musimy znaleźć taką nazwę B, żeby miała wspólne
desygnaty z A, ale żeby również istniały A nie będące
B oraz B nie będące A.

W naszym przypadku musi być to takie B, że
niektóre słonie tym są, ale też takie, że niektóre
słonie owym B nie są, oraz niektóre B nie są
słoniami.

Nazwą spełniającą takie warunki jest na przykład
afrykańskie zwierzę.

słoń

afrykańsk

ie

zwierzę

Są bowiem słonie żyjące w Afryce, są też słonie
mieszkające gdzie indziej (np. w Indiach), a także
zwierzęta żyjące w Afryce, nie będące słoniami.

Slajd

62/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Uwaga

Istnieje prosty nieformalny sposób pozwalający niemal
automatycznie stworzyć nazwę krzyżującą się z
dowolną podaną nazwą.

Aby utworzyć nazwę krzyżującą się z A (słoń)
należy:

(1)

Wziąć nazwę nadrzędną do A (na przykład zwierzę

do nazwy słoń).

(2)

Do nazwy tej dodać przymiotnik oznaczający cechę,

którą niektóre (ale nie wszystkie!) desygnaty A
posiadają (zwierzę żyjące w Afryce).

(3)

Otrzymamy wtedy nazwę krzyżującą się z A.

Slajd

63/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Dobrać nazwę krzyżującą w stosunku do nazwy A –
nieuczciwy polityk.

Ćwiczenie 4– zależności między

nazwami

Procedura tworzenia nazwy
krzyżującej się z podaną:

(1)

Wziąć nazwę nadrzędną do

A. (

2)

Do nazwy tej dodać

przymiotnik oznaczający
cechę, którą niektóre (ale nie
wszystkie!) desygnaty A
posiadają.

(1) Bierzemy nazwę nadrzędną do A:

(2) Do nazwy tej dodajemy cechę, jaką niektórzy
nieuczciwi politycy posiadają:

Otrzymujemy zatem nazwę człowiek mający
ponad 40 lat.

człowiek.

wiek powyżej 40
lat.

Slajd

64/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicje

Definicja to wyrażenie podające informacje o
znaczeniu jakiegoś słowa lub zwrotu.

Definicja taka składa się z trzech części:

Najczęściej spotykane są tak zwane definicje
równościowe (nazywane również normalnymi).

1. terminu definiowanego (tak zwanego
definiendum),

2. terminu definiującego (tak zwanego
definiensa)

3. zwrotu łączącego te dwa terminy – łącznika
definicyjnego.

Slajd

65/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykład

Zegar jest to urządzenie do pomiaru
upływu czasu.

termin definiowany

(definiendum)

termin definiujący

(definiens)

łącznik definicyjny

Slajd

66/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykład

„Student” oznacza osobę uczącą się na
wyższej uczelni.

termin definiowany

(definiendum)

termin definiujący

(definiens)

łącznik definicyjny

Slajd

67/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykład

„Polak” to osoba deklarująca narodowość
polską.

termin definiowany

(definiendum)

termin definiujący

(definiens)

łącznik definicyjny

Slajd

68/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykład

„Państwo europejskie” odnosi się do Polski, Francji,
Niemiec, itd..,

termin definiowany

(definiendum)

termin definiujący

(definiens)

łącznik definicyjny

Slajd

69/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Rodzaje definicji ze względu na

ich zadania.

Sprawozdawcze

(analityczne).

Regulujące.

Konstrukcyjne

(arbitralne).

Projektujące.

Slajd

70/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicja sprawozdawcza:

Wskazuje, jakie znaczenie ma czy też miał
kiedyś definiowany wyraz w pewnym języku.

Definicja sprawozdawcza „podaje sprawozdanie”
z tego, jak pewna grupa ludzi posługuje się czy
też posługiwała się pewnym wyrazem czy
wyrażeniem.

Slajd

71/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady definicji

sprawozdawczej:

Kopalinami są surowce mineralne,

wydobywane z ziemi metodami górniczymi.

Sumą dwóch liczb nazywamy wynik

dodawania tych liczb.

Księgarnia to sklep, w którym sprzedaje się książki.

Slajd

72/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicja projektująca:

Ustala znaczenie jakiegoś słowa na przyszłość.

W definicji tego rodzaju ustala się regułę
znaczeniową, która danemu wyrażeniu przypisuje
określone znaczenie.

Slajd

73/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady definicji

projektującej:

Przez „zboże” należy rozumieć w niniejszym
okólniku: żyto, pszenicę, proso, owies,
jęczmień, kukurydzę i grykę.

Za „matkę” uznawać będziemy odtąd
matkę genetyczną, tj. kobietę, od której
pochodzi zapłodniona komórka jajowa.

Slajd

74/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Różnice:

Definicje te podajemy
wtedy, gdy usiłujemy
opisać zastane znaczenie
pewnego terminu bądź,
gdy ktoś nie zna
ustalonego znaczenia
wyrazu.

Definicje
sprawozdawcze są
albo prawdziwe albo
fałszywe.

W definicjach tych
postanawiamy, zalecamy
bądź proponujemy, by w
jakimś języku posługiwać
się pewnym terminem w
określonym znaczeniu.

Sprawozdawcze

(analityczne).

Projektujące.

Definicjom tym nie
przysługuje wartość
logiczna.

Slajd

75/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicja regulująca i definicja

konstrukcyjna

Ustala na przyszłość
znaczenie pewnego
wyrazu
uwzględniając jednak
zastane (być może
niedostatecznie
określone) znaczenie
danego wyrazu.

Ustala znaczenie pewnego
wyrażenia na przyszłość
nie uwzględniając przy
tym dotychczasowego jego
znaczenia.

Regulująca.

Konstrukcyjna

(arbitralna).

Definicja

projektująca.

Slajd

76/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady definicji

regulujących:

Osoba wykwalifikowana to osoba mająca wykształcenie

niezbędne do wykonywania danej pracy.

Ciężka paczka to paczka ważąca 8 i więcej kilogramów.

Otyłym jest każdy, kto przekracza o 10 i więcej

procent normę wagi zalecanej dla jego wzrostu i

wieku przez Światową Organizację Zdrowia.

Slajd

77/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady definicji

konstrukcyjnych:

„Bąbel spekulacyjny” to sztuczne zawyżenie cen
wszystkich akcji na giełdzie wskutek dokonywania
wielu transakcji w bardzo krótkim czasie.

„Maraton” to seria kolokwiów dla studentów.

„Zbój” to kolokwium ostatniej szansy dla studenta.

Slajd

78/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicje regulujące - cd

Celem definicji regulującej jest:

uściślanie wyrażeń językowych po to, by uniknąć
nieporozumień, niezamierzonych interpretacji,
mylnych wykładni i pojęciowych nadużyć

by można się było definiowanymi wyrażeniami
sprawnie posługiwać w danym kontekście
teoretycznym lub praktycznym (w klasyfikacji,
analizie, formułowaniu problemu, debacie,
umowie, rozporządzeniu, negocjacjach).

Slajd

79/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Błędy w definicjach

sprawozdawczych:

Błędne koło bezpośrednie tzw. idem per
idem (tj. to samo przez to samo).

Błędne koło pośrednie (circulus in
definiendo).

Ignotum per ignotum, (tj. nieznane przez
nieznane).

Błędy nieadekwatności:

definicja za szeroka,
definicja za wąska,
definicja za szeroka i za wąska

zarazem,

błąd przesunięcia kategorialnego.

1.

2.

3.

4.

Slajd

80/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Idem per idem

Błędne koło bezpośrednie to sytuacja, w której
definiens zawiera definiowany termin.

Przykłady:

„Metaetyka to dział filozofii zajmujący się
problemami metaetycznymi.”

„Tolerancyjnym zwiemy człowieka
tolerującego inność.”

Slajd

81/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykład „z życia wzięty” – co tu jest

nie tak?

Definicja „drogi” w Kodeksie Drogowym:

Błędne koło: definiens bezpośrednio zawiera definiowany

termin (droga).

Idem per idem

„Droga" - wydzielony pas terenu składający się z
jezdni, pobocza, chodnika, drogi dla pieszych lub
drogi dla rowerów, łącznie z torowiskiem pojazdów
szynowych znajdującym się w obrębie tego pasa,
przeznaczony do ruchu lub postoju pojazdów, ruchu
pieszych, jazdy wierzchem lub pędzenia zwierząt.

Slajd

82/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Circulus in definiendo

Błędne koło pośrednie powstaje wtedy, gdy
jedno wyrażenie definiujemy za pomocą
drugiego, itd. , a w końcu ostatnie
definiujemy za pomocą pierwszego.

Przykład:

„Sędzia to osoba uprawniona do
wydawania wyroków sądowych.”

Jednocześnie

„Wyrok sądowy to decyzja
sędziego.”

Slajd

83/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ignotum per ignotum

Jest to definiowanie nieznanego terminu
przez termin równie nieznany.

Przykłady:

„Kwantyfikator to operator kwantyfikujący.”

„Bóg to byt, którego esencja jest identyczna z
egzystencją.”

„Kwark to cząstka elementarna o
ułamkowym ładunku, liczbie barionowej i
spinie.”

Slajd

84/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicja za wąska

Jest to sytuacja, gdy zakres definiendum
pozostaje w stosunku nadrzędności do
zakresu definiensa.

Przykłady:

„Nożyczki to przedmiot do cięcia
jedwabiu”.

„Szwagier to mąż
siostry”.

„Rolnik to wieśniak orzący ziemię”.

Slajd

85/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicja za szeroka

Ma miejsce wtedy, gdy zakres definiendum
pozostaje w stosunku podrzędności do
zakresu definiensa.

Przykłady:

„Ołówek to przedmiot do pisania”.

„Samochód to pojazd”.

„Człowiekiem zwiemy małpę
naczelną”.

Slajd

86/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Definicja i za szeroka i za

wąska

Występuje wtedy, gdy zakresy definiendum i
definiensa pozostają w stosunku krzyżowania
się.

Przykłady:

”Nożyce to narzędzie krawca”

.

„Prawnicy to osoby pracujące w kancelariach
prawnych”.

Slajd

87/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przesunięcie kategorialne

Ma miejsce wtedy, gdy zakresy definiendum i
definiensa wykluczają się.

Przykłady:

„Dyscyplina to karanie”.

„Miłość to para kochających się ludzi”.

„Książka jest zbiorem złożonym z okładki
i kartek.”

Slajd

88/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

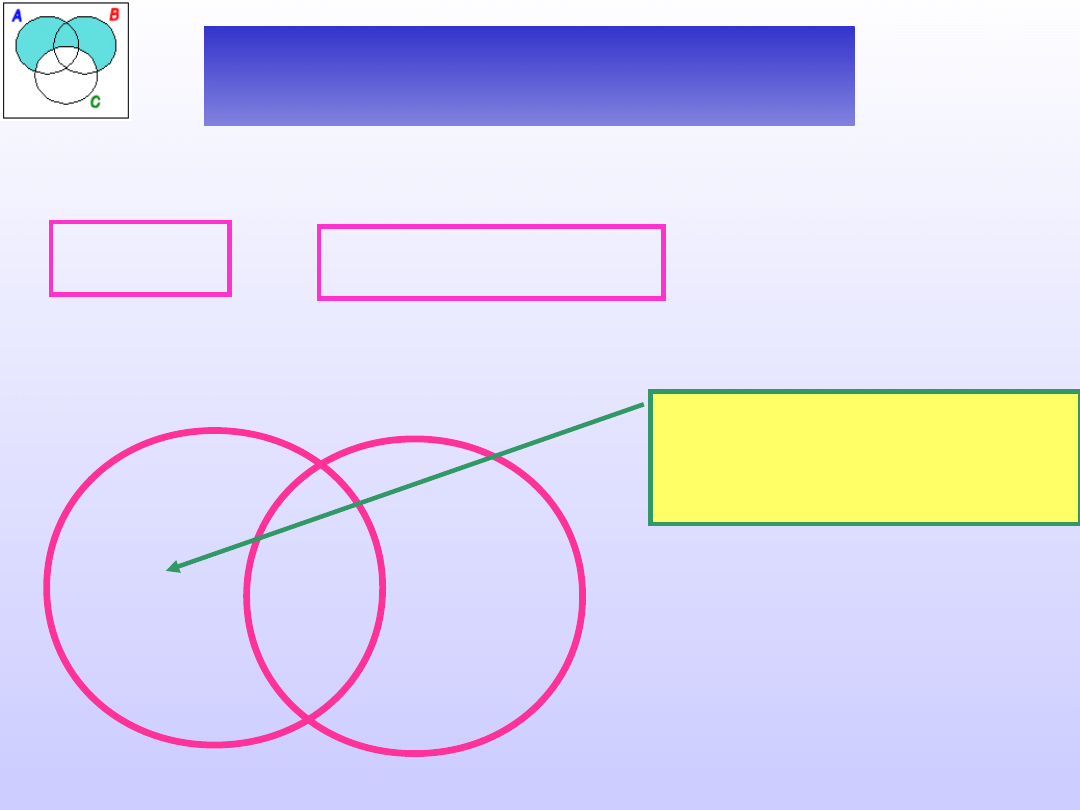
Badanie poprawności definicji

sprawozdawczych

Sprowadza się ono do określenia co
stanowi definiendum oraz definiens, a
następnie zbadania stosunków między
nimi.

Slajd

89/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie - badanie
poprawności definicji
sprawozdawczych

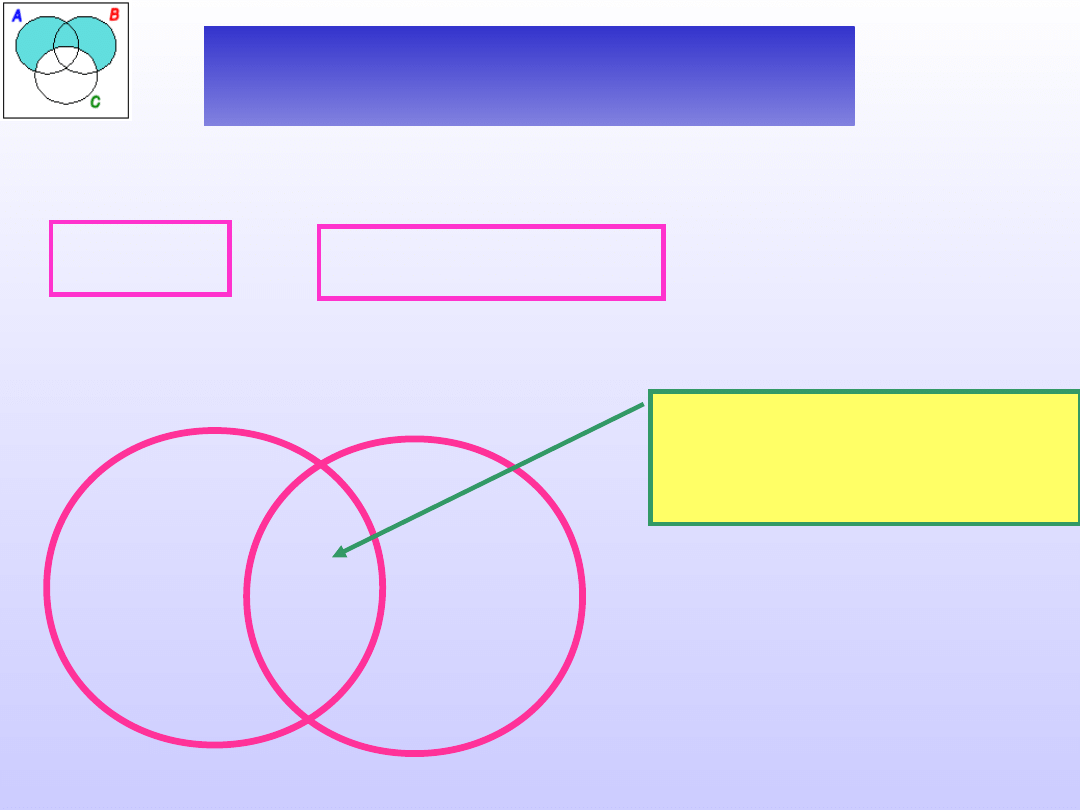
Sprawdzić poprawność definicji:

Termometr jest to przyrząd do
mierzenia.

A -

definiendum

B - definiens

D(A)

D(B)

_

Czy istnieje
termometr, który nie
jest przyrządem?

Slajd

90/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie - badanie
poprawności definicji
sprawozdawczych

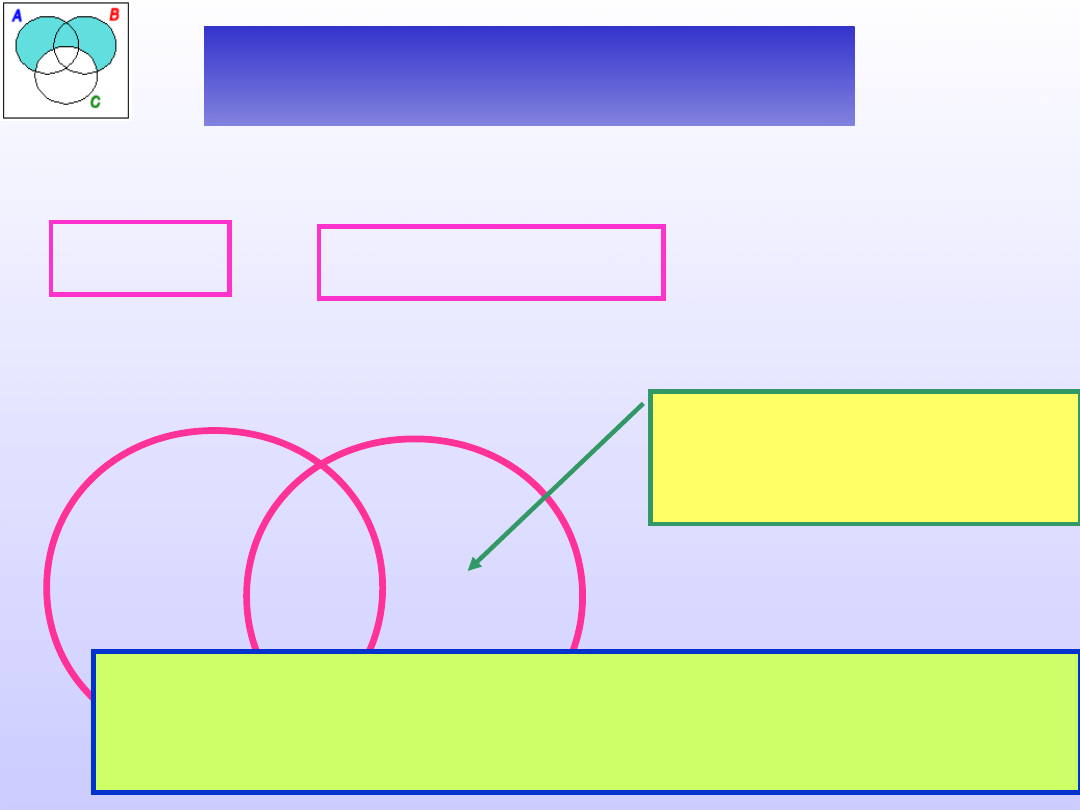
Sprawdzić poprawność definicji:

Termometr jest to przyrząd do
mierzenia.

A -

definiendum

B - definiens

D(A)

D(B)

_

Czy istnieje
termometr, który jest
przyrządem?

+

Slajd

91/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie - badanie
poprawności definicji
sprawozdawczych

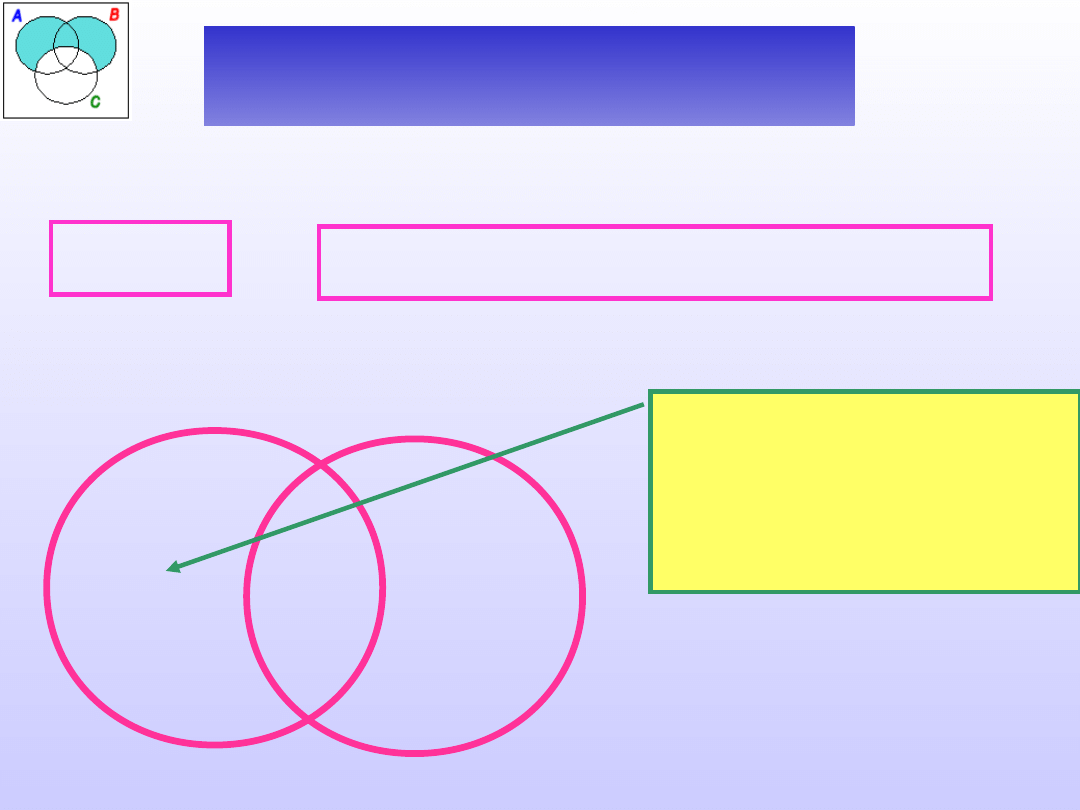
Sprawdzić poprawność definicji:

Termometr jest to przyrząd do
mierzenia.

A -

definiendum

B - definiens

D(A)

D(B)

_

Czy istnieje przyrząd,
który nie jest
termometrem?

+

+

Otrzymany rysunek wskazuje, że definiendum jest
podrzędne względem definiensa, a zatem badana
definicja jest za szeroka.

Slajd

92/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie - badanie
poprawności definicji
sprawozdawczych

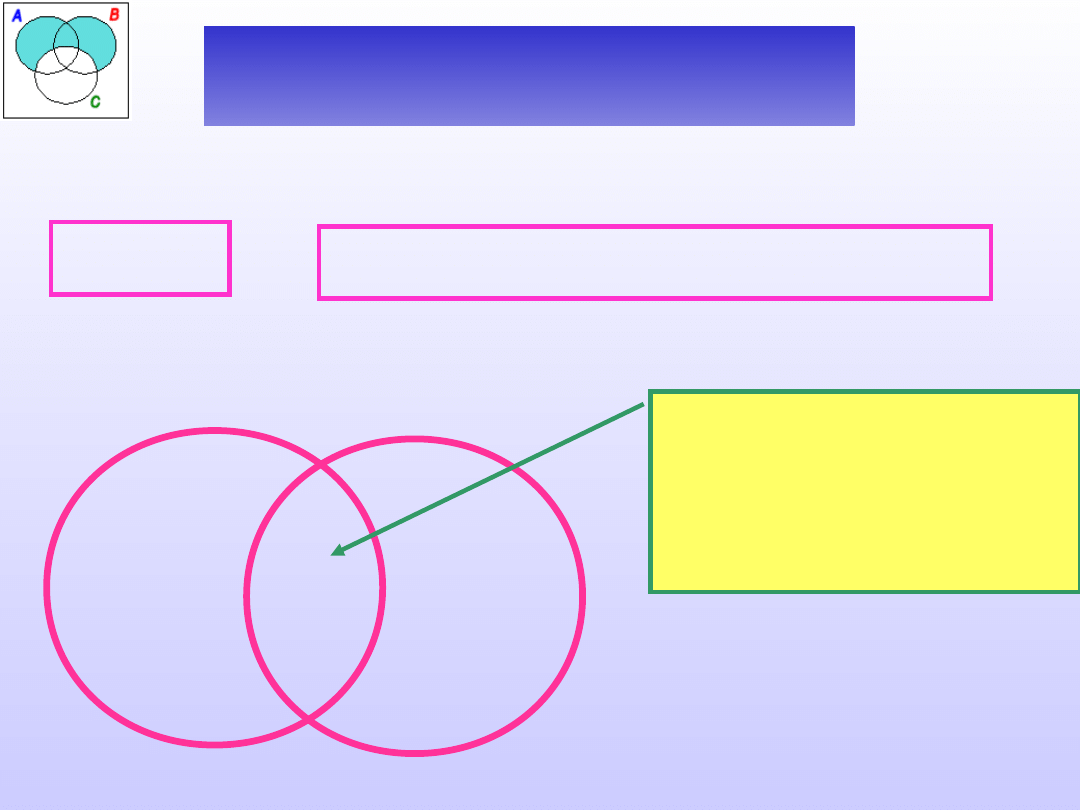
Sprawdzić poprawność definicji:

Termometr jest to przyrząd do mierzenia
temperatury powietrza.

A -

definiendum

B - definiens

D(A)

D(B)

+

Czy istnieje
termometr, który nie
jest przyrządem do
mierzenia
temperatury
powietrza?

Slajd

93/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie - badanie
poprawności definicji
sprawozdawczych

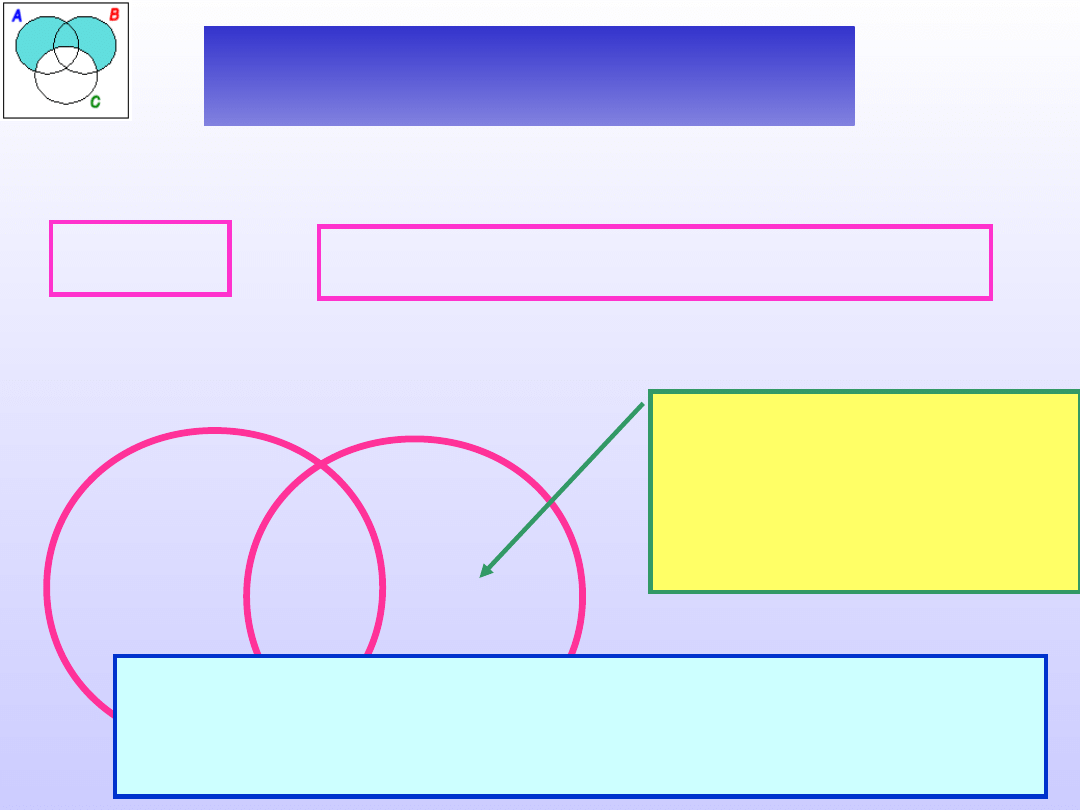
Sprawdzić poprawność definicji:

Termometr jest to przyrząd do mierzenia
temperatury powietrza.

A -

definiendum

B - definiens

D(A)

D(B)

+

Czy istnieje
termometr, który nie
jest przyrządem do
mierzenia
temperatury
powietrza?

+

Slajd

94/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ćwiczenie - badanie
poprawności definicji
sprawozdawczych

Sprawdzić poprawność definicji:

Termometr jest to przyrząd do mierzenia
temperatury powietrza.

A -

definiendum

B - definiens

D(A)

D(B)

+

Czy istnieje
przyrządem do
mierzenia
temperatury
powietrza, który nie
jest termometrem?

+

_

Diagram wskazuje na nadrzędność definiendum
względem definiensa, a więc badana definicja
jest za wąska.

Slajd

95/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przyczyny nieporozumień

słownych

Do najważniejszych i najciekawszych
przyczyn nieporozumień zaliczamy:

1. wieloznaczność słów,

2. wieloznaczność zwrotów językowych i wypowiedzi

złożonych,

3. ekwiwokacje i spory

słowne,

4. błąd amfibologii i figuralnego

myślenia.

Slajd

96/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Wieloznaczność słowa

Wieloznaczność słowa wynika przede
wszystkim z tego, że posiada ono więcej niż
jedno znaczenie.

Sposób użycia tego słowa czy kontekst
może być również źródłem wieloznaczności.

Slajd

97/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady wieloznaczności

słowa

Na mordy carów państwa patrzyły złym okiem.

Mama nie wypuściła mnie z powodu ciemnoty.

Car idąc do celu opierał się na mordzie.

Slajd

98/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Wieloznaczność zwrotów

językowych

Okrzyk: „Dajmy mu siana” co innego

znaczy

1. gdy grupka chłopców nachylona jest nad

znalezionym zwierzęciem, którego chcą
nakarmić albo zrobić mu legowisko ,

2. a co innego, gdy zamierzają oni ścisnąć z

dwóch stron siedzącego w ławce kolegę.

Slajd

99/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Wieloznaczność zwrotów

czasownikowych

Nieporozumienia mogą też powstać na skutek
wieloznaczności zwrotów czasownikowych
czy też specyficznego kontekstualnego ich

użycia.

– Czy Tadeusz pije alkohol?
– Pije.
– To zabierz mu natychmiast kieliszek.
– Nie mogę, bo go teraz nie ma, jest w pracy.

Slajd

100/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Ekwiwokacja

Błąd ekwiwokacji popełnia się wówczas, gdy w
jednym rozumowaniu kilkakrotnie używa się
pewnego słowa wieloznacznego w różnych
znaczeniach, sądząc błędnie, że
używa się go jednoznacznie.

Slajd

101/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady ekwiwokacji

Każde prawo ma prawodawcę.

Prawa przyrody są prawami.

Zatem: Prawa przyrody mają prawodawcę.

Slajd

102/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady ekwiwokacji

Każda kobieta jest kurą domową.

Każda kura domowa jest opierzona.

Zatem: każda kobieta jest opierzona.

Slajd

103/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady ekwiwokacji

Jeżeli Kowalski się spije, to śpi.

Jeżeli Kowalski śpi, to nie grzeszy.

Jeżeli Kowalski nie grzeszy, to jest święty.

A zatem: Jeżeli Kowalski się spije, to jest
święty.

Slajd

104/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Znaczenia dosłowne i

niedosłowne

Stosowanie wyrażeń idiomatycznych, obrazowych
czy metaforycznych upiększa sposób wypowiadania
się, pozwala na podkreślenie, wyostrzenie lub
wysubtelnienie sensu naszej wypowiedzi.

Może jednak być przyczyną
nieporozumień.

Slajd

105/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Znaczenia dosłowne i

niedosłowne

Pewne sformułowania metaforyczne mogą służyć
złagodzeniu wypowiedzi posiadającej niemiłą
treść.

Takie wypowiedzi nazywamy wypowiedziami
eufemistycznymi lub eufemizmami.

Przykład
y:

„Nie grzeszy urodą.”

= „Ale jest
brzydki!”.

„Córa Koryntu.”

= „Prostytutka”.

„Ma lepkie ręce.” = „Kradnie”.

Slajd

106/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Niebezpieczeństwa

Obrazowe wypowiedzi mogą być w pewnych
sytuacjach źródłem nieporozumień.

Jeśli ktoś pewne zwroty obrazowe, sformułowane
przez siebie czy przez kogoś innego bierze w
znaczeniu dosłownym i wysuwa stąd dziwne lub
fałszywe konsekwencje, to mówimy, że popełnia
błąd myślenia figuralnego.

Slajd

107/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady błędów myślenia

figuralnego

• Grażyna stanęła do walki z odkrytą

piersią.

• Z upływem lat Hrabia coraz słabiej

uciskał swoje kucharki i pokojówki.

• Komisja Edukacji Narodowej

obejmowała wszystkie dziewczęta.

Slajd

108/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Amfibolia

Jeśli ktoś wypowiada zdanie wieloznaczne
składniowo z powodu wadliwej budowy wypowiedzi
i nie uświadamia sobie tego, to popełnia błąd
amfibolii lub amfibologii.

Slajd

109/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady amfibolii

• Boryna był teściem żony syna Antka i

Hanki.

• Po uderzeniu w oczy rzucał się Kościuszko

trzymający szablę i miecz.

• Zginął piesek z zakręconym ogonkiem, do

którego była bardzo przywiązana jego

właścicielka.

Slajd

110/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

Przykłady amfibolii

• Na łące leżała Zosia, a przez jej środek

płynął strumyk.

• Lato mile spędzę w górach u kuzynek,

z których zejdę dopiero po wakacjach.

Slajd

111/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

I dalej:

• Po zebraniu makulatury, sprzedaliśmy ją

razem z panią.

• Tatuś kupił stary samochód do spółki ze

stryjem, którym dojeżdża do pracy.

• Zwiedziłem wieś koleżanki, która

przywiązana jest do tradycji.

Slajd

112/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

I dalej:

• Robak, ratując Tadeusza, strzelił do

niedźwiedzia, który nie wiedział, że jest jego
ojcem.

• Danusia ratując Zbyszka przed napaścią

dzikiego zwierza zabiła go.

• Idąc drogą dogoniła go bryczka.

Slajd

113/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

I jeszcze:

• Baryka zakopał precjoza wraz z żoną i

synkiem.

• Dopiero na ostatniej wycieczce nauczyłem się

odróżniać wronę i gawrona od siebie.

Slajd

114/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

I jeszcze:

• Kiedy ojciec wracał z koniem do domu, to chłopcy

pchali mu do pyska skórki od chleba.

• Ksiądz Robak strzelił do niedźwiedzia, który zwalił

się z hukiem i nie czekając na oklaski pobiegł do
domu.

Slajd

115/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

I jeszcze:

• Do uprawy roli Barbara nie nadawała się, więc Bogumił sam

ją uprawiał.

• Bił swoją żonę, z którą miał dzieci przy pomocy sznurka.

Slajd

116/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

I jeszcze:

• Kowalski wyrzucił śmieci razem z żoną.

• Sprawcą czynu jest brat Kowalskiego, który jest dobrze znany

organom ścigania.

Slajd

117/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje

A na koniec:

• A do kotletów była sałata, którą mamusia

przyprawiła potem.

• Kompozytor miał dużo pracy przy swoich

utworach, ale dzieci mu nie przeszkadzały,

więc je dalej tworzył po nocach.

Slajd

118/118

Tomasz Kowalski: Logika. Wykład 5: Nazwy i

definicje