Etapy realizacji badania

naukowego

• Planowanie badania

(zakres, populacja)

• Konstrukcja badania

(aparat losowania,

próba)

• Wykonanie badania

(baza danych)

• Analiza danych

(pakiet statystyczny)

• Prezentacja otrzymanych wyników
• Interpretacja

Konstrukcja badania

• Określenie badanej próby
• Reprezentatywność próby, aparat

losowania

• Określenie liczebności próby

Jaka ma być liczebność

próby?

• Zbyt duża – niepotrzebne koszty

badania

• Zbyt mała – uniemożliwia wykrycie

ważnych zjawisk medycznych

• Metoda obliczenia liczebności

próby zależy od stopnia złożoności
konstrukcji badania

• Przykłady obliczeń w STATISTICA

Analiza danych

• Dobór odpowiednich testów

statystycznych

• Przykłady obliczeń w STATISTICA:

test t Studenta i analiza wariancji
test chi-kwadrat
testy nieparametryczne
korelacja i regresja

Przedstawienie wyników i

interpretacja

• Wykresy
• Tabele

Cechy jakościowe:
płeć, zawód, diagnoza.szeregi
wielodzielcze.
-wyliczone wskaźniki struktury, natężenia i
poglądowości
-wykres słupkowy, kołowy.i inny
Cechy ilościowe: wzrost, masa ciała,wiek.

-wyliczone miary średnie i rozproszenia
bądź zestawienie wyników obserwacji w
szeregach szczegółowych, czy
rozdzielczych i wyliczanie wskaźników
struktury, natężenia i poglądowości
oraz wyliczanie miar średnich i
rozproszenia

Opis zebranego materiału

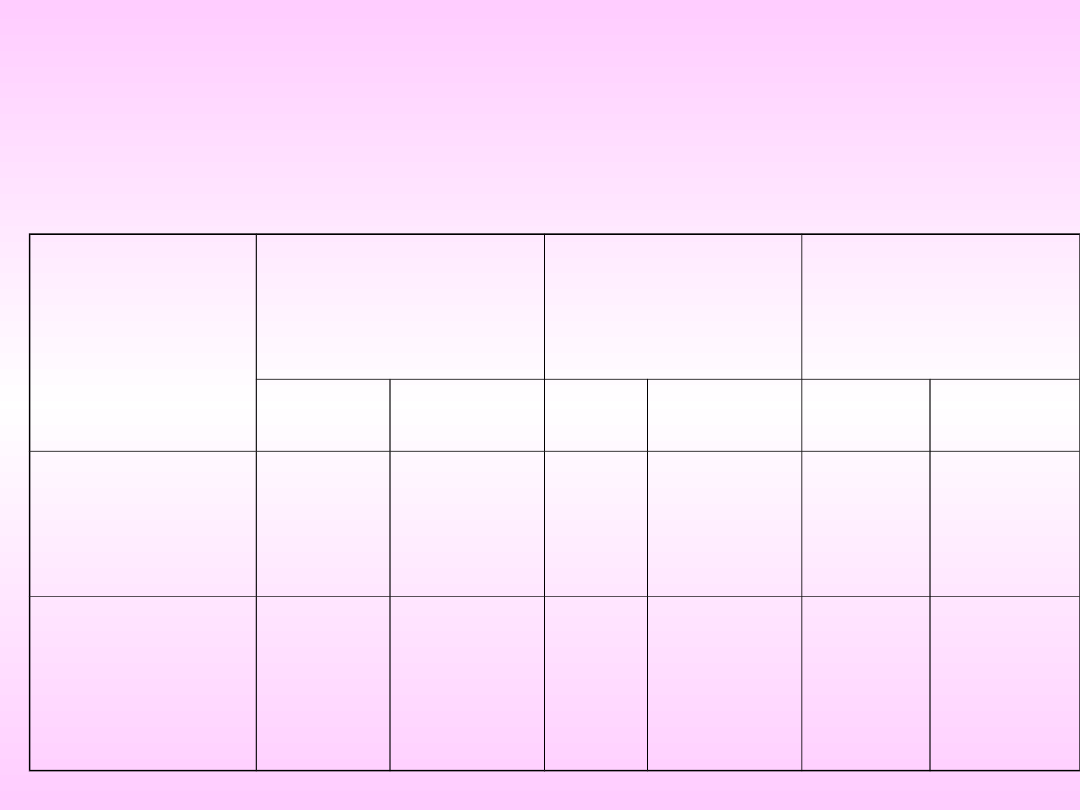
Cechy jakościowe

Częstość występowania, odsetki w

tablicach

Grupa

Kobiety

Mężczyźni

Razem

n

%

n

%

n

%

Cukrzyca

25

55,6

20

44,4

45

100,0

Bez

cukrzycy

45

60,0

30

40,0

75

100,0

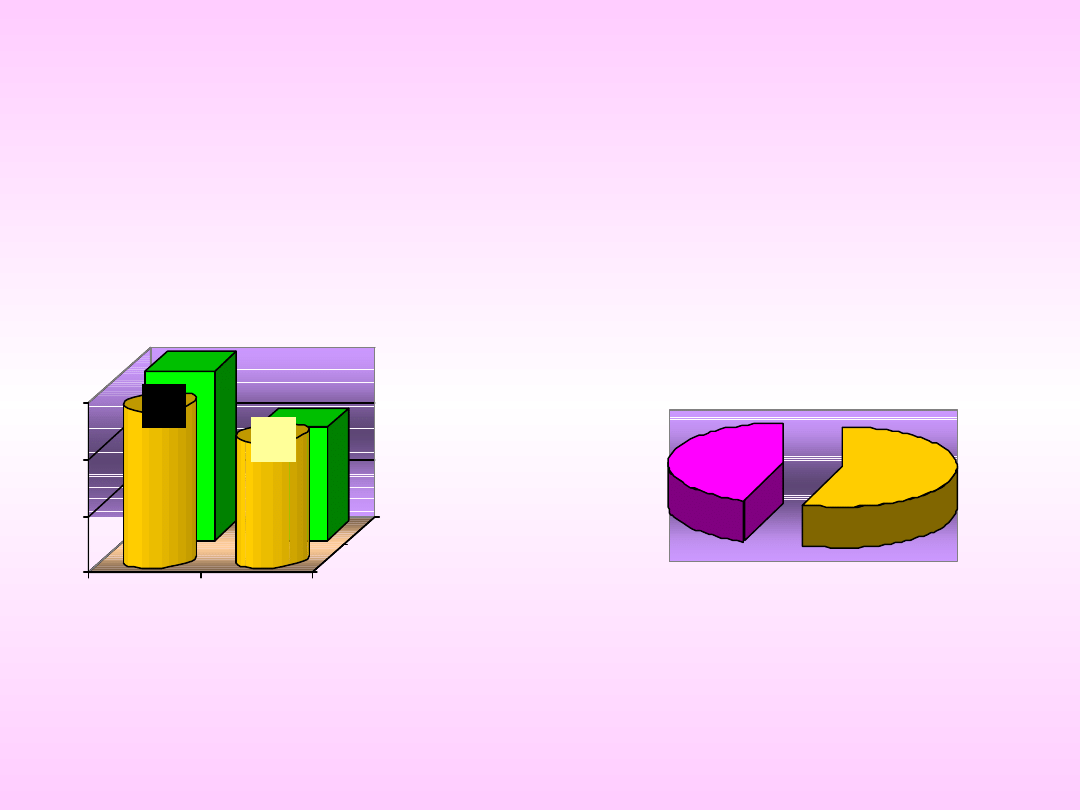
Graficzna prezentacja

60

40

55,6

44,4

0

20

40

60

%

Kobiety Mężczyźni

Cukrzyca

Bez cukrzycy

55,6

44,4

Cechy ilościowe

• Średnia, odchylenie standardowe, mediana, rozstęp,

tablice, wykres ramka-wąsy, szereg rozdzielczy,
histogram.

• Rozstęp:R= wartość maks. – wartość minim
• Długość przedziału d =

• Liczba przedziałów l jest tak dobrana, by długość

przedziału d była łatwa do dodawania, czyli w
miarę całkowita, lub z niedużą liczbą miejsc
dziesiętnych, przy czym 6< l <12 w zależności od
liczby pomiarów.

•

1j.m. to jest 1 jednostka miary, np. jeżeli wysokość jest
mierzona w centymetrach z jednym miejscem dziesiętnym
23,4 cm; 24,0 cm itd., to 1 j.m. wynosi 0,1 cm.

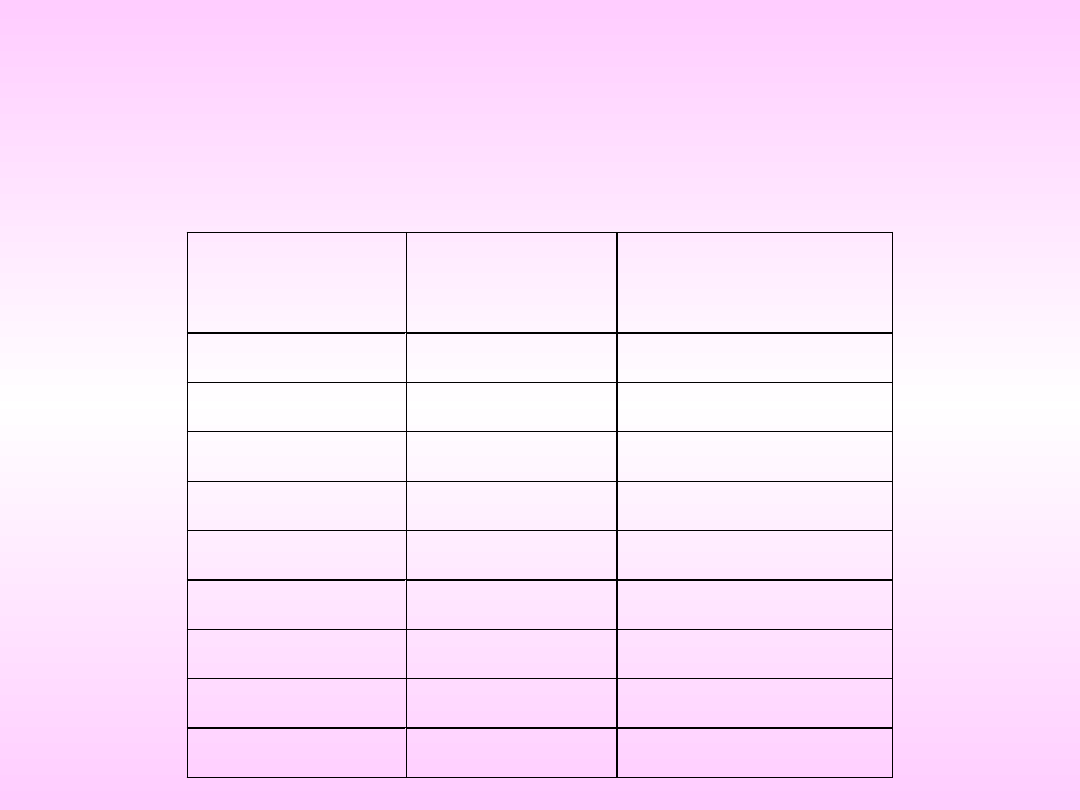
Przykład –masa ciała dzieci

min=3,5; max=45,4; R=45,4-

13,5=31,9; d =

jeżeli l=8 to d=4

P

r

z

e

d

z

i

a

ł

y

k

l

a

s

o

w

e

L

i

c

z

b

a

o

b

s

e

r

w

a

c

ji

i

n

P

r

a

w

d

o

p

o

d

o

b

i

e

ń

s

t

w

o

i

p

[

1

3

,5

–

1

7

,5

)

1

9

0

,1

8

[

1

7

,5

–

2

1

,5

)

2

2

0

,2

1

[

2

1

,5

–

2

5

,5

)

3

3

0

,3

1

[

2

5

,5

–

2

9

,5

)

1

6

0

,1

5

[

2

9

,5

–

3

3

,5

)

1

2

0

,1

1

[

3

3

,5

–

3

7

,5

)

2

0

,0

2

[

3

7

,5

–

4

1

,5

)

2

0

,0

2

[

4

1

,5

–

4

5

,5

)

1

0

,0

1

R

a

z

e

m

1

0

7

1

,0

0

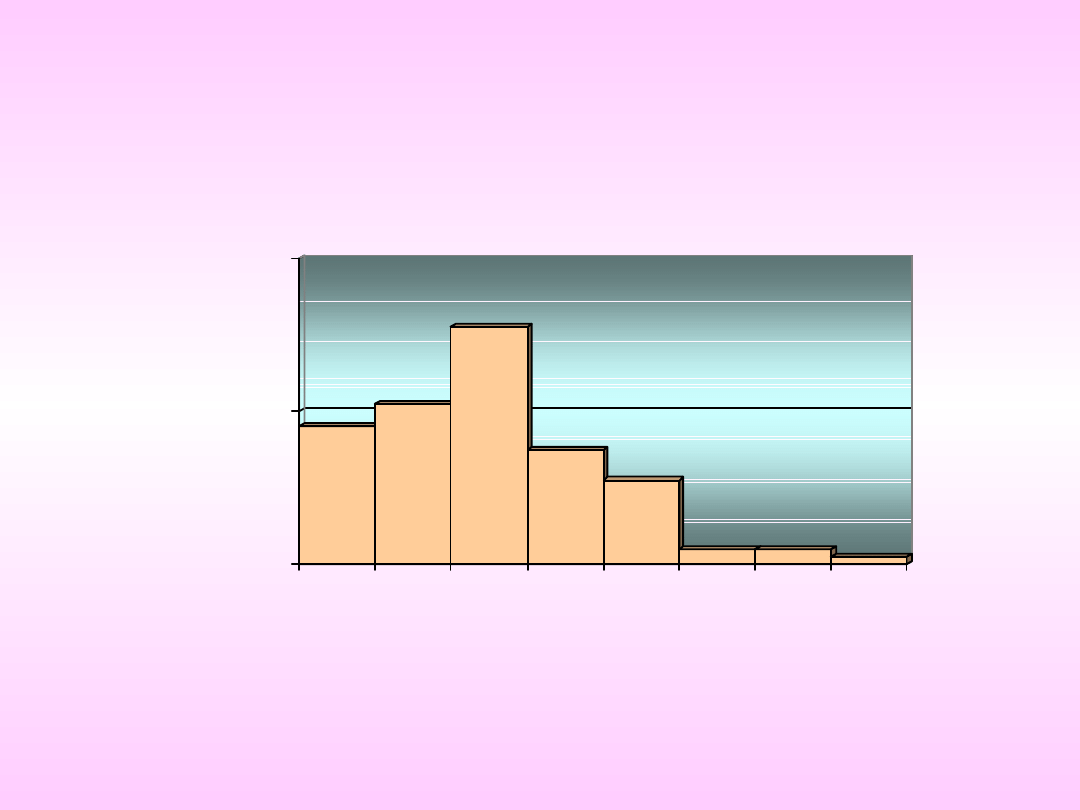
Graficzna prezentacja

0

0,2

0,4

pr

aw

do

po

do

bi

eń

st

w

o

[1

3,

5

–

17

,5

)

[1

7,

5

–

21

,5

)

[2

1,

5

–

25

,5

)

[2

5,

5

–

29

,5

)

[2

9,

5

–

33

,5

)

[3

3,

5

–

37

,5

)

[3

7,

5

–

41

,5

)

[4

1,

5

–

45

,5

)

Próba – populacja

Miary położenia i rozproszenia

Średnia arytmetyczna i odchylenie standardowe w populacji: .

Średnia arytmetyczna i odchylenie standardowe z próby:

n

x

x

n

i

i







1

1

)

(

1

2











n

x

x

s

n

i

i

gdzie:

n- liczba elementów w próbie,

x

i

– wartość i-tego elementu z próby

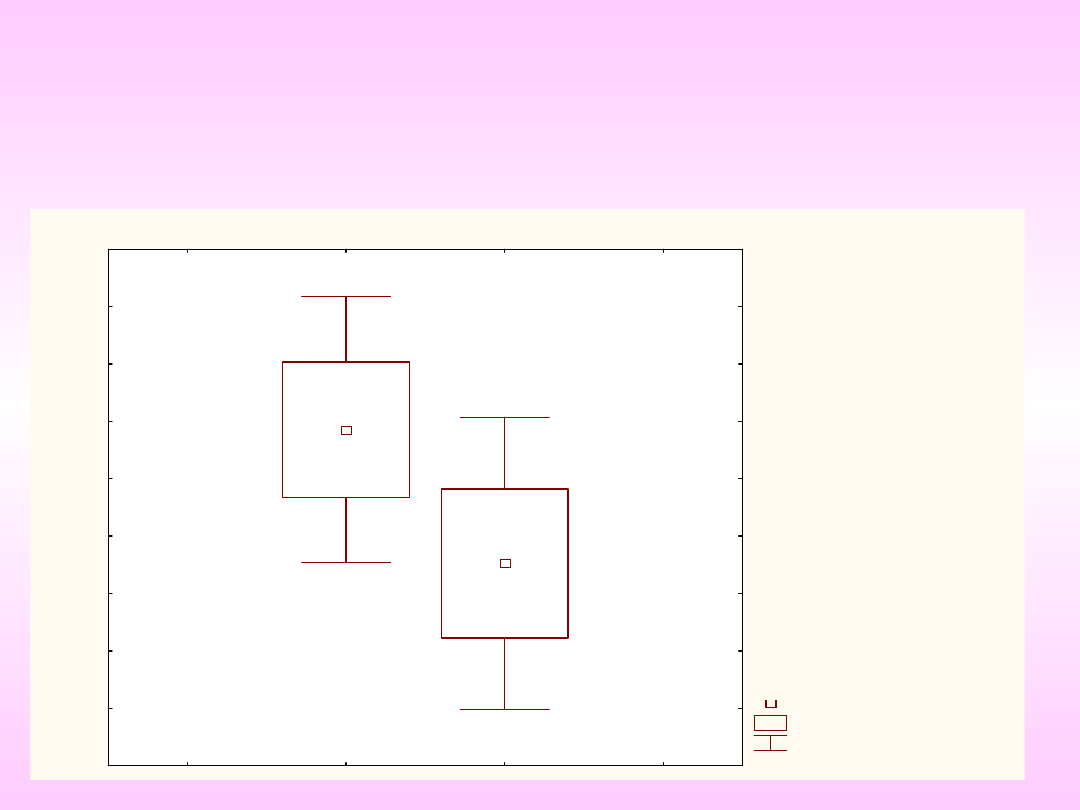
Graficzna prezentacja

Wykres ramka-wąsy:

Średnia
Średnia±Błąd std
Średnia±1,96*Błąd std

76

77

78

79

80

81

82

83

84

85

W

A

G

A

(

k

g

)

Błąd standardowy SE=

n

S

Rozstęp = wartość największa-wartość
najmniejsza
Mediana Me=wartość środkowa w
posortowanych danych
Modalna – wartość najczęściej
występująca
Są to miary położenia i rozproszenia
(zmienności)
Zadanie: s=4; SE=?
125,134,146,134,130
Me=? Modalna=?

Przedział ufności dla średniej

w populacji





- nieznana średnia w populacji,

• , s średnia i odchylenie standardowe

obliczone z próby dla cechy X, mającej
rozkład normalny, to

• P( -1,96s<



< +1,96s)=0,95

• Przykład =175; s=10, to
• P(155,4<



< 194,6)=0,95

ANALIZA

WSPÓŁZALEŻNOŚCI

Analiza struktury zjawisk dotyczyła jednej

cechy. W praktyce jednak bywa tak, że
badane jednostki statystyczne
charakteryzowane są przez kilka cech.
Cechy te nie są od siebie odizolowane,
mają na siebie wpływ oraz posiadają
wzajemne uwarunkowania. Dlatego często
zachodzi potrzeba badania
współzależności między tymi cechami.

Przeprowadzając analizę można spotkać

dwa rodzaje współzależności zmiennych:

1. Współzależność funkcyjną, polegającą

na tym, że zmiana wartości jednej

zmiennej pociąga określoną zmianę

wartości drugiej zmiennej.

2. Współzależność stochastyczną

(probabilistyczną), polegającą na tym,

że wraz ze zmianą jednej zmiennej

zmienia się rozkład prawdopodobieństwa

drugiej zmiennej. Szczególnym

przypadkiem zależności

stochastycznej jest zależność

korelacyjna.

Zależności korelacyjne zachodzą

wówczas, gdy określonym wartościom
jednej zmiennej odpowiadają ściśle
określone średnie wartości
drugiej zmiennej.

Zdarzają się jednak sytuacje, w

których nie istnieje
współzależność (korelacja) ale ma
miejsce zbieżność występowania
zjawisk. Taką zbieżność określa się
mianem korelacji pozornej.

Najczęściej spotykanymi metodami

wykrywania związków korelacyjnych są:

Metoda porównywania

przebiegu szeregów statystycznych.

Metoda graficzna.

y

i

0 x

i

y

i

0 x

i

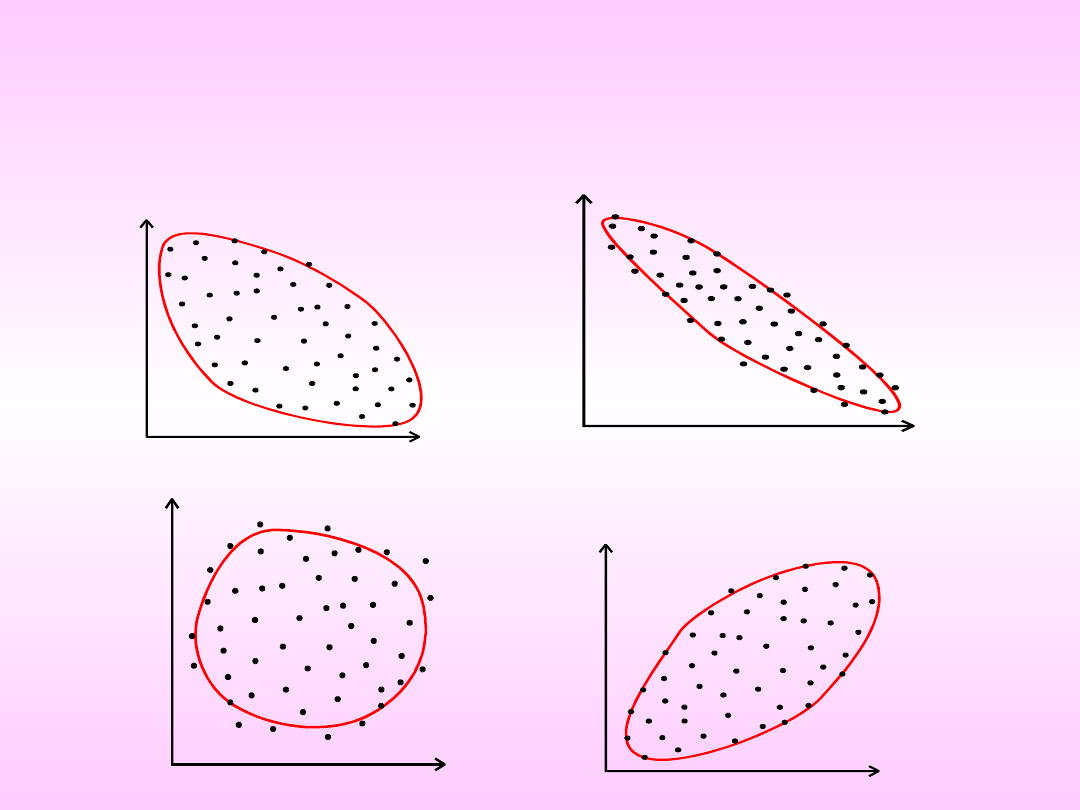
Związek ujemny (wzrost wartościchy X indukuje obniżanie

wartości cechy Y)

X

Y

X

Y

X

Y

X

Y

Związek dodatni

Brak związku

Cechę dwuwymiarową oznacza się jako

uporządkowaną parę (X,Y). Składowymi
mogą być zarówno cechy ilościowe
jak i jakościowe. To od tego, z jakimi cechami
mamy do czynienia zależy wybór sposobu
opisu współzależności.

Podstawą analizy jest zbiorowość

jednostek scharakteryzowanych parą
własności ,

gdzie i=1,2,...,n.
Badając zbiorowość jednostek pod względem

wyróżnionych cech otrzymuje się ciąg par wartości:



 







.

,

,...,

,

,

,

2

2

1

1

n

n

y

x

y

x

y

x





i

i

y

x ,

MIARY

WSPÓŁZALEŻNOŚCI

Do badania zależności między zmiennymi

X i Y wykorzystuje się najczęściej
współczynnik korelacji liniowej
Pearsona, będący miarą siły związku
prostoliniowego między dwiema
cechami mierzalnymi. Współczynnik ten
wylicza się ze wzoru:

gdzie:
cov(x,y) - kowariancja zmiennych X i Y





   

y

s

x

s

y

x

r

xy





,

cov

Kowariancja jest średnią

arytmetyczną iloczynu odchyleń
zmiennych X i Y od ich
średnich arytmetycznych:

 



 

















n

i

i

i

y

y

x

x

n

y

x

1

1

,

cov

Rozpatrując kowariancję uzyskać

można następujące informacje o
istniejącym związku pomiędzy
zmiennymi X i Y:

Jeżeli cov(x,y)>0 – dodatnia korelacja
Jeżeli cov(x,y)<0 – ujmena korelacja
Jeżeli cov(x,y)=0 – brak korelacji

Kowariancji nie można

stosować do bezpośrednich
porównań. Dlatego jest ona
standaryzowana przez odchylenia
standardowe, dzięki czemu otrzymuje
się współczynnik korelacji liniowej
Pearsona.

Właściwości współczynnika korelacji:
1.

Przyjmuje wartości z przedziału <-1;1>

2.

Dodatni znak świadczy o dodatnim, zaś
ujemny o ujemnym związku korelacyjnym

3.

Im tym związek
korelacyjny jest silniejszy.

Sposoby komentowania

współczynnika korelacji

:

a)

- współzależność nie występuje,

b) - słaby stopień współzależności,
c)

- umiarkowany (średni) stopień

współzależności,

d) - znaczny stopień współzależności,
e)

- wysoki stopień współzależności,

f)

- bardzo wysoki stopień

współzależności,

g) - całkowita (ścisła) współzależność
(zależność funkcyjna pomiędzy
badanymi cechami).

0



XY

r

3

,

0

0





XY

r

5

,

0

3

,

0





XY

r

7

,

0

5

,

0





XY

r

9

,

0

7

,

0





XY

r

1

9

,

0





XY

r

1



XY

r

• Współczynnik korelacji liniowej Pearsona

(dalej nazywany po prostu współczynnikiem

korelacji), wymaga, aby zmienne były

ciągłe. Określa on stopień proporcjonalnych

powiązań wartości dwóch zmiennych.

Wartość korelacji (współczynnik korelacji)

nie zależy od jednostek miary, w jakich

wyrażamy badane zmienne, np. korelacja

pomiędzy wzrostem i ciężarem będzie taka

sama bez względu na to, w jakich

jednostkach (cale i funty czy centymetry i

kilogramy) wyrazimy badane wielkości.

Określenie "proporcjonalne" znaczy zależne

liniowo, to znaczy, że korelacja jest silna,

jeśli może być opisana przy pomocy linii

prostej (nachylonej do góry lub na dół).

Analizę współzależności należy

uzupełnić o współczynnik
determinacji, będący kwadratem
współczynnika korelacji liniowej
Pearsona ( ).

Współczynnik determinacji

informuje, jaka część zmiennej
objaśnianej jest wyjaśniona przez
zmienną objaśniającą. Przy pomocy
tego współczynnika można
wnioskować, czy na zmienną
objaśniającą wpływają również inne
czynniki, nie podlegające badaniu.

2

xy

r

Prosta regresji: y=ax+b,

gdzie

a = cov(x,y)/

S; b= - a

• Linia, o której mowa, nazywa się linią regresji

albo linią szacowaną metodą najmniejszych
kwadratów, ponieważ jej parametry określane są
w ten sposób, by suma kwadratów odchyleń
punktów pomiarowych od tej linii była
minimalna. Zwróćmy uwagę, że fakt podnoszenia
odległości do kwadratu powoduje, iż
współczynnik korelacji reaguje na sposób
rozmieszczenia danych (jak to zobaczymy w
dalszej części opisu).

•  

x

y

yy

W sytuacji, gdy obserwacje

statystyczne dotyczące badanych
zmiennych są liczne, bazowanie na
wartościach szczegółowych może być
uciążliwe. W celu zapewnienia
przejrzystości zebranych danych
sporządza się wówczas tablicę korelacyjną.

Na skrzyżowaniu kolumn z

wierszami wpisuje się liczebności
jednostek zbiorowości statystycznej, u
których zaobserwowano jednoczesne
występowanie określonych wartości
i .

i

x

i

x

i

y

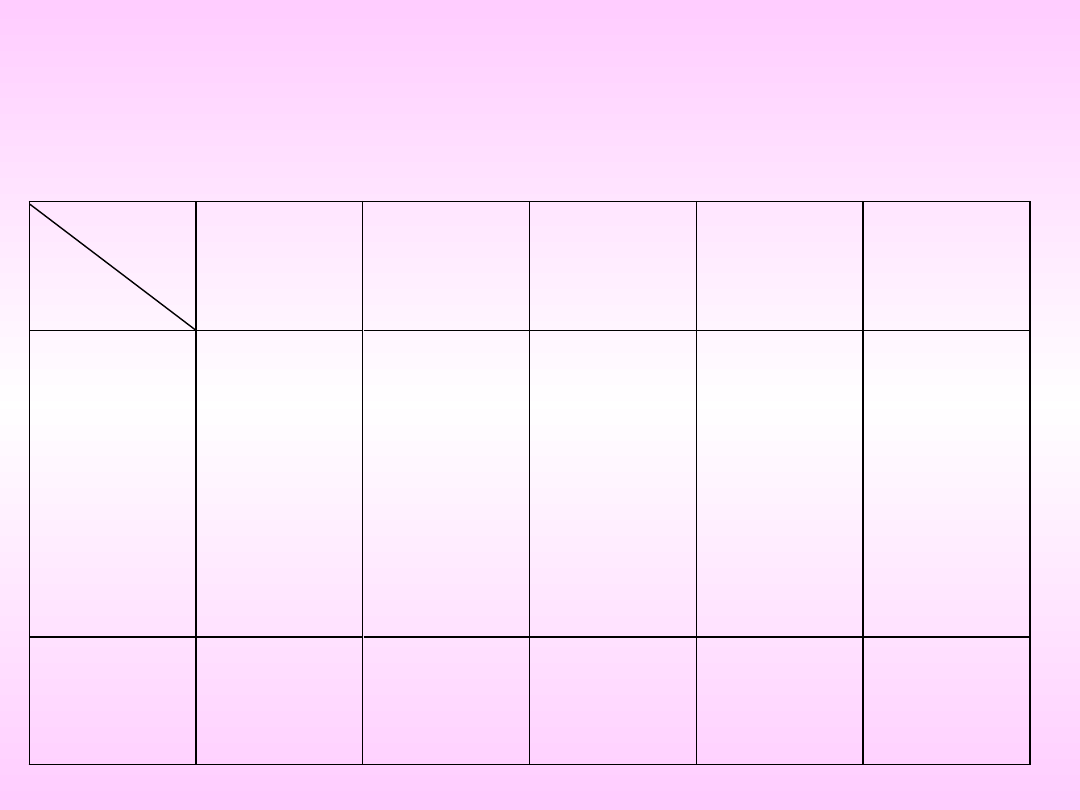
Schemat tablicy

korelacyjnej:

x

i

y

j

y

1

y

2

...

y

t

i

t

i

ij

n

n 



1

x

1

x

2

.
.
.

x

k

n

11

n

21

.
.
.

n

k1

n

12

n

22

.
.
.

n

k2

.
.
.
.
.
.

n

1t

n

2t

.
.
.

n

kt

n

1

n

2

.
.
.

n

k

j

k

i

ij

n

n 



1

n

.1

n

.2

…

n

.t

n

Przykład tabeli korelacyjnej.

Wykształcenie badanych osób

przebywających w Domach Pomocy

Społecznej z uwzględnieniem płci

Wykształcenie

Płeć

Żeńska

Męska

Liczba
podstawowe
%

53

86,9%

16

43,2%

Liczba
zawodowe

%

2

3,3 %

14

37,8 %

Liczba
średnie
%

6

9,8 %

5

13,5 %

Liczba

wyższe
%

0

0,0 %

2

5,4 %

Liczba
Razem

%

61

100,0 %

37

100,0 %

W tablicy korelacyjnej zawarte są

rozkłady brzegowe i warunkowe.
Rozkład brzegowy (por. ostatnia
kolumna określa rozkład brzegowy
cechy X, ostatni wiersz – rozkład
brzegowy cechy Y) prezentuje
strukturę wartości jednej zmiennej (X
lub Y) bez względu na kształtowanie
się wartości drugiej zmiennej.

Rozkłady brzegowe i warunkowe

mogą być scharakteryzowane pewnymi
sumarycznymi wielkościami (najczęściej
są to średnie arytmetyczne)

Średnie arytmetyczne z

rozkładów brzegowych wyznacza
się ze wzorów:

Średnie arytmetyczne z

rozkładów warunkowych oblicza
się następująco:

i

k

i

i

n

x

n

x









1

1

j

t

i

j

n

y

n

y









1

1

ij

k

i

i

j

j

n

x

n

x









1

.

1

ij

t

i

j

i

i

n

y

n

y









1

.

1

W sytuacji, gdy wraz ze

wzrostem (spadkiem) wartości jednej
zmiennej następuje wzrost (spadek)
warunkowych średnich drugiej
zmiennej, wówczas można stwierdzić
istnienie korelacji dodatniej
między zmiennymi. W sytuacji,
kiedy występuje przeciwny kierunek
zmian, można mówić o korelacji
ujemnej.

Jeżeli różnice pomiędzy

średnimi są takie same, tzn.:

wówczas związek między

zmiennymi jest liniowy.

1

2

3

1

2

...















t

t

x

x

x

x

x

x

1

2

3

1

2

...















k

k

y

y

y

y

y

y

Innym miernikiem korelacyjnego związku cech

jest współczynnik korelacji rang
Spearmana. Współczynnik ten stosowany
jest głównie do badania współzależności
cech niemierzalnych, bądź cechy mierzalnej i
niemierzalnej. Może być on również
stosowany w badaniu związku
korelacyjnego pomiędzy cechami
mierzalnymi (szczególnie w przypadku małej
próby).

Konstrukcja współczynnika korelacji

rang opiera się na zgodności pozycji, którą
zajmuje każda z odpowiadających sobie
wielkości we wzrastającym lub
malejącym szeregu wartości cechy.

Współczynnik korelacji rang Spearmana

(Q) wylicza się w oparciu o wyznaczone
różnice rang ( ) oraz liczby par
obserwacji (n):

przy czym:

gdzie:
- rangi zmiennej X oraz Y (i=1,2,...n)

n

n

d

Q

n

i

i













3

1

2

6

1

i

i

y

x

i

v

v

d





i

i

y

x

v

v ,

gdy

Współczynnik korelacji rang

przyjmuje wartości z przedziału
, a jego interpretacja
jest analogiczna do
współczynnika korelacji Pearsona

1



Q

0

1

2







n

i

i

d

1

1







Q

Przykład. W celu zbadania, czy istnieje związek
między zdyscyplinowaniem pacjentów względem
zaleceń personelu medycznego a wynikami
terapii na pewną dolegliwość poddano
obserwacji 10 pacjentów. Otrzymano
następujące wyniki obserwacji zestawione w
tabeli

:

Pacjent

Ranga

zdyscyply-

-nowanie

Ranga

terapii

Różnica

rang (d)

Kwadrat

różnicy

rang (d

2

)

1
2
3
4
5
6
7
8
9

10

6
2
5
1

10

4
9
3
8
7

4
1
5
3

10

7
6
2
9
8

2
1
0

-2

0

-3

3
1

-1
-1

4
1
0
4
0
9
9
1
1
1

Razem

0

30