Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Procesy Mechaniczne.

Proces mieszania

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Celem mieszania cieczy jest wyrównanie temperatur i stężenia. W przypadku cieczy
niejednorodnych (zawiesin i emulsji) mających tendencje do grawitacyjnego
rozwarstwienia, mieszanie stwarza stan równowagi dynamicznej  stężenie jest

wyrównane ale tylko tak długo jak mieszana jest zawiesina.

Mieszanie mechaniczne jest więc najpopularniejszą metoda zwiększania jednorodności
układu.

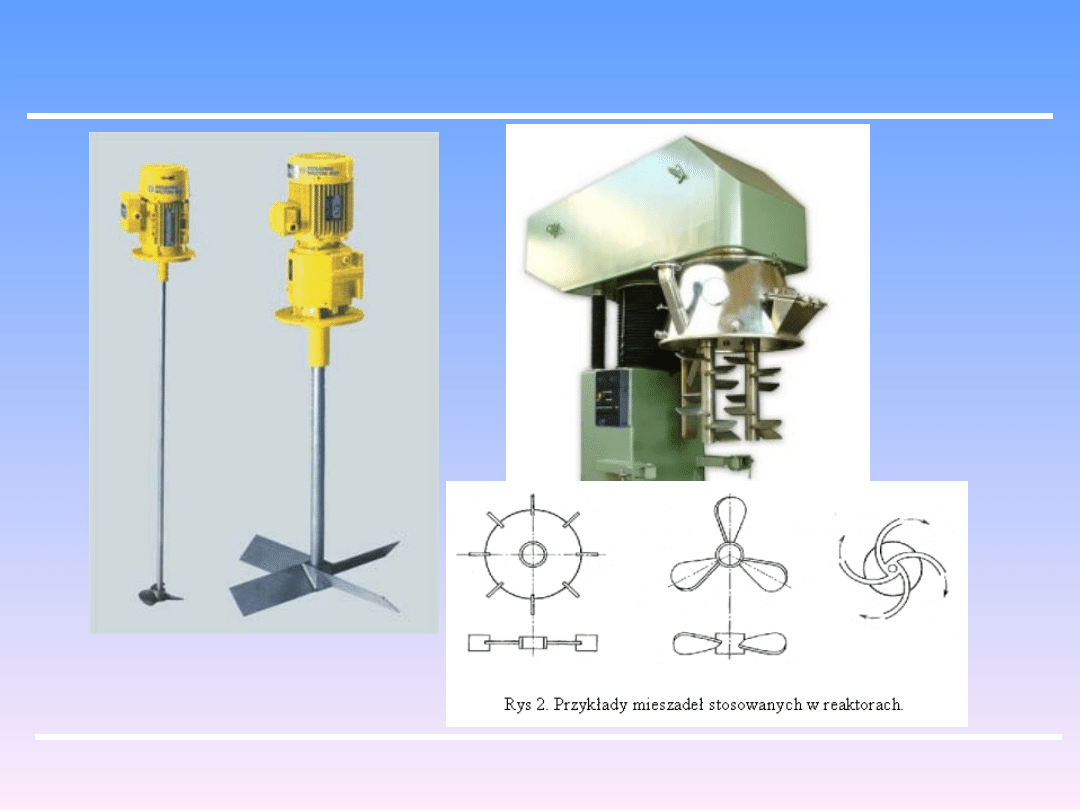
Proces ten przebiega najczęściej w aparatach zwanych mieszalnikami , wewnątrz
których umieszczone jest mieszadło.

Obroty mieszadła powodują powstanie zawirowań , co z kolei prowadzi do
przemieszczania się elementów płynu, a tym samym do mieszania się układu czyli
zwiększenia jego jednorodności.

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

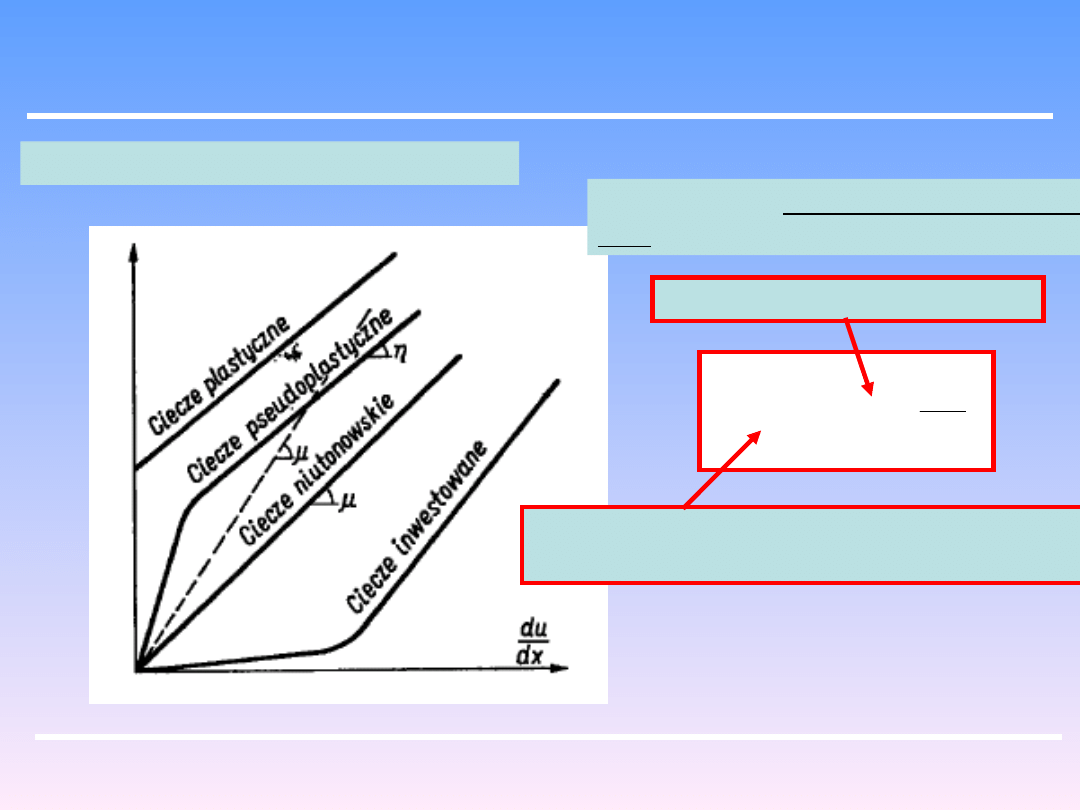
Ważna dla technik mieszania cieczy jest ich lepkość. Maleje ona ze wzrostem
temperatury, stąd wynika że w wyższych temperaturach mieszanie cieczy będzie
bardziej sprawne

Dla większości cieczy aktualne jest równanie lepkości (ciecze niutonowskie) (1)



















dx

du





naprężenie styczne

gradient prędkości u na kierunku x

lepkość dynamiczna

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

τ

Charakterystyki reologiczne cieczy:

2

3

1

W przypadku cieczy plastycznych
(2) aktualne jest równanie:





















dx

du







0

graniczne naprężenie styczne którego
przekroczenie jest warunkiem płynności

współczynnik plastyczności

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

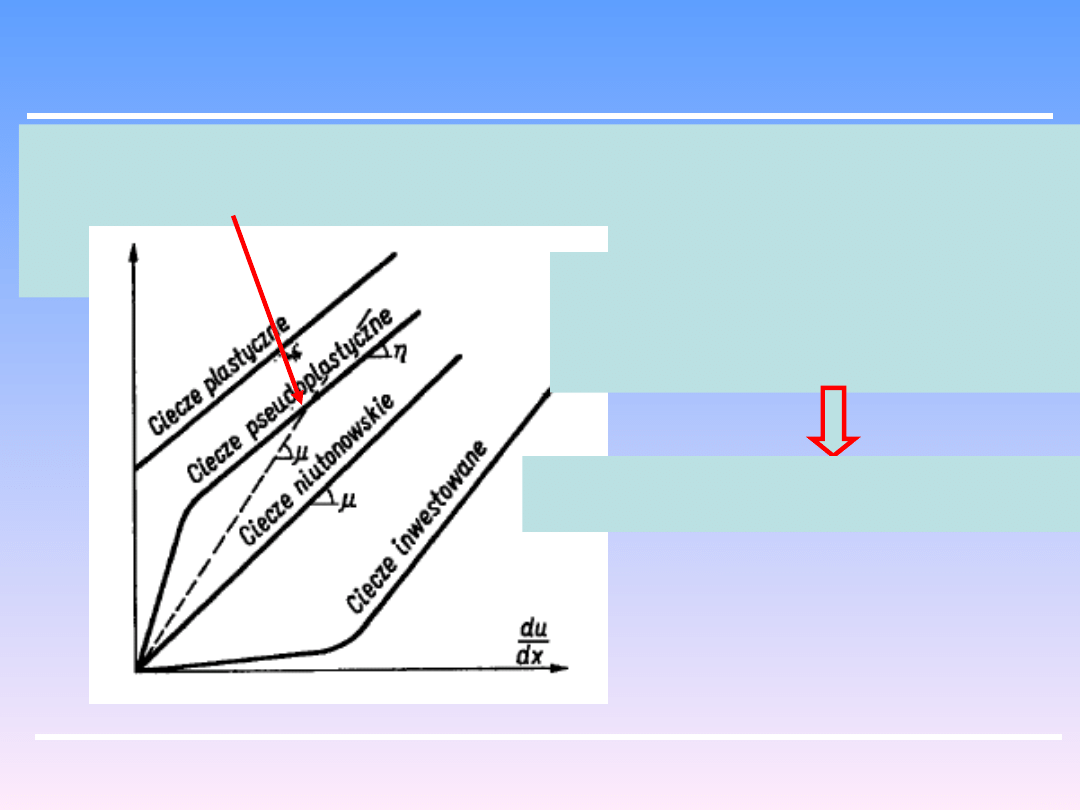
Stosownie do definicji lepkości – lepkość oznacza nachylenie odpowiedniego
promienia
z początku układu przechodzącego przez właściwy punkt na linii
charakterystycznej
dla danej cieczy:

τ

2

3

1

4

Jak wynika z przebiegu linii 2, lepkość
będzie wysoka przy wolnym mieszaniu
tej cieczy, a przy wyższych szybkościach
mieszania będzie maleć.

Należy wybrać pewne optimum szybkości
mieszania.

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

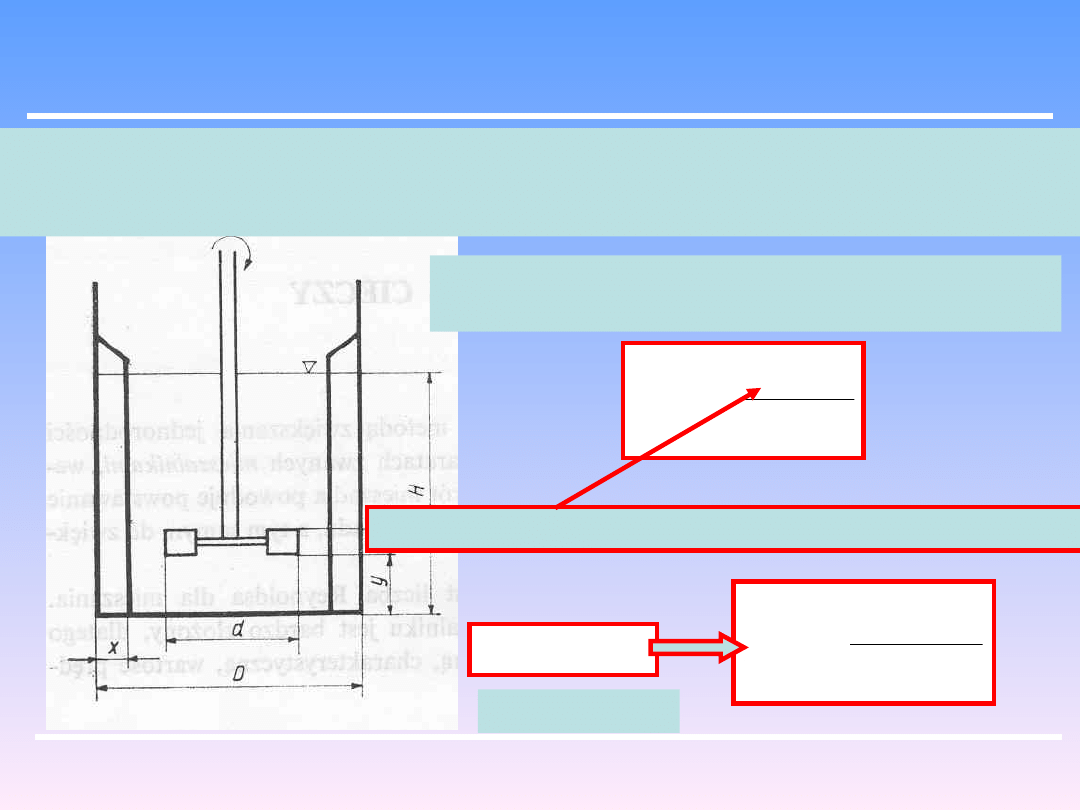
Ruch cieczy względem elementu ruchomego ( łapy wirnika ) może mieć charakter
laminarny, z łagodnym opływem względem tego elementu lub też z tworzeniem
się wirów za tym elementem  ruch burzliwy.

Miarą rodzaju ruchu jest liczba Reynoldsa dla
mieszania:











d

u

m

Re

prędkość obwodowa zewnętrznej krawędzi mieszadła

n

d

u



















2

Re

d

n

m

(pomijamy π)

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Tak zdefiniowana liczba Reynoldsa nie ma ogólnego charakteru, ponieważ jest
funkcja rodzaju stosowanego mieszadła oraz mieszalnika. Z tej przyczyny nie istnieje
jedna wartość rozgraniczająca obszar laminarny i turbulentny. Możemy przyjąć
że dla Re

m

< 50 mamy ruch laminarny.

Jednym z podstawowych zagadnień w procesie mieszania jest obliczanie mocy
niezbędnej do zapewnienia założonych warunków hydrodynamicznych.

moc
mieszania

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

h

dx

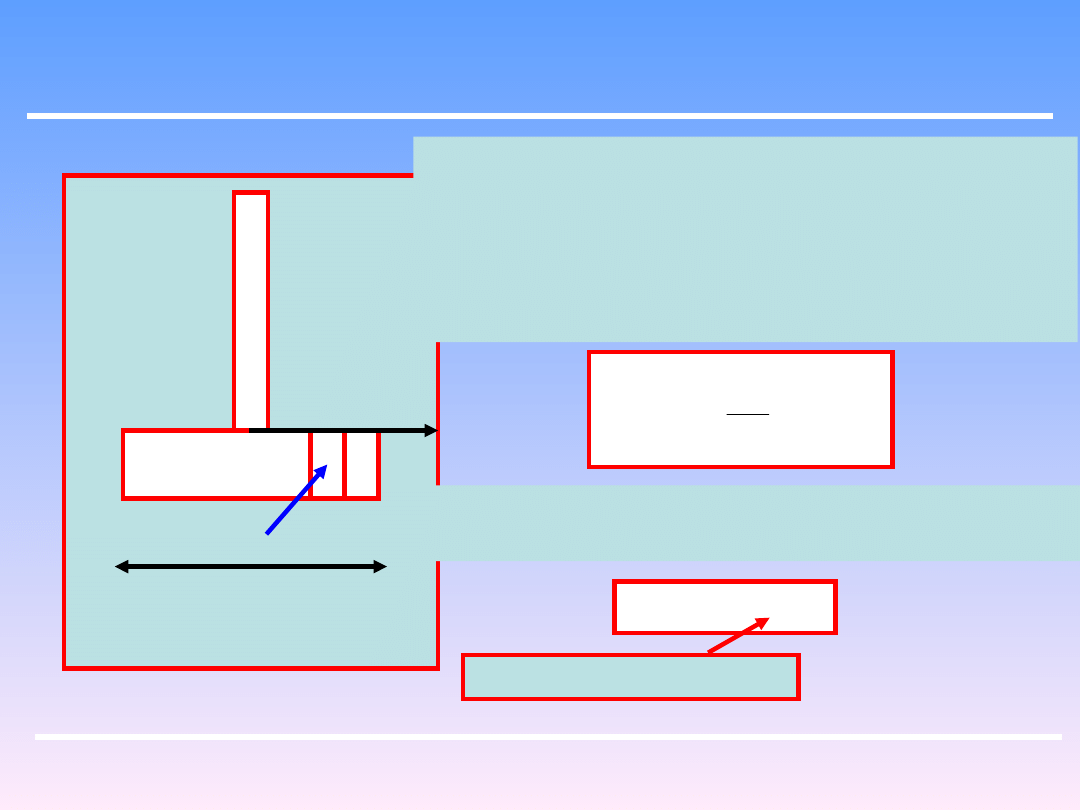
Weźmy pod uwagę zwykłe mieszadło łopatowe.
Element mieszający ma kształt płaskownika o
długości L i wysokości h. Dla różniczkowego
elementu tej łapy o długości dx i wysokości h
siła oporu stwarzanego przez płyn może być
opisana równaniem:

dF

u

dR













2

2

Powierzchnia elementu dF wyraża się iloczynem
h*dx. A prędkość obwodowa :

n

x

u











2

odległość od osi obrotu

x

dR

d

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Zużycie mocy możemy określić jako iloczyn siły dR i drogi wykonanej przez element
w jednostce czasu, czyli prędkości obwodowej u :

dR

u

dN









dx

h

n

x

n

x

dN

































2

2

2

2





2

2

3

3

3

dx

x

h

n

dN























Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Zależność tę można scałkować w granicach x od –d/2 do d/2. Układ jest symetryczny
więc można całkować w granicach od 0 do d/2 i wynik pomnożyć przez 2:

Wprowadzając stosunek h/d jako a  współczynnik charakteryzujący kształt łopaty





dx

x

d

a

n

N

d



















2

/

0

3

3

3

2







5

3

d

n

C

N



























C

n

d

N

3

5

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania













C

n

d

N

3

5

bezwymiarowa liczba mocy – liczba Newtona, Eulera

współczynnik oporów

stała

Współczynnik oporów λ jest funkcją liczby Reynoldsa i może być przedstawiony
równaniem :

m

b

Re





Wartości b i m zależą od typu mieszadła. Dla przepływu laminarnego m = 1, natomiast
przy silnej burzliwości m  0 , a więc λ dąży do wartości stałej.

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

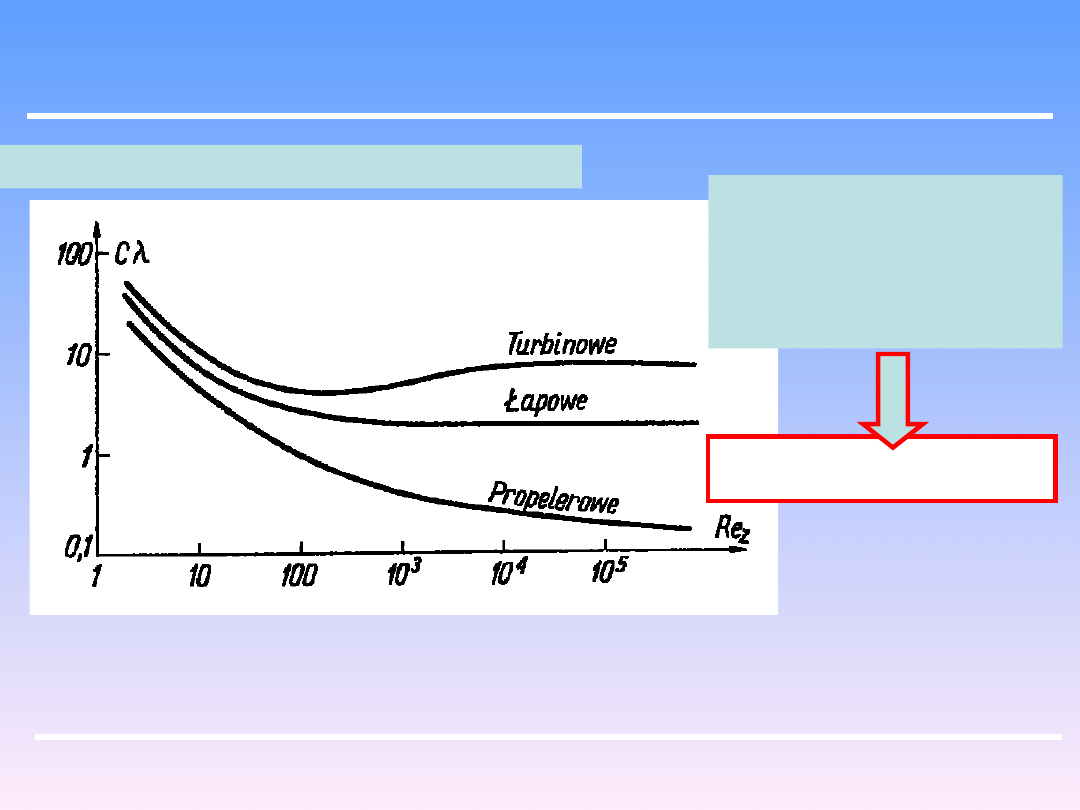
Dogodnie jest posługiwać się wykresami :

Dla każdego typu
mieszadła o określonych
wymiarach linia krzywa
dotyczy „liczby mocy”
jako funkcji liczby Re.



















3

5

n

d

C

N

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

m

b

Re





Jeżeli dla ruchu laminarnego uwzględnimy wartość m = 1 to wyrażenie na
współczynnik oporów przyjmie postać:

Re

b



















2

d

n

b

podstawiając do równania
na liczbę Newtona













C

n

d

N

3

5















3

5

n

d

C

N























3

5

2

n

d

d

n

b

C

N











2

3

n

d

K

N

moc mieszania laminarnego

wartość stała dla mieszadła

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Dla ruchu burzliwego λ = const











3

5

n

d

K

N

moc mieszania burzliwego











2

3

n

d

K

N











3

5

n

d

K

N

moc mieszania burzliwego

moc mieszania laminarnego

 wpływ lepkości cieczy

 wpływ gęstości cieczy

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

modelowanie mocy mieszania:

Dla dwóch mieszalników o podobnych parametrach geometrycznych, w których jest
mieszana ta sama ciecz, stosunek mocy mieszania jest następujący:

2

2

1

3

2

1

2

1





























n

n

d

d

N

N

dla obszaru laminarnego:

dla obszaru turbulentnego:

3

2

1

5

2

1

2

1





























n

n

d

d

N

N

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Przyjmuje się, że podobne warunki mieszania w obu mieszalnikach będą zachowane,
jeżeli moc właściwa, tj. moc przypadająca na jednostkę objętości mieszanego układu,
będzie w obu mieszalnikach taka sama.

Dla mieszalników w kształcie walca objętość wynosi:

3

2

2

d

d

H

d

D

d

d

H

d

d

D

V



































 









średnica zbiornika

wysokość poziomu cieczy średnica mieszadła

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Podobieństwo geometryczne zbiorników sprowadza się do ustalonych wartości
stosunków D/d i H/d :

3

2

1

2

1















d

d

V

V

Stosunek mocy właściwych:dla obszaru laminarnego:

2

2

1

3

1

2

2

1

2

2

1

1































n

n

d

d

N

N

V

N

V

N

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

dla obszaru turbulentnego:

3

2

1

2

2

1

3

1

2

2

1

2

2

1

1













































n

n

d

d

d

d

N

N

V

N

V

N

Stosunek mocy właściwych:

Przyrównując powyższe równania do jedności otrzymujemy:

dla obszaru laminarnego:

dla obszaru turbulentnego:

2

1

n

n 

3

2

1

2

2

1

















d

d

n

n

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Jeżeli zachowamy stałość liczby Re dla dwóch mieszalników geometrycznie podobnych:

2

1

Re

Re 

2

2

2

2

1

1

d

n

d

n







więc stosunek mocy: dla obszaru laminarnego:

1

2

1

2

1

2

2

2

1

2

1

Re

Re

D

D

d

d

d

d

N

N





















dla obszaru turbulentnego:

1

2

1

2

1

2

3

2

1

2

1

Re

Re

D

D

d

d

d

d

N

N





















Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Jeżeli zachowamy stałość prędkości obwodowej mieszadła dla dwóch mieszalników
geometrycznie podobnych:

2

1

u

u 

2

2

1

1

d

n

d

n







więc stosunek mocy: dla obszaru laminarnego:

2

1

2

1

2

1

2

2

2

1

1

2

1

D

D

d

d

d

d

n

d

n

d

N

N

























dla obszaru turbulentnego:

2

2

1

2

2

1

3

2

2

1

1

2

1















































D

D

d

d

d

n

d

n

N

N

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

d

1

D

1

H

1

n

1

Re

1

N

1

ta sama moc właściwa

układ przemysłowy

D/d i H/d zachowane
D

2

=10 * D

1

dla obszaru laminarnego:

1

2

n

n 

3

2

1

2

1

2















d

d

n

n

dla obszaru turbulentnego:

D/d = 3

10

1

3

10

3

3

3

1

1

2

1

2



















D

D

D

D

d

d

6

.

4

10

1

3

2

1

2

n

n

n





Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

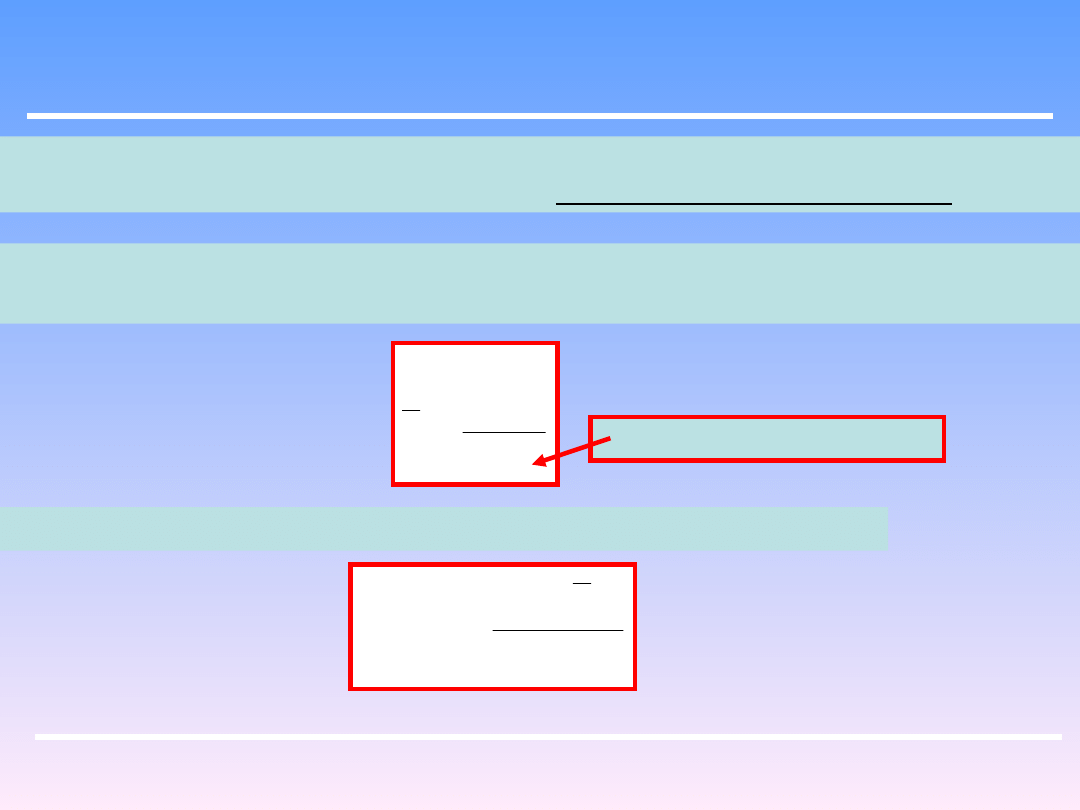
W przypadku mieszania układu niejednorodnego tj.: emulsja zawiesina, mieszanina
ciał sypkich bez cieczy itp. można określić efektywność wymieszania.

Pobiera się szereg próbek z różnych miejsc wymieszanego ośrodka i oznacza się w nich
skład x

i

(np. zawartość fazy stałej w zawiesinie). „Średnia z próbek” jest równa:

n

x

x

i

i





liczba pobranych próbek

Średnie zaś „odchylenie standardowe” określone jest następująco:















n

i

i

n

x

x

1

2

2

1



Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

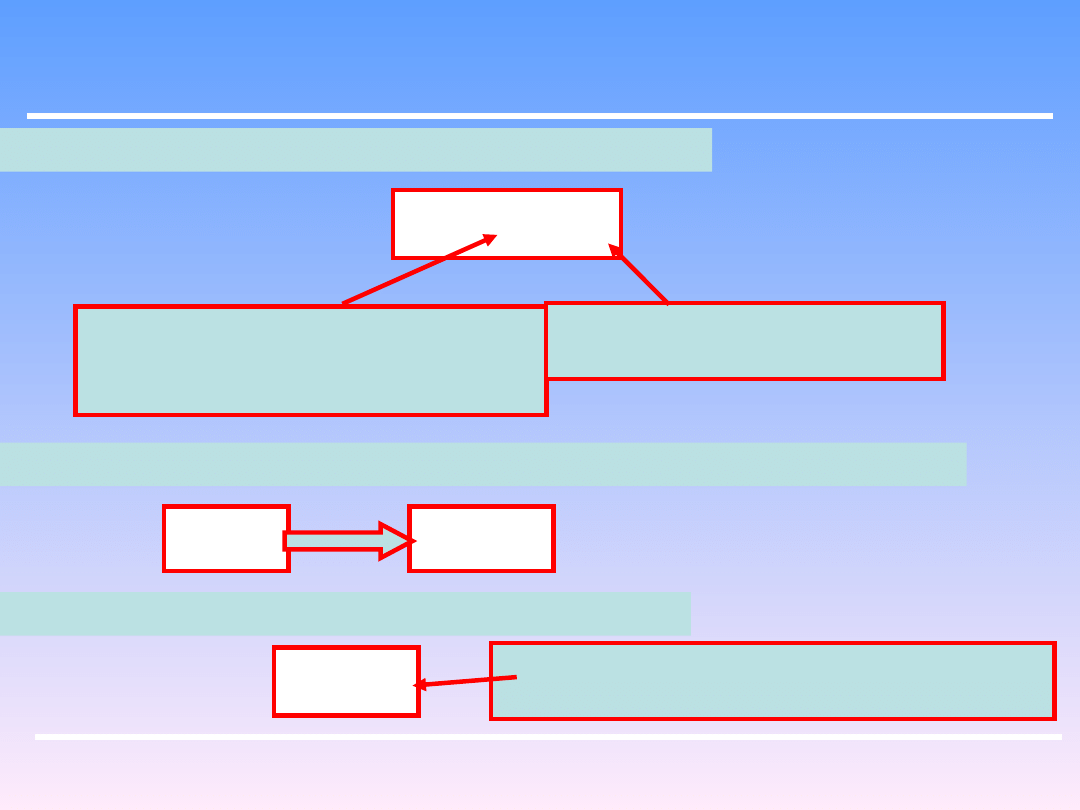
To średnie odchylenie σ

2

jest sumą dwóch udziałów:

2

2

2

m

r











odchylenie spowodowane małym
wymiarem próbki pobieranej do
analiz.

odchylenie spowodowane
niedoskonałością mieszania

W przypadku gdy mieszanie jest bardzo dobre (np.. trwa bardzo długo) :

0



m



2

2

r







W przypadku gdy mieszanie jeszcze nie nastąpiło :

2

0

2







odchylenie spowodowane początkowym
ułożeniem składników

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

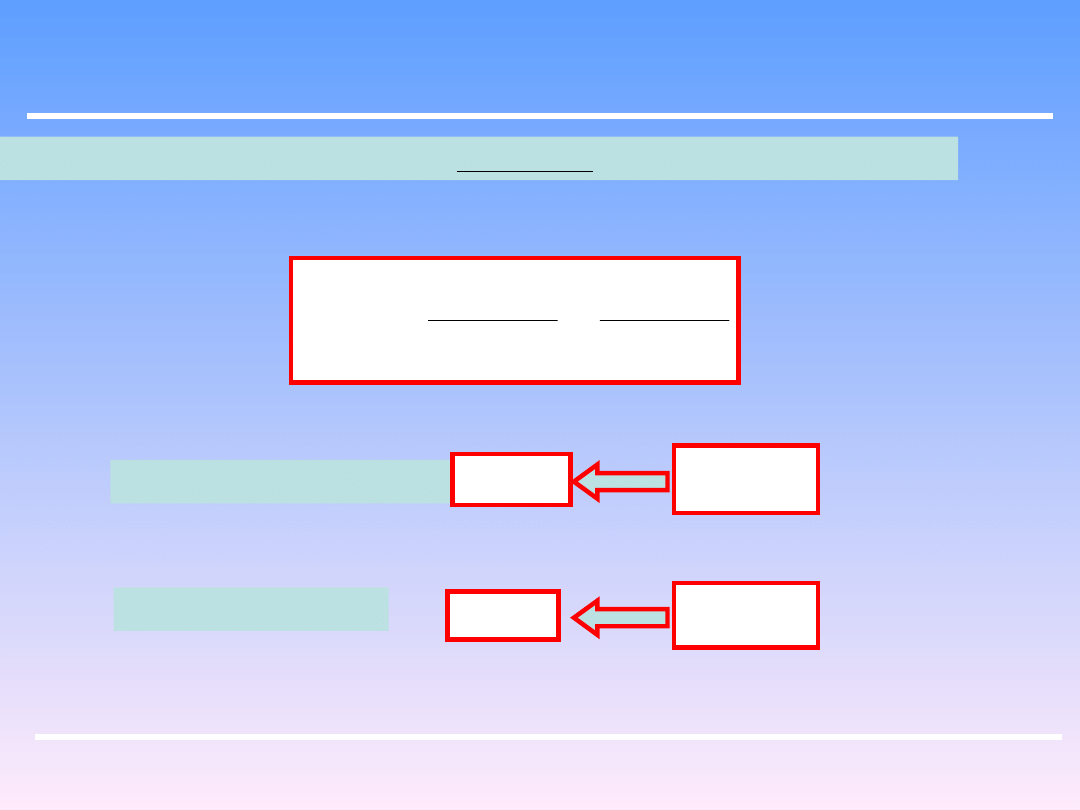
Miarą stopnia mieszania może być indeks M definiowany następująco:

2

2

0

2

2

0

2

2

0

2

2

1

r

r

r

M































Gdy nie ma mieszania :

0



M

2

0

2







Idealne mieszanie:

1



M

2

2

r







Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

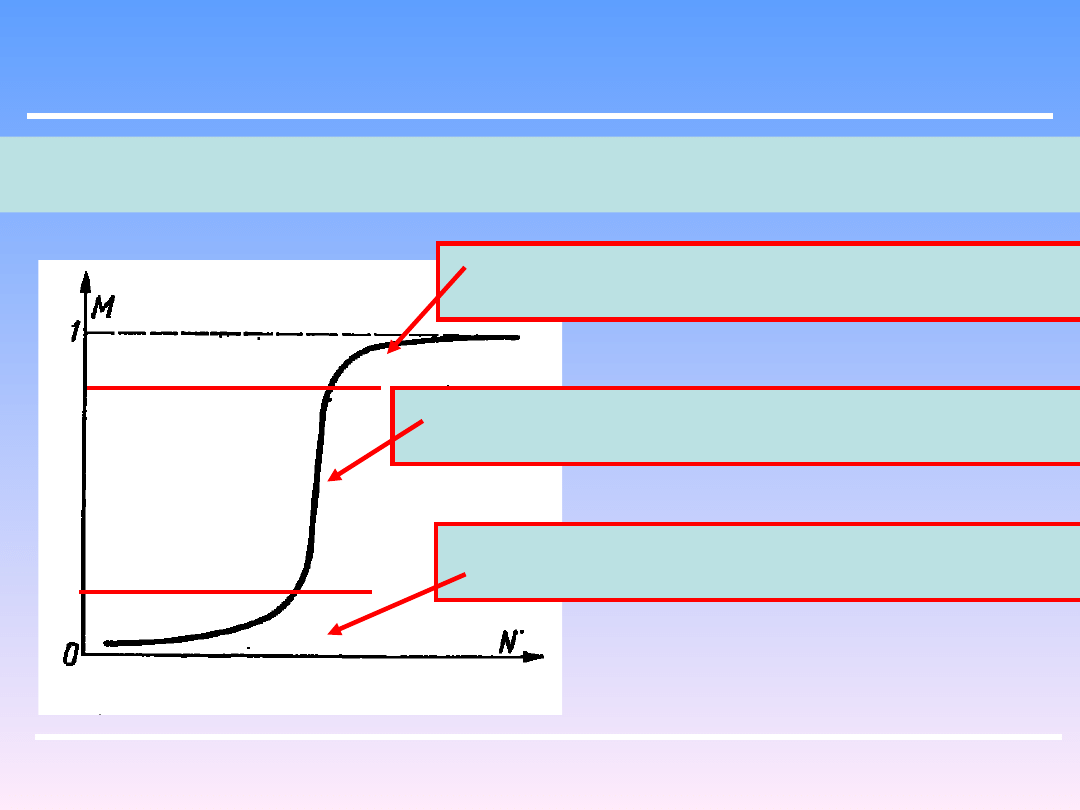
W miarę postępu procesu mieszania, wraz z upływem czasu t, indeks mieszania
zmienia się od 0 do 1 w sposób wykładniczy:

t

k

e

M







1

Tak więc wartość indeksu M jest miarą wymieszania układu.

W procesach rzeczywistych w których występują wyraźne różnice gęstości między
mieszanymi fazami, na skutek sedymentacji grawitacyjnej następować będzie
segregacja układu, w wyniku której nastąpi odchylenie od powyższego równania,
a mianowicie indeks M nie będzie dążył do 1 lecz do wartości niższej wynikającej
z równowagi pomiędzy mieszaniem a segregacją.

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Istnieje zależność między indeksem M a zużyciem mocy przez mieszadło. Zależność
ta przybiera kształt:

A) Indeks jest mały (słabe wymieszanie) przy zbyt
małym zużyciu mocy.

B) Szybki wzrost indeksu M, przy małym wzroście
mocy

C) Bardzo mały wzrost indeksu M przy wzroście
mocy .

A

B

C

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

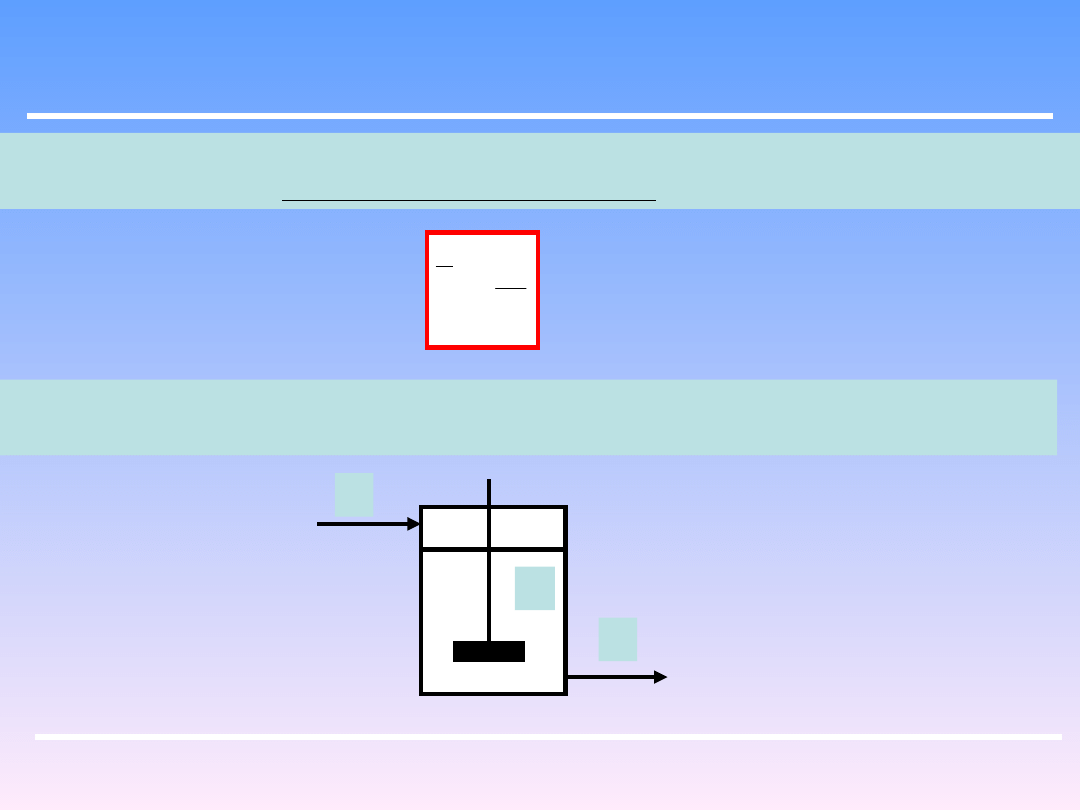
Jeżeli przez zbiornik z mieszadłem o objętości V przepływa strumień z prędkością
objętościową q , wówczas średni czas przebywania można zdefiniować następująco:

q

V





q

q

V

Zależnie od warunków mieszania płynu w zbiorniku różne elementy strumienia
mogą przebywać w tym zbiorniku krócej lub dłużej od τ.

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Wprowadźmy nową zmienną tzw. czas względny:









W wielu problemach procesowych interesuje nas rozkład czasu przebywania
w zbiorniku.

Można zdefiniować funkcję tzw. „funkcję wewnętrzną” – I tak aby jej iloczyn IdΘ
odpowiadał ułamkowi płynu zawartemu w zbiorniku który przebywał w nim
przez czas od Θ do Θ+d Θ.









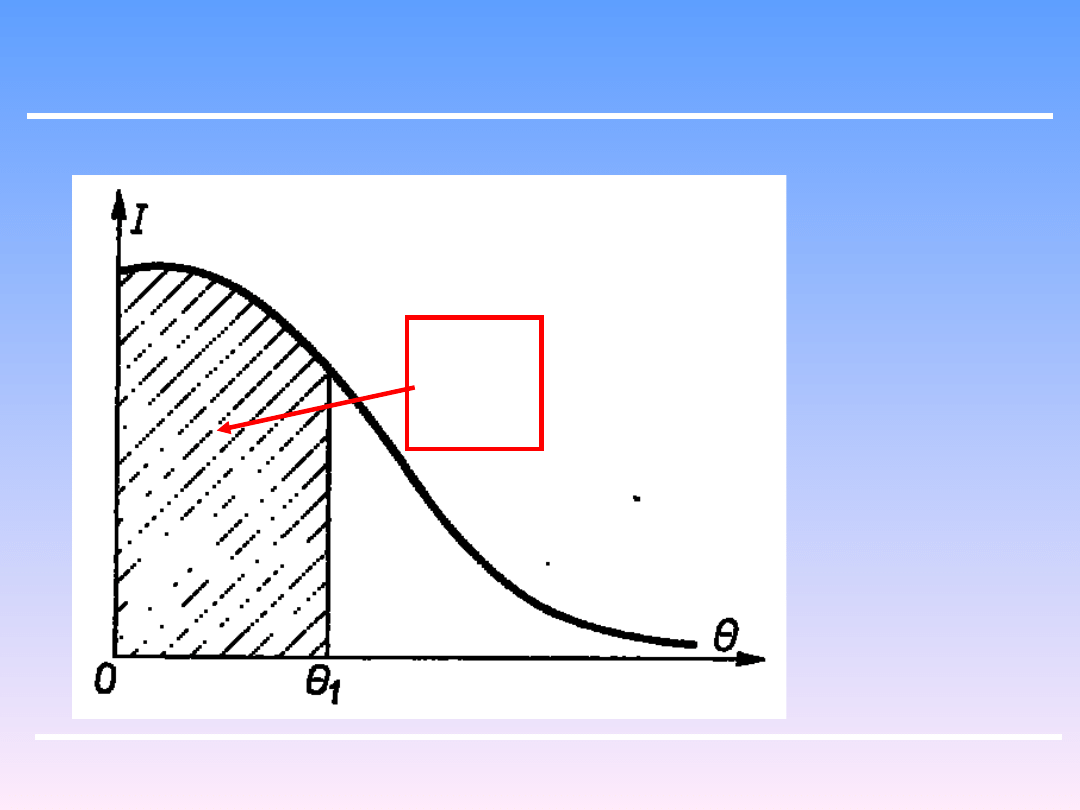
0

d

I

całka ta podaje więc ułamek płynu zawartego w zbiorniku
w danej chwili, który przebywał w nim przez czas od 0 do Θ

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania









1

0

d

I

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

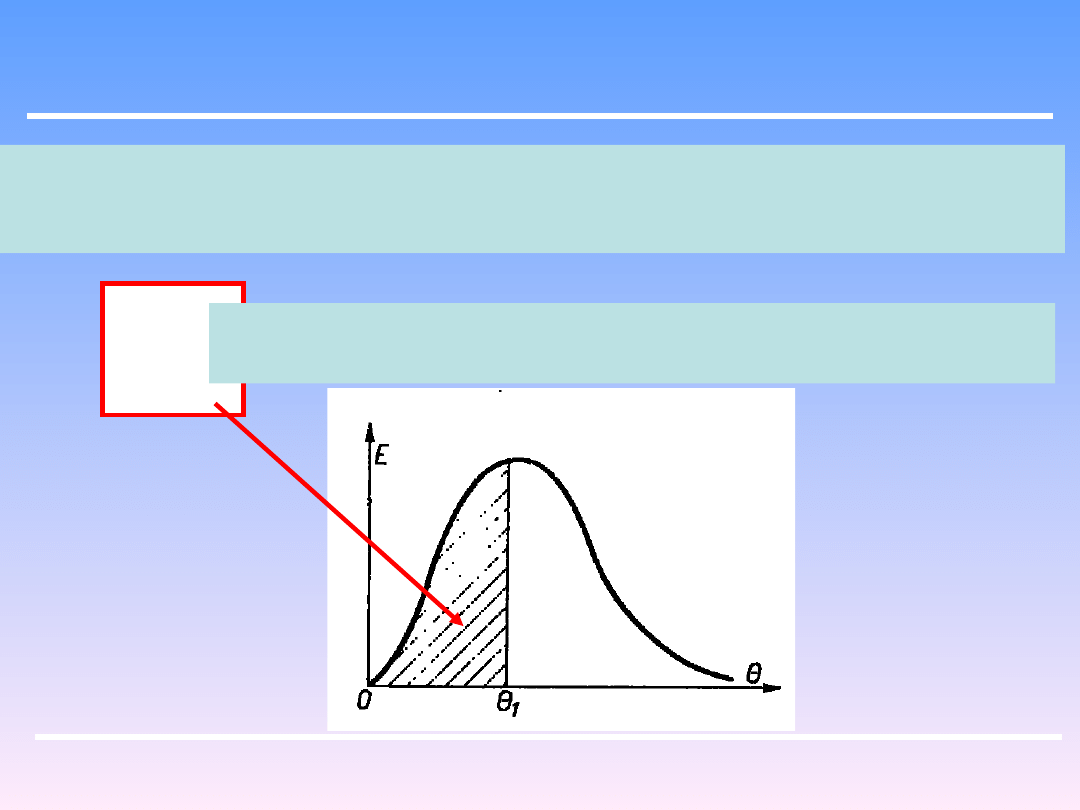
Analogicznie można zdefiniować funkcję „zewnętrzną” – E , tak że iloczyn EdΘ
podaje ułamek płynu w strumieniu wylotowym ze zbiornika, który przebywał
poprzednio w tym zbiorniku przez czas od Θ do Θ+dΘ. Stąd









1

0

d

E

całka ta podaje więc ułamek płynu w strumieniu wylotowym
w danej chwili, który przebywał w nim przez czas od 0 do Θ

1

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Pełne pole pod każdą z tych krzywych I i E w zakresie Θ od 0 do nieskończoności
jest równe 1.

1

0











d

I

1

0











d

E

Związek pomiędzy funkcjami I i E wynika z bilansu masowego:











d

E

I

1

E

d

dI







Funkcje te wykorzystywane są do modelowania funkcji rozkładu czasu przebywania

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

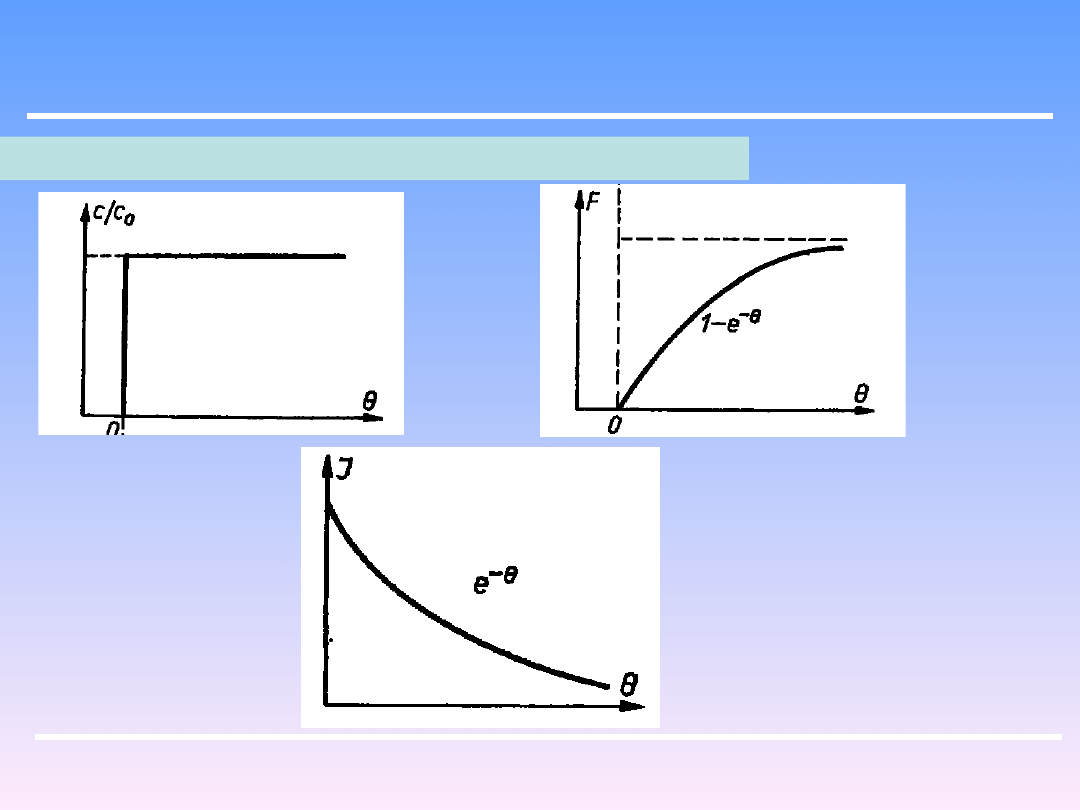
Funkcje rozkładu czasu przebywania można określić na podstawie badań dynamiki
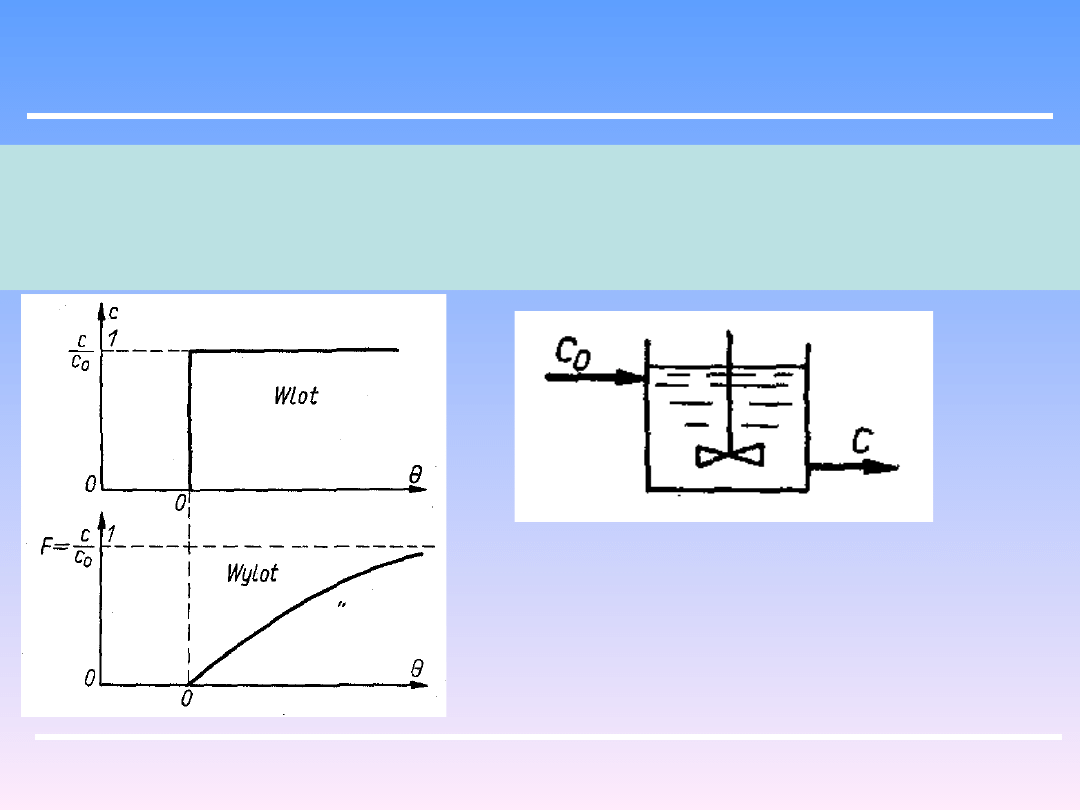
procesu. Badania te polegają na zastosowaniu impulsu skokowego w strumieniu
wlotowym (np.. dodatek indykatora o stężeniu C

0

). Na wylocie ze zbiornika stężenie

tego indykatora c będzie wzrastać nie skokowo ale tak jak na rys:

q

q

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Różniczkowy bilans masy dla układu wygląda następująco:





















d

I

c

V

d

q

c

d

q

c

0

0





dopływ indykatora odpływ indykatora

ogólna ilość w zbiorniku

ułamek porcji doprowadzonej
w czasie dτ

Uwzględniając definicję









q

V





0

c

c

F 





0

0

c

d

V

c

c

d

q

I





















0

0

c

c

c

I





F

I



1

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

A więc mierząc krzywe dynamiczne F łatwo określimy funkcje rozkładu czasu.

F

I



1

Dla kilku przypadków granicznych można określić charakterystyki dynamiczne bez
doświadczeń.

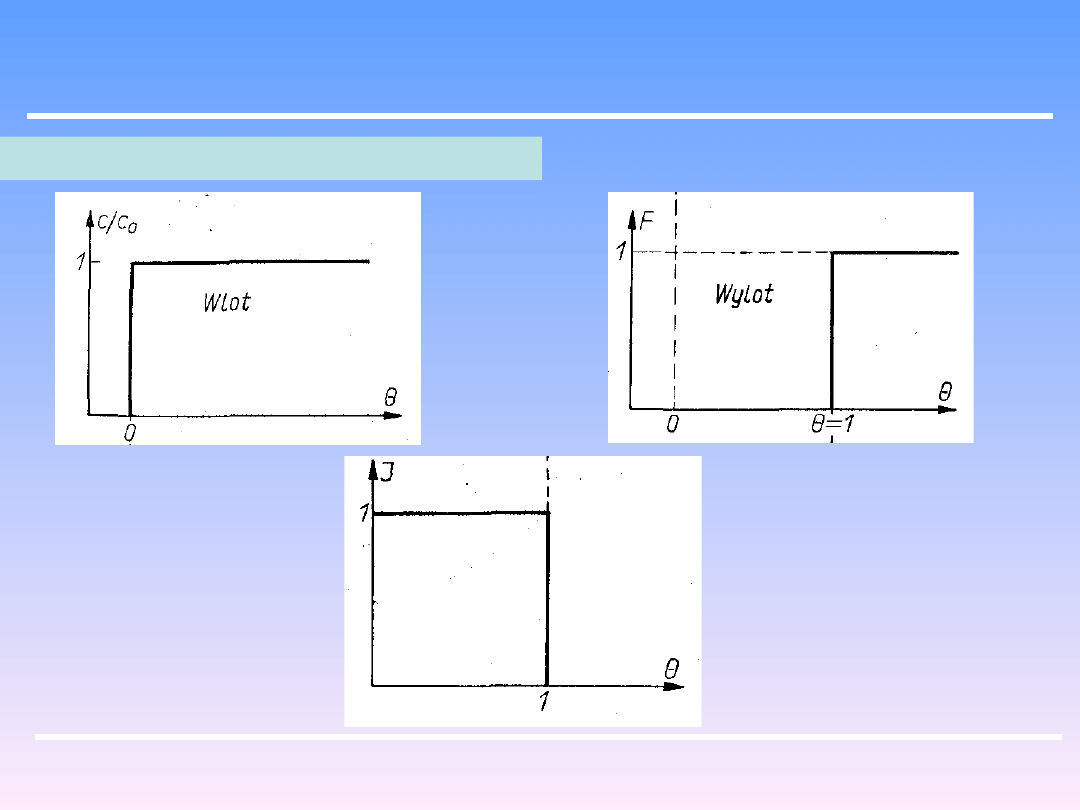
Przepływ tłokowy  w skutek braku mieszania impuls zadany na wlocie ukaże się

w niezmienionej postaci na wylocie po czasie względnym Θ = 1, czyli odpowiadającym
średniemu czasowi przebywania w układzie.

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Charakterystyka przepływu tłokowego:

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Drugim skrajnym przypadkiem jest zbiornik z idealnym wymieszaniem gdzie stężenie
jest jednakowe w każdym miejscu i stąd stężenie w strumieniu wylotowym jest takie
samo jak w zbiorniku.

równanie bilansowe różniczkowe:

dc

V

d

q

c

d

q

c



















0

wzrost stężenia indykatora w zbiorniku
w czasie dτ

Uwzględniając definicję









q

V





0

c

c

F 

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

otrzymujemy:









Fd

dF

d

Stąd po scałkowaniu i przekształceniu wynika charakterystyka dynamiczna :







 e

F 1

A stąd funkcja rozkładu czasu





e

I

Inżynieria Chemiczna i Procesowa

Wykład nr 8 : Procesy mechaniczne. Proces mieszania

Charakterystyka przepływu z idealnym wymieszaniem:

wlot

wylot