AE

AE

W + ĆW

W + ĆW

Zmienna wartość pieniądza w

Zmienna wartość pieniądza w

czasie

czasie

– metody dyskontowe

– metody dyskontowe

Bieżąca i przyszła wartość

Bieżąca i przyszła wartość

pieniądza

pieniądza

Wolisz otrzymać 100 złotych

dzisiaj, czy za rok???

100 zł (2009) > 100 zł (2010) > 100 zł

(2011) .....

O ile mniej wart jest pieniądz za rok???

Ile chciałbym otrzymać za rok aby

dzisiaj dobrowolnie zrezygnować z

dysponowania kwotą 100 złotych?

100 zł +

x

x

zł

konsumuję

Za rok

100 zł

inwestuję

100 zł

konsumuj

ę

Dziś

Ile wart jest

Ile wart jest

„x” ???

„x” ???

Jednakowa wartość

oceniana subiektywnie

przez inwestora

Miarą oczekiwań, czyli tempa zmiany

Miarą oczekiwań, czyli tempa zmiany

wartości pieniądza w czasie jest:

wartości pieniądza w czasie jest:

•

stopa

procentowa

stopa

procentowa

(jeżeli

chcemy

obliczyć wartość przyszłą znanej wartości
dzisiejszej)

•

stopa dyskontowa

stopa dyskontowa

(jeżeli znamy kwotę

przyszłą a chcemy ustalić jej wartość na
dziś).

Możliwe sytuacje dotyczące zmian wartości pieniądza w czasie:

Możliwe sytuacje dotyczące zmian wartości pieniądza w czasie:

•wartość bieżąca (PV – present value) lub wartość

przyszła (FV – future value)

•wartość pojedynczej płatności lub wartość strumienia płatności

•wartość strumienia jednolitych płatności (annuitety) lub

wartość strumienia zmiennych płatności

•obliczenia mogą być dokonywane przy stałej lub

zmieniającej się z okresu na okres stopie procentowej

•płatność jest dokonywana na początku lub na końcu okresu

•rozliczanie (kapitalizacja) wartości może być

dokonywane raz lub więcej razy w okresie roku.

1.

1.

Kalkulacja pojedynczej wartości

Kalkulacja pojedynczej wartości

przyszłej

przyszłej

(np. wpłata pieniędzy do

banku na kilka lat – ustala się kwotę
po upływie okresu lokaty)

Przykład 1
Ustal ile otrzymasz za trzy lata,

wpłacając dzisiaj 1000 zł na lokatę
oprocentowaną na 10% w skali
rocznej.

Aby rozwiązać to zadanie należy skorzystać z

formuły:

FV = PV*(1+i)

FV = PV*(1+i)

t

t

gdzie:
PV (wartość bieżąca) wynosi 1000 zł
i (stopa procentowa) wynosi 10%
t (okres) wynosi 3 lata

FV = 1000 * (1+0,1)

FV = 1000 * (1+0,1)

3

3

= 1331

= 1331

zł

zł

2.

2.

Liczenie wartości przyszłej stałych kwotowo

Liczenie wartości przyszłej stałych kwotowo

okresowych wpłat na rachunek.

okresowych wpłat na rachunek.

Oczekiwana

kwota obejmować będzie zarówno sumę wpłat jak
i zakumulowaną sumę odsetek od tych wpłat,
przy czym każdorazowo odsetki liczone są od
powiększającej się kwoty.

Przykład 2

Przez najbliższe 4 lata zamierzasz na koniec każdego

roku odkładać po 2000 zł na lokatę
oprocentowaną na 8% w skali roku. Ustal jaka
kwota znajdzie się na rachunku po upływie tego
okresu.

Aby rozwiązać to zadanie należy skorzystać

z formuły:

gdzie:
A (stała płatnośc roczna) 2000 zł
i 8%
t 4 lata





i

i

A

FV

t

A

1

1

*











zł

FV

A

9012

08

,

0

1

08

,

0

1

*

2000

4









Dla lepszego zrozumienia schematu

liczenia

2000 * (1,08)

3

= 2519,4

+ 2000 * (1,08)

2

= 2332,8

+ 2000 * (1,08) = 2160
+ 2000 = 2000

9012,2

9012,2

3.

3.

Liczenie wartości raty annuitetowej

Liczenie wartości raty annuitetowej

przy

znanej

wartości

bieżącej

przy

znanej

wartości

bieżącej

kapitału

kapitału

(np.

zaciągamy

kredyt

hipoteczny i ustalamy jaka będziemy
płacić ratę obsługi kredytu przez kolejne
30 lat);

Przykład 3
Zaciągnąłeś kredyt w wysokości 200 000 zł

na okres 30 lat przy oprocentowaniu 12%
w skali roku. Jaka będzie wysokość stałej
miesięcznej raty kredytowej.

Aby rozwiązać to zadanie należy skorzystać

z formuły:

gdzie:
• PV

A

(bieżąca wartość kapitału, który ma zostać spłacony

ratami annuitetowymi) 200 000 zł

• i 12%
• t 30 lat
• m (liczba podokresów) wynosi 12 (tyle ile miesięcy w roku)









1

1

1

*

*









t

t

A

i

i

i

PV

A

zł

A

2057

1

12

12

,

0

1

12

12

,

0

1

*

12

12

,

0

*

200000

12

*

30

12

*

30















 











 



4.

4.

Liczenie

wartości

bieżącej

zmiennych

Liczenie

wartości

bieżącej

zmiennych

przepływów

pieniężnych,

których

przepływów

pieniężnych,

których

spodziewamy się w przyszłości

spodziewamy się w przyszłości

– sytuacja

występująca w przypadku inwestycji rzeczowych;

Przykład 4

W ciągu najbliższych trzech lata masz otrzymać na

konto trzy wpłaty (na koniec każdego roku).
Pierwsza z nich wynosi 10 000, zaś każda następna
ma być o 50% wyższa w stosunku do kwoty z roku
poprzedniego. Ustal jaka jest wartość dzisiejsza
tych kwot przy stopie dyskontowej 10%.

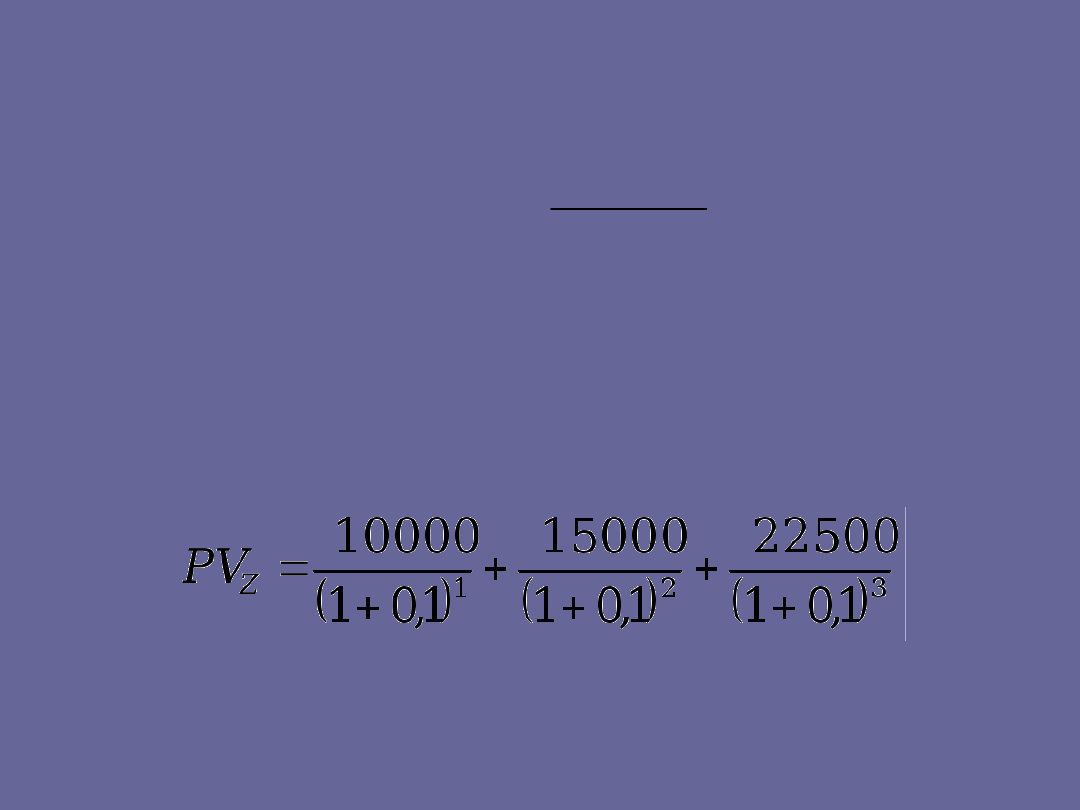
Aby rozwiązać to zadanie należy skorzystać

z formuły:

gdzie:
• Z

t

(kwota z okresu t) w naszym przypadku odpowiednio:

10 000 zł, 15 000 zł i 22 500 zł.

• i 10%
• t = 1,2,3





t

t

n

t

Z

i

Z

PV









1

0

Oznacza to, iż bieżąca wartość płatności to suma

9 091 zł + 12 397 zł + 16 905 zł = 38 393 zł.

9 091 zł + 12 397 zł + 16 905 zł = 38 393 zł.

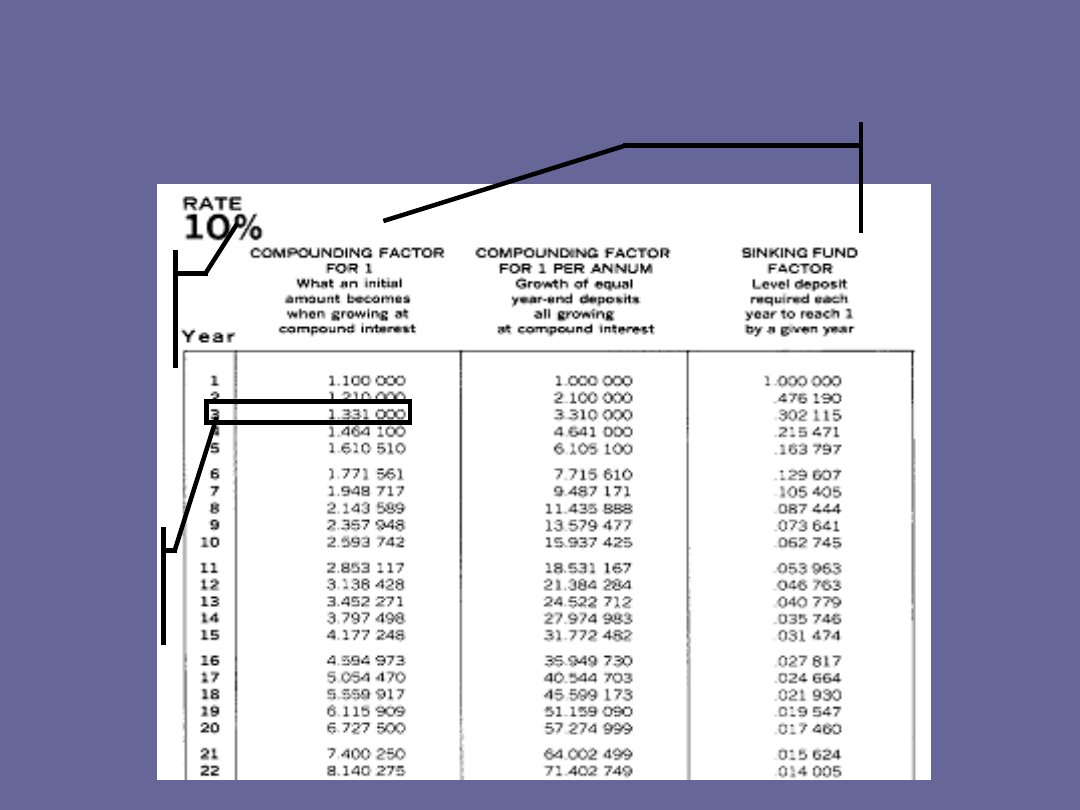
Tablice Banku Światowego

Tablice Banku Światowego

Krok 1 –
wybór stopy
procentowej

Krok 3 –
wybór
liczby lat

Krok 2 – wybór

odpowiedniej

formuły

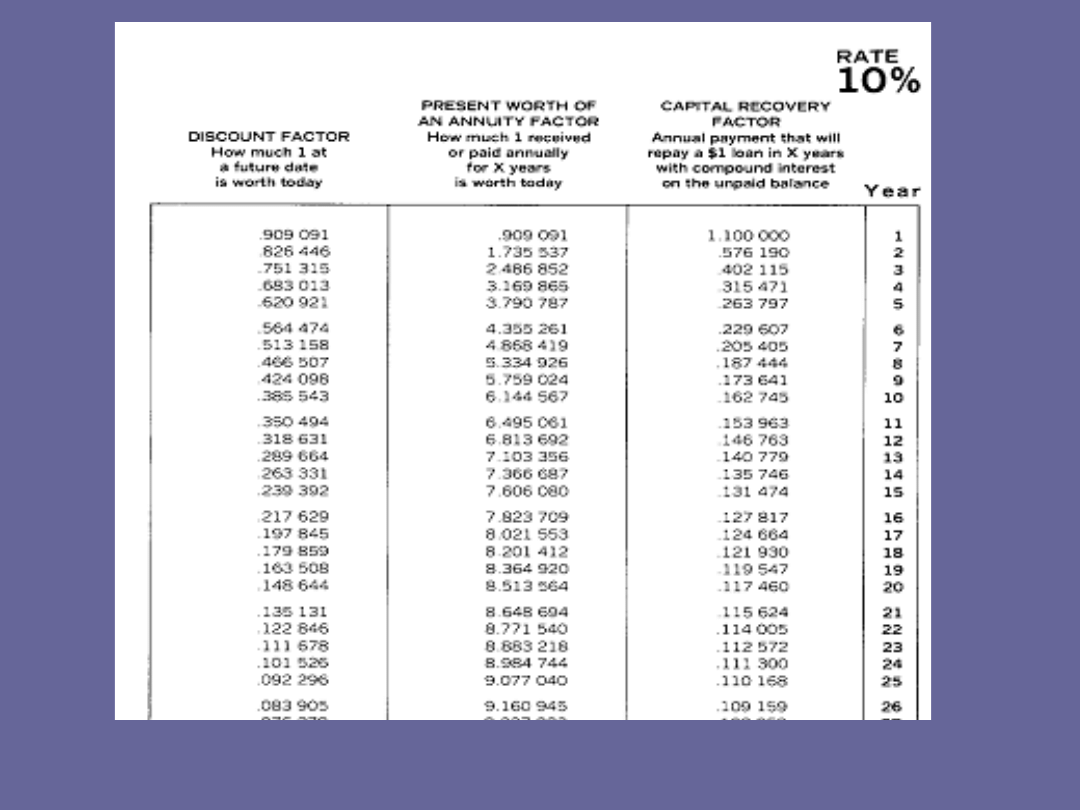
Źródło: J.P. Gittinger, Compounding and Discounting Tables for Project Analysis with a Guide to
Their Applications, EDI World Bank, Washington 1984.