Pochodna funkcji jednej
zmiennej

Iloraz różnicowy

Dana jest funkcja y=f(x) określona w pewnym przedziale

(a,b). Symbol x oznacza przyrost zmiennej niezależnej

x. Symbolem y (lub f) oznaczymy przyrost funkcji

odpowiadający przyrostowi x:

)

(

)

(

0

0

x

f

x

x

f

y











Def. Iloraz różnicowy funkcji f(x) w punkcie x

0

dla

przyrostu zmiennej niezależnej jest to stosunek:

x

x

f

x

x

f

x

y















)

(

)

(

0

0

3

x

x

f

x

x

f

x

y

x

y

x

x



























)

(

)

(

)

(

0

0

0

0

0

lim

lim

Definicja pochodnej

Pochodną funkcji y(x) w punkcie x

o

nazywamy

granicę
„ilorazu różnicowego”:

4

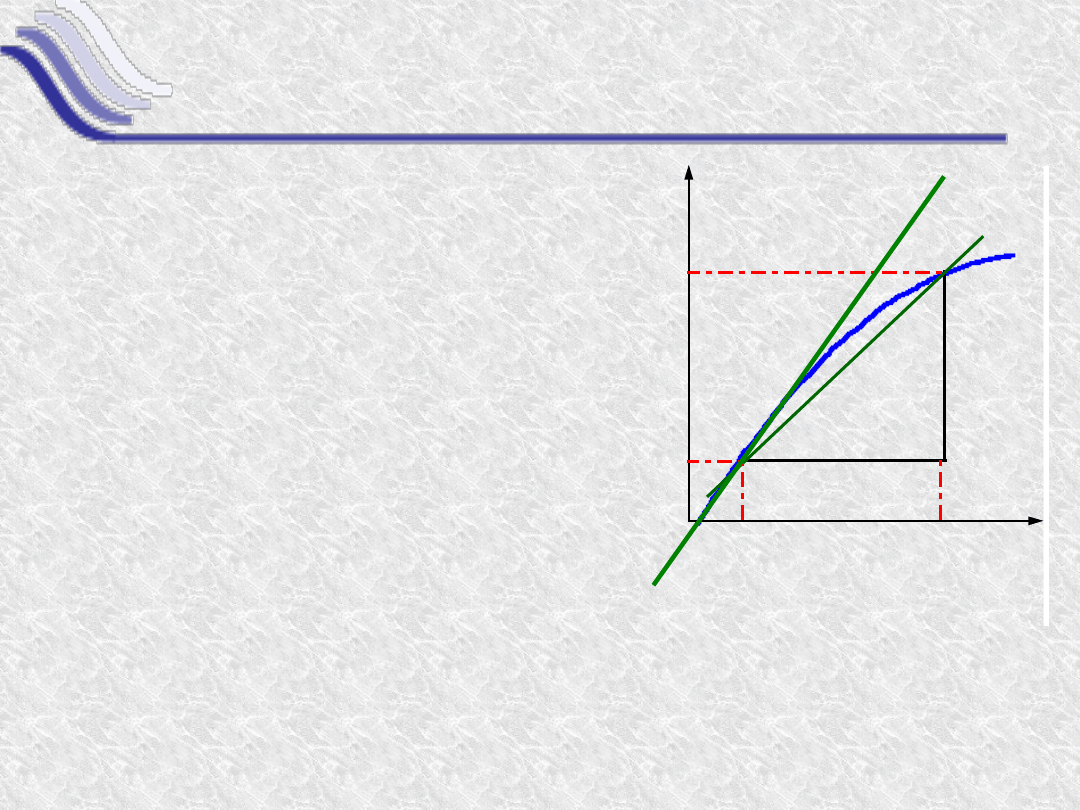
Interpretacja geometryczna

x





y

y

x

x

x+

x

y(x)

y(x+x)

Pochodna równa jest tangensowi kąta nachylenia
stycznej do osi OX.

Wartość ilorazu różnicowego
y/x jest tangensem kąta,

określającego

nachylenie

siecznej

, czyli linii, która

przecina krzywą w punktach
(x, y(x)) i (x+x, y(x+x)).

Kiedy x0, sieczna dąży

do stycznej do krzywej
w punkcie (x,y(x)).

Obliczanie pochodnych

2

1

( )'( )

'( ), (

)'( )

'( )

'( )

(

)'( )

'( ) ( )

( ) '( )

'( ) ( )

( ) '( )

( / )'( )

( ( ))

(

)'( )

'( ( )) '( )

1

(

)'( )

'( )

cf

x

cf x

f g x

f x

g x

f g x

f x g x

f x g x

f x g x

f x g x

f g x

g x

f g x

f g x g x

f

y

f x

-

=

+

=

+

=

+

-

=

=

=

g

o

)

(

g

f 

Wybrane wzory

7

0

0,5

1

1,5

2

0

0,5

1

1,5

2

x

0

x

1

x

2

x

3

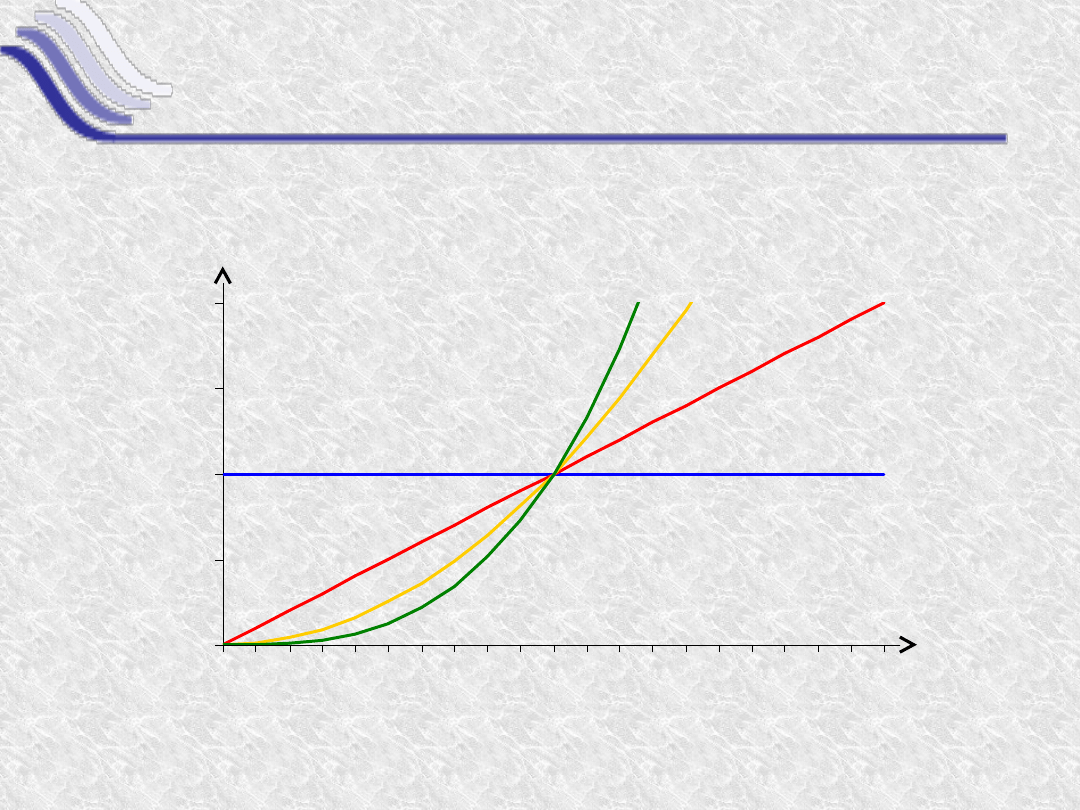
Funkcje potęgowe

Funkcje potęgowe mają postać y(x) = x

n

.

8

Pochodne funkcji potęgowych

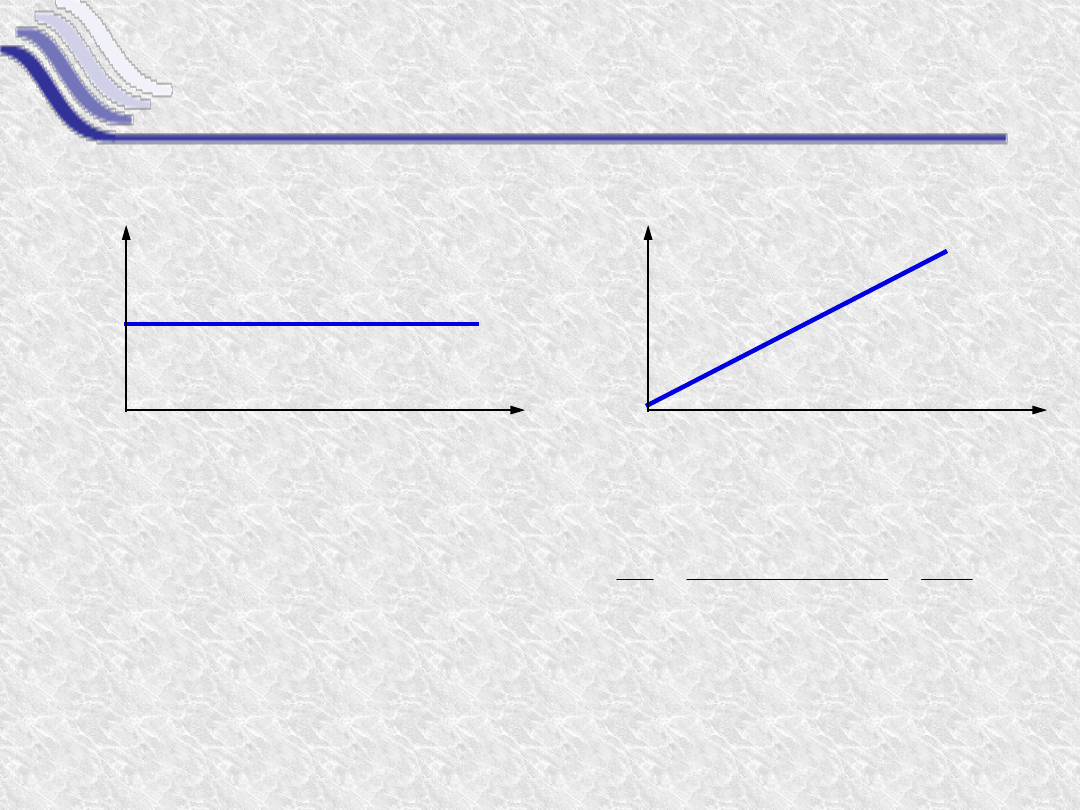
Funkcja stała y(x) = c

Licznik ilorazu
różnicowego jest równy:

y = y(x+ x) - y(x) = c-c

= 0

Pochodna funkcji stałej
jest równa zero.

y

x

Funkcja liniowa
y(x)=a·x

y

x

Iloraz różnicowy wynosi:

a

x

x

a

x

x

y

x

x

y

x

y























)

(

)

(

Pochodna funkcji liniowej
jest stała i wynosi a.

9

Iloraz różnicowy wynosi:

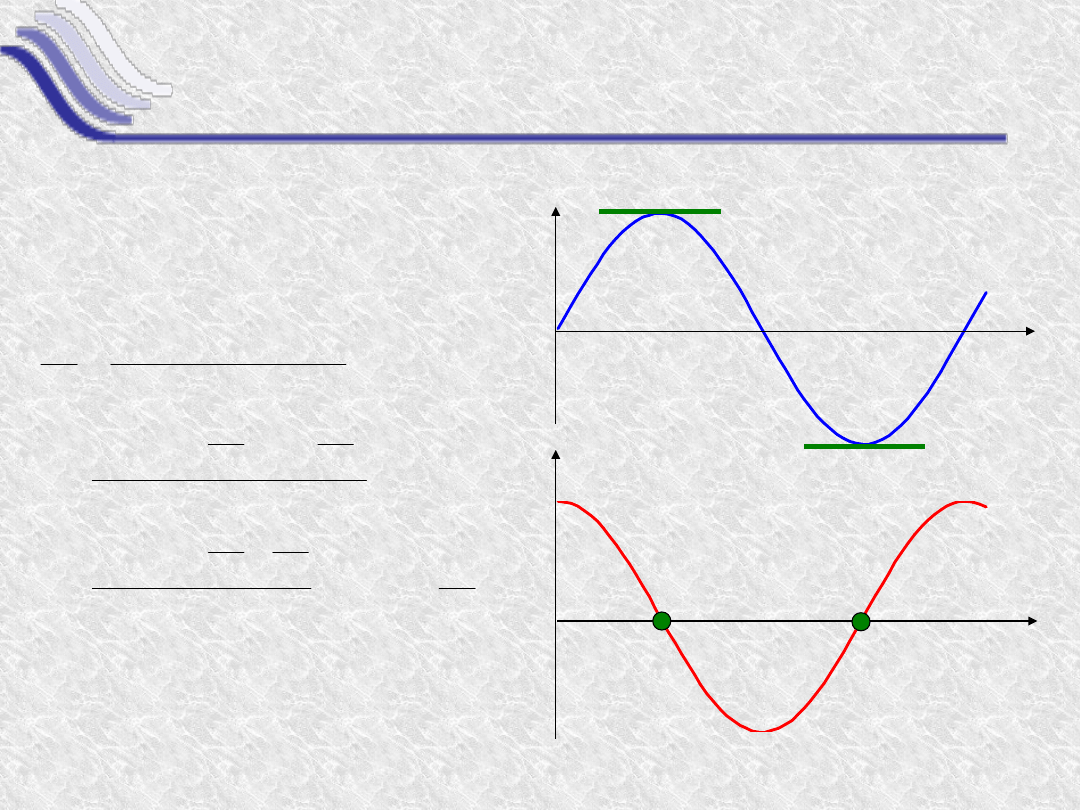
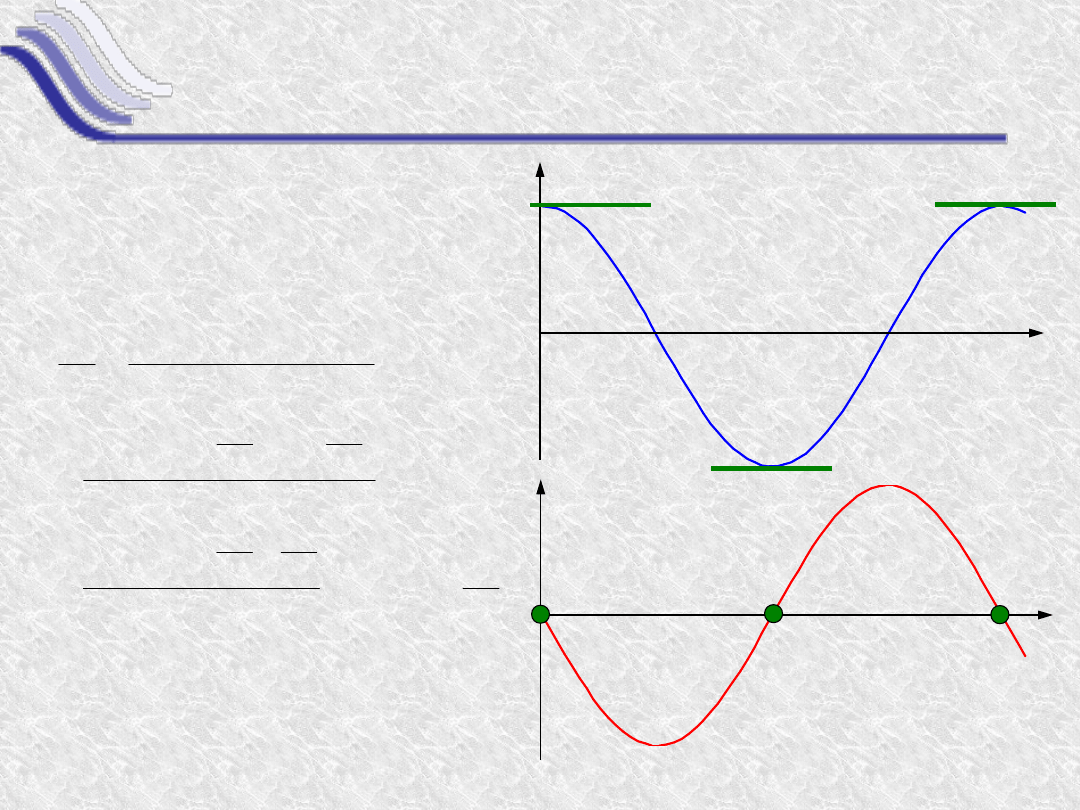
Pochodna funkcji sinus

Funkcja y(x) = sin(x)

Czyli

sin’(x) = cos(x)

















x

x

x

x

x

y

)

sin(

)

sin(















x

x

x

x

)

2

sin(

)

2

cos(

2

)

2

cos(

2

)

2

cos(

2

x

x

x

x

x

x



















y

x



2

0

y(x)=sin(x)

y

x



2

1

0

y’(x)=cos(x)

10

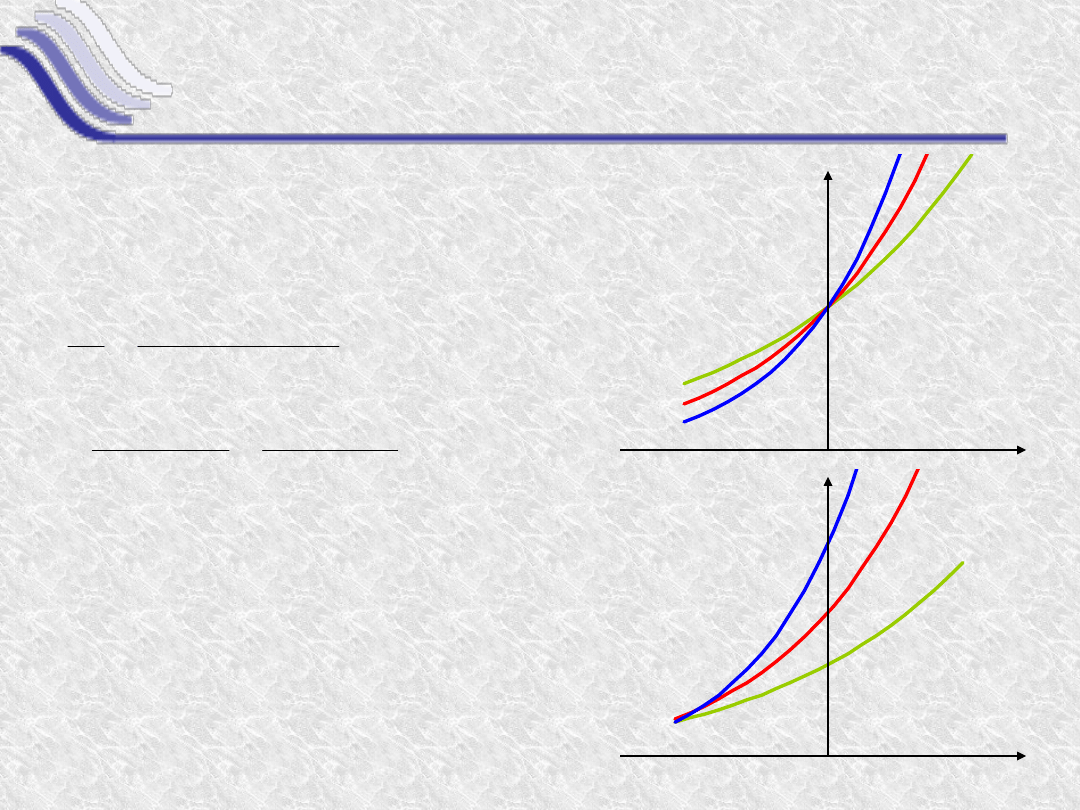
Pochodna funkcji cosinus

Funkcja y(x) = cos(x)

Iloraz różnicowy wynosi:

















x

x

x

x

x

y

)

cos(

)

cos(

Pochodną funkcji cosinus
jest -sinus

















x

x

x

x

)

2

sin(

)

2

sin(

2

)

2

sin(

2

)

2

sin(

2

x

x

x

x

x

x























y(x)=cos(x)

x

y



2



0

y’(x)=-sin(x)

y

x



2



0

Pochodna funkcji wykładniczej

Po obliczeniu granicy tego
ilorazu dla x dążącego do

zera, otrzymamy wzór
pochodnej:

1

x

y

2

x

4

x

e

x

1

x

y

2

x

ln2

e

x

4

x

ln4

Funkcja y(x) = a

x

Iloraz różnicowy wynosi:

















x

x

y

x

x

y

x

y

)

(

)

(

x

a

a

x

a

a

x

x

x

x

x





















)

1

(

(a

x

)’= a

x

lna

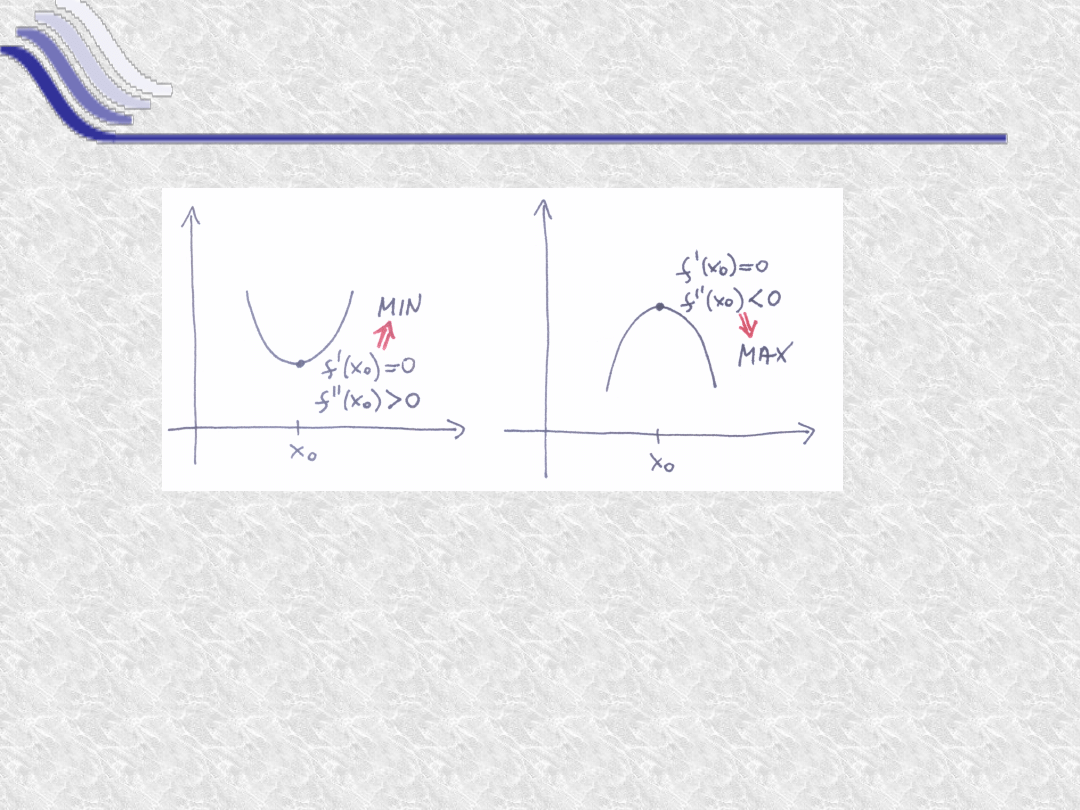
Tw. o ekstremach

Jeżeli :( , )

jest różniczkowalna w

( , )

i ma ma w tym punkcie ekstremum lokalne, to '( )=0

D (maksimum):

0:

( - ,

)

( )

( )

( )- ( )

( )- ( )

0 dla

' ( ) lim

0

-

-

podobnie

x c

f a b

R

c

a b

f c

x

c

c

f x

f c

f x f c

f x f c

x c

f

c

x c

x c

f

d

d

d

-

-

�

�

�

ޣ+�>$

�=�<ޣ

( )- ( )

' ( ) lim

0.

-

Ponieważ '( )

' ( )

' ( ), '( ) 0.

x c

f x f c

c

x c

f c

f

c

f

c f c

+

+

�

-

+

=

�

=

=

=

Tw. o ekstremach

1

2

1

2

2

1

2

1

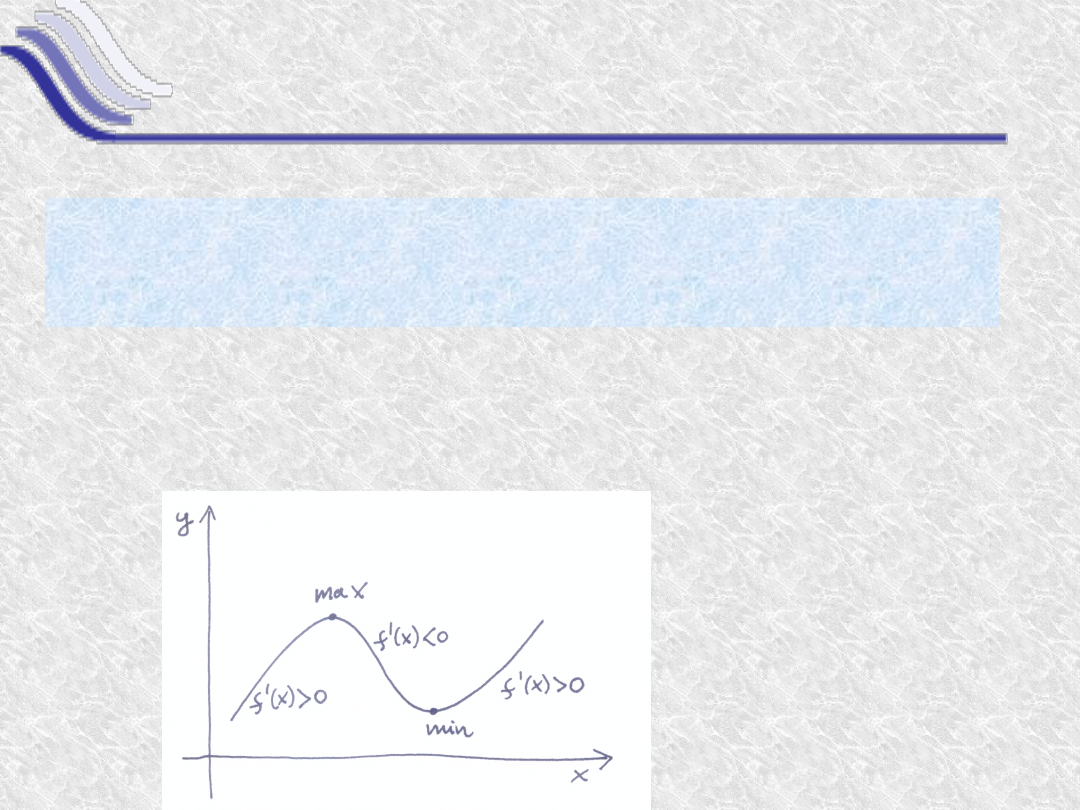
Tw. różniczkowalna w ( , )

'( ) 0 dla

( , )

( ) (silnie) rosnąca

'( ) 0 dla

( , )

( ) (silnie) malejąca

D: ,

( , ),

Z tw. Lagrange'a

( , ): ( )

( )

'( )(

)

Tw. różniczkow

f

a b

f x

x a b

f x

f x

x a b

f x

x x

a b x x

c a b f x

f x

f c x x

f

<

�

�

>

�

�

�

>

$ �

-

=

-

\

0

0

0

0

0

0

0

alna w ( , ),

( , )

'( ) 0 dla

( , ) i '( ) 0 dla

( , )

(silne) maksimum w

'( ) 0 dla

( , ) i '( ) 0 dla

( , )

(silne) minimum w

a b x

a b

f x

x a x

f x

x

x b

x

f x

x a x

f x

x

x b

x

�

<

�

>

�

�

>

�

<

�

�