WYKŁAD II

UKŁADY TRÓJFAZOWE SYMETRYCZNE

(Obliczenie układów)

1

prof. dr hab. inż. T. Niedziela

ELEKTROTECHNIKA II

Połączenie odbiornika

w gwiazdę

Połączenie odbiornika w gwiazdę

Układ trójfazowy jest symetryczny,

jeśli prądnica trójfazowa symetryczna jest

połączona z odbiornikiem symetrycznym (tzn. złożonym z

trzech identycznych

impedancji zespolonych

(Z

A

= Z

B

= Z

C

).

Z punktu widzenia sposobu połączenia źródła i odbiornika (jak już powiedziano)
możemy wyróżnić

pięć różnych układów podstawowych.

Jednak dla obliczeń

zasadnicze znaczenie ma sposób połączenia odbiornika.

Podłączenie źródła jest tu mniej istotne, ponieważ przeważnie odbiorniki są

dołączone do sieci systemu, w którym punkt neutralny transformatora trójfazowego,

w zależności od sposobu jego połączenia, może być uziemiony lub izolowany.

3

Układ trójfazowy czteroprzewodowy, do
którego dołączono odbiornik połączony
w gwiazdę z uziemionym punktem
neutralnym

4

Ten sam układ (

układ trójfazowy symetryczny z

odbiornikiem połączonym w gwiazdę

) może być

przedstawiony następująco. Dorysowanie źródła
ułatwia zrozumienie zależności występujących w
tym układzie.

5

5

Obliczenie układu

polega na

wyznaczeniu

prądów przewodowych i fazowych odbiornika,
napięć fazowych odbiornika oraz mocy czynnej,
biernej i pozornej pobieranej przez odbiornik.

Dla uproszczenia załóżmy ze

faza początkowa

napięcia

źródłowego (fazy A) jest równa zeru.

Napięcia fazowe źródeł (E

A,

E

B

, E

C

)

przedstawimy

w postaci zespolonej:

6

A

E

E

=

2

3

1

3

2

2

j

B

A

A

E

E e

E

j

p

-

�

�

-

=

=

- -

�

�

�

�

�

�

2

3

1

3

2

2

j

C

A

A

E

E e

E

j

p

�

�

-

=

=

- +

�

�

�

�

�

�

gdyż:

7

2

2

3

3

1

3

1

3

;

2

2

2

2

j

j

e

j

e

j

p

p

-

=- -

=- +

Z powyższych zależności (po dodaniu stronami) wynika, że:

0

A

B

C

E

E

E

+

+

=

W układzie trójfazowym symetrycznym gwiazda - gwiazda

potencjał punktu neutralnego (N) źródła jest równy

potencjałowi punktu neutralnego odbiornika (N’).

W takim razie jeżeli

w układzie trójfazowym symetrycznym gwiazda-gwiazda

potencjał

punktu neutralnego źródła jest równy potencjałowi punktu neutralnego odbiornika , to

E

A

= U

A

E

B

= U

B

E

C

= U

C

zatem

stwierdzamy, że w układzie trójfazowym symetrycznym

przy połączeniu

odbiornika w gwiazdę:

Suma wartości skutecznych zespolonych napięć fazowych

odbiornika jest równa zeru.

8

0

A

B

C

U

U

U

+

+

=

Wobec

równości

potencjałów

punktów

neutralnych N i N’ można te punkty zewrzeć,

zatem prądy fazowe odbiornikowe:

9

0

A

B

C

U

U

U

+

+

=

A

A

A

B

B

B

C

C

C

E

U

I

Z

Z

E

U

I

Z

Z

E

U

I

Z

Z

=

=

=

=

=

=

Ponieważ impedancja każdej fazy odbiornika
wynosi:

zatem

prądy fazowe

:

10

j

Z Ze

R jX

j

=

= +

2

2

3

3

2

2

3

3

j

j

A

A

A

j

j

j

B

B

A

j

j

j

C

C

A

E

I

e

I e

Z

E

I

e

e

I e

Z

E

I

e e

I e

Z

j

j

p

p

j

j

p

p

j

j

-

-

�

�

-

+

-

�

�

-

�

�

�

�

+

�

�

-

�

�

=

=

=

=

=

=

a

moduły prądów przewodowych (I

A

, I

B

, I

C

) są

odpowiednio:

Wniosek. Moduły prądów we wszystkich
fazach są jednakowe

, ponadto wartości

skuteczne zespolone:

11

A

A

B

C

p

E

I

I

I

I

Z

= = =

=

2

3

1

3

2

2

j

B

A

A

I

I e

I

j

p

-

�

�

-

=

=

- -

�

�

�

�

�

�

2

3

1

3

2

2

j

C

A

A

I

I e

I

j

p

�

�

=

=

- +

�

�

�

�

�

�

Zatem:

Wniosek.

Suma

wartości

skutecznych

zespolonych

prądów

fazowych

(przewodowych) jest równa zeru.

Stąd wynika,

że w układzie symetrycznym

prąd w przewodzie

neutralnym jest równy zeru.

Napięcie międzyfazowe

jest różnicą napięć

fazowych,

przy

czym

działania

należy

przeprowadzać

na

wartościach

skutecznych

zespolonych.

12

0

A

B

C

I

I

I

+ + =

Zatem:

Moduły napięć międzyfazowych są
sobie równe:

a

suma wartości skutecznych zespolonych

napięć międzyfazowych jest równa zeru,

czyli:

13

AB

A

B

BC

B

C

CA

C

A

U

U

U

U

U

U

U

U

U

=

-

=

-

=

-

AB

BC

CA

p

U

U

U

U

=

=

=

0

AB

BC

CA

U

U

U

+

+

=

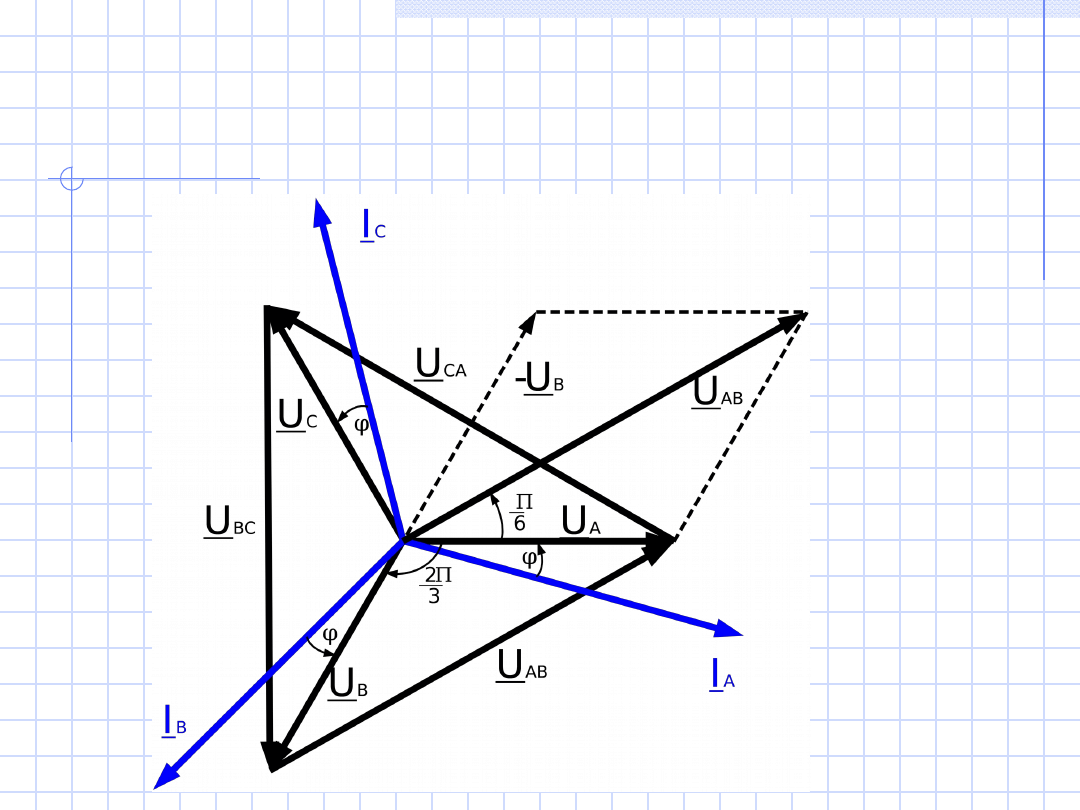
Na kolejnym rysunku zobrazujemy wyniki

naszych

obliczeń

w

postaci

wykresu

wektorowego napięć i prądów dla układu
trójfazowego symetrycznego przy podłączeniu
odbiornika w gwiazdę

14

Wykres wektorowy napięć i prądów dla
układu trójfazowego symetrycznego
przy połączeniu odbiornika w gwiazdę

15

Na wykresie wektorowym przedstawiliśmy

napięcia

fazowe

(U

A

, U

B

, U

C

),

międzyfazowe

(U

AB

, U

BC

, U

CA

)

oraz

prądy przewodowe, które są równe prądom
fazowym odbiornika

(I

A

, I

B

, I

C

) przy połączeniu

impedancji fazowych w gwiazdę.

Ponieważ

trzy wektory napięć międzyfazowych

(U

AB

,

U

BC

, U

CA

)

tworzą trójkąt

, zatem ich suma jest równa

zeru.

16

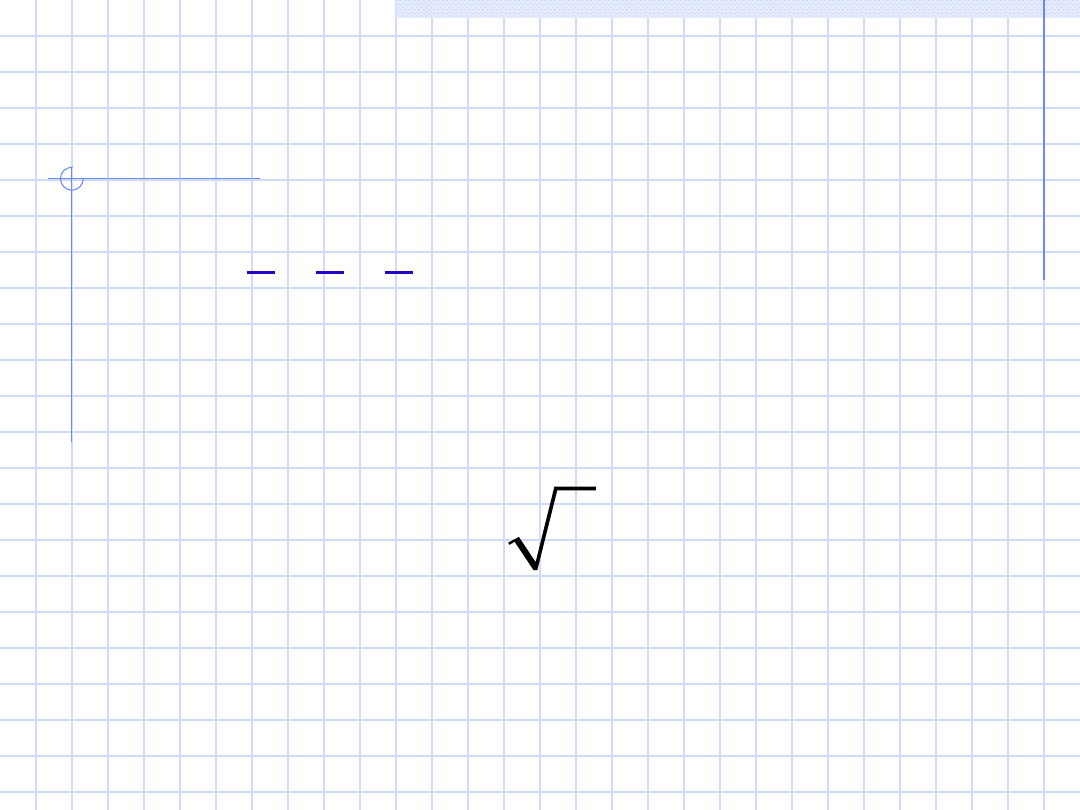
Z zależności dla trójkąta równoramiennego o
bokach U

A

, U

B

, U

AB

i o kątach 2π/3, π/6 i π/6

wynika że

moduł napięcia międzyfazowego

U

AB

= U

p

jest pierwiastek z 3 razy większy

od modułu napięcia fazowego U

f

,

czyli:

17

3

f

Up

U

=

Z zależności tej wynika, że w sieci o napięciu
fazowym U

f

= 220V, napięcie międzyfazowe:

Moc czynną P pobraną przez odbiornik
trójfazowy symetryczny

możemy obliczyć

jako potrójną wartość (3P

f

) mocy pobieranej

przez jedną fazę odbiornika:

przy czym R, jest rezystancją jednej fazy
odbiornika.

18

3 220 380

P

U

V

=

�

=

2

P

ff

ff

U I cos

RI

j

=

=

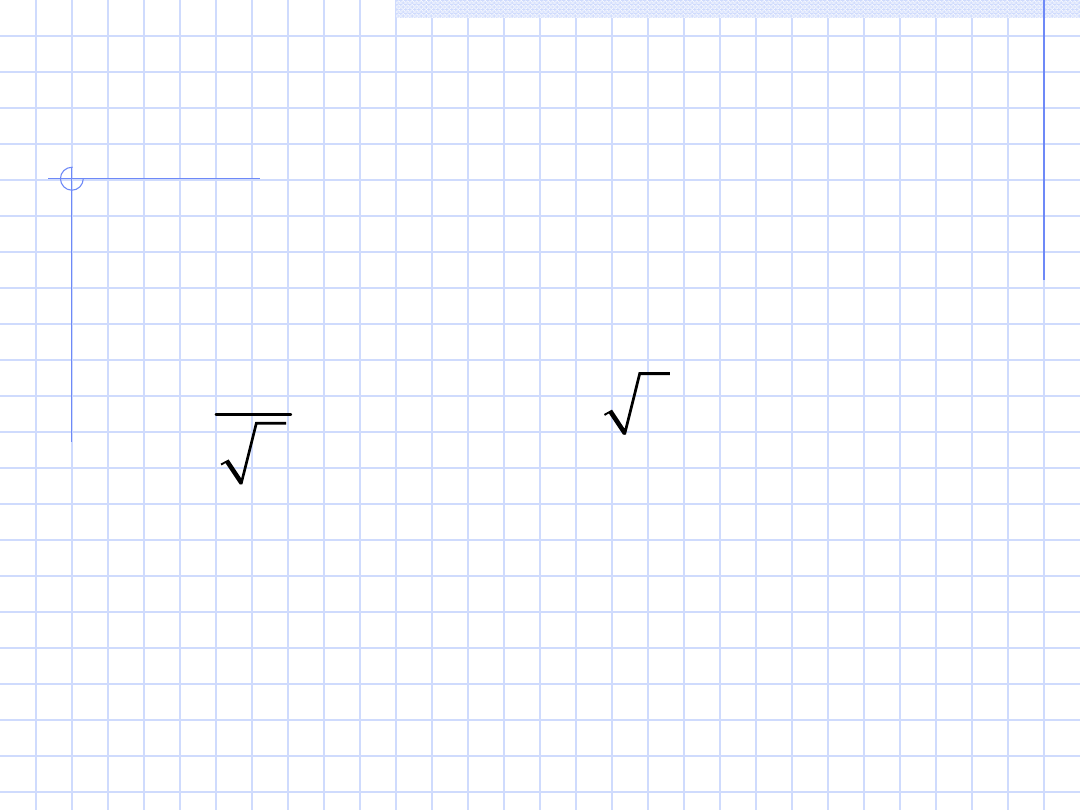
Zatem moc czynna

pobierana przez

odbiornik

trójfazowy symetryczny:

Po podstawieniu otrzymujemy ,

moc czynną P

jako:

Wzór ten jest najczęściej stosowany do
obliczania mocy czynnej P pobieranej przez
odbiornik trójfazowy symetryczny, gdyż
uzależnia moc od wartości związanych z
parametrami sieci zasilającej odbiornik (U

p

oraz

I

p

).

19

2

3P

3

ff

ff

P

U I cos

RI

j

=

=

=

3

cos

3

cos

3

p p

p p

P

U I

U I

j

j

=

=

DZIĘKUJĘ ZA UWAGĘ

WYKŁAD III

UKŁADY TRÓJFAZOWE SYMETRYCZNE

Połączenie odbiornika w trójkąt

21

prof. dr hab. inż. T. Niedziela

ELEKTROTECHNIKA II

Połączenie odbiornika w trójkąt

Na kolejnym rysunku zilustrujemy

układ

trójfazowy symetryczny

, w którym

odbiornik

połączono w trójkąt,

natomiast źródło w

gwiazdę.

Punktem wyjścia do naszych obliczeń

prądów

fazowych, napięć fazowych oraz mocy

czynnej, biernej i pozornej odbiornika

są

napięcia międzyfazowe.

Gdyby źródło było połączone np. w trójkąt,

wówczas napięcia międzyfazowe są

jednocześnie napięciami fazowymi źródła

.

22

B. Połączenie odbiornika w

trójkąt

Układ trójfazowy symetryczny z
odbiornikiem

połączonym w

trójkąt

23

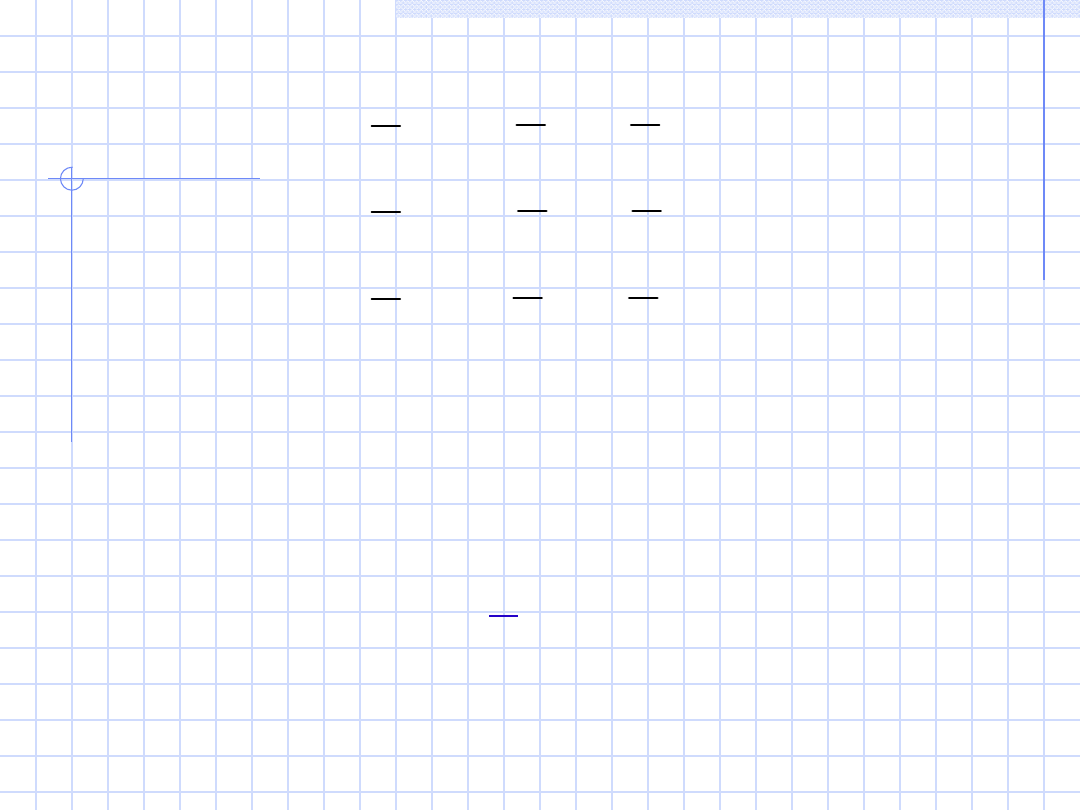
Wyznaczone za pomocą powyższych równań

napięcia międzyfazowe tworzą układ
trójfazowy symetryczny napięć

, przy czym

po założeniu

, że faza początkowa napięcia

międzyfazowego

U

AB

jest

równa

zeru

otrzymamy:

24

AB

A

B

BC

B

C

CA

C

A

U

E

E

U

E

E

U

E

E

=

-

=

-

=

-

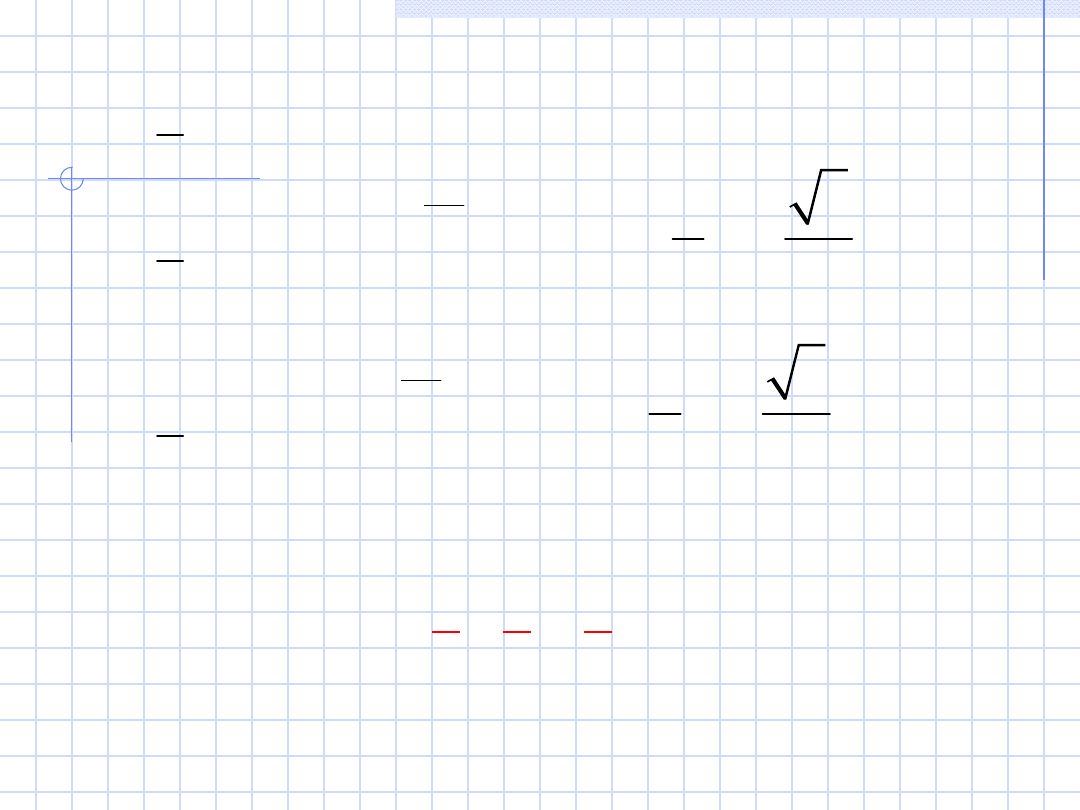
Z powyższych zależności wynika, że wektory

napięć fazowych (U

AB,

U

BC

, U

CA

) odbiornika tworzą

gwiazdę symetryczną gdzie ich suma jest równa
zero.

25

2

3

2

3

1

3

2

2

1

3

2

2

AB

AB

j

BC

AB

AB

j

CA

AB

AB

U

U

U

U e

U

j

U

U e

U

j

p

p

-

=

�

�

=

=

- -

�

�

�

�

�

�

�

�

=

=

- +

�

�

�

�

�

�

a moduły tych napięć (napięć

międzyfazowych) są jednakowe

(U

AB

= U

BC

= U

CA

= U

f

)

26

0

AB

BC

CA

U

U

U

+

+

=

Obliczone

napięcia międzyfazowe występują

na zaciskach odbiornika

, którego

impedancja każdej fazy

wynosi:

Prądy fazowe odbiornika (I

AB

, I

BC

, I

CA

)

możemy wyznaczyć z prawa Ohma dla
wartości skutecznych zespolonych:

27

j

Z Ze

R jX

j

=

= +

j

j

AB

AB

AB

AB

U

U

I

e

I e

Z

Z

j

j

-

-

=

=

=

Powyższe wyrażenia wskazują, że

wektory

prądów fazowych odbiornika tworzą gwiazdę
symetryczna ale opóźnioną o kąt

φ

w stosunku

do gwiazdy napięć fazowych.

28

2

2

3

3

2

2

3

3

j

j

j

BC

AB

BC

AB

j

j

j

CA

AB

CA

AB

U

U

I

e

e

I e

Z

Z

U

U

I

e e

I e

Z

Z

p

p

j

j

p

p

j

j

�

�

-

+

-

�

�

-

�

�

�

�

+

�

�

-

�

�

=

=

=

=

=

=

Przy czym:

Stwierdzamy więc, moduły prądów
fazowych płynących w gałęziach
odbiornika połączonego w trójkąt są
jednakowe i równe prądowi fazowemu I

f

.

29

AB

AB

BC

CA

f

U

I

I

I

I

Z

=

=

=

=

Zatem:

Wniosek.

Suma

wartości

skutecznych

zespolonych prądów fazowych jest równa zeru.

Prądy

przewodowe

obliczamy

jako

różnicę

odpowiednich

prądów fazowych

. Korzystając z

prawa Kirchhoffa dla kolejnych węzłów otrzymujemy:

30

2

3

2

3

1

3

2

2

1

3

2

2

j

BC

AB

AB

j

CA

AB

AB

I

I e

I

j

I

I e

I

j

p

p

-

�

�

-

=

=

- -

�

�

�

�

�

�

�

�

=

=

- +

�

�

�

�

�

�

0

AB

BC

CA

I

I

I

+

+

=

Moduły prądów przewodowych są sobie
równe,

tzn:

a

suma ich wartości skutecznych

zespolonych jest równa zeru,

czyli:

31

A

AB

CA

B

BC

AB

C

CA

BA

I

I

I

I

I

I

I

I

I

=

-

=

-

=

-

A

B

C

P

I

I

I

I

= = =

0

A

B

C

I

I

I

+ + =

Obliczenia przedstawimy na wykresie wektorowym.

Wykreślamy trzy

wektory napięć międzyfazowych

( faza początkowa U

AB

jest równa zeru).

Prąd fazowy

w każdej fazie jest opóźniony względem napięcia fazowego o

kąt φ.

Wektory prądów fazowych

( I

AB

, I

BC

, I

CA

) tworzą gwiazdę symetryczną.

Wektor prądu przewodowego

opóźnia się względem wektora prądu

fazowego o 30

0

.

32

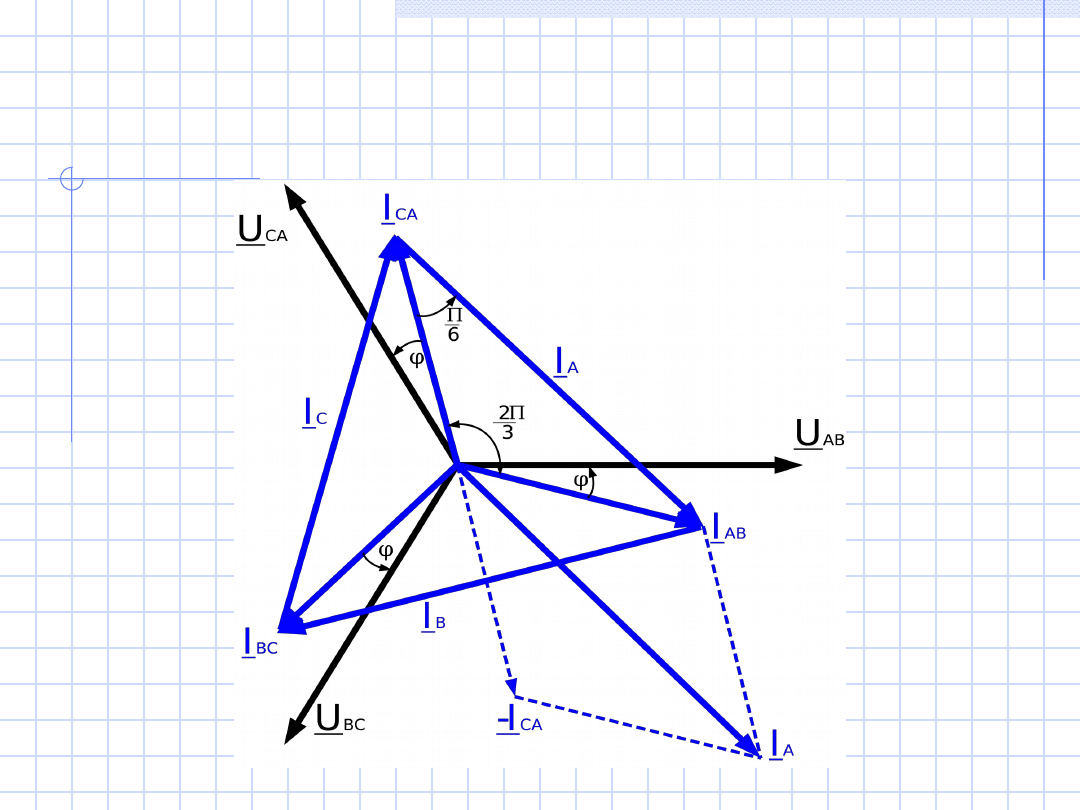
Wykres wektorowy prądów i napięć dla układu
trójfazowego symetrycznego przy połączeniu
odbiornika w trójkąt

33

Ponieważ trzy wektory prądów
przewodowych

(I

A

, I

B

, I

C

)

tworzą trójkąt,

zatem ich suma jest równa zeru

, co jest

zgodne z obliczeniami. Z zależności trójkąta
równoramiennego i kątów wynika, że

moduł

prądu przewodowego (I

A

=I

B

=I

C

=I

p

)

jest

pierwiastek z trzech razy większy od modułu
prądu fazowego

(I

AB

=I

BC

=I

CA

=I

f

) .

Dla odbiornika połączonego w trójkąt

, moc

pobieraną

przez

odbiornik

trójfazowy

symetryczny połączony w trójkąt obliczamy jako
potrójną wartość mocy pobieranej przez jedną
fazę a zatem

moc czynna P

:

34

3

f

Ip

I

=

2

3P

3

3

ff

ff

P

U I cos

RI

j

=

=

=

Przy czym R jest rezystancją jednej fazy
odbiornika.
Po podstawieniu I

f

=I

p

/3

1/2

oraz U

p

=U

f

moc

czynna P jest równa:

Podobnie

moc bierną Q

obliczymy jako potrójną

wartość mocy biernej, pobieranej przez jedną fazę.

Po uwzględnieniu zależności na I

f

oraz U

f

,

moc

pozorna S

:

35

3

cos

3

cos

3

p p

p p

P

U I

U I

j

j

=

=

2

3

sin

3

ff

f

Q

U I

XI

j

=

=

3

p p

S

U I

=

WNIOSKI:

1. Niezależnie od sposobu połączenia faz odbiornika

trójfazowego symetrycznego, odpowiednio moc czynną,
bierną i pozorną obliczamy z tych samych wzorów.

2. Do obliczania mocy odbiornika trójfazowego

symetrycznego połączonego w gwiazdę i trójkąt jest
potrzebna znajomość napięcia międzyfazowego, prądu
przewodowego i kata fazowego odbiornika.

3. Suma prądów fazowych i napięć fazowych odbiornika

trójfazowego symetrycznego połączonego zarówno w
gwiazdę i trójkąt jest równa zero.

36

DZIĘKUJĘ ZA UWAGĘ

37

Źródła:

„Elektrotechnika” – Bolkowski

Równania matematyczne napisano w

programie: MathType 5.0

Schematy układów elektrycznych w nakładce

programu MS Word.

38