POLITECHNIKA WROCŁAWSKA

Wydział Chemiczny

CHEMIA NIEORGANICZNA – PODSTAWY

WYKŁAD

ZWIĄZKI

KOMPLEKSOWE

A

B

B

B

B

B

B

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

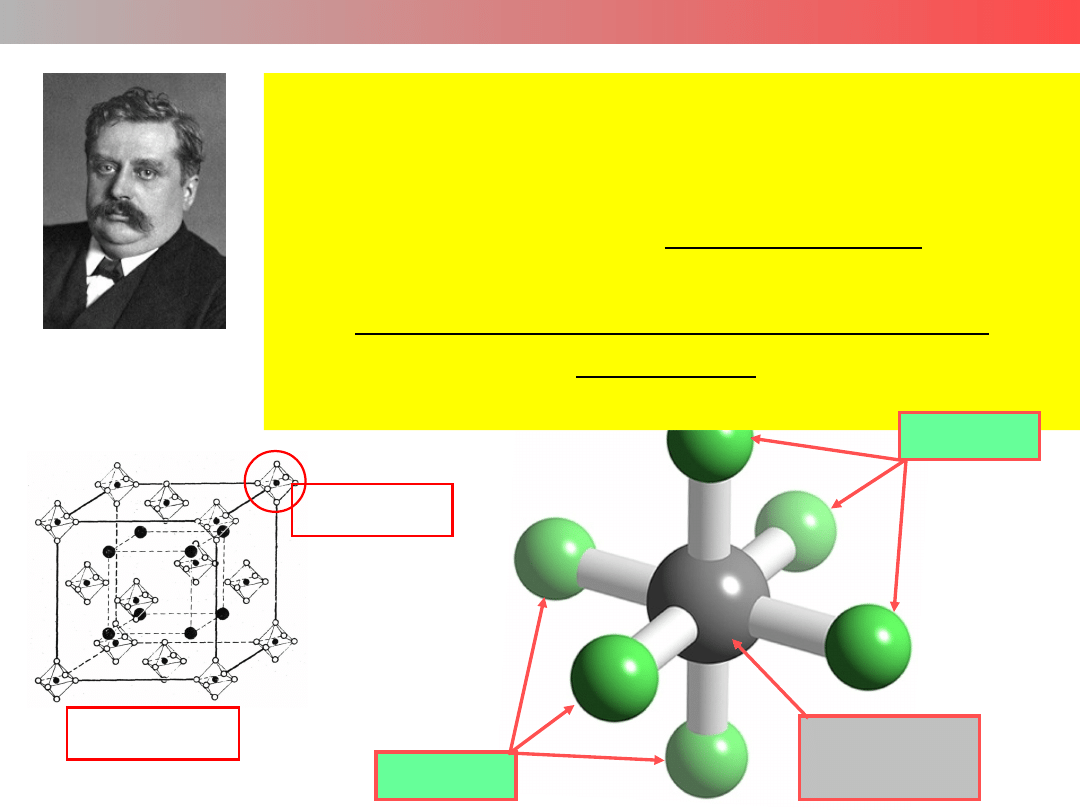
Związek lub jon kompleksowy to połączenie

w którym z atomem (jonem) A

związana jest większa liczba

innych atomów (jonów, grup) B

niż to wynika z ładunku lub stopnia

utlenienia

atomu (jonu) A.

K

2

[PtCl

6

]

[PtCl

6

]

2−

Atom (jon)

centralny

Ligandy

Ligandy

Alfred Werner

1866-1910

Nobel 1913

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Pt

IV

Cl

Cl

Cl

Cl

Cl

Cl

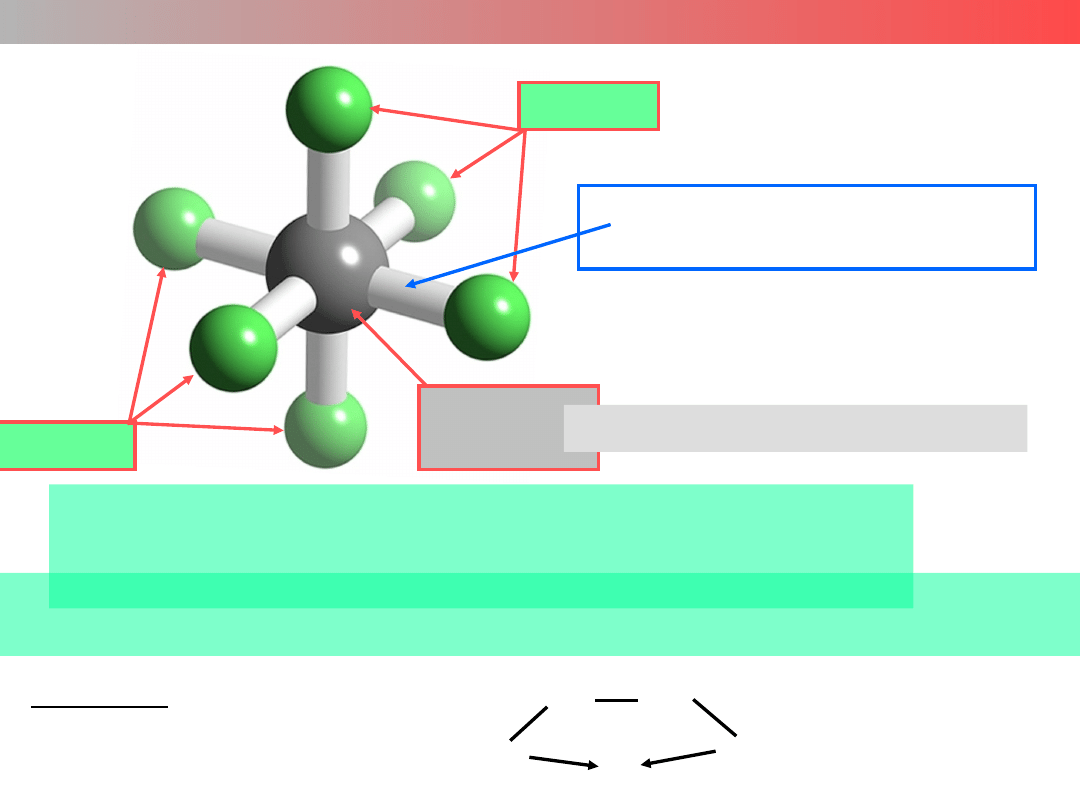
Atom (jon)

centralny

Ligandy

Ligandy

– głównie jony metali, metale

– obojętne cząsteczki lub aniony z wolną parą

elektronową,
:NH

3

, H

2

O:, :CO, NO: lub :Cl

–

,

:CN

–

, :OH

–

– cząsteczki organiczne z wieloma grupami posiadającymi

wolne pary elektronowe (ligandy wielokleszczowe)

Przykład: etylenodiamina

:NH

2

CH

2

CH

2

H

2

N:

M

Liczba wiązań metal-ligand

liczba koordynacyjna (LK)

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

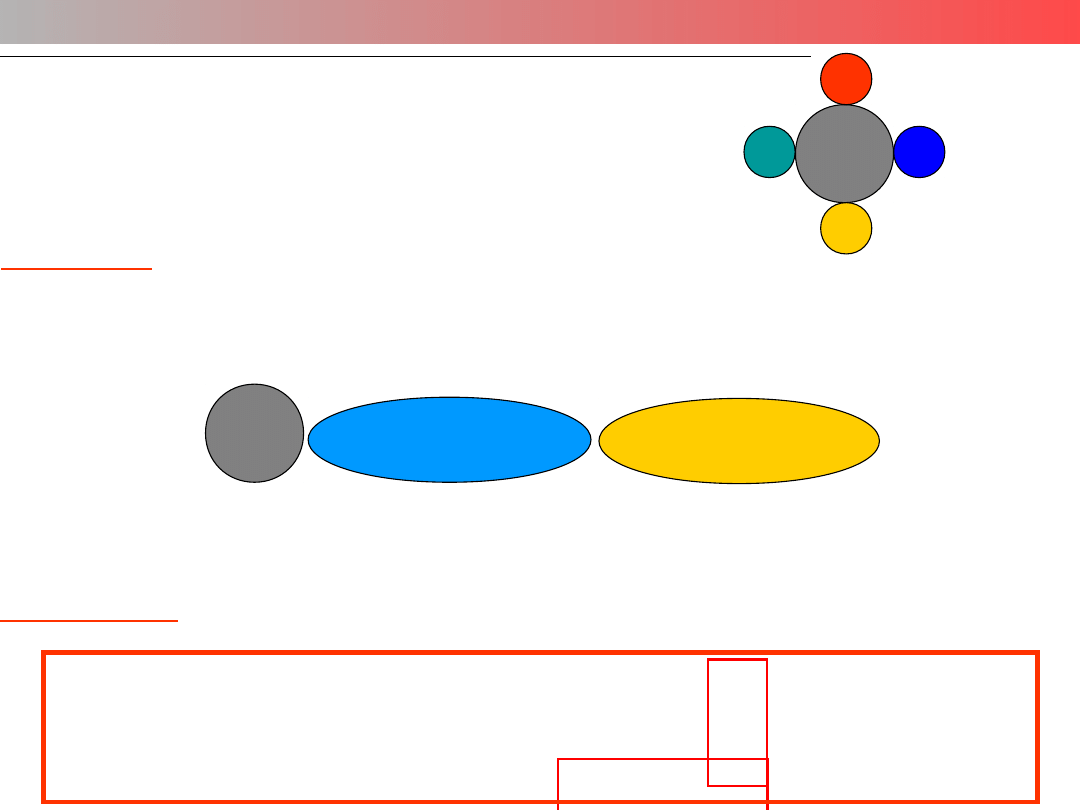
NOMENKLATURA (nazewnictwo)
ZWIĄZKÓW KOMPLEKSOWYCH

Atom
centr.

L

4

L

1

L

2

L

3

L-ligandy

[kation]

n+

[cząsteczka]

[anion]

n-

NOMENKLATURA KOORDYNACYJNA

WZÓR:

[

jednostki koordynacyjnej

]

Atom
centr.Ligandy anionowe alfabet.

Ligandy obojętne alfabet.

[

]

[Ni(CO)

4

]

[CoCl(NH

3

)

5

]

2+

[PtCl

6

]

2–

[CoBrCl(H

2

O)

2

(NH

3

)

2

]

+

Alfabetycznie wg. symboli we
wzorze

NAZWA:

[

jednostki koordynacyjnej

]

ligandy (wszystkie) alfabetycznie

atom
centralny

-u

-i

-

an

(

st. utl. atomu

centralnego

lub ładunek

jedn. koord.

)

wg. nazwy

binarnej

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

NAZWY wybranych LIGANDÓW:

H

2

O - akwa

NH

3

- amina

CO - karbonyl CN

–

- cyjano

OH

–

- hydrokso

NO - nitrozyl

NCS

–

- tiocyjanianoSH

–

- merkapto

PRZYKŁADY:

chlorek

penta

amina

chloro

kobaltu(III)

związek binarny (sól)

[Co

Cl

(NH

3

)

5

]

Cl

2

chlorek

penta

amina

chloro

kobaltu(2+)

[Co

4

(CO)

12

]

dodeka

karbonyl

tetra

kobalt(0)

heksa

cyjano

żelazian(II) żelaza(III)

związek binarny (sól)

Fe

4

[Fe

(CN)

6

]

3

[Co

(NH

3

)

6

]

[Cr

(CN)

6

]

3

związek binarny (sól)

heksa

cyjano

chromian(II)

heksa

amina

kobaltu(III)

[Pt

Cl

2

(NH

3

)

2

]

di

amina

di

chloro

platyna(II)

„cisplatyna”

[

(NH

3

)

5

Cr-

OH

-Cr

(NH

3

)

5

]Cl

5

chlorek

μ-hydrokso

bis(penta

amina

chromu(III))

[SnCl

3

]

–

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

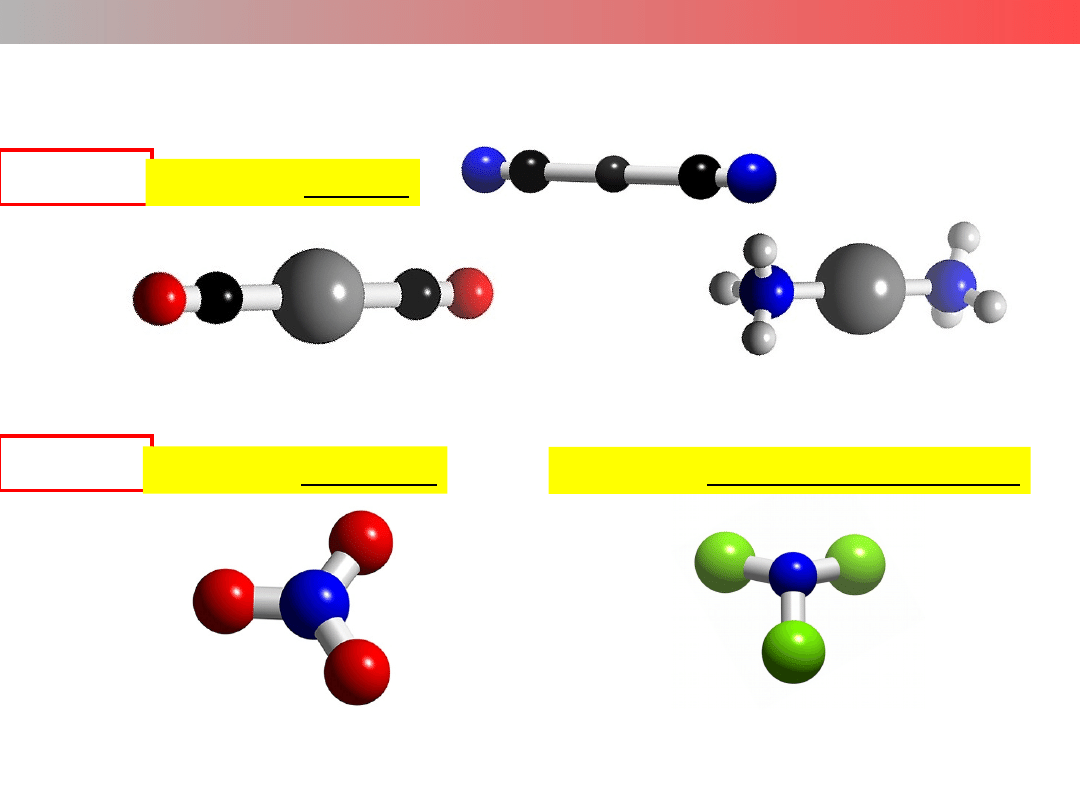
Liczba koordynacyjna (LK) – struktura kompleksu

LK = 2

struktura liniowa

[Au(CN)

2

]

–

[Ag(CO)

2

]+

[Ag(NH

3

)

2

]+

LK = 3

struktura trójkątna

[HgI

3

]

–

struktura piramidy trygonalnej

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

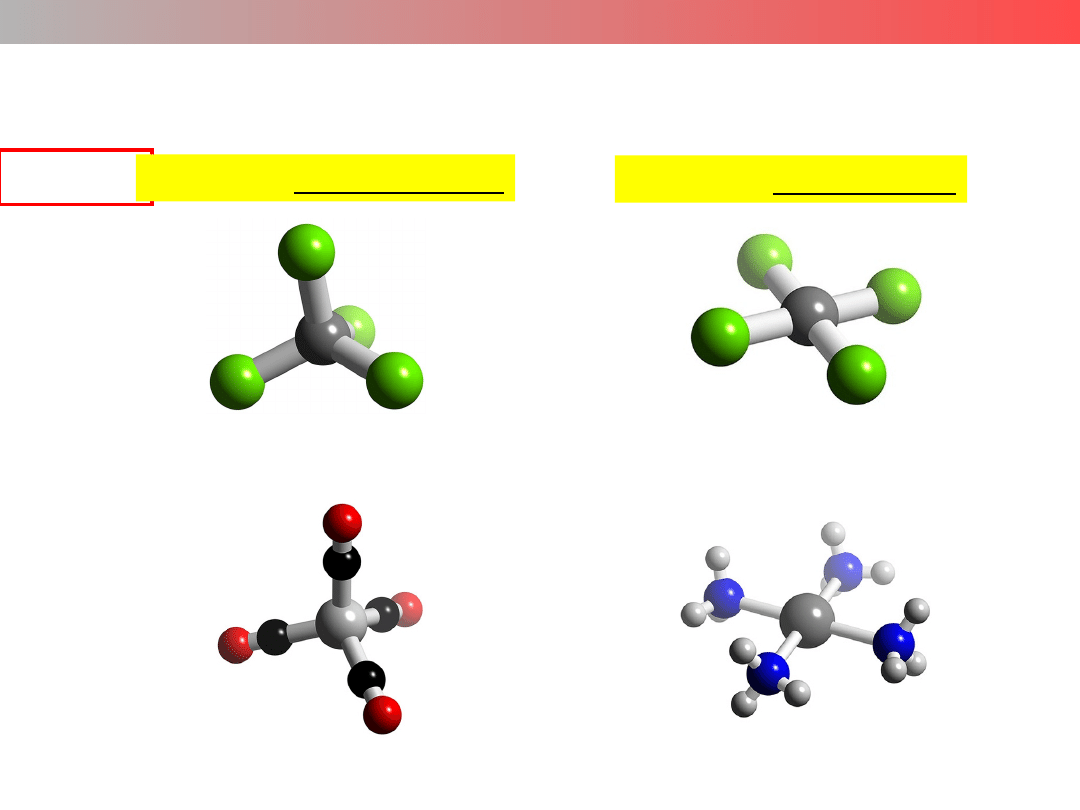
Liczba koordynacyjna (LK) – struktura kompleksu

LK = 4

struktura tetraedryczna

[FeCl

4

]

–

struktura kwadratowa

[PtCl

4

]

–

[Pt(NH

3

)

4

]

2+

[Ni(CO)

4

]

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

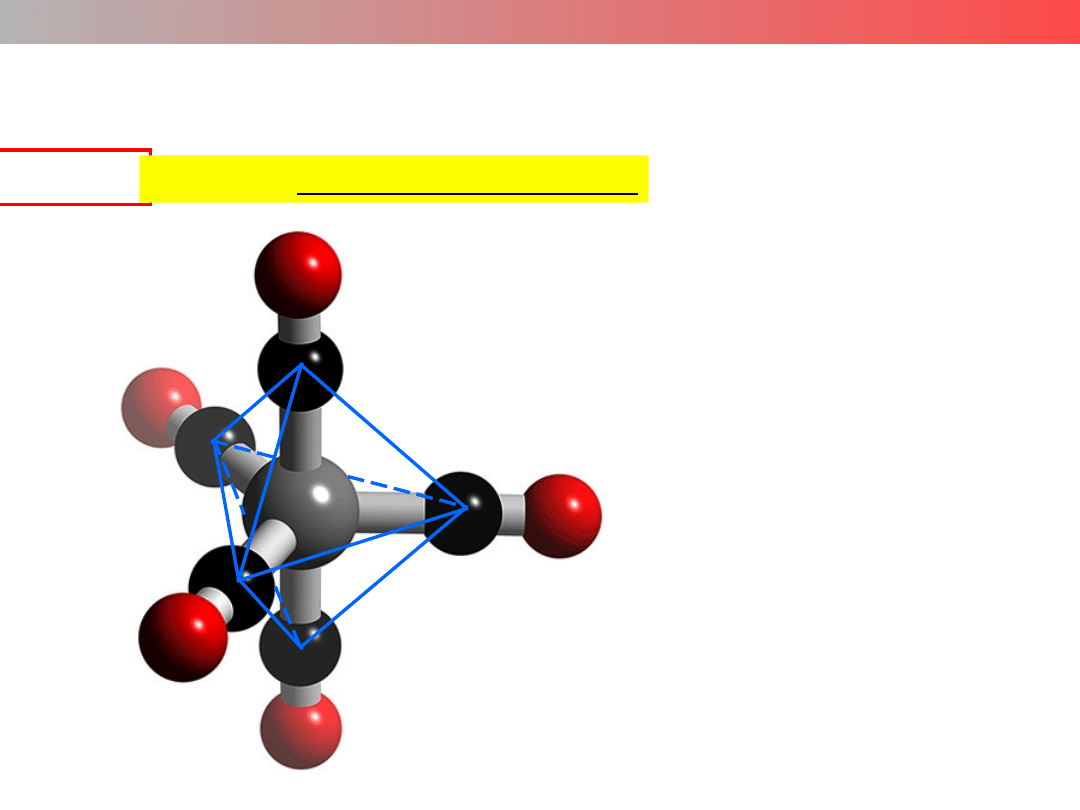
Liczba koordynacyjna (LK) – struktura kompleksu

LK = 5

struktura bipiramidy trygonalnej

[Fe(CO)

5

]

[Fe(CN)

6

]

3–

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Liczba koordynacyjna (LK) – struktura kompleksu

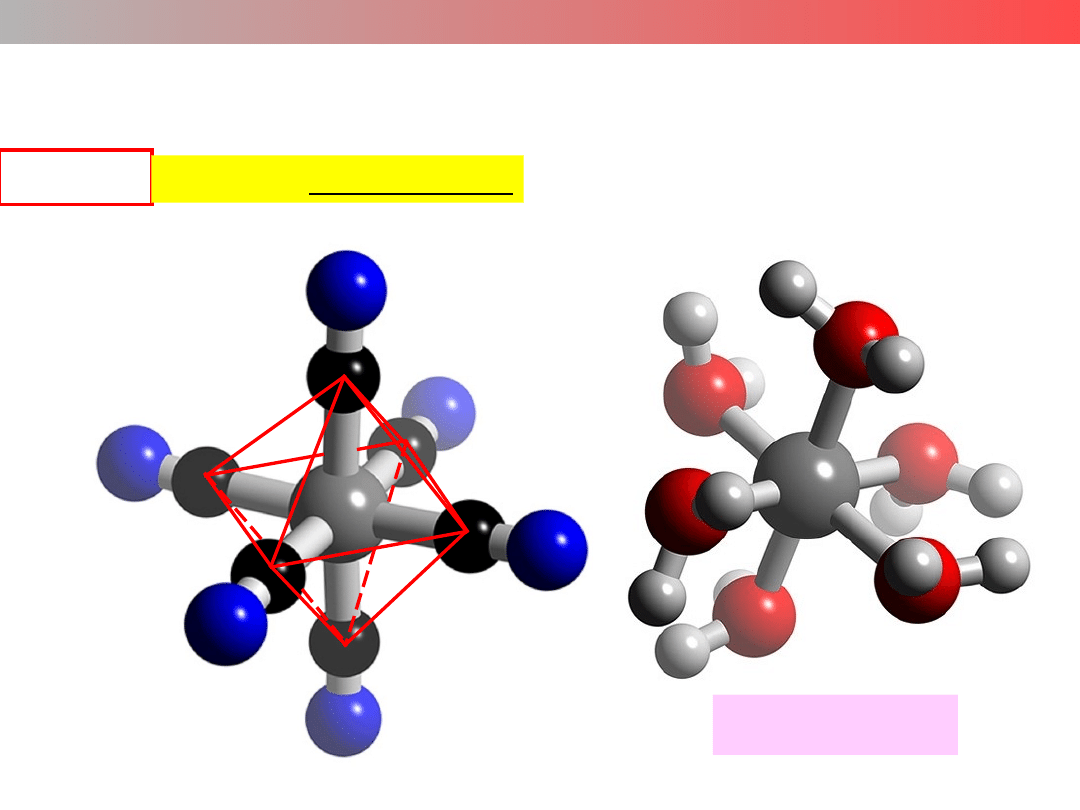
LK = 6

struktura oktaedryczna

[Co(H

2

O)

6

]

2+

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

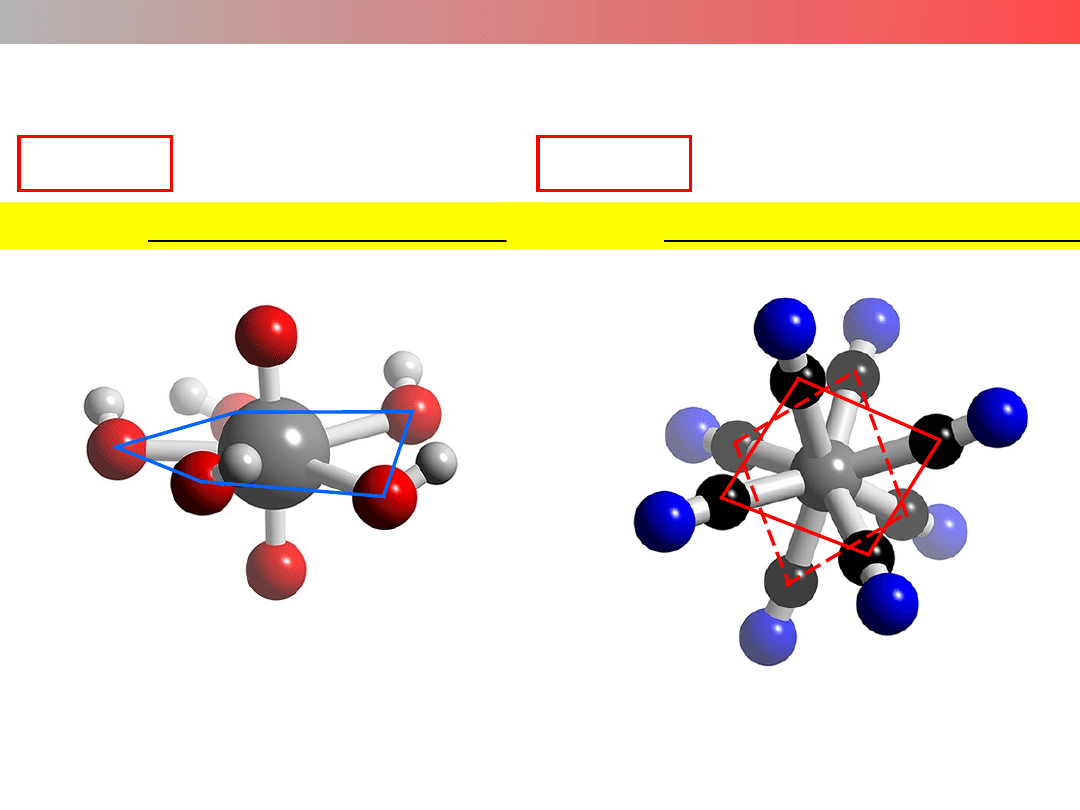
Liczba koordynacyjna (LK) – struktura kompleksu

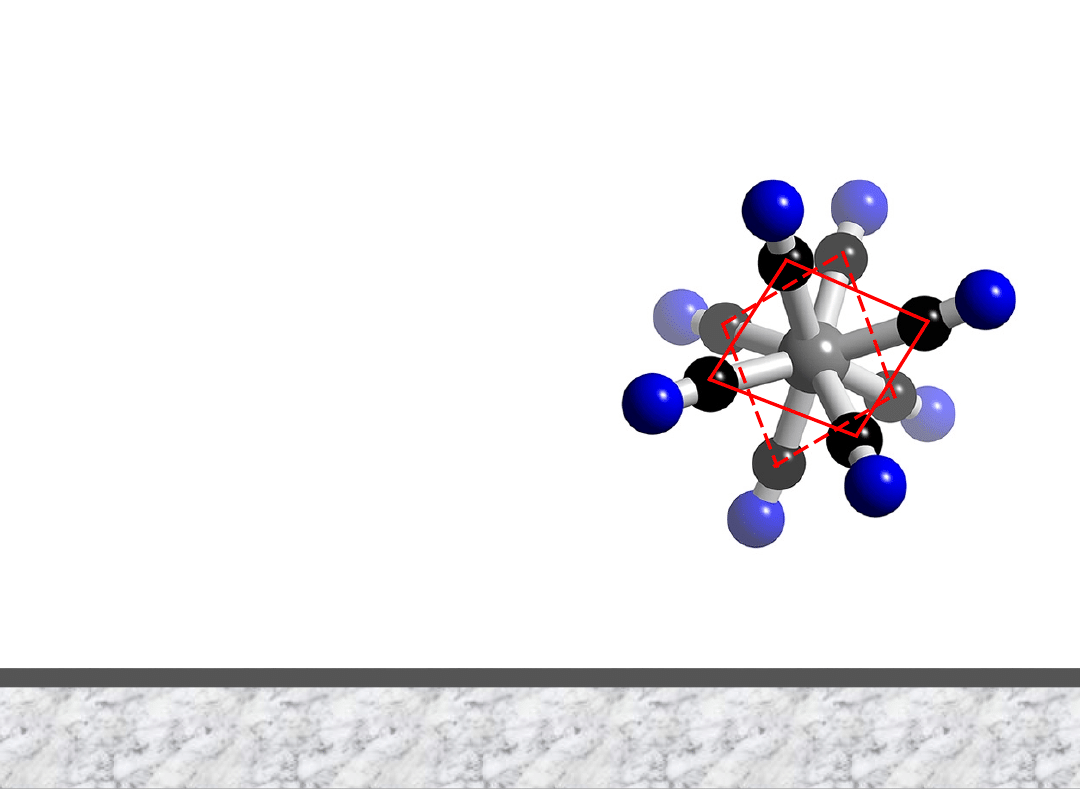
LK = 7

struktura bipiramidy pentagonalnej

[UO

2

(OH)

5

]

LK = 8

struktura antypryzmatu kwadratowgo

[Mo(CN)

8

]

3–

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

IZOMERIA ZWIĄZKÓW KOMPLEKSOWYCH

1. Izomeria strukturalna

a) izomeria jonowa

[CoBr(NH

3

)

5

]SO

4

i [Co(SO

4

)(NH

3

)

5

]Br

b) izomeria solwatacyjna

[Cr(H

2

O)

6

]Cl

3

i [CrCl

2

(H

2

O)

4

]Cl·2H

2

O

c) izomeria koordynacyjna

[Co(NH

3

)

6

][Cr(CN)

6

] i [Cr(NH

3

)

6

][Co(CN)

6

]

d) izomeria koordynacyjna

[Cr(SCN)(H

2

O)

5

]

2+

i [Cr(NCS)(H

2

O)

5

]

2+

jon pentaakwa(tiocyjanian-

S

)chromu(III) jon pentaakwa(tiocyjanian-

N

)chromu(III)

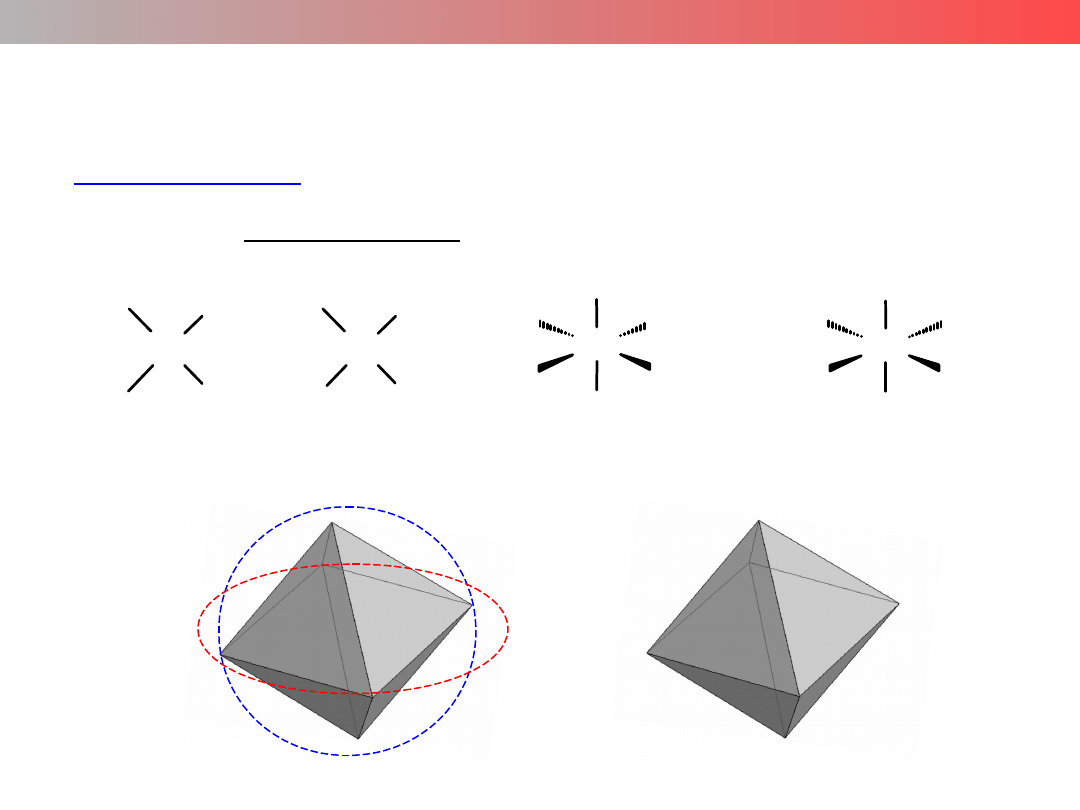
mer

B

B

B

A

A

A

fac

B

B

B

A

A

A

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

IZOMERIA ZWIĄZKÓW KOMPLEKSOWYCH

2.

Stereoizomeria

a) izomeria geometryczna

Cl

Cl

py

py

Pt

Cl

py

py

Cl

Pt

Cl

Ru

Cl

Ph

3

P

PPh

3

PPh

3

Ph

3

P

Cl

Ru

PPh

3

Ph

3

P

Cl

PPh

3

Ph

3

P

cis

trans

cis

trans

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

IZOMERIA ZWIĄZKÓW KOMPLEKSOWYCH

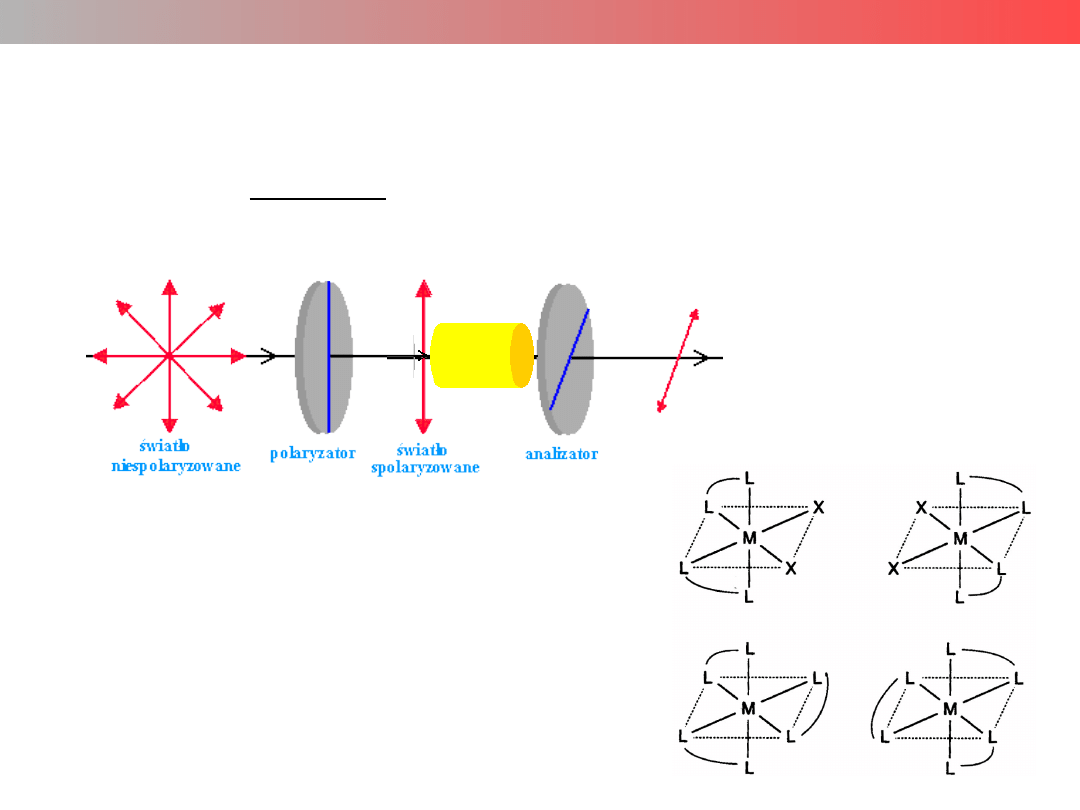
b) izomeria optyczna

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

M + L ⇆ ML

K

1

=

[ML]

[M] [L]

= β

1

ML + L ⇆ ML

2

K

2

=

[ML

2

]

[ML] [L]

β

2

= K

1

· K

2

REAKCJA

STAŁA

TRWAŁOŚCI

SKUMULOWANA

STAŁA TRWAŁOŚCI

M + 2L ⇆ ML

2

=

[ML

2

]

[M] [L]

2

ML

k-1

+ L ⇆ ML

k

K

k

=

[ML

k

]

[ML

k-1

] [L]

β

k

= Π K

n

M + kL ⇆ ML

k

=

[ML

k

]

[M] [L]

k

n=1

k

Równowagi tworzenia kompleksów

RÓWNOWAGI CHEMICZNE

W ROZTWORACH KOMPLEKSÓW

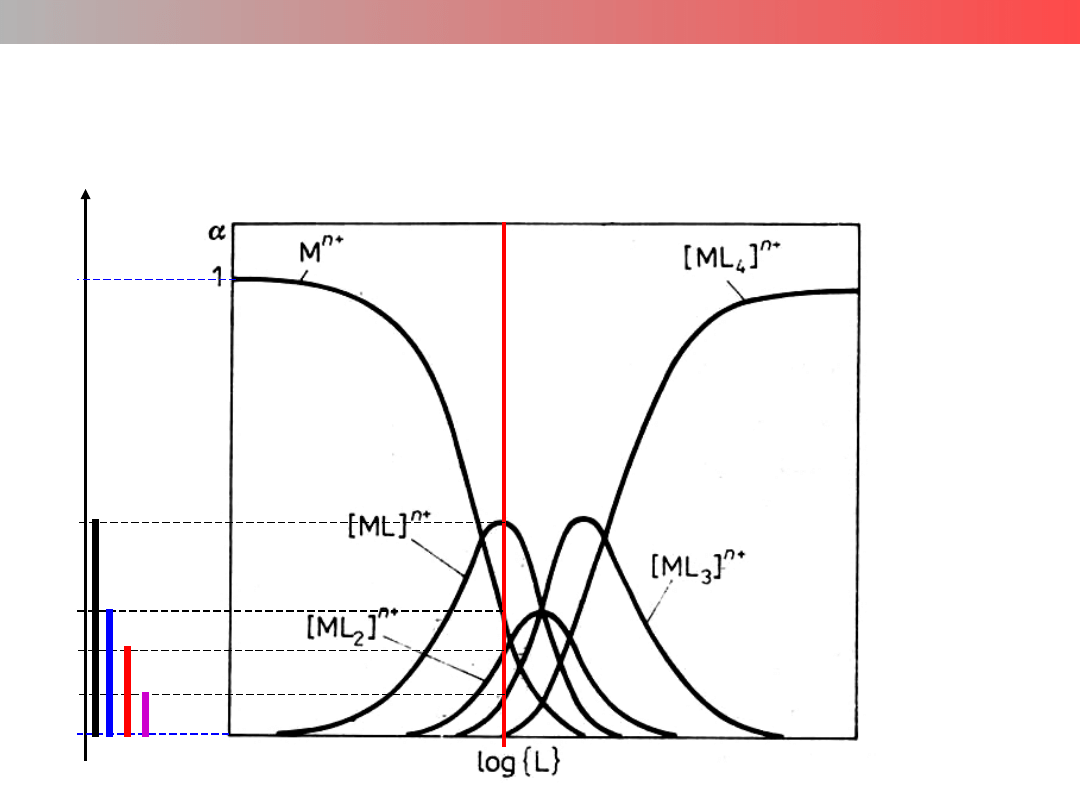
Krzywe podziału (specjacji)

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

RÓWNOWAGI CHEMICZNE

W ROZTWORACH KOMPLEKSÓW

% M

100

0

46

28

18

8

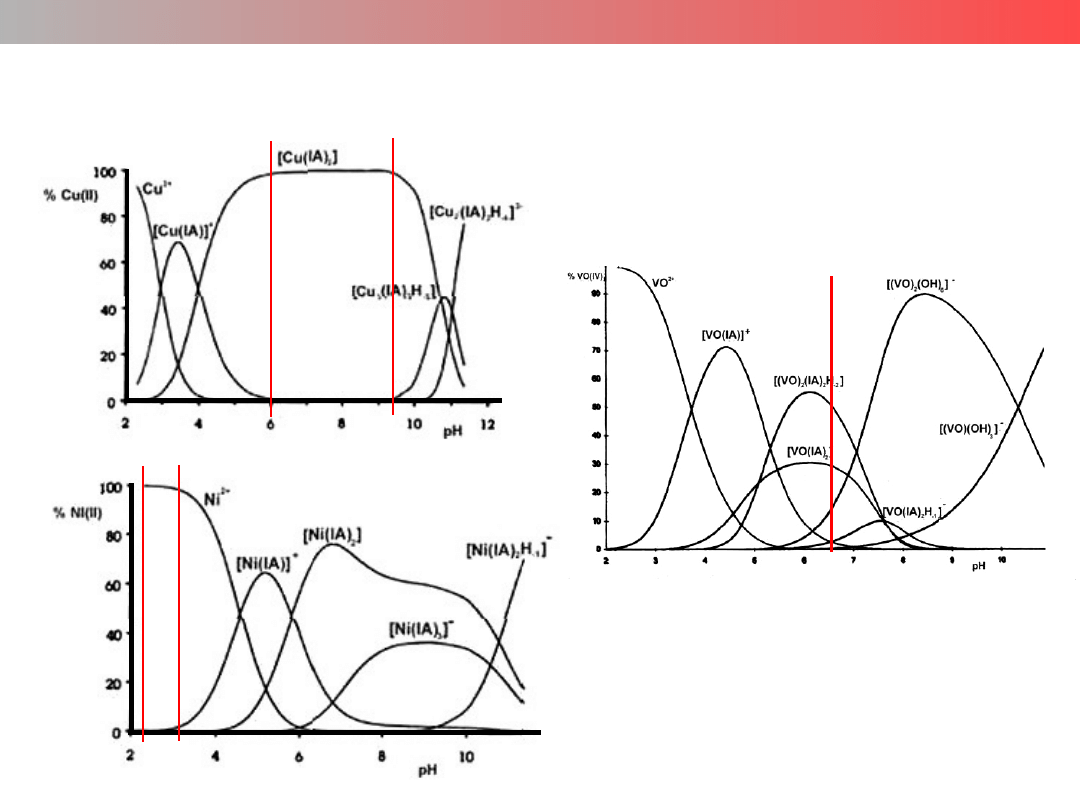
Krzywe podziału (specjacji)

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

tylko jedna

forma kompleksu

brak kompleksowania

współistnienie pięciu

form kompleksowych

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII ZWIĄZKÓW KOMPLEKSOWYCH

β

k

= Π K

n

M + kL ⇆ ML

k

=

[ML

k

]

[M] [L]

k

n=1

k

Podział (specjacja) metalu pomiędzy różne formy

Ułamek molowy metalu

w formie kompleksu

ML

n

x

n

=

[ML

n

]

c

M

c

M

–

stężenie

całkowite metalu

c

M

= [M] + [ML] + [ML

2

] + . . . [ML

k

]

[ML

n

] = β

n

· [M]·[L]

n

x

n

=

[ML

n

]

c

M

=

β

n

· [M]·[L]

n

[M] + β

1

· [M]·[L] + . . . β

k

· [M]·[L]

k

=

β

n

· [L]

n

1 + β

1

· [L] + . . . β

k

· [L]

k

x

n

=

[ML

n

]

c

M

?

x

M

= ?

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII ZWIĄZKÓW KOMPLEKSOWYCH

Ułamek molowy metalu

nieskompleksowanego

M

x

M

=

[M]

c

M

β

k

= Π K

n

M + kL ⇆ ML

k

=

[ML

k

]

[M] [L]

k

n=1

k

Podział (specjacja) metalu pomiędzy różne formy

c

M

–

stężenie

całkowite metalu

c

M

= [M] + [ML] + [ML

2

] + . . . [ML

k

]

x

M

=

[M]

c

M

=

[M]

[M] + β

1

· [M]·[L] + . . . β

k

· [M]·[L]

k

=

1

1 + β

1

· [L] + . . . β

k

· [L]

k

x

M

=

[M]

c

M

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Obliczyć stężenie wolnych jonów Sn+, jeżeli w 1,0 dm

3

1,0 M NaCl

rozpuszczono 0,65 g SnCl

2

, a pH tego roztworu wynosiło 4,0.

Stałe twardości kompleksów Sn(II) + Cl- wynoszą:
log 

1

= 1,51

log 

2

= 2,24

log 

3

= 2,03

log 

4

= 1,48

Masa molowa SnCl

2

= 189,6 g/mol

Rozwiązanie:

c

Sn

= 3,45·10

–3

[L] ≈ c

Cl

= 1,0

<<

=

1

1 + β

1

· [L] + . . . β

k

· [L]

k

x

M

=

[M]

c

M

3

48

,

1

03

,

2

24

,

2

51

,

1

4

4

3

3

2

2

1

M

10

90

,

2

5

,

344

1

10

10

10

10

1

1

L

L

L

L

1

1

x







































x

M

=

x

M

=

[M]

c

M

[M] = x

M

·

c

M

=

2,90 · 10

–3

· 3,45 · 10

–3

= 1,00 · 10

–5

M

Gdyby cały metal przeszedł
w kompleks [SnCl

4

]

2-

to stężenie

liganda zmalało by o
4·3,45·10

-3

= 0,0138 →1,38%

M

10

45

,

3

00

,

1

6

,

189

65

,

0

c

3

pocz

)

II

(

Sn











c

M

Założenie: stężenie wolnego

ligandu jest stałe,

równe początkowemu

Stężenie początkowe SnCl

2

:

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII NIEORGANICZNEJ

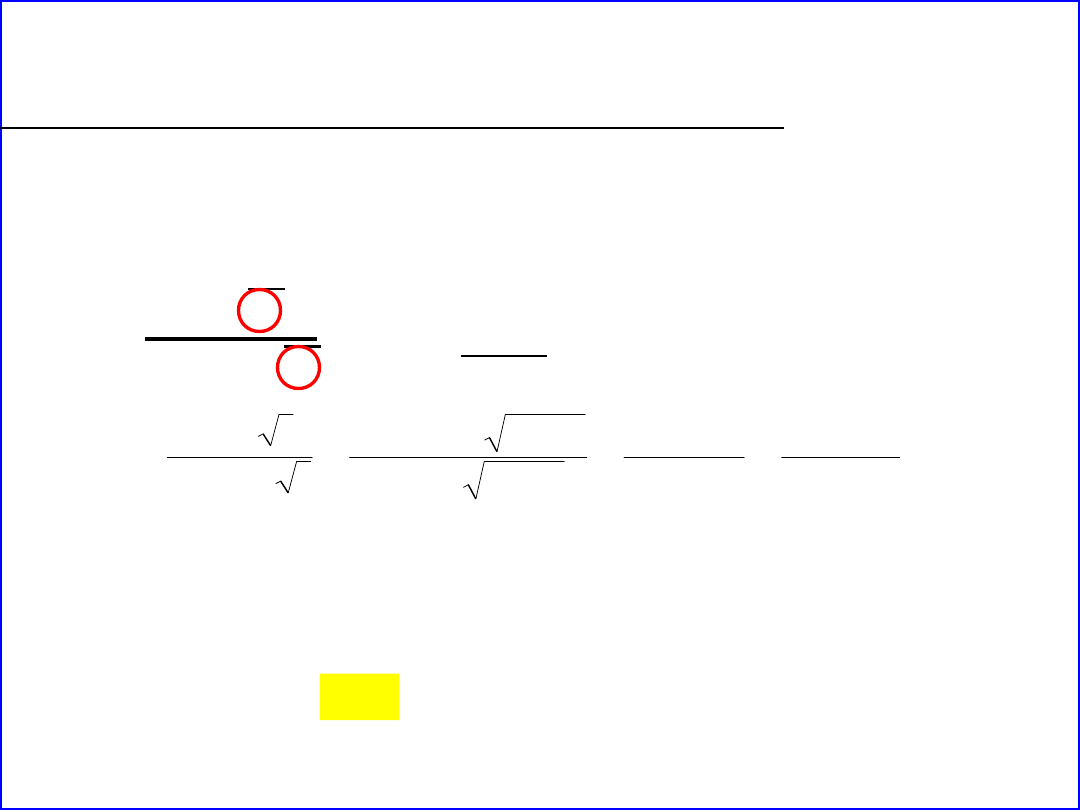
Oblicz pH ze stężenia lub aktywności jonów H

+

dla 1 dm

3

roztworu zawierającego 0,020 mola Na

2

SO

4

i

0,020 mola HCl.
a · B = 3,0; A = 0,51

Elektrolity – aktywność, wsp. aktywności, siła jonowa

a) pH na podstawie stężenia

c

HCl

= 0,020 = [H

+

]pH = –log 0,020 = 1,70

b) pH na podstawie aktywnościpH = –log a

H+

a

i

= c

i

· f

i

aktywność

stężenie

molowe

współczynnik

aktywności

1 + a B I

√

ln f

i

=

A z

i

2

I

√

I

– siła jonowa

I = ½ ∑

c

i

· z

i

2

I

= 1/2 (0,040 · 1

2

+ 0,020 · 2

2

+ 0,020 · 1

2

+ 0,020 · 1

2

=

0,080

Na

+

SO

4

2–

H

+

Cl

–

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII NIEORGANICZNEJ

Oblicz pH ze stężenia lub aktywności jonów H

+

dla 1 dm

3

roztworu

zawierającego 0,020 mola Na

2

SO

4

i 0,020 mola HCl.

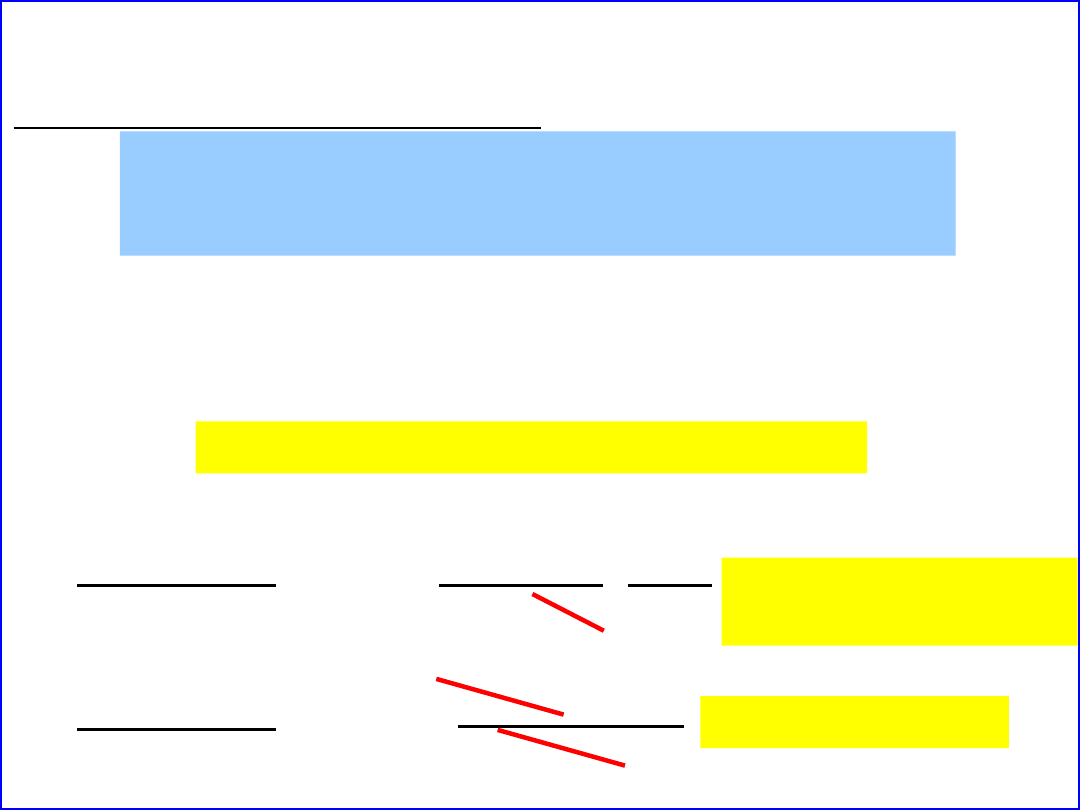
Elektrolity – aktywność, wsp. aktywności, siła jonowa

ln f

i

=

A z

i

2

I

1 + a B I

√

√

a · B = 3,0; A = 0,51

I

= 0,080

0780

,

0

283

,

1

1442

,

0

283

,

0

1

1442

,

0

080

,

0

0

,

3

1

080

,

0

1

51

,

0

I

B

a

1

I

Az

=

y

log

2

2

i

H

































H

y

= 10

-0,0780

= 0,836



H

a



H

c



H

y

= · = 0,020 · 0,836 = 0,0167

pH = - log 0,0167 = 1,78

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII NIEORGANICZNEJ

Oblicz stężenia molowe jonów w 0,010 M roztworze
H

2

CO

3

. Oblicz pH tego roztworu.

pKa1 = 6,04, pKa2 = 9,75

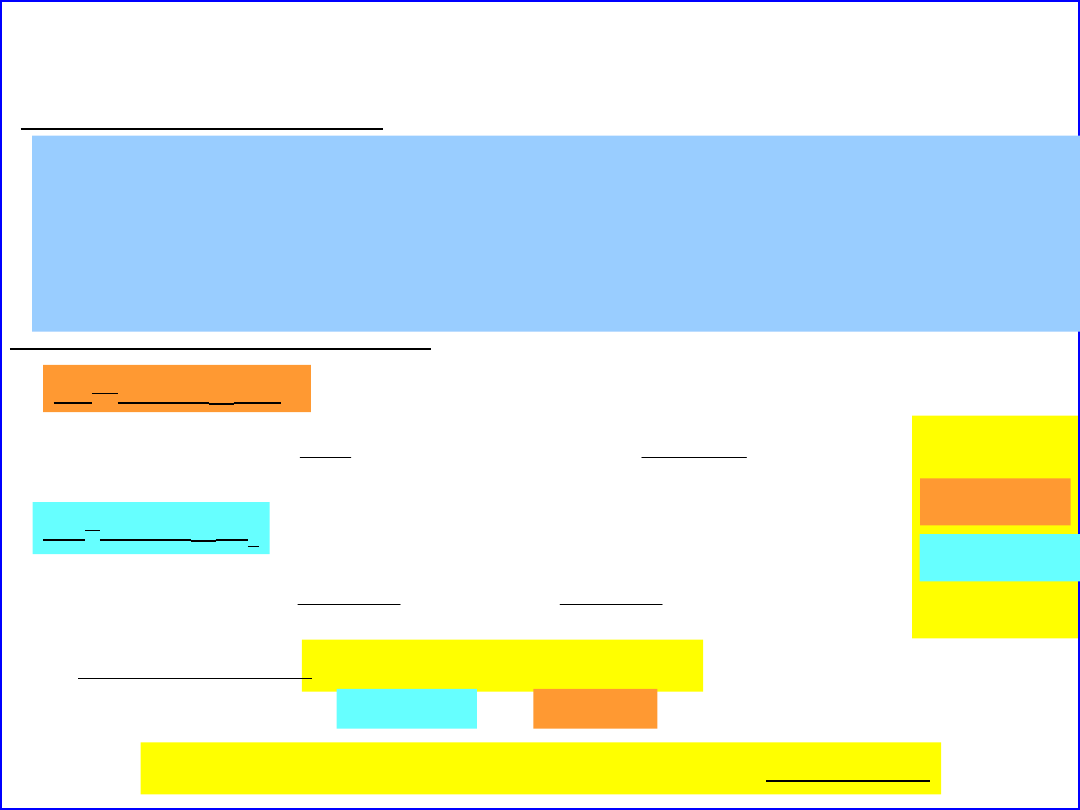
Elektrolity – kwasy wieloprotonowe

Dysocjacja H

2

CO

3

:

I stopień H

2

CO

3

⇆

H

+

+ HCO

3

-

II stopień HCO

3

–

⇆

H

+

+ CO

3

2–

Jony obecne w roztworze: H

+

, HCO

3

−

, CO

3

2−

Obliczamy [H

+

] i [HCO

3

]

−

- zaniedbujemy II stopień dysocjacji – [H

+

] ≈ [HCO

3

−

]

[H

2

CO

3

]

[H

+

]

· [HCO

3

−

]

K

a1

=

= 9,1·10

−7

=

[H

+

]

· [H

+

]

0,010 – [H

+

]

≈

[H

+

]

2

0,010

[H

+

]= 9,54·10

−5

=

[HCO

3

−

]

[HCO

3

−

]

[H

+

]

· [CO

3

2−

]

K

a2

=

= 2,7·10

−10

[HCO

3

−

]

[HCO

3

−

]

· [CO

3

2−

]

=

[CO

3

2−

] = 2,7·10

−10

Obliczamy [CO

3

]

2−

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII NIEORGANICZNEJ

Ogniwo składa się z elektrody cynowej zanurzonej w roztworze

SnCl

2

, o stężeniu 0,0100 mol/dm

3

, oraz elektrody platynowej

zanurzonej w roztworze o pH = 4,00 omywanej gazowym
wodorem pod ciśnieniem 101 kPa. Ile wynosi SEM tego
ogniwa?

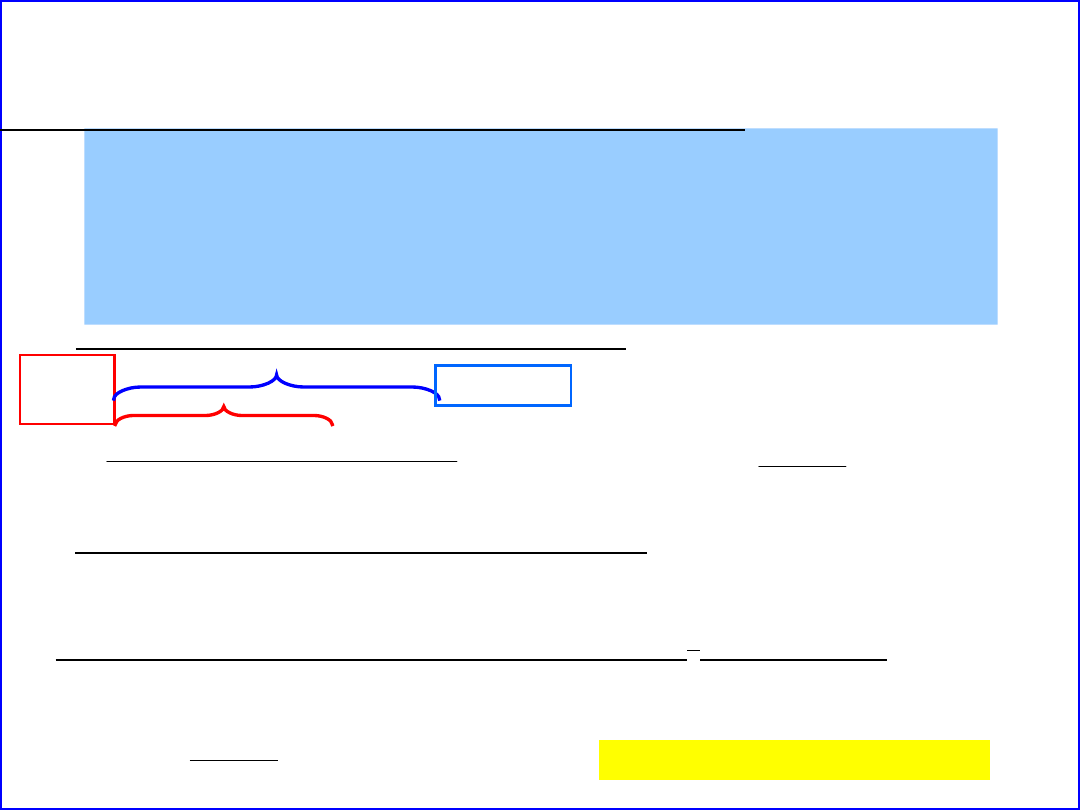
Elektrochemia – Ogniwa

V

136

,

0

E

Sn

/

Sn

o

2







Sn

2+

+ 2e  Sn

V

195

,

0

c

log

2

0592

,

0

136

,

0

c

ln

F

2

RT

E

E

2

2

2

2

Sn

Sn

o

Sn

/

Sn

Sn

/

Sn























2H

+

+ 2e  H

2

V

237

,

0

)

10

0

,

1

(

log

2

0592

,

0

c

log

2

0592

,

0

E

2

4

2
H

H

/

H

2



















redukcja

utlenianie

Pt, H

2

 H

+

 Sn

2+

 Sn

SEM = E

prawe

– E

lewe

= -0,195 – (-0,237) = + 0,042 V

Obliczamy potencjały półogniw

Schemat ogniwa:

utlenianie

redukcja

WYBRANE PROBLEMY OBLICZENIOWE

W CHEMII NIEORGANICZNEJ

Do 200 cm

3

10,00% roztworu HCl o gęstości 1,050 kg/dm

3

dodano 13,076 g metalicznego cynku. Obliczyć pH
otrzymanego roztworu. Założyć, ze cynk uległ
całkowitemu roztworzeniu.
M

Zn

= 65,38 M

HCl

= 36,46

Stechiometria np. roztwarzanie metali w kwasach

mola

,

,

,

cm

/

g

,

cm

5760

0

46

36

10

0

050

1

200

n

3

3

pocz

HCl









Obliczamy początkową liczność HCl i Zn:

masa
roztw.

masa HCl

mola

2000

,

0

38

,

65

076

,

13

n

pocz
Zn





Obliczamy liczność przereagowanego HCl:

Zn + 2HCl = ZnCl

2

+ H

2

1 : 2

mola

4000

,

0

2000

,

0

2

n

2

n

Zn

.

reak
HCl











Obliczamy końcową liczność, stężenie jonów H

+

(kwasu) i pH:

mola

1760

,

0

4000

,

0

5760

,

0

n

.

kon
HCl







3

H

dm

/

mol

8800

,

0

200

,

0

1760

,

0

c







0555

,

0

8800

,

0

log

pH







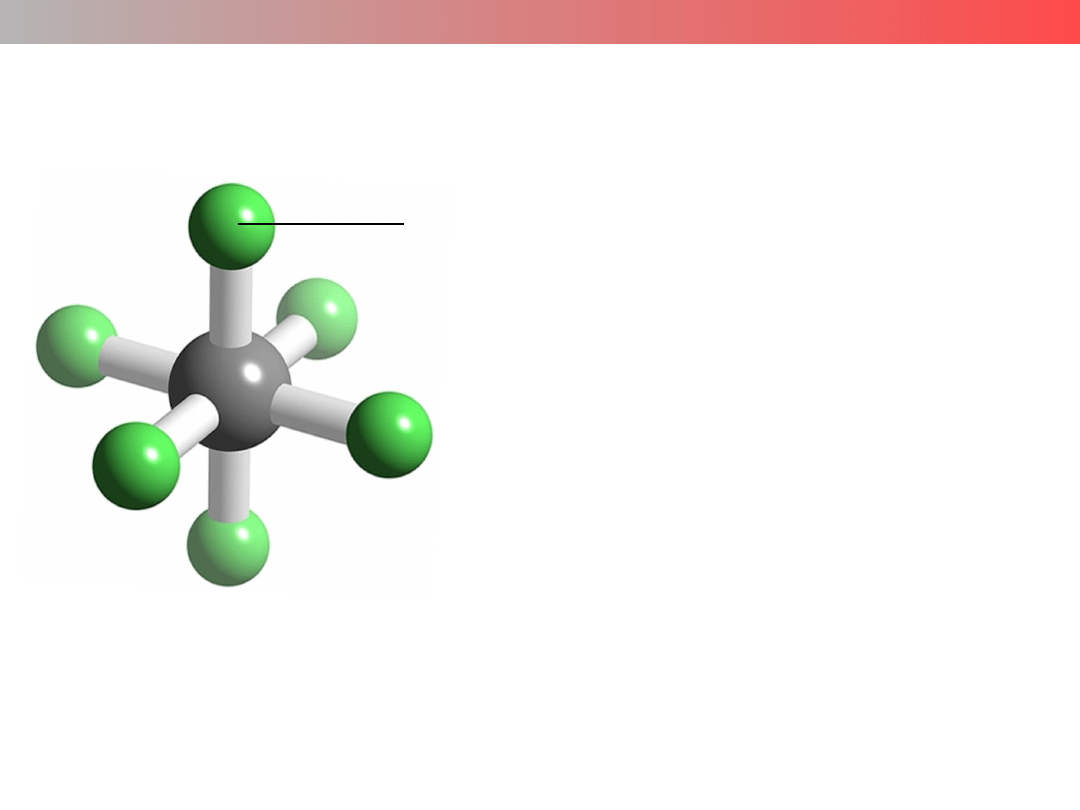
Wykład 9 – ZWIĄZKI KOMPLEKSOWE

TEORIA POLA KRYSTALICZNEGO

w CHEMII KOORDYNACYJNEJ

M

L

L

L

L

L

L

Założenie: Ligandy traktuje się jedynie jako

punktowe, ujemne ładunki elektryczne
mające wpływ na energie orbitali d.

Teoria Pola Krystalicznego wyjaśnia m. in.:

– różnice w trwałości kompleksów

– barwy kompleksów

– właściwości magnetyczne kompleksów

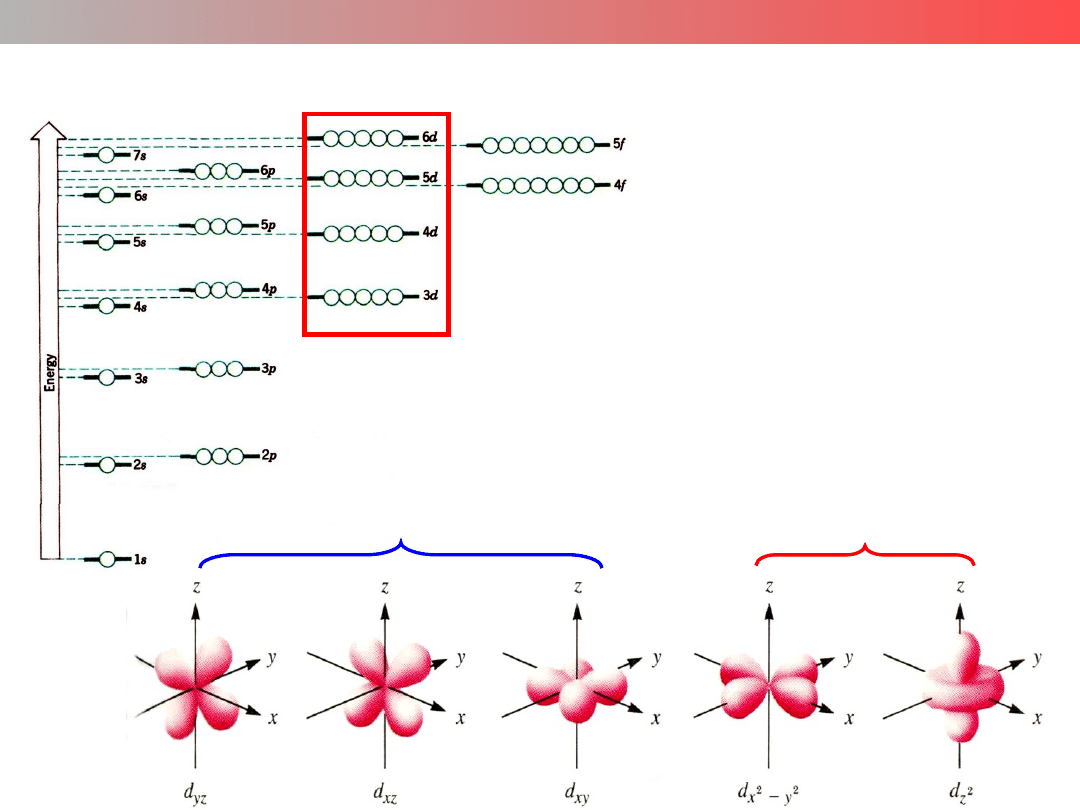
Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Diagram energetyczny orbitali atomowych

Metale przejściowe –
pierwiastki d-elektronowe

Orbitale

d

orbitale "leżą" na osiach

orbitale "leżą" pomiędzy osiami

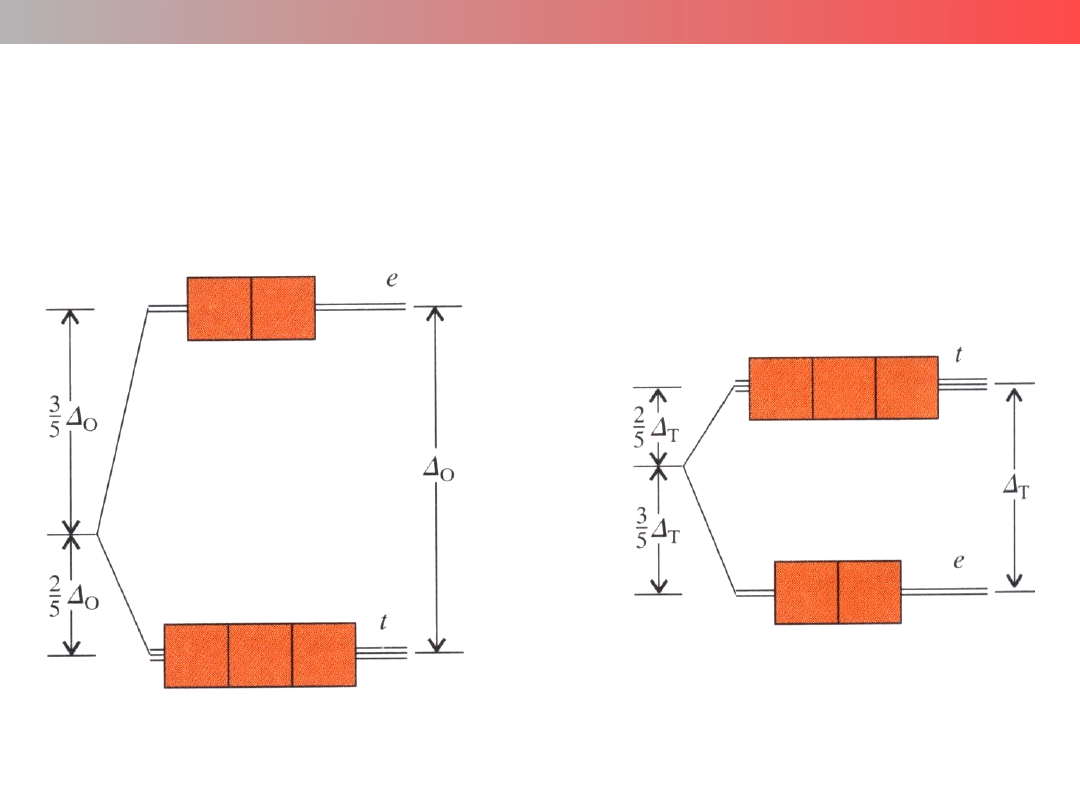
Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Orbitale d

w polu oktaedrycznym O

h

Orbitale d

w polu tetraedrycznym T

d

Δ

o

> Δ

t

Δ

o

≈ 9/4Δ

t

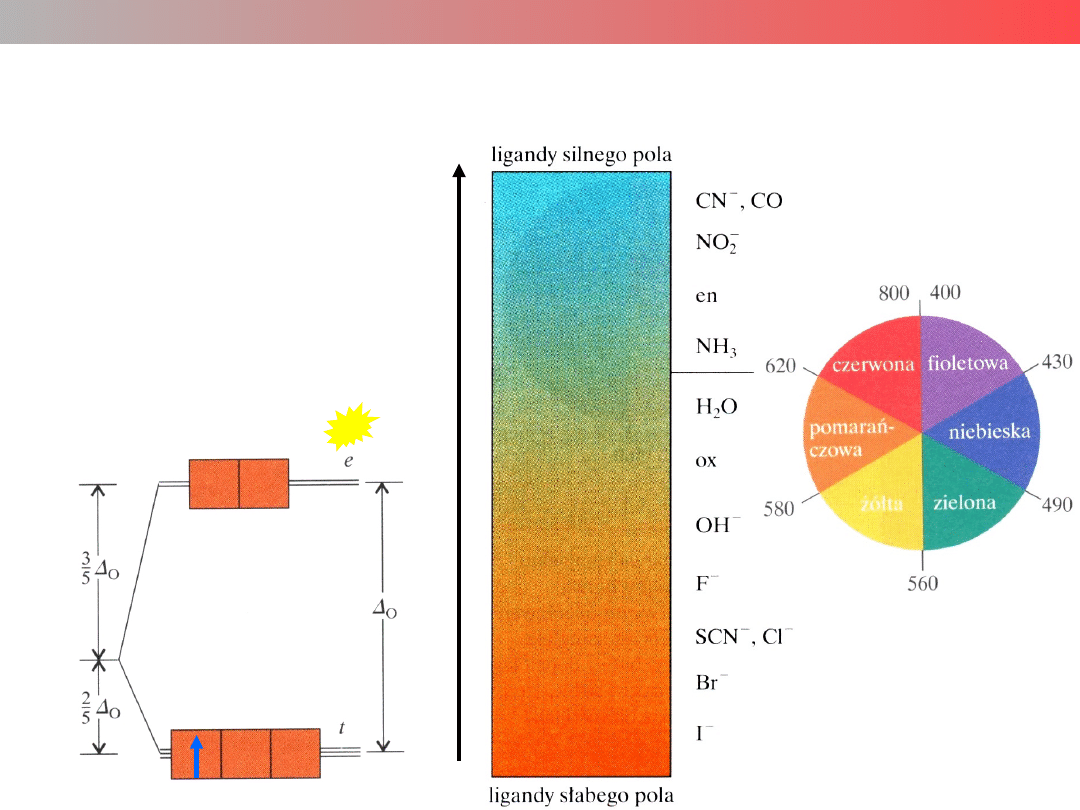
Wykład 9 – ZWIĄZKI KOMPLEKSOWE

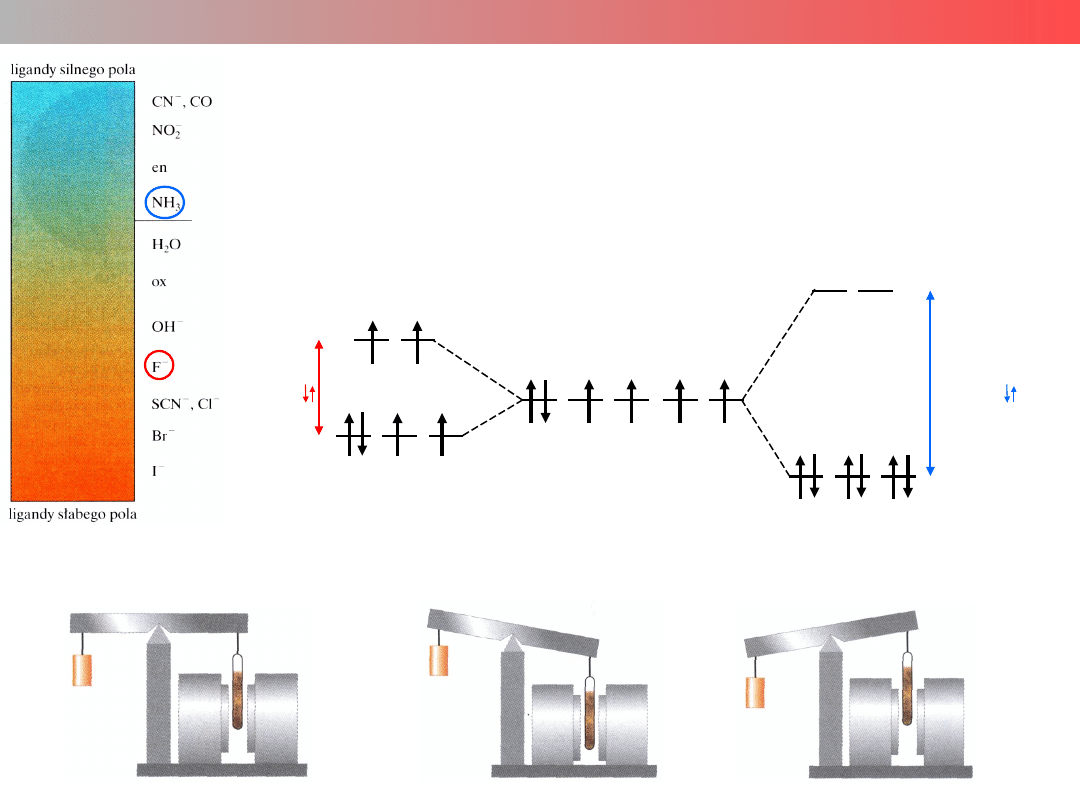
Szereg spektrochemiczny ligandów

Wielkość parametru Δ
zależy od rodzaju ligandów

Parametr Δ wyznacza się
poprzez pomiar wielkości
kwantów
absorbowanych podczas
przejścia elektronu z poziomu
t na poziom e (dla pola O

h

)

hν = Δ

o

ν

Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Kompleksy wysoko- i nisko-spinowe

Rodzaj ligandów (poprzez parametr Δ) ma wpływ na
obsadzenie elektronami rozszczepionych poziomów d, co
wywołuje różnice we właściwościach magnetycznych
kompleksów.

[CoF

6

]

3−

[Co(NH

3

)

6

]

3+

Co

3+

- d

6

S = 4·1/2 =

2

S =

0

Badanie właściwości magnetycznych substancji

paramagnetyk

diamagnetyk

brak pola mgt.

paramagnetyk

diamagnetyk

Δ<E

Δ>E

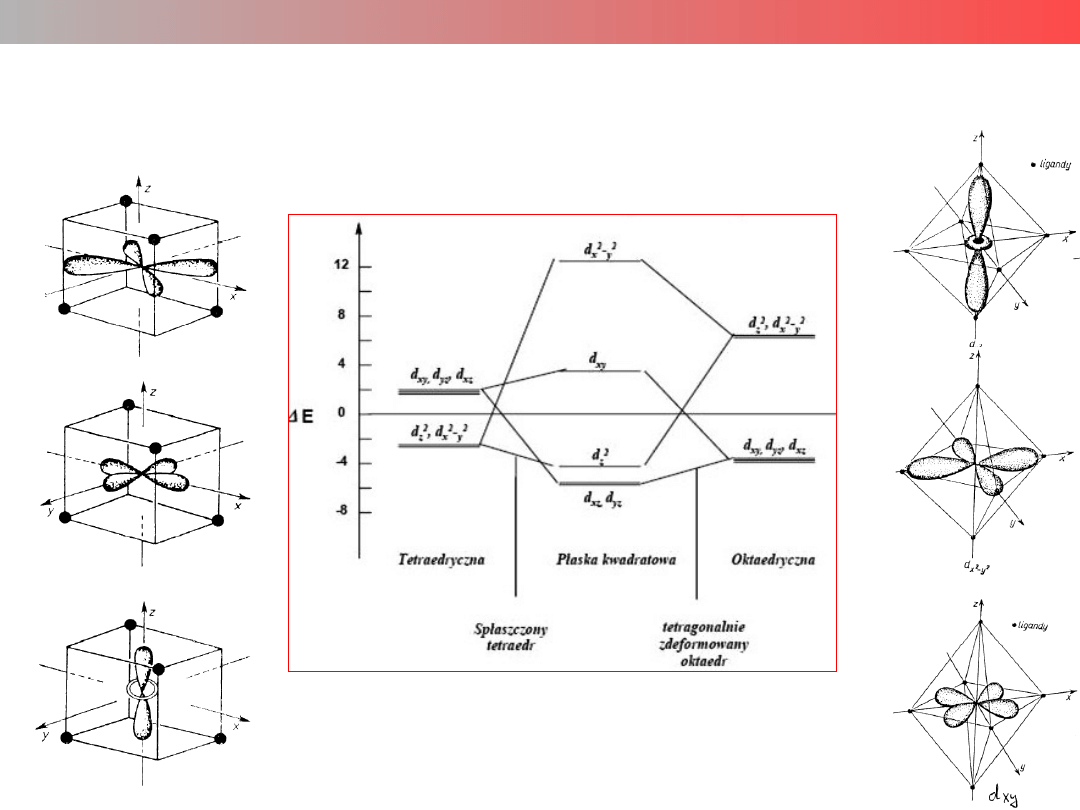
Wykład 9 – ZWIĄZKI KOMPLEKSOWE

Rozkład energetyczny orbitali d w kompleksach o różnej symetyrii