Wykład 8

Ruch falowy

1. Własności ruchu falowego

2. Prędkość fazowa i grupowa

3. Interferencja fal

4. Fale stojące

5. Dudnienia

6. Zjawisko Dopplera

1. Własności ruchu falowego

• Fale powstające w ośrodkach sprężystych (np. fale dźwiękowe). Drgania ośrodka 

wokół  położenia  równowagi  są  przekazywane  na  kolejne  części  ośrodka.  Sam 
ośrodek nie przesuwa się, a jedynie jego elementy wykonują drgania.  

      Np. fale na powierzchni wody.

 

• Fala  dobiegające  do  danego  przedmiotu  wprawiają  go  w  ruch  drgający 

przekazując mu energię (na duże odległości). 

        Energia  fal    =  energia  kinetyczna  +  potencjalna  cząstek 

ośrodka.

Cechą  charakterystyczną  fal  jest  to,  że  przenoszą  energię  poprzez 
materię  dzięki  przesuwaniu  się  zaburzenia  w  materii  a  nie  dzięki 
ruchowi postępowemu samej materii

. 

Do  rozchodzenia  się  fal  mechanicznych 

potrzebny  jest  ośrodek 

-  jego 

właściwości sprężyste decydują o prędkości rozchodzenia się fali.

FALE MECHANICZNE

Podział fal ze względu na:

(A)  kierunek drgań cząstek względem kierunku rozchodzenia 

się fali:

•  fale poprzeczne (np. lina)

•  fale podłużne (np. sprężyna, głos)

(B)  czoło  fali  (powierzchnia  łącząca  punkty  o  jednakowych 

zaburzeniach w danej chwili):

• fale płaskie (w jednym kierunku)
• fale kuliste 

2. Prędkość fazowa, równanie 

falowe

y = f(x), t = 0

Przykłąd: długi sznur naciągnięty w kierunku x, wzdłuż którego biegnie fala 
poprzeczna, y – przemieszczenie cząsteczek sznura sznura.

Po czasie t   fala przesuwa się o vt  w prawo (v - prędkość fali), czyli

               y = f(x  vt), t 

 

(fala w prawo)

Kształt fali jest taki sam w chwili 

t = 0 i t

 mamy, więc równanie fali - 

określamy funkcję 

f

. 

Obserwujemy  

wybraną część fali

 (czyli określoną 

fazę

) – chcemy, żeby 

wartość 

y

 (np. maksimum - amplituda) była cały czas takie samo, więc 

x 

 vt

 

musi być też taki sam, tzn. że gdy czas t rośnie - musi rosnąć x (czyli ruch w 
prawo).

                            

               y = f(x + vt)       

(fala w lewo)

 

Dla wybranej 

fazy

 mamy:

 

x vt = const.

 
Różniczkując względem  t  otrzymujemy

0

v

d

d





t

x

v

d

d



t

x

v - 

prędkość fazowa

              dla danego 

t

 - równanie 

f(x)

                                    

i

 

dla danego miejsca sznura 

x

 - równanie 

f(t).

Jeżeli fala biegnie w prawo to po czasie t 

)

(

2

sin

t

x

A

y

v









Równanie fali biegnącej

T  -  okres  czyli  czas,  w  którym  fala  przebiega  odległość 

równą 



 :                  



 = vT

 , czyli











 



T

t

x

A

y





2

sin

W danej chwili  

t

  taka sama faza jest w punktach      

x, x + 

, x + 2, x + 3

 

itd., oraz danym miejscu  

x

  faza powtarza się w chwilach        

t, t + T, t +2T

, 

itd. 

Po wprowadzeniu: k = 2/

 - liczby falowej i  = 2/T – częstości

 

y = A sin(kx-



t)

 

fala biegnąca w prawo

 

y = A sin(kx+



t)

 

fala biegnąca w lewo.

stąd 

prędkość fazowa fali v

   jest dana wzorem

 

 

Dla  danego  x

  otrzymujemy 

równanie  ruchu  harmonicznego 

prostego

.

v



t

x

d

d

 v = 



/T = 



/k 

lub

Pomiar prędkości fali v - badamy przemieszczanie się w czasie 

wybranej część fali

 czyli 

określonej fazy

. 

Prędkość fali zależy od:

- 

sprężystości ośrodka

 (dla sznura jest określona poprzez napinającą 

go siłę 

F

), 

- 

bezwładności ośrodka

 (związanej z masą sznura 

m

 oraz jego 

długością 

l

). 

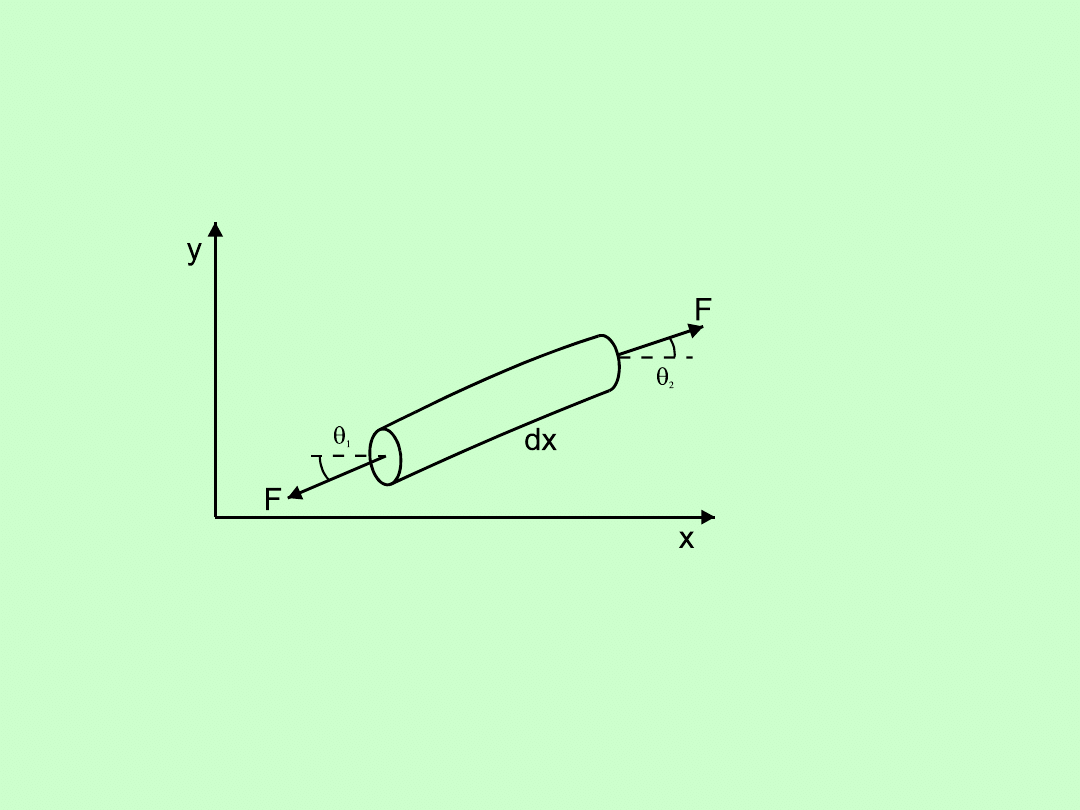
Rozpatrzmy mały wycinek sznura o długości 

dx

   i  masie 

dm =



 dx

  

  (gdzie    =  m/l          tj.  masa  przypadająca  na  jednostkę  długości 
sznura) .

. 

θ

1

, θ

2

 - kąty pomiędzy końcami wycinka sznura a osią 

x. 

Dla małych kątów   

θ  sin θ   dy/dx

Wypadkowa pionowa siła

 tj. siła wychylająca sznur w kierunku y wynosi :

1

2

1

2









F

F

F

F

F

wyp









sin

sin

Z II zasady dynamiki 

F=ma=m(dv/dt)

2

1

2

)

(

)

(

v

t

y

dx

dx

t

t

v

dm

Fd

F

F

F

y

y

wyp

























2











2

)

(

t

y

dx

Fd







2





stąd

2

2

t

y

F

x















lub

(Uwaga: pochodne 
cząstkowe, bo funkcja 
y = f (x,t) – dwie zmienne). 

Uwzględniając, że 

θ = y/x

 otrzymujemy 

2

2

2

2

t

y

F

x

y













Równanie falowe

Podstawmy do tego równania odpowiednie pochodne 
funkcji 

)

sin(

)

,

f(

t

x

k

A

t

x

y









)

sin(

t

x

k

A

t

y















2

2

2

)

sin(

t

x

k

Ak

x

y













2

2

2

2

2





F

k 





F

k





v

W wyniku podstawienia

otrzymujemy

 skąd możemy obliczyć prędkość fali: 

Sinusoidalna fala może być przenoszona wzdłuż struny z prędkością 

niezależną od amplitudy i częstotliwości. 

2

2

2

2

2

1

t

y

x

y









v



Równanie falowe struny możemy zapisać w 
postaci: 

Otrzymane 

równanie falowe

 stosuje się do wszystkich 

rodzajów rozchodzących się fal.

 Np. fale dźwiękowych czy elektromagnetycznych

. 

 

y

1

 = A sin(kx – 



t – 



)

              y

2

 = A sin(kx – 



t) 

3. Interferencja fal

Rozważmy dwie fale o równych częstotliwościach i amplitudach ale 
o fazach różniących się o 



. 

fala wypadkowa (

zasada superpozycji

) jest sumę 

                 y = y

1

 + y

2

.

Korzystając ze wzoru na sumę sinusów otrzymujemy:

 

                  y = 2A cos(/2) sin(kx – t – /2)

 

 

Jest równaniem fali sinusoidalnej o amplitudzie 2Acos(



/2). 

Dla 

 = 0 fale spotykają się zgodnie w fazie (wzmacniają), 

dla 

 = 180 wygaszają. 

Rozważmy  teraz  dwa  ciągi  falowe  biegnące  w  przeciwnych 

kierunkach tzn.

 

y

1

 = A sin(kx – 



t)

                                       y

2

 = A sin(kx + 



t)

np. falę padającą i odbitą.

Fala  wypadkową
 

                      y = y

1

 + y

2

 = 2A sinkx cost

 

 

Równanie fali stojącej.

 

Zauważmy,  że  cząstki  drgają  ruchem  harmonicznym  prostym.  Cząstki 

mają tę samą częstość ale 

różną amplitudę

 zależną od położenia cząstki x. 

Punkty  kx  =  /2,  3/2,  5/2,  itd.  czyli  x  =  /4,  3/4,  5/4  itd.  mające 

maksymalną amplitudę nazywamy 

strzałkami

 

Punkty  kx  =  ,  2,  3  itd.  czyli  x  =  /2,  ,  3/2  itd.  mające  zerową 

amplitudę nazywamy 

węzłami

. 

4. Fale stojące

Układ drgający

Jeżeli  struna  zamocowana  na  obu  końcach  zostanie  najpierw 

wygięta  a  następnie  puszczona,  to  wzdłuż  struny  rozchodzą  się 
drgania  poprzeczne.  Zaburzenia  te  odbijają  się  od  zamocowanych 
końców i w wyniku interferencji powstaje 

fala stojąca

. 

Drgania  struny  wytwarzają  w  otaczającym  powietrzu 

dźwiękowe 

fale podłużne

 (fale akustyczne). 

Warunkiem powstawania fal, jest nieruchomość obu końców struny, 

czyli istnienie 

węzłów fali stojącej

 na tych końcach (mogą powstać 

fale stojące o różnej długości). 

n

L

n

2





Długości fal spełniają związek: 



F

L

n

L

n

f

n

2

2





v

v

T









v

a częstotliwość rezonansów:

ale

Najniższa częstość - 

częstość podstawowa,

 

a 

pozostałe 

wyższymi 

harmonicznymi

 

(alikwotami).

Cztery rodzaje drgań jakie powstają w strunie o 
długości L zamocowanej na końcach są pokazane na 
rysunku poniżej. 

Takie fale stojące nazywamy

 

rezonansami

.

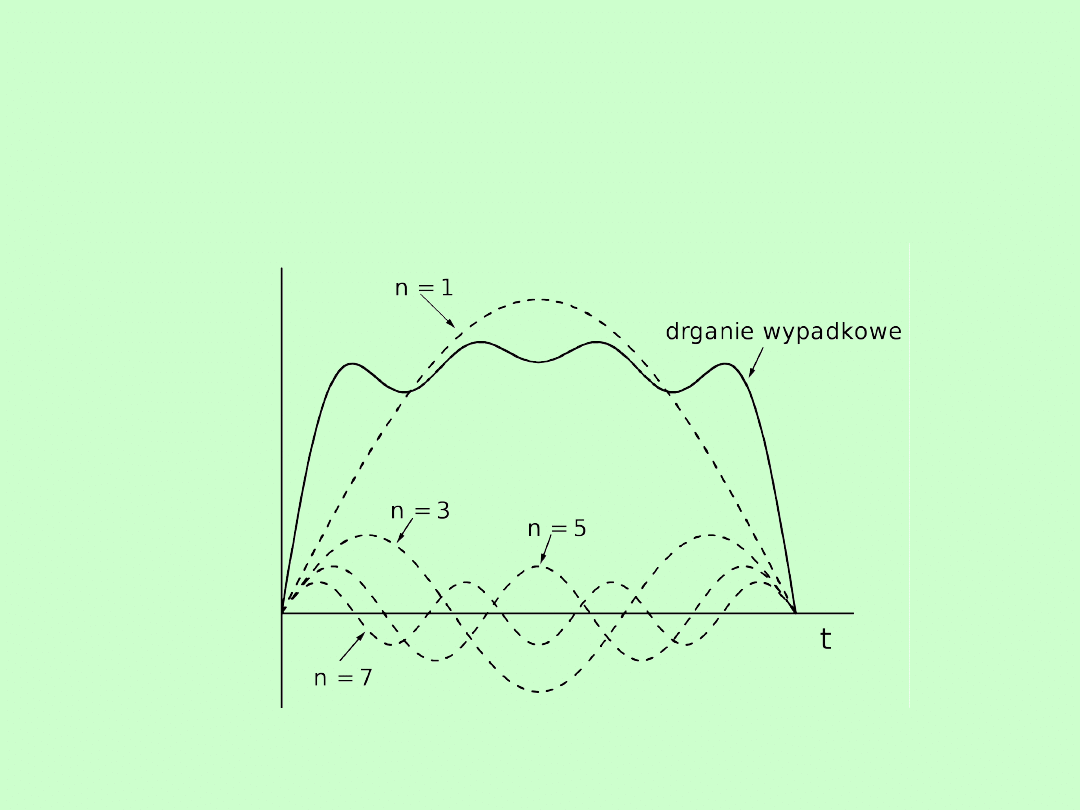
W  drganiach  oprócz  drgania  podstawowego  występują  również 

drgania  harmoniczne

,  a  dźwięki  jakie  odbieramy  są  wynikiem 

nakładania się tych drgań. 
O  jakości  instrumentu  (jego  barwie)  decyduje  właśnie  to  ile 
alikwotów jest zawarte w dźwięku i jakie są ich natężenia. 
Przykładowo, 

drganie wypadkowe struny

 będące złożeniem 

tonu 

podstawowego  (n  =  1)

  i 

wyższych  harmonicznych  (n  =  3,  5,  7)

  o 

różnych amplitudach jest pokazane na rysunku poniżej.

Wypadkowe drganie

 (chociaż okresowe) 

nie jest harmoniczne

 (nie 

daje się opisać funkcją sinus lub cosinus).

 

5. Dudnienia ‑ modulacja amplitudy

Superpozycja fal - 

interferencja w przestrzeni

 (dodawanie fal o tej 

samej częstości). 

Interferencja w czasie

 - pojawia się gdy przez dany 

punkt  w  przestrzeni  przebiegają  w  tym  samym  kierunku  fale  o 
trochę różnych częstotliwościach. 

Wychylenie wywołane przez jedną falę ma postać
 

y

1

 = Acos2



v

1

t

 y

2

 = Acos2



v

2

t

więc 

y = y

1

 + y

2

 = A(cos2



v

1

t + cos2



v

2

t)

Ze wzoru na sumę cosinusów 

t

v

v

t

v

v

A

y











 













2

2

cos

2

2

cos

2

2

1

2

1





Drgania wypadkowe - drgania o częstości
 

v

srednie

 = (v

1

 + v

2

)/2

 która jest średnią dwóch fal, i o amplitudzie (wyrażenie w nawiasie 
kwadratowym) zmieniającej się w czasie z częstością 
 

v

amp

 = (v

1

 – v

2

)/2

 
Jeżeli częstotliwości v

1

 i v

2

 są bliskie siebie to amplituda zmienia się 

powoli. Mówimy, że mamy do czynienia z modulacją amplitudy AM 
(stosowana np. w odbiornikach radiowych). 

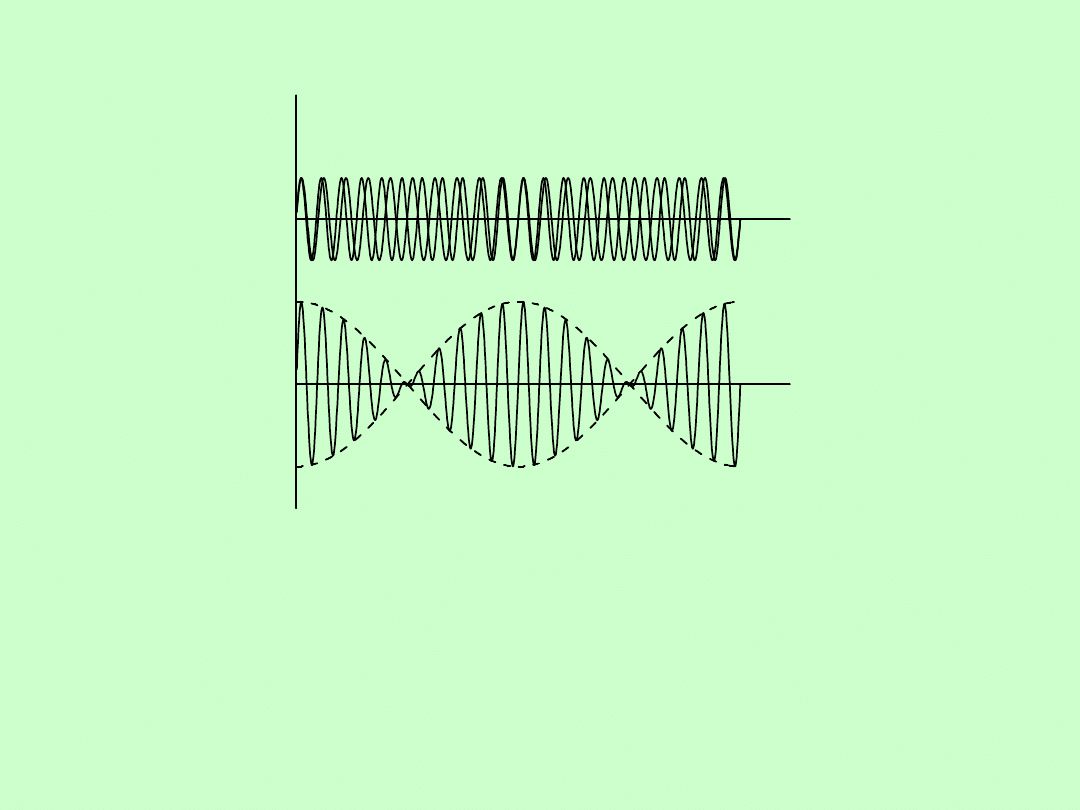
Dla fal dźwiękowych modulacja amplitudy - 

dudnienienia

 - przejawia 

się jako zmiana głośności nazywana (rysunek).

y

y

t

t

 

6. Zjawisko Dopplera

Źródło dźwięku spoczywa, a obserwator porusza się w kierunku źródła 
z prędkością 

v

o

. Nieruchomy obserwator odbierał by 

vt/



 fal w czasie 

t

. Teraz odbiera jeszcze dodatkowo 

v

o

t/



 fal. 

Częstość słyszana przez obserwatora 

v

t

t

t

v

o

o

o

v

v

v

v

v

v

v



















'

v

v

v

o

v

v





'











 



z

o

v

v

v

v

v

v



'

gdzie v' - częstość odbierana przez obserwatora, v - częstość źródła, 
v - prędkość fali, v

o

 - prędkość obserwatora, v

z

 - prędkość źródła. 

Znaki "górne" w liczniku i mianowniku odpowiadają zbliżaniu się, a 
znaki dolne oddalaniu się obserwatora i źródła.