Metody sieciowe

rozwiązywania obwodów

liniowych prądu

sinusoidalnego w stanie

ustalonym

Zagadnienia

• Metoda oczkowa
• Metoda węzłowa
• Zasada superpozycji
• Twierdzenia o zastępczym źródle energii

(Thevenina – źródło napięcia, Nortona –
prądu)

• Bilans mocy obwodu
• Dopasowanie gałęzi pasywnej do obwodu

(ze względu na moc czynną)

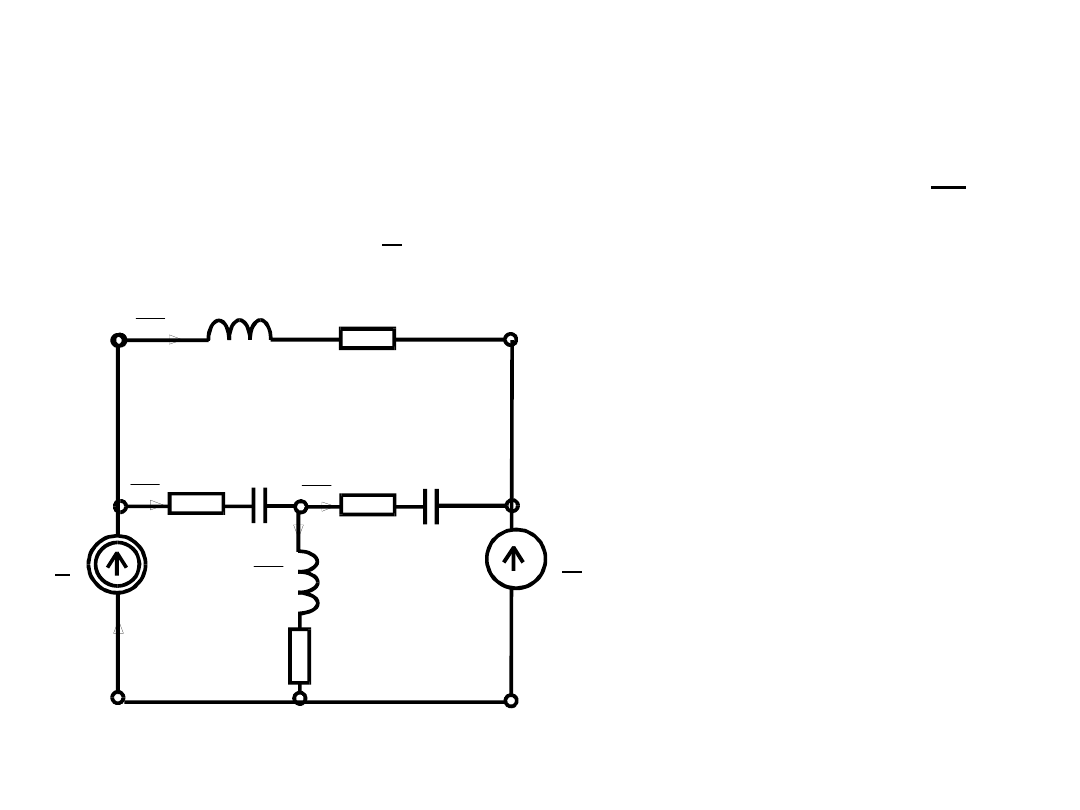
Zadanie 1

Stosując zasadę superpozycji
wyznaczyć prąd w gałęzi 4. Dane: E
= 50e

j90°

V, J = 2e

j180°

A,

R

1

= 50 ,

R

2

= 80 ,

R

3

= 80 ,

R

4

= 30 ,

X

C1

= 50 ,

X

L2

= 80 ,

X

C3

= 50 ,

X

L4

= 80 .

4

2

3

1

I

I

I

I

R

R

C

C

L

L

R

R

4

2

3

1

4

2

3

1

J

E

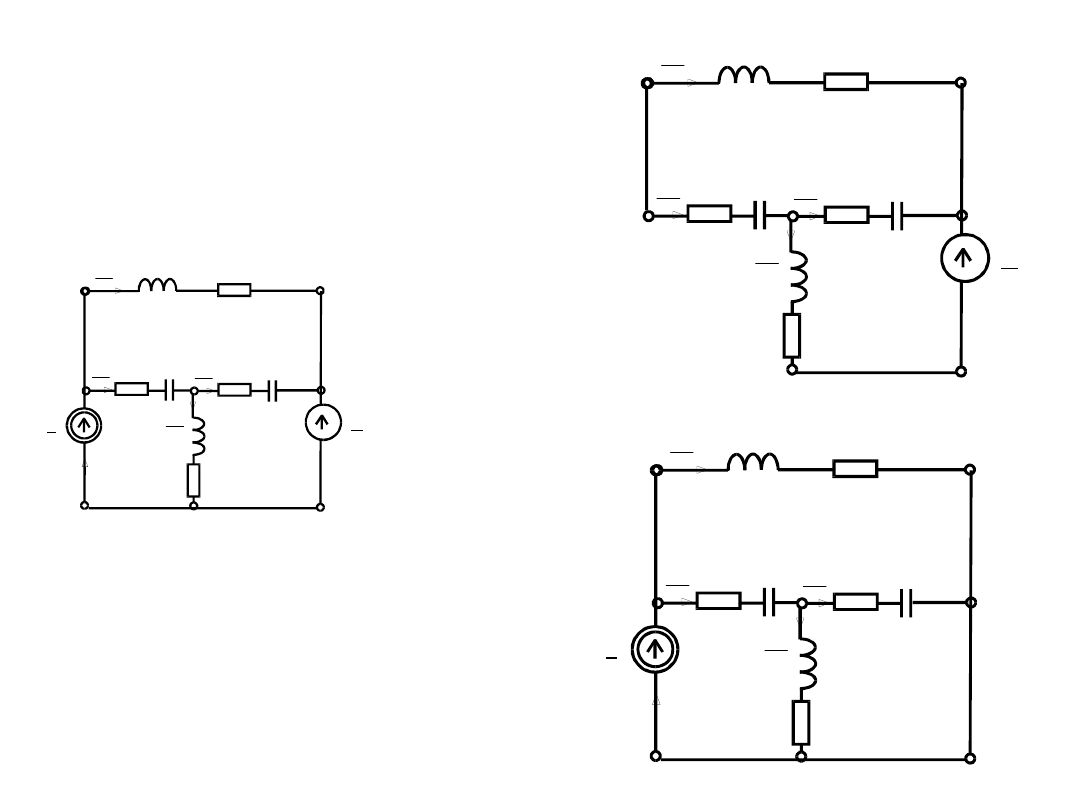
Zasada
superpozycji:

Rozdzielenie źródeł:
I

4

= I

4

E

+ I

4

J

4

2

3

1

I

I

I

I

R

R

C

C

L

L

R

R

4

2

3

1

4

2

3

1

J

E

4

E

E

E

E

2

3

1

I

I

I

I

R

R

C

C

L

L

R

R

4

2

3

1

4

2

3

1

E

4

J

J

J

J

2

3

1

I

I

I

I

R

R

C

C

L

L

R

R

4

2

3

1

4

2

3

1

J

=

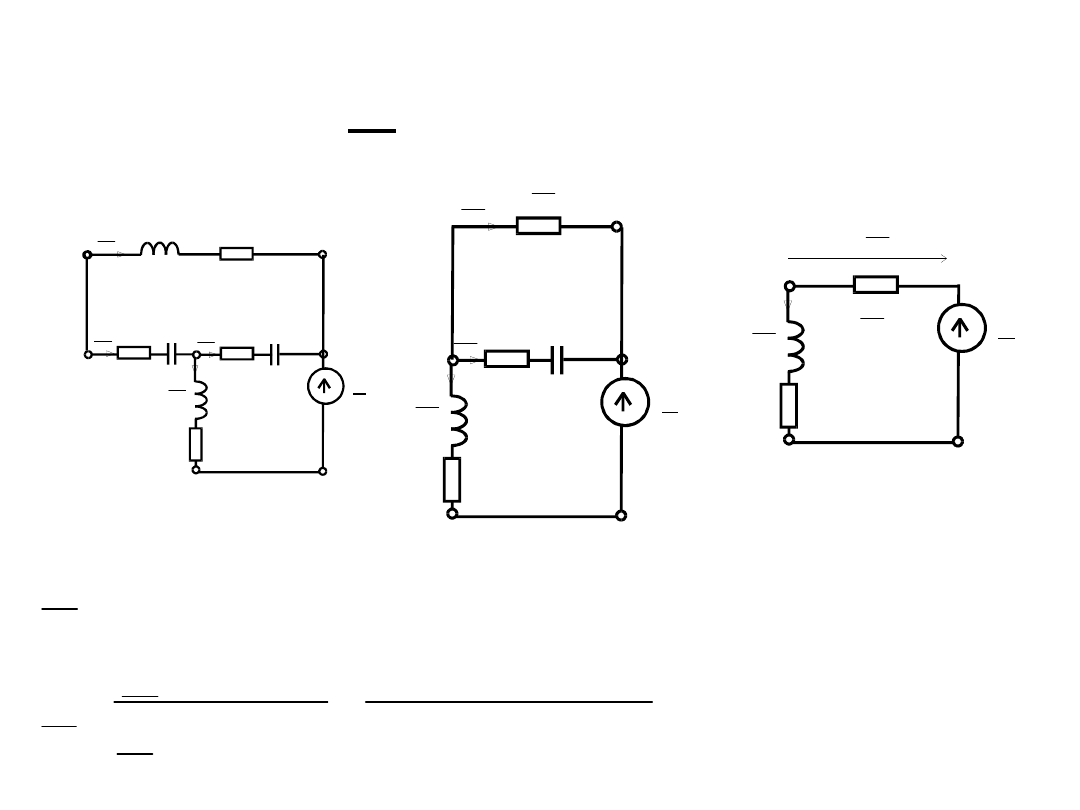
Obwód E

4 E

E

E

E

2

3

1

I

I

I

I

R

R

C

C

L

L

R

R

4

2

3

1

4

2

3

1

E

4

E

E

E

2

3

I

I

I

Z

R

C

L

R

4

2

3

2

3

E



E

2

I

R

L

Z

U

2

2

3

3

E





















30

80

1

4

4

1

4

j

X

X

j

R

R

Z

C

L



 



























77

.

3

8

.

49

20

160

50

80

30

80

3

3

4

3

3

4

3

j

j

j

j

jX

R

Z

jX

R

Z

Z

C

C

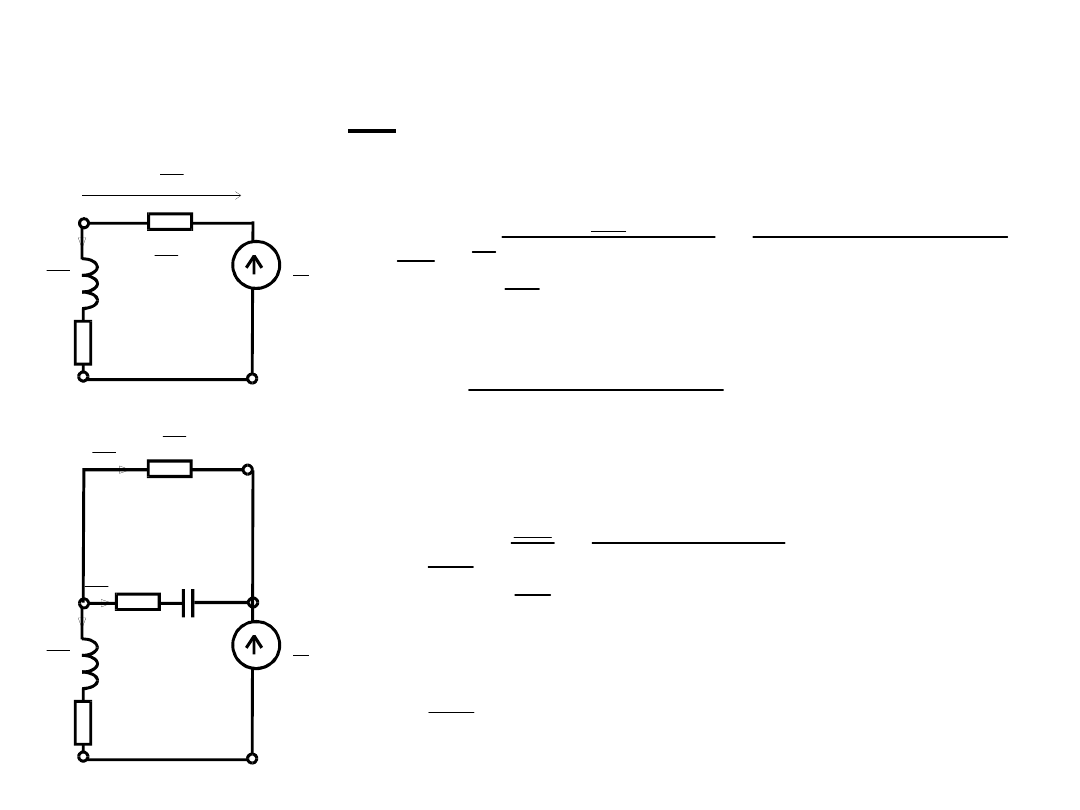
Obwód E

E

2

I

R

L

Z

U

2

2

3

3

E



















23

.

76

8

.

129

77

.

3

8

.

49

50

2

2

3

3

3

j

j

j

jX

R

Z

Z

E

U

L













30

80

63

.

13

46

.

9

4

3

4

j

j

Z

U

I

E

4

E

E

E

2

3

I

I

I

Z

R

C

L

R

4

2

3

2

3

E





V

j

j

j

j

63

.

13

46

.

9

23

.

76

8

.

129

77

.

3

8

.

49

50











A

j

I

E

110

.

0

160

.

0

4







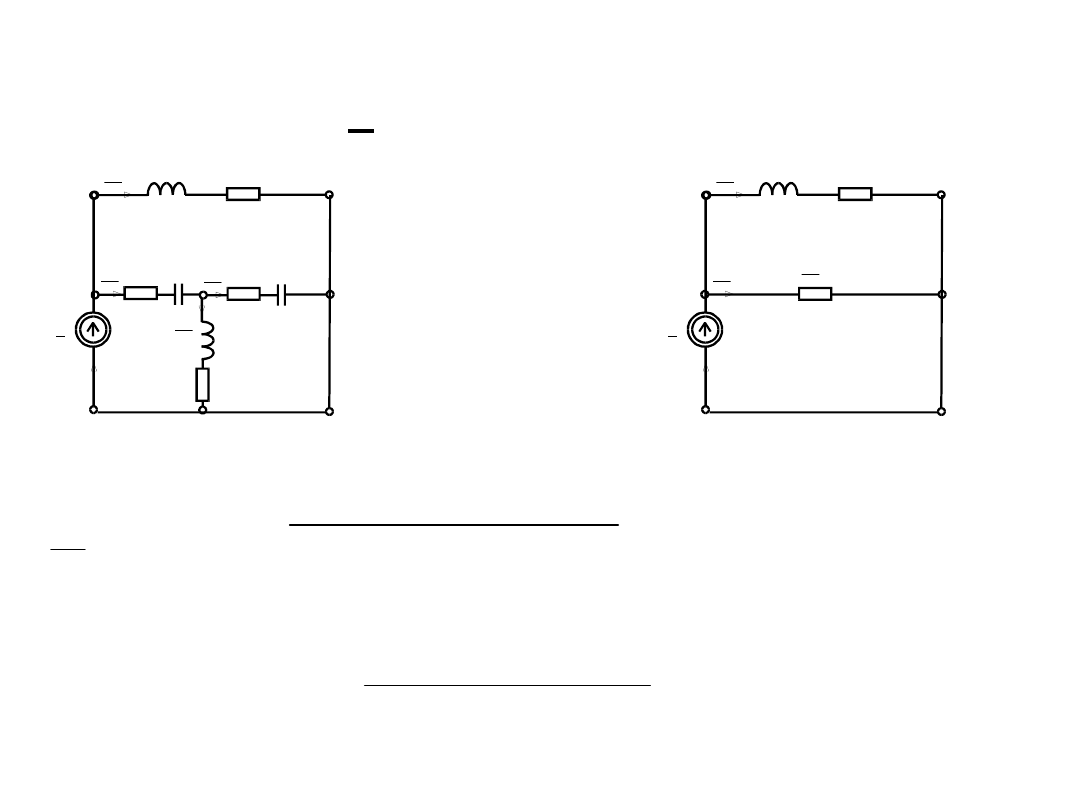
Obwód J





























3

2

3

2

3

3

2

2

1

1

3

C

L

C

L

C

X

X

j

R

R

jX

R

jX

R

jX

R

Z

4

J

J

J

J

2

3

1

I

I

I

I

R

R

C

C

L

L

R

R

4

2

3

1

4

2

3

1

J

























283

.

47

51

.

115

30

160

50

80

80

80

50

50

j

j

j

j

j

4

J

J

1

I

I

Z

R

L

3

4

4

J



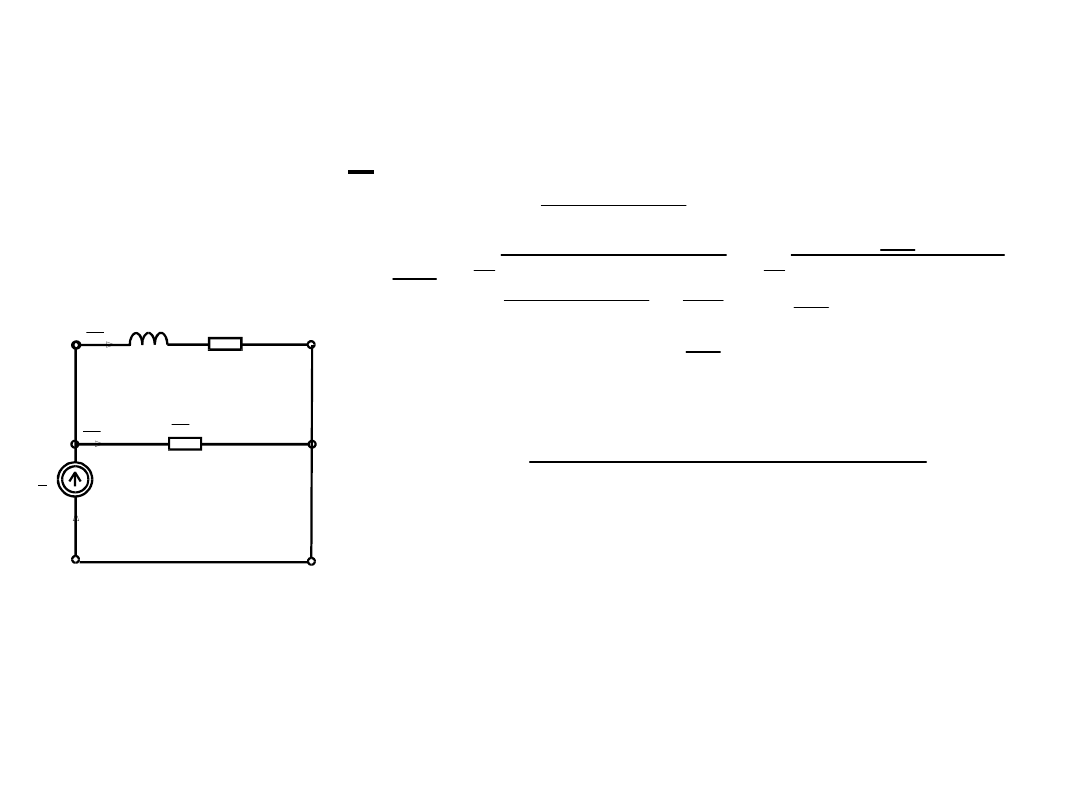
Obwód J















80

30

283

.

47

51

.

115

283

.

47

51

.

115

2

j

j

j

4

J

J

1

I

I

Z

R

L

3

4

4

J

















4

4

3

3

3

4

4

4

4

4

1

1

1

L

L

L

J

jX

R

Z

Z

J

Z

jX

R

jX

R

J

I

A

j 958

.

0

372

.

1







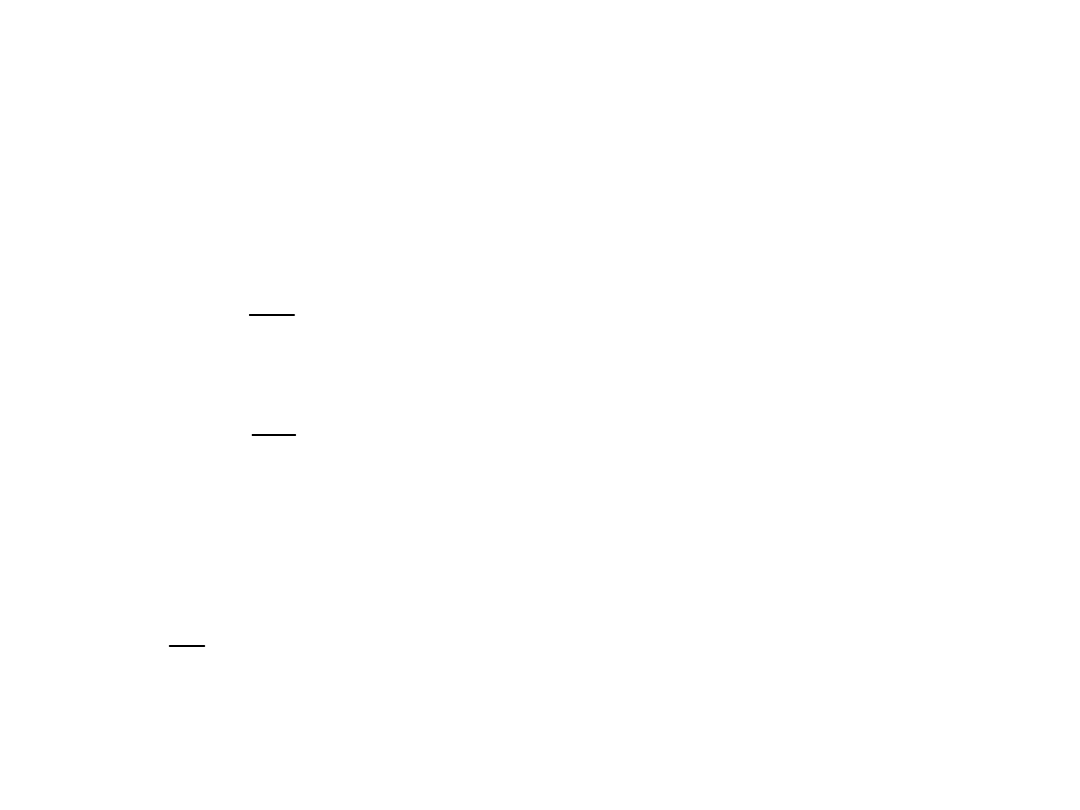
Wynik:

A

j

I

E

110

.

0

160

.

0

4







A

j

I

J

958

.

0

372

.

1

4







A

j

I

848

.

0

532

.

1

4







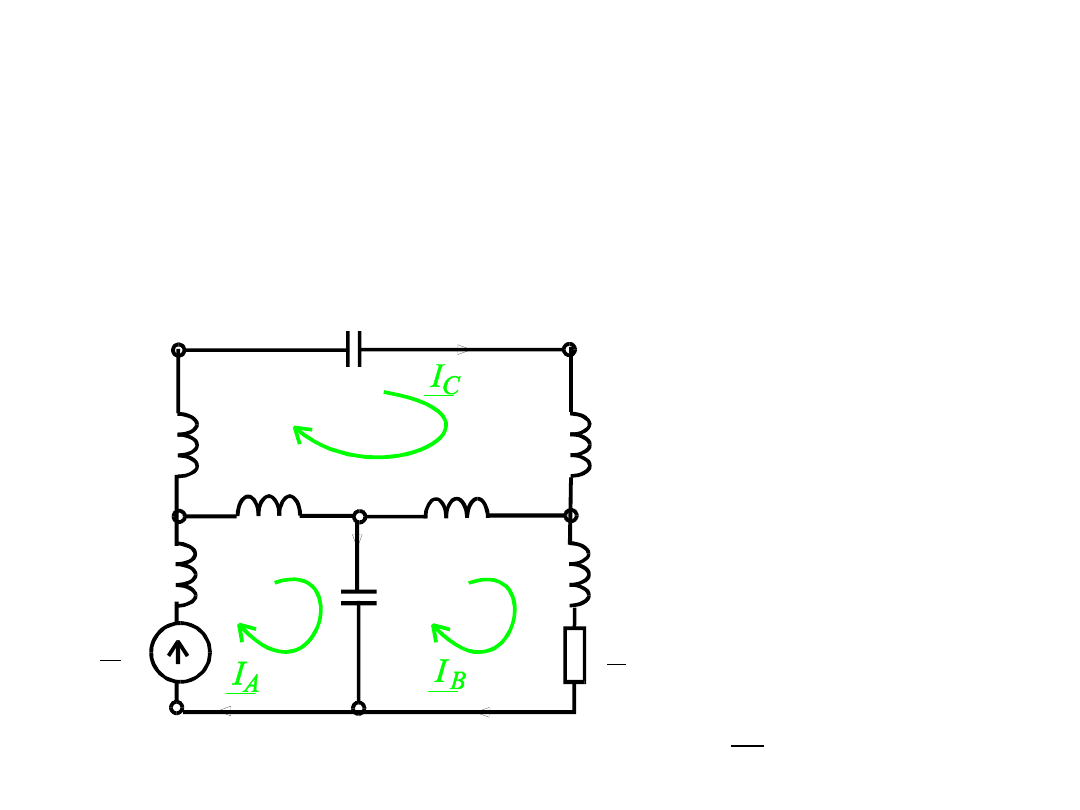
Zadanie 2

Obliczyć prądy gałęziowe stosując
metodę oczkową. Dane: e(t)=
10cos(10

6

t+60) V,

L

1

= 4 mH,

L

2

= 1 mH,

C

1

= 0.5 nF,

C

2

= 0.16(6)

nF,
L

M

= 1 mH,

Z = -j1 k

Z

C

C

L

L

L

L

L

L

2

1

M

M

1

1

2

2

E

Reaktancje obwodu

wynoszą:

X

L1

= 4 k, X

L2

= 1 k,

X

C1

= 2 k, X

C2

= 6 k,

X

M

= 1 k,

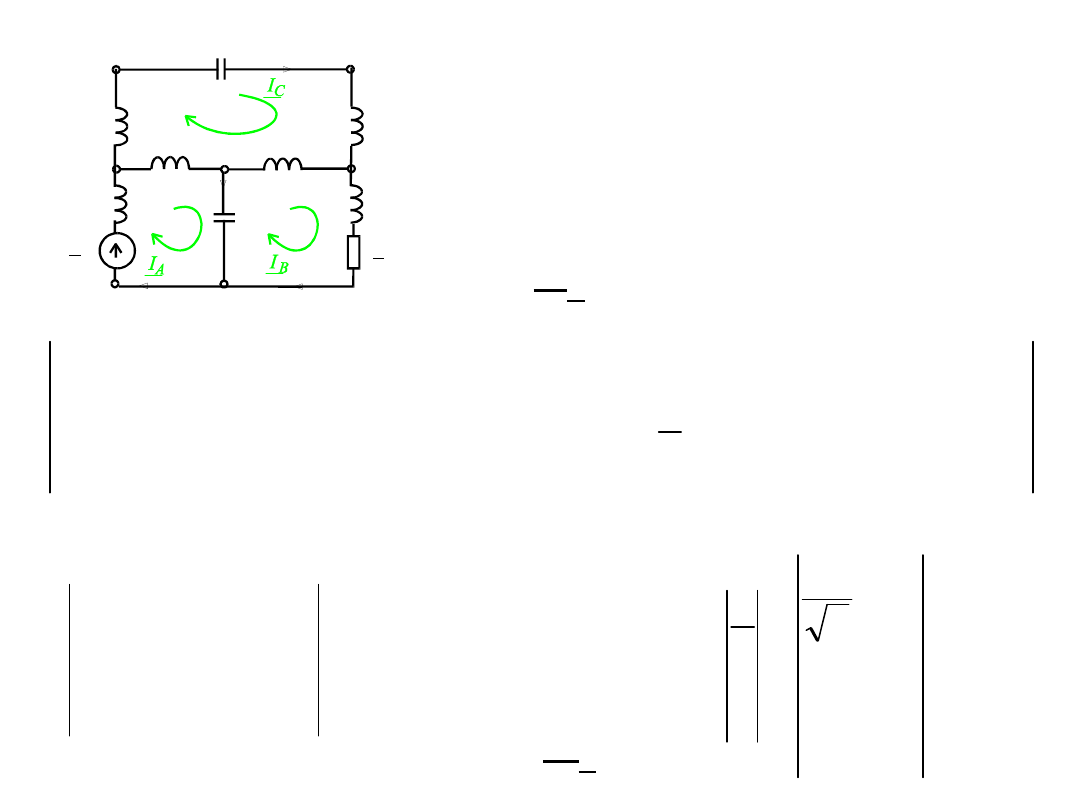
Macierz
impedancji
obwodowych:
[Z

0

]=

Wektor

napięć

obwodowy

ch [E

0

]=













2

2

1

1

1

1

1

1

2

2

C

M

L

M

M

M

C

M

L

C

M

C

C

M

L

X

X

X

j

jX

jX

jX

Z

X

X

X

j

jX

jX

jX

X

X

X

j























2

1

1

1

2

2

1

2

3

j

j

j

j

j

j

j

j

j













V

e

E

j

0

0

2

10

0

0

60





Z

C

C

L

L

L

L

L

L

2

1

M

M

1

1

2

2

E

Równanie prądów

obwodowych:

Przybiera postać:

Skąd: I

A

= 10/0.7e

-j30°

mA,

I

B

= 10e

j150°

mA, I

C

= 0 mA.

    

0

0

0

E

I

Z

































































0

0

2

10

2

1

1

1

2

2

1

2

3

60



j

C

B

A

e

I

I

I

j

j

j

j

j

j

j

j

j

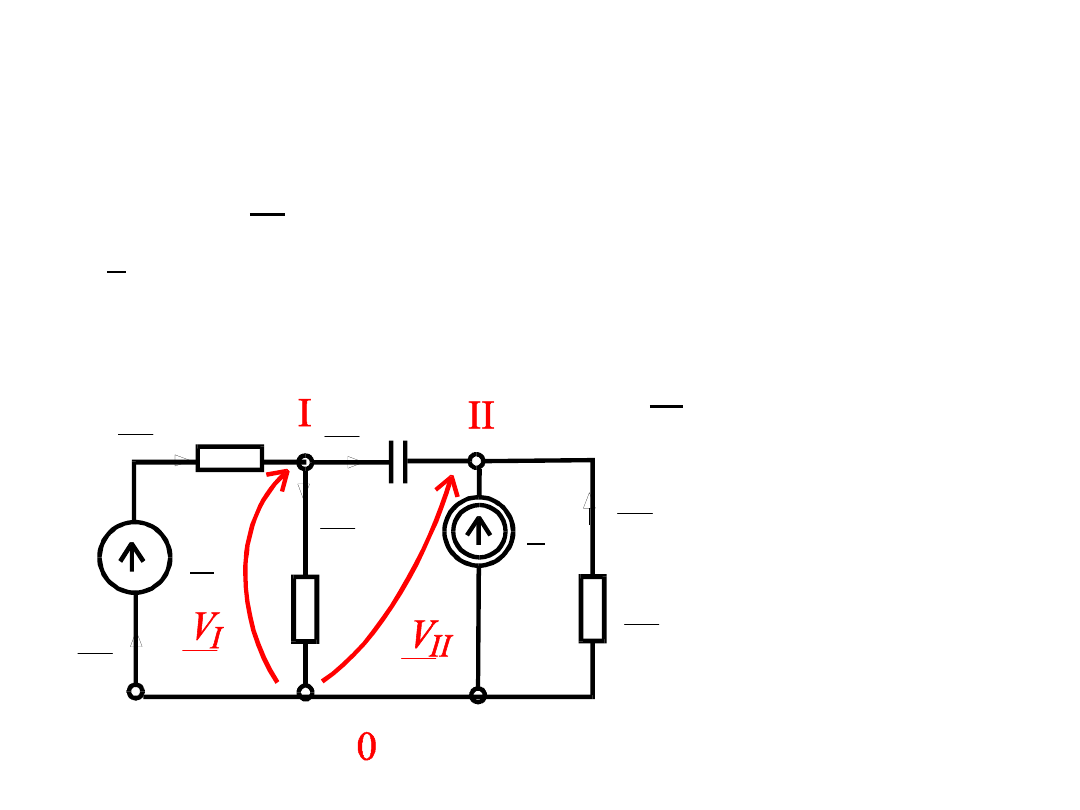
Zadanie 3

Obliczyć prądy gałęziowe stosując
metodę potencjałów węzłowych.
Dane: E = 3 V,
J = j0.1 mA,



= 10

5

rd/s, R= 10 k,

C = 1 nF,
Z = 16.67(1+j)
k.

0

R

C

E

E

0

I

I

I

I

I

R

Z

C

R

J

E

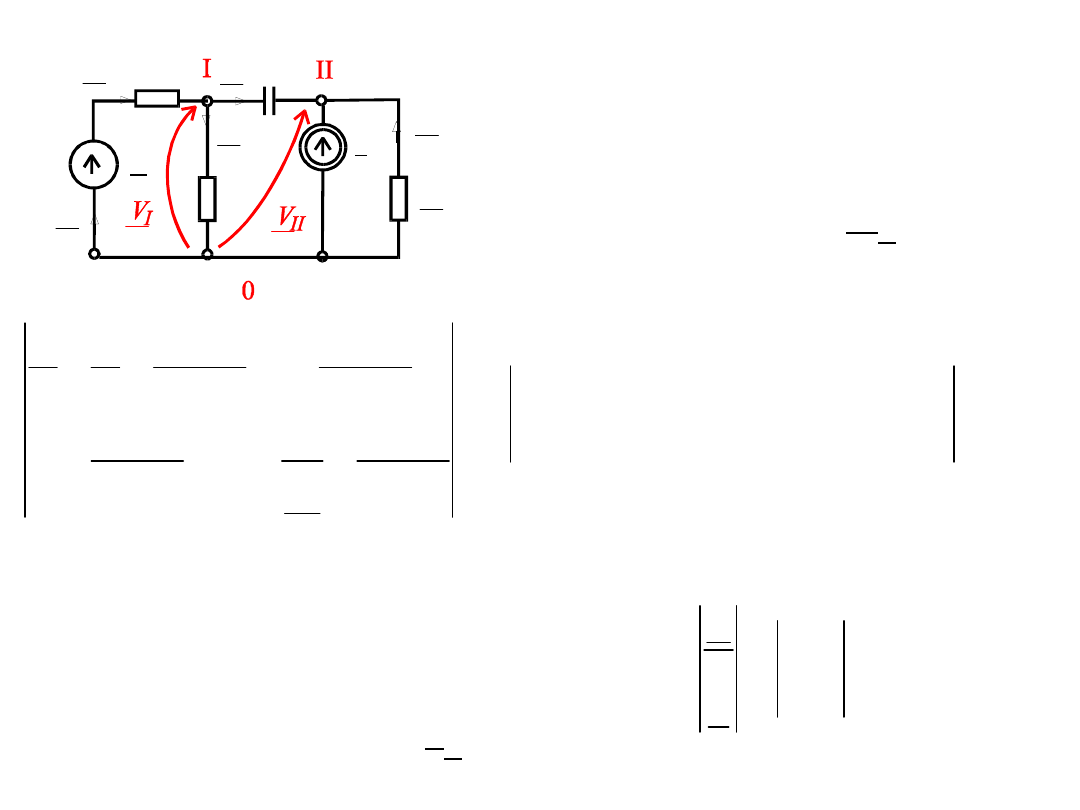
Macierz admitancji
węzłowych: [Y

0

]=

Wektor prądów

węzłowych

[J

0

]=

C

C

C

C

jX

Z

jX

jX

jX

R

R



















1

1

1

1

1

1

1

0

mS

j

j

j

j

j

1

.

0

03

.

0

03

.

0

1

.

0

1

.

0

1

.

0

2

.

0













mA

j

J

R

E

1

.

0

3

.

0



0

R

C

E

E

0

I

I

I

I

I

R

Z

C

R

J

E

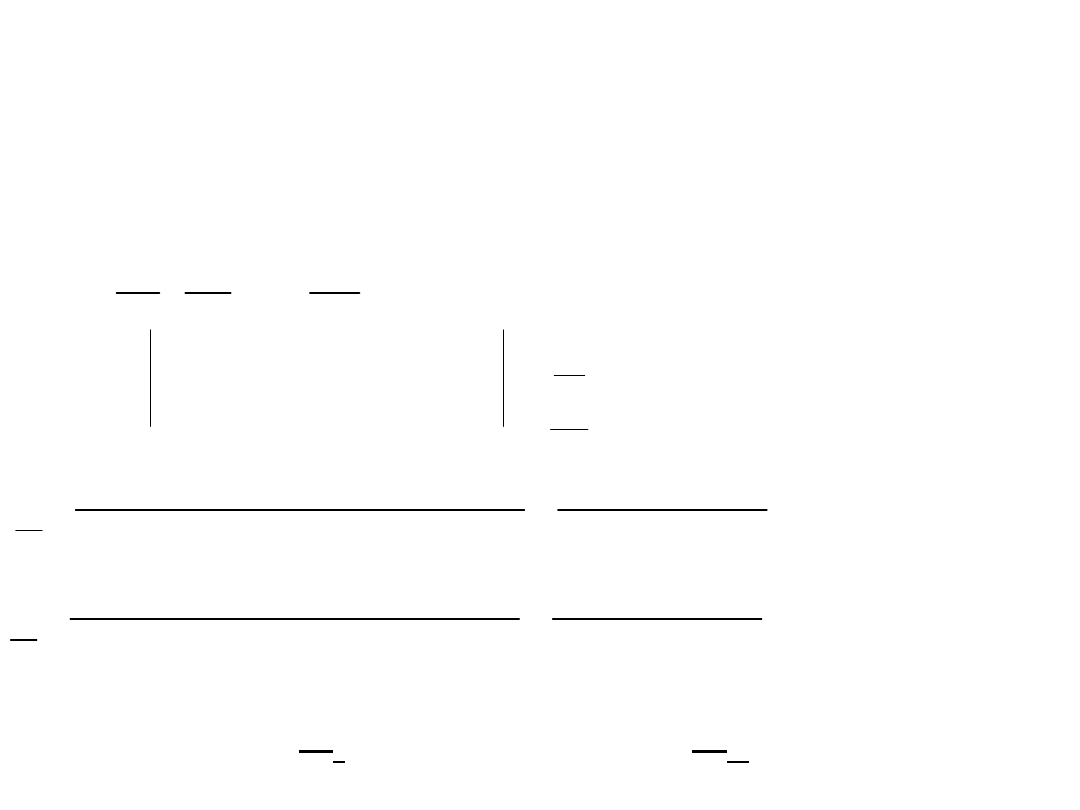
Równanie potencjałów

węzłowych:

Przybiera postać:

Skąd: V

I

= 1.366

-j22°

V, V

II

=

0.239e

-j11°

V.

    

0

0

0

J

V

Y











































1

.

0

3

.

0

97

.

0

03

.

0

1

.

0

1

.

0

1

.

0

2

.

0

j

V

V

j

j

j

j

II

I













 



V

j

j

j

j

j

j

j

j

j

V

I

515

.

0

265

.

1

197

.

0

081

.

0

291

.

0

001

.

0

1

.

0

97

.

0

03

.

0

1

.

0

2

.

0

1

.

0

1

.

0

97

.

0

03

.

0

3

.

0

2











































 



V

j

j

j

j

j

j

j

j

j

V

I

046

.

0

235

.

0

197

.

0

081

.

0

05

.

0

01

.

0

1

.

0

97

.

0

03

.

0

1

.

0

2

.

0

1

.

0

3

.

0

1

.

0

2

.

0

1

.

0

2































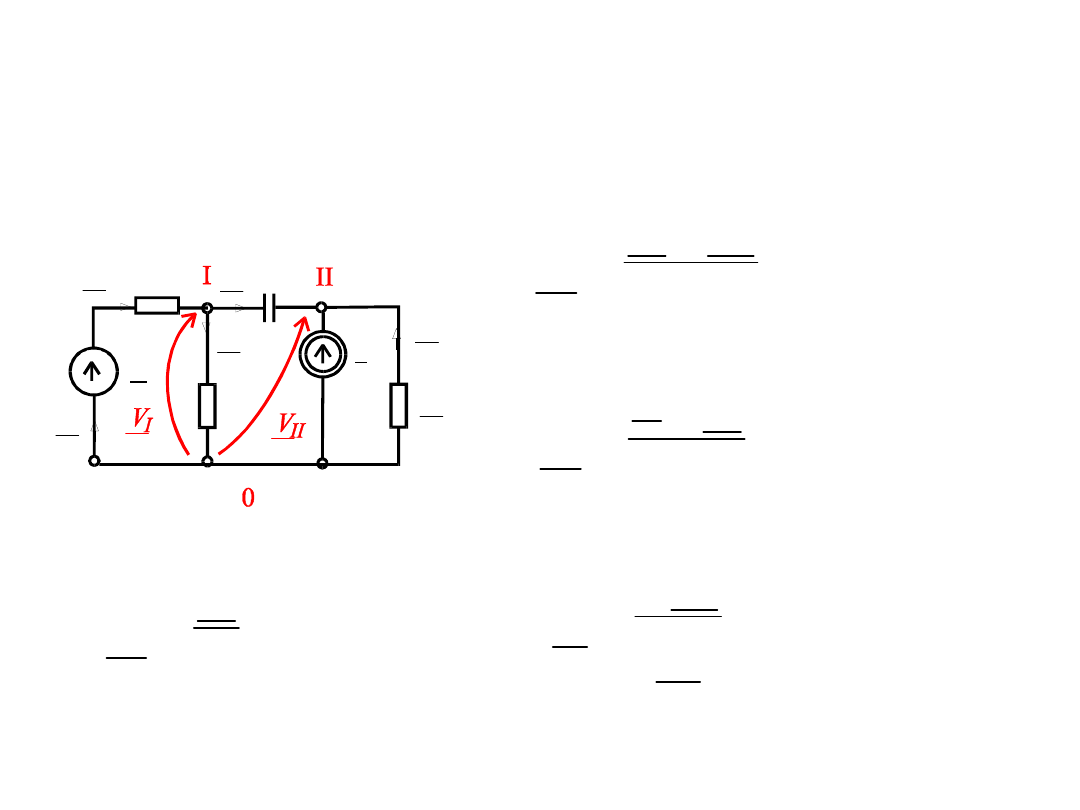
Prądy gałęziowe wyznacza

się:

0

R

C

E

E

0

I

I

I

I

I

R

Z

C

R

J

E

C

II

I

C

jX

V

V

I







R

V

E

I

I

E





R

V

I

I

R



0

0

Z

V

I

II





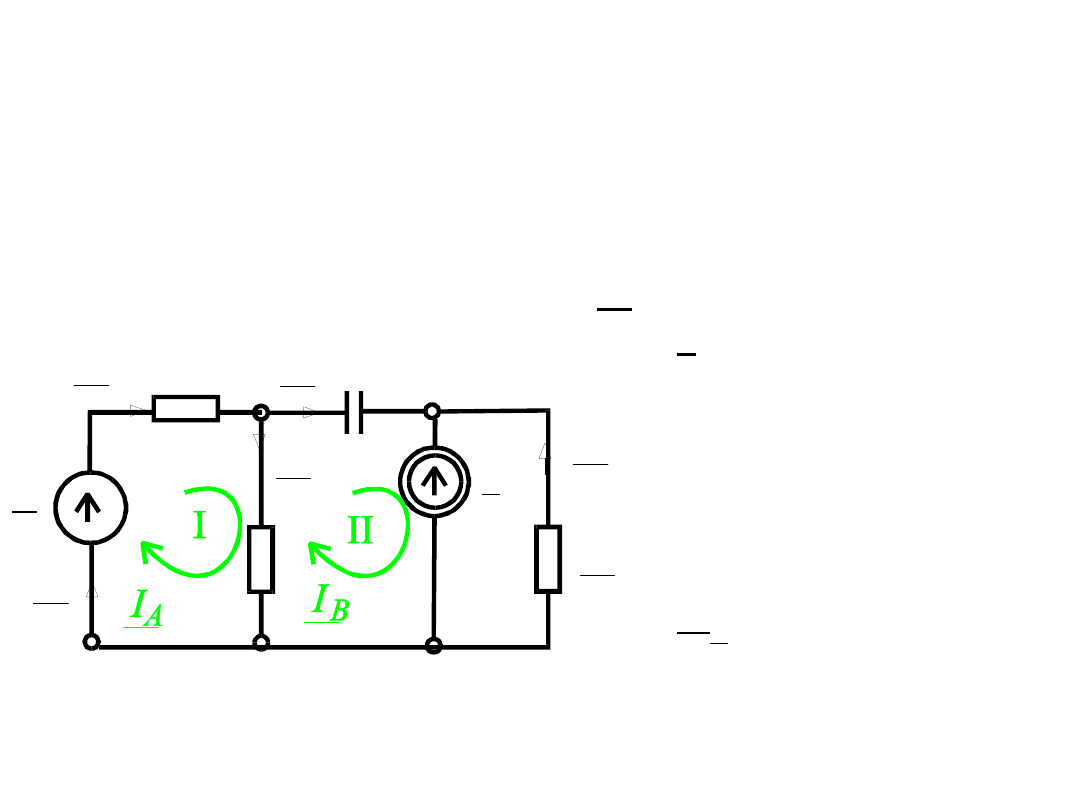
Zadanie 4

Zadanie poprzednie rozwiązać
stosując metodę prądów
obwodowych. Dane: E = 3 V,

J = j0.1 mA,
= 10

5

rd/s,

R= 10 k,
C = 1 nF,
Z

0

=

16.67(1+j) k

0

R

C

E

E

0

I

I

I

I

I

R

Z

C

R

J

E