Sylogizmy i ich

poprawność

Logika. Wykład
7

dr Tomasz Kowalski

Slajd

2/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Sylogizm

Sylogizm, to pewien ściśle określony rodzaj
wnioskowania.

Sylogizm zawsze składa się z trzech zdań
kategorycznych: dwóch przesłanek i wniosku.

Slajd

3/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Każdy sędzia jest uczciwy.
Żaden przestępca nie jest

uczciwy.
-------------------------------------------

--
Żaden przestępca nie jest

sędzią.

Przykład sylogizmu

W sylogizmie zawsze występują trzy

nazwy.

Slajd

4/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Każdy

sędzia

jest

uczciwy

.

Żaden

przestępca

nie jest

uczciwy

.

-------------------------------------------

--
Żaden

przestępca

nie jest

sędzią

.

Przykład sylogizmu

W sylogizmie zawsze występują trzy

nazwy.

Slajd

5/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwagi

W sylogizmie ważne jest, które nazwy oznaczymy
jaką zmienną.

Przyjęte jest, aby symbole S oraz P zarezerwować
odpowiednio dla podmiotu i orzecznika
występujących we wniosku.

Tradycyjnie nazwę oznaczoną przez S nazywamy
terminem mniejszym sylogizmu, nazwę oznaczoną
P – terminem większym, natomiast nazwę M –
terminem średnim.

Trzecia nazwa – ta, której nie ma we wniosku, a
która jest w obu przesłankach – oznaczana jest
symbolem M.

Slajd

6/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Przesłanka większa – jest to przesłanka, w której
występuje termin większy (P).

Uwagi - cd

Przesłanka mniejsza – jest to przesłanka, w
której występuje termin mniejszy (S).

Slajd

7/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Każdy

sędzia

jest

uczciwy

.

Żaden

przestępca

nie jest

uczciwy

.

-------------------------------------------

--

Żaden

przestępca

nie jest

sędzią

.

P a M

S – przestępca

(termin

mniejszy)

Przykład sylogizmu

Przesłanka większa

Przesłanka mniejsza

P – sędzia

(termin większy)

M – uczciwy człowiek

(termin średni)

S e M

S e P

Slajd

8/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

M P

P M

M P

P M

S M

S M

M S

M S

-------

-------

-------

-------

S P

S P

S P

S P

Ze względu na rozmieszczenie terminów w
przesłankach wyróżnia się cztery figury
sylogistyczne:

Figury sylogistyczne

Slajd

9/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

M P

P M

M P

P M

S M

S M

M S

M S

-------

-------

-------

-------

S P

S P

S P

S P

Z każdej figury można uzyskać 64 różne tryby
sylogistyczne.

Figury sylogistyczne

Łącznie istnieje 256 trybów sylogistycznych.

Poprawnych trybów sylogistycznych jest 24 (po 6 w
każdej figurze).

Slajd

10/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby sylogistyczne

Spośród 24 trybów poprawnych, 19 uznaje się za
podstawowe.

Pozostałych 5 trybów wynika z tych 24
podstawowych np. na podstawie kwadratu
logicznego.

Slajd

11/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby sylogistyczne

Wszystkie niezawodne tryby sylogistyczne
otrzymały w średniowieczu swoje nazwy tak
skonstruowane, by kolejne trzy samogłoski
występujące w tych nazwach wskazywały typ
zdania kolejno: przesłanki większej, mniejszej i
wniosku.

Dla łatwiejszego zapamiętania 19
podstawowych trybów sylogistycznych, ułożono
heksametrem z ich nazw wiersz.

Autorstwo tego wiersza przypisuje się
wybitnemu filozofowi trzynastowiecznemu,
Piotrowi Hiszpanowi, późniejszemu papieżowi
Janowi XXI.

Slajd

12/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Wiersz Piotra Hiszpana

Barbara, Celarent, Darii, Ferioque prioris

Cesare, Camestres, Festino, Baroco
secundae

Tertia Darapti, Disamis, Datisi, Felapton,

Bocardo, Ferison habet. Quarta insuper
addidit

Bamalip, Camenes, Dimatis, Fesapo,
Fresison.

Slajd

13/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby figury I

B

a

rb

a

r

a

C

e

l

a

r

e

nt D

a

r

i

i

F

e

r

i

o

M

P M

P M

P M

P

S

M S

M S

M S

M

---------- ----------- ----------- ----------

S

P S

P S

P S

P

a

a

a

Slajd

14/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby figury I

B

a

rb

a

r

a

C

e

l

a

r

e

nt D

a

r

i

i

F

e

r

i

o

M

a

P M

e

P M

a

P M

e

P

S

a

M S

a

M S

i

M S

i

M

---------- ----------- ----------- ----------

S

a

P S

e

P S

i

P S

o

P

M

a

P M

e

P

S

a

M S

a

M

---------- -----------

S

i

P S

o

P

Ponadto trybami figury I są:

Slajd

15/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby figury II

Cesare Camestres Festino Baroco

P e M P a M P e M P a M

S a M S e M S i M S o M

---------- ----------- ---------- ----------

S e P S e P S o P S o P

Ponadto trybami figury II są:

P e M P a M
S a M S e M

---------- -----------

S o P S o P

Slajd

16/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby figury III

Darapti Disamis Datisi Felapton Bocardo

Ferison

M a P M i P M a P M e P M o P M

e P

M a S M a S M i S M a S M a S M

i S

---------- ----------- ------------ ----------- ----------- ----------

S i P S i P S i P S o P S o P S

o P

Slajd

17/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Tryby figury IV

Bamalis Camenes Dimatis Fesapo Fresison

P a M P a M P i M P e M P e M

M a S M e S M a S M a S M i S

----------- ------------ ----------- ----------- ------------

S i P S e P S i P S o P S o P

Ponadto trybem figury IV jest:

P a M

M e S

------------

S o P

Slajd

18/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Sprawdzanie poprawności

sylogizmu

Sylogizm to pewien rodzaj wnioskowania.

Sprawdzenie poprawności sylogizmu, to nic
innego jak sprawdzenie poprawności tego
wnioskowania.

Slajd

19/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Sprawdzanie poprawności

sylogizmu

Reguła jest niezawodna, gdy nie jest możliwa
sytuacja, aby przesłanki były prawdziwe, natomiast
wniosek był fałszywy.

Innymi słowy:

W przypadku niezawodnej reguły, jeśli przesłanki
są prawdziwe, to prawdziwy musi być również i
wniosek.

Slajd

20/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Sprawdzanie poprawności

sylogizmu

W teorii sylogizmów poprawność wnioskowań
badać można:

1. przy pomocy tzw. diagramów Venna,

2. przy pomocy tzw. reguły pięciu.

Slajd

21/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Metoda diagramów Venna

W diagramach Venna przy pomocy kół symbolizujemy
zbiory obiektów określanych przez poszczególne nazwy,
czyli zakresy tych nazw.

Znaki „+” oraz „–” stawiane w częściach tych kół
informować będą, że w danym obszarze na pewno coś
się znajduje lub też, że na pewno niczego tam nie ma.

Slajd

22/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Metoda diagramów Venna

S

P

+

Stawiamy znak „+” w tej części
rysunku.

S i P

Niektóre S są

P.

Pewien S jest

P.

Zdanie to oznacza, że istnieją

jakieś obiekty w części

wspólnej S oraz P.

Na temat pozostałych obszarów
diagramu zdanie S i P niczego
nie mówi, dlatego nic do nich
nie wpisujemy.

Slajd

23/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Metoda diagramów Venna

S

P

+

Stawiamy znak „+” w
części S znajdującej się
poza zbiorem P.

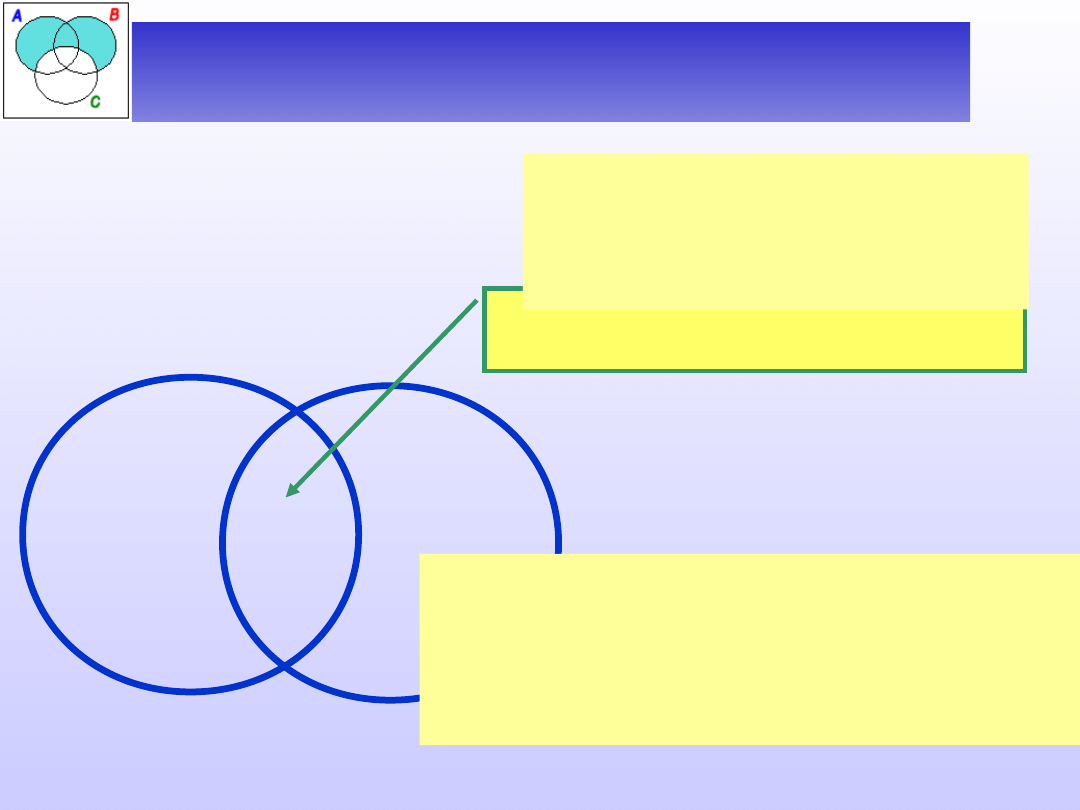
S o P

Niektóre S nie

są P.

Pewien S nie

jest P.

Zdanie to informuje, iż na
pewno istnieją obiekty
należące do zbioru S, a
jednocześnie nie należące
do P

Na temat pozostałych obszarów
diagramu zdanie S o P niczego
nie mówi, dlatego nic do nich
nie wpisujemy.

Slajd

24/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Metoda diagramów Venna

S

P

_

Stawiamy znak „–” w części
wspólnej tych zbiorów.

S e P

Żadne S nie są P.

Żaden S nie jest

P.

Zdanie to stwierdza, że nie
istnieją żadne obiekty
należące jednocześnie do
zbiorów S i P.

Zdanie typu S e P nie informuje o
istnieniu jakichkolwiek obiektów
będących desygnatami nazw S lub P,
dlatego też niczego nie wpisujemy w
pozostałe obszary diagramu.

Slajd

25/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwaga

W praktyce, przy sprawdzaniu poprawności
sylogizmu, będziemy czasem korzystali z
założenia, że obiekty będące desygnatami danej
nazwy na pewno istnieją.

Najczęściej jednak będziemy wpisywali do
diagramu tylko to, co dane zdanie wprost
stwierdza, pomijając informacje, jakie mogą z
niego dodatkowo wynikać przy pewnych
założeniach.

Slajd

26/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Metoda diagramów Venna

S

P

_

Stawiamy znak „–” poza
częścią wspólną tych zbiorów.

S a P

Każde S jest P.

Zdanie to informuje, że cokolwiek
możemy nazwać S, podpada również
pod nazwę P.
Nie ma w związku z tym żadnych
obiektów S nie będących
jednocześnie P.

Zdanie to nie informuje, że
jakiekolwiek S faktycznie
istnieje – stwierdza jedynie, że
jeżeli coś jest S (o ile w ogóle
istnieje) to jest również P.
Dlatego też nie stawiamy znaku
„+” w części środkowej.

Slajd

27/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

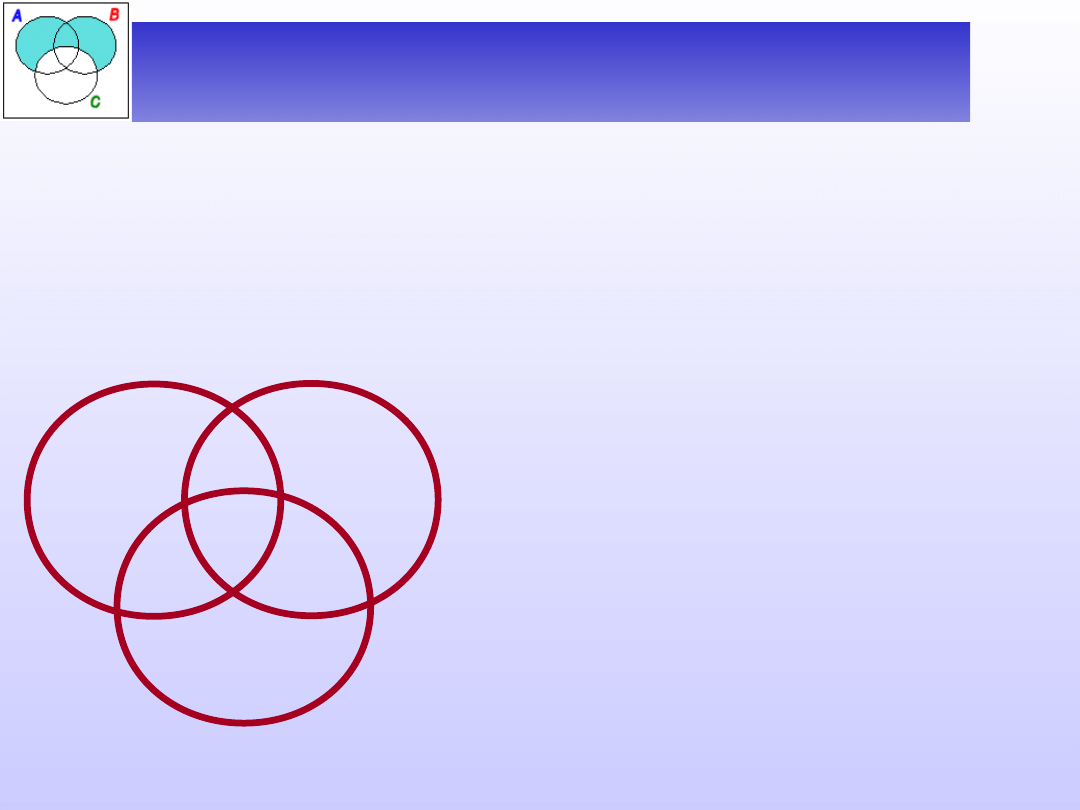
Diagramy dla trzech nazw

W każdym sylogizmie występują trzy nazwy. Dlatego
też do sprawdzania poprawności sylogizmów
potrzebna jest umiejętność ilustrowania
poszczególnych zdań kategorycznych na diagramach
złożonych z trzech kół.

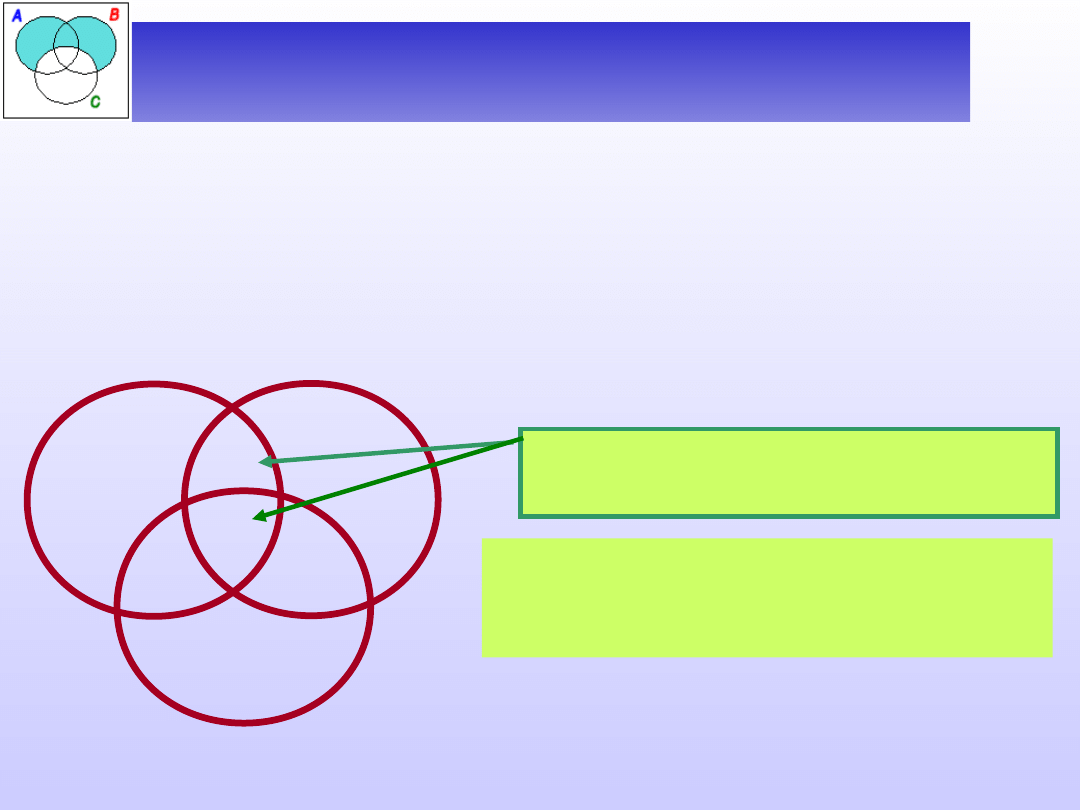
S

P

M

Slajd

28/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Diagramy dla trzech nazw

Dla zdań ogólnych sprawa jest prosta – rysunki
stanowią zwykłe rozszerzenie diagramów
sporządzanych dla dwóch nazw.

S

P

_

M

W tym przypadku pusty musi
być cały obszar zbioru S
leżący poza P.

S a P

Każde S jest P.

_

Ponieważ obszar ten składa się z
dwóch części, musimy postawić
znaki „–” w obu tych kawałkach.

Slajd

29/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

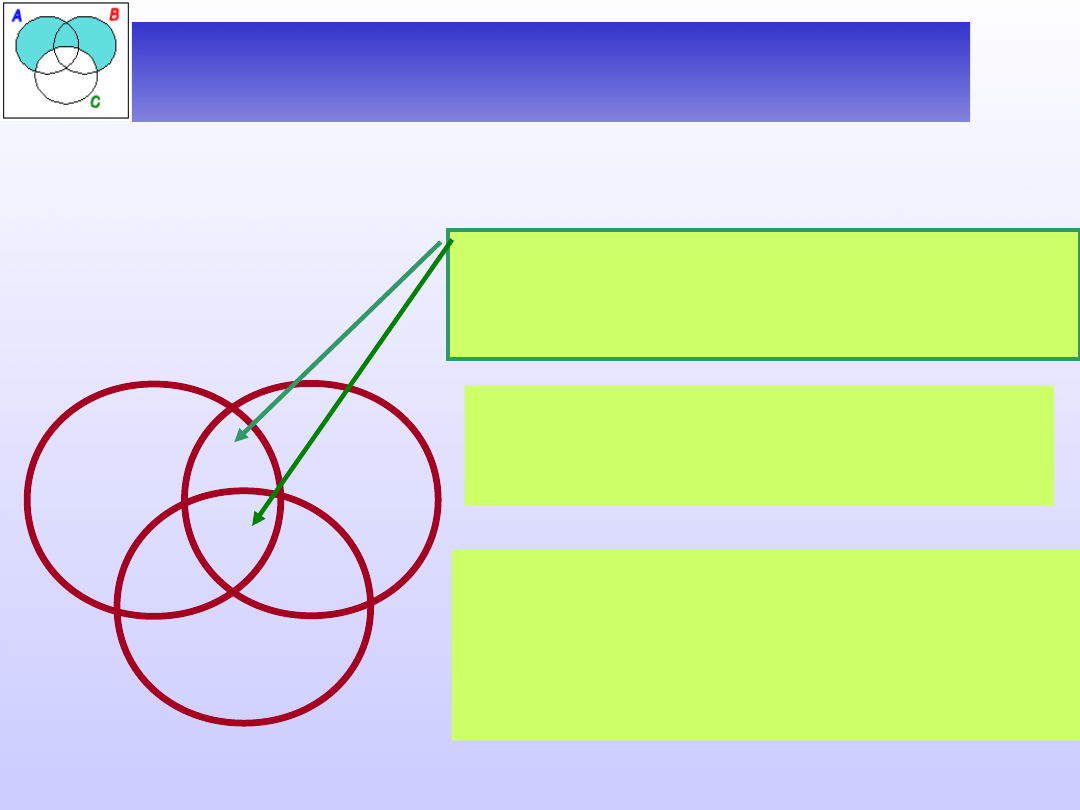
Diagramy dla trzech nazw

Dla zdań ogólnych sprawa jest prosta – rysunki
stanowią zwykłe rozszerzenie diagramów
sporządzanych dla dwóch nazw.

S

P

_

M

W tym przypadku pusty musi
pozostać obszar wspólny tych
zbiorów.

S e P

Żadne S nie jest

P.

_

Ponieważ obszar ten składa się z
dwóch części, musimy postawić
znaki „–” w obu tych kawałkach.

Slajd

30/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

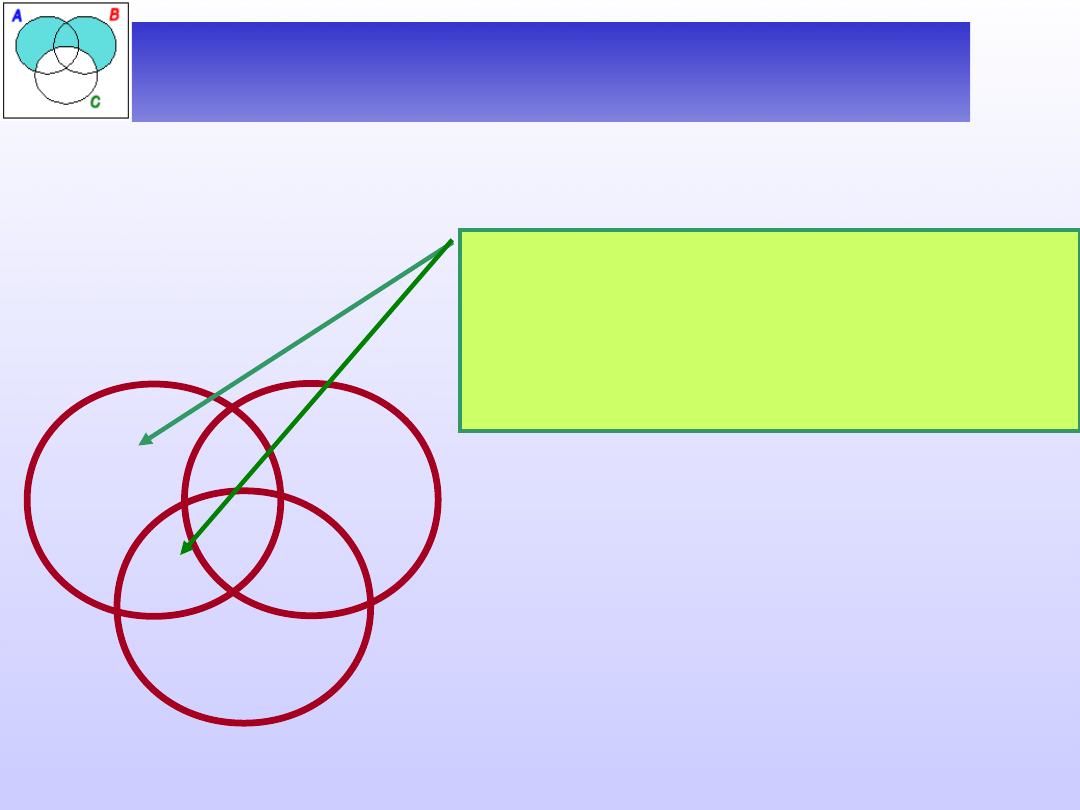
Diagramy dla trzech nazw

W przypadku zdań szczegółowych sytuacja przedstawia
się nieco inaczej.

S

P

+?

M

Zdanie informuje, że istnieją pewne
obiekty w części wspólnej zbiorów S
oraz P, ale w której z dwóch części
tego zbioru – nie wiadomo.

S i P

Niektóre S są P.

Pewien S jest P.

+?

Wpisujemy symbole „+” w
odpowiednich częściach ze
znakami zapytania.

Pytajniki te oznaczają, że w danym
obszarze na pewno jakieś elementy
się znajdują, ale nie wiadomo w w
którym fragmencie tego obszaru –
w jednym, drugim, czy obydwu.

Slajd

31/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Diagramy dla trzech nazw

W przypadku zdań szczegółowych sytuacja przedstawia
się nieco inaczej.

S

P

+?

M

Zdanie to informuje, że na pewno
istnieją jakieś elementy w części
zbioru S znajdującej się poza
zbiorem P, ale nie określa, w
którym fragmencie tego obszaru –
w jednym, drugim, czy obydwu.

S o P

Niektóre S nie

są P. Pewien S

nie jest P.

+?

Slajd

32/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwagi

Przy wypełnianiu diagramów Venna warto
pamiętać, że:

Zdania ogólne (S a P oraz S e P) dają nam zawsze
minusy na diagramach, natomiast zdania
szczegółowe (S i P oraz S o P) – plusy.

Minusy są zawsze „pewne” (bez znaków
zapytania) – wynika to z tego, że gdy jakiś obszar
ma być pusty, to pusta musi być każda jego część.

Plusy są „niepewne” – gdy w danym obszarze, coś
się znajduje, to nie oznacza to, że wiemy w której
jego części.

Slajd

33/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

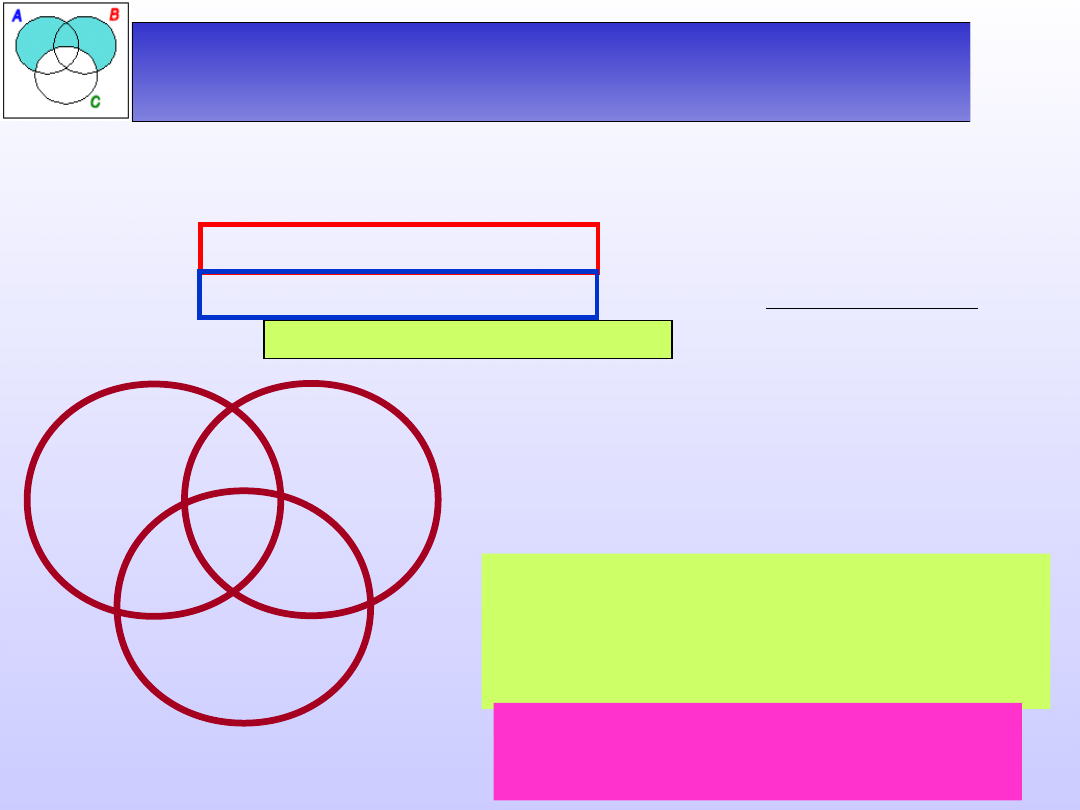
Sprawdzanie poprawności

sylogizmu

Badanie poprawności sylogizmów przy pomocy
diagramów Venna składa się z dwóch kroków:

Wpisujemy do diagramu plusy i minusy, o których
informują przesłanki sylogizmu.

Sprawdzamy, czy wypełniony zgodnie z
przesłankami diagram gwarantuje nam
prawdziwość wniosku.

1

.

2

.

Slajd

34/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Sprawdzanie poprawności

sylogizmu

Zdania będącego wnioskiem sylogizmu nie
ilustrujemy na diagramie.

Musimy jedynie rozstrzygnąć, co w diagramie
powinno się znajdować, aby był on prawdziwy, a
następnie sprawdzić, czy nasz diagram spełnia te
warunki.

Jeżeli rysunek gwarantuje prawdziwość konkluzji,
oznacza to, że sylogizm jest poprawny.

Jeśli nie mamy pewności co do prawdziwości
wniosku, oznacza to, że sylogizm jest niepoprawny.

Slajd

35/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

Każdy jamnik jest psem.

Każdy pies jest ssakiem.

Zatem: Każdy jamnik jest

ssakiem.

S - jamnik

P - ssak

M – pies

S a M

M a

P

S a P

_

S

jamnik

P

ssak

M

pies

_

_

_

Aby ta konkluzja była
prawdziwa, pusty musi być
obszar zbioru S leżący poza
zbiorem P.

Badany sylogizm jest

poprawny.

Slajd

36/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Każdy milioner jest bogaty.

Niektórzy bogaci

ludzie nie są szczęśliwi.

Zatem: Niektórzy milionerzy nie są

szczęśliwi.

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - milioner

P – ktoś, kto

jest szczęśliwy

M – bogaty człowiek

S a M

M o

P

S o P

+?

S

milion

er

P

szczęśli

wy

M

bogat

y

_

_

+?

Aby ta konkluzja była prawdziwa,
coś powinno znajdować się w
obszarze zbioru S leżącym poza
zbiorem P.

Badany sylogizm nie jest

poprawny.

Plus ze znakiem zapytania nie daje

pewności!

Slajd

37/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Żaden mędrzec nie jest fanatykiem

jednej idei. Niektórzy uczeni są

fanatykami jednej idei.

Zatem: Niektórzy uczeni nie są

mędrcami.

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - uczony

P - mędrzec

M – fanatyk jednej

idei

P e M

S i

M

S o P

+

S

uczon

y

P

mędrz

ec

M

fanaty

k

_

_

Aby ta konkluzja była
prawdziwa, coś powinno się
znajdować w części zbioru S
leżącej poza P.

Badany sylogizm jest

poprawny.

Slajd

38/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Niektórzy politycy są nacjonalistami.

Każdy nacjonalista

jest ograniczony.

Zatem: Niektórzy politycy są

ograniczeni

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - polityk

P – ktoś

ograniczony

M – nacjonalista

S i M

M a

P

S i P

_

S

polity

k

P

ograniczo

ny

M

nacjonalis

ta

+?

+?

_

Aby ta konkluzja była

prawdziwa, coś musi się

znajdować w części wspólnej

zbioru S i zbioru P.

Badany sylogizm jest

poprawny.

Slajd

39/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwaga

Aby uniknąć wymazywania symboli w diagramie i
zastępowania ich innymi, najlepiej jest zaczynać
wypełnianie diagramu od tej przesłanki, która daje
nam „pewne” informacje (a więc zdania typu „a”
bądź „e”, niezależnie, czy jest ono pierwsze, czy
drugie w sylogizmie).

Slajd

40/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Niektórzy wykładowcy są dobrymi

fachowcami. Każdy dobry

fachowiec dużo zarabia.

Zatem: Każdy wykładowca dużo

zarabia.

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - wykładowca

P – ktoś, kto dużo

zarabia

M – dobry fachowiec

S i M

M a

P

S a P

_

S

wykładow

ca

P

dużo

zarabia

M

fachowi

ec

+?

+?

Aby ta konkluzja była prawdziwa, w

części zbioru S leżącej poza P nie

powinno być żadnych elementów.

Badany sylogizm nie jest

poprawny.

_

Slajd

41/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwaga

Przy badaniu poprawności sylogizmów zawsze
należy przyjąć milczące założenie, że terminy
oznaczane symbolami S, P oraz M nie są nazwami
„pustymi”.

Założenie o niepustości terminów nie jest
wykorzystywane zbyt często, jednak czasami jest
ono konieczne, aby właściwie ocenić poprawność
sylogizmu.

Slajd

42/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Każdy pies jest ssakiem.

Każdy ssak jest kręgowcem.

Zatem: Niektóre kręgowce są

psami.

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - kręgowiec

P – pies

M – ssak

P a M

M a

S

S i P

_

S

kręgowi

ec

P pies

M

ssak

_

_

_

Aby ta konkluzja była prawdziwa,

coś powinno znajdować się w części

wspólnej zbiorów S i P.

Badany sylogizm jest

poprawny.

+

Korzystamy z

niepustości nazwy P.

Slajd

43/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwaga

Czasem wynik sprawdzenia poprawności sylogizmu
może wydać się dość dziwny lub nawet ewidentnie
sprzeczny ze zdrowym rozsądkiem.

Slajd

44/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Żaden ptak nie jest ssakiem.

Niektórzy ludzie są ptakami.

Zatem: Niektórzy ludzie

nie są ssakami.

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - człowiek

P – ssak

M – ptak

M e P

S i

M

S o P

+

S-

człowie

k

P-ssak

M-

ptak

_

_

Aby ta konkluzja była
prawdziwa, coś powinno
znajdować się w obszarze zbioru
S leżącym poza zbiorem P.

Badany sylogizm jest

poprawny.

Slajd

45/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Błąd materialny sylogizmu

Sylogizm powyższy jest poprawny ponieważ jego
wniosek wynika logicznie z przesłanek.

We wnioskowaniu popełniono błąd polegający na
przyjęciu fałszywej przesłanki, co w konsekwencji
doprowadziło do otrzymania fałszywego wniosku.

Błąd taki nazywany jest błędem
materialnym.

Slajd

46/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Każdy pies jest ssakiem.

Niektóre ssaki mają czarną

sierść. Zatem:

Niektóre psy mają czarną sierść.

Ćwiczenie – metoda diagramów

Venna

Sprawdzić poprawność sylogizmu:

S - pies

P - coś z czarną

sierścią

M – ssak

S a M

M i

P

S i P

+?

S-pies

P- coś z

czarną

sierścią

M-

ssak

_

_

+?

Aby ta konkluzja była prawdziwa,
coś powinno znajdować się w
części wspólnej zbiorów S i P.

Badany sylogizm nie jest

poprawny.

Slajd

47/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Uwaga

Sylogizm ten jest niepoprawny, ponieważ pomimo
prawdziwości przesłanek i wniosku, wniosek nie
wynika logicznie z przesłanek.

To, że wszystko są to zdania prawdziwe, jest
pewnego rodzaju zbiegiem okoliczności, a nie
zachodzących pomiędzy nimi związków logicznych.

Slajd

48/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Sprawdzanie poprawności

sylogizmów

Metoda diagramów Venna nie jest jedynym
sposobem, w jaki można badać poprawność
sylogizmu.

Sprawdzenie poprawności sylogizmu może się
odbywać poprzez zbadanie, czy spełnia on wszystkie
warunki sformułowane w tzw. metodzie pięciu reguł.

Jeżeli sylogizm spełnia wszystkie reguły to
należy go uznać za poprawny; jeśli nie spełnia
on choć jednego warunku – świadczy to o jego
niepoprawności.

Slajd

49/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Termin rozłożony

W metodzie pięciu reguł konieczna jest
znajomość pojęcia terminu rozłożonego w
zdaniu kategorycznym.

Jeżeli zdanie udziela nam informacji o całym
zakresie jakieś nazwy (czyli o jej wszystkich
desygnatach), to nazwa ta jest terminem
rozłożonym w tym zdaniu.

Slajd

50/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Przykłady

W zdaniu: Każde S jest P mowa jest o wszystkich S.

Oznacza to, że w zdaniu S a P nazwa S jest terminem
rozłożonym.

Zdanie: Żadne S nie jest P informuje nas, że ani
jeden desygnat nazwy S nie jest desygnatem nazwy
P, ani też żaden desygnat P nie jest desygnatem S –
a więc stwierdza fakt dotyczący całych zakresów
obu tych nazw.

W zdaniu S e P rozłożone są zatem oba terminy.

Jeżeli zdanie udziela nam informacji
o całym zakresie jakieś nazwy (czyli
o jej wszystkich desygnatach), to
nazwa ta jest terminem rozłożonym
w tym zdaniu.

Slajd

51/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Przykłady

W zdaniu Niektóre S są P mowa jest tylko o
niektórych S, które są „niektórymi” P.

W zdaniu S e P żaden z terminów nie jest więc
rozłożony.

Zdanie Niektóre S nie są P stwierdza, że
niektórych desygnatów nazwy S nie ma w całym
zakresie nazwy P.

W zdaniu S o P rozłożony jest termin P.

Jeżeli zdanie udziela nam informacji
o całym zakresie jakieś nazwy (czyli
o jej wszystkich desygnatach), to
nazwa ta jest terminem rozłożonym
w tym zdaniu.

Slajd

52/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Termin rozłożony - inaczej

Termin, który jest podmiotem zdania ogólnego lub
orzecznikiem zdania przeczącego, jest terminem
rozłożonym.

W skrócie:

S

a P – rozłożony termin S

S

e

P

– rozłożone obydwa terminy –

S oraz P
S i P – żaden termin nie jest
rozłożony
S o

P

– rozłożony termin P.

Slajd

53/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – wyznaczanie terminów

rozłożonych

Podkreślić terminy rozłożone w zdaniach:

Niektórzy prawnicy są pracownikami

administracyjnymi.

Nie ma terminów rozłożonych!

Podmiot zdania ogólnego lub orzecznik
zdania przeczącego jest terminem
rozłożonym.

To jest zdanie szczegółowo-

twierdzące.

Slajd

54/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – wyznaczanie terminów

rozłożonych

Podkreślić terminy rozłożone w zdaniach:

Żaden sędzia nie jest prokuratorem.

Podmiot zdania ogólnego lub orzecznik
zdania przeczącego jest terminem
rozłożonym.

To jest zdanie ogólno-

przeczące.

Slajd

55/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – wyznaczanie terminów

rozłożonych

Podkreślić terminy rozłożone w zdaniach:

Każdy wyrok jest podpisany przez sędziego.

Podmiot zdania ogólnego lub orzecznik
zdania przeczącego jest terminem
rozłożonym.

To jest zdanie ogólno-

twierdzące.

Slajd

56/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – wyznaczanie terminów

rozłożonych

Podkreślić terminy rozłożone w zdaniach:

Niektórzy ludzie nie są uprzejmi.

Podmiot zdania ogólnego lub orzecznik
zdania przeczącego jest terminem
rozłożonym.

To jest zdanie szczegółowo-

przeczące.

Slajd

57/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – wyznaczanie terminów

rozłożonych

Podkreślić terminy rozłożone w zdaniach:

Niektórzy ludzie są nieuprzejmi.

Nie ma terminów rozłożonych!

Podmiot zdania ogólnego lub orzecznik
zdania przeczącego jest terminem
rozłożonym.

To jest zdanie szczegółowo-

twierdzące.

Slajd

58/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – wyznaczanie terminów

rozłożonych

Podkreślić terminy rozłożone w zdaniach:

Tylko osoby z wykształceniem prawniczym są

notariuszami.

Każdy notariusz jest osobą z wykształceniem

prawniczym.

Podmiot zdania ogólnego lub orzecznik
zdania przeczącego jest terminem
rozłożonym.

To jest zdanie ogólno-

twierdzące.

Slajd

59/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Warunki poprawności

sylogizmu:

1. Termin średni musi być przynajmniej w jednej

przesłance rozłożony.

2. Przynajmniej jedna przesłanka musi być zdaniem

twierdzącym.

3. Jeśli jedna z przesłanek jest zdaniem przeczącym, to i

wniosek musi być zdaniem przeczącym.

4. Jeśli obie przesłanki są zdaniami twierdzącymi, to i

wniosek musi być twierdzący.

5. Jeśli jakiś termin ma być rozłożony we wniosku,

to musi być i rozłożony w przesłance.

Slajd

60/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Sprawdzić poprawność sylogizmu:

Żaden mędrzec nie jest fanatykiem jednej idei.

Niektórzy uczeni są fanatykami jednej idei.

Zatem: Niektórzy uczeni nie są

mędrcami.

S - uczony

P - mędrzec

M – fanatyk jednej

idei

P e M

S i

M

S o P

Slajd

61/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

1. Termin średni musi być przynajmniej w jednej

przesłance rozłożony.

2. Przynajmniej jedna przesłanka musi być

zdaniem twierdzącym.

3. Jeśli jedna z przesłanek jest zdaniem przeczącym,

to i wniosek musi być zdaniem przeczącym.

4. Jeśli obie przesłanki są zdaniami twierdzącymi,

to i wniosek musi być twierdzący.

5. Jeśli jakiś termin ma być rozłożony we wniosku,

to musi być i rozłożony w przesłance.

1.

2.

3.

4.

5.

+

+

+

+

+

P e M

S i

M

S o P

Badany sylogizm jest poprawny

Slajd

62/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Sprawdzić poprawność sylogizmu:

Każdy jamnik jest psem.

Każdy pies jest ssakiem.

Zatem: Każdy jamnik jest

ssakiem.

S - jamnik

P - ssak

M – pies

S a M

M a

P

S a P

Slajd

63/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

1. Termin średni musi być przynajmniej w jednej

przesłance rozłożony.

2. Przynajmniej jedna przesłanka musi być

zdaniem twierdzącym.

3. Jeśli jedna z przesłanek jest zdaniem przeczącym,

to i wniosek musi być zdaniem przeczącym.

4. Jeśli obie przesłanki są zdaniami twierdzącymi,

to i wniosek musi być twierdzący.

5. Jeśli jakiś termin ma być rozłożony we wniosku,

to musi być i rozłożony w przesłance.

1.

2.

3.

4.

5.

+

+

+

+

+

S a M

M a

P

S a P

Badany sylogizm jest poprawny

Slajd

64/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Sprawdzić poprawność sylogizmu:

Niektórzy politycy są nacjonalistami.

Każdy nacjonalista jest

ograniczony. Zatem:

Niektórzy politycy są ograniczeni.

S - polityk

P – ktoś

ograniczony

M – nacjonalista

S i M

M a

P

S i P

Slajd

65/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

1. Termin średni musi być przynajmniej w jednej

przesłance rozłożony.

2. Przynajmniej jedna przesłanka musi być

zdaniem twierdzącym.

3. Jeśli jedna z przesłanek jest zdaniem przeczącym,

to i wniosek musi być zdaniem przeczącym.

4. Jeśli obie przesłanki są zdaniami twierdzącymi,

to i wniosek musi być twierdzący.

5. Jeśli jakiś termin ma być rozłożony we wniosku,

to musi być i rozłożony w przesłance.

1.

2.

3.

4.

5.

+

+

+

+

+

Badany sylogizm jest poprawny

S i M

M a

P

S i P

Slajd

66/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Sprawdzić poprawność sylogizmu:

Niektórzy wykładowcy są dobrymi

fachowcami. Każdy dobry fachowiec

dużo zarabia. Zatem: Każdy

wykładowca dużo zarabia.

S - wykładowca

P – ktoś, kto dużo

zarabia

M – dobry fachowiec

S i M

M a

P

S a P

Slajd

67/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

1. Termin średni musi być przynajmniej w jednej

przesłance rozłożony.

2. Przynajmniej jedna przesłanka musi być

zdaniem twierdzącym.

3. Jeśli jedna z przesłanek jest zdaniem przeczącym,

to i wniosek musi być zdaniem przeczącym.

4. Jeśli obie przesłanki są zdaniami twierdzącymi,

to i wniosek musi być twierdzący.

5. Jeśli jakiś termin ma być rozłożony we wniosku,

to musi być i rozłożony w przesłance.

1.

2.

3.

4.

5.

+

+

+

+

_

Badany sylogizm nie jest

poprawny

S i M

M a

P

S a P

Slajd

68/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Sprawdzić poprawność sylogizmu:

Każdy milioner jest bogaty.

Niektórzy bogaci ludzie nie są

szczęśliwi. Zatem: Niektórzy

milionerzy nie są szczęśliwi.

S - milioner

P – ktoś, kto jest

szczęśliwy

M – bogaty człowiek

S a M

M o

P

S o P

Slajd

69/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Ćwiczenie – metoda 5 reguł

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

Zdanie
przeczące

Zdanie
twierdzące

termin rozłożony

…o…

…i…

Zdanie szczegółowe

…e…

…a…

Zdanie ogólne

1. Termin średni musi być przynajmniej w jednej

przesłance rozłożony.

2. Przynajmniej jedna przesłanka musi być

zdaniem twierdzącym.

3. Jeśli jedna z przesłanek jest zdaniem przeczącym,

to i wniosek musi być zdaniem przeczącym.

4. Jeśli obie przesłanki są zdaniami twierdzącymi,

to i wniosek musi być twierdzący.

5. Jeśli jakiś termin ma być rozłożony we wniosku,

to musi być i rozłożony w przesłance.

1.

2.

3.

4.

5.

_

Badany sylogizm nie jest

poprawny

S a M

M o

P

S o P

Slajd

70/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Do sali wchodzi bardzo czymś zdenerwowany
matematyk:

- Wszyscy idioci proszę wstać!

Nikt się nie rusza. Nagle podnosi się jeden
student.

- Gratulacje! - cieszy się profesor i pyta ironicznie:

- Dlaczego uważa się Pan za idiotę?

- Wcale się nie uważam, tylko głupio mi, że pan
profesor tak sam stoi...

Slajd

71/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność

Student weterynarii pływał na egzaminie. W końcu
dostał Pytanie Ostatniej Szansy: "Czy owieczce można
zrobić aborcję?"

Niestety, nie wiedział, więc wyleciał z dwóją.
Zmartwiony poszedł do baru, usiadł w kącie i powoli
upija się na smutno rozmyślając o pytaniu.

Barman co jakiś czas na niego zerka, w końcu
podchodzi i zagaduje:

- Coś niewyraźnie Pan wygląda, jakieś kłopoty?

- Niech mi Pan powie, czy owieczce można zrobić
aborcję?

- Nie mam pojęcia, ale coś mi się widzi, że nieźle sobie
Pan życie skomplikował...

Slajd

72/72

Tomasz Kowalski: Logika. Wykład 7: Sylogizmy i ich

poprawność