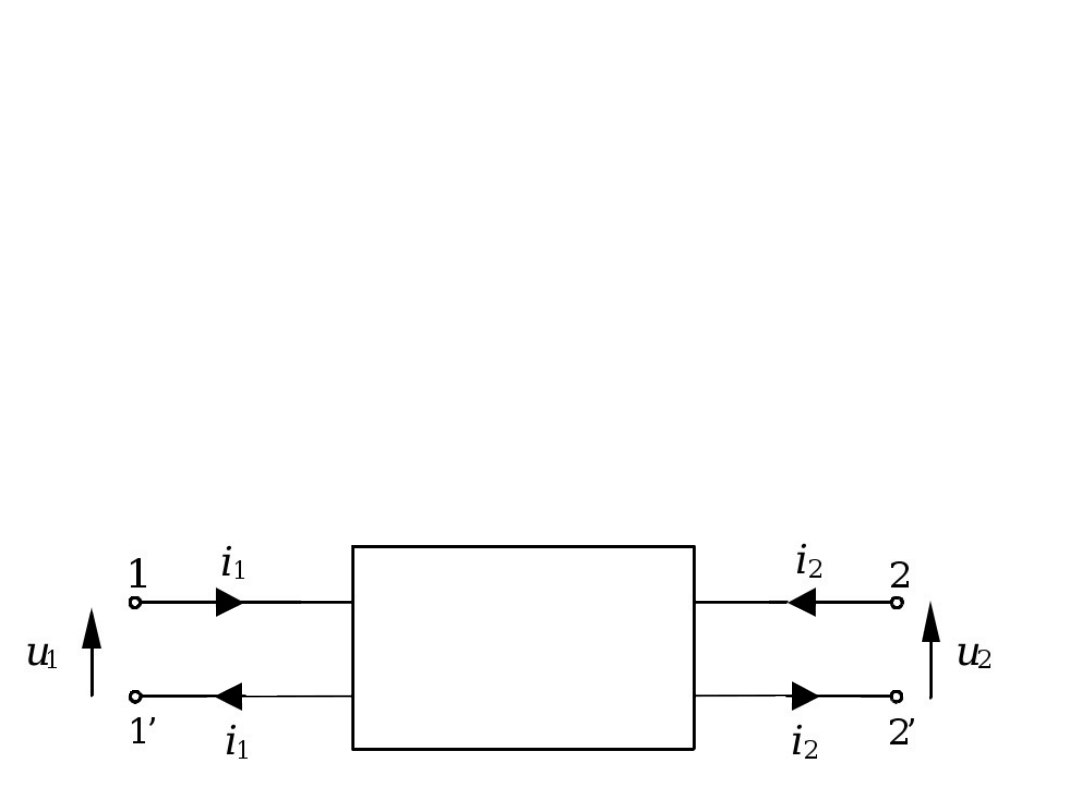
Czwórniki

Czwórnikiem nazywamy obwód 4-
zaciskowy, w którym utworzone są
dwie pary końcówek mających tę
właściwość, że w parze płynie ten
sam prąd.

zaciski 11’ – zaciski wejściowe
zaciski 22’ – zaciski wyjściowe

Czwórniki SLS, przy zerowych
warunkach początkowych dadzą
się zapisać co najmniej w jednej z
sześciu podanych postaci

Równanie impedancyjne



























2

1

2

1

i

i

u

u

Z















22

21

12

11

z

z

z

z

Z

- macierz
impedancyjna

Równanie admitancyjne



























2

1

2

1

u

u

i

i

Y















22

21

12

11

y

y

y

y

Y

- macierz
admitancyjna

Równanie łańcuchowe





























2

2

1

1

i

u

i

u

A

Równanie łańcuchowe odwrotne





























1

1

2

2

i

u

i

u

B

Równanie hybrydowe



























2

1

2

1

u

i

i

u

H

Równanie hybrydowe odwrotne



























2

1

2

1

i

u

u

i

F

Macierze Z, Y, A, B, H, F, opisujące
czwórniki, nazywamy

macierzami

charakterystycznymi.

Elementy

macierzy charakterystycznych są
funkcjami zmiennej zespolonej s.

Czwórniki nazywamy

równoważnymi

, jeżeli mają

identyczne macierze
charakterystyczne.

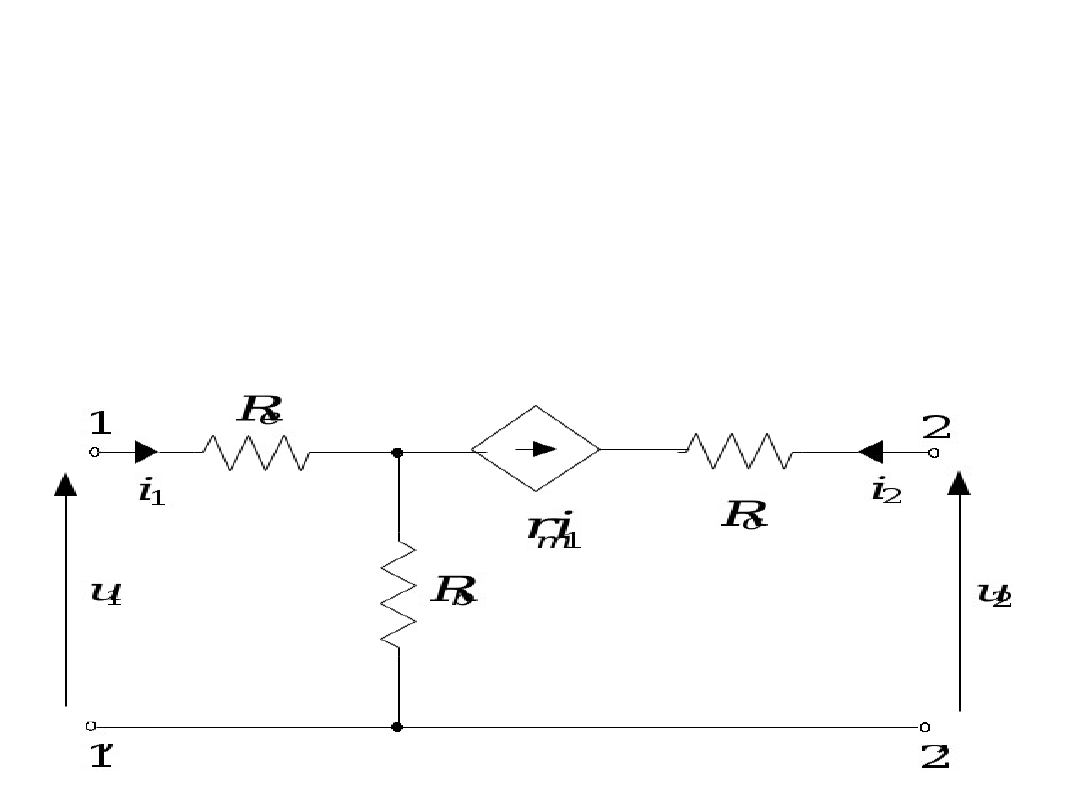
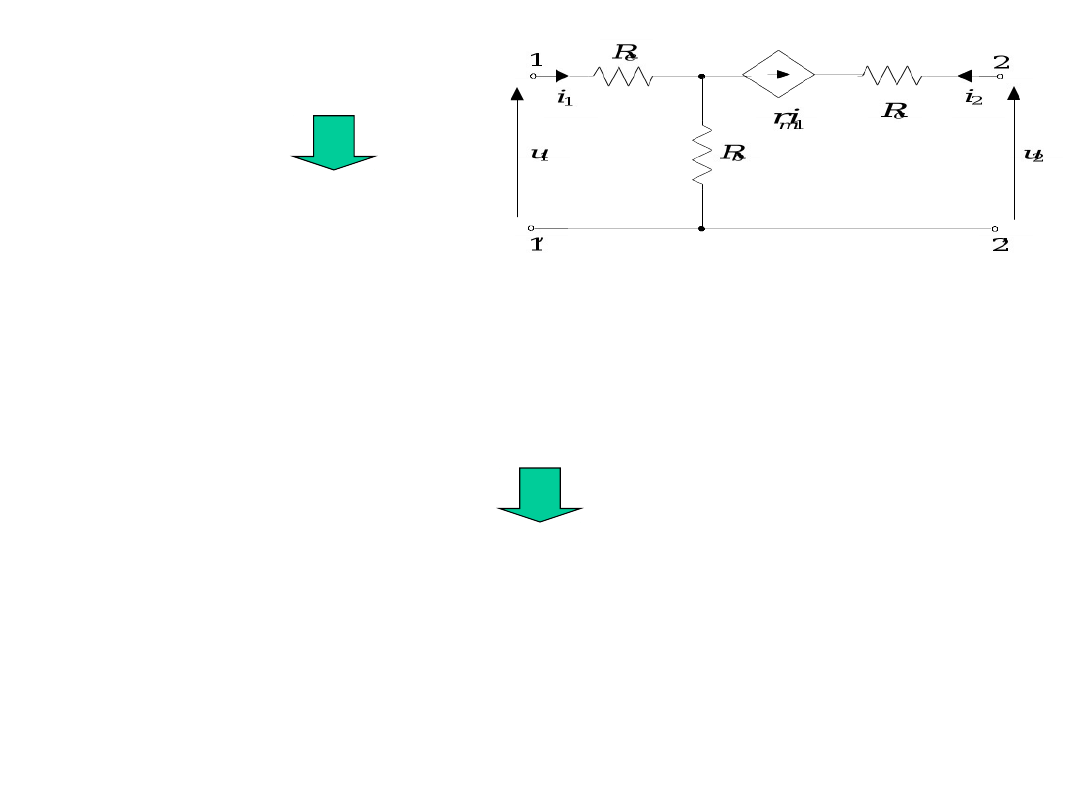
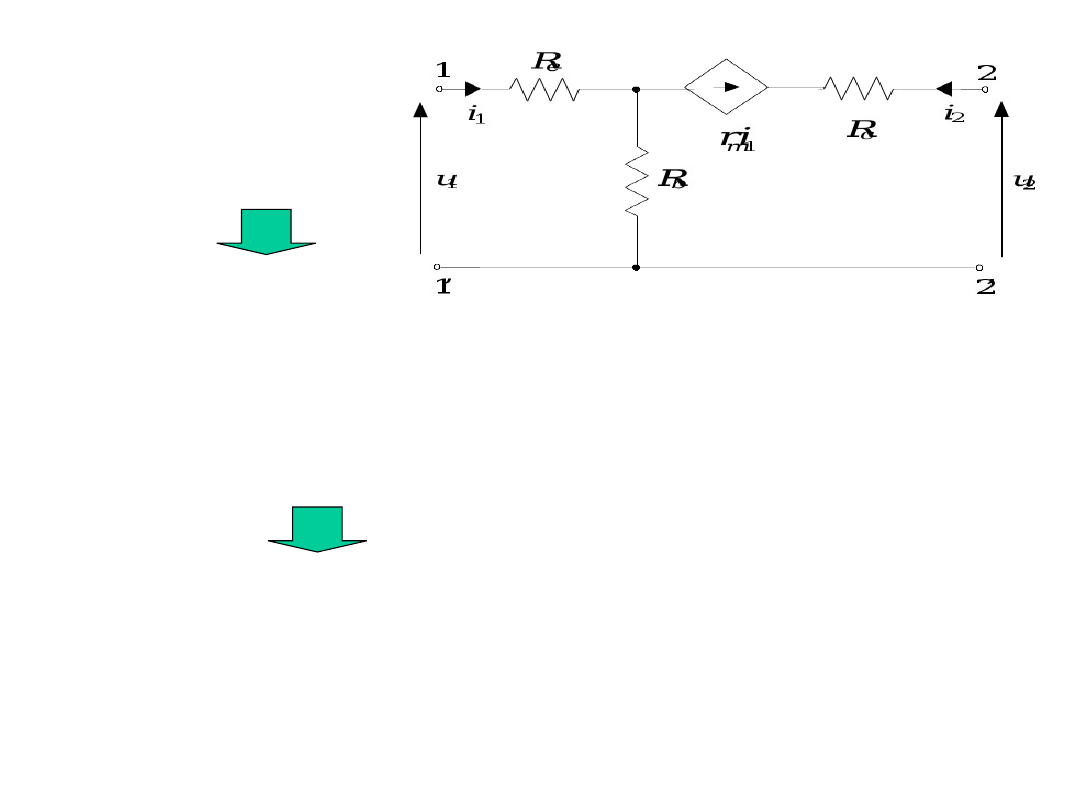
Przykład

wyznacz opis impedancyjny czwórnika



























2

1

22

21

12

11

2

1

i

i

z

z

z

z

u

u

0

2

1

1

11





i

i

u

z

0

2

1

2

21





i

i

u

z

0

1

2

1

12





i

i

u

z

0

1

2

2

22





i

i

u

z

0

2



i





1

1

i

R

R

u

b

e





1

1

2

i

R

i

r

u

b

m





b

e

R

R

z





11

b

m

R

r

z





21

0

1



i

2

1

i

R

u

b







2

2

i

R

R

u

c

b





b

R

z 

12

c

b

R

R

z





22





















c

b

m

b

b

b

e

R

R

r

R

R

R

R

Z

1



Z

Y



































11

21

12

22

z

z

z

z

Y

21

12

22

11

det

z

z

z

z











Z

Uwaga
 
W celu zbudowania żądanych równań
czwórnikowych nie jest konieczne
rozpatrywanie stanów zwarcia i
rozwarcia.

Wystarczy sformułować układ równań
opisujących obwód na podstawie praw
Kirchhoffa i Ohma, a następnie
rozwiązać go względem odpowiedniej
pary zmiennych.





2

1

1

1

i

i

R

i

R

u

b

e











2

1

1

2

2

i

i

R

i

R

r

i

R

u

b

c

m

c

























2

1

1

i

R

i

R

R

u

b

b

e









 



2

1

2

i

R

R

i

r

R

u

c

b

m

b









wyznaczamy u

1

i u

2

w funkcji i

1

i i

2

–

- otrzymujemy opis impedancyjny





2

1

1

1

i

i

R

i

R

u

b

e











2

1

1

2

2

i

i

R

i

R

r

i

R

u

b

c

m

c





















wyznaczamy u

1

i i

1

w funkcji u

2

i i

2

–

- otrzymujemy opis łańcuchowy







  

2

2

1

i

r

R

R

R

R

R

r

R

u

r

R

R

R

u

m

b

c

b

e

b

m

e

m

b

b

e



















 

2

2

1

1

i

r

R

R

R

u

r

R

i

m

b

c

b

m

b













Przekształcanie macierzy

charakterystycznych

Interesuje nas związek pomiędzy
elementami dowolnych dwóch,
spośród sześciu, macierzy
charakterystycznych.
Znajomość takich zależności
pozwala na łatwe przejście od
jednego opisu czwórnika do
innego, bardziej w danym
zagadnieniu użytecznego.
Związki takie łatwo wyprowadzić
lub można skorzystać z
odpowiedniej tabeli (13.1 z cz II)

Czwórniki prawidłowe i

zdegenerowane

Czwórnik nazywamy prawidłowym,
jeżeli ma wszystkie macierze
charakterystyczne.

Czwórnik jest prawidłowy wtedy i
tylko wtedy, kiedy ma
którąkolwiek z macierzy Z, Y, A, B,
H, F, nieosobliwą i o wszystkich
elementach różnych od zera.

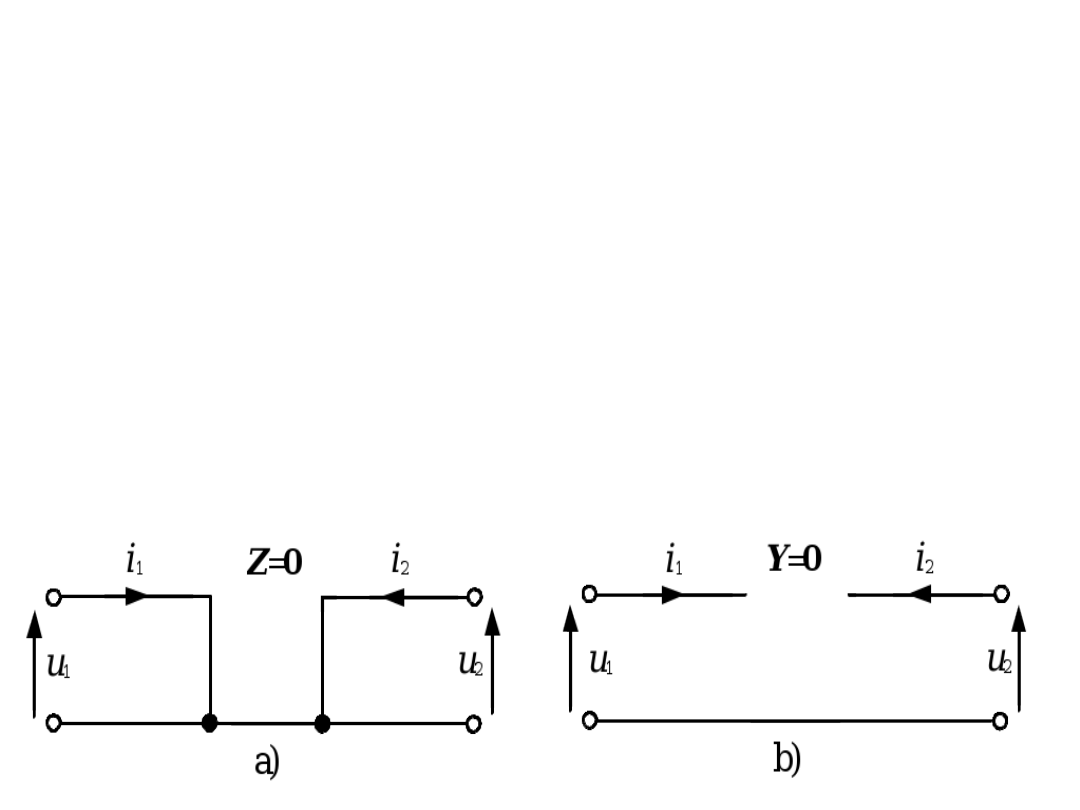
Czwórnik, który nie jest
prawidłowy, nazywamy

zdegenerowanym

.

Czwórnik mający tylko jedną
macierz charakterystyczną
nazywamy

czwórnikiem zerowym

.

Macierz charakterystyczna
czwórnika zerowego ma wszystkie
elementy równe zeru.

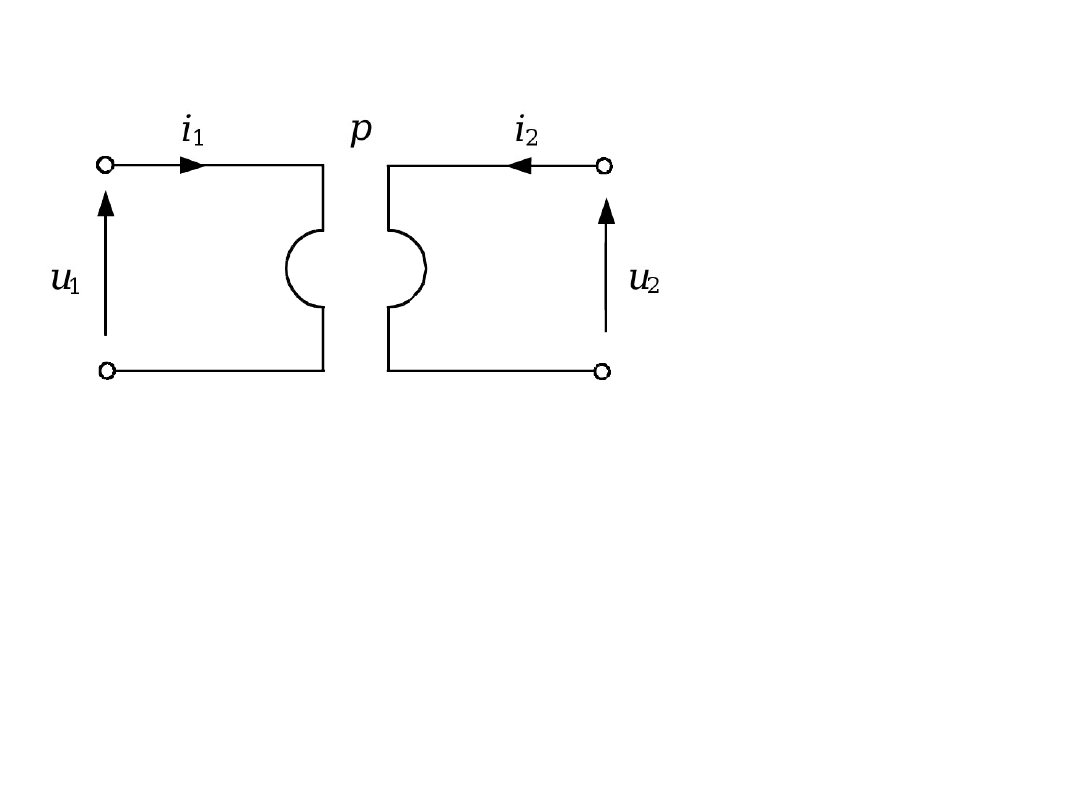
Transformator idealny

2

1

pu

u 

2

1

1

i

p

i























p

p

0

0

1

B

























0

0

1

1

1

p

p

H

F

Transformator idealny nie ma
macierzy Z i Y.

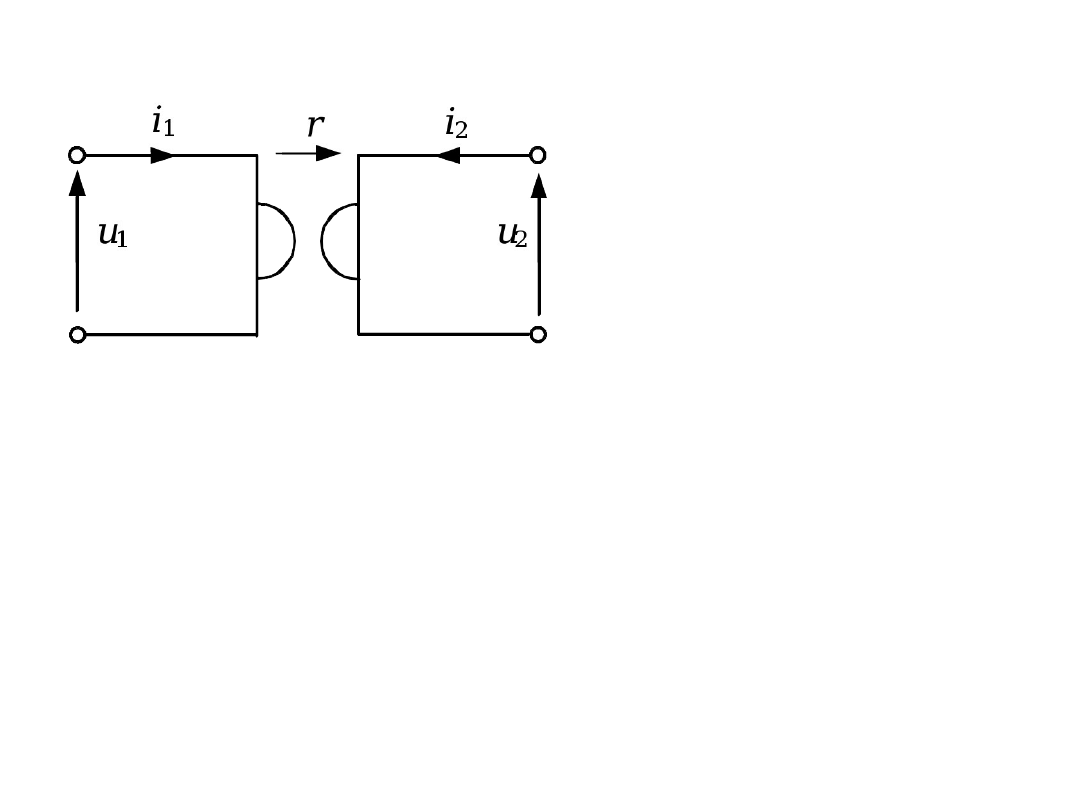
Żyrator idealny

,

i

r

u

,

i

r

u

1

2

2

1























0

0

r

r

Z

















0

0

1

r

r

A

Żyrator idealny nie ma macierzy H i F

Odwracalność i symetria

czwórnika

czwórnik przy zerowych
warunkach początkowych w dwóch
stanach

 

   





T

1

2

1

1

1

u

u



u

 

   





T

1

2

1

1

1

i

i



i

 

   





T

2

2

2

1

2

u

u



u

 

   





T

2

2

2

1

2

i

i



i

stany są wynikiem działania pewnych
wymuszeń prądowych lub
napięciowych od strony zacisków
pierwotnych i wtórnych

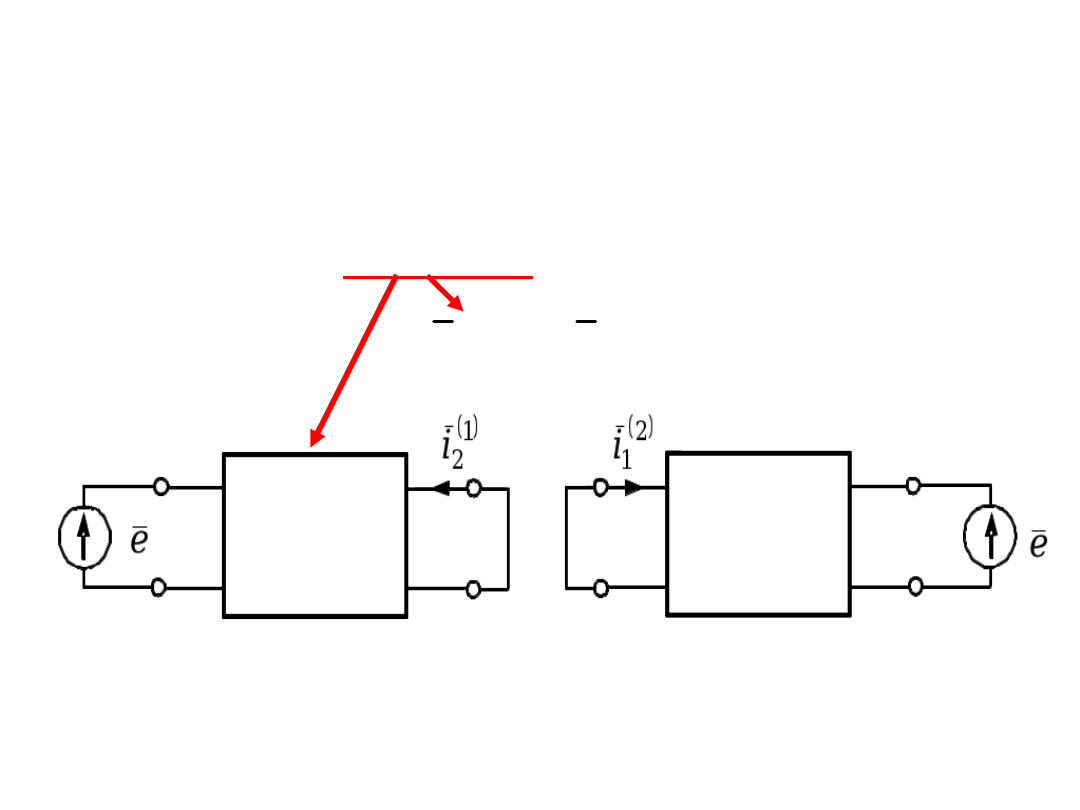
Czwórnik nazywamy odwracalnym

,

jeżeli dla każdej pary jego stanów
zachodzi równość

 

 

 

 

 

 

1

T

2

2

T

1

i

u

i

u



   

   

   

   

1

2

2

2

1

1

2

1

2

2

1

2

2

1

1

1

i

u

i

u

i

u

i

u







W przeciwnym przypadku
czwórnik jest nieodwracalny.

Twierdzenie

Warunkiem koniecznym i
wystarczającym do tego, aby
czwórnik opisany równaniem
admitancyjnym był odwracalny,
jest spełnienie zależności

21

12

y

y 

.

f

f

h

h

z

z

21

12

21

12

21

12

1

det

1

det















B

A

F

H

B

A

Z

Twierdzenie

Czwórnik jest odwracalny wtedy i
tylko wtedy, kiedy spełnia twierdzenie
o wzajemności (oczkowe lub węzłowe)

 

 

2

1

1

2

i

i 

Przykład

Transformator idealny opisany
równaniem łańcuchowym











































2

2

1

1

1

0

0

i

u

p

p

i

u

jest czwórnikiem odwracalnym

1

det 

A

Czwórniki symetryczne

W klasie czwórników odwracalnych
wyodrębniamy podklasę czwórników
symetrycznych.

W czwórniku symetrycznym
zamiana zacisków wejściowych i
wyjściowych nie powoduje
żadnych zmian w opisie
matematycznym tego czwórnika.

2

1

u

u 

2

1

i

i 

1

det

1

det

22

11

22

11

22

11

22

11













F

H

b

b

a

a

y

y

z

z

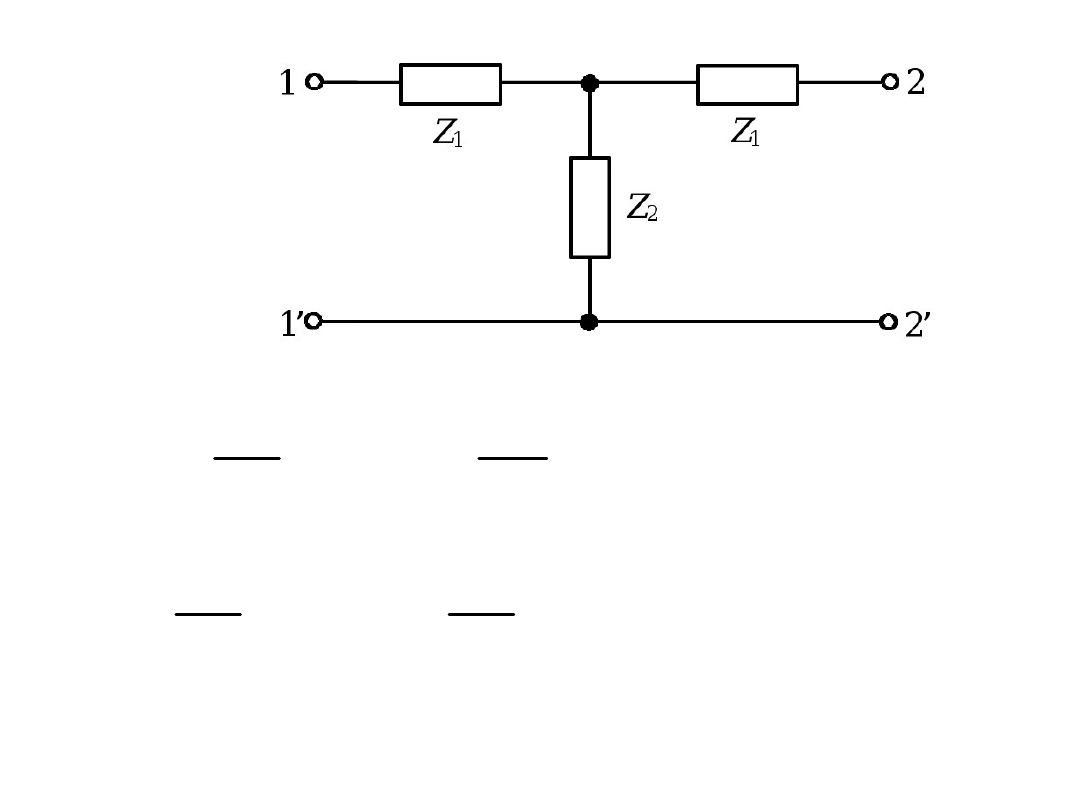
Przykład

































2

1

2

2

2

1

1

2

1

1

1

2

1

z

z

z

z

z

z

z

z

A

1

det 

A

22

11

a

a 

czwórnik jest więc symetryczny