
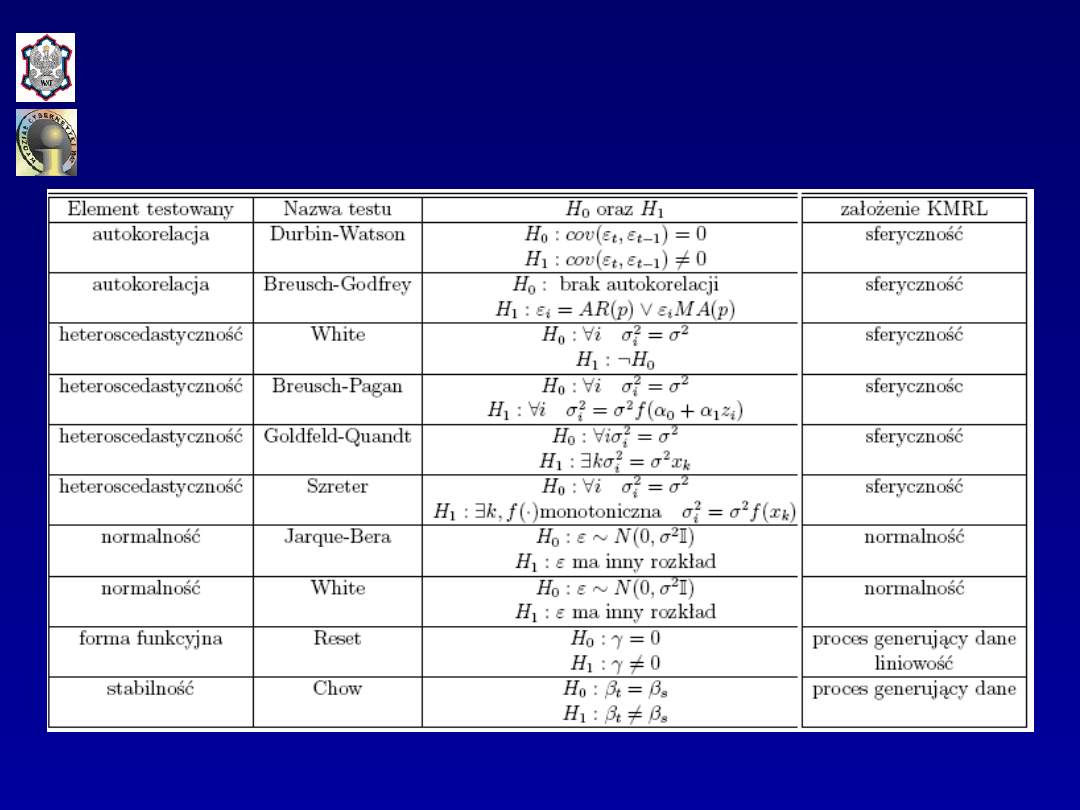
Weryfikacja
jednorównaniowego modelu
ekonometrycznego

Weryfikacja modelu
ekonometrycznego
Weryfikacja modelu obejmuje badanie:
•zgodności modelu z danymi empirycznymi,
•istotności ocen parametrów strukturalnych,
•reszt modelu (założeń dotyczących składnika losowego).
Badanie dopuszczalności modelu ekonometrycznego zwykle
polega na rozpatrzeniu
:
•dopasowania
modelu do danych empirycznych (próby).
Najczęściej stosowanymi miarami dopasowania są
współczynniku zbieżności i współczynniku determinacji
,
•dokładności
szacunku parametrów strukturalnych.
Najczęściej stosowanymi miarami dokładności są
standardowe błędy oszacowania parametrów
oraz
względne
błędy
oszacowania parametrów
.
Ocena wyrazistości modelu ekonometrycznego jest
formułowana na podstawie
współczynnika zmienności
losowej.
2
GK (WEiP(2) - 2011)
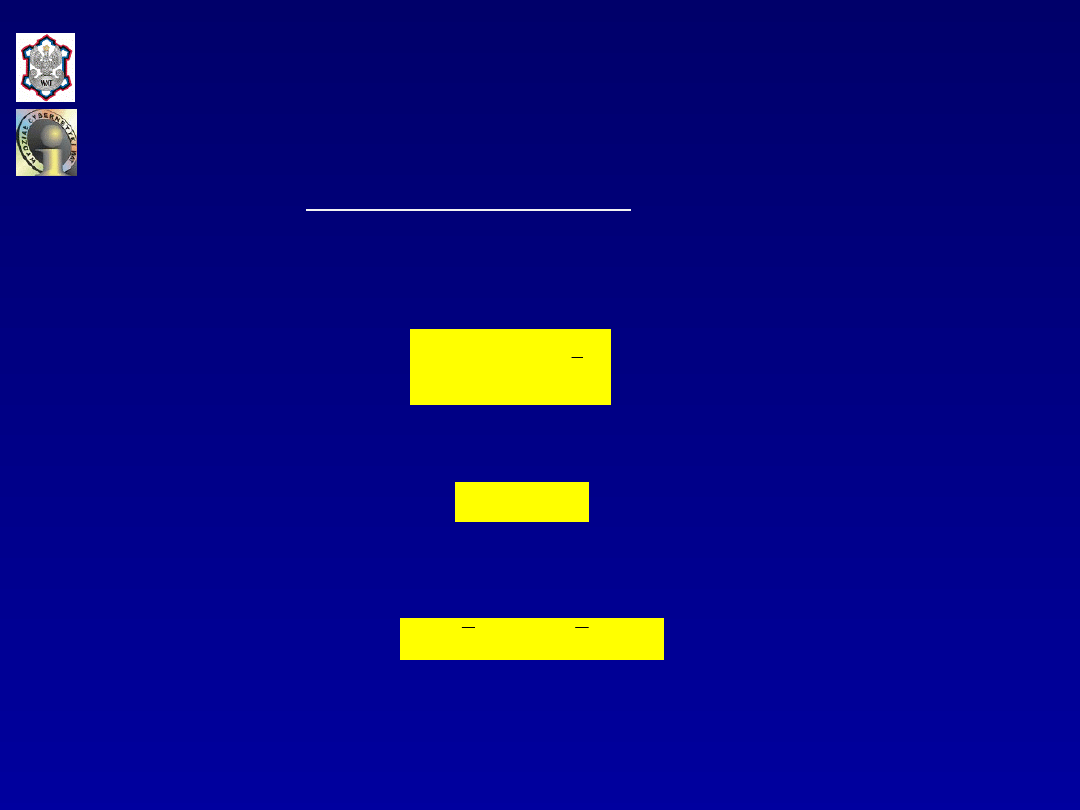
Miarą stopnia dopasowania uzyskanej
hiperpłaszczyzny regresji w próbie do danych empirycznych,
tworzących tę próbę jest miara uzyskana z dekompozycji
zmienności zmiennej objaśnianej.
Całkowita zmienność zmiennej objaśnianej wyraża
się następującą zależnością:
Z drugiej strony
i po odjęciu od obydwu stron wartości oczekiwanej zmiennej
objaśnianej otrzymuje się:
.
n
1
t
2
t
)
y
(y
SST
t
t
t
e
y
y
ˆ
.
)
ˆ
(
t
t
t
e
y
y
y
y
Weryfikacja dopuszczalności
modelu ekonometrycznego
3
GK (WEiP(2) - 2011)

Uwzględniając ostatnią równość w zależności
SST
otrzymuje
się:
Analizując ostatni składnik powyższego wyrażenia otrzymuje
się:
Ponieważ oraz więc
i ostatecznie
Weryfikacja dopuszczalności
modelu ekonometrycznego
.
ˆ
ˆ
ˆ
n
1
t
t
t
n
1
t
2
t
n
1
t
2
t
n
1
t
2
t
t
n
1
t
2
t
)e
y
y
(
2
e
)
y
y
(
)
e
)
y
y
((
)
y
(y
SST
k
1
i
n
1
t
t
it
i
n
1
t
t
0
n
1
t
t
k
1
i
it
i
0
n
1
t
t
t
e
x
a
e
)
y
(a
)e
y
x
a
(a
)e
y
y
(ˆ
0
e
n
1
t
t
0
e
x
n
1
t
t
it
0
)e
y
y
(
n
1
t
t
t
ˆ
.
ˆ
n
1
t
2
t
n
1
t
2
t
n
1
t
2
t
e
)
y
y
(
)
y
(y
SST
4
GK (WEiP(2) - 2011)

Zatem
zmienność całkowita
jest sumą
zmienności
objaśnionej
(SSR)
i
zmienności nieobjaśnionej
(SSE)
przy czym
oraz
n
1
t
2
t
)
y
y
(
SSR
ˆ
.
n
1
t
2
t
e
SSE
SSE
SSR
SST
Weryfikacja dopuszczalności
modelu ekonometrycznego
5
GK (WEiP(2) - 2011)

Podzielenie stronami rozpatrywanej zależności przez
SST
daje w wyniku:
Wyrażenia
noszą nazwy odpowiednio
współczynnika determinacji
i
współczynnika zbieżności
. Obydwa przyjmują wartości z
przedziału
[0,1]
.
Wartości współczynnika determinacji bliższe
1
,
a współczynnika zbieżności bliższe
0
oznaczają lepsze
dopasowanie modelu do danych empirycznych.
.
2
2
R
SST
SSE
SST
SSR
1
n
1
t
2
t
n
1
t
2
t
2
)
y
(y
)
y
y
(
SST
SSR
R
ˆ
n
1
t
2
t
n
1
t
2
t
2
)
y
(y
e
SST
SSE
Weryfikacja dopuszczalności
modelu ekonometrycznego
6
GK (WEiP(2) - 2011)

Weryfikacja dopuszczalności
modelu ekonometrycznego
Współczynnik determinacji
w zapisie macierzowym wyraża się
następującą zależnością:
Współczynnik zbieżności
zapisie macierzowym wyraża się
następującą zależnością:
Dla liniowego modelu ekonometrycznego współczynnik
determinacji
może być również definiowany jako kwadrat
współczynnika korelacji z próby pomiędzy wartościami
empirycznymi i teoretycznymi zmiennej objaśnianej, tj:
.
2
2
T
T
2
T
2
T
T
y
n
y
y
e
e
1
y
n
y
y
y
n
y
X
a
R
.
2
2
T
T
2
T
T
T
T
y
n
y
y
e
e
y
n
y
y
y
X
a
y
y
.
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
2
n
1
t
n
1
t
2
t
2
t
n
1
t
t
t
2
n
1
t
n
1
t
2
t
2
t
n
1
t
t
t
2
2
y
2
y
2
y
y
2
)
y
y
(
)
y
(y
)
y
y
)(
y
(y
)
y
y
(
)
y
(y
)
y
y
)(
y
(y
σ
σ
)
y
cov(y,
r
R
7
GK (WEiP(2) - 2011)

Współczynnik determinacji
może być obliczany zawsze, ale
jego interpretacja w kategoriach zmienności objaśnionej i
nieobjaśnionej oraz jego własności są zachowywane tylko przy
spełnieniu poniższy trzech następujących warunków:
•w populacji generalnej prawdziwa relacja pomiędzy zmienną
objaśnianą a objaśniającą musi być liniowa,
•parametry strukturalne modelu muszą być estymowane za
pomocą
KMNK
,
•model musi zawierać wyraz wolny, gdyż w przeciwnym przypadku
R
2
(-
,1]
.
Wadą współczynnika determinacji jest to, że jest on
niemalejącą
funkcją liczby zmiennych objaśniających
w modelu, zatem nie
może być wykorzystywany do porównywania modeli o różnej
liczbie zmiennych objaśniających. Wady tej nie posiada coraz
powszechniej stosowany
skorygowany (scentrowany)
współczynnik determinacji
postaci:
gdzie:
R
2
- współczynnik determinacji,
k
– liczba zmiennych
objaśniających,
n
–
liczba obserwacji zmiennych wykorzystanych
do oszacowania parametrów strukturalnych modelu,
e
t
– reszty
modelu.
Weryfikacja dopuszczalności
modelu ekonometrycznego
.
)
(1-R
n-k-1
k
-
R
n-k-1
1
n
)
R
(1
1
R
2
2
2
2
8
GK (WEiP(2) - 2011)

Relacje pomiędzy
współczynnikiem determinacji
i
skorygowanym (scentrowanym) współczynnikiem determinacji
:
•
,
•
,
•
może przyjmować wartości ujemne.
Współczynnik determinacji
i
skorygowany (scentrowany)
współczynnik determinacji
oraz przedstawione wnioski są
uprawnione tylko w przypadku, gdy w estymowanym modelu
ekonometrycznym
występuje wyraz wolny
. W przeciwnym
przypadku
współczynnik determinacji
może przyjmować
wartości z przedziału
(-
, 1]
, co podważa sens jego stosowania.
1,
k
dla
2
2
R
R
,
1
R
1
R
2
2
2
R
Weryfikacja dopuszczalności
modelu ekonometrycznego
9
GK (WEiP(2) - 2011)

W przypadku, gdy w estymowanym modelu
nie występuje
wyraz wolny
, stosuje się dwa podejścia do oceny dopasowania
modelu do danych empirycznych:
za pomocą
zmodyfikowanego (niescentrowanego)
współczynnika determinacji
postaci:
za pomocą
kwadratu współczynnika korelacji liniowej
pomiędzy wartościami empirycznymi i teoretycznymi
zmiennej objaśnianej
, tj.
Obydwie wymienione miary są unormowane i przyjmują
wartości z przedziału
[0, 1]
.
,
~
n
1
t
2
t
n
1
t
2
t
2
y
e
1
R
.
ˆ
2
y
y
r
Weryfikacja dopuszczalności
modelu ekonometrycznego
10
GK (WEiP(2) - 2011)
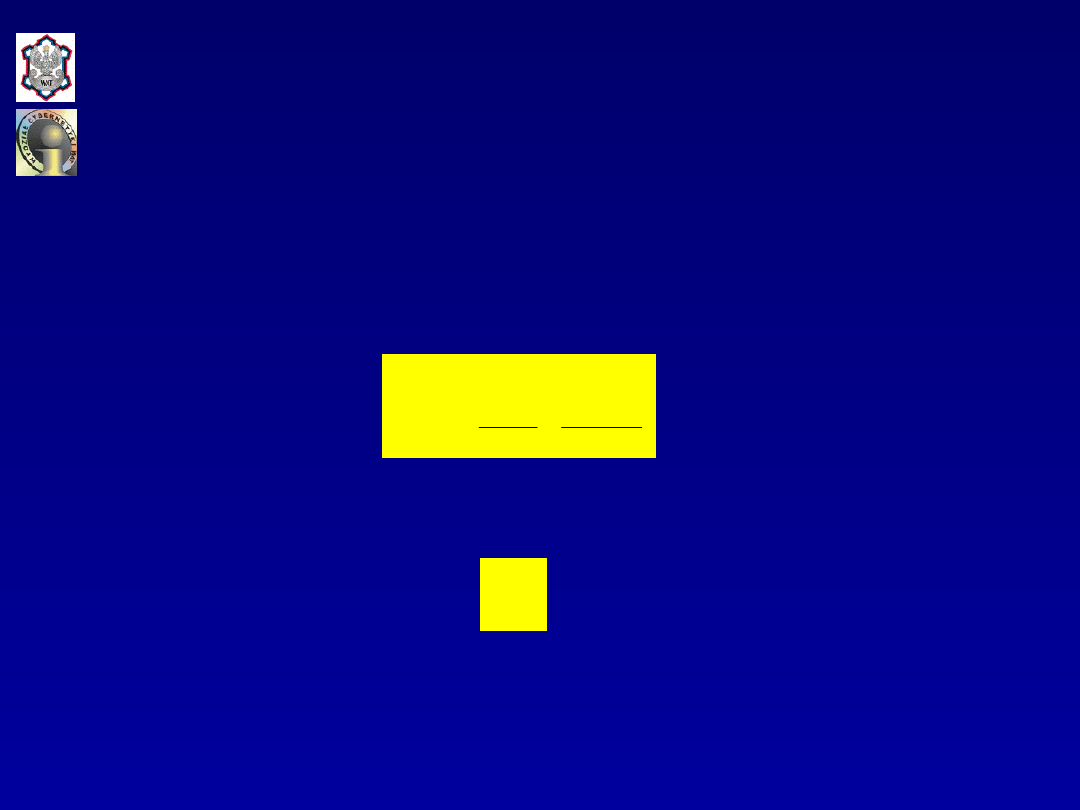
Innym wskaźnikiem wykorzystywanym do oceny dobroci
dopasowania do danych empirycznych różnych modeli , w tym
modeli bez stałej oraz modeli nieliniowych względem
parametrów, jest tzw.
kryterium informacyjne Akaike (AIC)
.
Wyraża się ono następującą formułą:
Rozpatrywane kryterium uwzględnia wpływ nadmiernej liczby
zmiennych objaśniających na spadek wartości
Zgodnie z tym kryterium włączenie dodatkowej zmiennej
objaśniającej jest zasadne wtedy, gdy maleje wartość
AIC
.
.
n
1
k
2
n
e
ln
AIC
n
1
t
2
t
.
n
t
2
t
e
1
Weryfikacja dopuszczalności
modelu ekonometrycznego
11
GK (WEiP(2) - 2011)
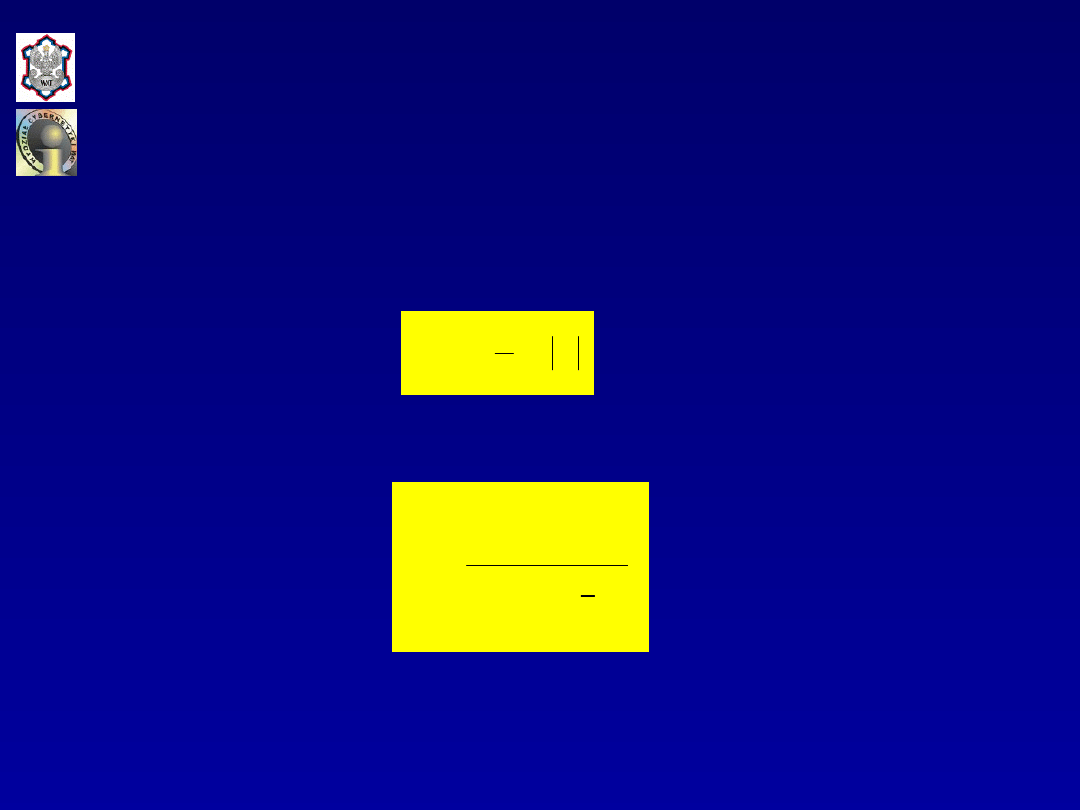
Rzadziej wykorzystywane miary jakości dopasowania modelu
do danych empirycznych:
•średni błąd względny
•współczynnik Theila
,
e
n
1
MAE
n
1
t
t
..
ˆ
n
1
t
2
t
n
1
t
2
t
t
2
)
y
(y
)
y
y
(
U
Weryfikacja dopuszczalności
modelu ekonometrycznego
12
GK (WEiP(2) - 2011)

Miarą wyrazistości modelu jest
współczynnik
zmienności, losowej
postaci:
Współczynnik ten informuje jaką część wartości średniej
zmiennej objaśnianej stanowi odchylenie standardowe
reszt modelu. Mniejsze wartości współczynnika
informują o lepszym dopasowaniu modelu do danych
empirycznych. Procedura weryfikacji wyrazistości polega
modelu na przyjęciu wartości krytycznej współczynnika
(zwykle w praktyce nie więcej niż
0,1
) i przyjęciu
modelu, gdy obliczona dla niego wartość współczynnika
W
e
jest nie większa od krytycznej. W przeciwnym
przypadku model jest oceniany jako dopasowany słabo
do danych empirycznych i powinien on być
„poprawiony”.
.
y
S
W
e
e
Weryfikacja wyrazistości
modelu ekonometrycznego
13
GK (WEiP(2) - 2011)

Weryfikacja istotności ocen parametrów
strukturalnych modelu ekonometrycznego obejmuje
najczęściej:
•określenie standardowych błędów oszacowania
parametrów
,
•testowanie hipotez o zerowej wartości parametrów
,
•określeniu przedziałów ufności dla parametrów
.
Określanie
standardowych błędów oszacowania parametrów
strukturalnych modelu
opiera się na znajomości macierzy
kowariancji postaci:
przy czym oszacowanie wariancji składnika losowego
wyznacza się z zależności
:
Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
1
T
2
e
2
X)
(X
S
(a)
D
.
1
k
n
e
1
k
n
e
e
S
n
1
t
2
t
T
2
e
14
GK (WEiP(2) - 2011)

Na głównej przekątnej macierzy wariancji i
kowariancji
D
2
(a)
znajdują się oszacowania wariancji
KMNK
-
estymatora parametrów strukturalnych modelu. Pierwiastki
kwadratowe z tych oszacowań wariancji noszą nazwę
średnich
(albo standardowych)
błędów oszacowania
parametrów
.
Średnie błędy oszacowania parametrów
0
,
1
,…,
i
,…,
k
wyznacza się z zależności:
przy czym
d
ii
jest
i-tym
elementem z głównej przekątnej
macierzy
D
2
(a)
.
Weryfikacja istotności parametrów strukturalnych
modelu
0
,
1
,…,
i
,…,
k
ma na celu stwierdzenie, czy
zmienne objaśniające istotnie oddziałują na zmienną
objaśnianą, tj. czy oceny wartości parametrów strukturalnych
modelu istotnie różnią się od
zera
(0). W przypadku, gdy
wartość parametru strukturalnego nie różni się statystycznie
od zera, przyjmuje się, że zmienna objaśniająca, z którą jest
związany w modelu ten parametr nieistotnie oddziałuje na
zmienną objaśnianą, co powinno skutkować jej usunięciem z
modelu, a taki zredukowany model musi być ponownie
estymowany i weryfikowany.
,
...,k
0,1,
i
,
d
)
S(a
ii
i
Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
15
GK (WEiP(2) - 2011)

Weryfikacja istotności ocen parametrów
strukturalnych modelu przebiega w dwóch:
etap1
- testowanie hipotezy o poprawności specyfikacji
postaci funkcyjnej modelu (testowanie stabilności postaci
analitycznej modelu); w przypadku, gdy hipoteza o
poprawności specyfikacji modelu zostanie odrzucona należy
zmienić postać funkcyjną modelu i procedurę estymacji oraz
weryfikacji modelu powtórzyć od nowa,
etap2
– jest wykonywany wtedy, gdy na
etapie1
zostanie
pozytywnie zweryfikowana hipoteza
o poprawności
specyfikacji postaci funkcyjnej modelu i polega na
testowanie istotności ocen indywidualnie każdego parametru
strukturalnego modelu.
Najczęściej stosowanym testem
poprawności specyfikacji
postaci funkcyjnej modelu
jest
test
Ramsey’a (test RESET)
.
Może być on stosowany jedynie do modeli
ekonometrycznych, których parametry strukturalne zostały
oszacowane za pomocą KMNK.
Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
16
GK (WEiP(2) - 2011)

Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
Weryfikowany jest model postaci:
którego parametry strukturalne zostały oszacowane za pomocą
KMNK.
Na tej podstawie tworzony jest rozszerzony (testowy) model
postaci:
Który jest również estymowany za pomocą MNK.
Weryfikowaną hipotezą (zerową) jest hipoteza postaci:
wobec hipotezy alternatywnej postaci:
gdzie
b
j
(j=1,2,…,p-1)
oznaczają oszacowania parametrów
strukturalnych
j
modelu rozszerzonego.
k
1
i
t
it
i
0
t
,n
1,2,
t
,
ε
x
α
α
y
...
,
...
ˆ
,n
1,2,
t
,
η
y
β
x
α
α
y
t
1
p
1
j
1
j
t
j
k
1
i
it
i
0
t
0
b
b
b
:
H
1
p
2
1
0
...
0
b
:
H
j
1
1)
,p
1,2,
(j
...
17
GK (WEiP(2) - 2011)

Sprawdzianem weryfikującym prawdziwość hipotezy zerowej jest
statystyka postaci:
gdzie
e
– wektor reszt modelu weryfikowanego,
u
– wektor reszt
modelu rozszerzonego,
(p-1)
– liczba nowych parametrów
strukturalnych uwzględnionych w modelu rozszerzonym
(najczęściej przyjmuje się
2
p
5
,
k
–
liczba zmiennych
objaśniających w modelu weryfikowanym,
R
e
2
i
R
u
2
- współczynniki
determinacji, odpowiednio dla modelu weryfikowanego i
rozszerzonego.
W przypadku prawdziwości hipotezy zerowej statystyka
F
ma rozkład
F-Snedecora o
ν
1
=p-1
i
ν
2
=n-(k+p)
stopniach swobody. Brak
podstaw do odrzucenia hipotezy zerowej występuje wtedy, gdy
wartość statystyki
F
jest nie większa od wartości krytycznej
F
*
rozkładu F-Snedecora dla przyjętego poziomu istotności i stopni
swobody
ν
1
i
ν
2
(
F
F
*
), co oznacza, że postać modelu
weryfikowanego jest dobrana poprawnie. Jeżeli wartość statystyki
F
jest większa od wartości krytycznej
F
*
(
F
>F
*
), hipoteza zerowa
jest odrzucana na rzecz hipotezy alternatywnej, co oznacza, że
model weryfikowany ma niewłaściwą postać funkcyjną.
1
p
p)
(k
n
R
1
R
R
1
p
p)
(k
n
u
u
u
u
e
e
F
2
u
2
e
2
u
T
T
T
Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
18
GK (WEiP(2) - 2011)

Innym testem
poprawności specyfikacji postaci
funkcyjnej modelu
jest
test oparty na uogólnionym
teście
Walda
.
Testowaną hipotezą jest hipoteza zerowa postaci:
wobec hipotezy alternatywnej:
Sprawdzianem prawdziwości hipotezy zerowej jest statystyka
postaci:
gdzie
R
2
oznacza współczynnik determinacji dla
rozpatrywanego modelu.
W przypadku prawdziwości hipotezy zerowej
statystyka
F
ma rozkład F-Snedecora o
ν
1
=k
i
ν
2
=n-k-1
stopniach swobody.
0
α
α
α
:
H
k
2
1
0
...
.
...
0
α
:
H
i
1
,k)
1,2,
(i
k
n-k-1
1-R
R
F
2
2
Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
19
GK (WEiP(2) - 2011)

Indywidualne testowanie istotności parametrów
strukturalnych modelu ekonometrycznego przyjmuje dla każdego
parametru formę weryfikacji hipotezy zerowej o tym, że badany
parametr
i
ma wartość równą
0
(zeru), tj.
wobec hipotezy alternatywnej
Sprawdzianem hipotezy zerowej jest statystyka postaci
która w przypadku prawdziwości hipotezy zerowej i normalnego
rozkładu składników losowych ma rozkład t-Studenta o
ν=n-k-1
stopniach swobody.
Brak podstaw do odrzucenia hipotezy zerowej występuje wtedy, gdy
wartość statystyki
t
jest nie większa od wartości krytycznej
t
/2,v
rozkładu t-Studenta dla przyjętego poziomu istotności
i stopni
swobody
ν
(
t
t
/2,v
), co oznacza, że zmienna objaśniająca związana
z weryfikowanym parametrem nie oddziałuje istotnie na zmienną
objaśnianą; zmienna powinna zostać usunięta z modelu, a model
ponownie estymowany i weryfikowany. Jeżeli wartość statystyki
t
jest większa od wartości krytycznej
t
/2,v
(
t
> t
/2,v
), hipoteza zerowa
jest odrzucana na rzecz hipotezy alternatywnej, co oznacza, że
zmienna objaśniająca związana z weryfikowanym parametrem
istotnie oddziałuje na zmienną objaśnianą.
0
α
:
H
i
0
.
0
α
:
H
i
1
)
S(a
a
t
i
i
i
Weryfikacja istotności ocen
parametrów strukturalnych
modelu ekonometrycznego
20
GK (WEiP(2) - 2011)

Weryfikacja składnika losowego zwykle obejmuje badanie:
losowości składnika losowego,
normalności składnika losowego,
autokorelacji składnika losowego,
homoskedastyczności składnika losowego.
Weryfikacja składnika losowego modelu ekonometrycznego
opiera się na badaniu reszt tego modelu. Wymieniona wyżej
kolejność badań nie jest przypadkowa i ma na celu możliwie
szybkie zakwestionowanie modelu przy zastosowaniu możliwie
najprostszych środków.
Weryfikacja składnika losowego
modelu ekonometrycznego
21
GK (WEiP(2) - 2011)

Weryfikacja losowości
składnika losowego ma na celu
pośrednie zweryfikowanie hipotezy o trafności wyboru postaci
analitycznej modelu. Weryfikowaną hipotezą zerową jest hipoteza
postaci:
wobec hipotezy alternatywnej
Do weryfikacji hipotezy o losowości składnika losowego najczęściej
jest stosowany
test serii Walda-Wolfowitza
, oparty na liczbie serii
występujących w ciągu reszt modelu. Zasadnicze etapy tego testu
są następujące:
uporządkowanie ciągu reszt według rosnących wartości wybranej
zmiennej objaśniającej,
reszty dodatnie są oznaczane „
+
”, a ujemne – „
–
”; reszty zerowe -
usuwane z ciągu,
wyznacza się liczbę serii
S
, a serią jest każdy podciąg kolejnych
reszt, którym przypisano wyłącznie takie same znaki „
+
” lub „
–
”,
Dla liczby reszt dodatnich (
n
+
) oraz ujemnych (
n
-
) i przyjętego
poziomu istotności
γ
z tablic warunkowego rozkładu liczby serii
brane są dwie liczby krytyczne
S
γ/2
i
S
1-γ/2
,
jeżeli
S
γ/2
< S< S
1-γ/2
, to nie ma podstaw do odrzucenia hipotezy
zerowej.
,n)
(t=1,2,...
,
+ε
x
+...+a
x
+α
x
+α
=α
y
:
H
t
it
k
it
2
it
1
0
t
0
.
,n)
(t=1,2,...
,
+ε
x
+...+a
x
+α
x
+α
α
y
:
H
t
it
k
it
2
it
1
0
t
1
Weryfikacja składnika losowego
modelu ekonometrycznego
22
GK (WEiP(2) - 2011)

Dla dużych prób
,
tj. w przypadku, gdy
n
+
(liczba reszt
dodatnich) oraz
n
-
(liczba reszt ujemnych) są równe co najmniej
20
, do weryfikacji hipotezy zerowej o losowości składnika
losowego nożna stosować sprawdzian postaci:
który przy prawdziwości hipotezy zerowej ma rozkład
N(0,1)
.
Dla przyjętego poziomu istotności
γ
z tablic dystrybuanty
rozkładu
N(0,1)
odczytywany jest kwantyl rzędu
1-γ/2
równy
u
1-γ/2
.
Jeżeli
|u|
>
u
1-γ/2
, hipoteza zerowa jest odrzucana, a w przeciwnym
przypadku – nie ma podstaw do jej odrzucenia
.
1
n
n
n
n
n
n
n
2n
n
n
2
n
n
n
n
2
1
S
u
2
Weryfikacja składnika losowego
modelu ekonometrycznego
23
GK (WEiP(2) - 2011)
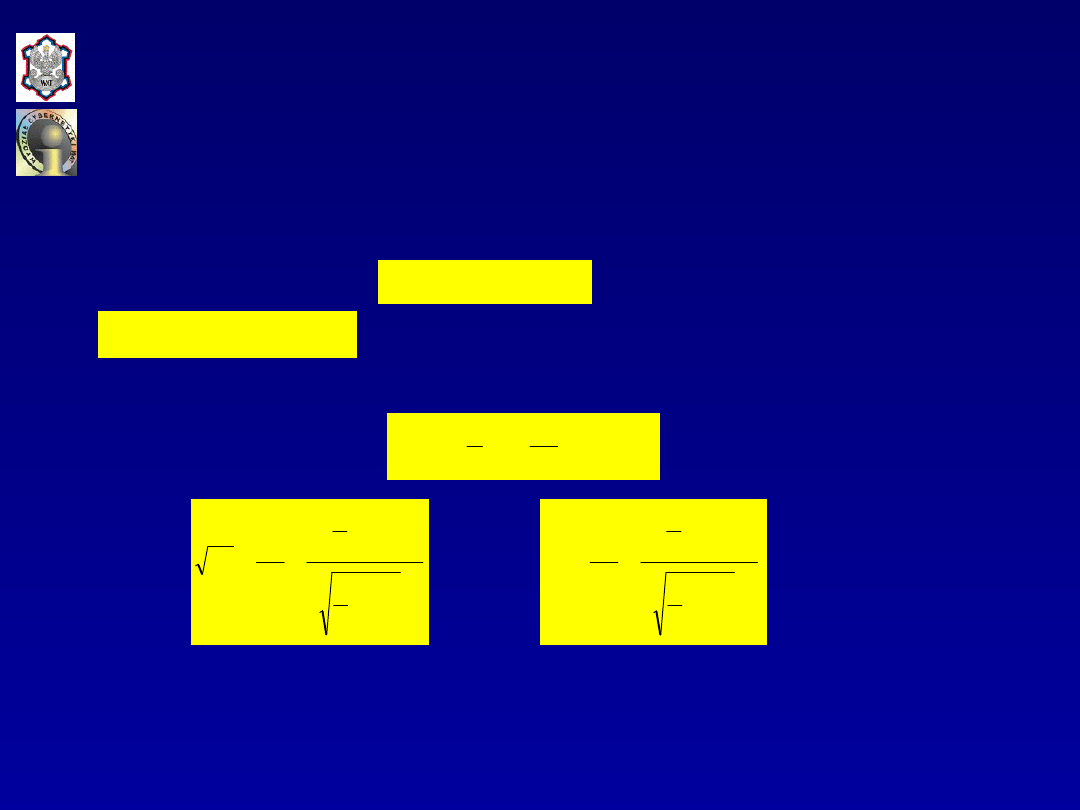
Weryfikacja składnika losowego
modelu ekonometrycznego
Do
weryfikacji normalności rozkładu składnika losowego
modelu, ze często jest stosowany (szczególnie dla dużych prób)
test
C.M. Jarque
i
A.K. Bera (JB)
, oparty na współczynnikach
asymetrii (skośności) i skupienia (kurtozy). Weryfikacji
podlega hipoteza zerowa wobec hipotezy
alternatywnej
Sprawdzianem prawdziwości hipotezy zerowej jest statystyka
postaci:
gdzie:
oraz
Przy założeniu prawdziwości hipotezy zerowej sprawdzian
JB
ma
rozkład
2
o
ν = 2
stopniach swobody. Hipoteza zerowa jest
odrzucana, gdy wartość
JB
jest większa od wartości krytycznej
2*
rozkładu
2
dla przyjętego poziomu istotności
γ
i liczby stopni
2
.
σ
m,
N
~
ε
:
H
0
.
σ
m,
N
~
ε
:
H
1
2
2
1
3)
(B
24
1
B
6
1
n
JB
3
n
1
t
2
t
n
1
t
3
t
3
3
1
e
n
1
e
n
1
S
μ
B
.
e
n
1
e
n
1
S
μ
B
4
n
1
t
2
t
n
1
t
4
t
4
4
2
24
GK (WEiP(2) - 2011)

Jedno z założeń metody KMNK dotyczy braku
autokorelacji składnika losowego
, która występuje wtedy, gdy
składniki losowe dotyczące różnych obserwacji (danych
empirycznych) są ze sobą skorelowane.
Skutki wystąpienia autokorelacji, to przede wszystkim:
utrata efektywności przez estymatory parametrów
strukturalnych uzyskane za pomocą KMNK, chociaż nadal
pozostają nieobciążone,
estymator macierzy wariancji i kowariancji parametrów
strukturalnych modelu
D
2
(a)
jest estymatorem obciążonym
rzeczywistej macierzy wariancji i kowariancji tych
parametrów,
w przypadku istnienia dodatniej autokorelacji (najczęściej
obserwowana
w praktyce) występuje zjawisko pozornej większej dokładności
oszacowania parametrów strukturalnych modelu
(niedoszacowanie wariancji), co powoduje, że testy mogą
wykazać, iż wartości oszacowań parametrów strukturalnych są
istotnie różne od zera podczas, gdy w rzeczywistości tak nie
jest,
przeszacowanie (zawyżenie) wartości współczynnika
determinacji.
Weryfikacja składnika losowego
modelu ekonometrycznego
25
GK (WEiP(2) - 2011)

Weryfikacja składnika losowego
modelu ekonometrycznego
Do pomiaru stopnia autokorelacji składników
losowych przyjmuje się współczynnik postaci:
gdzie
cov(
t
,
t-1
)
oznacza kowariancję pomiędzy
t
i
t-1
;
D(
t
)
i
D(
t-1
)
–
odchylenia standardowe
t
i
t-1
odpowiednio.
Najpopularniejszym testem do weryfikacji hipotezy o
istnieniu autokorelacji pierwszego rzędu jest test
Durbina-
Watsona (DW)
, w którym weryfikowaną hipotezą zerową jest
hipoteza postaci:
wobec jednej z następujących alternatywnych:
,
...,n
2,3,
t
,
)
)D(ε
D(ε
)
,ε
cov(
ε
ρ
1
t
t
1
t
t
0
ρ
:
H
0
,
0
ρ
:
H
1
.
0
ρ
:
H
1
,
0
ρ
:
H
1
26
GK (WEiP(2) - 2011)

Weryfikacja składnika losowego
modelu ekonometrycznego
Sprawdzianem w teście
DW
jest statystyka postaci:
gdzie: ponieważ
Statystyka
d
przyjmuje wartości z przedziału
[0,4]
.
W przypadku prawdziwości hipotezy zerowej statystyka
d
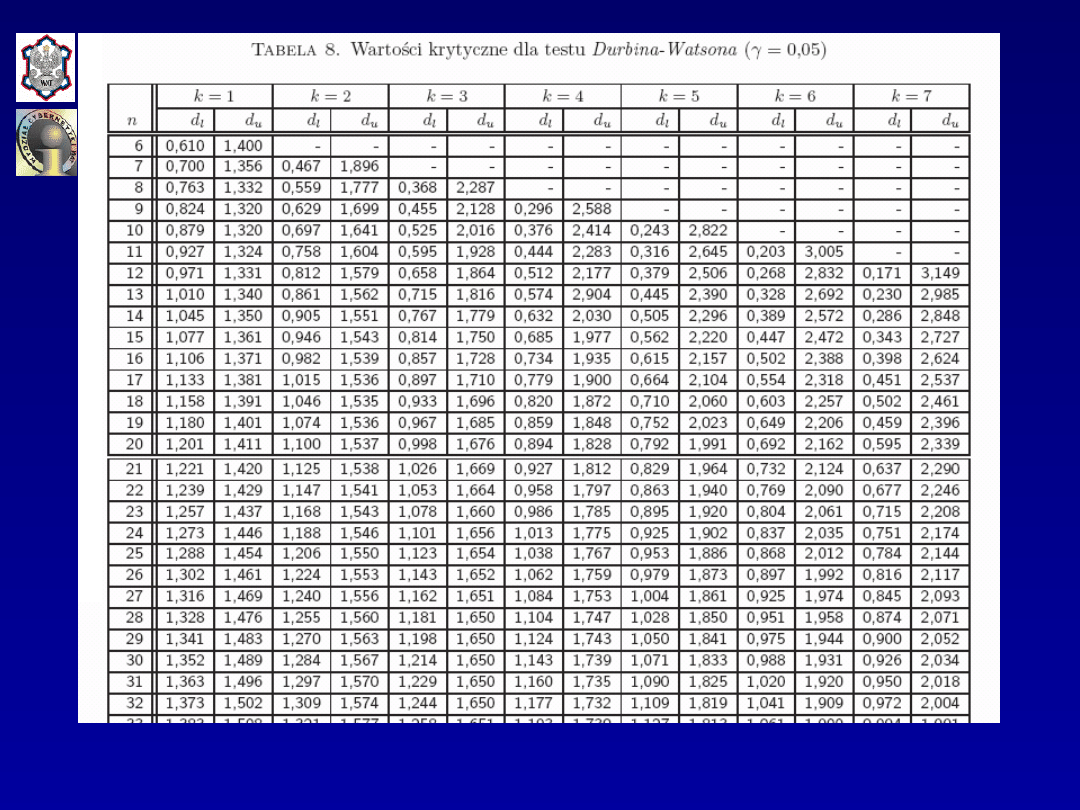
ma rozkład Durbina-Watsona. Z tabeli wartości krytycznych
testu DW
dla przyjętego poziomu istotności
γ
,
liczności
danych empirycznych
n
oraz liczby parametrów
strukturalnych w modelu
k
odczytywane są dwie liczby:
d
L
i
d
U
.
ρ
1
2
e
e
e
e
2
e
e
)
e
(e
d
n
1
t
2
t
n
2
t
2
1
t
n
2
t
1
t
t
n
2
t
2
t
n
1
t
2
t
n
2
t
2
1
t
t
ˆ
n
1
t
2
t
n
2
t
1
t
t
e
e
e
ρ
ˆ
.
n
2
t
2
1
t
n
2
t
2
t
n
1
t
2
t
e
e
e
27
GK (WEiP(2) - 2011)
W praktyce, wyboru którejkolwiek z hipotez
alternatywnych dokonuje się na podstawie analizy wartości
współczynnika autokorelacji rzędu I
obliczonego na
podstawie reszt modelu z zależności:
gdzie
Jeżeli
r
1
< 0
, wybierana jest hipoteza lewostronna, a
w przypadku, gdy
r
1
> 0
– hipoteza prawostronna.
n
2
t
2
1
t
1
t
n
2
t
2
t
t
n
2
t
1
t
1
t
t
t
1
e
e
e
e
e
e
e
e
r
.
n
2
t
1
t
1
t
n
1
t
t
t
e
1
n
1
e
,
e
n
1
e
Weryfikacja składnika losowego
modelu ekonometrycznego
28
GK (WEiP(2) - 2011)

W przypadku, gdy nie przewiduje się występowanie
autokorelacji
(r
1
0, najczęstsze założenie)
dla hipotezy
zerowej alternatywną jest hipotez dwustronna postaci:
W tym przypadku weryfikacja prawdziwości hipotezy zerowej
następuje na podstawie następujących relacji wartości
statystyki
d
obliczonej z próby i wartości krytycznych
d
L
oraz
d
U
:
gdy
0< d< d
L
- hipoteza zerowa jest odrzucana
;
istnieje
dodatnia
autokorelacja
składnika losowego,
gdy
d
U
< d< 4-d
U
-
nie ma podstaw do odrzucenia hipotezy
zerowej o braku autokorelacji
składnika losowego,
gdy
4-d
L
< d< 4
- hipoteza zerowa jest odrzucana
;
istnieje
ujemna
autokorelacja
składnika losowego,
gdy
d
L
d d
U
lub
4-d
U
d 4-d
L
test Durbina-Watsona nie
rozstrzyga
o tym, czy autokorelacja wystąpiła, czy nie
(obszar niekonkluzywności testu
DW
).
.
0
ρ
:
H
1
Weryfikacja składnika losowego
modelu ekonometrycznego
29
GK (WEiP(2) - 2011)

Odrzucenie
H
0
Istnieje
autokorelacja
dodatnia
( > 0)
?
Brak podstaw
do odrzucenia
H
0
( = 0)
?
Odrzucenie
H
0
Istnieje
autokorelacja
ujemna
( < 0)
0
d
L
d
U
4-d
U
4-
d
L
4
Graficzna interpretacja obszarów krytycznych dla testu
Durbina-Watsona w przypadku hipotezy alternatywnej
postaci:
.
0
ρ
:
H
1
Weryfikacja składnika losowego
modelu ekonometrycznego
30
GK (WEiP(2) - 2011)
31
GK (WEiP(2) - 2011)

Test Durbina-Watsona w omówionej poprzednio postaci może
być stosowany, gdy:
w modelu uwzględnia się wyraz wolny,
składnik losowy ma rozkład normalny,
zmienne objaśniające nie są losowe,
w zbiorze zmiennych objaśniających nie występują zmienne z
przesuniętym czasem (opóźnione).
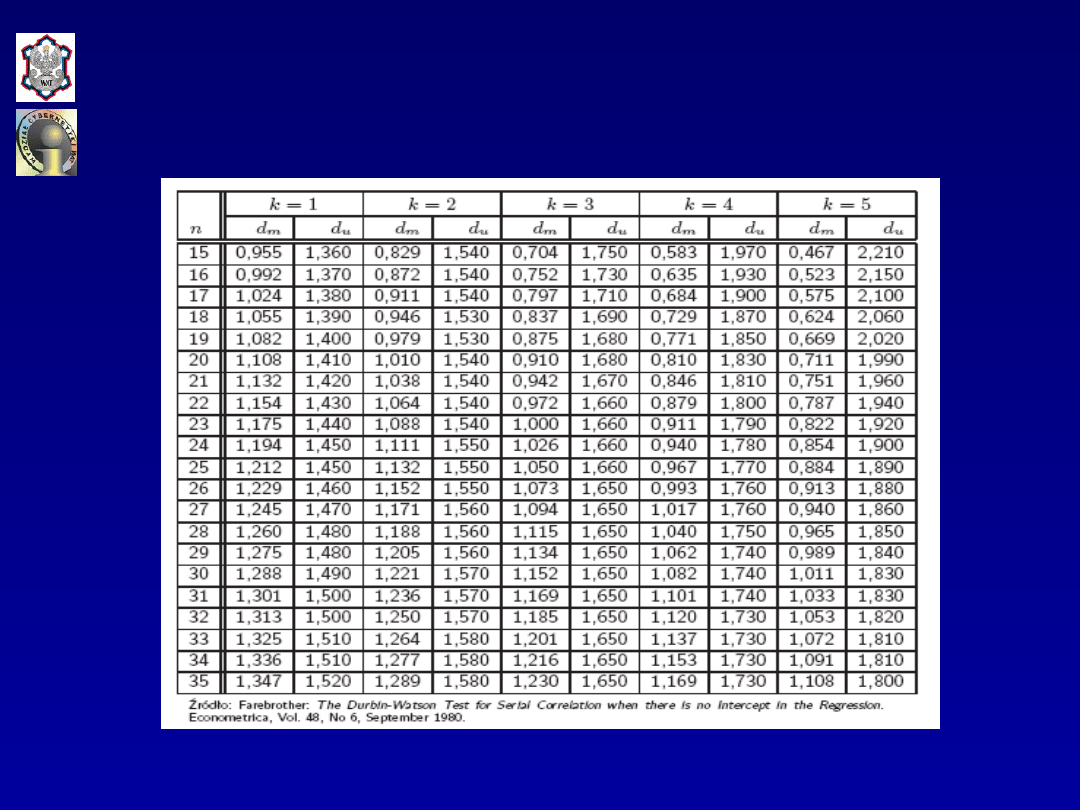
W przypadku, gdy model nie zawiera wyrazu wolnego
stosuje się również test Durbina-Watsona z tym, że
wyznaczanie wielkości granicznych statystyki
DW
, tj.
wielkości
d
L
i
d
U
odbywa się na podstawie innych tablic, w
których
d
L
zostało zastąpione przez
d
m
.
Weryfikacja składnika losowego
modelu ekonometrycznego
32
GK (WEiP(2) - 2011)
Weryfikacja składnika losowego
modelu ekonometrycznego
33
GK (WEiP(2) - 2011)

Istotną wadą testu Durbina–Watsona jest istnienie
obszarów niekonkluzywności, w których nie można podjąć decyzji
co do odrzucenia bądź nieodrzucenia hipotezy zerowej o braku
autokorelacji. W tym przypadku należy zastosować inne testy, np
.
test istotności współczynnika korelacji
,
test Breuscha-Godfrey’a
(BG)
. Test
BG
zwykle jest stosowany w przypadku, gdy
n>30
. W
przypadku, gdy
n>60
często jest stosowany
test von Neumanna
(Q)
.
Test
Breuscha-Godfrey’a (BG)
może być stosowany również w
przypadku testowania zjawiska autokorelacji rzędu wyższego niż
1
. Postępowanie przy teście
BG
przebiega następująco:
oszacowanie parametrów strukturalnych pierwotnego
(badanego) modelu ekonometrycznego i wyznaczenie jego reszt,
utworzenie modelu pomocniczego ze zmienną objaśnianą w
postaci reszt
z modelu pierwotnego
gdzie :
x
it
- zmienne objaśniające pierwotnego modelu
ekonometrycznego,
p
- największy rząd badanej autokorelacji
składnika losowego (w praktyce na ogół przyjmuje się (
p
5
),
Weryfikacja składnika losowego
modelu ekonometrycznego
,n
2,
1,p
p
t
,
ξ
e
λ
x
β
β
e
t
p
1
j
j
t
j
k
1
i
it
i
0
t
...
34
GK (WEiP(2) - 2011)
sformułowanie hipotezy zerowej
wobec
alternatywnej
oszacowanie parametrów strukturalnych modelu
pomocniczego i obliczenie dla niego współczynnika
determinacji
R
2
.
Sprawdzianem
testu BG
jest statystyka postaci:
która w przypadku prawdziwości hipotezy zerowej ma
asymptotyczny rozkład
2
z
ν = p
stopniami swobody.
Hipoteza zerowa jest odrzucana, gdy wartość sprawdzianu
2
jest większa od wartości krytycznej
2*
rozkładu
2
dla
przyjętego poziomu istotności
γ
i liczby stopni
ν
, co
oznacza istnienie autokorelacji rzędu
p
.
0
λ
λ
λ
:
H
p
2
1
0
...
,
...
0
λ
:
H
i
1
,p)
1,2,
(i
2
2
R
p
n
χ
Weryfikacja składnika losowego
modelu ekonometrycznego
35
GK (WEiP(2) - 2011)

Weryfikacja homoskedastyczności składnika losowego.
W
przypadku, gdy zróżnicowanie wariancji składnika losowego
zależy tylko od jednej zmiennej powinny być stosowane testy
Goldfelda-Quandta i Harrisona-McCabe’a. Jeżeli jednak
zróżnicowanie wariancji składnika losowego zostało
spowodowane łącznie przez więcej niż jedną zmienną
objaśniającą, należy stosować inne testy np.
test Breuscha-
Pagana
lub
White’a
. Warunkiem stosowania tych testów jest
dysponowanie dużą próbą (
n-k-1>30
). Opierają się one na
koncepcji potraktowania reszt z oszacowanego modelu
pierwotnego jako zmiennych objaśnianych (po odpowiednim
przekształceniu) w modelu pomocniczym, w którym
zmiennymi objaśniającymi są zmienne objaśniające modelu
pierwotnego oraz ich kombinacje (w teście White’a).
Sprawdzianem w tych testach jest statystyka oparta na
współczynniku determinacji obliczonym dla modelu
pomocniczego, która przy założeniu prawdziwości hipotezy
zerowej o braku zróżnicowania wariancji składnika
losowego ma rozkład
2
.
Weryfikacja składnika losowego
modelu ekonometrycznego
36
GK (WEiP(2) - 2011)

Zastosowanie
testu Breuscha-Pagana (BP)
wymaga
uprzedniego określenia zbioru tych zmiennych
objaśniających, które są podejrzewane o wpływanie na
zmienność wariancji składnika losowego ( w teście mogą
być uwzględnione wszystkie zmienne objaśniające). Dalej
te zmienne będą oznaczane przez
Z = {z
1t
, z
2t
, …,z
mt
}
.
Procedura testowania
testem BP
jest następująca:
oszacowanie parametrów strukturalnych modelu
pierwotnego
i wyznaczenie jego reszt
e
t
,
wyznaczenie wartości estymatora wariancji resztowej
postaci:
,n)
1,2,
(t
t
kt
k
2t
2
1t
1
0
t
ε
x
α
x
α
x
α
α
y
...
,
...
,
ˆ
n
e
σ
n
1
t
2
t
2
Weryfikacja składnika losowego
modelu ekonometrycznego
37
GK (WEiP(2) - 2011)

utworzenie i oszacowanie parametrów strukturalnych
modelu pomocniczego:
gdzie
obliczenie dla modelu pomocniczego wyjaśnionej sumę
kwadratów:
,
...
ˆ
,n
1,2,
t
,
σ
e
π
2
2
t
t
,n)
1,2,
(t
,
η
z
β
z
β
z
β
β
π
t
mt
m
2t
2
1t
1
0
t
...
...
.
ˆ
n
1
t
2
t
π
π
ESS
Weryfikacja składnika losowego
modelu ekonometrycznego
38
GK (WEiP(2) - 2011)

Testowaną hipotezą jest hipoteza zerowa postaci:
wobec hipotezy alternatywnej:
.
Sprawdzianem prawdziwości hipotezy zerowej jest statystyka
postaci:
która ma asymptotyczny rozkład
2
o
ν = m
stopniach
swobody.
Hipoteza zerowa o homoskedastyczności składnika
losowego jest odrzucana, gdy wartość sprawdzianu
BP
jest
większa od wartości krytycznej
2*
rozkładu
2
dla przyjętego
poziomu istotności
γ
i liczby stopni
ν
.
0
β
β
β
:
H
m
2
1
0
...
.
...
0
β
:
H
i
1
,m)
1,2,
(i
ESS
2
1
BP
Weryfikacja składnika losowego
modelu ekonometrycznego
39
GK (WEiP(2) - 2011)

Procedura testowania
testem White’a
jest następująca:
oszacowanie parametrów strukturalnych modelu
pierwotnego
i wyznaczenie jego reszt
e
t
,
utworzenie modelu pomocniczego w następującej postaci i
oszacowanie jego parametrów strukturalnych:
obliczenie współczynnika determinacji
R
2
dla modelu
pomocniczego.
,n)
1,2,
(t
t
kt
k
2t
2
1t
1
0
t
ε
x
α
x
α
x
α
α
y
...
,
...
,n
1,2,
t
t
1
k
1
i
k
1
i
j
jt
it
C
i
j
k
1
i
k
1
i
2
it
k
i
k
1
i
it
i
0
2
t
η
x
x
β
x
β
x
β
β
e
2
i
...
Weryfikacja składnika losowego
modelu ekonometrycznego
40
GK (WEiP(2) - 2011)

Testowaną hipotezą jest hipoteza zerowa postaci:
wobec hipotezy alternatywnej:
.
Sprawdzianem prawdziwości hipotezy zerowej jest
statystyka postaci:
która ma asymptotyczny rozkład
2
o
=2k+C
k
2
stopniach
swobody.
Hipoteza zerowa o homoskedastyczności składnika
losowego jest odrzucana, gdy wartość sprawdzianu
nR
2
jest
większa od wartości krytycznej
2*
rozkładu
2
dla przyjętego
poziomu istotności
γ
i liczby stopni
ν
.
0
β
β
β
:
H
2
k
C
2k
2
1
0
...
.
...
0
β
:
H
i
k
1
)
C
,2k
1,2,
(i
2
2
nR
Weryfikacja składnika losowego
modelu ekonometrycznego
41
GK (WEiP(2) - 2011)

Wybór odpowiedniego testu do wykrywania
heteroskedastyczności zależy od znajomości możliwej jej
formy funkcyjnej. Jeżeli są znane zmienne odpowiedzialne za
heteroskedastyczność i zależy ona od nich liniowo, należy
użyć testu
Breuscha-Pagana (BP)
.
W przypadku, gdy za
istnienie heteroskedastyczności odpowiada tylko jedna
zmienna poleca się stosowanie testu
Goldfelda-Quandta
(GQ)
, szczególnie, gdy ta zmienna jest zmienną dyskretną.
W przypadku nieznanej postaci funkcyjnej
heteroskedastyczności może być stosowany najbardziej
ogólny test
White’a
, chociaż ma on ograniczoną moc.
Weryfikacja składnika losowego
modelu ekonometrycznego
42
GK (WEiP(2) - 2011)
Weryfikacja składnika losowego
modelu ekonometrycznego
43
GK (WEiP(2) - 2011)

Uogólniony model regresji
liniowej
Założenia
standardowego modelu ekonometrycznego
wymagają
sferyczności składnika losowego
, tj,:
co oznacza jednoczesne zachodzenie warunków:
•homoskedastyczności składnika losowego (stała w czasie i
skończona wariancja):
• brak autokorelacji (niezależność) składnika losowego:
I
σ
εε
E
ε
D
2
T
2
,
2
2
t
t
2
σ
ε
E
ε
D
.
0
τ
0,
ε
ε
E
,ε
ε
Cov
τ
t
t
τ
t
t
44
GK (WEiP(2) - 2011)

Jeżeli nie zostanie spełnione założenie dotyczące
homoskedastyczności składnika losowego, to mówi się, że
składnik losowy jest
heteroskedastyczny
. Jeżeli nie zostanie
spełnione założenie braku autokorelacji składnika losowego,
to mówi się, że występuje
autokorelacja
składnika losowego.
Przypadek niespełnienia obydwu wymienionych wymagań
określa się mianem
niesferyczności
składnika losowego.
Uwzględnienie
niesferyczności
składnika losowego jest
równoważne zastąpieniu macierzy jednostkowej
I
dodatnio
określoną symetryczną macierzą
o wymiarach
(n
n)
,
co
oznacza, że w modelu zostanie uwzględniona jednocześnie
heteroskedastyczność
składnika losowego (różne elementy
diagonalne macierzy
)
i jego
autokorelacja
(niezerowe
elementy macierzy
poza główną przekątną). Tworzony jest w
ten sposób
uogólniony model regresji liniowej
.
45
GK (WEiP(2) - 2011)
Uogólniony model regresji
liniowej

Definicja
uogólnionego modelu regresji liniowej
:
uogólnionym modelem regresji liniowej jest model postaci:
spełniający warunki:
gdzie
•
-
macierz dodatnio określona,
•
X
– nielosowa macierz wartości zmiennych objaśniających o
wymiarach
(n
(k+1))
i
r(X) = 1+k
n
.
Nie tracąc ogólności rozważań przyjmuje się, że
tr(
) = n
.
ε
Xα
y
Ω
σ
εε
E
ε
D
oraz
0
ε
E
2
T
2
46
GK (WEiP(2) - 2011)
Uogólniony model regresji
liniowej

Estymacji (oceny, oszacowania) parametrów
strukturalnych rozpatrywanego uogólnionego modelu regresji
dokonuje się za pomocą
Uogólnionej Metody Najmniejszych
Kwadratów (UMNK)
,
której istota polega na minimalizacji
„uogólnionej sumy kwadratów odchyleń” postaci:
.
Rozwijając powyższe wyrażenie uzyskuje się:
.
Różniczkując
(a)
po wektorze
a
otrzymuje się:
.
a
1
T
e
Ω
e
a
ψ
min
.
y
Ω
X
2a
Xa
Ω
X
a
y
Ω
y
Xa
y
Ω
Xa
y
e
Ω
e
a
ψ
1
T
T
1
T
T
1
T
1
T
1
T
.
y
Ω
2X
Xa
Ω
2X
a
a
ψ
1
T
1
T
47
GK (WEiP(2) - 2011)
Uogólniony model regresji
liniowej

Przyrównując uzyskane wyrażenie do
0
(zera)
otrzymuje się układ równań normalnych postaci:
którego rozwiązanie daje poszukiwane oszacowanie
parametrów strukturalnych modelu:
przy czym symbol (
*
) został użyty dla odróżnienia od
oszacowania uzyskanego za pomocą KMNK.
Zgodnie z uogólnieniem Aitkena twierdzenia Gaussa-
Markowa o metodzie najmniejszy kwadratów, uzyskany
estymator
a
*
jest najlepszym nieobciążonym estymatorem
liniowym wektora parametrów strukturalnych
dla
uogólnionego modelu regresji liniowej.
,
y
Ω
X
Xa
Ω
X
1
T
1
T
y
Ω
X
X)
Ω
(X
a
1
T
1
1
T
*
48
GK (WEiP(2) - 2011)
Uogólniony model regresji
liniowej

Dla rozpatrywanego modelu oszacowaniem macierzy
wariancji i kowariancji estymatorów parametrów
strukturalnych jest:
przy czym
S
2
e
jest nieobciążonym estymatorem wariancji
2
składnika losowego postaci:
W praktycznych zastosowaniach zwykle korzysta się z
przekształceń danych empirycznych opierając się na
wnioskach w następującego twierdzenia: ponieważ macierz
jest macierzą symetryczną i dodatnio określoną, więc takie
same własności posiada do niej macierz odwrotna
--1
, zatem
istnieje taka nieosobliwa macierz
P
, że
.
.
S
2
e
1
k
n
e
Ω
e
1
T
1
1
T
2
e
*
2
X)
Ω
(X
S
)
(a
D
.
1
T
T
Ω
P
P
I
P
Ω
P
oraz
49
GK (WEiP(2) - 2011)
Uogólniony model regresji
liniowej

Mnożąc obie strony modelu
przez macierz
P
uzyskuje się model postaci z danymi
przetransformowanymi:
gdzie:
,
Stąd wynika, że do estymacji modelu z danymi
przetransformowanymi może być stosowana
KMNK
, a
uzyskane za jej pomocą oszacowania
a
są równe uzyskanym za
pomocą
UMNK
dla danych pierwotnych, tj.:
,
Pε
ε
PX,
X*
Py,
y
*
*
.
I
σ
P
PΩ
σ
P
Pεε
E
Pε
Pε
E
εε
E
2
T
2
T
T
T
T
,
*
*
*
ε
α
X
y
.
*
a
y
Ω
X
X
Ω
X
Py
P
X
PX
P
X
y
X
X
X
a
1
T
1
1
T
T
T
1
T
T
*
T
*
1
*
T
*
ε
Xα
y
50
GK (WEiP(2) - 2011)
Uogólniony model regresji
liniowej

Estymacja parametrów modelu w
przypadku
heteroskedastyczności
składnika losowego
51
GK (WEiP(2) - 2011)
1. Uogólniona metoda najmniejszych kwadratów.
W przypadku
wystąpienia zjawiska heteroskedastyczności
składnika losowego
i przy braku jego autokorelacji oraz
zachowaniu pozostałych założeń Gaussa-Markowa
macierz
wykorzystywana w
UMNK
jest macierzą diagonalną postaci:
Jako elementy diagonalne macierzy
najczęściej w praktyce
są wykorzystywane z modelu pierwotnego:
• wartości wybranej zmiennej objaśniającej:
• wartości zmiennej objaśnianej (empiryczne i teoretyczne):
•
wartości reszt modelu:
.
n)
(n
nn
22
11
ω
...
0
0
:
...
:
:
0
...
ω
0
0
...
0
ω
Ω
,
2
it
it
x
,
x
,
ˆ
2
t
2
t
y
,
y
.
2
t
t
e
,
e

52
GK (WEiP(2) - 2011)
Estymacja parametrów modelu w
przypadku
heteroskedastyczności
składnika losowego
2. Ważona metoda najmniejszych kwadratów.
Rozpatrywana metoda polega na tym, że dane empiryczne,
stanowiące podstawę do szacowania parametrów
strukturalnych modelu pierwotnego
zostają przekształcone za pomocą odpowiednio dobranych
wag
, a następnie wykorzystane do powtórnego oszacowania
parametrów strukturalnych tego modelu za pomocą
KMNK
.
Istotę metody można przedstawić w postaci następującego
postępowania:
1.Estymowanie modelu pierwotnego.
2.Zbudowanie modelu pomocniczego opartego na resztach
modelu pierwotnego w jednej z następujących wersji:
przy czym za zmienne objaśniające
z
tj
(j=1,2,…,s)
przyjmuje
się zmienne objaśniające
x
ti
(i=1,2,…,k)
lub
ich funkcje
lub
tylko zmienne
x
ti
podejrzewane o spowodowanie wystąpienia
heteroskedastyczności.
,n
1,2,
t
,
v
z
β
z
β
z
β
β
e
I
t
st
s
2t
2
1t
1
0
2
t
...
...

53
GK (WEiP(2) - 2011)
Estymacja parametrów modelu w
przypadku
heteroskedastyczności
składnika losowego
2. Ważona metoda najmniejszych kwadratów (cd).
Zakłada się, że składnik losowy
v
t
występujący w modelu (I)
spełnia warunki Gaussa-Markowa, które umożliwiają
stosowanie KMNK do estymacji tego modelu. Niech
oznaczają teoretyczne wartości zmiennej objaśnianej
Wagi
t
są obliczane jako:
,n
1,2,
t
,
e
2
t
...
ˆ
.
...,n
1,2,
t
,
e
2
t
.
...
ˆ
,n
1,2,
t
,
e
1
2
t
t

54
GK (WEiP(2) - 2011)
Estymacja parametrów modelu w
przypadku
heteroskedastyczności
składnika losowego
2. Ważona metoda najmniejszych kwadratów (cd).
W przypadku, gdy nie wszystkie teoretyczne wartości
zmiennej objaśnianej w modelu (I) są dodatnie, przyjmuje się
jeden z następujących modeli (model II lub III):
Wagi
t
są obliczane jako w przypadku
modelu (II)
oraz w przypadku modelu (III).
,n
1,2,
t
,
e
2
t
...
ˆ
,n
1,2,
t
,
1
t
t
...
ˆ
.
,
...
...
ln
...
...
,n
1,2,
t
,n
1,2,
t
2
t
t
t
st
s
2t
2
1t
1
0
t
t
t
t
st
s
2t
2
1t
1
0
t
e
,
v
z
β
z
β
z
β
β
,
e
,
v
z
β
z
β
z
β
β
II
III
,n
1,2,
t
,
1
t
t
...
ˆ
exp

55
GK (WEiP(2) - 2011)
Estymacja parametrów modelu w
przypadku
heteroskedastyczności
składnika losowego
2. Ważona metoda najmniejszych kwadratów (cd).
Wyznaczone wagi
t
, (t=1,2,…,n)
służą do transformacji
danych empirycznych modelu pierwotnego według
następującej zasady:
Estymowany jest model
.
...
...
,
,
,n
1,2,
t
,k;
1,2,
0
i
,
x
x
y
y
t
it
*
it
t
t
*
t
.
n
t=1,2,...,
,
+ε
x
+...+a
x
+α
x
+α
x
=α
y
t
*
kt
k
*
2t
2
*
1t
1
*
0t
0
*
t

2. Ważona metoda najmniejszych kwadratów
(cd)
4. Transformacja danych empirycznych:
.
5. Oszacowanie parametrów strukturalnych modelu postaci:
w którym
x
0t
=
q
t
(t=1,2,…,n)
.
,n
1,2,
t
,k;
1,2,
0
i
,
q
x
x
q
y
y
t
it
*
it
t
t
*
t
,
,n)
(t=1,2,...
,
+ε
x
+...+a
x
+α
x
+α
x
=α
y
t
*
kt
k
*
2t
2
*
1t
1
*
0t
0
*
t
Estymacja parametrów modelu w
przypadku
heteroskedastyczności
składnika losowego
56
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
W przypadku wystąpienia
zjawiska autokorelacji składnika
losowego
zagadnienie to rozpatruje się przy następujących
założeniach:
•
składnik losowy jest homoskedastyczny oraz zachowane są
pozostałe założenia Gaussa-Markowa,
• składniki losowe są generowane w procesie autoregresji rzędu I,
oznaczanego przez
AR(1)
, który opisuje się za pomocą następującego
równania:
,
gdzie:
- współczynnik autokorelacji,
– składnik losowy, o którym
zakłada się, że ma zerową wartość oczekiwaną, tj.
E(
) = 0
oraz, że
jest sferyczny, tj.
D
2
(
) =
2
I
.
1
ρ
,n;
1,2,
t
,
η
ρε
ε
t
1
t
t
57
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
Uwzględniając charakter rekurencyjny relacji opisującej
t
,
można napisać, że:
.
Stąd wartość oczekiwana i wariancja składnika losowego
przy istnieniu jego autokorelacji wynosi:
1
ρ
,n;
1,2,
t
,
η
ρ
ε
0
τ
τ
t
τ
t
1
ρ
założenia
z
bo
2,
1,t
t,t
dla
założenia
z
bo
2
2
η
0
τ
τ
2
η
0
τ
2
τ
t
τ
2
t
2
t
t
2
ε
t
2
τ
t
0
τ
τ
t
τ
0
τ
τ
t
τ
t
ρ
1
σ
ρ
σ
η
E
ρ
ε
E
ε
E
ε
E
σ
ε
D
0
η
E
0,
η
E
ρ
η
ρ
E
ε
E
,
58
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
Kowariancja składnika losowego
przy istnieniu jego
autokorelacji jest równa:
Z powyższej zależności wyznacza się współczynnik autokorelacji rzędu
, który jest równy:
2
ε
τ
2
τ
s
s
t
s
τ
2
τ
s
s
t
s
τ
τ
s
s
t
s
1
τ
0
p
p
t
p
τ
s
s
t
s
0
p
p
t
p
τ
t
t
τ
t
τ
t
t
t
τ
t
t
σ
ρ
η
ρ
E
ρ
η
ρ
ρ
η
ρ
η
ρ
E
η
ρ
η
ρ
E
ε
ε
E
ε
E
ε
ε
E
ε
E
,ε
ε
Cov
τ
2
ε
τ
t
t
ρ
σ
,ε
ε
Cov
59
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
W rozpatrywanym przypadku macierz wariancji i kowariancji
składnika losowego modelu jest postaci:
1
...
ρ
ρ
:
...
:
:
ρ
...
1
ρ
ρ
...
ρ
1
ρ
1
σ
1
...
ρ
ρ
:
...
:
:
ρ
...
1
ρ
ρ
...
ρ
1
σ
εε
E
ε
D
2
n
1
n
2
n
1
n
2
2
η
2
n
1
n
2
n
1
n
2
ε
T
2
60
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
W przypadku wystąpienia
zjawiska
autokorelacji
składnika losowego
przy spełnieniu
pozostałych warunków Gaussa-Markowa do
estymacji parametrów strukturalnych modelu stosuje
się :
• uogólnioną metodę najmniejszych kwadratów
(UMNK),
• metodę Cochrane’a-Orcutta,
• metodę Prais’a-Winsten’a,
• metodę różniczki zupełnej,
• ważoną metodę najmniejszych kwadratów
(WMNK).
61
GK (WEiP(2) - 2011)

1. Uogólniona metoda najmniejszych
kwadratów
W przypadku wystąpienia
zjawiska autokorelacji
składnika
losowego
i przy braku jego heteroskedastyczności oraz zachowaniu
pozostałych założeń Gaussa-Markowa
w UMNK wykorzystuje się
symetryczną macierz
postaci:
n
n
2
n
1
n
2
n
1
n
1
...
ρ
ρ
:
...
:
:
ρ
...
1
ρ
ρ
...
ρ
1
Ω
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
62
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
1. Uogólniona metoda najmniejszych
kwadratów
Stąd
oraz
.
1
ρ
0
0
0
ρ
ρ
1
0
0
0
0
0
ρ
1
ρ
0
0
0
ρ
ρ
1
ρ
0
0
0
ρ
1
ρ
1
1
Ω
2
2
2
2
1
1
ρ
0
0
0
0
1
0
0
0
0
0
1
ρ
0
0
0
0
1
ρ
0
0
0
0
ρ
1
ρ
1
1
P
2
2
63
GK (WEiP(2) - 2011)
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
1. Uogólniona metoda najmniejszych
kwadratów (cd)
Transformacja modelu pierwotnego
za pomocą macierzy
P
do postaci
polega na przemnożeniu wszystkich pierwotnych wartości (wszystkich
danych empirycznych) wszystkich zmiennych modelu pierwotnego,
łącznie z wektorem wyrazów wolnych przez elementy macierzy
P
, z
uwzględnieniem
czynnika skalującego lub bez niego, a następnie zastosowanie
KMNK do modelu po transformacji. Podobnie, czynnik skalujący może być
opuszczony lub uwzględniony w macierzy
-1
.
*
*
*
ε
α
X
y
ε
Xα
y
2
ρ
1
1
64
GK (WEiP(2) - 2011)

Transformacja modelu pierwotnego
z uwzględnieniem
czynnika
skalującego polega na wykonaniu następujących operacji:
• dla
t = 1
• dla
t = 2,3,…,n
.
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
1. Uogólniona metoda najmniejszych
kwadratów (cd)
,k
0,1,2,
i
,
ρ
1
ρx
x
x
ρ
1
ρy
y
y
2
1
i,t
it
*
it
2
1
t
t
*
t
,k
0,1,2,
i
,
x
x
y
y
i1
*
i1
1
*
1
2
ρ
1
1
65
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
1. Uogólniona metoda najmniejszych
kwadratów (cd)
Transformacja modelu pierwotnego
bez uwzględnienia
czynnika
skalującego polega na wykonaniu następujących operacji:
• dla
t = 1
• dla
t = 2,3,…,n
.
,k
0,1,2,
i
,
ρx
x
x
ρy
y
y
1
t
i
it
*
it
1
t
t
*
t
,
,k
0,1,2,
i
,
ρ
1
x
x
ρ
1
y
y
2
i1
*
i1
2
1
*
1
2
ρ
1
1
66
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
Bezpośrednie stosowanie UMNK jest trudne, gdyż zazwyczaj
nie jest znana macierz
ponieważ nie są znane występujące w niej
współczynniki autokorelacji składnika losowego. W praktyce korzysta
się więc z różnych oszacowań tych współczynników, głównie
autokorelacji rzędu I, która najczęściej występuje w problemach
rzeczywistych. Spośród wielu oszacowań współczynnika autokorelacji
rzędu I, najczęściej są stosowane dwa następujące:
(Goldberger)
(serial correlation) –
zalecany
Oszacowania współczynnika autokorelacji rzędu I są wykorzystywane
w
metodach
Cochrana-Orcutta ora Prais’a-Winsten’a.
n
2
t
2
1
t
n
2
t
2
t
n
2
t
1
t
t
e
e
e
e
ρ
ˆ
n
1
t
2
t
n
2
t
1
t
t
e
e
e
1
n
1
k
n
ρ
ˆ
67
GK (WEiP(2) - 2011)

2. Metoda Cochrane’a-Orcutta
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
Me
toda
CO
jest metodą iteracyjną i jest szczególnym
przypadkiem UMNK. Może być stosowana w przypadku występowania
autokorelacji rzędu I składnika losowego
. Jest ona mniej dokładna od
UMNK, ale znacznie prostsza w praktycznym stosowaniu.
Rozważa się liniowy model ekonometryczny dla dwóch
kolejnych okresów:
t
oraz
t-1
, tj.
1
t
k
1
i
1
i,t
i
0
1
t
t
k
1
i
it
i
0
t
ε
x
α
α
y
ε
x
α
α
y
68
GK (WEiP(2) - 2011)

2. Metoda Cochrane’a-Orcutta (cd)
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
Po przemnożeniu drugiego równania przez współczynnik
autokorelacji składnika losowego i odjęciu od siebie stronami tych
równań otrzymuje się model postaci:
.
Należy zauważyć, że składnik losowy powyższego modelu jest
zmienną losową
t
określoną wcześniej zależnością:
o własnościach:
E(
) = 0
oraz
D
2
(
) =
2
I
, zgodnych z założeniami
KMNK, tj. Gaussa-Markowa.
1
t
t
k
1
i
1
i,t
it
i
0
1
t
t
ρε
ε
ρx
x
α
ρ
1
α
ρy
y
1
ρ
,n;
1,2,
t
,
η
ρε
ε
t
1
t
t
69
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
W rozpatrywanej metodzie transformacja modelu pierwotnego
za pomocą macierzy
P
do postaci
polega na
przemnożeniu
wszystkich oryginalnych wartości (wszystkich danych empirycznych)
wszystkich zmiennych modelu oryginalnego, łącznie z wektorem
wyrazów wolnych przez elementy macierzy
P
, która ma wymiar
(n-1)
n
i jest postaci:
*
*
*
ε
α
X
y
ε
Xα
y
2. Metoda Cochrane’a-Orcutta (cd)
n
1
n
2
1
ρ
0
0
0
0
1
0
0
0
0
0
ρ
0
0
0
0
1
ρ
0
0
0
0
1
ρ
ρ
1
1
P
70
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
2. Metoda Cochrane’a-Orcutta (cd)
W metodzie
CO
macierz
P
spełnia następującą zależność:
przy czym macierz
Θ
jest macierzą kwadratową rzędu
n
, w której tylko
pierwszy element jest różny od
zera
(0) i jest równy
1
.
Zatem, bez uwzględnienia czynnika skalującego macierzy
P
,
transformacja danych modelu oryginalnego będzie polegała na
wykonaniu następujących operacji:
,
a następnie zastosowaniu KMNK do modelu po transformacji.
,n
2,3,
t
,k;
0,1,2,
i
,
x
ρ
x
x
y
ρ
y
y
1
t
i
it
*
it
1
t
t
*
t
,
ˆ
ˆ
Θ
Ω
ρ
1
P
P
1
2
T
71
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
2. Metoda Cochrane’a-Orcutta (cd)
Rozpatrywana metoda jest metodą iteracyjną, której algorytm
jest następujący:
1.
Oszacowanie za pomocą zależności
wartości współczynnika autokorelacji rzędu I reszt na podstawie
reszt wyestymowanego modelu z oryginalnymi wartościami
zmiennych, tj. na podstawie modelu:
.
ρˆ
ε
Xα
y
n
2
t
2
1
t
n
2
t
2
t
n
2
t
1
t
t
e
e
e
e
ρ
ˆ
72
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
2. Metoda Cochrane’a-Orcutta (cd)
2.
Przeprowadzenie transformacji wszystkich oryginalnych wartości
zmiennych modelu (łącznie z wyrazem wolnym) za pomocą
następujących przekształceń:
.
Transformacji
nie podlegają
pierwsze wartości
wszystkich zmiennych
modelu – są one opuszczane. Zatem, liczba danych dla modelu po
transformacji jest równa
n-1
.
3.
Estymacja za pomocą KMNK modelu po tranformacji
.
,n
2,3,
t
,k;
0,1,2,
i
,
x
ρ
x
x
y
ρ
y
y
1
t
i
it
*
it
1
t
t
*
t
,
ˆ
ˆ
*
*
*
ε
α
X
y
73
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
2. Metoda Cochrane’a-Orcutta (cd)
4.
Wstawienie do modelu oryginalnego ocen parametrów
strukturalnych z wyestymowanego modelu po transformacji, tj. ocen
a*
i wyliczenie z modelu oryginalnego wektora reszt
e
:
.
5.
Obliczenie kolejnej wartości współczynnika autokorelacji na
podstawie reszt
e
wyznaczonych w
pkt 4
i przejście do
pkt 2
algorytmu.
Postępowanie iteracyjne (algorytm) jest zatrzymywane, gdy dwa
kolejne przybliżenia współczynnika autokorelacji (z iteracji
s
oraz
s+1
)
różnią się nie więcej niż zadana dokładność obliczeń
, tj. gdy:
.
*
Xa
y
e
ζ
ρ
ρ
1
s
s
ˆ
ˆ
74
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
3. Metoda Prais’a-Winsten’a
W metodzie Cochrane’a-Orcutta w procesie transformacji
oryginalnych wartości zmiennej objaśnianej i zmiennych objaśniających
nie są uwzględniane ich pierwsze wartości. Ten mankament eliminuje
metoda Prais’a-Winsten’a. Metoda
PW
jest realizowana według algorytmu
metody
CO
, przy czym transformacja dotyczy
wszystkich wartości
oryginalnych zmiennych modelu i jest dokonywana według zależności:
.
,k
0,1,2,
i
,n,
2,
t
,k
0,1,2,
i
1,
t
1
i,t
it
*
it
1
t
t
*
t
2
i1
*
i1
2
1
*
1
ρx
x
x
ρy
y
y
ρ
1
x
x
ρ
1
y
y
75
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
4. Metoda różniczki zupełnej
Metoda różniczki zupełnej (metoda pierwszych różnic) jest
stosowana do szacowania parametrów strukturalnych modelu w
przypadku występowania dodatniej autokorelacji pierwszego rzędu
odchyleń składnika losowego, której współczynnik
1
.
Idea tej metody polega na przekształceniu pierwotnych danych
empirycznych zmiennej objaśnianej i zmiennych objaśniających w ich
pierwsze różnice, tj. na wyznaczeniu:
.
1
i,t
it
it
1
t
t
t
x
x
Δx
y
y
Δy
,n)
2,3,
t
,k;
1,
(i
76
GK (WEiP(2) - 2011)

4. Metoda różniczki zupełnej (cd)
Po wyznaczeniu różnic zmiennych modelu otrzymuje się
następujące macierze danych empirycznych po transpozycji:
k
1
n
1
k,n
1
2,n
1
1,n
k2
22
12
k1
21
11
1
1
n
1
n
2
1
Δx
Δx
Δx
Δx
Δx
Δx
Δx
Δx
Δx
ΔX
,
Δy
Δy
Δy
Δy
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
77
GK (WEiP(2) - 2011)

Za pomocą KMNK szacuje się parametry strukturalne modelu postaci:
w którym nie występuje wyraz wolny.
Oszacowanie parametrów strukturalnych modelu wyznacza się z
zależności:
1)
,n
1,2,
(t
,
Δε
Δx
α
Δx
α
Δx
α
Δy
t
kt
k
2t
2
1t
1
t
ΔXΔy
ΔX
ΔX
a
1
T
Δ
)
(
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
4. Metoda różniczki zupełnej (cd)
78
GK (WEiP(2) - 2011)
Oszacowanie wyrazu wolnego, występującego w modelu
pierwotnym, wyznacza się z następującej zależności:
Oszacowanie macierzy wariancji i kowariancji estymatora
parametrów strukturalnych modelu ma postać:
k
1
i
i
i
0
x
a
y
a
1
1
T
1
2
e
2
ΔX
X
(Δ
S
(a)
D
)
4. Metoda różniczki zupełnej (cd)
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
79
GK (WEiP(2) - 2011)

gdzie
oznacza macierz pierwszych różnic zmiennych
objaśniających, w której pierwsza kolumna zawiera same jedynki,
natomiast
jest oszacowaniem wariancji odchyleń składnika losowego, przy czym
e
jest wektorem reszt modelu pierwotnego.
1
k
n
e
e
S
T
2
e
ΔX
ΔX
1
1
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
4. Metoda różniczki zupełnej (cd)
80
GK (WEiP(2) - 2011)

Jedną z lepszych, ale bardziej pracochłonnych metod jest
metoda zaproponowana przez Hildretha i Liu, należąca do tzw. metod
przeszukiwania „po kracie”. Algorytm tej metody jest następujący:
1.
Wybierana jest wartość początkowa współczynnika autokorelacji rzędu
I z przedziału
[-1,1]
. W przypadku braku innych przesłanek wybiera się
= -1
.
2.
Wybierany jest krok poszukiwań (wielkość „oczka kraty”), tj. krok
zmiany wartości współczynnika autokorelacji oznaczany przez
. Na
ogół wartość tego kroku przyjmuje się równą 0,01 lub mniejszą, zależnie
od żądanej dokładności określenia wartości współczynnika autokorelacji.
Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
5. Metoda Hidretha-Liu
81
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
5. Metoda Hidretha-Liu
3.
Przeprowadzenie transformacji oryginalnych danych z
wykorzystaniem ustalonego współczynnika
według takiej samej
procedury jak w metodzie Cocgrane’-Orcutta, tj. według
.
4.
Estymacja za pomocą KMNK modelu przetransformowanego, tj.
modelu
.
5.
Obliczenie i zarejestrowanie zmienności nieobjaśnionej
SSE
modelu
z
pkt
4
po estymacji, tj. obliczenie
.
,n
2,3,
t
,k;
0,1,2,
i
,
ρx
x
x
ρy
y
y
1
t
i
it
*
it
1
t
t
*
t
,
*
*
*
ε
α
X
y
1
n
1
t
t
e
SSE
2
82
GK (WEiP(2) - 2011)

Estymacja parametrów modelu w
przypadku
autokorelacji
składnika
losowego
5. Metoda Hidretha-Liu
6.
Zwiększenie wartości współczynnika autokorelacji
o
, tj.
+
i
jeżeli ta zwiększona wartość nie przekracza
1
lub innej z góry
ustalonej liczby - przejście, do
pkt 3
algorytmu.
7.
Wybór najlepszego oszacowania parametrów strukturalnych modelu:
za najlepsze oszacowanie parametrów strukturalnych modelu
oryginalnego przyjmuje się oszacowanie parametrów z modelu
przetransformowanego, który charakteryzuje się najmniejszą
wartością
SSE
.
83
GK (WEiP(2) - 2011)

84
GK (WEiP(2) - 2011)
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
- Slide 82
- Slide 83
- Slide 84
Wyszukiwarka
Podobne podstrony:
indukcyjnosc wzajemna cw. WEiP marzec 2011
Sprawozdanie 4 (WEiP 2011)
Sprawozdanie 1 (WEiP-2011), WAT, semestr VII, Wprowadzenie do ekonometrii i prognozowania
Ćwiczenie 1 (WEiP-2011), WAT, semestr VII, Wprowadzenie do ekonometrii i prognozowania
Ćwiczenie 4 (WEiP=2011), WAT, SEMESTR VII, wprowadzenie do ekonometrii i prognozowania
Sprawozdanie 4 (WEiP-2011), SEMESTR VII
WEiP (3 Podstawy prognozowania 2011)
Sprawozdanie 2 (WEiP 2011)
Sprawozdanie 4 (WEiP-2011)A lach, WAT, SEMESTR VII, wprowadzenie do ekonometrii i prognozowania, Ćwi
Maciej Iwancz Sprawozdanie 4 (WEiP-2011), WAT, SEMESTR VII, wprowadzenie do ekonometrii i prognozowa
Sprawozdanie 5 (WEiP 2011)
WEiP (4 Prognozowanie na podstawie modeli ekonometrycznych 2011)
Sprawozdanie 1 (WEiP 2011)
WEiP (1 Model jednorównaniowy 2011)
Sprawozdanie 3 (WEiP 2011)
więcej podobnych podstron