1

Prognozowanie procesów

ekonomicznych c.d.

Średnie błędy predykcji ex-

post

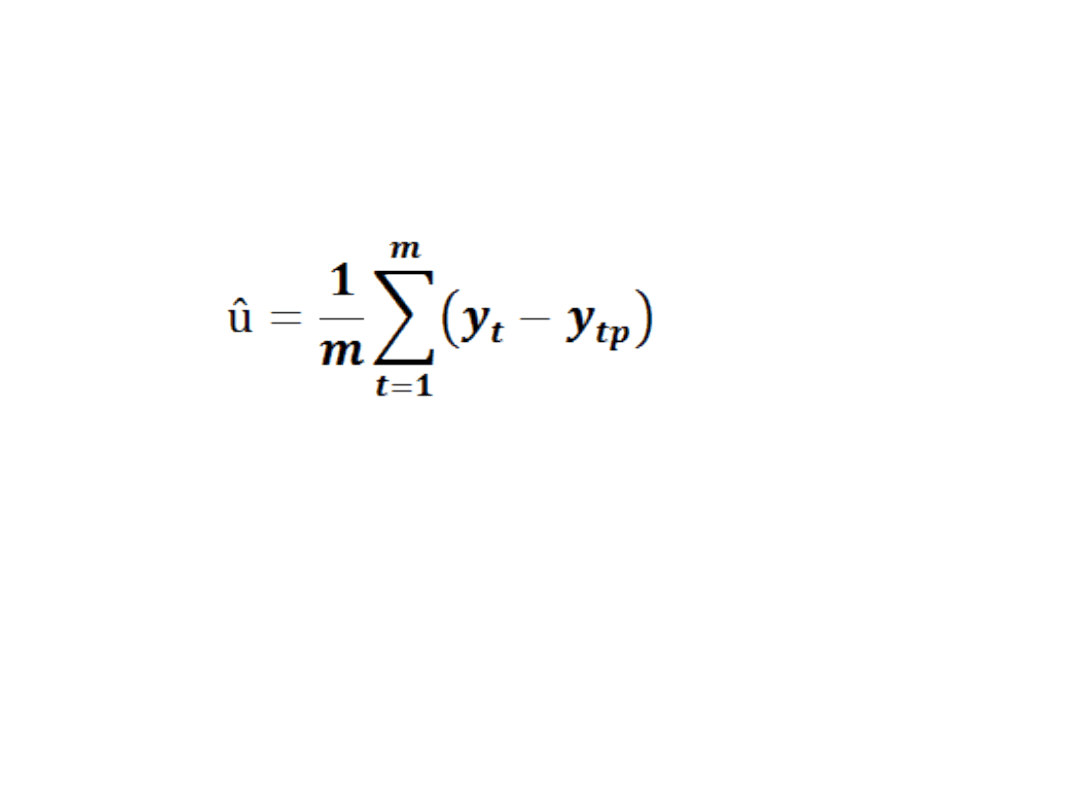
2

Średni błąd predykcji

• gdzie t = 1,……,m jest okresem

empirycznego sprawdzania
dokładności prognoz.

• Jeśli predykcja była nieobciążona to

û ≈ 0.

3

• Jeśli û ≠ 0, to okres empirycznego

sprawdzania dokładności prognoz

można podzielić na kilka podokresów,

aby przekonać się, czy nadzieja

matematyczna błędów predykcji jest

stacjonarna, czy też wykazuje

określone tendencje (np. wzrostu).

• Udział obciążenia prognozy w średniej

wartości wielkości prognozowanej ,

jeśli û ≠ 0 jest równy:

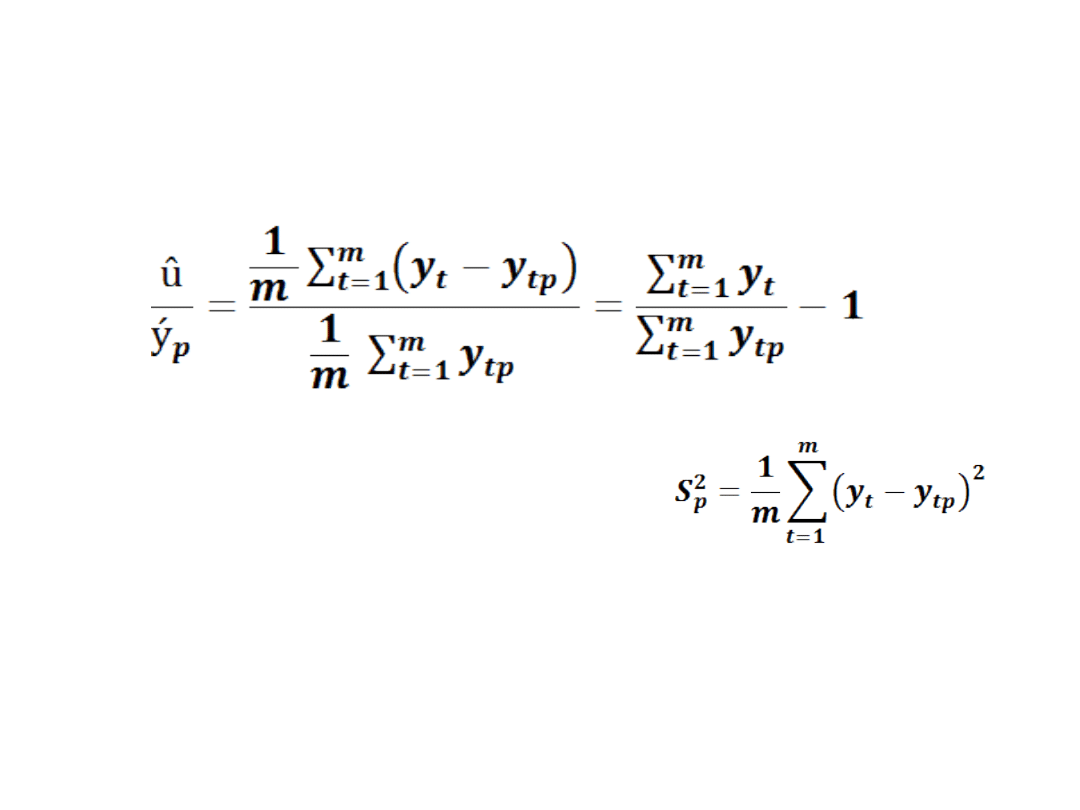
4

Wariancja predykcji

• Empiryczna wariancja predykcji
•
• Pierwiastek kwadratowy z powyższej

wariancji jest empirycznym średnim
błędem predykcji.

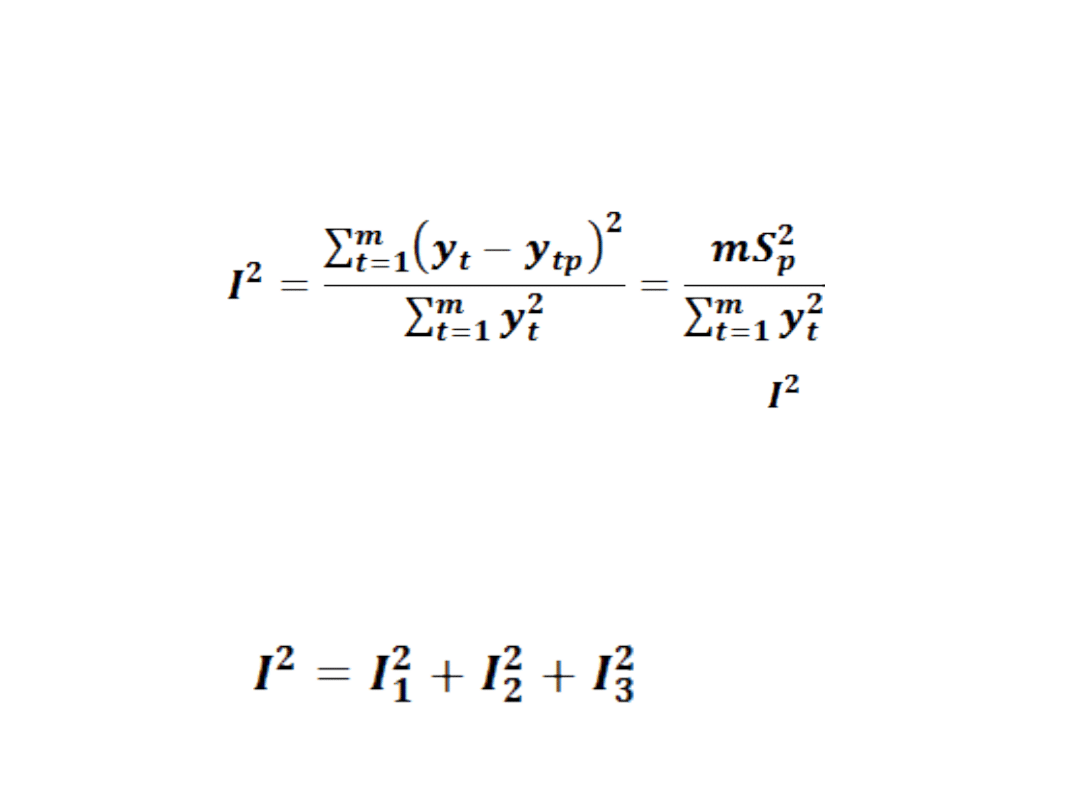
5

Współczynnik Theila

• I, a więc pierwiastek kwadratowy z

jest przeciętnym względnym błędem

predykcji w okresie weryfikacji prognoz.

• Współczynnik Theila można rozłożyć na

trzy składniki o określonej interpretacji.

•

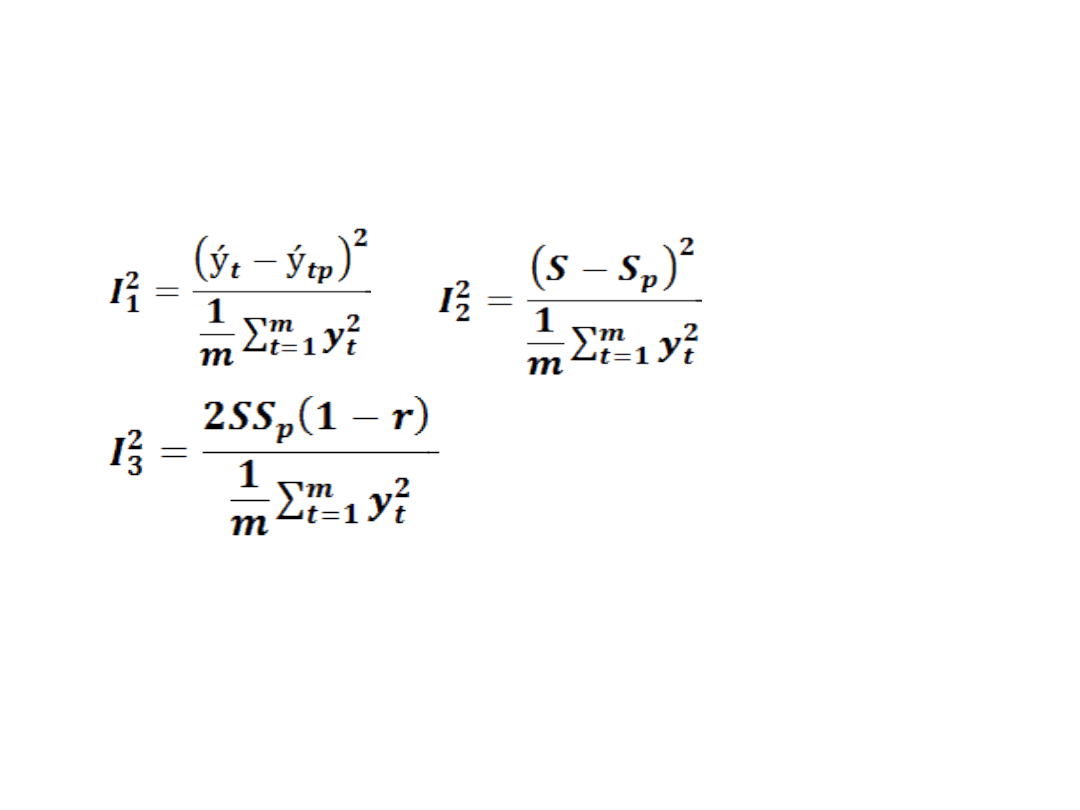
6

Współczynniki Theila

• Gdzie S jest odchyleniem

standardowym obserwacji y

t ,

r jest

współczynnikiem korelacji między y

t

oraz y

tp

w okresie weryfikacji prognoz

7

• informuje jaka część ogólnych

rozmiarów błędów predykcji jest
wynikiem obciążenia predykcji,

• odzwierciedla rozmiary błędów

wynikających z niedostatecznej
elastyczności predykcji,

• jest miernikiem błędów

wynikających z niedoskonałej
predykcji punktów zwrotnych.

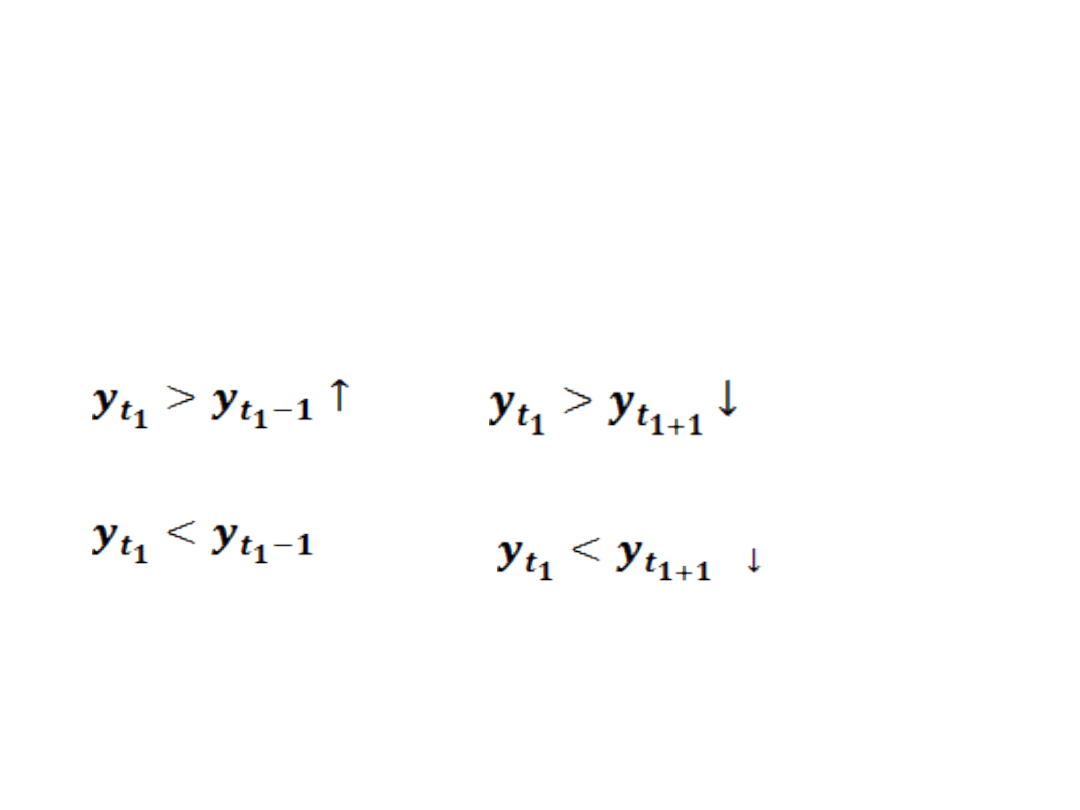
8

Punkty zwrotne.

• Punkty zwrotne występują w

okresie t

1

, jeżeli zrealizuje się

jedna z następujących par
nierówności.

• oraz
•
• ↓ oraz

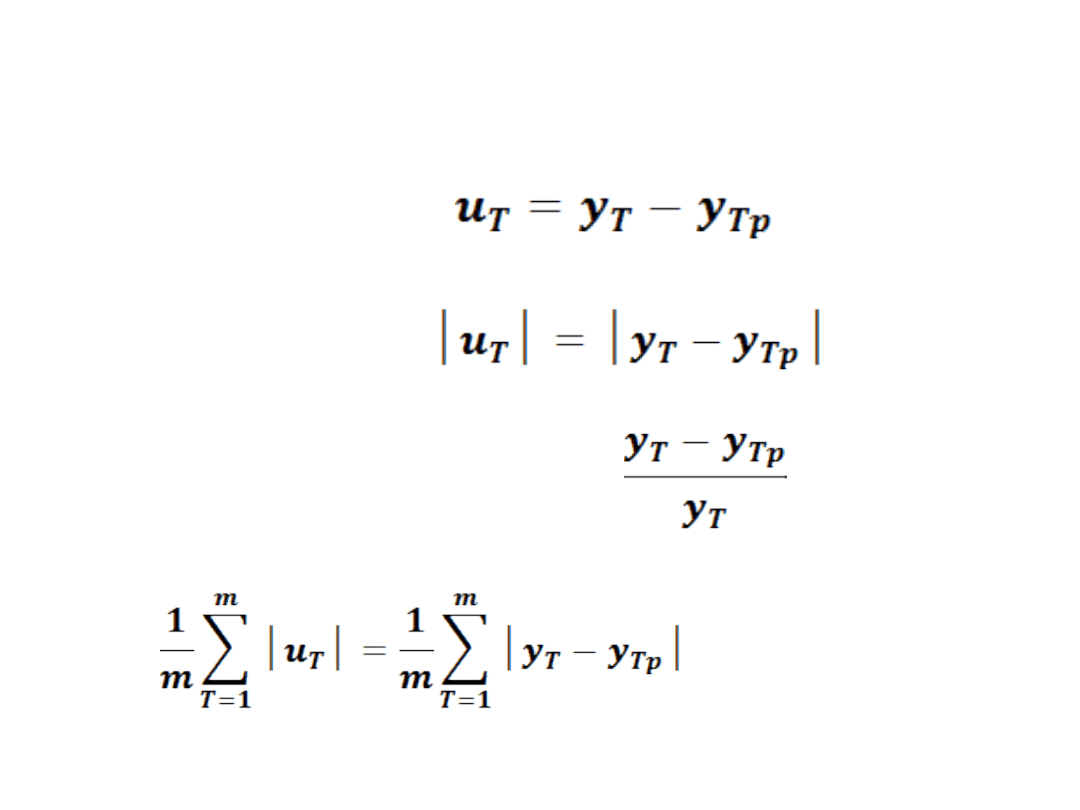
9

Inne mierniki dokładności

prognoz

ex-post

• Błąd prognozy

• Błąd absolutny
•
• Względny błąd prognozy
• Średni absolutny błąd prognoz

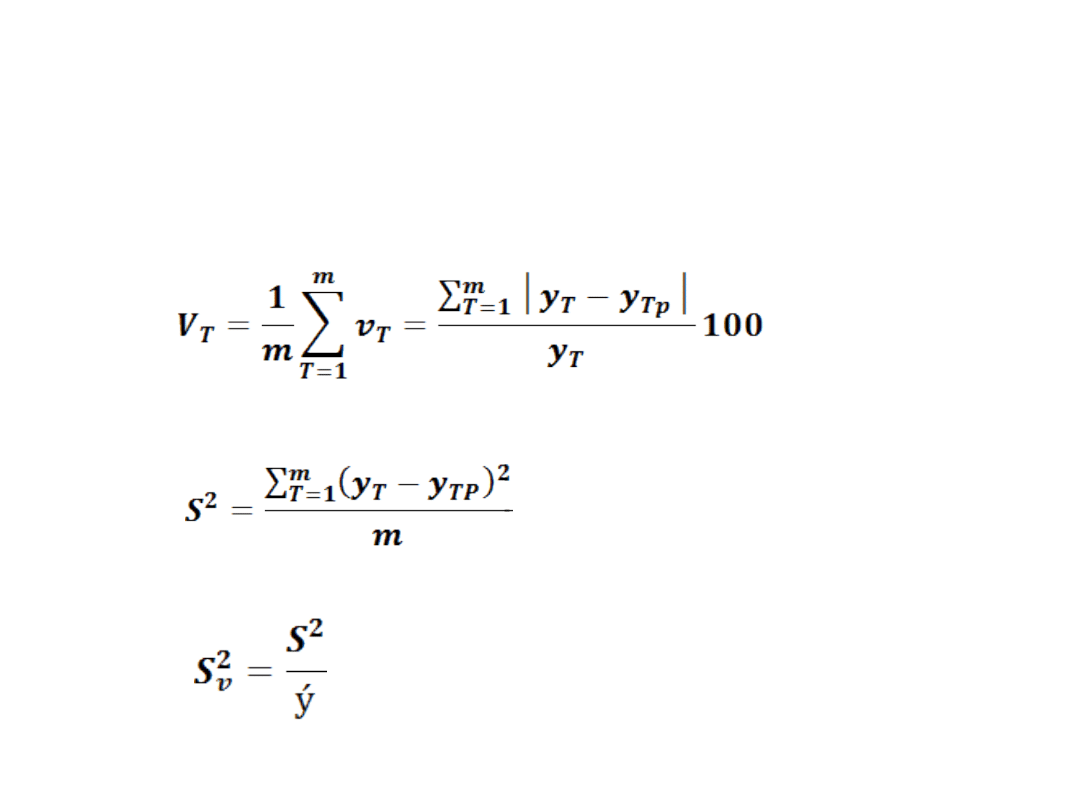
10

Średnie błędy prognoz

c.d.

• Średni względny błąd prognoz

•
• Średni kwadratowy błąd prognoz
•
• Względny średni kwadratowy

błąd prognoz

11

Główne cele prognozowania

ekonomicznego.

• Obszary zainteresowania prognozami –

państwa, przedsiębiorców, organów

władzy samorządowej, organizacji

społecznych – to przede wszystkim:

• PKB, lub stopa wzrostu PKB,

• Stopa bezrobocia,

• Poziom inflacji,

• Wzrost wynagrodzeń,

• Popyt konsumpcyjny,

• Rezerwy walutowe.

• Prognozy powyższych wielkości służą

podejmowaniu optymalnych decyzji .

12

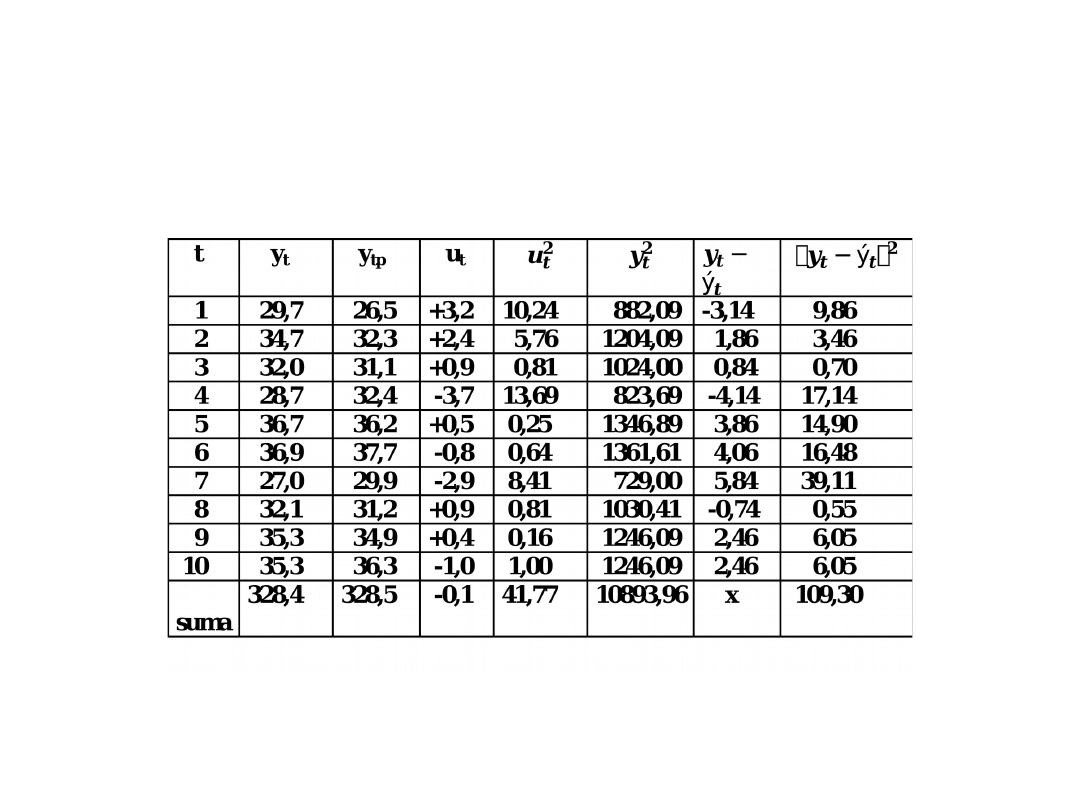
Tablica 1. Wartości

realizacji oraz prognozy i

reszty (przykład).

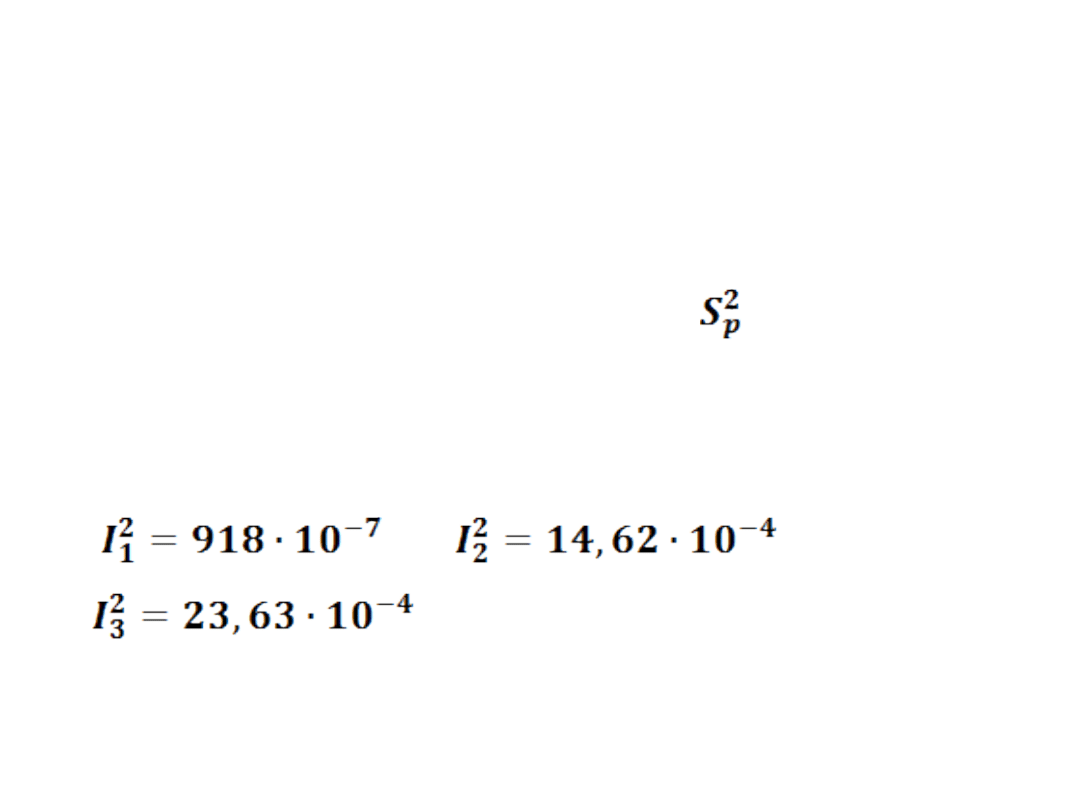
13

Przykład c.d.

• Wartość û wynosi 0,01, a więc jest

bliska zeru i wskazuje na brak

obciążenia predykcji.

• Empiryczna wariancja predykcji

wynosi 4,18, a więc empiryczny średni

błąd predykcji jest równy 2,044.

• Współczynniki Theila są równe: I

2

=

0,003834,

•

•

• I = 0,0619.

•

 

14

WIELORÓWNANIOWE MODELE

EKONOMETRYCZNE

• Zmienne endogeniczne – zmienne

objaśniane przez równania modelu.

• Zmienne egzogeniczne – zmienne, których

wartości określane są poza modelem.

• Zmienne endogeniczne i zmienne

egzogeniczne mogą być opóźnione, bądź
nieopóźnione.

• Opóźnione zmienne endogeniczne i

wszystkie zmienne egzogeniczne tworzą
zbiór zmiennych z góry ustalonych.

15

Postacie modelu i zmienne

endogeniczne

• Postać strukturalna modelu jest zapisem

związków istniejących między zjawiskami

ekonomicznymi (opis struktury).

• Postać zredukowana modelu jest zapisem

jednokierunkowych związków między zmiennymi

endogenicznymi i zmiennymi z góry ustalonymi.

• m – liczba nieopóźnionych zmiennych

endogenicznych

•

- liczba zmiennych endogenicznych

nieopóźnionych występujących w danym

równaniu,

• m2

- liczba zmiennych endogenicznych

nieopóźnionych występujących w pozostałych

równaniach modelu.

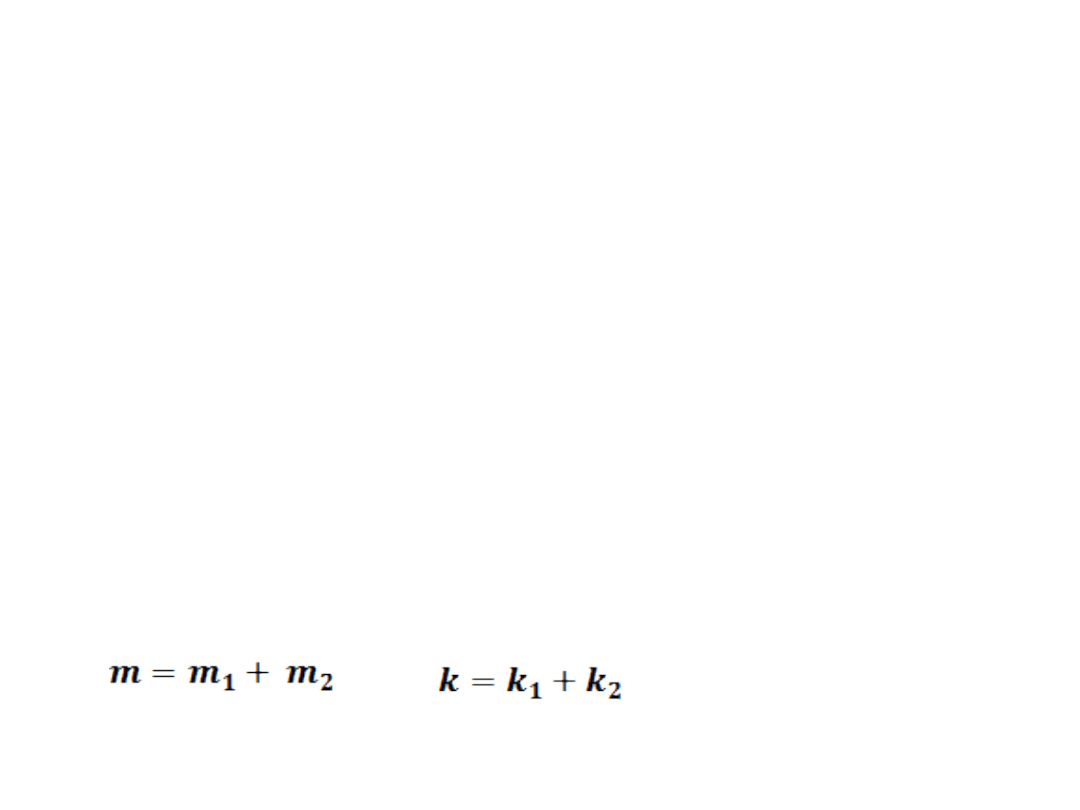
16

Zmienne z góry ustalone

• k – liczba zmiennych z góry

ustalonych występujących w
modelu:

• k1

- liczba zmiennych z góry

ustalonych występujących w
danym równaniu modelu,

• k2 - liczba pozostałych zmiennych

z góry ustalonych.

•

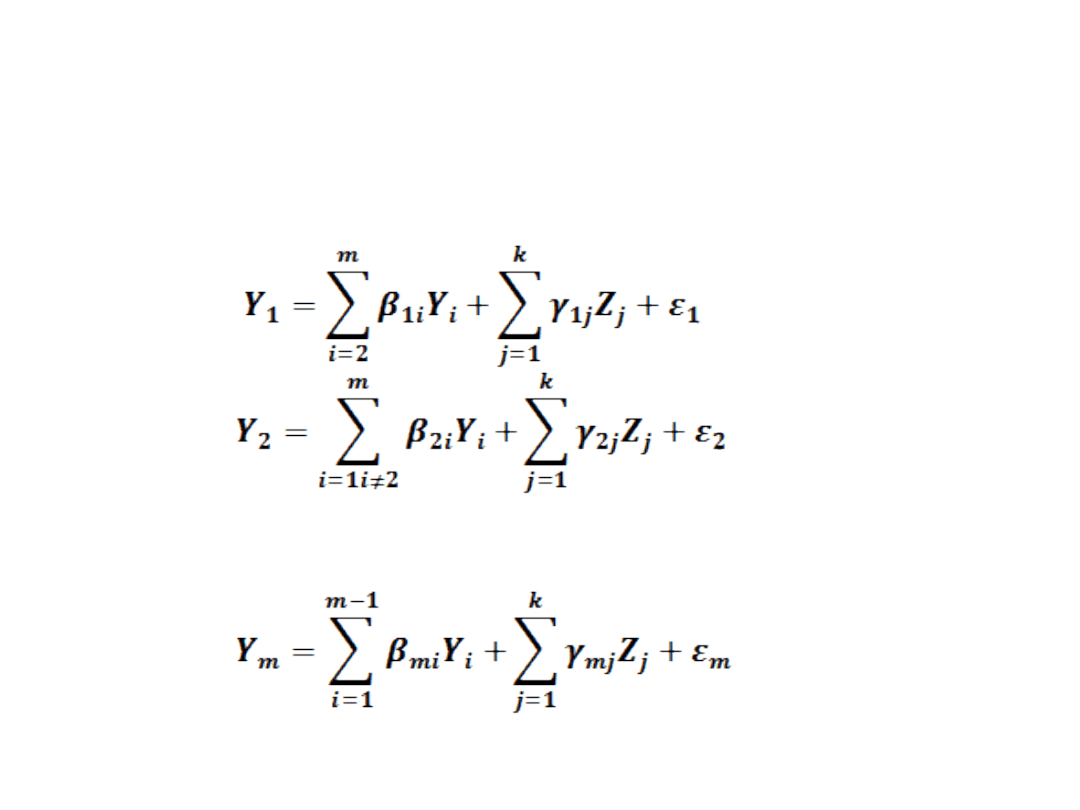
17

Strukturalna postać

modelu:

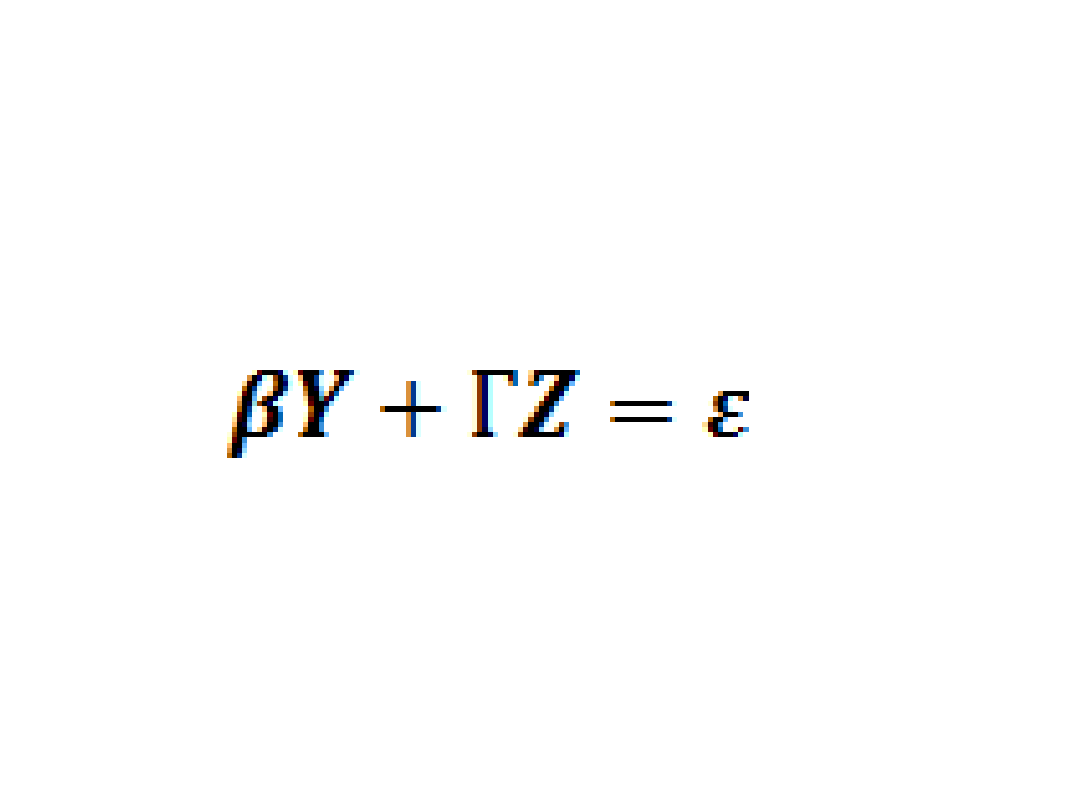
18

Zapis macierzowy

• m - zmiennych endogenicznych Y

1

,………., Y

m

• k - zmiennych z góry ustalonych Z

1

, …….., Z

k

• β – jest macierzą o wymiarach [ m x m]

parametrów przy zmiennych endogenicznych

nieopóźnionych,

• Y – jest wektorem [m x 1] zmiennych

endogenicznych,

19

• Γ – jest macierzą parametrów o

wymiarach [m x k] stojących przy
zmiennych z góry ustalonych,

• Z – jest wektorem zmiennych z

góry ustalonych o wymiarach
[k x 1] ,

• ε – jest wektorem składników

losowych o wymiarach [m x 1].

20

Klasyfikacja modeli

wielorównaniowych

• Budowa macierzy β jest kryterium

klasyfikującym modele ekonometryczne

wielorównaniowe.

• Jeżeli β jest macierzą diagonalną o jedynkach

na głównej przekątnej i zerach w pozostałych

miejscach to model jest modelem prostym.

• Jeżeli macierz β jest macierzą trójkątną ( lub

może być po przestawieniu równań lub

zmiennych) to model jest modelem

rekurencyjnym. W modelu rekurencyjnym

powiązania między nieopóźnionymi zmiennymi

endogenicznymi są jednokierunkowe.

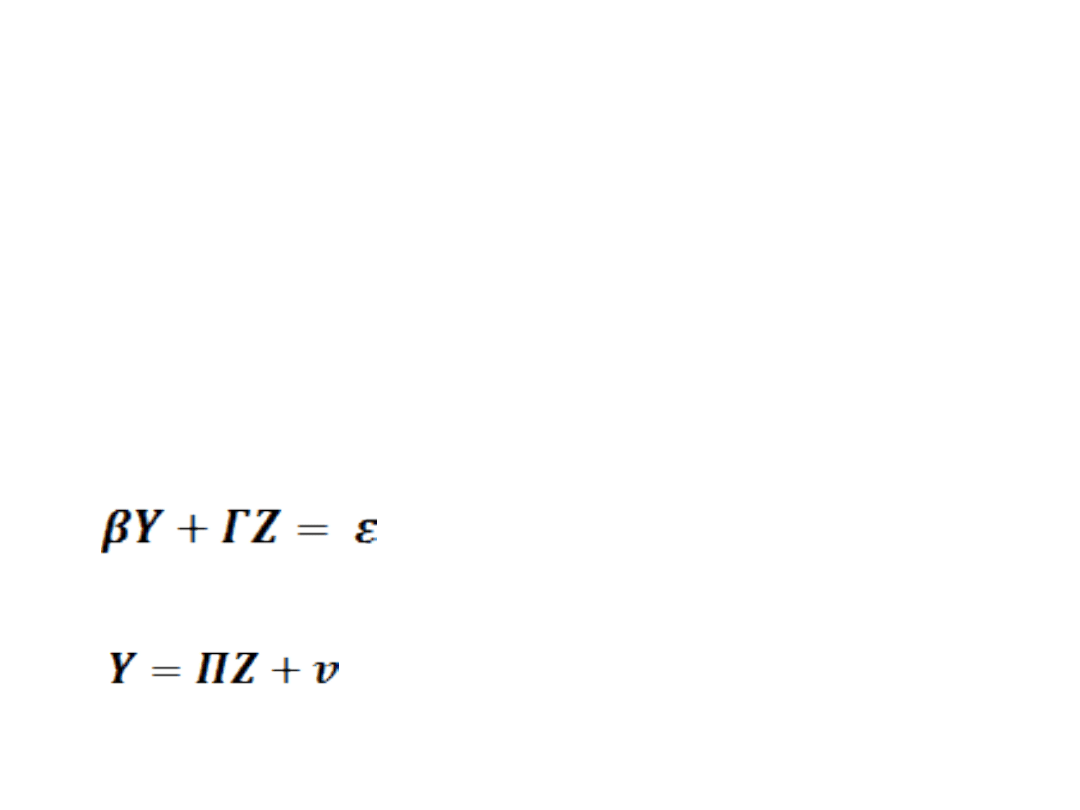
21

• Jeżeli macierz β jest macierzą

dowolną to model jest modelem o
równaniach współzależnych, o
wielokierunkowych powiązaniach
między zmiennymi endogenicznymi.

•

postać strukturalna modelu,

•

postać zredukowana modelu.

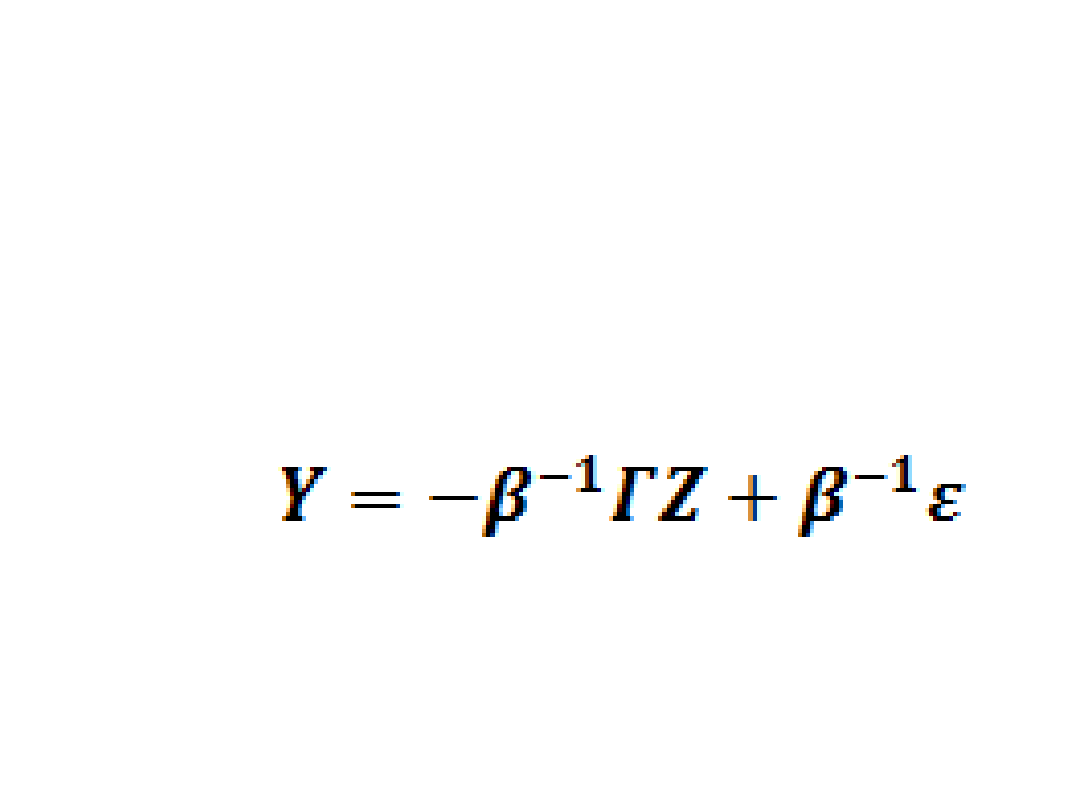
22

• Jeżeli macierz β jest nieosobliwa, to

mnożąc lewostronnie równanie
postaci strukturalnej przez macierz
odwrotną do macierzy β mamy:

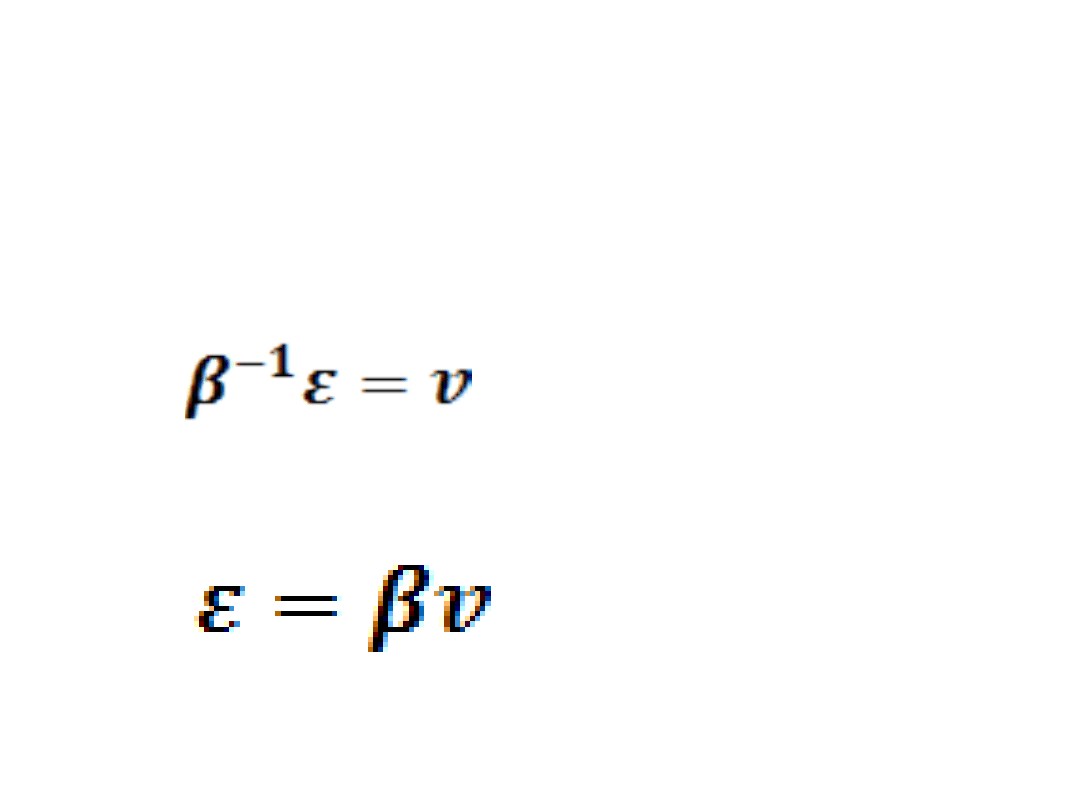
23

• Zależności między wektorami

składników losowych obydwu postaci
modeli:

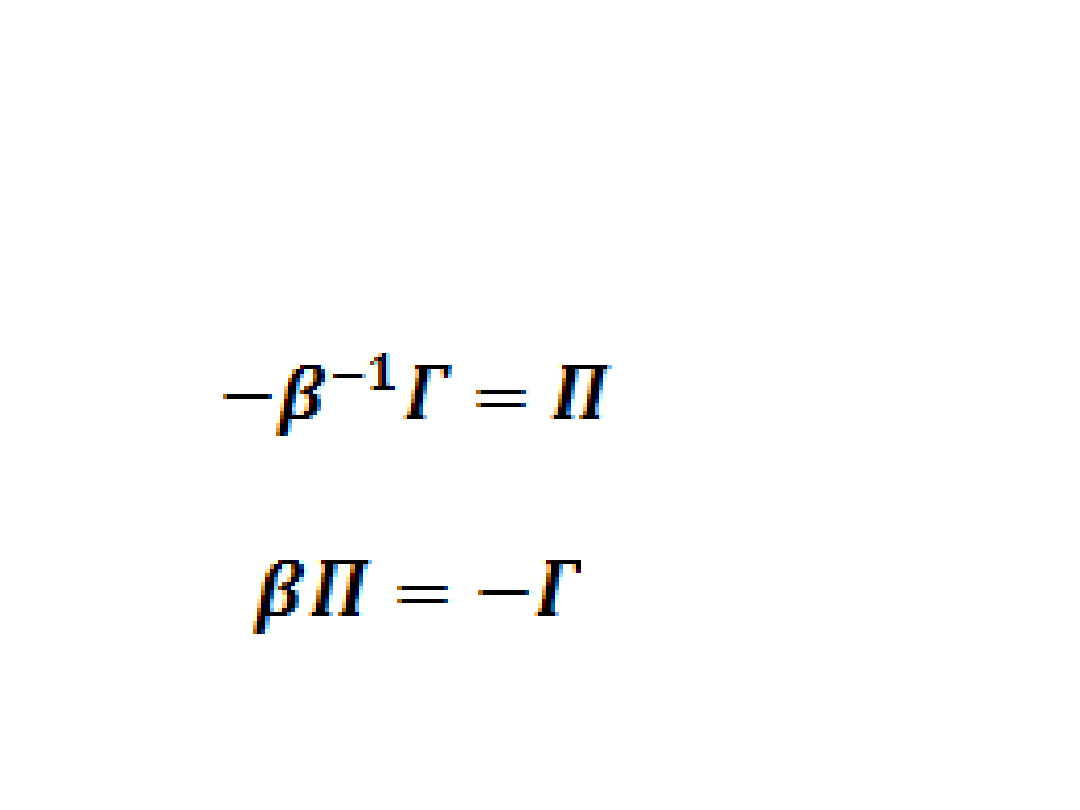
24

• Zależności między macierzami

parametrów obydwu postaci modelu:

• lub