SPC Statistical Process Control

Panowanie nad zmiennością procesów

przyczyny przypadkowe, proces kontrolowany statystycznie

przyczyny wyjątkowe

Karty Shewharta

Miary położenia:

średnia arytmetyczna, mediana, dominanta

Miary dyspersji:

Rozstęp: R = x_max - x_min

Odchylenie standardowe: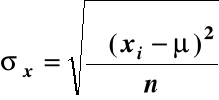

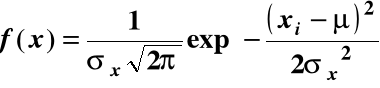
Z procesu pobiera się próby, dla każdej oblicza się odpowiednie charakterystyki, np.
, odchylenie standardowe tej średniej i rozstęp.

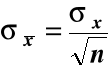
, a

Załóżmy, że μ = 20,0 g, σ_x= 0,6 g, próby o n=4, σ_x = =0,6/2 = 0,3 a więc μ ± 3σ_x = 20 ±0,9

Karta kontrolna x

(GLK - to górna linia kontrolna, DLK to dolna linia kontrolna, LC to linia centralna)

x, g

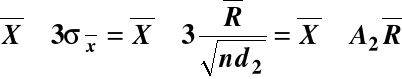
d₂ współczynnik Hartleya

Konfiguracje punktów wskazujące na występowanie przyczyn wyjątkowych

(Pitt Hy, SPC for the Rest of us, Addison-Weseley Publishing Company, Inc.; litery A,B,C,D

oznaczają poszczególne kryteria omówione w tekście)

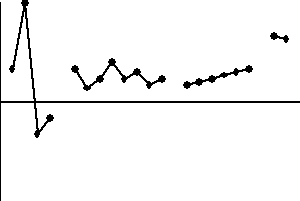
A/ pojedynczy punkt znajduje się poza linią kontrolną,

B/ osiem kolejnych punktów znajduje się po jednej stronie linii kontrolnej,

C/ pięć kolejnych punktów jest po tej samej stronie liniii centralnej i mają tendencję rosnącą lub malejącą,

D/ dwa kolejne punkty znajdują się tuż przy jednej z linii kontrolnych.

Konfiguracje punktów wskazujące na występowanie przyczyn wyjątkowych wg L.S.Nelsona.

1. Jeden punkt poza strefą A

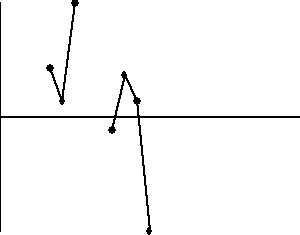
2. Dziewięć punktów po kolei w strefie C lub poza nią.

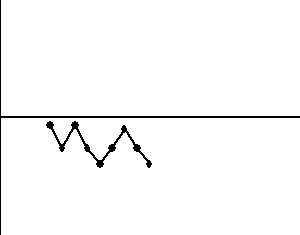
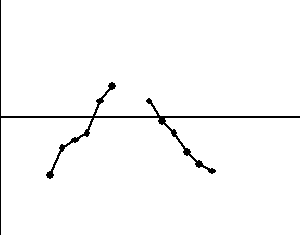
3. Sześć punktów po kolei wykazuje tendencję rosnącą lub malejącą

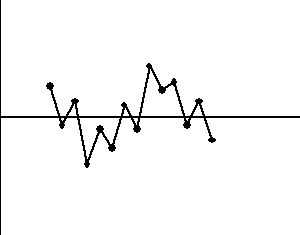
4. Czternaście punktów po kolei, których wartości na przemian rosną i maleją

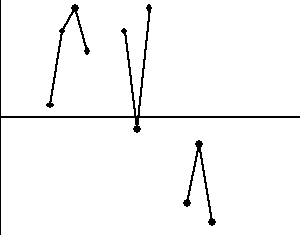
5. Dwa z trzech kolejnych punktów w strefie A lub poza nią

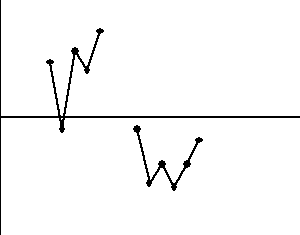
6. Cztery z pięciu kolejnych punktów w strefie B lub poza nią

7. Piętnaście kolejnych punktów w strefie C

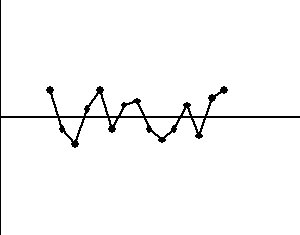
8. Osiem kolejnych punktów po obu stronach linii centralnej, ale żaden z nich nie znajduje się w strefie C

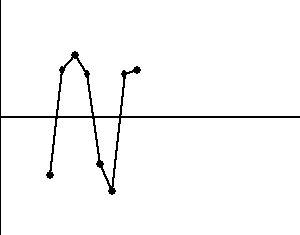
Karty średniej i karty rozstępu z naniesionymi punktami

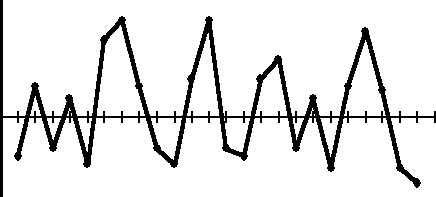
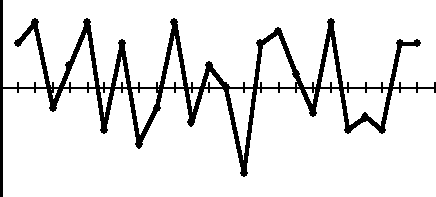
Schematyczne przedstawienie procesów o różnej zdolności jakościowej

a)

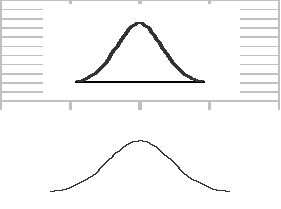
b)

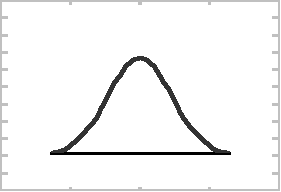
c)

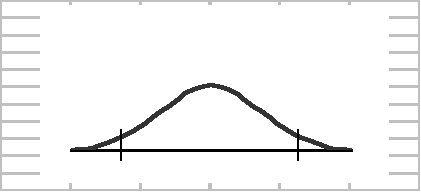
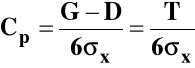
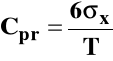
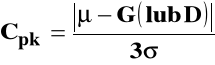
I .Proces dostarcza elementy o masie

20 +/- 4 g, a odchylenie standardowe dla wytworzonych elementów wynosi 0,6 g.

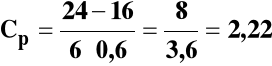
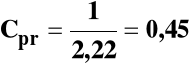
II. Średnia przyjmie najpierw μ₁ = 22 g, następnie μ₂=17 g i wreszcie μ₃ = 20 g.

C_pk wyniosą odpowiednio:

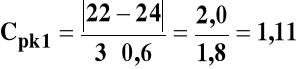
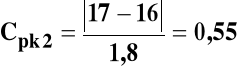
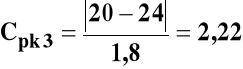
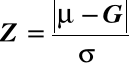
Jeżeli Z=6, to 6σ =

Można wykazać, że gdy Z=6, to C_p= 2,0

59,0

UCL_X 57,5 -

55,0 -

52,5 -

52,5

Center line 50,0 -

47,5 -

45,0 -

LCL_X 42,5 -

Time

Genichi Taguchi

O jakości produktu decyduje strata przekazywana przez ten produkt społeczeństwu, licząc od chwili, gdy produkt ten został udostępniony odbiorcy.

Zmienność procesów, zmienność produktów

Wartość pożądana, target value

Tolerancja

Funkcja strat, quality loss, loss function

Strata, L(x)

A

m - Δ m m + Δ x

T

Tradycyjny model funkcji strat

Strata

Straty Straty nie Straty

występują

x

T

Analityczna postać funkcji strat L(x)

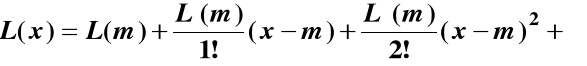
L(x) = 0 gdy x=m, dla x=m funkcja przyjmuje minimum, więc L′(m) = 0. Pomijając składniki o potęgach większych od 2 otrzymujemy:

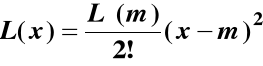
lub prościej:

L(x) = k (x-m)²

gdzie k = L′′(m)/2!

L(x) = A, gdy x-m =Δ. W takim razie A=kΔ², a k = A/Δ²

.

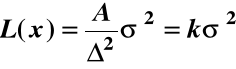
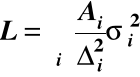
Funkcja strat, gdy przedziały tolerancji po obu stronach wartości m są różne

Strata, L(x)

A₁

A₂

m - Δ₁ m m + Δ₂ x

T

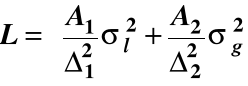
minimenty, the smaller the better, m=0

optymenty, the nominal the best, 0 < m < +∞

maksymenty, the larger the better, m = +∞

Wprowadźmy nową zmienną z zdefiniowaną jako:

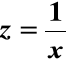
Dla tak zdefiniowanej zmiennej pożądaną wartością (target value) będzie m = 0, a górną granicą tolerancji 1/Δ. W takim razie funkcja strat:

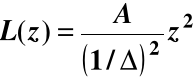
lub

,

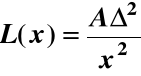
a dla zbioru n elementów o różnym x

przy czym w tym wypadku

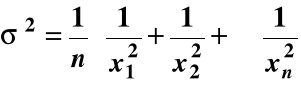
Załóżmy, że w ciągu 10 dni realizujemy zlecenie polegające na wytworzeniu 100 000 płytek. Każdego dnia wybieramy w sposób przypadkowy 1 płytkę i poddajemy ją analizie. Ponieważ proces wytwórczy jest kontrolowany statystycznie zakładamy, że 10 pobranych płytek jest reprezentatywną próbką całości. Odbiorca zażądał aby grubość płytki wynosiła 1,00000 cm (a więc m = 1,00000 cm) oraz określił tolerancję tak, że Δ=0,00010 cm Strata spowodowana odrzuceniem płytki niemieszczącej się w dopuszczalnej tolerancji wynosi A = 10 zł. Wykonane pomiary wykazały następujące grubości płytek:

1,000010 1, 000020 1,000010 0, 999990 0,999995 1,000005 1,000020 1,00000 0,999998 0,999990.

σ²=(1/10)[(1,000010 - 1,000000)² +(1,000020 - 1,000000)² +.....+ (0,999990 - 1,000000)²] = 1,2× 10 ^-10 cm².

L =[10/ (0,00010)²]× 1,2 ×10^-10 = 1,2 zł/płytkę.

Dla całej partii 100 000 × 1,2 = 120 000 złotych.

Tolerancja

m - Δ m m + Δ

Δ = 5, T = 10

Dla fabryki A, rozkład normalny,

σ = (1/6) T, C_p=1,00

Dla fabryki B, rozkład prostokątny,

σ =
T C_p=0,58

koszt naprawy telewizora, 2$/aparat. W obu fabrykach koszt takich napraw jest ten sam. Z rys. wynika, że Δ= 5 jednostek, to znaczy, że T = 10 jednostek. Ponieważ Δ=5 a A=2, więc

k=A/Δ² = 2.0$/5² = 0.08 $/ap.jed.².

Strata w fabryce A :

L = k σ² =0.08 (10/6)² = 0.222 $/aparat

Strata w fabryce B:

L = k σ² =0.08 (100/12)² = 0.667 $/aparat

Fabryka	Target value	σ^2	L	% braków
A	m	100/36	o.222$	0.27
B	m	100/12	0.667$	0.00

Fabryka A zamierza ograniczyć odchylenia od wartości pożądanej, tak aby σ = 10/8, (a nie 10/6), dodatkowy koszt z tym związany: 0,05 $/aparat

Nowa strata: L=0.08(10/8)²=0.125 $/aparat

Ale 0,125 + 0,05 = 0,175 $/aparat

:

Netto: 0.222-0.175=0.047$/aparat

Fabryka B:

decyzja o zmniejszeniu tolerancji do ± (2/3) Δ, bez zmian w technologii, lecz przez zaostrzenie kontroli jakości, 1/3 produkcji nie jest dopuszczana do sprzedaży lecz idzie do poprawki.

Nowa strata:

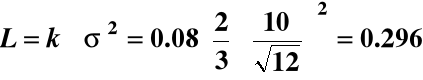
$/aparat

koszty napraw 1/3 produkcji,

0.333× 2$ = 0,666 $/aparat

L= 0,296 +0,666 =0.962$/aparat.

Praca pochodzi z serwisu www.e-sciagi.pl

x

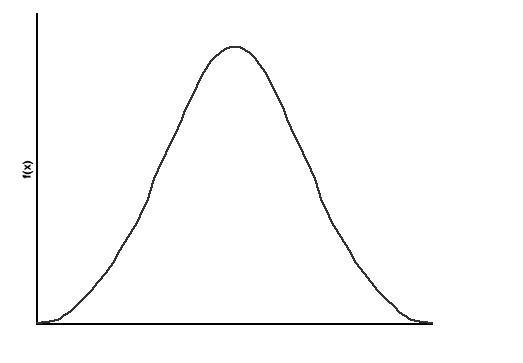
99,73%

95,44%

68,26%

-3
-2



2
3

GLK

20,9

LC

20,0

czas

19,1

DLK

DLK

GLK

D

C

B

A

C

B

A

B

C

A

GLK

DLK

GLK

A

B

C

C

A

B

DLK

B

GLK

DLK

A

B

C

C

A

B

GLK

DLK

A

B

C

C

A

GLK

DLK

A

B

C

C

B

A

GLK

DLK

A

B

C

C

B

A

GLK

DLK

A

B

C

C

B

A

GLK

DLK

A

B

C

C

B

A

DLK

GLK

GLK

DLK

G

D

G

D

G

D

a

lub 45%

Fabryka B

Fabryka A

---