Teoria Chaosu

Teoria Chaosu

Definicja

Teoria chaosu zakłada, że złożoność
badanych zjawisk może być rezultatem ich
właściwości polegającej na wykładniczym
rozbieganiu się początkowo bliskich
trajektorii układu w ograniczonym obszarze
przestrzeni fazowej. Do modelowania tego
typu zjawisk wykorzystuje się powszechnie
tzw. Inteligentne systemy obliczeniowe, a w
szczególności sieci neuronowe.

Jerzy Zieliński “Inteligentne systemy w zarządzaniu”

Teoria Chaosu

Definicja

Chaos jest rozumiany jako ruch
nieregularny, stan nieporządku, u podstaw
którego leżą jednak prawa
deterministyczne. Ruch chaotyczny jest
określony równaniami nieliniowymi, które
jednoznacznie wyznaczają ewolucję układu
w czasie przy określonych warunkach
początkowych. Przyszłość układu jest
jednoznacznie wyznaczona przez jego
historię i prawa, którym podlega.

Mariusz Michno “Teoria chaosu a rynki kapitałowe”

Teoria Chaosu

Podstawowe pojęcia - przestrzeń fazowa

Przestrzeń fazowa - jest to przestrzeń
której współrzędnymi są wszystkie
wielkości potrzebne aby opisać
trajektorię danego układu.
Dla punktu materialnego są to trzy
współrzędne położenia i trzy
współrzędne prędkosci ciała

Teoria Chaosu

Podstawowe pojęcia - fraktal

Fraktale to obiekty, których wymiar
nie jest liczbą całkowitą

Teoria Chaosu

Podstawowe pojęcia - atraktor

Atraktorem jest pewien obszar,
trajektoria lub punkt w przestrzeni
fazowej, do którego w miarę upływu
czasu zmierzają rozwiązania równań,
czyli trajektorie rozpoczynające sie w
róznych punktach przestrzeni
fazowej.

Teoria Chaosu

Bifurkacja

Bifurkacja - rozdwojenie trajektorii
układu wynikające z sytuacji w której
odbywa się ruch

Teoria Chaosu

Podstawowe pojęcia - układ ergodyczny

Dla układu ergodycznego trajektoria
w przestrzeni fazowej przechodzi z
upływem czasu przez każdy punkt
powierzchi stałej energii tego układu

Teoria Chaosu

Kalendarium

▪

1834 - J. Russel obserwuje solitonową falę wodną

▪

1871 - hipoteza ergodyczności Maxwella-Boltzmana

▪

1890 - Poincare bada zredukowany problem Hilla

▪

1895 - teoria turbulencji O.Reynoldsa

▪

1904 - konstrukcja krzywych Kocha

▪

1916 - konstrukcja dywanu Sierpińskiego

▪

1928 - konstrukcja gąbki Mengera

▪

1958 - A.Kołmogorow definiuje entropię metryczną

▪

1962 - M.Henon odkrywa chaotyczny ruch gwiazd w

centrum galaktyki

▪

1963 - równania i atraktor Lorenza

Teoria Chaosu

Fraktale

▪

Fraktale są formami geometrycznymi,

zawartymi w dziale matematyki, który opisuje i
analizuje nieregularnosci oraz zlożoność struktur
rzeczywistego świata.

▪

Twórcą i odkrywcą tej geometrii jest, urodzony

w 1924 roku w Warszawie, Benoit Mandelbrot.

▪

Nazwa fraktale pochodzi od łacinskiego

frangere – lamać.

▪

Matematyka definiuje fraktale jako zwarte

podzbiory topologicznej przestrzeni metrycznej
S, charakteryzowane przez wymiar fraktalny D i
miare fraktalna μ.

Teoria Chaosu

Fraktale - cechy

●

Samopodobienstwo

●

Symetria

●

Wymiar fraktalny nie jest liczbą

całkowitą

●

Brak jednoznacznego kształtu

●

Nie są określone wzorem

matematycznym, tylko zależnością
rekurencyjną

Teoria Chaosu

Fraktale - cechy

●

Badania nieregularności fraktali

●

Opis procesów chaotycznych zachodzących

w układach dynamicznych

●

Przetwarzanie i kodowanie obrazów

cyfrowych – kompresja fraktalna

●

Modelowanie tworów naturalnych dla celów

realistycznej grafiki komputerowej

●

Badanie struktury łancuchów DNA

●

Badanie samopodobnych struktur

harmonicznych wystepujacych w muzyce

Teoria Chaosu

Fraktale klasyczne - zbiór Cantora

Każdy odcinek domknięty dzieli sie na trzy
równe części i usuwa sie z niego część
środkową bez jej brzegów.

Teoria Chaosu

Fraktale klasyczne - trójkąt Sierpińskiego

Trójkąt równoboczny jest dzielony na
cztery mniejsze, a następnie usuwany
jest środkowy trójkąt, operacja
wykonywana jest w pętli

Teoria Chaosu

Fraktale klasyczne - gąbka Mengera

Ściany dowolnego sześcianu dzieli się na 9
kwadratów przystających. Następnie wiercone
są dziury o przekroju kwadratowym,
zaczynając od środkowego kwadratu, na wylot,
do środkowego kwadratu na przeciwnej
ścianie.

Teoria Chaosu

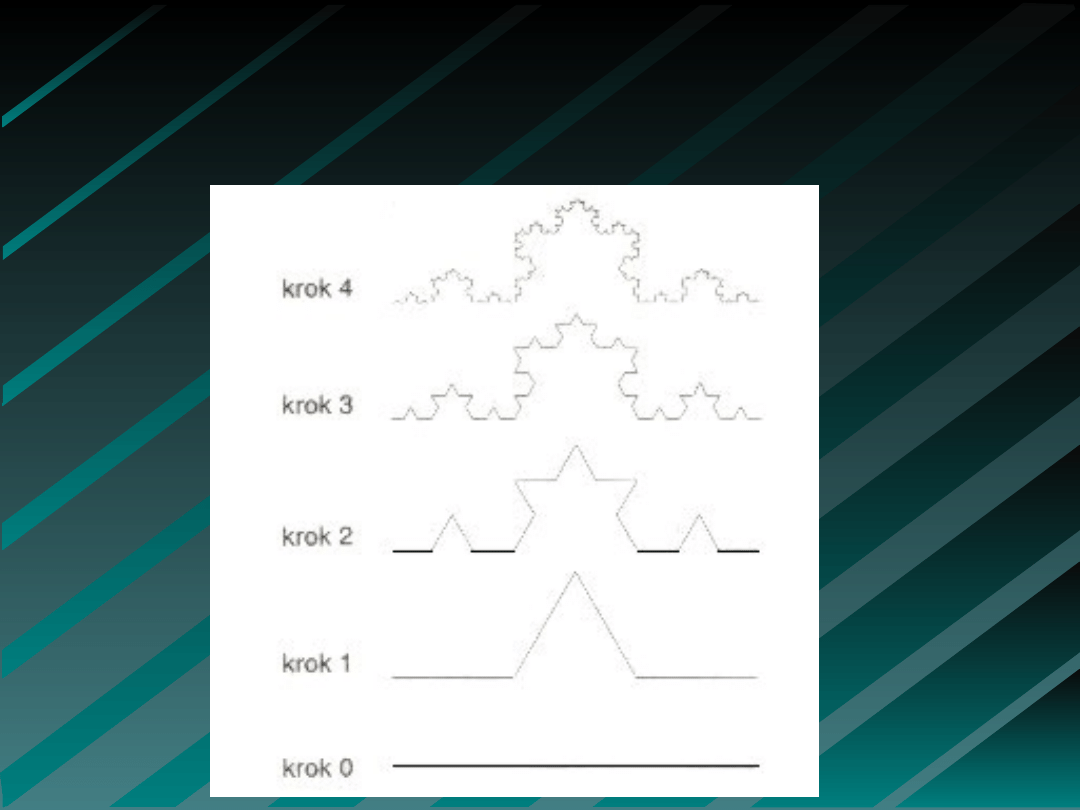
Fraktale klasyczne - krzywe Kocha

Teoria Chaosu

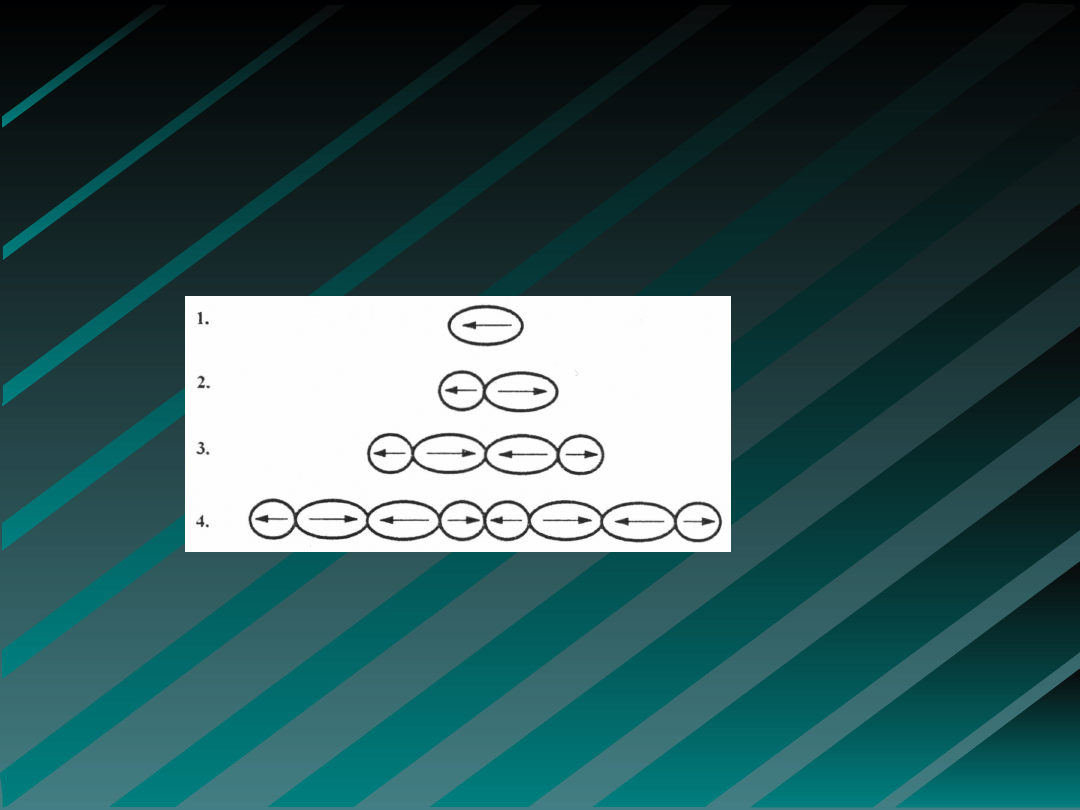
L - system

Kolejne kroki podziałów komórkowych glonu
anabaena catenula

Jeśli podziałowi ulega komórka, której
powstanie spowodowało rozrost w kierunku
lewym (prawym), wówczas jej potomkami
będą: mała komórka powodująca rozrost w
lewo (prawo) oraz większa komórka
powodująca rozrost w prawo (lewo).

Teoria Chaosu

L - system

Przykłady roślinnych struktur rozgałęzionych.

Teoria Chaosu

Układy ergodyczne

Kiedy układ złożony z dużej liczby
składników może być prawidłowo
opisany za pomocą praw statystycznych ?

▪

Entropia Kołmogorowa

▪

Wykładniki Lapunowa

Teoria Chaosu

Atraktory

Pewien obszar, trajektoria, lub punkt w
przestrzeni fazowej, do którego z
upływem czasu zmierzają rozwiązania
równań, czyli trajektorie rozpoczynające
się w róznych punktach przestrzeni
fazowej.

Basen przyciągania - zbiór tych warunków
początkowych, dla których trajektoria
zmierza do danego atraktora.

Teoria Chaosu

Atraktory - cykl graniczny

Cykl graniczny atraktor występujący w
przestrzeni dwuwymiarowej , zamknięta
trajektoria, dzieląca przestrzeń fazową na
dwa rozłączne obszary. Trajektorie
rozpoczynające się w obszarze
wewnętrznym rozkręcają się i zbliżają do
cyklu, a trajektorie zewnętrzne zwijają się.

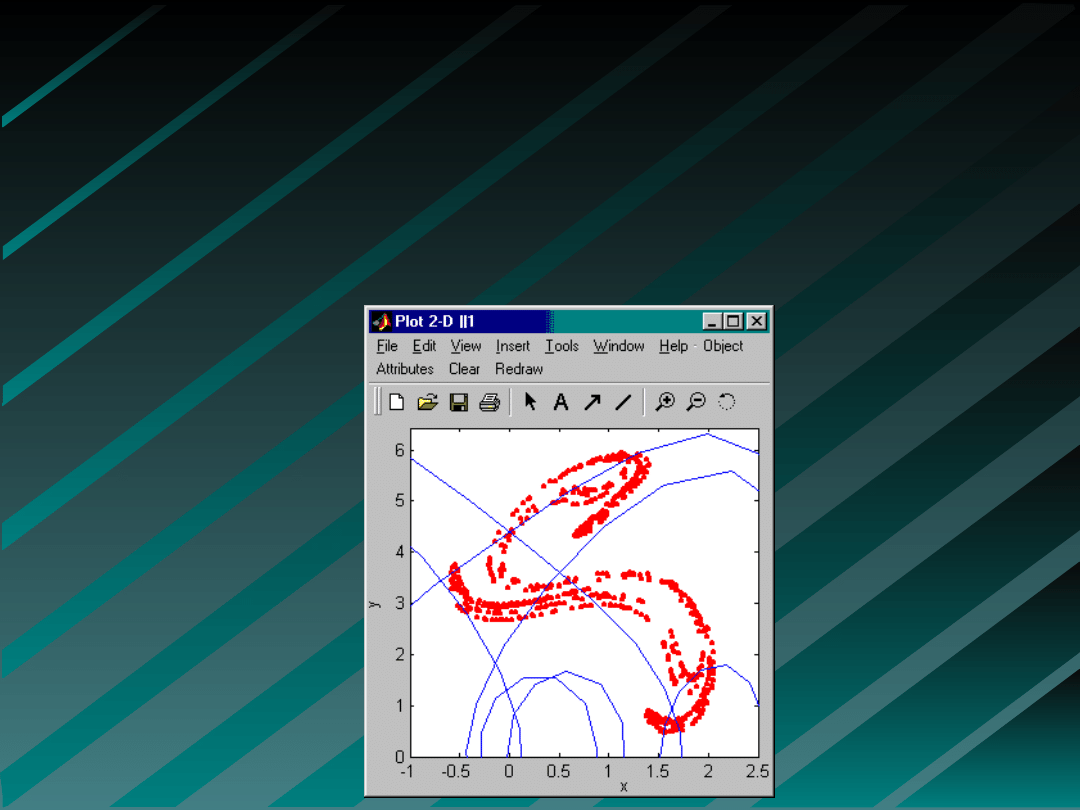
Teoria Chaosu

Atraktory - cykl przekrój Poincarego

Badane są punkty w których trajektorie
występujące w przestrzeni fazowej
przecinają określoną płaszczyznę.

Teoria Chaosu

Atraktory - znane atraktory

▪

Atraktor Lorenza

▪

Atraktor Henona

▪

Atraktor Roslera

Teoria Chaosu

Atraktory - znane atraktory

W 1960 roku w Massachusetts Institute of
Technology, meteorolog Edward Lorenz
zdołał skonstruować prosty model.
Zawierał on trzy równania różniczkowe,
przy pomocy których chciał opisać
przemiany zachodzące w atmosferze pod
wpływem promieniowania słonecznego
nagrzewającego powierzchnię Ziemi.

Teoria Chaosu

Atraktory - scenariusze przejścia do chaosu

▪

Intermitencja - okresy regularnego

ruchu przeplatają się z okresami
zachowania chaotycznego

▪

Scenariusze Rulle’a-Takensa-

Newhous’a - oparta na bifrukacji Hopfa

▪

Bifurukacja Feingenbauma

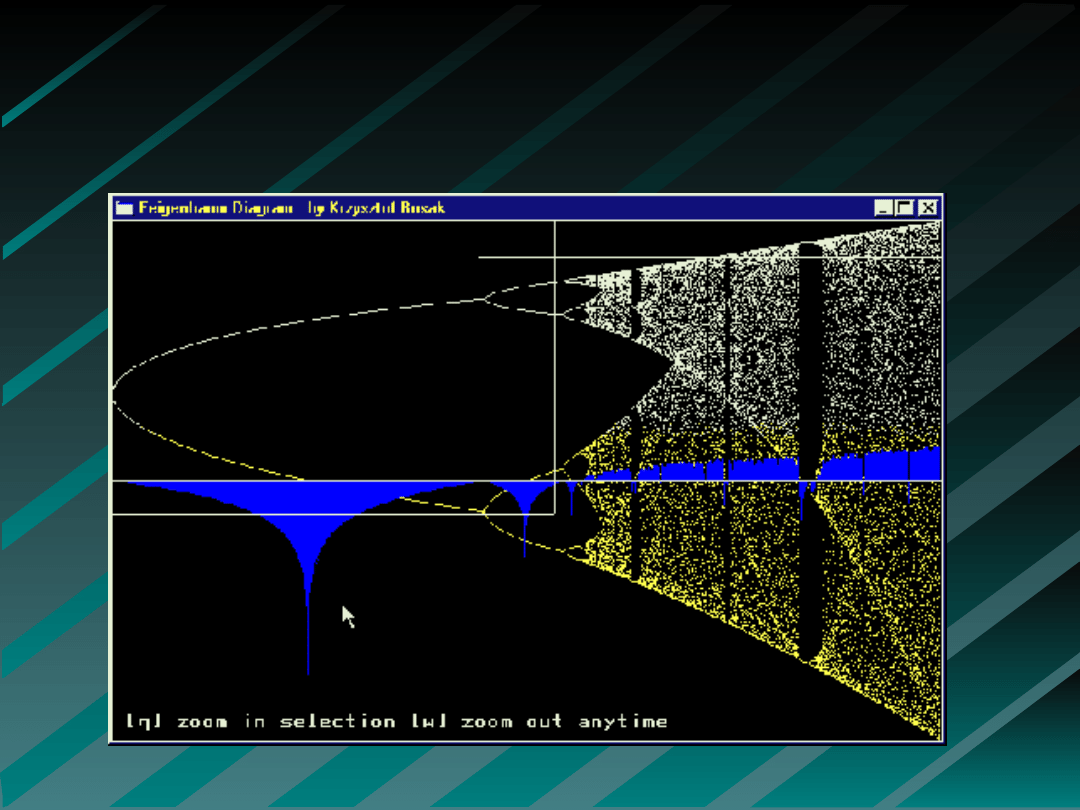
Teoria Chaosu

Bifurkacja Feigenbauma

Teoria Chaosu

Atraktor w gospodarce

Atraktor w gospodarce jest to każde duże
skupisko lub natężenie procesów
gospodarczych, rejestrowanych obecnie
najczęściej wyłącznie w pamięciach dużych
sieci komputerowych, obsługujących banki i
giełdy finansowe. Atraktor jest mechanizmem
dodatniego sprzężenia zwrotnego związanego
z ruchem kapitału, jest potwierdzoną
eksperymentalnie regułą nasilania się
procesów gospodarczych w tych miejscach,
gdzie są one już intensywne. Atraktory
ekonomiczne wyłaniają się z graficznych
prezentacji danych w postaci wykresów i tabel,
ilustrujących statystyczne skutki miliardów
przeprowadzanych codziennie operacji
finansowych