Zmienne losowe ciągłe

dr Tomasz Kowalski

Wykład 24

Slajd 2 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Funkcja gęstości

Funkcję f nazywamy gęstością pewnej
zmiennej losowej X, jeżeli

1. ( ) 0 dla

,

f x

x R

�

�

2.

( )

1.

f x dx

+�

- �

=

�

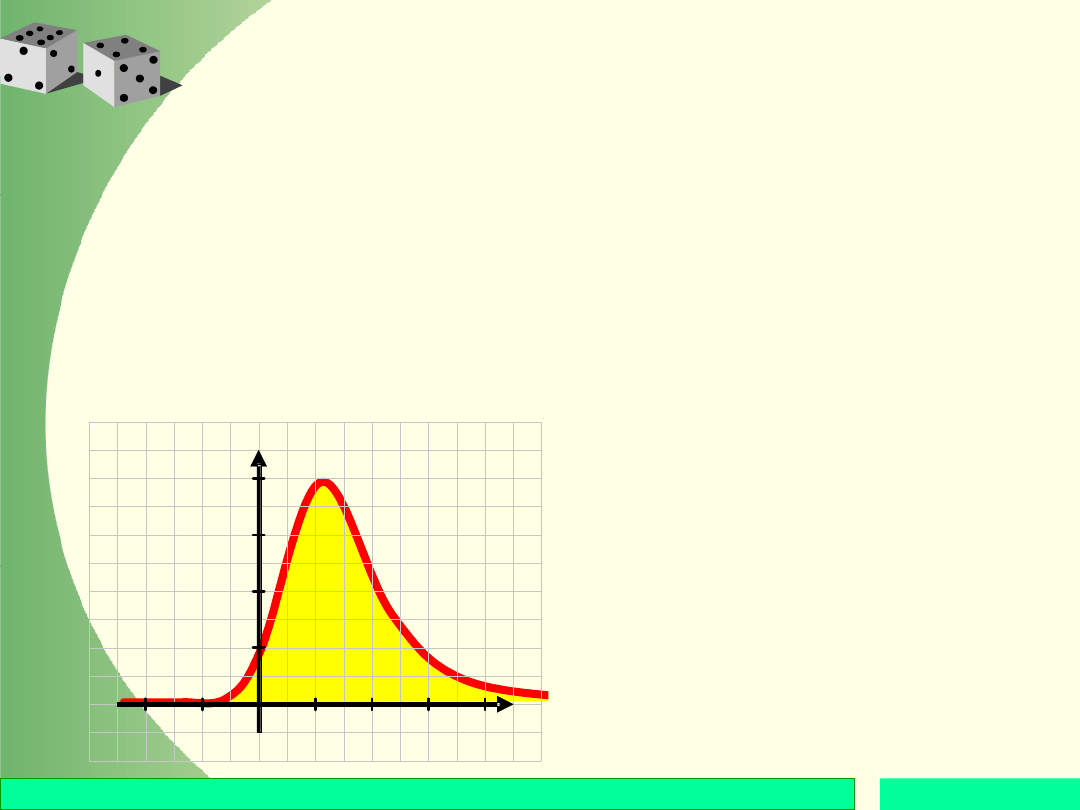
Warunek 2. definicji zwany
warunkiem unormowania
oznacza, że wykres funkcji f
i oś OX ograniczają obszar
o polu równym 1.

X

y

f x

 ( )

Pole = 1

Slajd 3 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Uwaga

Jeżeli f(x) = 0 na przedziale

(a, b), to

( )

0.

b

a

f x dx =

�

Slajd 4 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

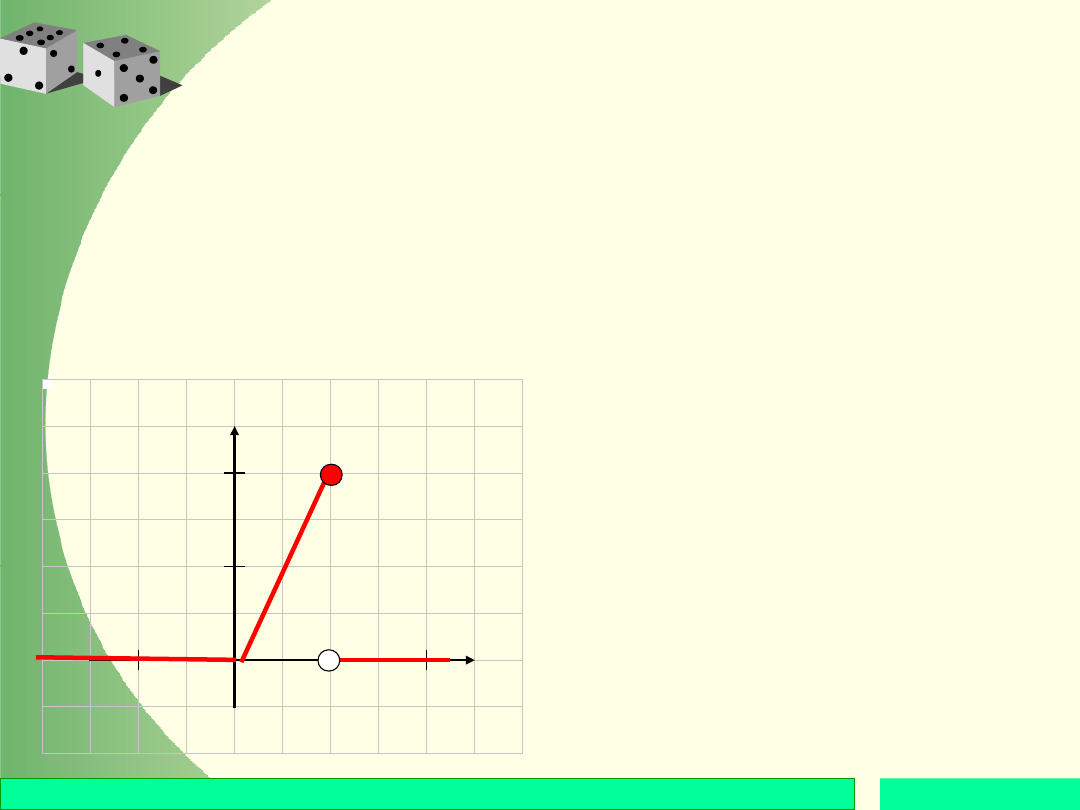
Przykład

Wykazać, że funkcja f określona
wzorem:

jest gęstością pewnej zmiennej
losowej X. Naszkicować wykres
gęstości.

2

dla 0

1,

( )

0 dla pozost. .

x

x

f x

x

� �

�

=�

�

-1

1

2

X

2

1

1. ( ) 0 dla

.

f x

x R

�

�

Na podstawie wykresu
stwierdzamy:

Slajd 5 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

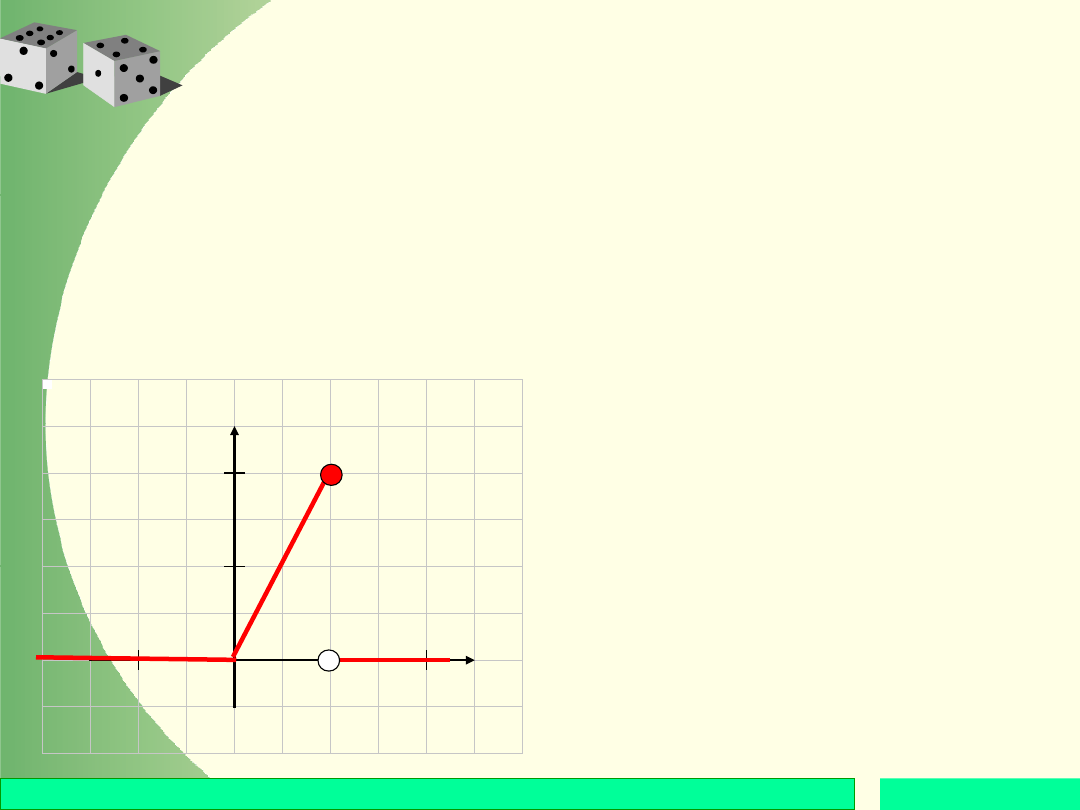
Przykład

Wykazać, że funkcja f określona
wzorem:

jest gęstością pewnej zmiennej
losowej X. Naszkicować wykres
gęstości.

2

dla 0

1,

( )

0 dla pozost. .

x

x

f x

x

� �

�

=�

�

-1

1

2

X

1

2

0

1

0

1

( )

0

2

0

f x dx

dx

xdx

dx

�

�

- �

- �

=

+

+

=

�

� �

�

1

1

1

2

0

0

0

0

2

0

2

1

xdx

xdx

x

� �

+

+ =

=

=

� �

�

�

2.

( )

1.

f x dx

+�

- �

=

�

Istotnie:

Slajd 6 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Zmienne losowe ciągłe

Zmienna losowa X jest ciągła, jeżeli istnieje
funkcja gęstości f taka, że dla każdych a  b

zachodzi zależność

(

)

( ) .

b

a

P a X b

f x dx

� � =

�

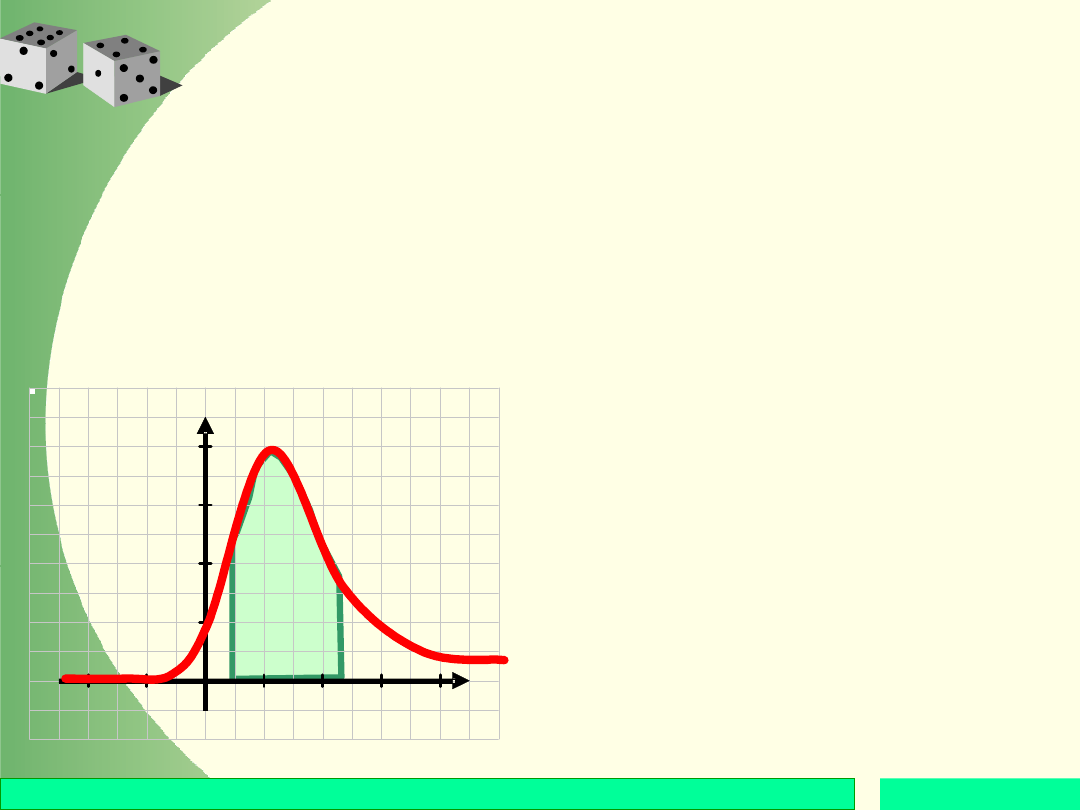
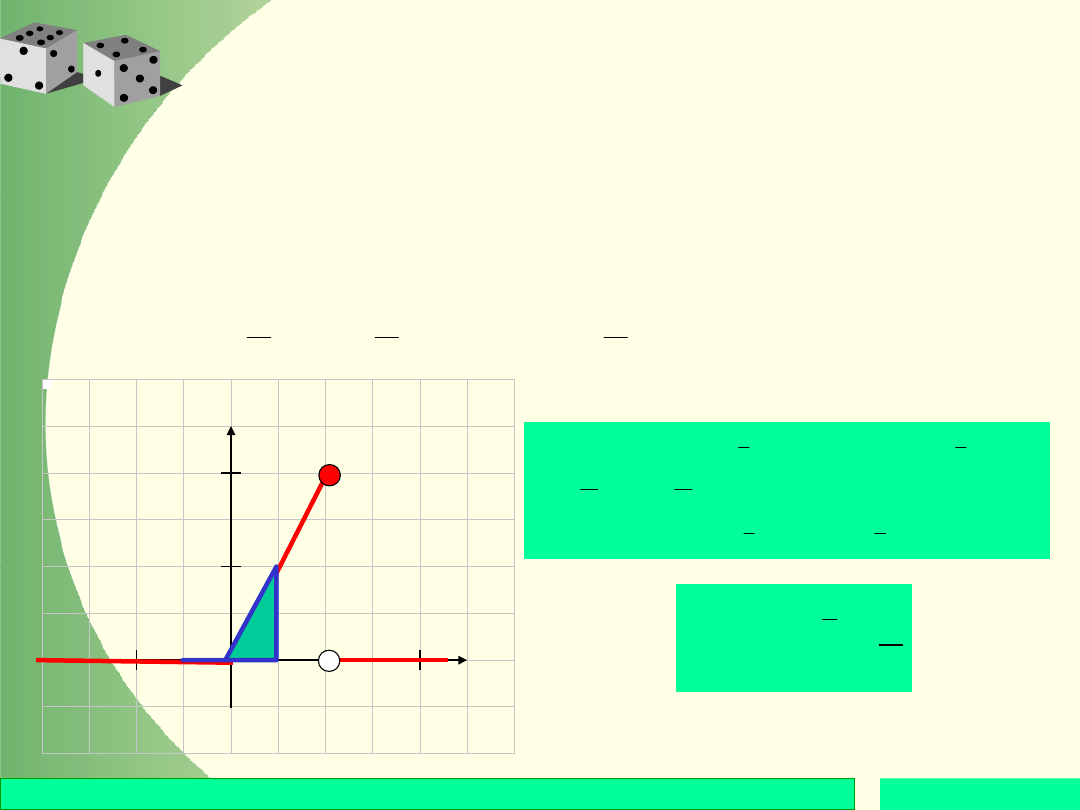
Interpretując geometrycznie
całkę występującą po prawej
stronie ostatniej zależności
otrzymujemy, że
prawdopodobieństwo przyjęcia
przez zmienną losową X
wartości z przedziału [a, b]
jest równa polu obszaru
rozpościerającego się nad tym
przedziałem poniżej funkcji
gęstości.

X

y

f x

 ( )

a b

Slajd 7 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

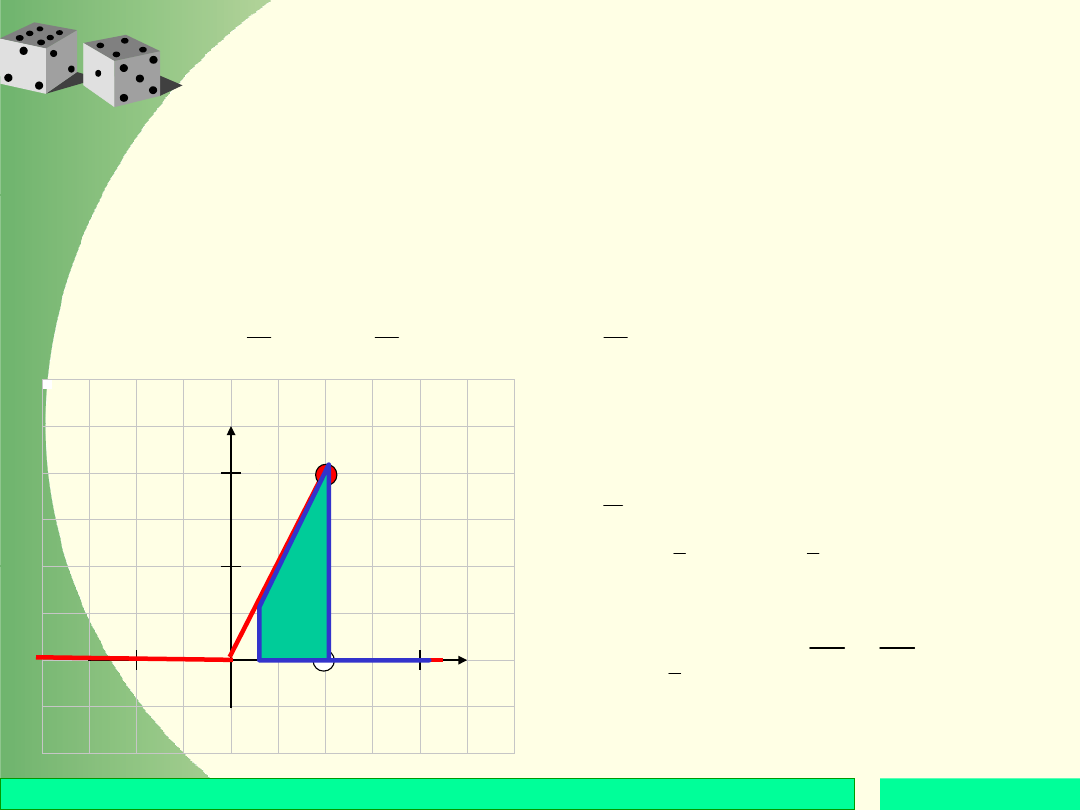
Przykład

Rozpatrzmy funkcję gęstości pewnej zmiennej
losowej X:

Obliczyć prawdopodobieństwa:

2

dla 0

1,

( )

0 dla pozost. .

x

x

f x

x

� �

�

=�

�

-1

1

2 X

2

1

1

1

2

a) (

), b) (

).

2

2

3

P

X

P X

-

� �

�

1

1

0

2

2

1

1

0

2

2

1

1

( )

0

2

2

2

P

X

f x dx

dx

xdx

-

-

�

�

-

� � =

=

+

=

�

�

�

�

�

� �

1

2 2

0

1

0 [ ]

4

x

= +

=

-½

½

Slajd 8 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

-1

1

2 X

1

2

Przykład

Rozpatrzmy funkcję gęstości pewnej zmiennej
losowej X:

Obliczyć prawdopodobieństwa:

2

dla 0

1,

( )

0 dla pozost. .

x

x

f x

x

� �

�

=�

�

1

1

1

a) (

), b) (

).

2

2

4

P

X

P X

-

� �

�

1

1

1

1

4

4

1

( )

2

0

4

P X

f x dx

xdx

dx

+�

+�

�

�

� =

=

+

=

�

�

�

�

�

�

�

1
4

2 1

1 15

[ ]

0 1

.

16 16

x

=

+ = -

=

¼

Slajd 9 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Dystrybuanta zmiennej losowej ciągłej

Z definicji dystrybuanty zmiennej losowej X:

F(x) = p(X < x)

wynika, że jeżeli f jest funkcją gęstości tej
zmiennej, to

( )

(

)

( ) .

x

F x

P X x

f t dt

- �

=

< =

�

Slajd 10 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Własności dystrybuanty zmiennej losowej

ciągłej

1. Dla każdego xR mamy 0  F(x)  1.

2. lim ( )

(

) 0, lim ( )

(

) 1.

x

x

F x

F

F x

F

�- �

�+�

= - � =

= +� =

3. F jest funkcją niemalejącą.

4. F jest funkcją ciągłą w każdym

punkcie.

Slajd 11 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Uwaga

W przypadku, gdy X jest zmienną
losową ciągłą o dystrybuancie F
prawdziwe są zależności:

(

)

(

)

( )

( ).

(

)

(

)

P a X b
P a X b

F b F a

P a X b
P a X b

� � �

�

� < �

=

-

�

< � �

�

< < �

Slajd 12 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

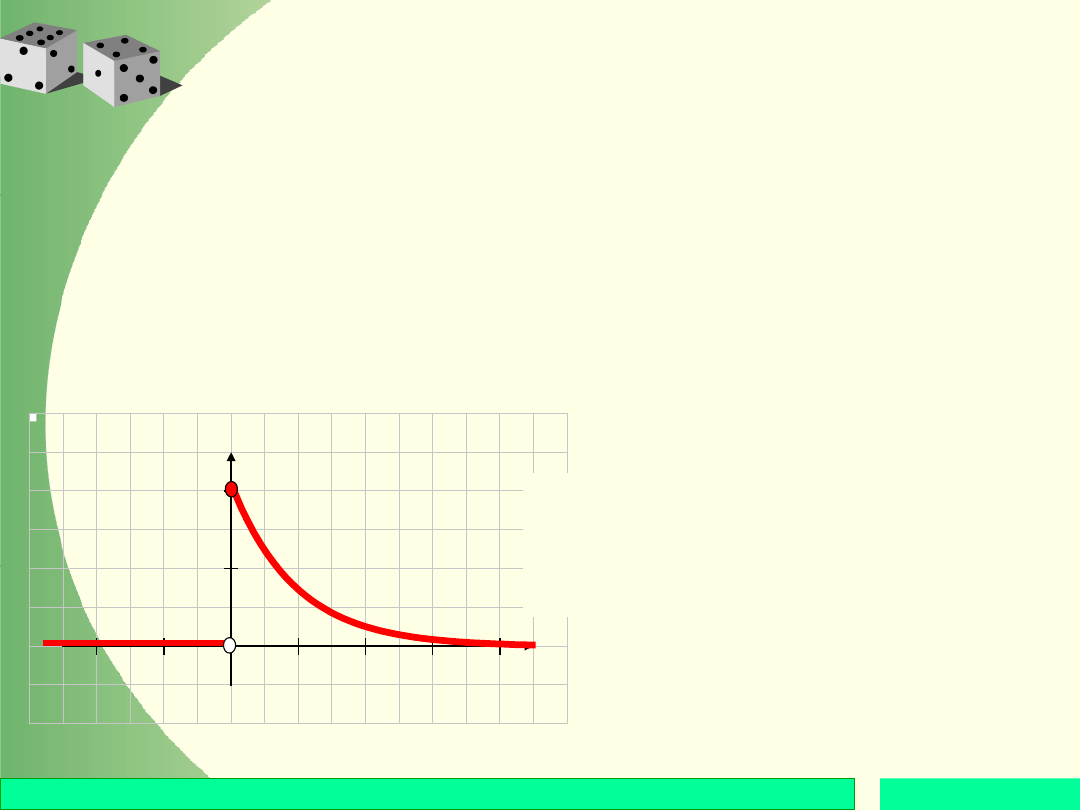
Przykład

Wykazać, że funkcja f jest gęstością pewnej
zmiennej losowej.

f x

x

e

x

x

( )

,















0

0

0

dla

dla

Naszkicować wykres gęstości. Wyznaczyć dystrybuantę
i sporządzić jej wykres. Obliczyć P(1 X  2), a

następnie zinterpretować otrzymaną liczbę na wykresie
gęstości i dystrybuanty.

X

1

2

0

3 4

1

0,
5

-1

-2

y = f(x)

1. ( ) 0 dla

.

f x

x R

�

�

0

0

0

0

2.

( )

0

0

1

x

x

f x dx

dx

e dx

e

e

e

+�

+�

+�

-

-

- �

- �

- �

�

�

=

+

= + -

=

�

�

=-

+ =

�

� �

Funkcja f jest więc
gęstością
prawdopodobieństwa
pewnej zmiennej losowej
X.

Slajd 13 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

f x

x

e

x

x

( )

,















0

0

0

dla

dla

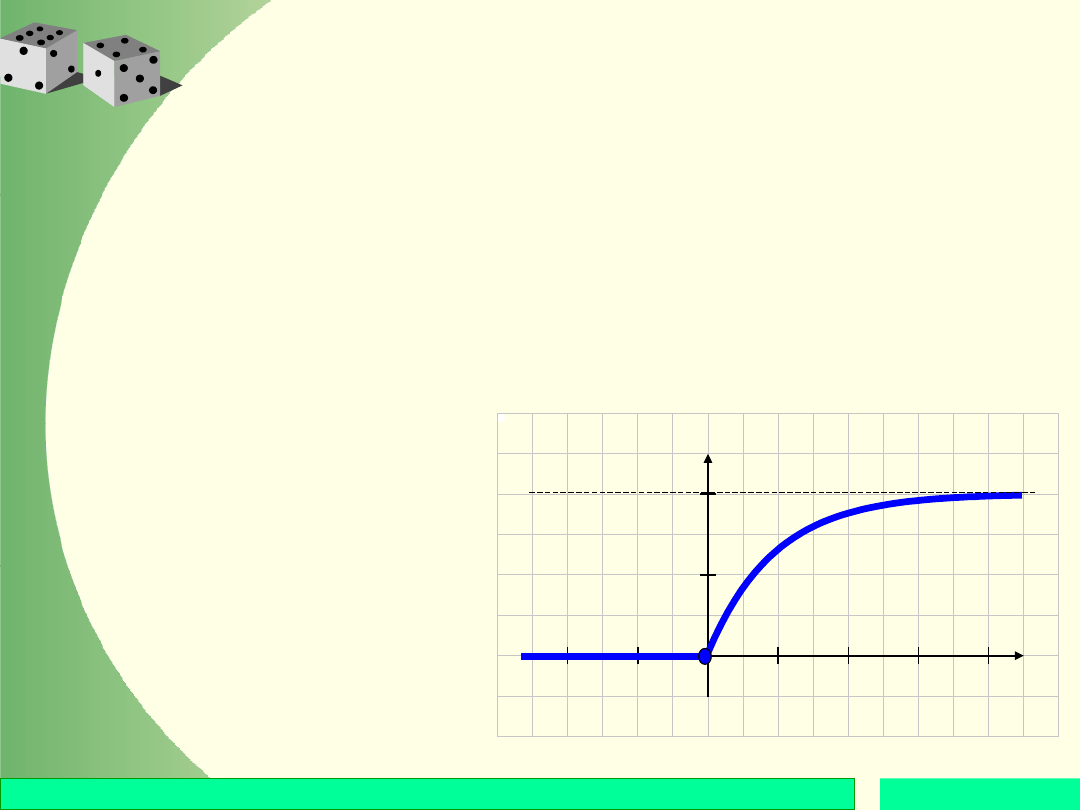
Wyznaczanie
dystrybuanty:

( )

( )

0

0.

x

x

F x

f t dt

dt

- �

- �

=

=

=

�

�

Gdy x  0, to

Gdy x < 0, to

0

0

( )

( )

0

x

x

t

F x

f t dt

dt

e dt

-

- �

- �

=

=

+

=

�

� �

0

0

0

1

x

t

x

x

e

e

e

e

-

-

-

�

�

= + -

=-

+ = -

�

�

X

1

2

0

3

4

1

0,
5

-1

-2

y = F(x)

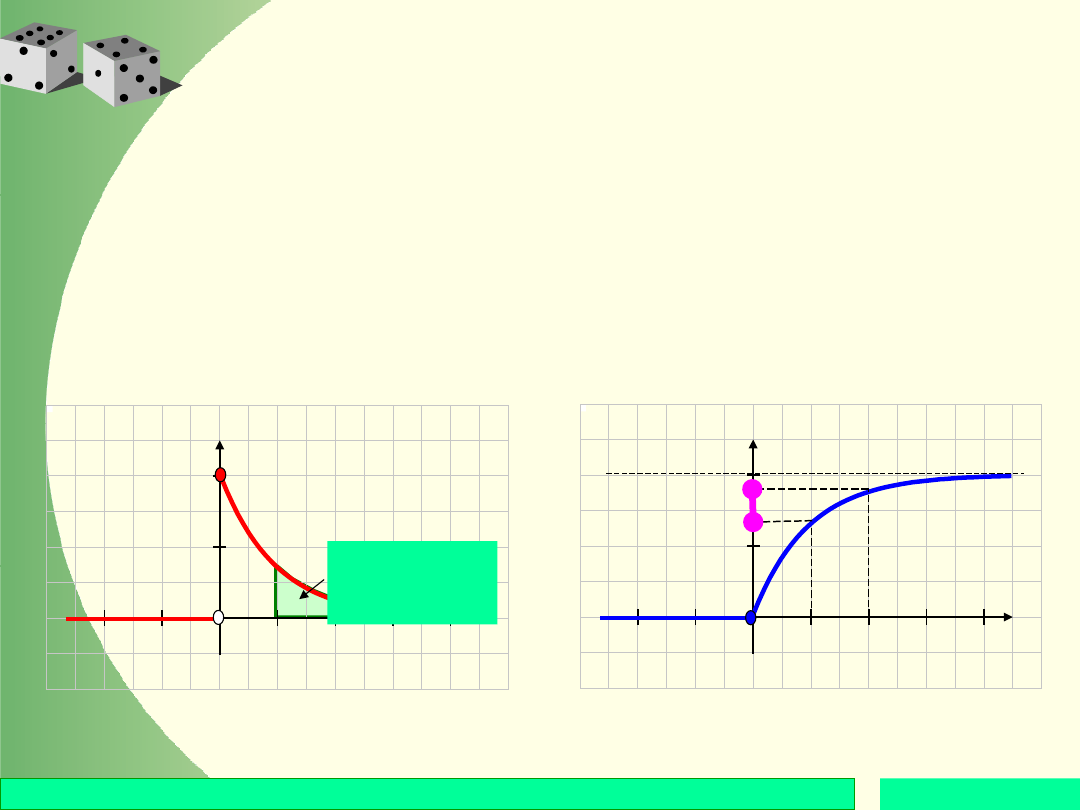
Slajd 14 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

f x

x

e

x

x

( )

,















0

0

0

dla

dla

2

2

2

2

1

1

1

1

(1

2)

( )

0,2325

x

x

P

X

f x dx

e dx

e

e

e

-

-

-

-

�

�

� � =

=

= -

=-

+

=

�

�

�

�

X

1 2

0

3 4

1

F(2)

-
1

-
2

y =
F(x)

X

1 2

0

3 4

1

0,
5

-
1

-
2

y =
f(x)

F(1)

P(1 X

 2)

P(1 X  2)=F(2)-

F(1)

Slajd 15 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Gęstość prawdopodobieństwa a

dystrybuanta

Funkcja gęstości zmiennej losowej ciągłej X i jej
dystrybuanta są ze sobą ściśle związane.

Na podstawie funkcji gęstości f można określić
dystrybuantę F oraz na odwrót: na podstawie
dystrybuanty można wyznaczyć funkcję gęstości
f.

Prawdziwe jest stwierdzenie:

Jeżeli x jest punktem ciągłości gęstości f, to F

/

(x) = f (x).

Slajd 16 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

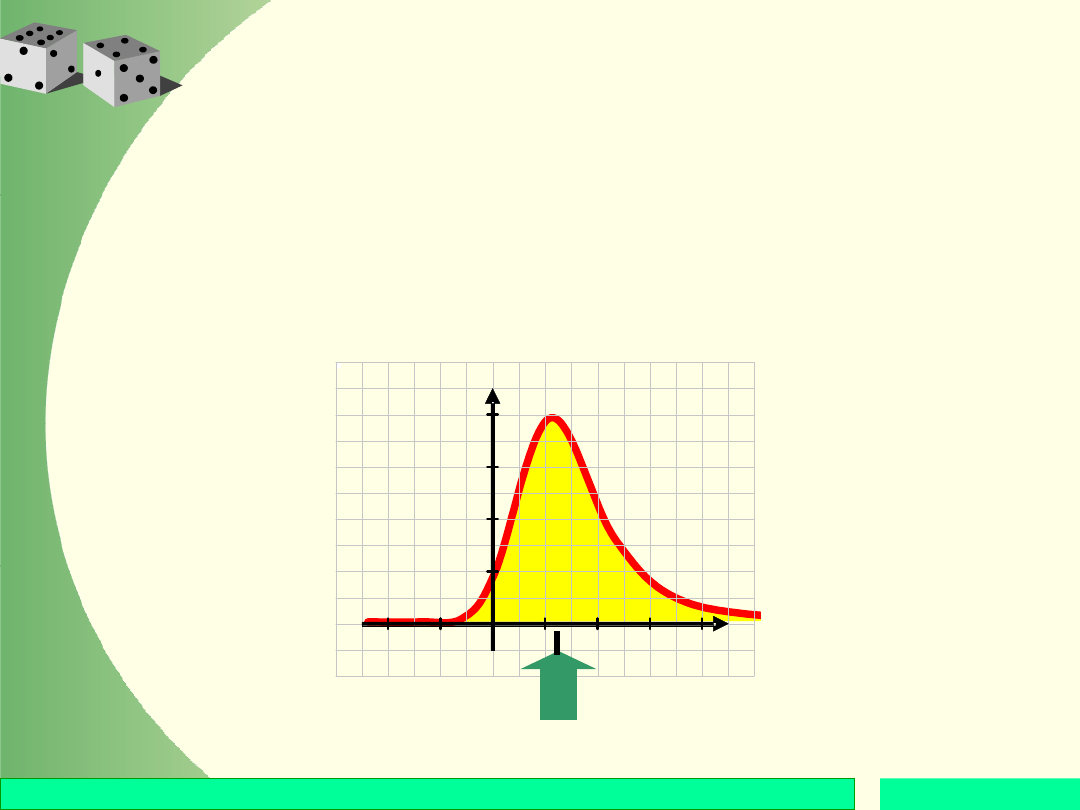
Wartość oczekiwana zmiennej

ciągłej

Wartością oczekiwaną zmiennej losowej ciągłej X
nazywamy liczbę oznaczaną przez E(X) i równą:

( )

( ) .

E X

xf x dx

+�

- �

=

�

Slajd 17 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

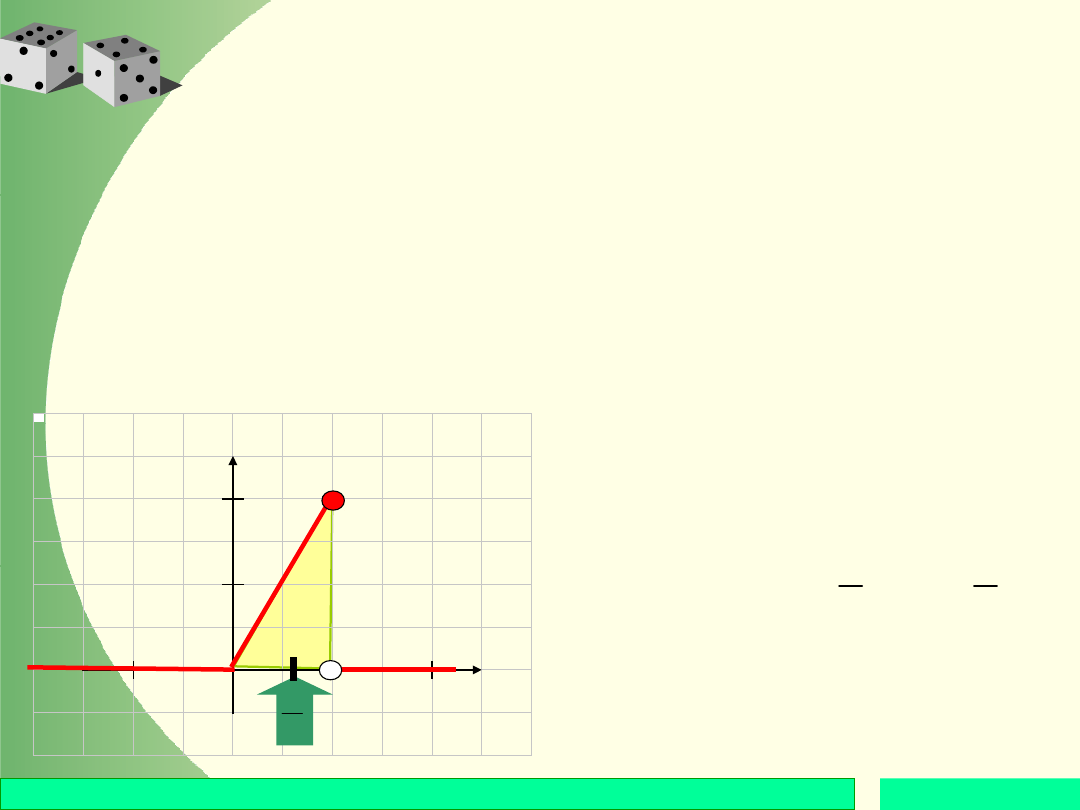
Wartość oczekiwana

zmiennej ciągłej

Liczba E(X) pokazuje, w którym punkcie osi
poziomej należy podeprzeć obszar ograniczony
osią OX i wykresem gęstości, aby znajdował się on
w stanie równowagi.

X

y

f x

 ( )

Pole = 1

( )

E X

Slajd 18 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

Niech X będzie zmienną losową o gęstości

2

dla 0

1,

( )

0 dla pozost. .

x

x

f x

x

� �

�

=�

�

Obliczyć wartość oczekiwaną. Zinterpretować na
wykresie funkcji gęstości.

1

0

1

1

2

3

0

0

( )

( )

2

2

2

2

3

3

E X

xf x

x xdx

x dx

x

+�

- �

=

=

�

=

�

�

=

=

=

�

�

�

�

�

�

�

-1

1

2 X

1

2

y = f(x)

2
3

Slajd 19 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Wariancja zmiennej

losowej

Liczbę E(X – E(X))

2

nazywamy wariancją

zmiennej X i oznaczamy przez D

2

(X).

Pierwiastek z wariancji nazywamy odchyleniem
standardowym zmiennej losowej X i oznaczamy
symbolem



.

Liczba ta jest nieujemna.

Slajd 20 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

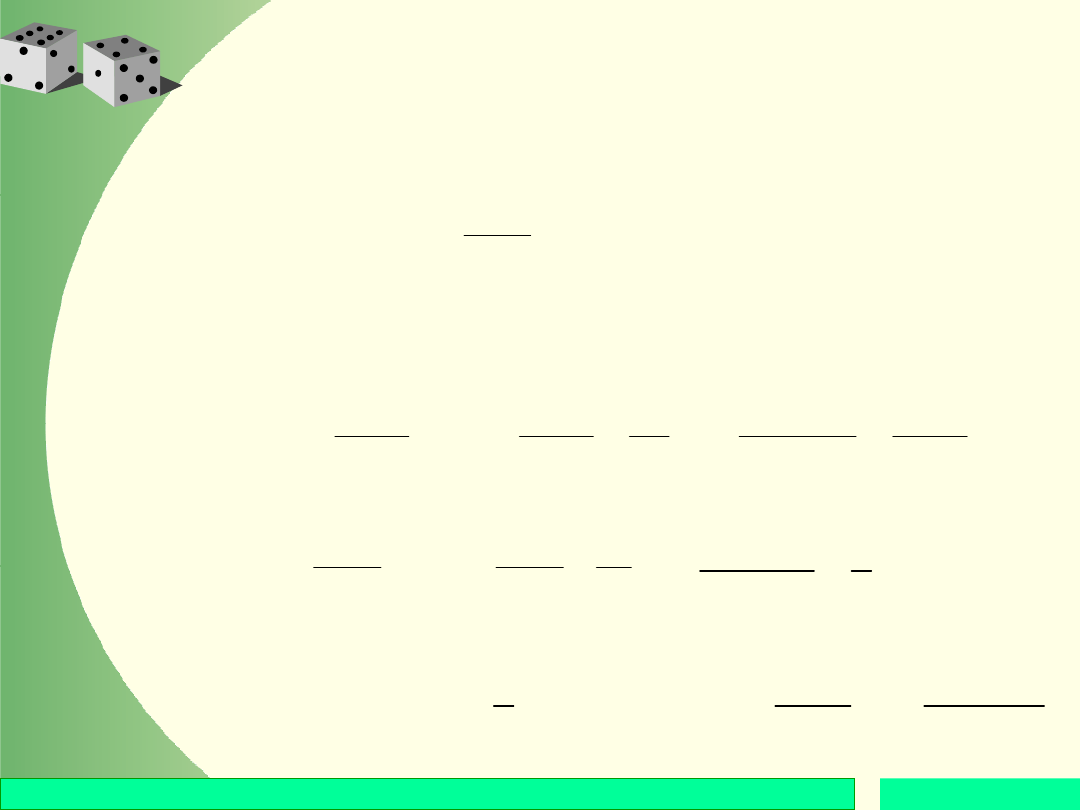
Wariancja zmiennej

losowej

Wariancja zmiennej losowej X wyraża się
wzorem

D

2

(X) = E(X

2

) – (E(X))

2

,

gdzie E(X) oznacza wartość oczekiwaną zmiennej
X ,

2

2

(

)

( )

E X

x f x dx

+�

- �

=

�

a w przypadku zmiennej ciągłej:

Slajd 21 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

Niech X będzie zmienną losową o gęstości:

1

gdy

[ ; ],

( )

0

dla pozost. .

x a b

f x

b a

x

�

�

�

=

-

�

�

�

Obliczyć wartość oczekiwaną oraz wariancję tej
zmiennej losowej.

3

2

2

2

1

1

(

)

( )

3

b

b

a

a

x

E X

x f x dx

x dx

b a

b a

+�

- �

� �

=

=

=

�

=

� �

-

-

� �

�

�

3

3

2

2

1

(

)

3(

) 3

b

a

a

ab b

b a

-

=

+ +

-

D X

E X

E X

a

ab b

a b

a b

2

2

2

2

2

2

2

1

3

2

12

( )

(

) [ ( )]

(

) (

)

(

)



















2

2

2

1

1

( )

( )

2

2(

)

2

b

b

a

a

x

b

a

a b

E X

xf x dx

xdx

b a

b a

b a

+�

- �

� �

-

+

=

=

=

�

=

=

� �

-

-

-

� �

�

�

Slajd 22 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

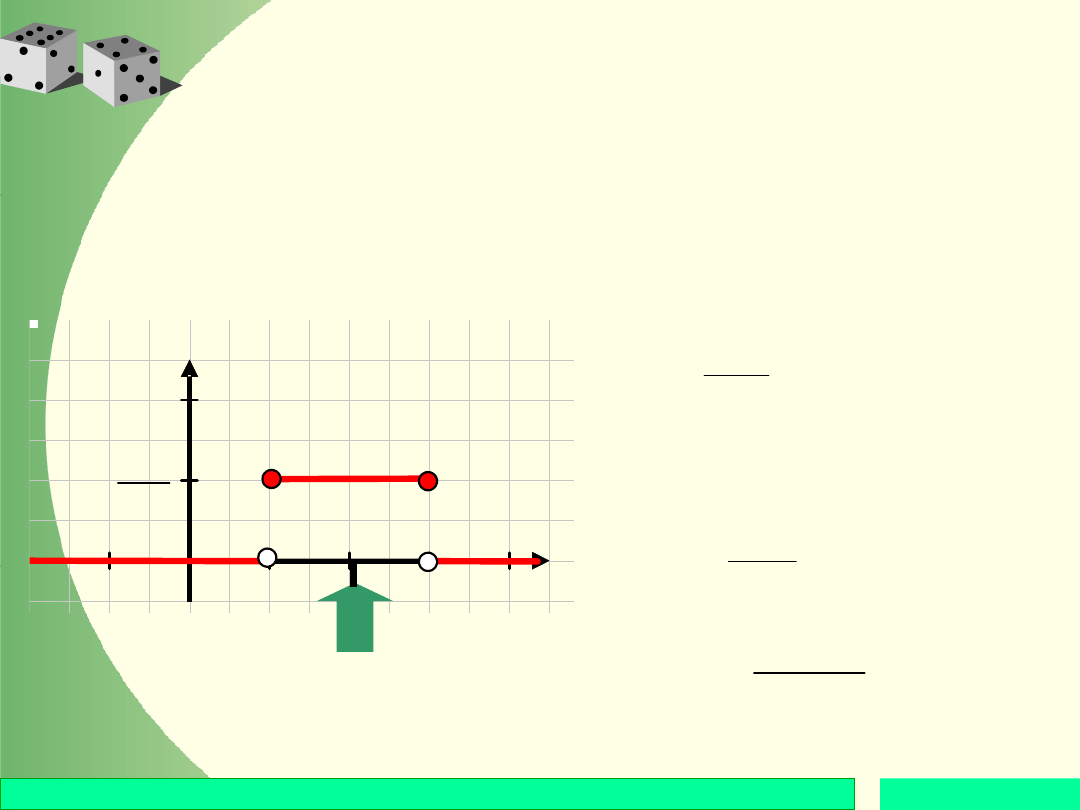
Zmienna losowa o rozkładzie

jednostajnym

Zmienna losowa X ma rozkład jednostajny na
przedziale [a; b], jeżeli funkcją gęstości tej zmiennej
jest funkcja określona wzorem:

[ ]

1

gdy

; ,

( )

0

dla pozost. .

x a b

f x

b a

x

�

�

�

=

-

�

�

�

X

a b

1

b a



( )

2

a b

E X

+

=

2

2

(

)

( )

12

a b

D X

-

=

( )

E X

Slajd 23 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

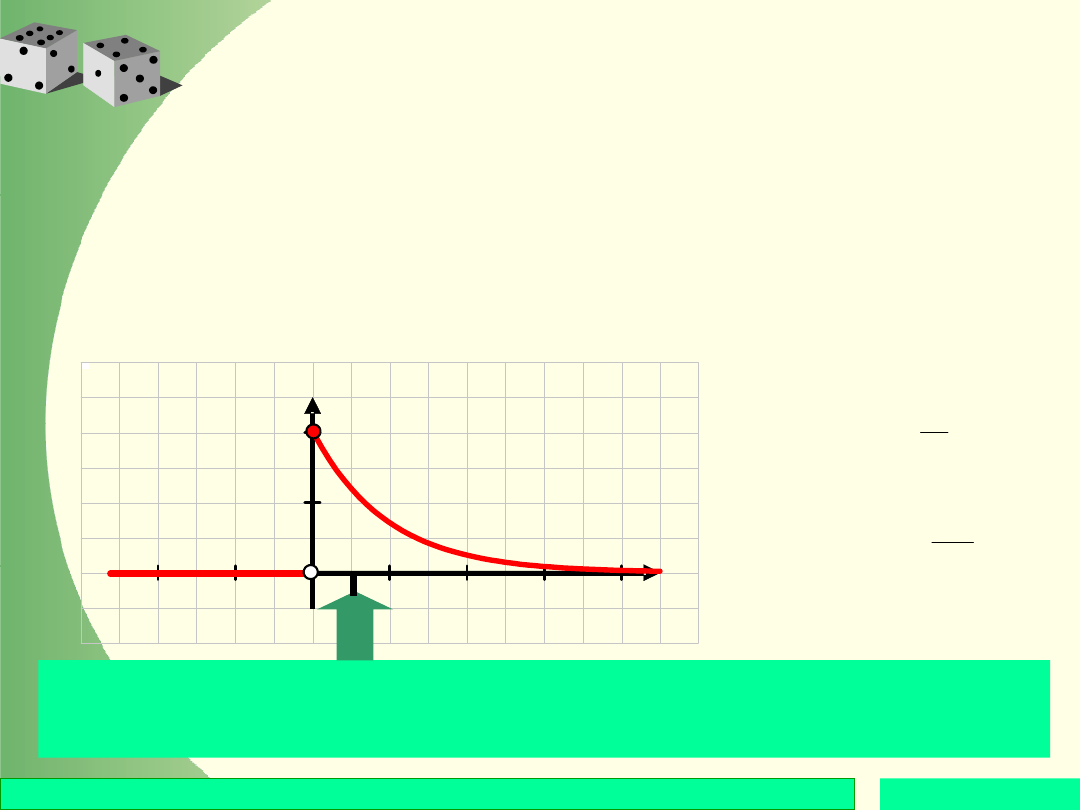
Zmienna losowa o rozkładzie

wykładniczym

Zmienna losowa X ma rozkład wykładniczy o
parametrze



> 0, jeżeli przyjmuje wyłącznie

wartości nieujemne, a funkcja gęstości tej zmiennej
wyraża się wzorem:

dla

0,

( )

0

dla pozost. .

x

e

x

f x

x

l

l

-

�

�

�

=�

�

�

Czas bezawaryjnej pracy wielu urządzeń można
opisywać zmienną o rozkładzie wykładniczym.

X

1

2

0

3

4



-1

-2

y = f(x)

E X

( ) 

1



D X

2

2

1

( ) 



( )

E X

Slajd 24 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

Czas świecenia żarówki (w godzinach) opisuje
zmienna losowa X o gęstości danej wzorem:

0,001

0,001

dla

0,

( )

0

dla pozost. .

t

e

t

f t

t

-

�

�

׳

�

=�

�

�

Obliczyć prawdopodobieństwo, że żarówka:
a) świecić będzie co najmniej 500 godzin,
b) przepali się w drugim tygodniu świecenia.

(

500)

P X �

=

500

( )

f t dt

+�

=

�

0,001

500

0,001

t

e

dt

+�

-

�

=

�

0,001

500

t

e

+�

-

=-

0.5

0,607.

e

e

- �

-

=-

+

=

a)

Slajd 25 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

Czas świecenia żarówki (w godzinach) opisuje
zmienna losowa X o gęstości danej wzorem:

0,001

0,001

dla

0,

( )

0

dla pozost. .

t

e

t

f t

t

-

�

�

׳

�

=�

�

�

Obliczyć prawdopodobieństwo, że żarówka:
a) świecić będzie co najmniej 500 godzin,
b) przepali się w drugim tygodniu świecenia.

(168

336)

P

X

� �

=

336

168

( )

f t dt =

�

336

0,001

168

0,001

t

e

dt

-

�

=

�

336

0,001

168

t

e

-

=-

0,336

0,168

0,7118 0,8437 0,1319.

e

e

-

-

=-

+

=-

+

=

b)

Slajd 26 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

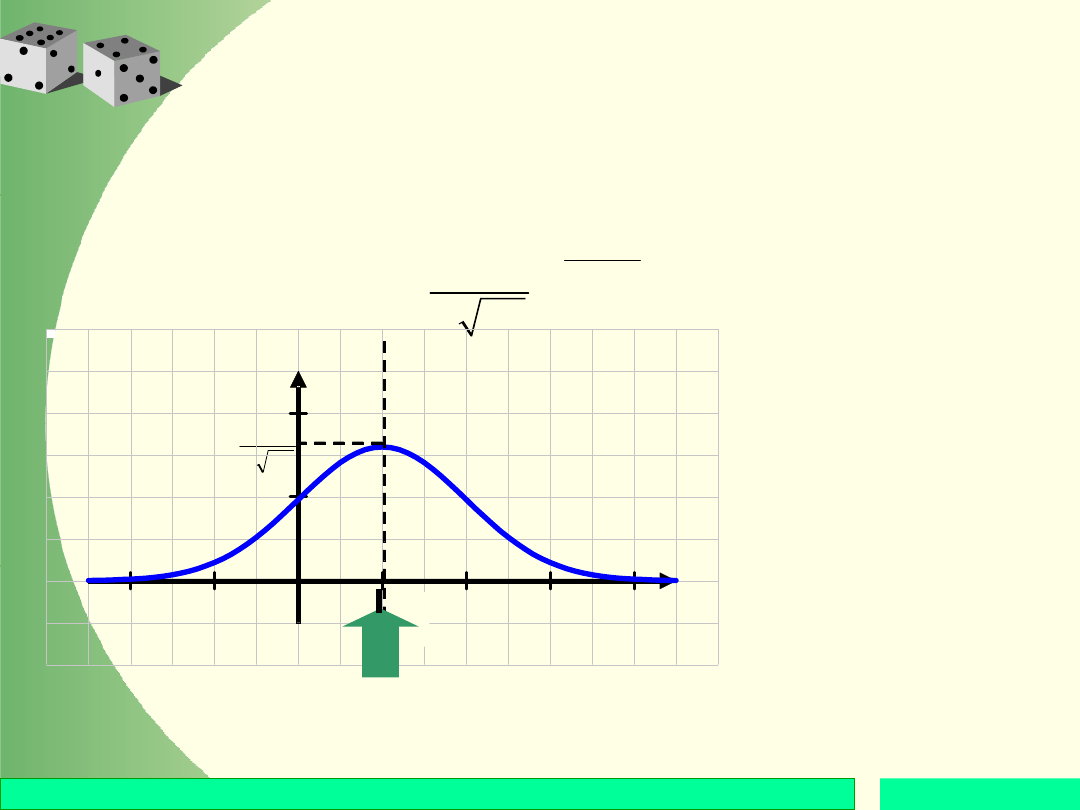
Zmienna losowa o rozkładzie

normalnym

Zmienna losowa X ma rozkład normalny o
parametrach



i



, jeżeli jej gęstość wyraża się

wzorem

2

(

)

2

2

1

( )

.

2

x

f x

e

m

s

s

p

-

-

=

Z badań wynika, że wzrost i waga ludzi, błędy
pomiarów mogą być traktowane jako zmienne
losowe o rozkładach normalnych.

2

2

( )

,

( )

E X
D X

m

s

=

=

Y

1

2

 

m

X



( )

E X

Slajd 27 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

- jest symetryczna względem prostej x =



,

- w punkcie x =



osiąga wartość

maksymalną,

- ramiona funkcji mają punkty przegięcia dla
x =



- σ

oraz x =



+ σ,

- kształt funkcji gęstości zależy od wartości

parametrów:



i σ. Parametr



decyduje o przesunięciu

krzywej,
natomiast parametr σ decyduje o

„smukłości” krzywej.

Funkcja gęstości w rozkładzie
normalnym:

Slajd 28 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

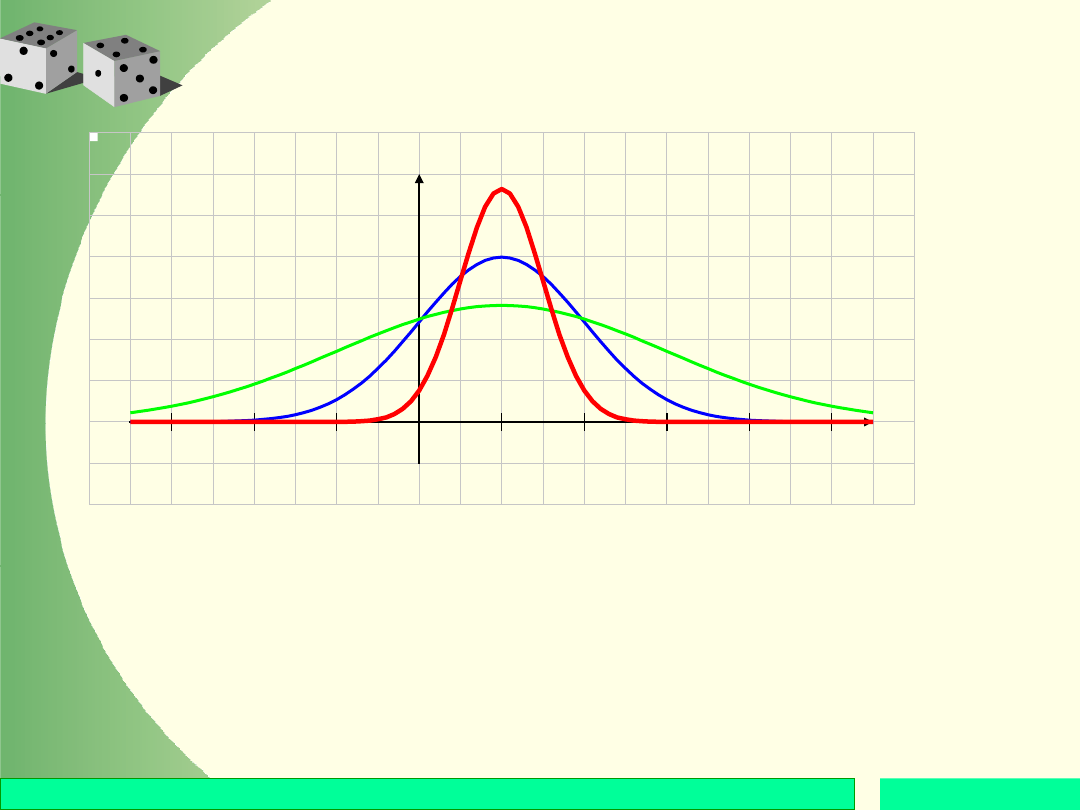
Wpływ parametru



-3

-2

-1

1

2

3

4

5 X

Y

Powyższe wykresy gęstości funkcji rozkładu
normalnego otrzymano przy



= 1 oraz trzech

różnych parametrach



.

Wykresy te pokazują, że wartość oczekiwana



nie

wpływa na kształt wykresu funkcji gęstości rozkładu
normalnego.

Slajd 29 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

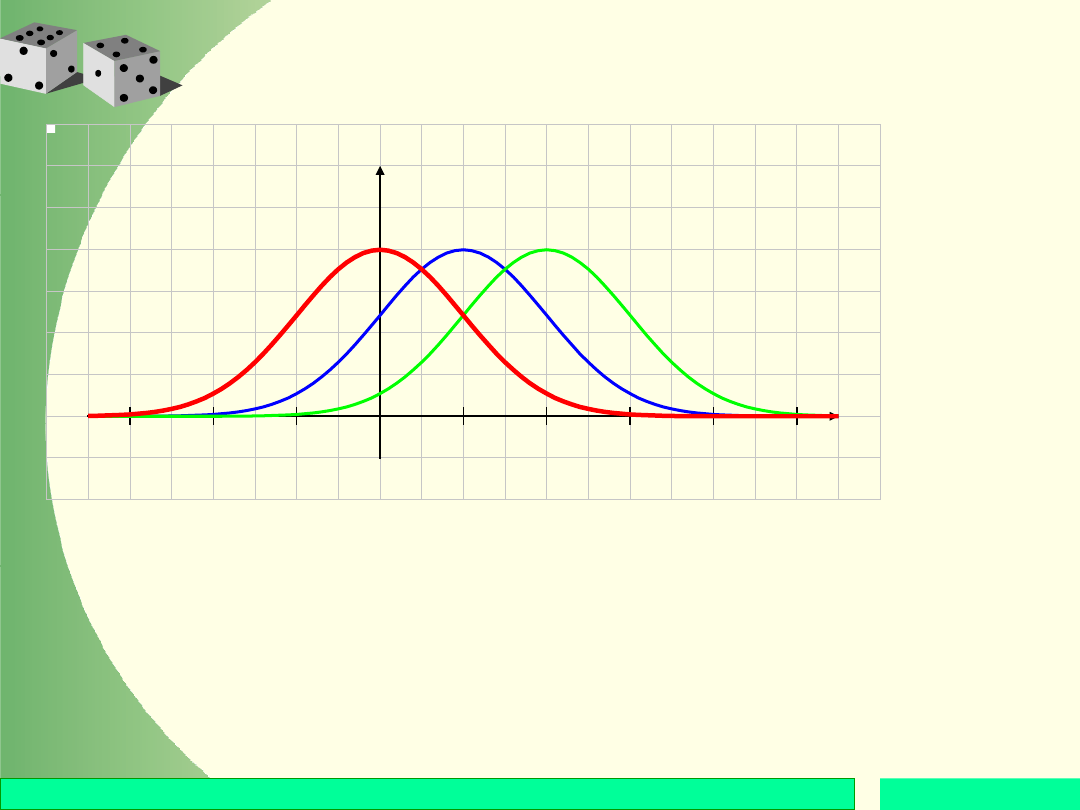
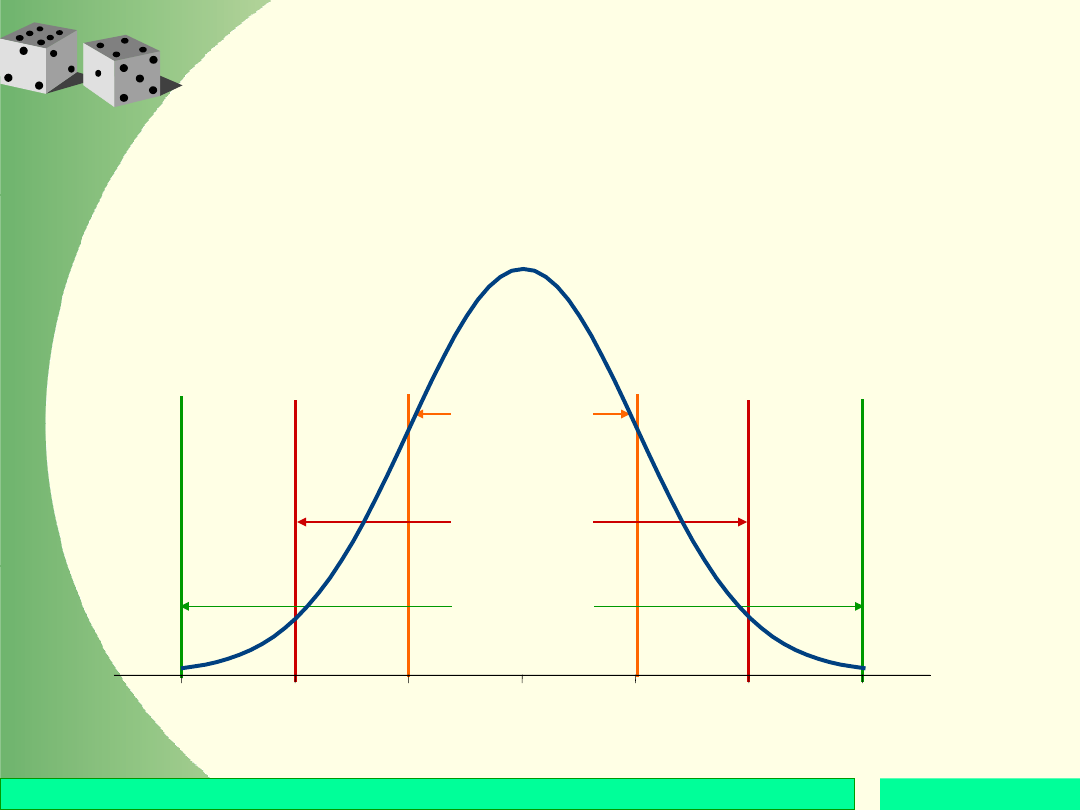
Wpływ parametru



-3

-2

-1

1

2

3

4

5

X

Y

Powyższe wykresy gęstości funkcji rozkładu
normalnego otrzymano przy



= 1 oraz trzech

różnych parametrach



.

Wykresy te pokazują, że wariancja



2

jest miarą

rozproszenia wartości zmiennej losowej wokół jej
wartości oczekiwanej.

Slajd 30 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Zmienna losowa o rozkładzie

normalnym

68,3 %

95,5 %

99,7 %

m - 3



m -
2



m -



m

m +



m + 2

 m + 3

Jeżeli zmienna losowa ma rozkład normalny to:

- 68,3 % jej wartości mieści się w przedziale (m - σ; m + σ),
- 95,5 % jej wartości mieści się w przedziale (m - 2σ; m + 2σ),

- 99,7 % jej wartości mieści się w przedziale (m- 3σ; m + 3σ).

Slajd 31 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Obliczanie

prawdopodobieństw rozkładu

normalnego

Dowodzi się, że jeżeli zmienna X ma rozkład
normalny o parametrach



i



, to zachodzi wzór:

(

)

(

)

(

)

b

a

P a X b

m

m

s

s

-

-

� � =F

- F

gdzie  oznacza funkcję Laplace’a.

Slajd 32 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

Wzrost dorosłych ludzi (w cm) jest zmienną losową
posiadającą rozkład normalny o parametrach



=

170 i



= 15. Obliczyć, jaka część ludzi ma wzrost:

a) mieszczący się w przedziale [160;180], b)
powyżej 200.

180 170

160 170

(160

180)

(

)

(

)

15

15

P

X

-

-

� �

=F

- F

=

(0,67)

( 0,67)

=F

- F -

=

2 (0,67) 2 0,2486 0,4972

= F

= �

=

Slajd 33 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

Przykład

Wzrost dorosłych ludzi (w cm) jest zmienną losową
posiadającą rozkład normalny o parametrach



=

170 i



= 15. Obliczyć, jaka część ludzi ma wzrost:

a) mieszczący się w przedziale [160;180], b)
powyżej 200.

200 170

(200

)

(

)

(

)

15

P

X

-

� <+� =F +� - F

=

0,5 0,4772 0,0228

=

-

=

0,5

(2)

=

- F

=

Slajd 34 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe

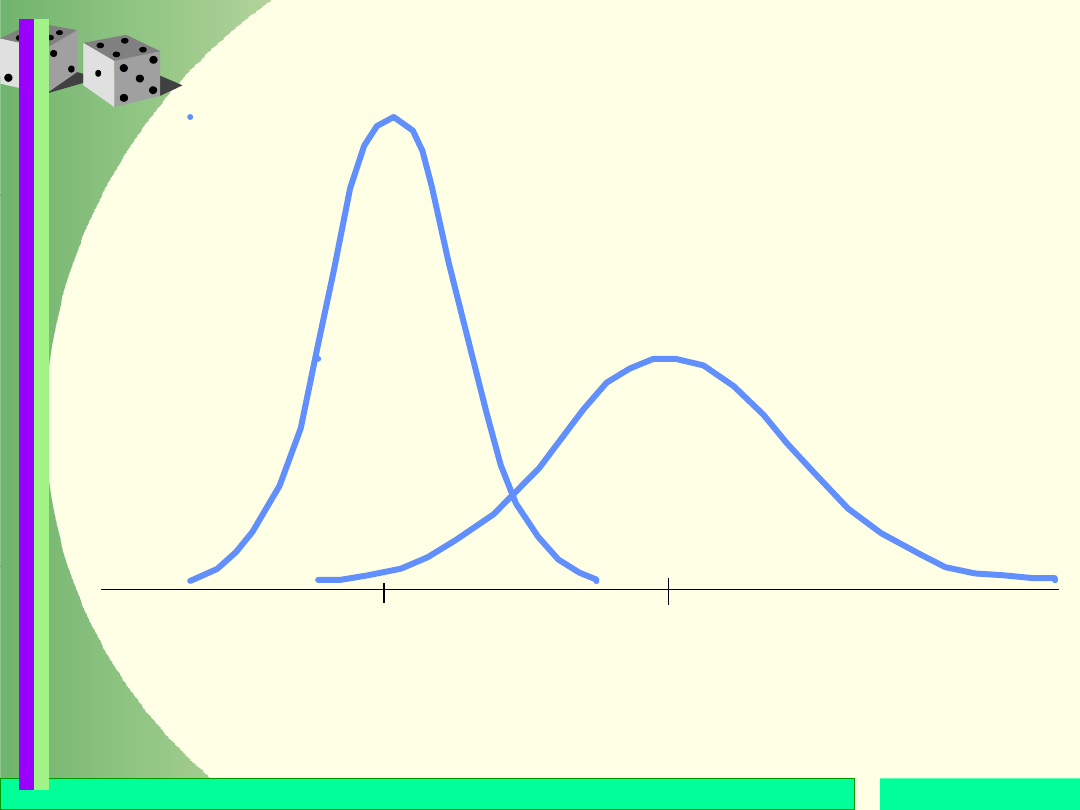
Mężczyź

ni:

µ = 172



= 7

172

160

Wzrost (w cm)

Krzywe wzrostu kobiet i mężczyzn (w cm)

Kobiety:

µ = 160

 = 6,3

Slajd 35 / 35

Tomasz Kowalski. Matematyka. Wykład 24. Zmienne losowe ciągłe