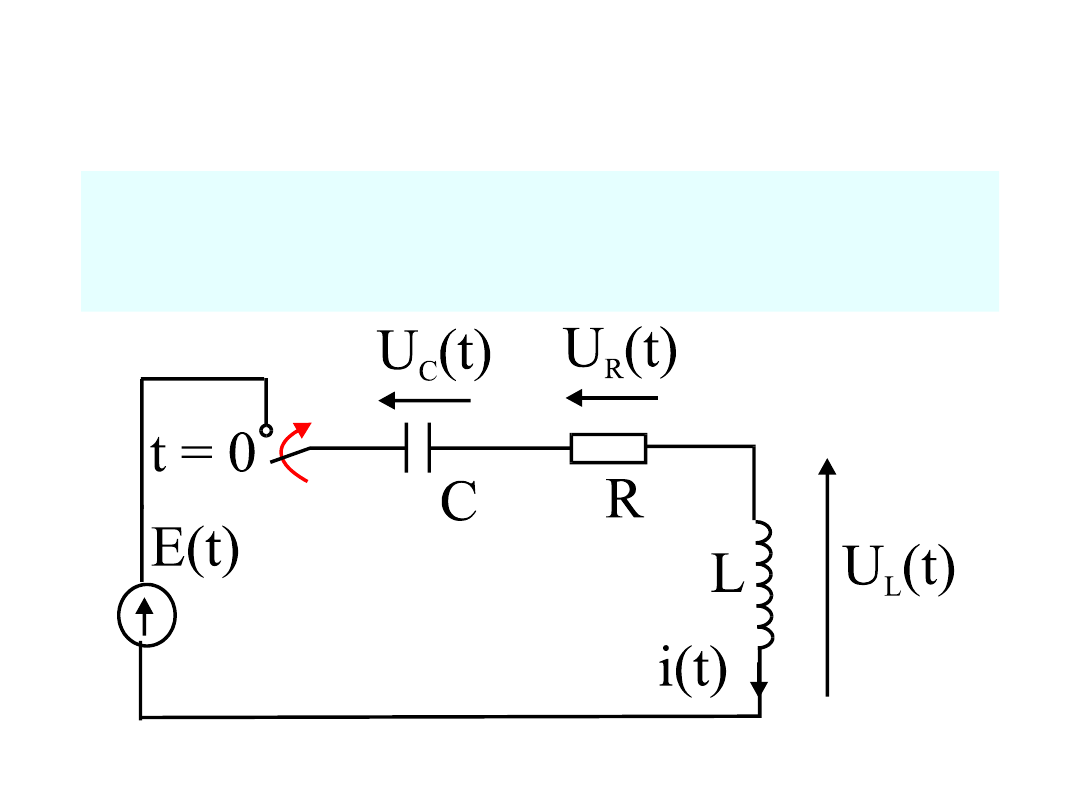
1
Stany nieustalone - w obwodzie
rezonansowym
Przykład 6. Obliczyć przebiegi prądu i napięć w
obwodzie przyjmując zerowe warunki
początkowe.
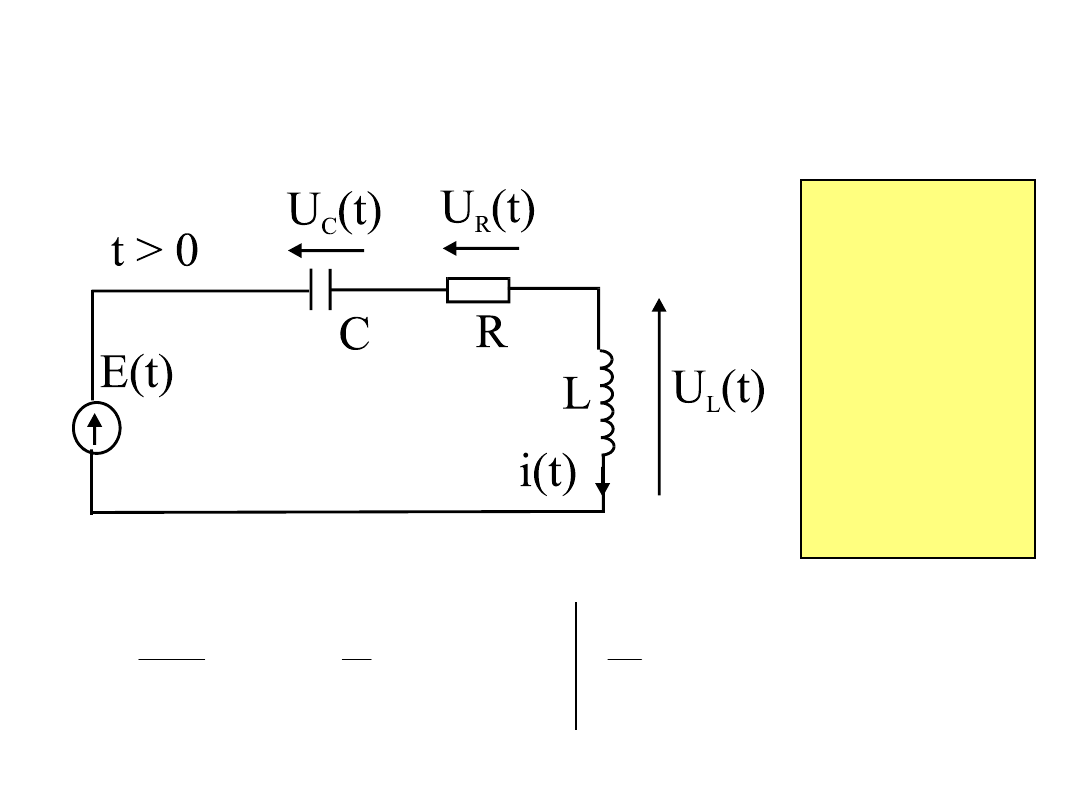
2
Stany nieustalone - w obwodzie
rezonansowym
E
dt
t
i
C
t
Ri
dt
t
di
L
1
0
0
i
0
i
E
U
C
0
0
C
U
0
L
U
dt
d
3
Podstawiamy -
Gdzie:
jest pulsacją
rezonansową obwodu,
a
jest współczynnikiem
tłumienia obwodu.
Stany nieustalone - w obwodzie
rezonansowym
0
1
2
2
t
i
C
dt
t
di
R
dt
t
i
d
L
0
2
2
0
2
2
t
i
dt
t
di
dt
t
i
d
LC
1
0
L
R
2
st
Ae
t
i
4
Stany nieustalone - w obwodzie
rezonansowym
0
2
2
0
2
s
s
Otrzymujemy do
rozwiązania równanie
którego pierwiastkami
są:
2
0
2
1
s
2
0
2
2
s
t
t
e
A
e
A
t
i
2
0
2
2
0
2
2
1
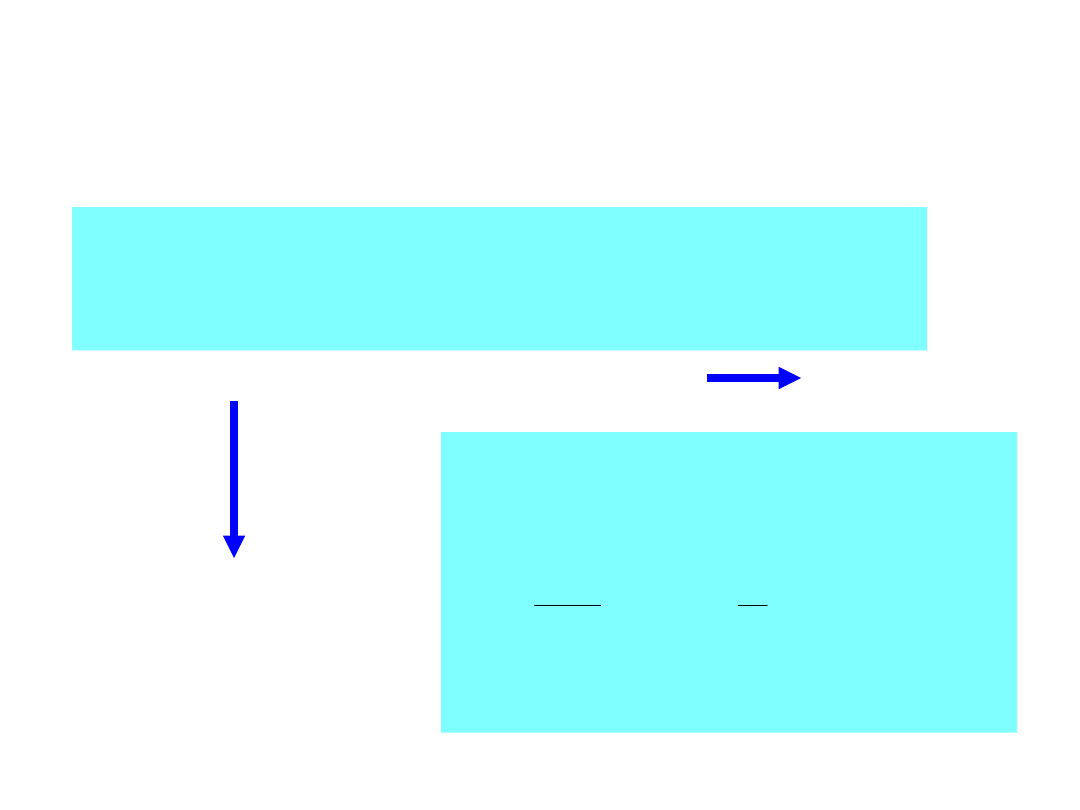
5
Aby znaleźć wartość stałej A
1
,
należy rozwiązać równanie
dla chwili czasu t = 0
+
.
Stany nieustalone - w obwodzie
rezonansowym
• Przypadek aperiodyczny -
2
>
0
2
, czyli
Q < 1/2,
otrzymamy dwa pierwiastki rzeczywiste
t
s
t
s
e
A
e
A
t
i
2
1
2
1
0
0
i
1
2
A
A
t
s
t
s
e
A
e
A
t
i
2
1
1
1
E
dt
t
i
C
t
Ri
dt
t
di
L
1
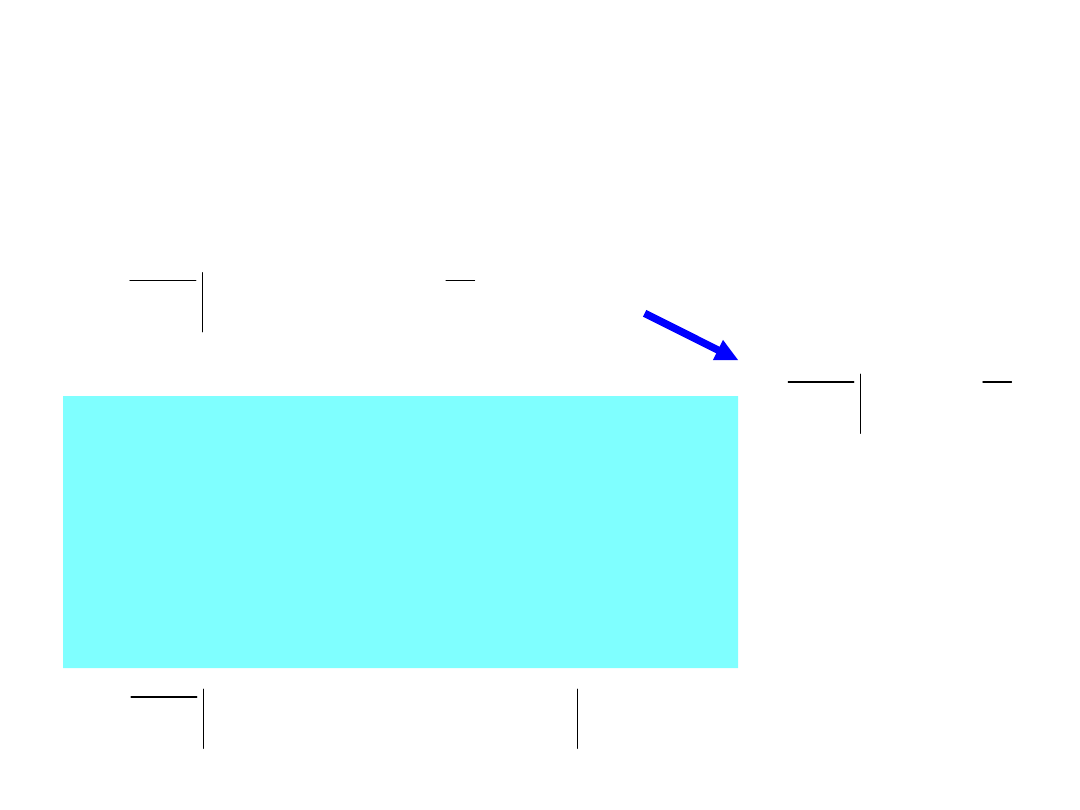
6
Stany nieustalone - w obwodzie
rezonansowym
E
dt
t
i
C
Ri
t
dt
t
di
L
0
0
1
0
0
L
E
t
dt
t
di
0
Oraz obliczyć pochodną prądu z
zależności
i znaleźć jej wartość dla chwili
czasu t = 0
+
.
t
s
t
s
e
A
e
A
t
i
2
1
1
1
1
2
1
1
2
1
1
0
0
2
1
A
s
s
t
e
A
s
e
A
s
t
dt
t
di
t
s
t
s
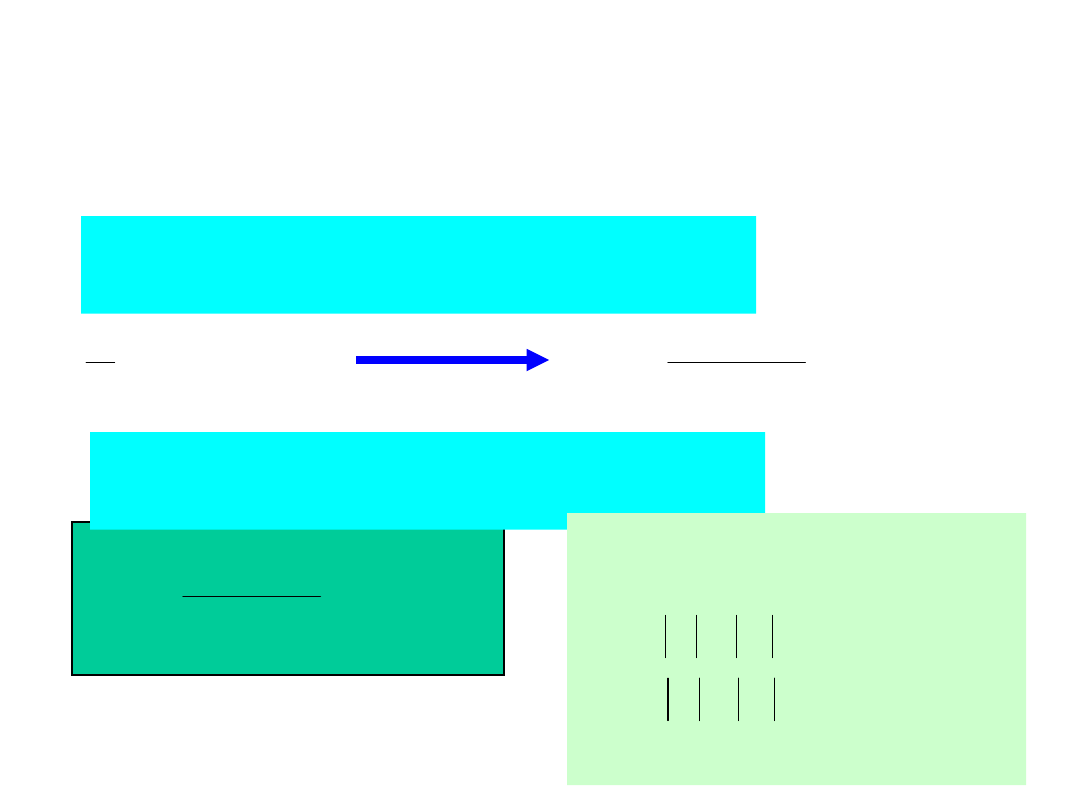
7
Stany nieustalone - w obwodzie
rezonansowym
Porównując obydwa równania
uzyskamy:
1
2
1
A
s
s
L
E
2
1
1
s
s
L
E
A
Stąd wyrażenie na prąd przyjmie
postać:
t
s
t
s
e
e
s
s
L
E
t
i
2
1
2
1
Ponieważ s = 1/,
można rozważyć dwa
przypadki:
2
1
2
1
1
s
s
2
1
2
1
2
s
s
8
Stany nieustalone - w obwodzie
rezonansowym
Przypadek
1):
t
s
t
s
e
s
s
L
E
e
s
s
L
E
t
i
2
1
2
1
2
1
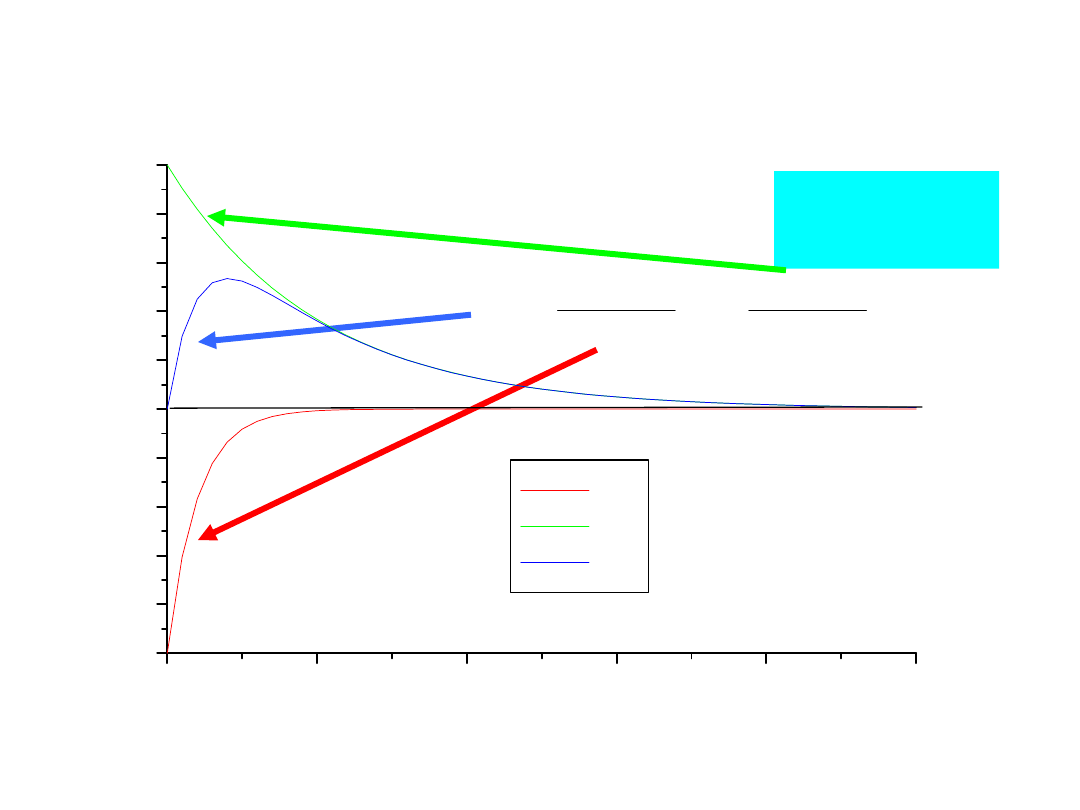
0
1
2
3
4
5
-10
-8
-6
-4
-2
0
2
4
6
8
10
i1a
i1b
i1
P
rz
e
bi
eg
i
p
rą
d
ó
w
Czas - t
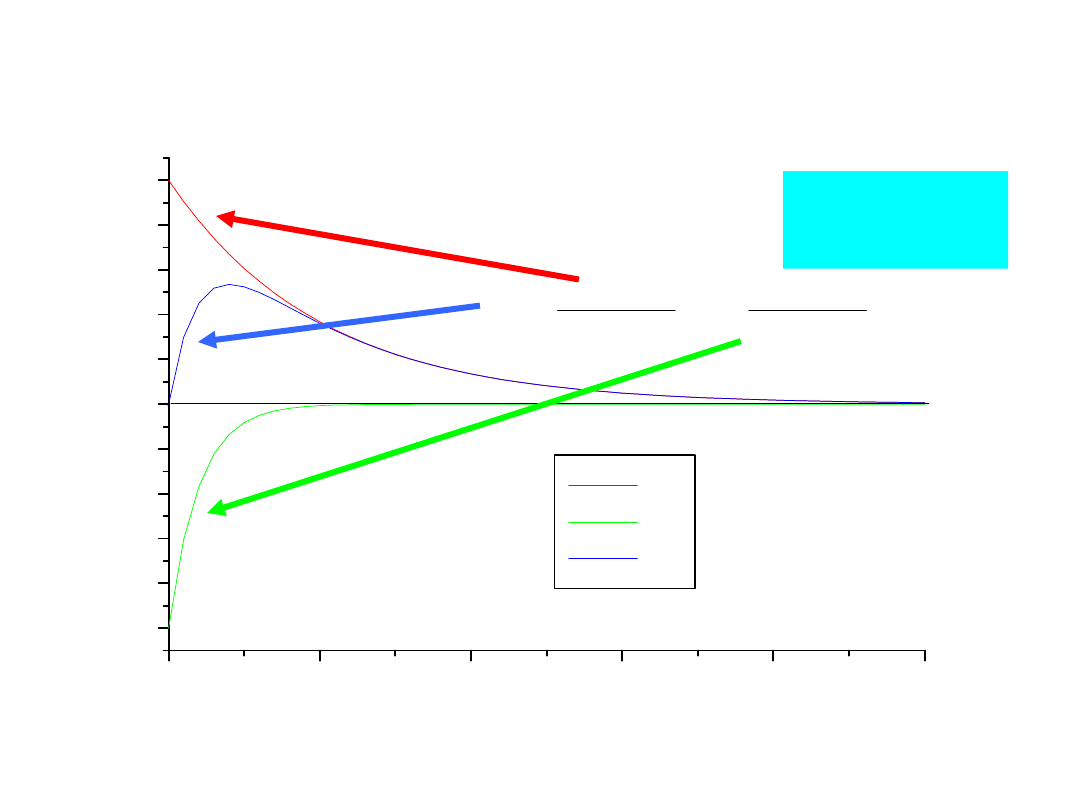
9
0
1
2
3
4
5
-10
-8
-6
-4
-2
0
2
4
6
8
10
i2a
i2b
i2
P
rz
e
bi
eg
i
p
rą
dó
w
Czas - t
Stany nieustalone - w obwodzie
rezonansowym
Przypadek
2):
t
s
t
s
e
s
s
L
E
e
s
s
L
E
t
i
2
1
2
1
2
1
10
Pełne rozwiązanie równania różniczkowego
drugiego rzędu powinno zawierać dwie stałe. W
tym celu stosujemy metodę uzmienniania stałej.
Stany nieustalone - w obwodzie
rezonansowym
• Przypadek aperiodyczny - krytyczny:
2
=
0
2
,
czyli Q = 1/2,
otrzymamy jeden pierwiastek rzeczywisty
dwukrotny
t
t
s
Ae
e
A
A
t
i
12
2
1
t
e
t
A
t
i
0
2
2
0
2
2
t
i
dt
t
di
dt
t
i
d
0
2
2
0
2
2
t
t
t
e
t
A
dt
e
t
A
d
dt
e
t
A
d
11
Stany nieustalone - w obwodzie
rezonansowym
0
2
2
2
2
t
t
t
t
t
e
t
A
e
t
A
e
dt
t
dA
e
t
A
e
dt
t
dA
dt
d
0
2
2
2
2
2
2
2
t
t
t
t
t
t
t
e
t
A
e
t
A
e
dt
t
dA
e
t
A
e
dt
t
dA
e
dt
t
dA
e
dt
t
A
d
0
2
2
t
e
dt
t
A
d
0
2
2
dt
t
A
d
12
Stany nieustalone - w obwodzie
rezonansowym
0
2
2
dt
t
A
d
1
A
dt
t
dA
2
1
A
t
A
t
A
Pełne rozwiązanie równania różniczkowego
drugiego rzędu przyjmie postać:
t
t
e
A
te
A
t
i
2
1
0
0
i
0
2
A
t
te
A
t
i
1
13
Stany nieustalone - w obwodzie
rezonansowym
Aby znaleźć wartość stałej A
1
,
należy rozwiązać równanie
dla chwili czasu t = 0
+
.
E
dt
t
i
C
t
Ri
dt
t
di
L
1
L
E
t
dt
t
di
0
t
te
A
t
i
1
dt
d
t
e
A
dt
t
di
t
1
1
1
0
A
t
dt
t
di
L
E
A
1
t
te
L
E
t
i
14
Stany nieustalone - w obwodzie
rezonansowym
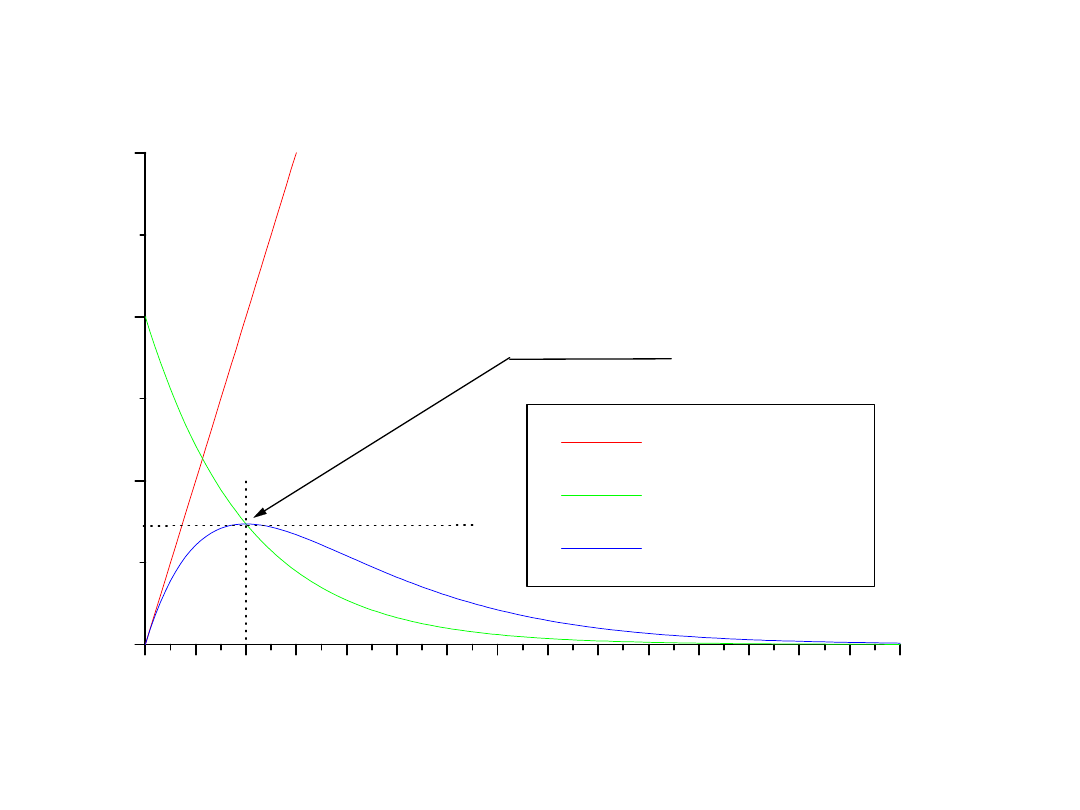
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5
0,0
0,5
1,0
1,5
t = 1 /
(E/L)t
e
-
t
i(t) = (E/L)te
-
t
P
rz
eb
ie
g
p
rą
du
Czas - t
15
Stany nieustalone - w obwodzie
rezonansowym
• Przypadek oscylacyjny -
2
<
0
2
, czyli Q
> 1/2,
otrzymamy dwa pierwiastki zespolone
sprzężone.
t
s
t
s
e
A
e
A
t
i
2
1
2
1
0
0
i
1
2
A
A
t
s
t
s
e
A
e
A
t
i
2
1
1
1
2
2
0
1
j
s
2
2
0
2
j
s
16
Oznaczając pulsację drgań
własnych obwodu
rezonansowego
można napisać:
Stany nieustalone - w obwodzie
rezonansowym
2
2
0
r
t
j
t
j
r
r
e
A
e
A
t
i
1
1
t
j
t
j
t
r
r
e
e
e
A
t
i
1
j
e
e
e
jA
t
i
t
j
t
j
t
r
r
2
2
1
t
sin
e
jA
t
i
r
t
1
2
17
Stany nieustalone - w obwodzie
rezonansowym
Aby znaleźć wartość stałej A
1
,
należy rozwiązać równanie
dla chwili czasu t = 0
+
.
E
dt
t
i
C
t
Ri
dt
t
di
L
1
L
E
t
dt
t
di
0
1
2
0
A
j
t
dt
t
di
r
t
cos
e
jA
t
sin
e
jA
dt
t
di
r
t
r
r
t
1
1
2
2
1
2
A
j
L
E
r
L
j
E
A
r
2
1
t
sin
e
jA
t
i
r
t
1
2
t
sin
e
L
E
t
i
r
t
r
18
Stany nieustalone - w obwodzie
rezonansowym
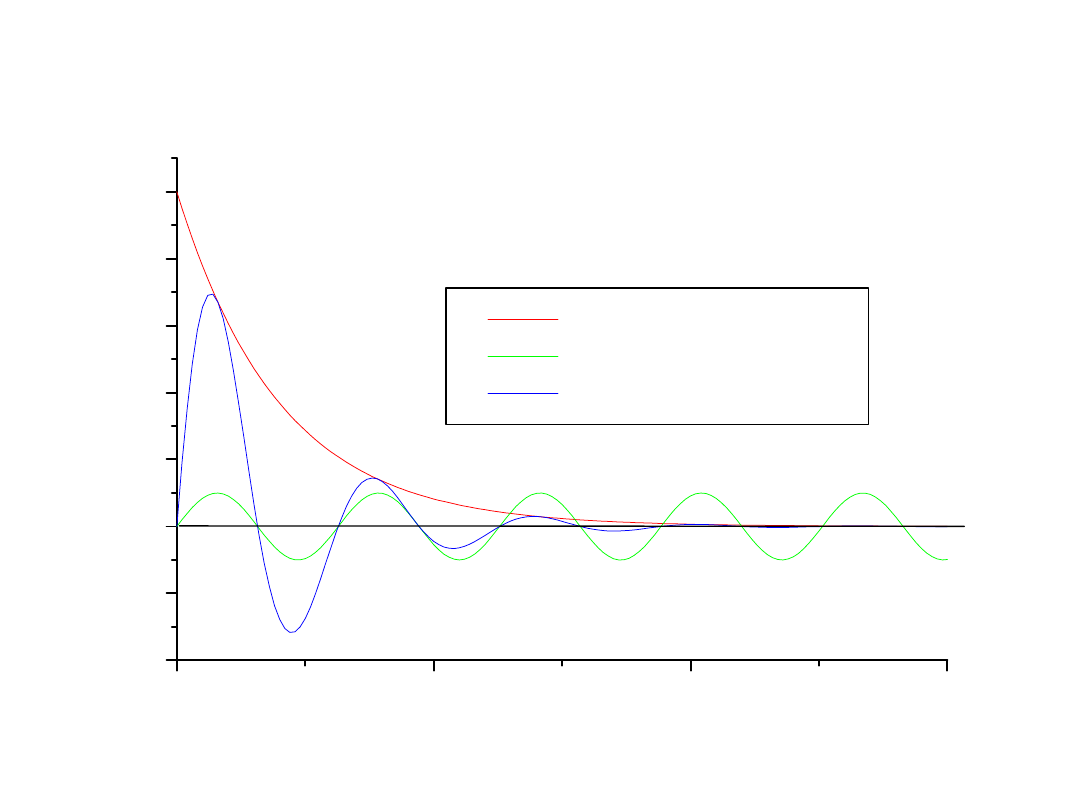
0,0
0,5
1,0
1,5
-4
-2
0
2
4
6
8
10
(E/L
r
)exp(-
t)
sin(
r
t)
(E/L
r
)exp(-
t)sin(
r
t)
P
rz
eb
ie
g
p
rą
d
u
Czas - t
19
Transformacja Laplace’a
dt
e
t
f
t
f
s
f
st
0
L
Funkcja f(s) jest funkcją zmiennej zespolonej
.
Przekształcenie Laplace’a jest jednostronne.
Funkcja f(s) nie
zależy od przebiegu funkcji f(t) dla czasów t < 0.
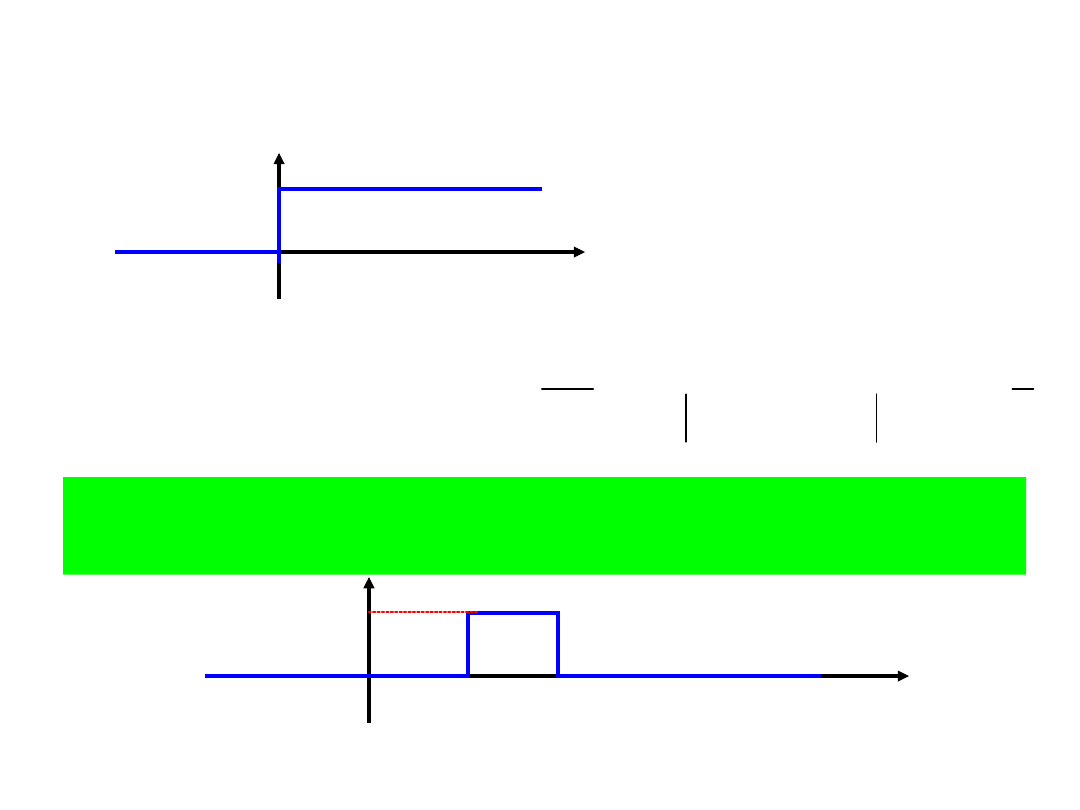
j
s
• Transformata funkcji
jednostkowej
0
0
0
1
1
t
dla
t
dla
t
t
1
t
0
1
20
t
1
t
Transformacja Laplace’a
s
t
e
t
e
s
dt
e
t
t
f
s
f
st
st
st
1
0
1
1
0
L
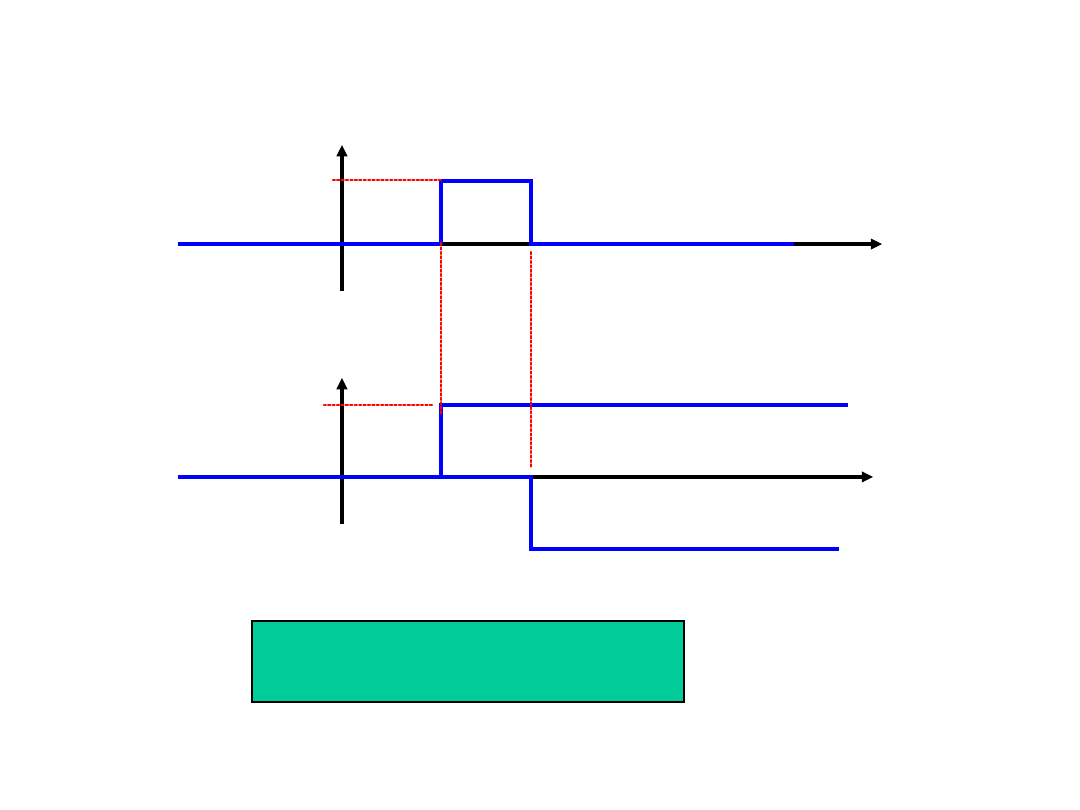
• Obliczyć transformatę funkcji przedstawionej na
rysunku
t
f
t
1
2
0
0
1
A
21
Transformacja Laplace’a
t
f
t
0
t
f
t
1
2
0
2
1
1
1
t
t
A
t
f
1
2
A
A
22
dt
e
t
A
dt
e
t
A
t
f
s
f
st
st
2
1
2
1
1
1
L
Transformacja Laplace’a
2
1
s
s
e
e
s
A
s
f
dy
e
y
Ae
dx
e
x
Ae
s
f
sy
s
sx
s
0
0
1
1
2
1
x
t
1
y
t
2

23
Własności transformacji Laplace’a
• Twierdzenie o przesunięciu (własność 1):
Jeżeli istnieje to dla 0
spełniona jest
relacja
s
f
t
f
L
s
f
e
t
t
f
s
1
L
• Twierdzenie o liniowości (własność 2):
Jeżeli istnieją transformaty: ,
to dla dowolnych współczynników a
1
, a
2
spełniona
jest relacja
s
f
t
f
1
1
L
s
f
t
f
2
2
L
s
f
a
s
f
a
t
f
a
t
f
a
2
2
1
1
2
2
1
1
L
24
Oznaczmy:
Własności transformacji Laplace’a
• Twierdzenie 3:
Transformata funkcji gdzie n = 1, 2,
3, .........
może być obliczona według następującego przepisu:
n
t
t
f
1
1
1
n
n
n
n
n
s
!
n
t
ds
d
t
L
L
Obliczmy transformatę funkcji
f(t) = t
dt
e
t
t
f
s
f
st
0
L
t
f
t
t
'
g
e
st
25
Własności transformacji Laplace’a
Istnieje następujący
związek:
dt
t
g
t
'
f
t
g
t
f
dt
t
'
g
t
f
0
0
0
1
dt
e
s
e
s
t
dt
e
t
t
f
s
f
st
st
st
L
t
'
g
e
st
Jeżel
i
st
st
e
s
e
t
g
1
0
2
0
2
0
0
1
1
1
s
e
s
dt
e
s
dt
e
t
t
f
s
f
st
st
st
L

26
Własności transformacji Laplace’a
• Twierdzenie 4:
Jeżeli istnieje transformata funkcji f(t) równa
to istnieje nastepujący związek:
n
n
n
n
ds
s
f
d
t
f
t
1
L
s
f
t
f
L
• Twierdzenie o przesunięciu w dziedzinie s
(własność 5):
Jeżeli istnieje transformata funkcji f(t) równa
to dla dowolnego istnieje nastepujący związek:
s
f
t
f
e
t
L
s
f
t
f
L

27
Własności transformacji Laplace’a
s
f
dt
e
t
f
dt
e
t
f
e
t
f
e
t
s
st
t
t
0
0
L
Przesunięcie w dziedzinie zmiennej s koresponduje
z mnożeniem funkcji f(t) przez czynnik
eksponencjalny w dziedzinie czasu t.
Przesunięcie w dziedzinie zmiennej t powoduje
pomnożenie funkcji f(s) przez odpowiedni czynnik
eksponencjalny.
s
f
t
f
e
t
L
s
f
e
t
t
f
s
1
L
28
• Twierdzenie 6:
Jeżeli istnieje transformata funkcji f(t) równa
to dla dowolnych współczynników a > 0
istnieje nastepujący związek:
Własności transformacji Laplace’a
s
f
t
f
L
a
s
f
a
at
f
1
L
0
0
dt
e
at
f
dt
e
at
f
at
f
at
a
s
st
L
Oznaczm
y:
x
at
a
dx
dt
a
s
f
a
dx
a
e
x
f
x
f
at
f
x
a
s
1
1
0
L
L
29
Własności transformacji Laplace’a
• Twierdzenie o pochodnej (własność 7):
Jeżeli istnieje transformata funkcji f(t) równa
oraz istnieje pochodna funkcji f(t) równa f’(t) dla t >
0, to istnieje
nastepujący związek:
gdzie -
0
t
f
s
sf
t
'
f
L
s
f
t
f
L
t
f
lim
t
f
t
0
0
t
sin
t
f
t
cos
t
'
f
1
1
1
1
2
1
2
2
s
j
s
j
s
j
j
e
e
t
sin
t
f
jt
jt
L
L
L
Własnoś
ć 5
0
0
0
sin
t
f

30
Niech
Własności transformacji Laplace’a
1
0
2
s
s
t
f
s
sf
t
'
f
L
t
cos
t
g
1
1
1
2
1
2
2
s
s
j
s
j
s
e
e
t
cos
t
g
jt
jt
L
L
L
• Twierdzenie o całce (własność 8):
Jeżeli istnieje transformata funkcji f(t) równa
to istnieje nastepujący związek:
dla całki
oznaczonej
s
s
f
dt
t
f
L
s
f
t
f
L
s
f
s
s
f
f
dt
t
f
t
0
0
0
L
31
Własności transformacji Laplace’a
t
sin
dt
t
f
t
g
t
cos
t
f
Niech
1
1
2
s
s
s
f
dt
t
f
L
1
2
s
s
t
cos
t
f
L
L
1
1
2
s
t
sin
t
g
L
L
Niech
t
cos
t
f
c
t
sin
t
f
s
2
2
s
t
sin
t
f
s
L
L
2
2
s
s
t
cos
t
f
c
L
L
32
Własności transformacji Laplace’a
Przykład 7. Obliczyć transformatę funkcji
1
1
2
2
t
t
t
f
1
1
9
1
6
1
2
t
t
t
t
f
Niech t’ = t
- 1
't
't
't
't
f
1
9
6
2
't
't
't
't
't
't
f
1
9
1
6
1
2
't
't
't
't
't
't
f
1
9
1
6
1
2
L
L
L
L
33
s
't
9
1
9
L
Własności transformacji Laplace’a
2
2
6
1
6
1
6
1
6
s
s
't
ds
d
't
't
L
L
3
2
2
2
2
2
1
1
1
s
s
ds
d
't
ds
d
't
't
L
L
3
2
2
6
9
s
s
s
't
f
L
2
2
6
9
s
s
s
e
t
f
s
L
Na mocy
własności 1, dla
= 1
34
Własności transformacji Laplace’a
Przykład 8. Obliczyć transformatę funkcji
T
t
te
t
f
t
1
T
t
Te
T
t
e
T
t
T
t
Te
T
t
Te
T
t
te
t
f
t
t
t
t
t
1
1
1
1
1
T
T
e
e
T
t
e
Te
T
t
e
T
t
e
t
f
T
t
T
T
t
T
1
1
dt
e
t
f
t
f
s
f
st
0
L
35
Własności transformacji Laplace’a
0
0
1
1
dt
e
T
t
e
Te
dt
e
T
t
e
T
t
e
s
f
st
T
t
T
st
T
t
T
0
0
1
1
dt
e
t
e
e
Te
dt
e
t
te
e
e
s
f
st
t
sT
T
st
t
sT
T
Własność 1) - o
przesunięciu
Oznaczm
y
0
0
1
1
dt
e
t
e
Te
dt
e
t
t
e
e
s
f
st
sT
T
st
sT
T
t
Zatem
s
Te
s
e
s
f
T
s
T
s
t
2
Własność
4)
36
s
Te
s
e
s
f
T
s
T
s
t
2
Własność
5)
Własności transformacji Laplace’a
s
T
s
e
s
Te
s
e
s
f
T
s
T
s
T
s
1
2
2
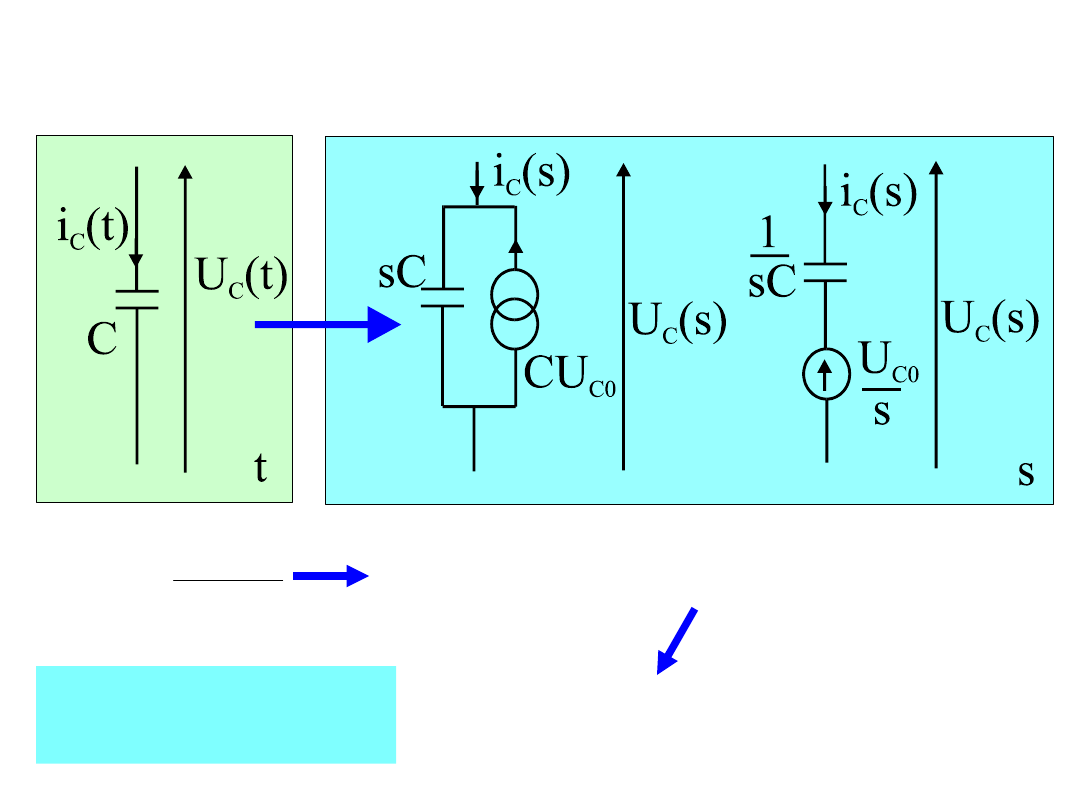
37
Opis operatorowy obwodu
dt
t
dU
C
t
i
C
C
dt
e
t
CU
t
i
s
i
st
'
C
C
C
0
L
Na mocy
własności 7
0
C
C
C
U
s
sU
C
s
i
Z(s
)
Y(s)
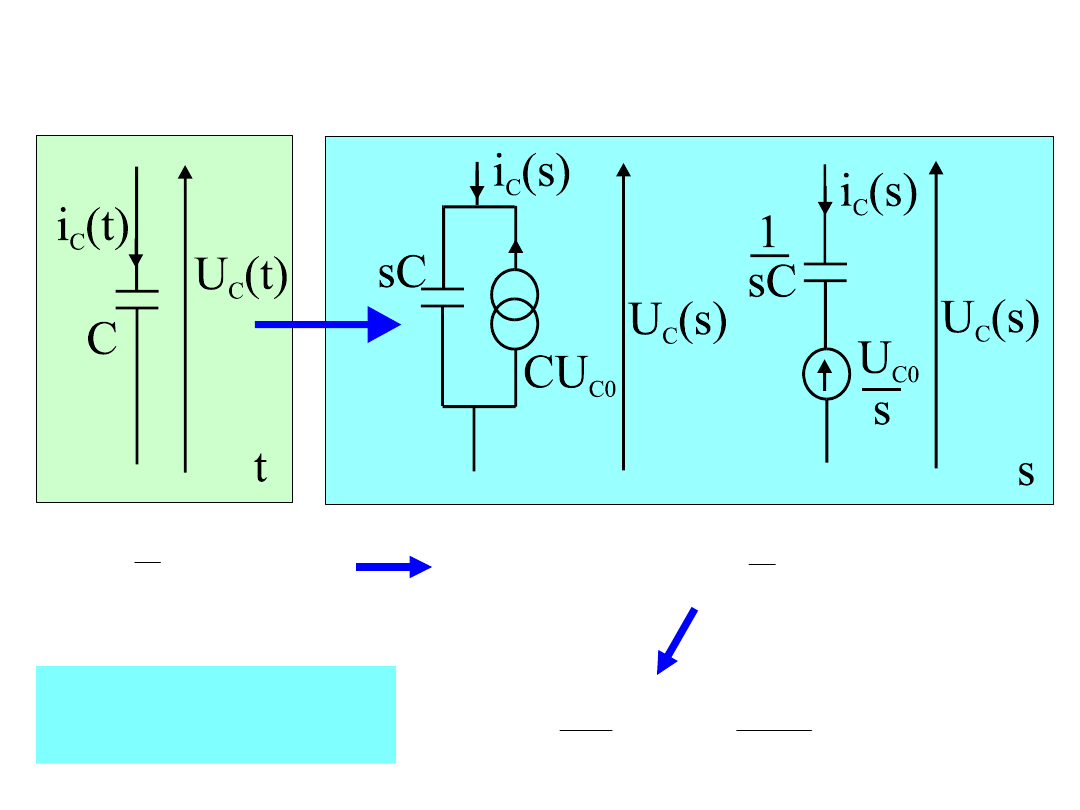
38
Opis operatorowy obwodu
t
C
C
C
U
dt
t
i
C
t
U
0
0
1
dt
e
U
dt
t
i
C
t
U
s
U
st
C
C
C
C
0
0
0
1
L
Na mocy
własności 8
s
U
s
i
sC
s
U
C
C
C
0
1
Z(s
)
Y(s)
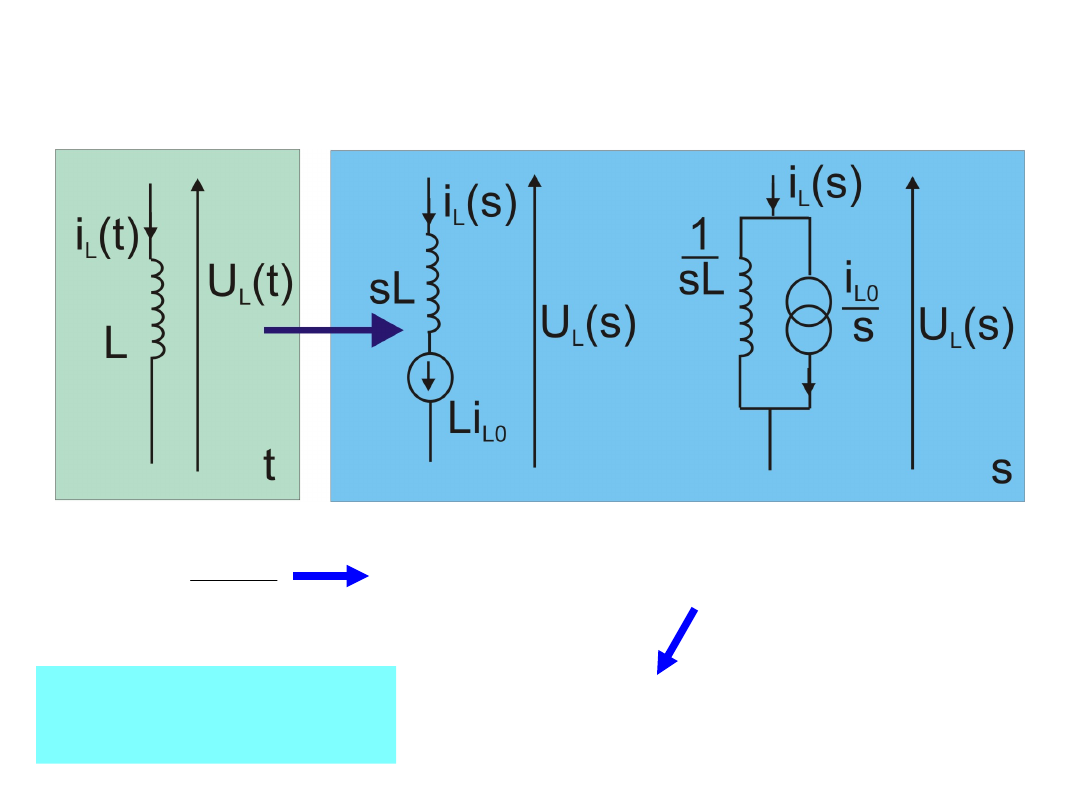
39
Opis operatorowy obwodu
dt
t
di
L
t
U
L
L
dt
e
t
Li
t
U
s
U
st
'
L
L
L
0
L
Na mocy
własności 7
0
L
L
L
i
s
si
L
s
U
Z(s
)
Y(s)
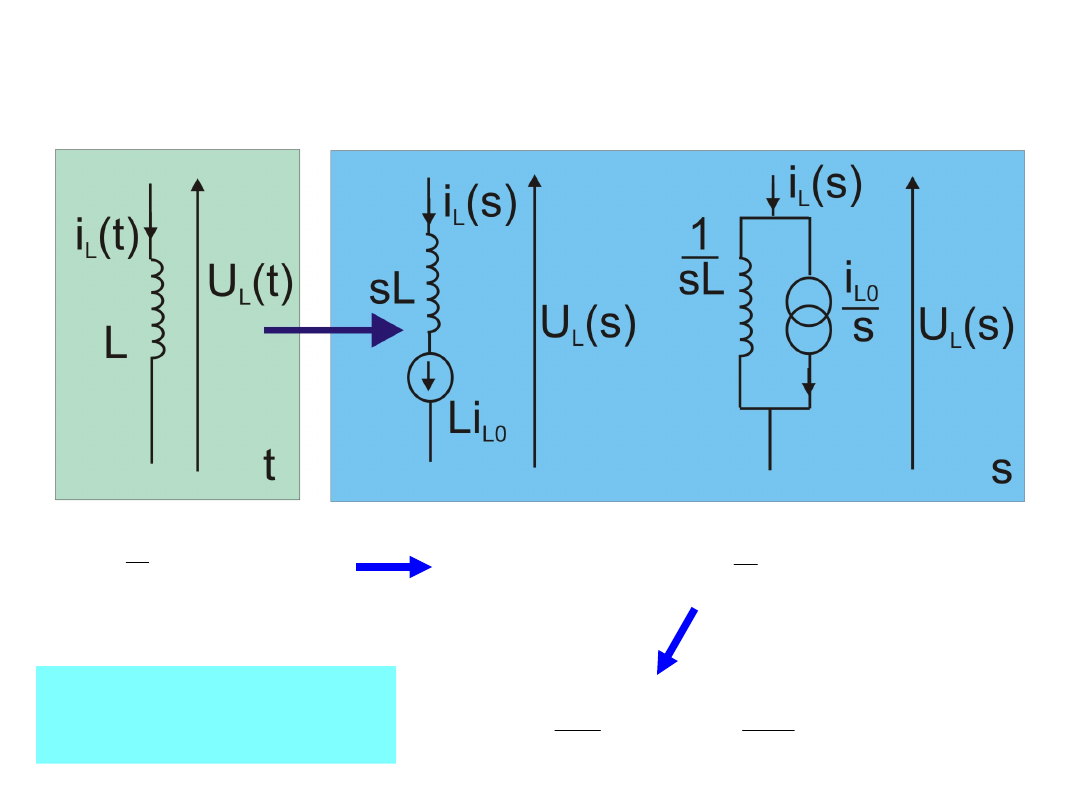
40
Opis operatorowy obwodu
0
0
1
L
t
L
L
i
dt
t
U
L
t
i
dt
e
i
dt
t
U
L
t
i
s
i
st
L
L
L
L
0
0
0
1
L
Na mocy
własności 8
s
i
s
U
sL
s
i
L
L
L
0
1
Z(s
)
Y(s)
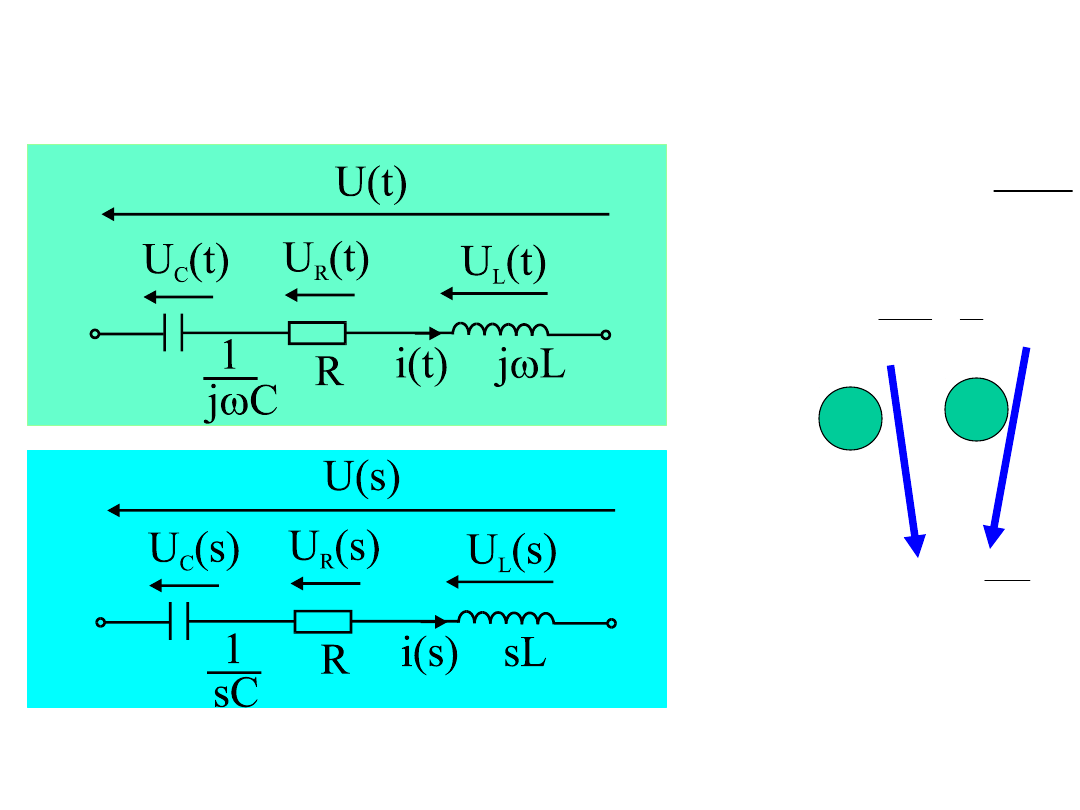
41
Opis operatorowy obwodu
C
j
L
j
R
j
Z
1
dt
t
i
C
dt
t
di
L
R
t
i
t
U
1
sC
sL
R
s
i
s
U
1
W7
W
8
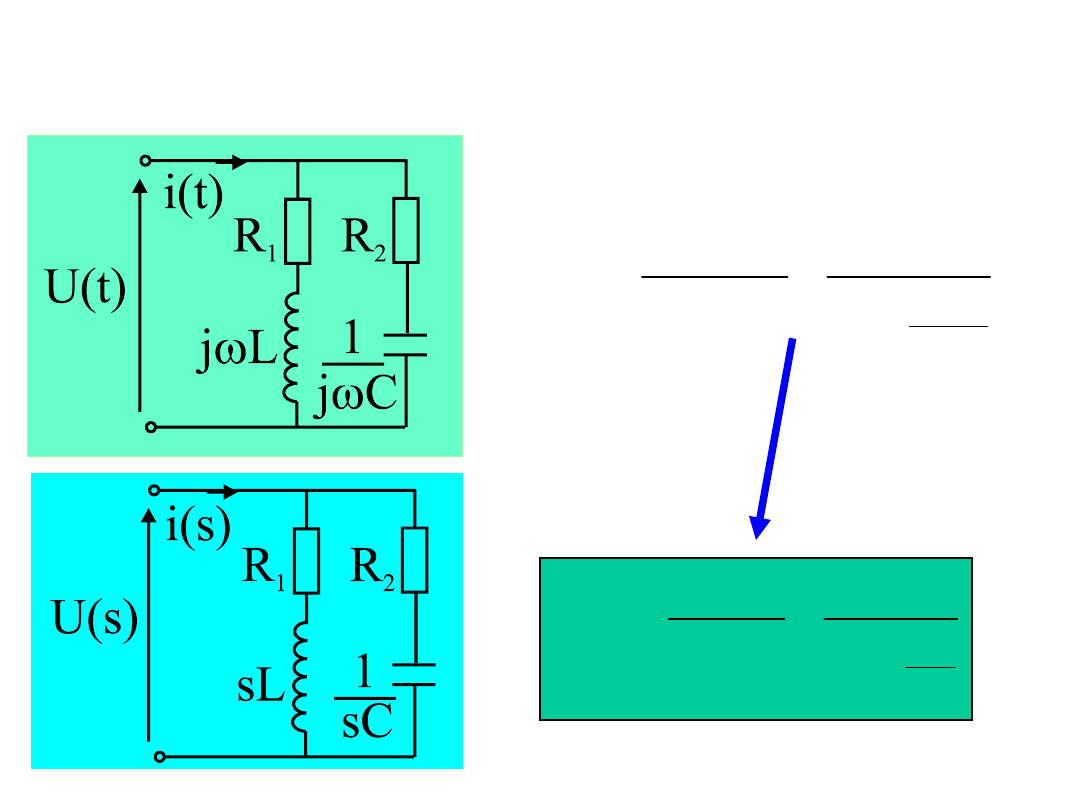
42
Opis operatorowy obwodu
C
j
R
L
j
R
j
Y
1
1
1
2
1
sC
R
sL
R
s
Y
1
1
1
2
1
43
Zastosowanie transformacji Laplace’a
do rozwiązywania obwodów w stanie
nieustalonym
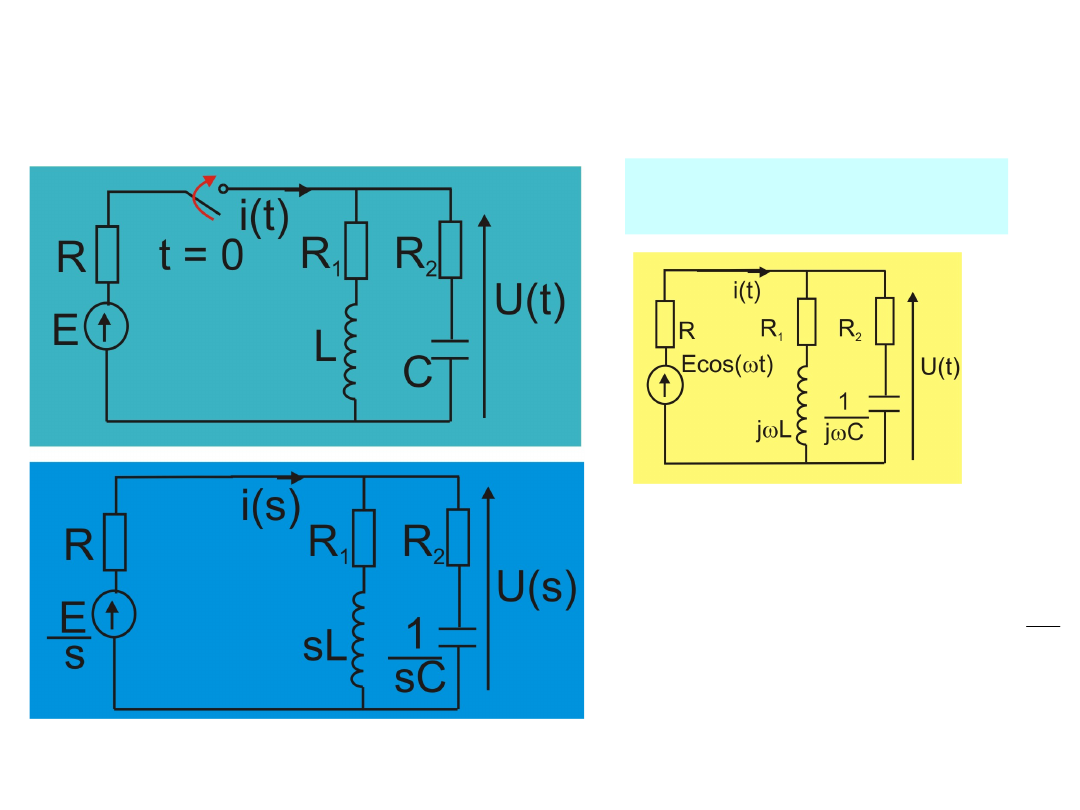
44
Zastosowanie transformacji Laplace’a
do rozwiązywania obwodów w stanie
nieustalonym
0
1
s
E
dt
e
E
t
E
st
L
Analogia dla przebiegów
harmonicznych
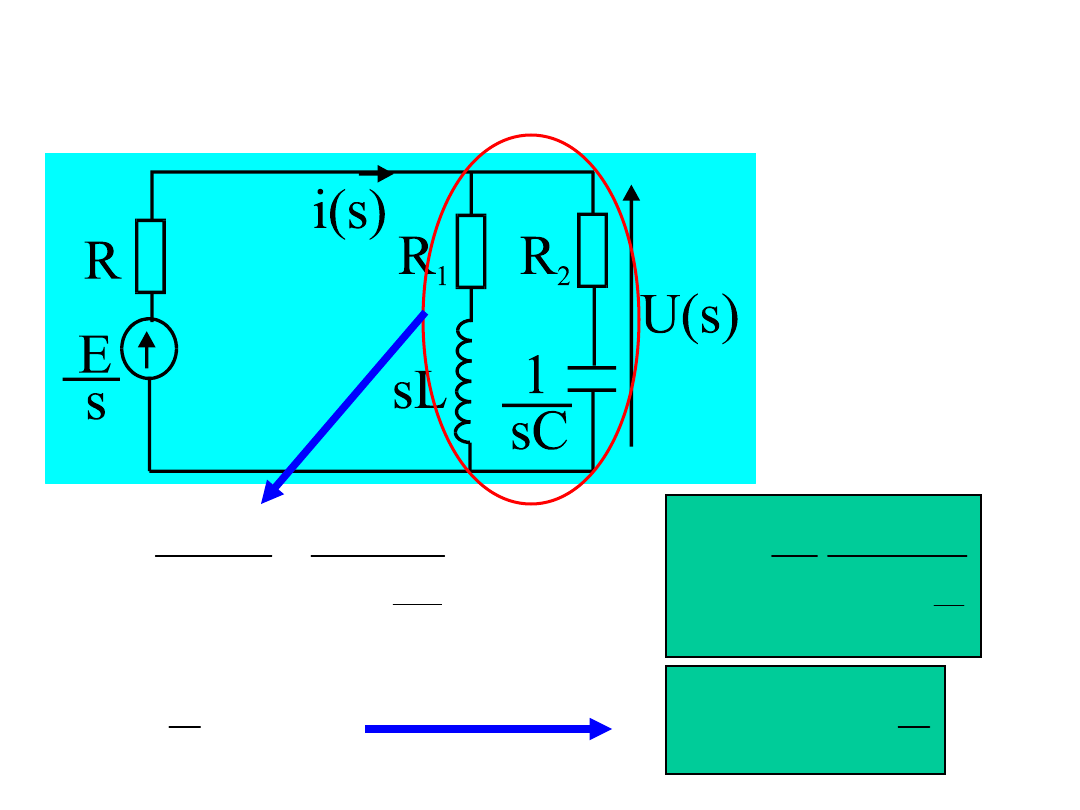
45
Zastosowanie transformacji Laplace’a
do rozwiązywania obwodów w stanie
nieustalonym
sC
R
sL
R
s
Y
1
1
1
2
1
R
s
Y
s
Y
Rs
E
s
i
1
s
U
s
E
R
s
i
s
E
R
s
i
s
U
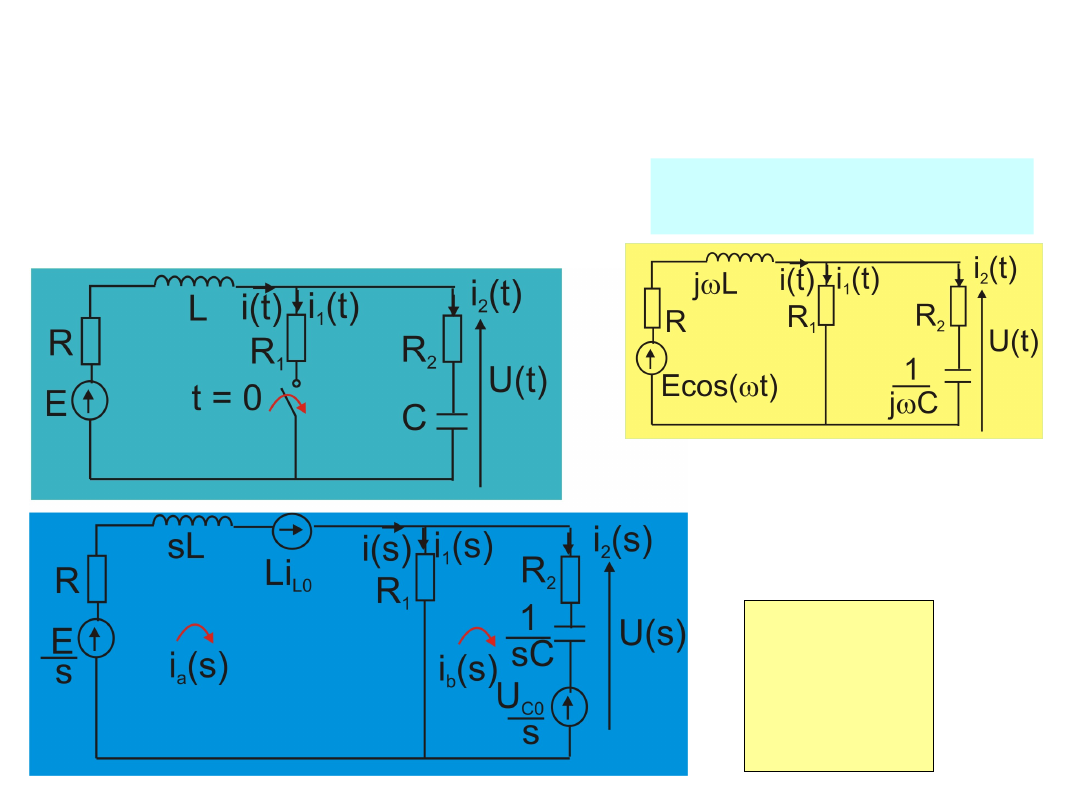
46
Zastosowanie transformacji Laplace’a
do rozwiązywania obwodów w stanie
nieustalonym
E
U
C
0
0
0
L
i
Analogia dla przebiegów
harmonicznych

47
Zastosowanie transformacji Laplace’a
do rozwiązywania obwodów w stanie
nieustalonym
t
C
U
dt
t
i
C
t
i
t
i
R
t
i
R
t
i
t
i
R
dt
t
di
L
t
Ri
E
0
0
2
2
1
2
2
2
1
1
0
s
U
s
s
i
C
s
i
s
i
R
s
i
R
s
i
s
i
R
s
Lsi
s
Ri
s
E
C
b
b
a
b
b
a
a
a
0
1
2
1
1
0

48
s
i
sC
R
R
s
i
R
s
U
s
i
R
s
i
R
sL
R
s
E
b
a
C
b
a
1
2
1
1
0
1
1
Zastosowanie transformacji Laplace’a
do rozwiązywania obwodów w stanie
nieustalonym
s
i
s
i
s
Z
s
Z
s
Z
s
Z
s
E
s
E
b
a
bb
ba
ab
aa
b
a
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
Wyszukiwarka
Podobne podstrony:
Tois 5 Stany nieustalone 1
08 Stany nieustalone w obwodach RLCid 7512 ppt
SPRAWKO STANY NIEUSTALONE, Elektrotechnika, Elektrotechnika
stany nieustalone w RC, Elektrotechnika-materiały do szkoły, Elektrotechnika
03 stany nieustalone
C7a Stany nieust RLC 2012
instrukcja - stany nieustalone, Elektrotechnika AGH, Semestr III zimowy 2013-2014, semestr III, seme
Stany nieustalone w obwodach RL, RC, RLC, ˙wiczenie II-13
stany nieustalone w obwodach z elemetami rc
8 Stany nieustalone w obwodach Nieznany
Stany nieustalone w obwodach elektrycznych o stałych skupionych 2
stany nieustalonerc, Politechnika Lubelska
Cw1 Stany nieustalone RL RC
stany nieustalone 2
wyklad 1 stany nieustalone II rzedu cz1
01 Stany Nieustaloneid 2945 Nieznany (2)
więcej podobnych podstron