METODY

KOMPUTEROWE W

MECHANICE

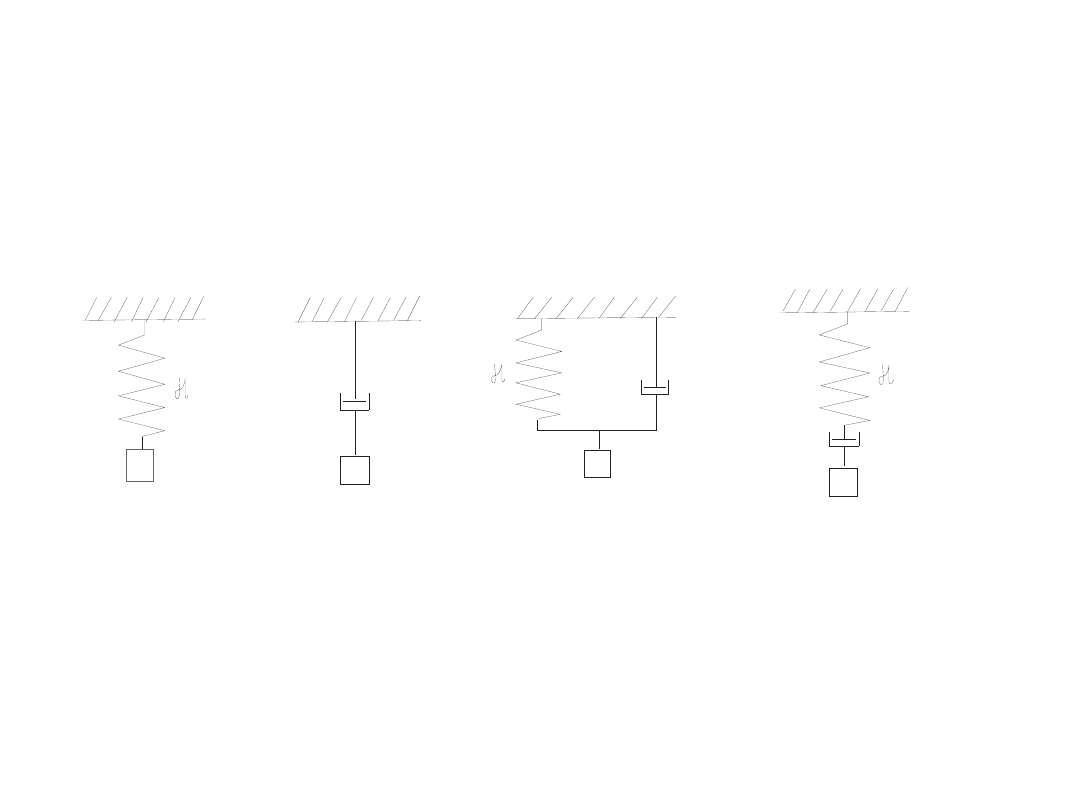
MODELE DRGAŃ

Hooke

Newton

Voigt-Kelvin

Maxwell

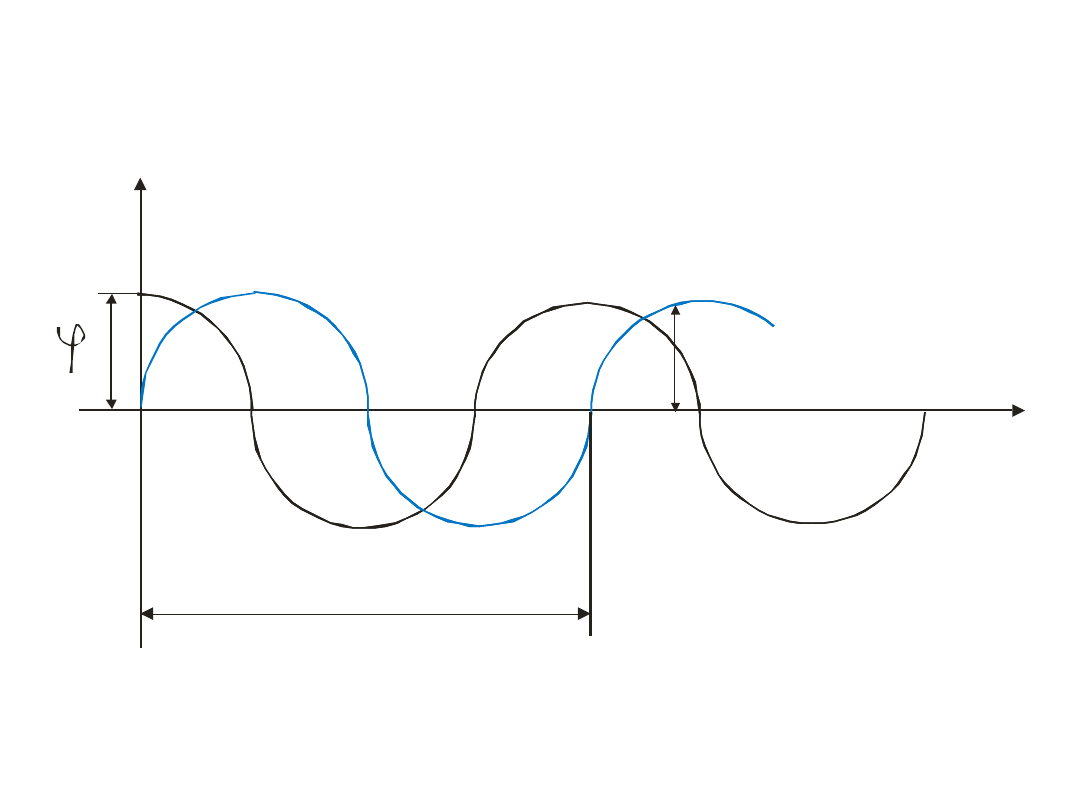
P

o

– przesunięcie fazowe,

a

p

- amplituda max,

f – częstotliwość drgań (ilość wahnięć na sekundę),
x(t) – wychylenie,
x – współrzędna, która określa chwilowe położenie ruchomego

punktu,

T – czas,
x˙ - prędkość
ω – częstotliwość drgań
χ - współczynnik proporcjonalności pomiędzy siłą a

wychyleniem





































s

rad

T

2Π

dt

dx

x

s

1

T

1

f

)

t

cos(

a

x(t)

t

cos

a

x(t)

T)

(t

x

(t)

x

T)

x(t

x(t)

0

p

p















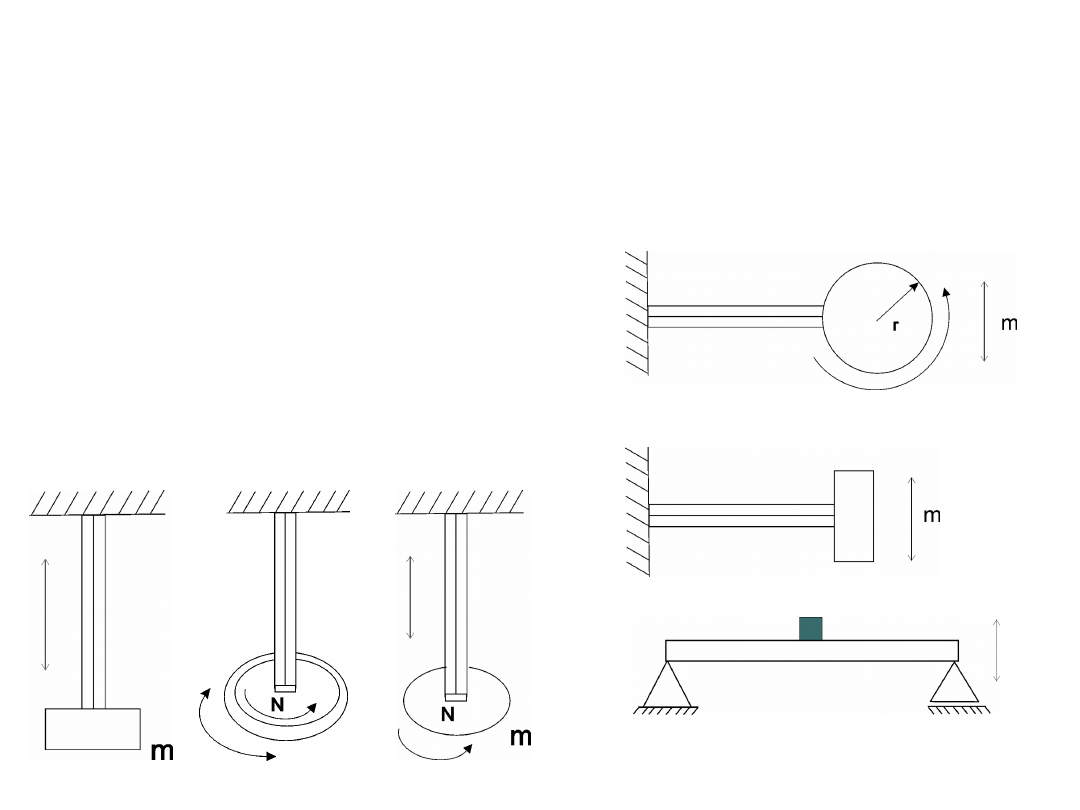
Klasyfikacja i podział drgań

1. Ze względu na ilość stopni swobody.
s – ilość niezależnych uogólnionych

współrzędnych, których określają
chwilowe położenie układu.

a) Drgania o 1 stopniu swobody
b) Drgania o 2 stopniach swobody.
c) Drgania o 3 stopniach swobody.
d) Drgania o 4 stopniach swobody.
e) Drgania o wielu stopniach swobody.

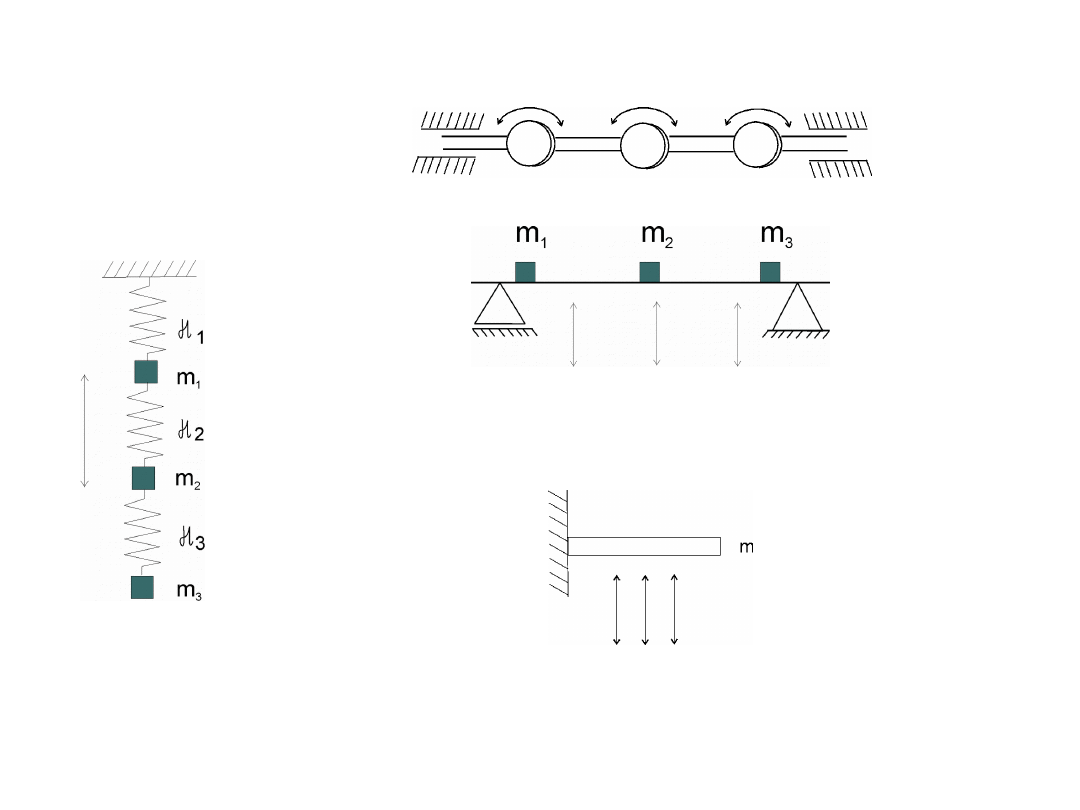
2. Ze względu na charakter odkształceń sprężystych drgającego układu.

a) drgania podłużne
b) drgania poprzeczne (gięte)
c) drgania skrętne
d) drgania złożone
e) drgania dowolne

Drgania podłużne

Drgania poprzeczne

Drgania skrętne złożone i dowolne

Drgania o nieskończonej liczbie stopni swobody

3. Ze względu na przyczyny wywołujące drgania.

a) Drgania własne (swobodne) – Są to drgania, które wywołane są jednorazowym wytrąceniem układu z położenia równowagi sprężystej.

b) Drgania wymuszone – Są to drgania, które wzbudzone są siłami zewnętrznymi, zmieniającymi się w czasie T.
P(t) = P0 sinγt
P0 – stała siła
γ- częstość drgań
t – czas
P(t) – drgania wymuszone

c) Drgania parametryczne – Są to drgania, które są wywołane okresową zmianą parametru układu np.: jego sztywność.
P(t)=P0sinγt

d) drgania samowzbudne – Są to drgania, które wzbudzane są przez siły spowodowane samym ruchem np.: siły tarcia.

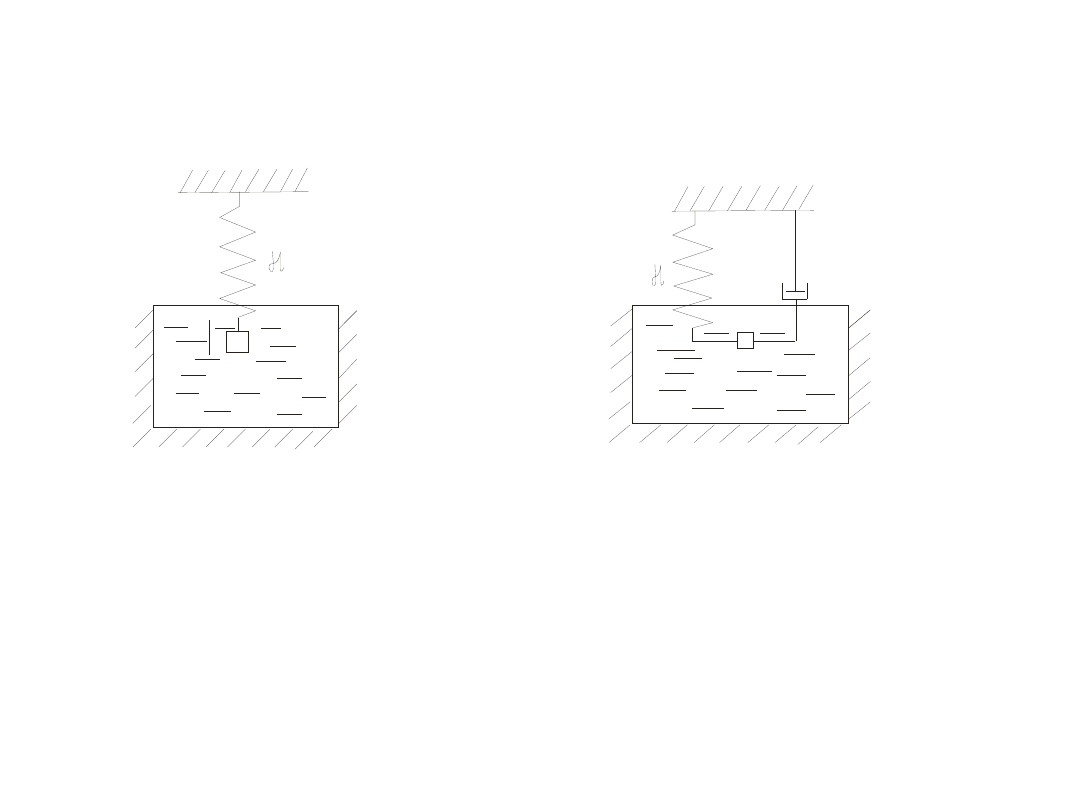
4. Ze względu na możliwości
występowania oporów.

Modele drgań tłumionych

5. Ze względu na opis matematyczny ruchu.

a) Drgania tłumione – to takie ,gdzie występuje opór.
Szeregowy model Maxell-a

b) Drgania nietłumione – bez oporów.
równoległy model Voight-Kelvin-a

Stałe sprężystości układu o jednym stopniu swobody.

s – uogólnione przemieszczenie

S – uogólniona siła

χ- stała sprężystości

Stałą sprężystości (χ) układu o jednym stopniu swobody nazywamy iloraz uogólnioną

siły do uogólnionego przemieszczenia w miejscu przyłożenia siły w kierunku jej
działania.

a) Ruch postępowy

b) Ruch obrotowy

zenie

przemieszc

siłi

m

N

x

P













kąą

moment

rad

Nm

M















Stałe sprężystości układu o wiązaniach połączonych.

a) Połączenie szeregowe.

st.sprężystości zastępcza

Połączenie szeregowe podstawowy warunek to inaczej warunek przemieszczeń. Pod
zadanym obciążeniem Q i całkowitym przemieszczeniem równe jest xxxxxxxxxxxxxxx

i

i

i

i

i

i

z

i

i

i

i

p

i

S

x

Q

S

S

S

Q

x

Q

x

x

x

x

x

x































































...

1

1

...

1

1

1

...

...

2

1

2

1

2

1

2

1

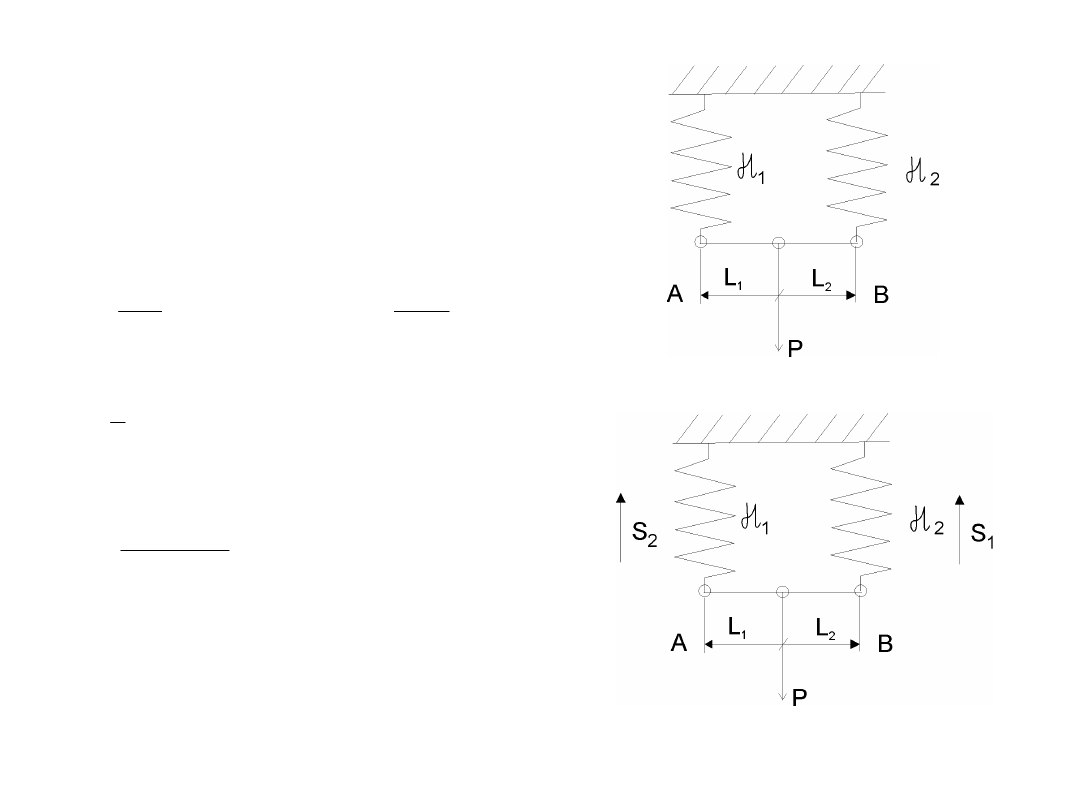
b) Połączenie równoległe.

Warunki równowagi
x - przemieszczenie

- wydłużenie sprężyn

- st.sprężystości zastępcza

2

2

2

1

2

1

2

i

z

2

1

1

2

1

2

2

1

df

2

1

2

1

2

2

2

1

1

1

1

2

1

2

2

1

2

1

χ

λ

χ

λ

χ

χ

χ

x

λ

x

λ

x

Pλ

S

,

Pλ

S

χ

P

x

1

λ

λ

l

l

l

λ

,

l

l

l

λ

0

)Pl

l

(l

S

0

P

*

S

S

λ

,

λ









































 
 

l

l

l

l

3

1

3

2

2

1





E

E

E





2

1

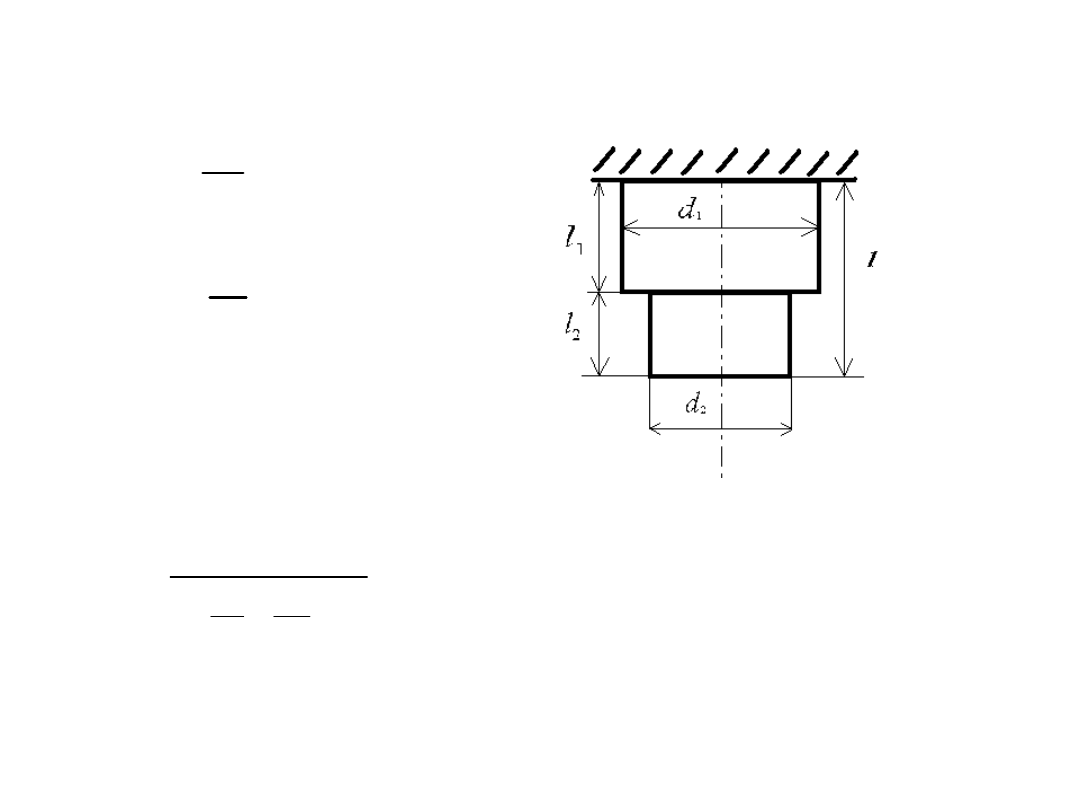
Zad. 1 Określić zastępczą siłę sprężystości H

2

.











2

1

1

2

1













i

i

2



i

s

S





x

Q





1

1

2

1

1

1

l

EF

l

Q

EF

Ql

l











2

2

1

2

2

2

l

EF

l

Q

EF

Ql

l






























2

2

1

1

l

Q

l

Q





















4

4

2

2

2

2

1

1

d

F

d

F















m

N

l

EF

1

1

1













m

N

l

EF

2

2

2



1

2

2

2

2

1

1

2

2

1

2

2

1

1

2

1

4

4

l

d

l

d

l

F

l

F

l

EF

l

EF















Czyli:

1

2

2

2

2

1

1

1

2

1

l

d

l

d

l

EF







rad

l

EF

d

d

l

l

l

EF

2

1

2

2

2

1

1

2

1

1

2

1

































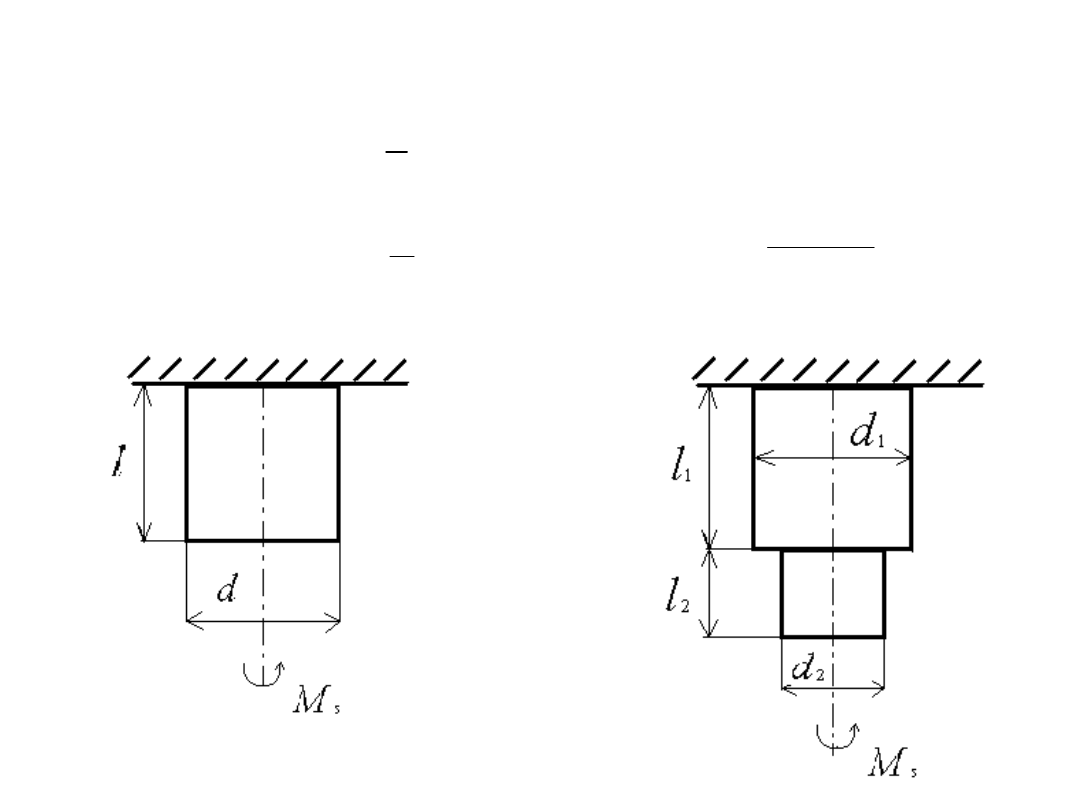
Zad. 2 Określić zastępczą stałą sprężystości gdy

mm

d

mm

d

10

14

2

1





l

l

l

l

3

2

3

1

2

1





E

E

E





2

1

)

1

(

2







E

G

I

II

0

GI

l

M

S

S





32

4

0

d

I

















rad

Nm

l

GI

M

0





1

01

1

l

GI





2

02

2

l

GI





32

4

1

01

d

I





32

4

2

02

d

I





4

2

1

2

1

2

1















d

d

l

l





2

1

1

2

1













Dla ruchu obrotowego:

red

l

GI

d

d

GI

l

l

l

2

01

4

2

1

1

2

1

01

2

1



































Analiza wyników

 

m

l

d

d

l

l

l

l

red

33

,

1

1

2

2

1

1

2

1

2



































 

m

l

d

d

l

l

l

l

red

94

,

1

1

4

2

1

1

2

1

2



































Sztywność układu

0

GI

Przy skręcaniu jest większa

niż przy rozciąganiu

0

0

EI

GI 

Zmiana średnicy pręta ma większy wpływ przy
skręcaniu na podatność w porównaniu z
rozciąganiem.

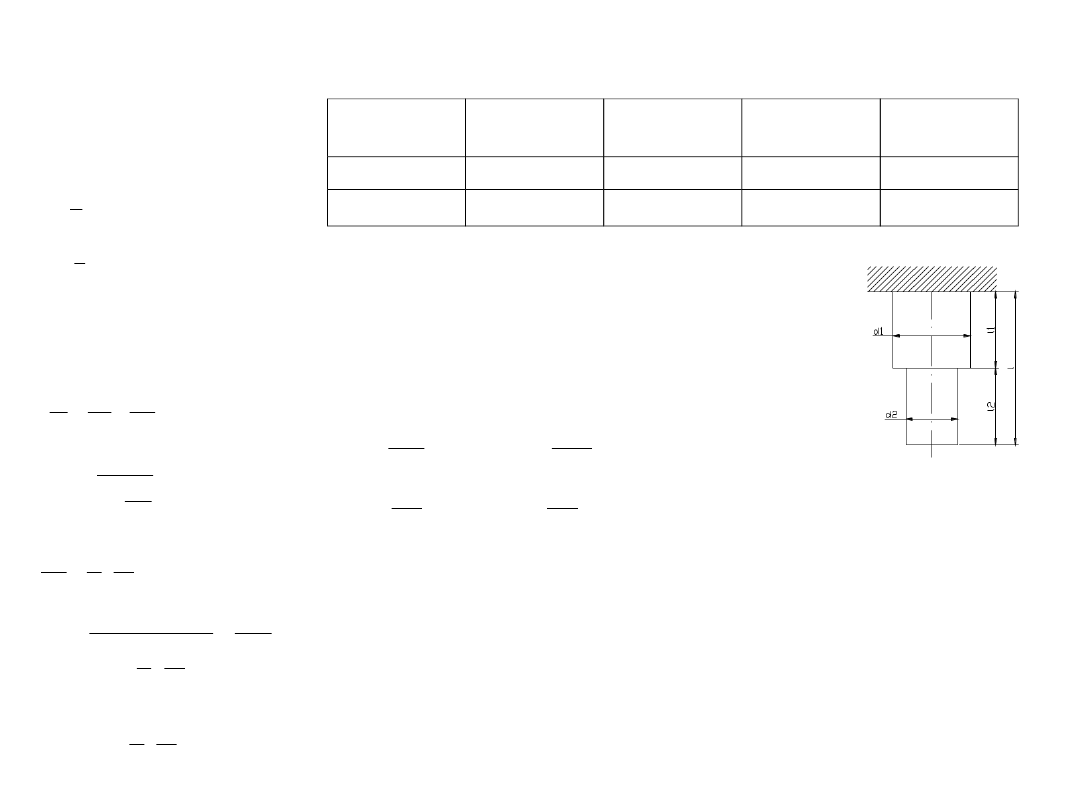
Zad.1
Dane:
d1= 14 mm
d2=10 mm

l

l

3

2

1



l

l

3

1

2



E

1

=E

2

=E

Tabela

d

1

d

1

d

2

d

2

Δl

14mm

20mm

10mm

26mm

Η

H

1

H

2

H

1

=H

2

H

2

=H

3

Określić zastępczą stałą sprężystości układu przedstawionego na rysunku

2

1

1

1

2

1









i

H

H

H

2

1

1

1

H

H

H

H

Z





1

1

1

1

l

F

E

H 

2

2

2

2

l

F

E

H 

4

2

1

1

d

F





4

2

2

2

d

F





2

2

1

1

2

2

1















d

d

l

l

H

H

zred

Z

l

F

E

d

d

l

l

l

F

E

H

1

1

2

2

1

1

2

1

1

1

1

































































2

2

1

1

2

1

1

d

d

l

l

l

l

zred

Obl:

1

1

1

1

l

F

E

H 

2

2

2

2

l

F

E

H 

4

2

1

1

d

F 



4

2

2

2

d

F





2

86

,

153

4

2

14

14

,

3

1

mm

mm

F







2

5

,

78

4

2

10

14

,

3

2

mm

mm

F







4

5

1

10

01

,

2

16

86

,

153

10

1

,

2















H

4

5

1

10

06

,

2

8

5

,

78

10

1

,

2















H

4

5

10

01

,

1

68

,

31

86

,

153

10

1

,

2















Z

H

68

,

31

10

14

16

8

1

16

2



































zred

l

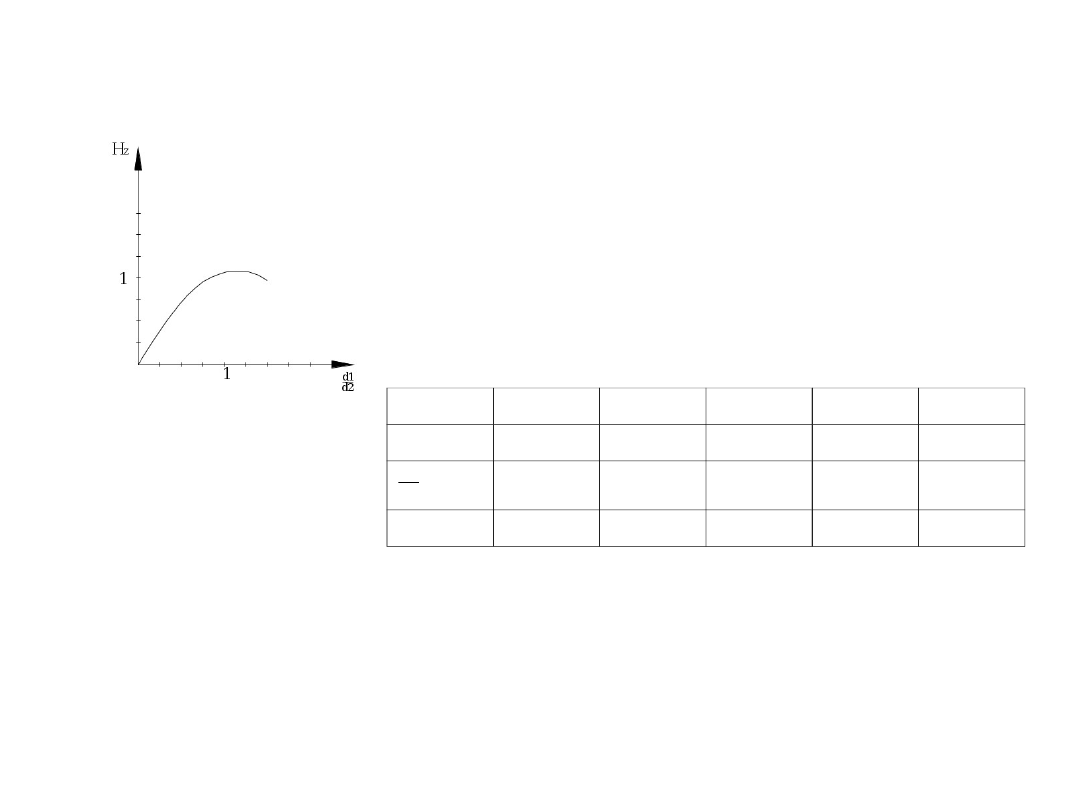
I przypadek

E

1

=E

2

=E

Zmienne d

1

, d

2

2

1

d

d

d

1

14

18

20

24

30

d

2

10

12

16

18

12

1,4

1,5

1,25

1,33

1,36

H

z

1,01

0,95

1,13

1,07

1,05

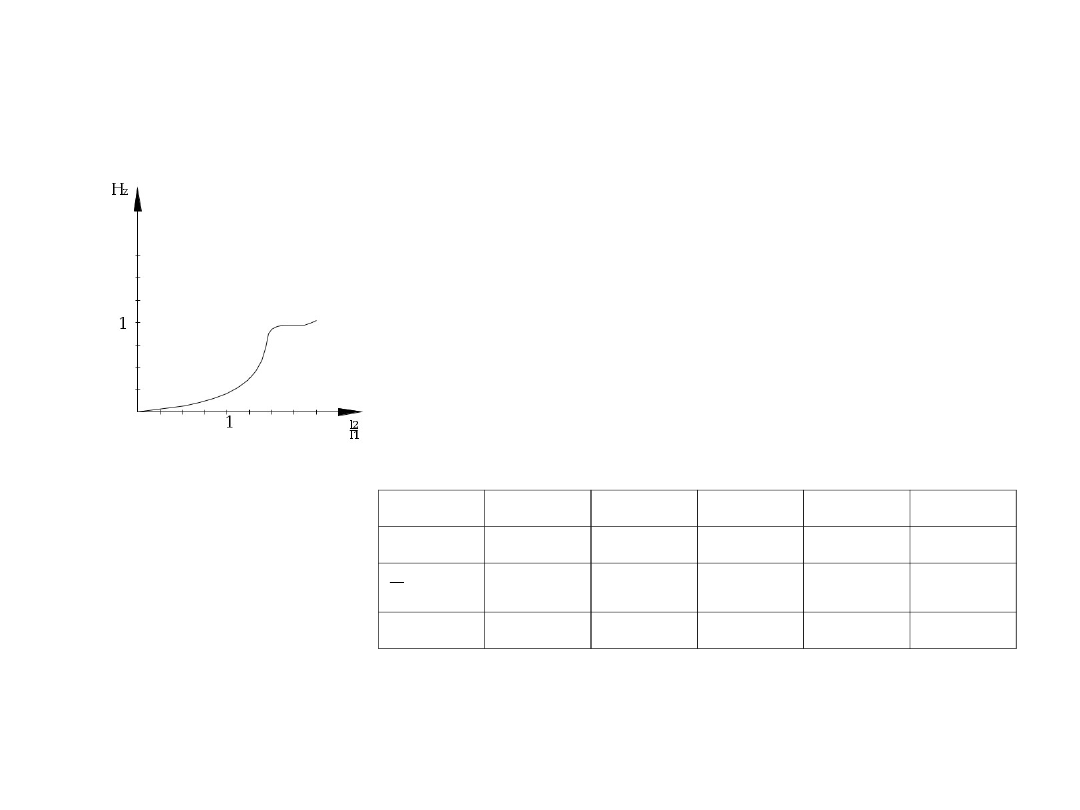
II przypadek

E

1

=E

2

=E

Zmienne l

1

, l

2

1

2

l

l

l

1

16

20

30

36

40

l

2

8

12

16

20

25

2

1,66

1,85

1,8

1,6

H

z

1,01

0,92

0,98

0,96

0,64

Stałe d

1

, d

2

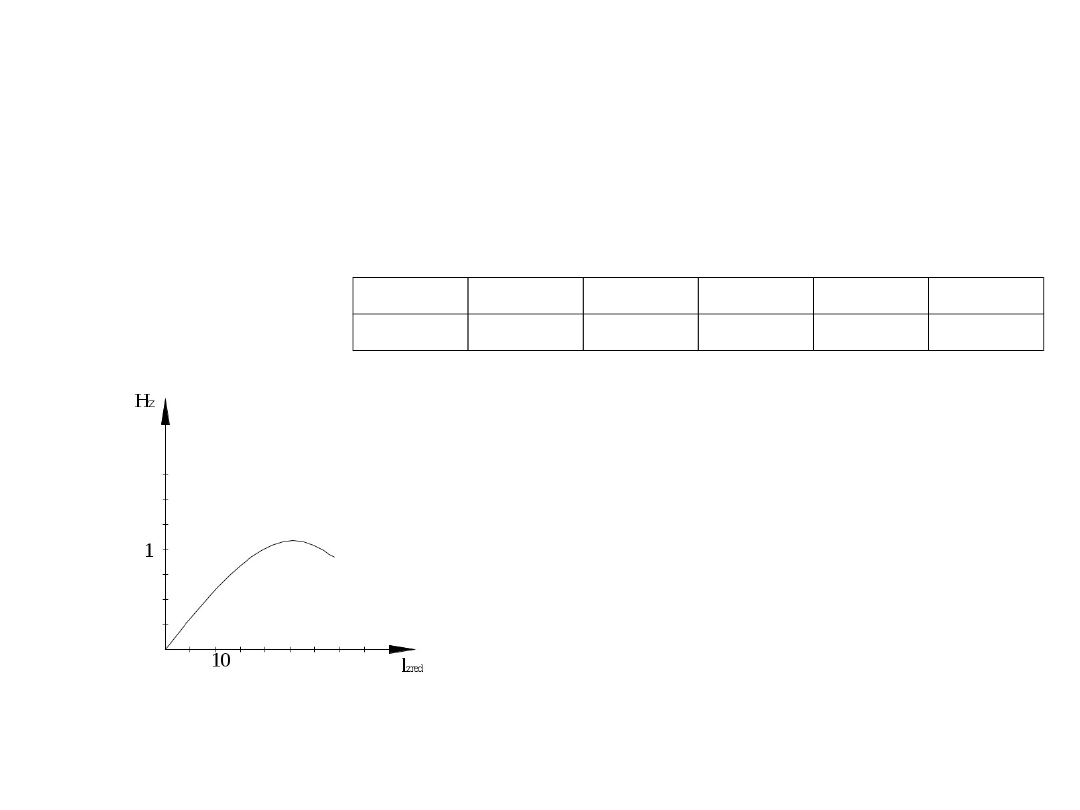
III przypadek

E

1

=E

2

=E

H

z

1,01

0,92

0,98

0,96

0,64

l

zred

31,68

34,81

32,72

33,42

35,6