Zadania

ćwiczenia 2

1

Należność od niewypłacalnego dłużnika

przedsiębiorstwa wynosi 100.000 zł. Wstępna analiza

wykazała, że firma może liczyć na odzyskanie jedynie

części należności w kwocie 50.000 zł. ale dopiero po

zakończeniu procesu upadłościowego, który potrwa

około dwóch lat. Przedsiębiorstwo korzysta z

długoterminowego kredytu bankowego, od którego

odsetki wynoszą 16%, ale naliczane są co kwartał.

Czy propozycja jednego z dłużników niewypłacalnej

firmy odkupienia należności za 38.000 zł. w gotówce

jest korzystna dla przedsiębiorstwa?

Odp. TAK, bo PV możliwej do odzyskania

należności = 37 160 zł
 

2

Firma LAS wydała 4 mln zł na wykarczowanie
działki i zasadzenie na niej młodych
świerków. Drzewa wyrosną za 6 lat i
wówczas firma spodziewa się uzyskać ze
sprzedaży choinek7 mln zł. Jaka jest
oczekiwana stopa dochodu z tego
przedsięwzięcia?

Odp. r = 9,77%

3

Kierownictwo przedsiębiorstwa planuje w

przyszłości kupić urządzenia produkcyjne. W

związku z tym zamierza zgromadzić w ciągu

dziesięciu lat kapitał w wysokości 200.000 zł.

Ile przedsiębiorstwo musi rocznie wpłacać na

rachunek bankowy, oprocentowany na 5% w

skali roku, aby kwotę tę zgromadzić, jeżeli:

1. płatności następują z dołu,
2. płatności następują z góry.

Odp. 1. 15 900,78 zł
2. 15 143,60 zł

4

Student ma zamiar wypłacać ze swojego
konta kwotę 1 200zł co miesiąc na pokrycie
wydatków przez następne 2 lata. Jeżeli
rachunek jest oprocentowany stopą w
wysokości 12%, to ile trzeba mieć dzisiaj,
aby pokryć te wydatki?

5

Firma ANEKS otrzymała następujące
propozycje zapłaty za wystawioną na
sprzedaż działkę budowlaną: I – zapłata
natychmiastowa w kwocie 120 tys. zł, II –
dwie płatności roczne z góry po 63 tys. zł, III
– sześć płatności półrocznych po 25 tys. zł z
dołu. Który z tych wariantów (wszyscy
oferenci są wiarygodni pod względem
wypłacalności) wybrać, jeśli oprocentowanie
obligacji skarbowych wynosi 6%?

6

Firma MAD musi zapłacić kredytodawcy na
koniec kolejnych lat: 10 000 zł, 8 000 zł, 6
000 zł, 4 000 zł. Jeśli firma chciałaby
zrestrukturyzować swój zadłużenie i spłacić
je w sześciu równych ratach na koniec
każdego z kolejnych lat, to ile wyniesie rata
przy uzgodnionym z kredytodawcą
oprocentowaniu w wysokości 10%? Jaką
część trzeciej raty stanowić będzie spłata
odsetek?

7

Firma BELLA rozpatruje opłacalność
udzielenia pożyczki w kwocie 150 tys. zł w
zamian za 6 rocznych wpłat z dołu w
wysokości 30 tys. zł. Czy warto udzielić tej
pożyczki, jeśli stopa dochodu z obligacji
długoterminowych wynosi 7%? Przy jakiej
stopie procentowej opłacalność pożyczki i
lokaty w obligacje byłaby taka sama?

 

8

Firma WRÓBEL rozpatruje opłacalność
zakupu certyfikatu depozytowego za 10 tys.
zł w zamian za 5 rocznych wypłat z dołu w
wysokości 22 tys. zł. Czy warto nabyć ten
certyfikat, jeśli stopa dochodu z
alternatywnych zastosowań kapitału wynosi
6%? Jakie wypłaty zrównoważyłyby koszty
zakupu certyfikatu?

9

Jeden z klientów hurtowni AS zalega z
płatnościami. Uzgodniono plan spłaty po 1
000 zł miesięcznie, z doliczeniem odsetek w
wysokości 2% miesięcznie od zaległej sumy.
Jeżeli dług obecnie wynosi 22 000 zł, to ile
dokładnie czasu potrzeba na całkowitą
spłatę zobowiązania?

10

 

Spółka BETTAN ponosi corocznie wydatki

z tytułu leasingu maszyn w wysokości 3
540 zł. W celu ich pokrycia zamierza
pozyskać nowego udziałowca. Jeżeli nowy
udział wyniesie 20 tys. zł i może być
ulokowany przy oprocentowaniu 12%, na
jak długo wystarczy tych środków?

11

Senior chce skorzystać z hipoteki odwróconej na swoje

mieszkanie i zaproponowano mu następujące formy

płatności: 

•dostaje od razu 300 000 zł,

•dostaje od razu 200 000 zł, a po dwóch latach dostaje
140 000 zł,

•będzie dostawał co roku przez 5 lat z góry 75 000 zł

(pierwsza płatność od razu),

•będzie dostawał 19 000 zł co roku z góry do końca

życia.
Która forma płatności jest najkorzystniejsza dla

seniora, jeśli roczna stopa procentowa wynosi 6%.
 

12

Co jest bardziej opłacalne: ulokowanie w
banku 15 000 zł na 8% czy zakup za taką
samą kwotę papierów wartościowych, który
przyniesie po 120 zł w końcu każdego z
następnych 3 lat i 15 120 zł w końcu
czwartego roku?

Zadania – wycena papierów

wartościowych

1.

Obligacje A i B mają 8% kupony
odsetkowe, wartość nominalną 100zł.,
roczne płatności odsetek. Obligacja A
będzie wykupiona za 2 lata, zaś
obligacja B ma 15 lat do wykupu.
•Jak zmienią się ceny obu obligacji, jeżeli
stopy procentowe wzrosną do 10%?
•Jak zmienią się ceny obu obligacji, jeżeli
stopy procentowe spadną do 6%?

2.

Jakich wpływów z emisji 50 000

obligacji 5-letnich o wartości
nominalnej 100 zł, stopie odsetkowej
6% może oczekiwać spółka DINO,
jeśli obecnie rentowność
alternatywnych inwestycji kształtuje
się na poziomie 5%, a koszty emisji
wyniosą 3%?

3.

Jakich wpływów z emisji 100 000

obligacji 5-letnich zerokuponowych o
wartości nominalnej 100 zł, jeśli
obecnie rentowność alternatywnych
inwestycji kształtuje się na poziomie
5%, a koszty emisji wyniosą 3%?

4.

Czy za obligację o wartości nominalnej
100 zł., terminie wykupu za 3 lat,
stopie odsetkowej 6% i półrocznych
płatnościach odsetek warto zapłacić 95
zł, jeśli rentowność alternatywnych
inwestycji wynosi 8%?

5.

Przedsiębiorstwo BIS wyemitowało 6-

cio procentowe obligacje, które za 5
lat zostaną wykupione za 100 zł.
Obecnie obligacje te oferowane są po
96,26 zł. Jaka jest dochodowość tej
inwestycji, w tym dochodowość
bieżąca i dochodowość z tytułu
przyrostu kapitału?

Analiza fundamentalna

- analiza makrootoczenia,
- analiza sektorowa,
- analiza sytuacyjna spółki (ocena spółki

na tle całej gałęzi),

- analiza finansowa spółki (wykorzystująca

wskaźniki płynności, rentowności,
zadłużenia, sprawności działania oraz
wskaźniki rynku kapitałowego).

- wycena akcji.

Wskaźniki rynku kapitałowego

7.

Spółka wypłaciła dywidendę w
wysokości 50 PLN na 1 akcję. Oczekuje
się, że poziom dywidendy w kolejnych
latach pozostanie bez zmian. Jeśli
oczekiwana stopa zwrotu dla akcji tej
spółki wynosi 16%, jaka będzie wartość
akcji?

8.

Spółka wypłaca dywidendę w
wysokości 5 PLN rocznie na akcję. Ile
warta jest akcja tej spółki przy
założeniu, że po 4 latach zostanie
sprzedana za 800 PLN, a wymagana
stopa zwrotu wynosi 8%?

9.

Posiadaczowi 1 akcji firma X wypłaci za
rok 50 zł dywidendy, za dwa lata 75 zł,
a za trzy 85 zł. Przewiduje się, że 1
akcja za trzy lata osiągnie cenę 500 zł.
Pożądana stopa zwrotu wynosi 20 %.
Jaka jest obecna wartość tej akcji?

10.

Czy inwestor powinien nabyć akcje
zwykłe firmy X, jeśli cena rynkowa akcji
wynosi 100 zł, a inwestor planuje ich
sprzedaż po 3 latach. Przewidywana
wartość dywidendy w 3 latach
posiadania akcji kolejno wynosi 8,10,
12 zł, a oczekiwana po 3 latach cena
akcji 130 zł. Rynkowa stopa dochodu
kształtuje się na poziomie 15 %.

11.

Wymagana stopa zwrotu wynosi 8%. Firma
wypłaca dywidendę w wysokości 70 zł. Oblicz
ceny akcji, przy założeniach:
•modelu stałej dywidendy
•modelu stałego wzrostu dywidendy (wzrost o
6% rocznie)
•modelu dwóch faz (wzrost o 6% przez 2 lata,
a następnie o 3%)
•modelu trzech faz (wzrost o 6% przez 2 lata,
przez kolejne 2 lata o 3%, a następnie o 2%).

12.

Spółka nie planuje wypłat dywidend w

ciągu najbliższych czterech lat, w piątym
roku zakłada się dywidendę w wysokości
2,5 zł, w późniejszym okresie firma
zamierza utrzymać stałe tempo wzrostu
dywidendy na poziomie 5% rocznie. Jaką
maksymalną cenę warto zapłacić za 1
akcję tej spółki, jeśli wymagana stopa
dochodu z takiej inwestycji wynosi 22%?

13.

Spółka DREEMIM zamierza pozyskać na
realizację zadań inwestycyjnych kwotę 2
mln zł z emisji akcji. Jeśli zarząd deklaruje
wypłatę dywidendy w wysokości 2 zł na 1
akcję i jej wzrost w następnych latach
corocznie o 5%, a inwestorzy oczekują
stopy zwrotu na poziomie 19%, zaś koszty
emisji szacowane są na 3,5%, to ile akcji
trzeba wyemitować aby zgromadzić
niezbędne środki?

14.

Rozpatrujemy akcję zwykłą, z której dywidenda wynosi
obecnie20 zł. Koszt kapitału własnego wynosi 20 % .
1.Oszacować cenę tej akcji, korzystając z trzech
modeli :

- modelu stałej stopy wzrostu

dywidendy,

równej 10 %,

2. modelu dwóch faz, gdzie w pierwszym etapie

przez 10 lat stopa wzrostu dywidendy

wynosi 15 %, a następnie 10 %,

3. modelu trzech faz, gdzie w pierwszym etapie
przez 5 lat stopa wzrostu wynosi 15 %,
następnie przez 5 lat regularnie spada co
roku o jeden punkt procentowy, aby po 10
latach osiągnąć stałą stopę równą 10 %.

15.

Możesz kupić obligację, która przyniesie
po roku 1000 zł odsetek rocznie przez 3
lata, a po tym okresie możesz ją
wymienić na 20 akcji spółki X. Wiedząc,
że zostanie wyemitowanych 20 000 szt.
akcji, wskaźnik P/E wyniesie 4, a zysk
netto przedsiębiorstwa 5 000 000 zł,
oblicz za ile warto kupić taką obligację.
Przyjmij stopę zwrotu 10 %. 

Koszt kapitału

Ogólnie to relacja dochodu oczekiwanego

przez dawców kapitału z działalności
przedsiębiorstwa i wartości
zaangażowanego przez nich kapitału.

Z drugiej strony to cena, jaką powinna

firma zapłacić za prawo do dysponowania
każdą złotówką pozyskiwanego kapitału.

Koszt kapitału stanowi stopę zwrotu, którą

powinna generować firma ze swoich
inwestycji, aby utrzymywana była wartość
przedsiębiorstwa.

Koszt kapitału - podstawowe

pojęcia

32

Kapitał, który „kosztuje” przedsiębiorstwo to

kapitał zainwestowany, tj. zobowiązania od

których płacone są odsetki oraz kapitał

własny.

Kalkulacja kosztu kapitału polega na

oszacowaniu oddzielnie kosztów długu i

kosztu kapitału własnego, a następnie

wyliczenie średniego ważonego kosztu

kapitału (WACC - weighted awerage cost of

capital), w którym struktura kapitału(relacja

kapitału własnego i obcego) określa wagi

kapitału obcego i własnego.

Kalkulacja kosztu kapitału

33

34

35

Koszt kredytu

Historyczne:
 Rynkowe,
 Księgowe.
Docelowa struktura finansowa.
Wagi krańcowe.
Optymalna struktura kapitału.

Wagi w formule WACC

36

1.

Cena akcji spółki NETT wynosi 312,5

zł, ostatnia wypłacono dywidendę w
wysokości 13 zł na akcję i przewiduje
się wzrost dywidend w stałym tempie
1,5% rocznie. Jaki jest koszt kapitału
własnego tej spółki?

2.

Kapitał spółki TRASAT składa się z 1mln akcji
zwykłych (55%) i kredytu bankowego. Cena
akcji wynosi 120 zł, ostatnio wypłacono
dywidendę w wysokości 5 zł na akcję i
przewiduje się wzrost dywidend w stałym
tempie 4% rocznie. Oprocentowanie kredytu
bankowego kształtuje się na poziomie 10%.
Stopa podatku dochodowego wynosi 19%. Jaką
wartość ma kapitał całkowity spółki TRASAT?
Jaki jest średni ważony koszt kapitału tej
spółki ?

3.

Przedsiębiorstwo WEZYR ma wartość 1,5mln
zł. Jest ono finansowane z kapitału własnego i
kredytu. Spółka ostatnio wypłaciła dywidendę
w wysokości 3 zł/1 akcję i zarząd deklaruje jej
wzrost o 4% rocznie. Inwestorzy oczekują
17% stopy zwrotu z akcji. Oprocentowanie
kredytu wynosi 11%. Proszę zaproponować
taką strukturę kapitałową, aby średni ważony
koszt kapitału nie przekraczał 14%. Stopa
podatku dochodowego wynosi 19%.

4.

Firma NIP posiada wskaźnik dług /
kapitał własny równy 1,5. Średni ważony
koszt kapitału wynosi 11%, takie też jest
oprocentowanie długu. Stopa obciążenia
tej firmy podatkiem dochodowym to
20%. Ile wynosi koszt kapitału własnego
firmy NIP? Ile wynosiłby średni ważony
koszt kapitału, gdyby wskaźnik dług /
kapitał własny wynosił 1,0?

5.

Firma finansuje swoją działalność w 40% kapitałem
własnym oraz w 60% kapitałem obcym. Prognozuje
się, że zyski i dywidendy z akcji zwykłych tej spółki
będą rosły w tempie 10% rocznie. Aktualna cena
rynkowa akcji tej spółki wynosi 50 PLN, wartość
ostatnio wypłaconej dywidendy na jedną akcję
wyniosła 6 PLN. Oblicz średni ważony koszt kapitału
tej spółki, jeżeli wiadomo, że dług firmy stanowi
kredyt oprocentowany 10% w skali roku, a stopa
podatku dochodowego wynosi 19%.
Odpowiedź: WACC = 0,141

6.

Spółka AS dysponuje kapitałem w wysokości 800 tys. zł, na który
składają się:
a/ akcje uprzywilejowane o wartości rynkowej 40 tys. zł., o
koszcie 15%,
b/ akcje zwykłe o wartości rynkowej 500 tys. zł., o koszcie 20%,
c/ obligacje o wartości rynkowej 160 tys. zł., o oprocentowaniu
10%,
d/ kredyt bankowy w wysokości 100 tys. zł., o oprocentowaniu
12%.
Stopa podatku dochodowego wynosi 20%.
Obliczyć średni ważony koszt kapitału spółki AS. Jak zmieniłby
się ten koszt, gdyby spółka zaciągnęła dodatkowo kredyt
bankowy w kwocie 200 tys. zł., oprocentowany w/g stopy 11%?

• 

7.

•Kapitał akcyjny 750 000 zł -
•Kredyt długoterminowy 75 000 zł – 25%
•Kredyt krótkoterminowy 250000 zł - 22%
•Obligacje długoterminowe 100 000 zł - 23%
•Obligacje zamienne 5000 zł - 19%

Firma planuje wypłacić swoim akcjonariuszom
coroczną dywidendę na poziomie 0,50 zł, bieżąca
cena akcji to 3 zł , tempo wzrostu dywidendy to 5%.
•Oblicz koszt kapitału własnego oraz ogólny koszt
kapitału firmy z uwzględnieniem stopy podatku
procentowego 19%.

8.

Spółka planuje zrealizować projekt inwestycyjny, którego
nakład początkowy wynosi 200 000 zł:
Z akcji uprzywilejowanych, o wartości 30 000 zł,
dywidenda wynosi 10 zł a ich cena rynkowa 40 zł.
Udział kapitału własnego pochodzącego z zysków
zatrzymanych i akcji zwykłych stanowi 50% kapitału, ich
cena rynkowa to 30 zł, dywidenda wypłacona za 2009 rok
to 3 zł, natomiast za 2010 rok to 3,3 zł. Przewiduje się, że
tempo wzrostu dywidendy utrzyma się na dotychczasowym
poziomie.
Pozostały kapitał finansowany jest z kredytu, którego koszt
to 8% w skali roku przy comiesięcznej kapitalizacji odsetek.
Podatek to 19%.
Jaki jest średni ważony koszt kapitału?

Modele wyceny aktywów

kapitałowych

1.

Proszę ustalić i zinterpretować współczynnik
beta (ß) spółki MEGX, przyjmując, że:
- odchylenie standardowe stóp zwrotu z akcji
spółki MEGX wynosi 0,09,
- wariancja stóp zwrotu z rynku wynosi 0,0049,
- współczynnik korelacji pomiędzy stopą
zwrotu z rynku akcji i stopą zwrotu z akcji
spółki MEGX wynosi 0,77.
• 

2.

Załóżmy, ze stopa wolna od ryzyka r

f

= 5%.

Przypuśćmy, że oczekiwana stopa zwrotu z
rynku wynosi r

M

= 15%, a odchylenie

standardowe stopy zwrotu z rynku δ

M

= 20%.

Rozważmy papier wartościowy, który ma
kowariancję stopy zwrotu ze stopą rynkową
cov(r, r

M

) = 0,03.

Współczynnik β takiego papieru wynosi:

Oczekiwana stopa zwrotu z tego aktywu wynosi?

3.

Beta akcji „Y” wynosi 1,59, a jej oczekiwany
dochód jest równy 25%. Beta akcji „Z”
wynosi 0,44, a jej oczekiwany dochód jest
równy 12%. Czy akcje te są prawidłowo
wycenione, jeśli rentowność bonów
skarbowych kształtuje się na poziomie 6%,
a premia za ryzyko rynkowe wynosi 11,3%?
Proszę wykreślić linię papierów
wartościowych i wyniki analizy zaznaczyć
na wykresie. 

4.

Oprocentowanie bonów skarbowych wynosi
5,5%, a stopa zwrotu z przeciętnej akcji
10,5%. Jeżeli współczynnik β spółki
STORNO wynosi 1,4, oczekiwana
dywidenda 8 zł, stopa stałego wzrostu
dywidendy 5%, to czy cena na poziomie 75
zł jest ceną równowagi? Czy jest to akcja
przewartościowana czy
niedowartościowana? Proszę wyniki
obliczeń przedstawić na wykresie.

Inwestycje – ocena

względna

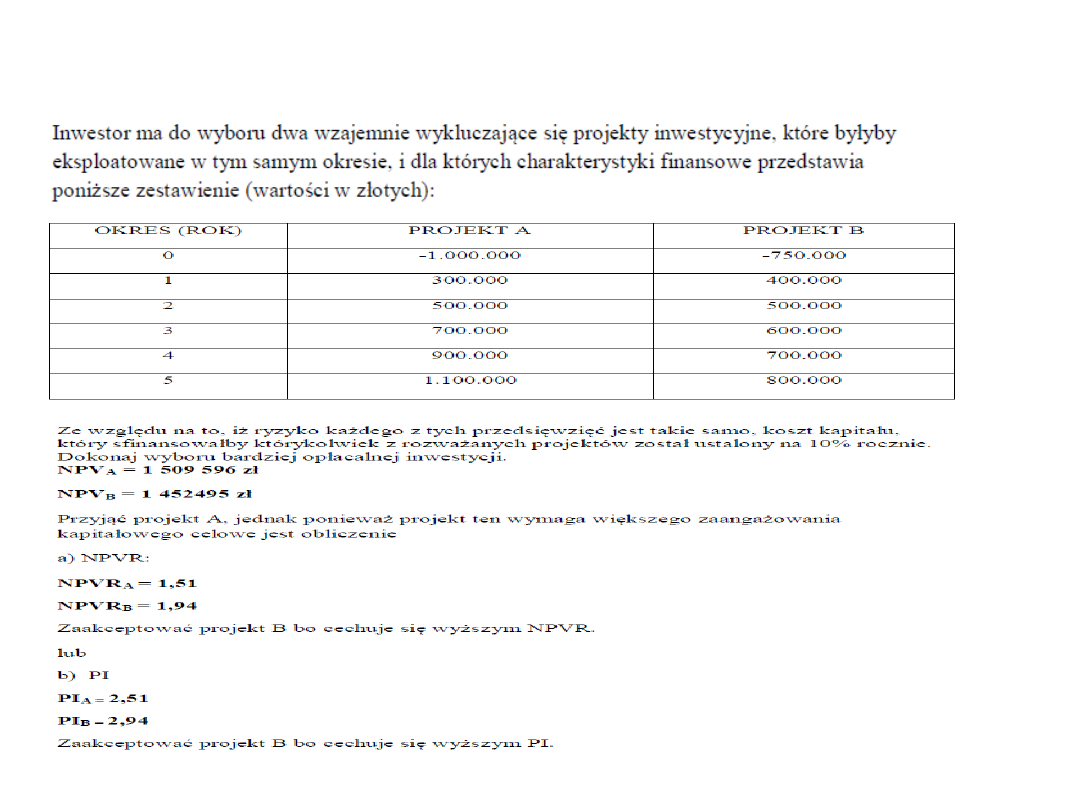
1.

Przedsiębiorca rozważa realizację dwóch niezależnych od siebie
inwestycji A i B.
Nakłady na realizację inwestycji A szacuje się na 100 000 zł, a na
inwestycję B przewiduje się 80 000 zł.
Oczekuje się, że roczne wpływy z realizacji inwestycji A wyniosą
35 000 zł przez kolejnych 5 lat, przy czym przedsiębiorca szacuje,
że dla tej inwestycji właściwa będzie stopa dyskontowa k =8%.
Oczekuje się, że roczne wpływy z realizacji inwestycji B wyniosą
22 000 zł przez kolejnych 8 lat, przy czym przedsiębiorca ocenia,
że dla tej inwestycji właściwa będzie stopa dyskontowa k =13%.
Stosując kryterium NPV wskaż, którą inwestycję powinien wybrać
do realizacji przedsiębiorca. 
NPV

A

= 39 744,5 zł NPVR

A

= 1,1356

NPV

B

= 27 573,6 zł NPVR

B

= 1,3787

Wybrać B

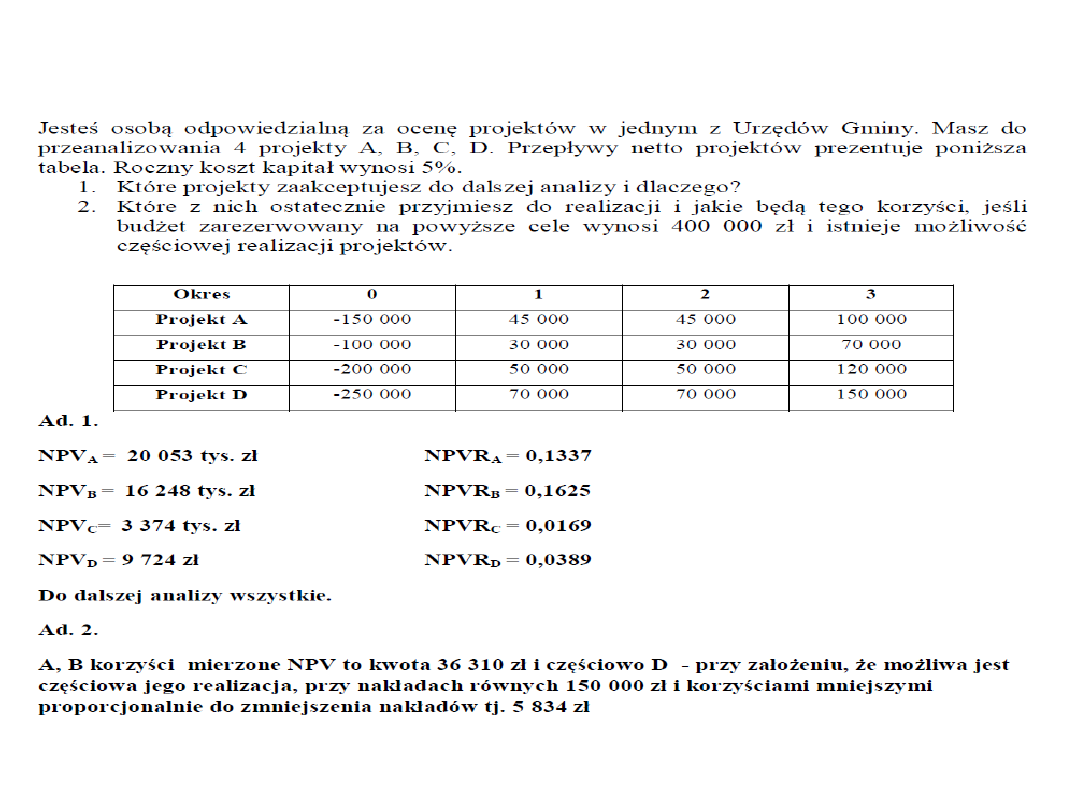
2.

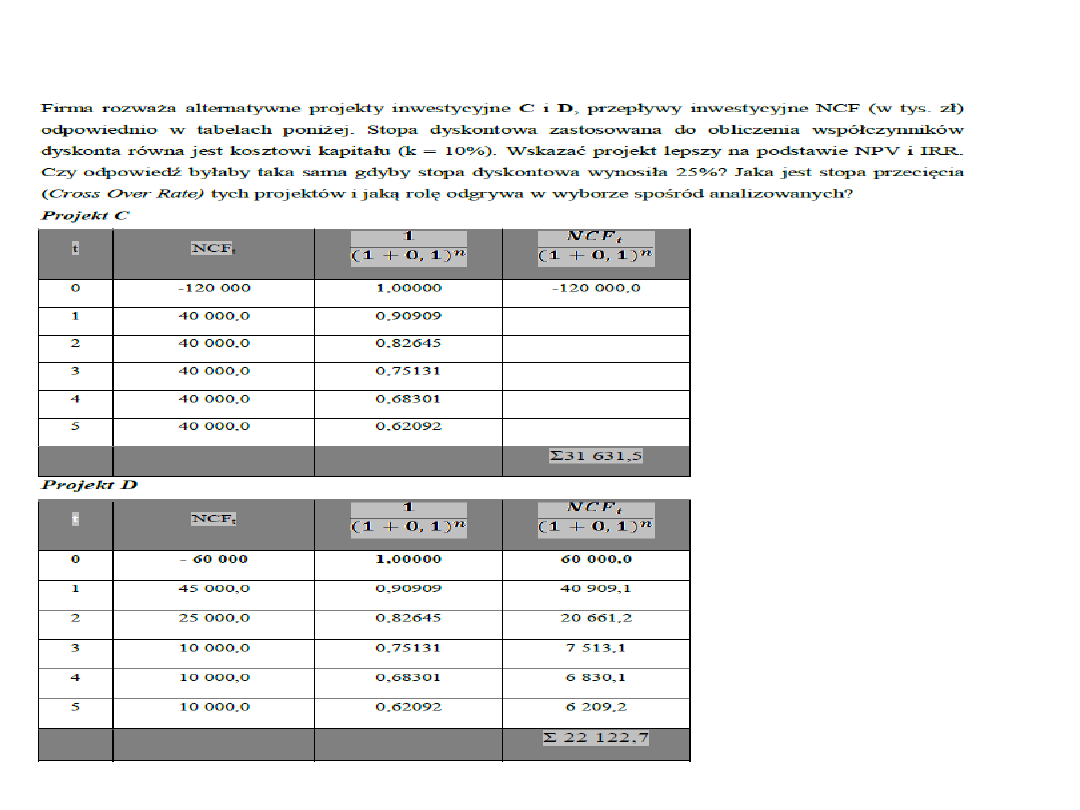
3.

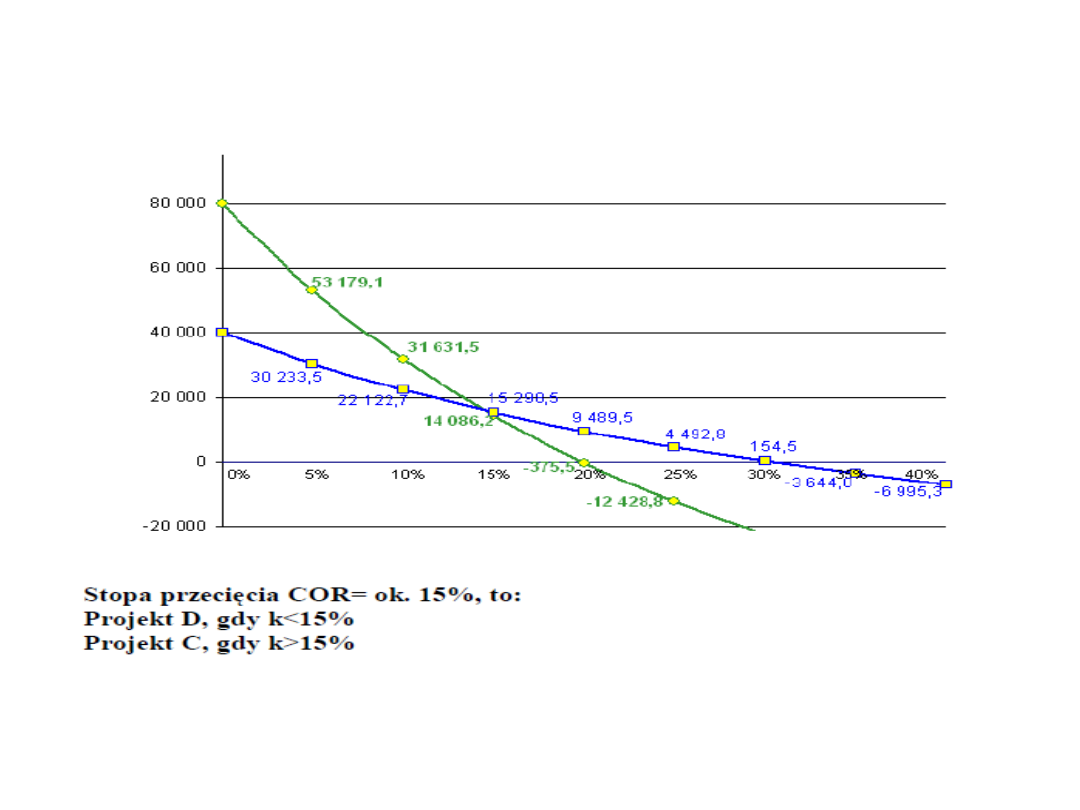
4. Stopa przecięcia

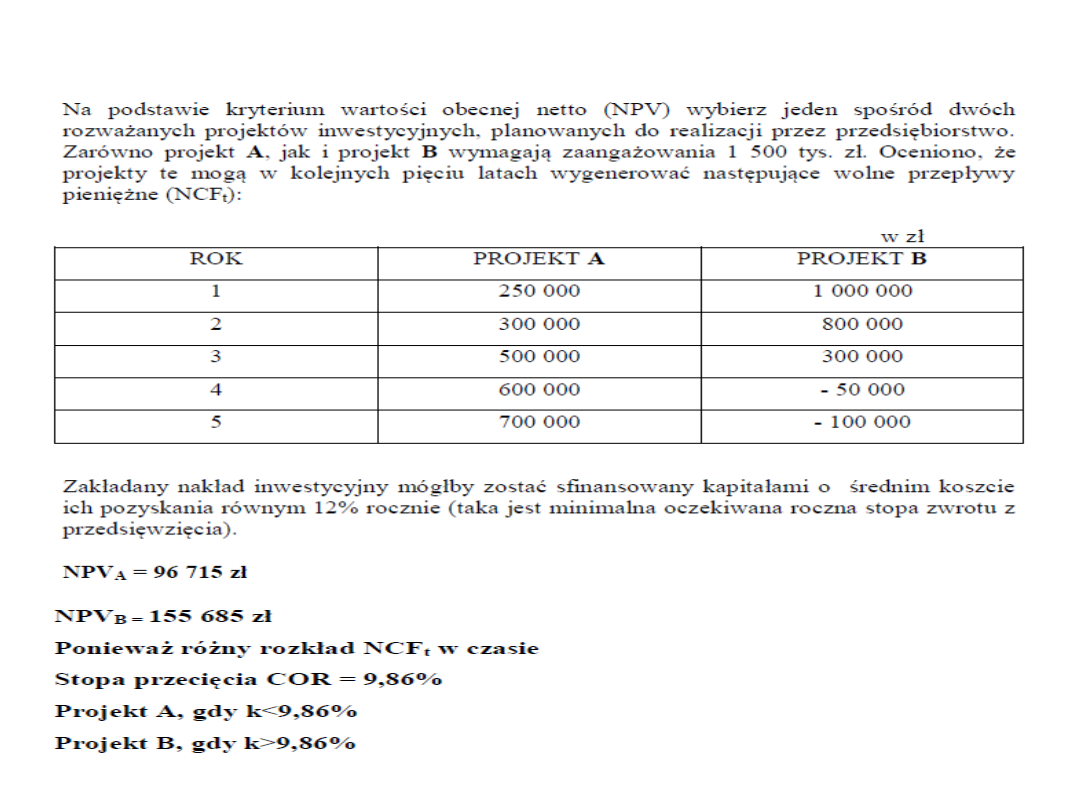
5.

6.

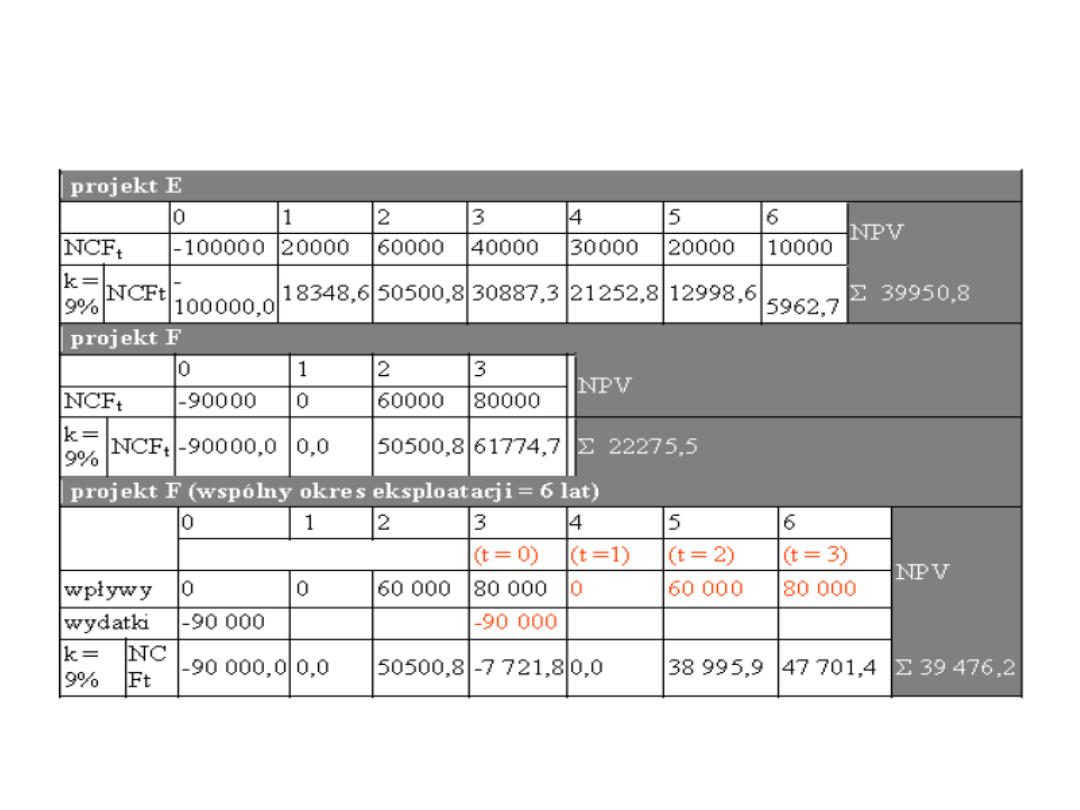
7. Metoda zastępowań

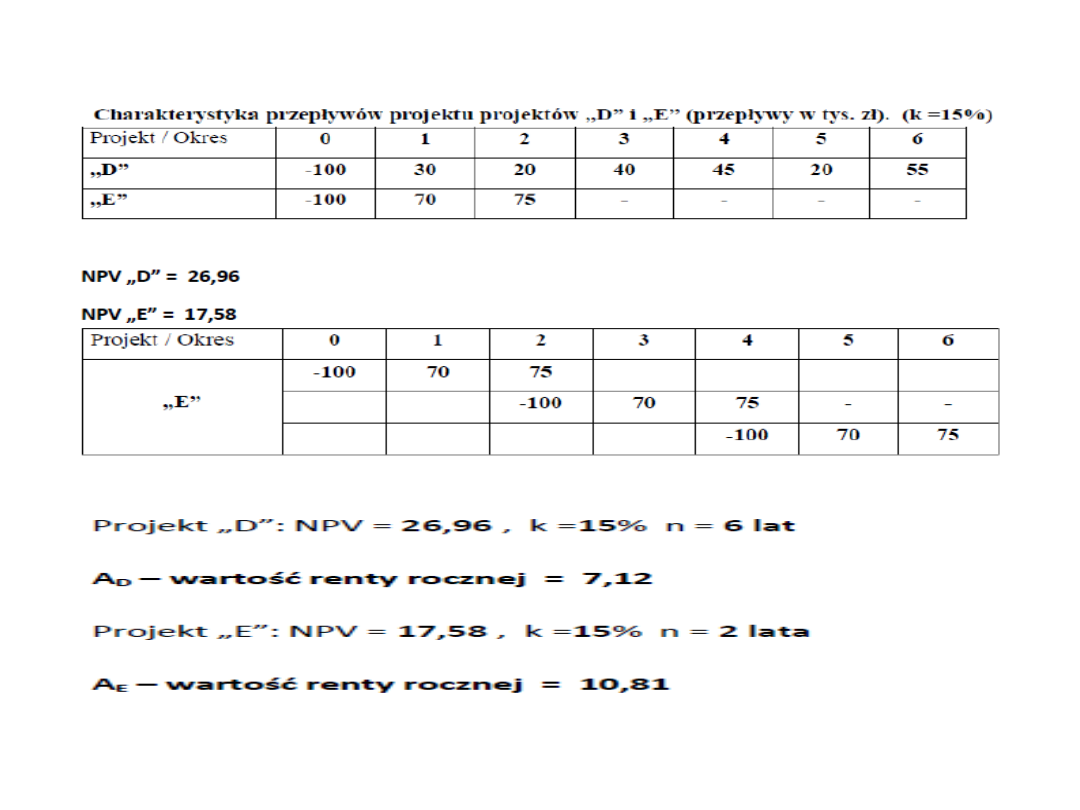
8.

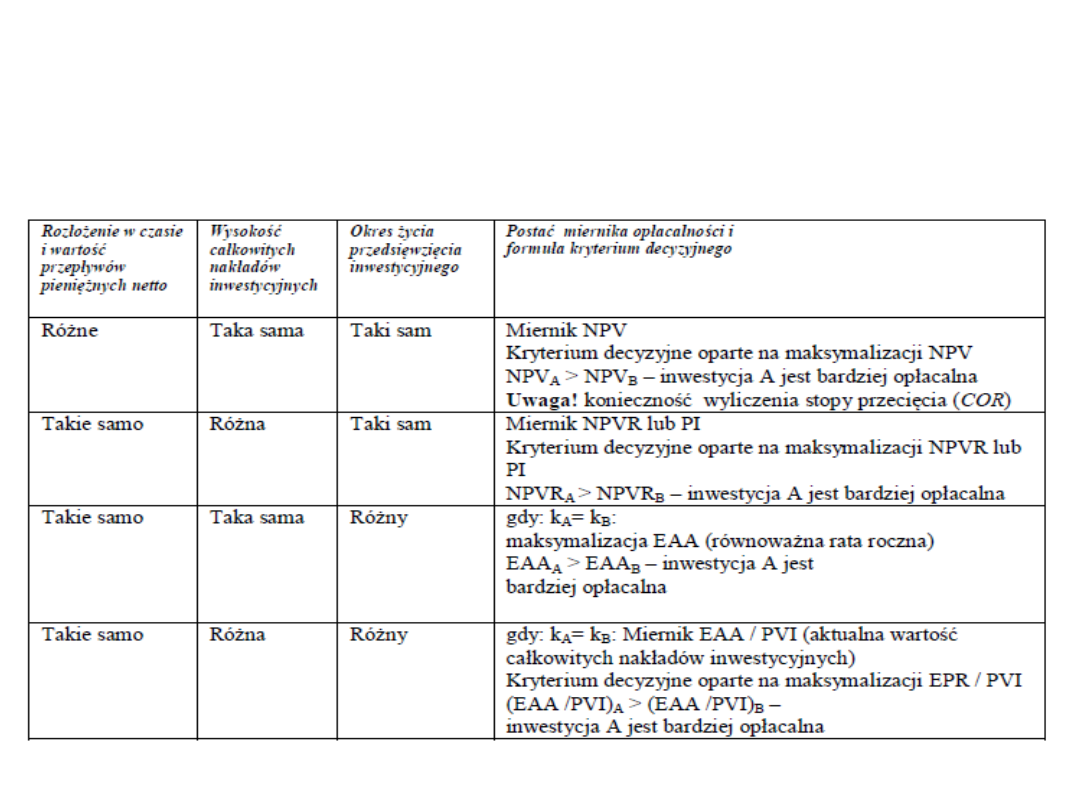
Zestawienie metod względnej opłacalności
inwestycji wraz z odpowiednimi kryteriami
decyzyjnymi

źródło:

W. Rogowski Względny rachunek opłacalności inwestycji. Katedra

Analizy Działalności Przedsiębiorstwa SGH

Instrumenty pochodne

Instrumenty pochodne

1.

Załóżmy, że 2-miesięczna stopa wolna od
ryzyka wynosi 6% w skali roku, cena jednej
akcji to 30 PLN, a w ciągu najbliższych 6
miesięcy nie jest spodziewana wypłata
dywidendy. Ile wynosi właściwa cena
rozliczeniowa? Jaki będzie wynik
sprzedawcy i nabywcy, jeśli cena
rozliczeniowa wyniesie 31,20 PLN, a
kontrakt opiewa na 500 akcji?

2.

1.

Poziom indeksu WIG-20 równa się 2233 punkty, stopa
wolna od ryzyka 6%,stopa dywidendy z indeksu 2%.
Po jakiej cenie terminowej zostanie otwarta pozycja
długa dla kontraktu sześciomiesięcznego? Jaka jest
cena teoretyczna kontraktu?

2.

Inwestor kupił portfel akcji wchodzących w skład
WIG 20 za 20 tys. zł, które w ciągu 3 miesięcy
obniżyły swoją wartość do 14 tys. zł. 10%?
Jednocześnie, spodziewając się spadku indeksu WIG
20, inwestor zajął pozycję krótką na 2 kontraktach
terminowych na indeks WIG 20. Indeks zmalał z 2580
pkt. do 2180 pkt.

Ile zarobił lub stracił inwestor? (1 pkt.

indeksowy=10 zł)

3.

Analityk Bloomberg Money Desk oblicza cenę
terminową 9-miesięcznego kontraktu forward
opiewającego na akcje brytyjskiego Banku
Budownictwa S.A., notowanego na giełdzie
londyńskiej. Cena akcji aktualnie wynosi 94
GBP. Analityk przyjmuje, że wolna od ryzyka
stopa procentowa jest równa 7% oraz że po 3,
6 i 9 miesiącach Bank Budownictwa S.A.
wypłaci dywidendę w wysokości 1,25 GBP na
akcję, a po 12 miesiącach nie wypłaci
dywidendy. Oblicz cenę kontraktu.

4.

1.

Kurs gotówkowy dolara wynosi 3,4264. Dostępny jest
6-miesięczny kontrakt forward na 200000 PLN po
kursie 3,6218. Załóżmy, że złotowa stopa procentowa
to 5,5%, a stopa w strefie dolarowej to 2,65%. Jaka
jest właściwa cena rozliczeniowa tego kontraktu
walutowego?

2.

Importer za miesiąc ma zapłacić za otrzymane towary
i chcąc zabezpieczyć się przed wzrostem kursu
dolara rozważa zakup kontaktu terminowego. Kurs
natychmiastowy wynosi obecnie 3,4513zł/1USD,
natomiast oprocentowanie WIBOR 1M dla PLN
3,6200%. Oprocentowanie LIBOR USD 1M wynosiło
w tym samym czasie 1,3509%. Po jakim kursie
(terminowym) importer kupi dolary za 30 dni?

5.

5.

20 marca eksporter dokonał sprzedaży towaru do

20 marca eksporter dokonał sprzedaży towaru do

Niemiec na kwotę 1 mln EUR. Zgodnie z umową jego

Niemiec na kwotę 1 mln EUR. Zgodnie z umową jego

partner niemiecki zapłaci dopiero 20 czerwca. Przez

partner niemiecki zapłaci dopiero 20 czerwca. Przez

ten czas eksporter wystawiony jest na duże ryzyko

ten czas eksporter wystawiony jest na duże ryzyko

cenowe. Jeżeli cena euro spadnie (w stosunku do

cenowe. Jeżeli cena euro spadnie (w stosunku do

złotego) może on ponieść niemałe straty. W związku z

złotego) może on ponieść niemałe straty. W związku z

tym eksporter postanawia zabezpieczyć się na rynku

tym eksporter postanawia zabezpieczyć się na rynku

futures, na którym czerwcowe ceny euro są dla niego

futures, na którym czerwcowe ceny euro są dla niego

satysfakcjonujące. Eksporter sprzedaje 20 „dużych”

satysfakcjonujące. Eksporter sprzedaje 20 „dużych”

kontraktów czerwcowych (1 kontrakt opiewa na

kontraktów czerwcowych (1 kontrakt opiewa na

50000 euro, a więc 20 kontraktów opiewa na 1 mln

50000 euro, a więc 20 kontraktów opiewa na 1 mln

EUR) w cenie 3,4523 zł

EUR) w cenie 3,4523 zł

Rynek gotówkowy

Rynek gotówkowy

3,3650

3,3650

Cena kontraktu na marzec

Cena kontraktu na marzec

3,3670

3,3670

Cena kontraktu na kwiecień

Cena kontraktu na kwiecień

3,3945

3,3945

Cena kontraktu na czerwiec

Cena kontraktu na czerwiec

3,4523.

3,4523.

Jaki będzie wynik eksportera, jeśli kurs kasowy w dniu

Jaki będzie wynik eksportera, jeśli kurs kasowy w dniu

wygasania kontraktu wynosił 3,4325?

wygasania kontraktu wynosił 3,4325?

6.

Amerykański farmer - dostawca pszenicy na
rynek ocenia swoje przyszłe zbiory, które
zbierze we wrześniu, na 50 000 ton. 1
kwietnia kontrakt terminowy na pszenicę na
10 000 ton kosztuje $700, a we wrześniu
$800. Czy sprzedawca przyjął właściwą
strategię zabezpieczającą, jeżeli sprzedał
już w kwietniu 5 kontraktów po 10 000 ton?
Jakie są konsekwencje jego decyzji?

7. Cena kontraktu na stopę
procentową - specyfikacja

Ceny nie są podawane w wartościach
nominalnych, ale jako różnica: 100 minus
oprocentowanie w stosunku rocznym. Skutek
tego jest następujący:
•Przykładowo cena kontraktu 85,40 implikuje
terminową stopę procentową 14,60% (100 -
14,60 = 85,40). Jest to oczywiście
oprocentowanie w stosunku rocznym.
•Wzrost cen kontraktów oznacza spadek
terminowych stóp i odwrotnie

8.Wartość TIKU (12,5 zł)

• W przypadku kontraktu na 3M WIBOR

wielkość

nominalna kontraktu to 500 tys. zł.

A więc 0,01% tej

kwoty wynosi 50 zł. Jednak jest to oprocentowanie w
stosunku rocznym, a zatem za 3 miesiące kwota ta
wyniesie odpowiednio czterokrotnie mniej, czyli 12,5 zł

.

• W przypadku kontraktu na 1M WIBOR

wielkość

nominalna kontraktu to 1 500 tys. zł

. A więc 0,01%

tej kwoty wynosi 150 zł. Jednak tak samo jak w
poprzednim przypadku, jest to oprocentowanie w
stosunku rocznym. Za 1 miesiąc kwota ta wyniesie
dwunastokrotnie mniej - także 12,5 zł.

Aby obliczyć swój zysk: kupując kontrakt w cenie 87,60 i

sprzedając go po 88,00 zarabiamy 40 tików, czyli 500 zł.

9.

Jaki będzie wynik inwestora, który kupił
kontrakt na 6 M WIBOR po cenie 93,5, a
następnie zamknął pozycję po cenie 95?

Zmiana stóp procentowych:

Liczba uzyskanych tików:

Wynik inwestora:

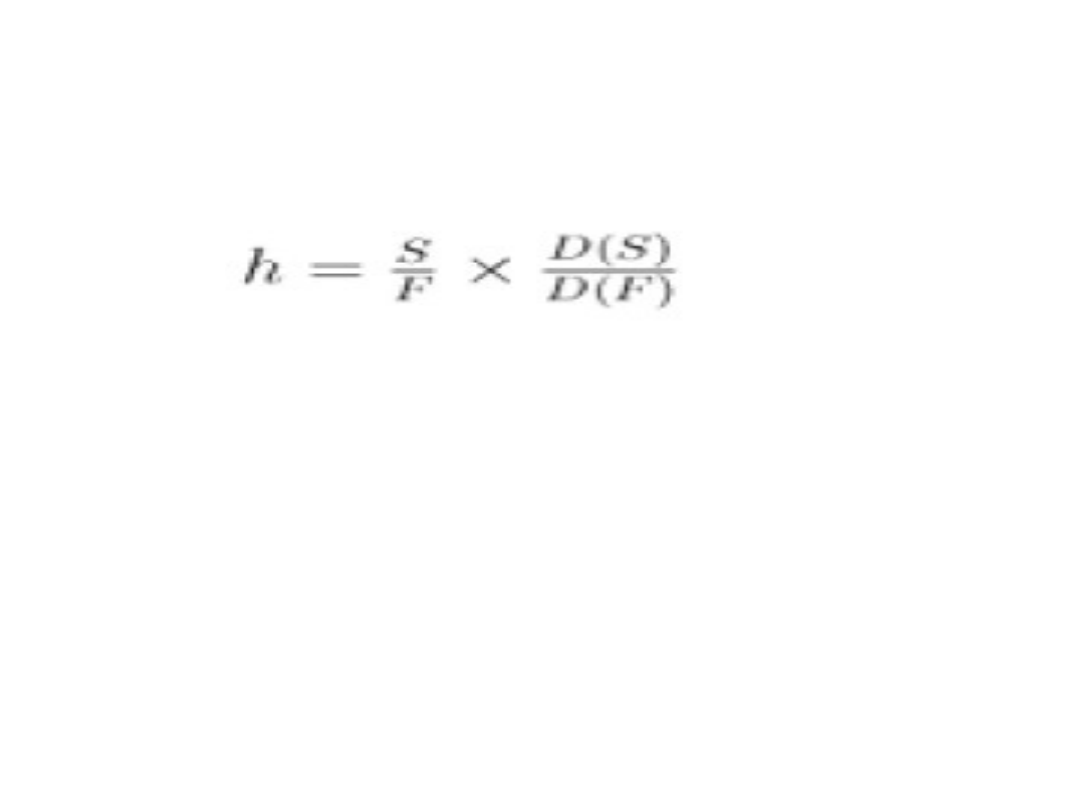
9.Współczynnik
zabezpieczenia

gdzie:
S - wartość nominalna instrumentu zabezpieczanego
F - wartość nominalna instrumentu bazowego
kontraktu futures
D(S) - czas trwania (duration) instrumentu
zabezpieczanego w latach (czyli 3 miesiące to 0,25
lat)
D(F) - czas trwania instrumentu bazowego kontraktu
futures w latach

10.

Inwestor zakupił w maju 52 tygodniowe bony skarbowe po

Inwestor zakupił w maju 52 tygodniowe bony skarbowe po

840 tys. zł za 1 000 tys. zł wartości nominalnej, które

840 tys. zł za 1 000 tys. zł wartości nominalnej, które

zamierza odsprzedać za 3 miesiące, czyli na 9 miesięcy

zamierza odsprzedać za 3 miesiące, czyli na 9 miesięcy

przed terminem wykupu. Obawia się jednak wzrostu stóp

przed terminem wykupu. Obawia się jednak wzrostu stóp

procentowych co zaowocowałoby spadkiem cen papierów

procentowych co zaowocowałoby spadkiem cen papierów

wartościowych.

wartościowych.

Cena bonów na 9 miesięcy przed wykupem 875 000 zł.

Cena bonów na 9 miesięcy przed wykupem 875 000 zł.

Inwestor chciałby uzyskać ze swojej inwestycji

Inwestor chciałby uzyskać ze swojej inwestycji

przynajmniej kwotę, jaką mógłby dziś otrzymać sprzedając

przynajmniej kwotę, jaką mógłby dziś otrzymać sprzedając

bony wygasające za 9 miesięcy.

bony wygasające za 9 miesięcy.
•

Ile kontraktów musi kupić?

Ile kontraktów musi kupić?

Cena bonów na 9 miesięcy przed wykupem 842 100 zł

Cena bonów na 9 miesięcy przed wykupem 842 100 zł

Sprzedaje zatem 6 wrześniowych kontraktów po 79.00.

Sprzedaje zatem 6 wrześniowych kontraktów po 79.00.
•

Futures na 3M WIBOR Czerwiec'98 

Futures na 3M WIBOR Czerwiec'98 

 74,90

 74,90

11.

Zgodnie z prognozami inwestora stopy wzrosły, a
więc ceny bonów spadły. Na rynku gotówkowym
uzyskał on: -842 100 zł - 840 000 zł = 2 100 zł,
-w stosunku do cen sprzed 3 miesięcy poniósł stratę
w wysokości 875 000 zł - 842 100 zł = 32 900
Na rynku futures zamknął swoje pozycję (kupił
kontrakty futures) po 74,90. Uzyskał 410 tików
(79,00-74,90) zysku na kontrakcie, czyli: 6 × 410 ×
12,5 =
30 750 zł.
A więc widać, że zyski z rynku futures pokryły
prawie w całości straty z rynku gotówkowego.

12. Jednostka transakcyjna dla
kontraktów walutowych

- dla kontraktów na USD 10 000 USD,
- dla kontraktów na EURO 10 000

EUR.

13. Jednostka notowania dla
kontraktów terminowych na walut

- dla kontraktów na USD/PLN - 100 USD,
- dla kontraktów na EURO/PLN - 100 EUR.
minimalny krok notowania dla: - dla kontraktów na

USD 0,01 PLN/100 USD, - dla kontraktów na
EURO 0,01 PLN/100 EUR.

wartość minimalnego kroku notowania wynosi dla

obu klas kontraktów 1 PLN.

[wartość minimalnego kroku notowania =

jednostka transakcyjna x minimalny krok
notowania = 10 000 USD x 0,01 PLN/100 USD =
1 PLN]

14.

CFD (

CFD (

Contract For Difference) - to kontrakt różnic

Contract For Difference) - to kontrakt różnic

kursowych, instrument pochodny, lewarowany,

kursowych, instrument pochodny, lewarowany,

pozwalający zarabiać na zmianach kursów walutowych,

pozwalający zarabiać na zmianach kursów walutowych,

cen towarów, akcji i poziomów indeksów giełdowych.

cen towarów, akcji i poziomów indeksów giełdowych.

Transakcja na kontraktach CFD dają możliwość kupna

Transakcja na kontraktach CFD dają możliwość kupna

lub sprzedaży określonej ilości walut, towarów i akcji

lub sprzedaży określonej ilości walut, towarów i akcji

bez konieczności dysponowania środkami

bez konieczności dysponowania środkami

pokrywającymi całą wartość kontraktu - wystarczy

pokrywającymi całą wartość kontraktu - wystarczy

zabezpieczenie, zwane depozytem, gwarantujące

zabezpieczenie, zwane depozytem, gwarantujące

rozliczenie transakcji w przypadku niekorzystnego dla

rozliczenie transakcji w przypadku niekorzystnego dla

inwestora ruchu kursów walutowych.

inwestora ruchu kursów walutowych.

Podstawowe wielkości depozytów to 1% dla

Podstawowe wielkości depozytów to 1% dla

kontraktów walutowych, 2 i 3 % dla CFD na towary i

kontraktów walutowych, 2 i 3 % dla CFD na towary i

indeksy oraz 7 % dla CFD indeksowych.

indeksy oraz 7 % dla CFD indeksowych.

15. CFD

Kontrakty CFD są instrumentami wysoce
wystandaryzowanymi i obrót nimi podlega szczegółowym
uregulowaniom. Jednostką transakcyjną dla CFD to jeden
kontrakt - w przypadku walut znany jako LOT, który
oznacza zakup lub sprzedaż 100 000 jednostek jednej
waluty za drugą. W przypadku CFD na towary, akcje i
indeksy, wielkość kontraktu wynika ze zdefiniowanej
specyfikacji.
Można zawierać transakcje o nominale większym lub
mniejszym od 1 lota, kupując lub sprzedając jego
wielokrotność. Przykładowo, aby nabyć 150tys USD za PLN
należy zawrzeć transakcję kupna 1,5 lotów na USD/PLN.
Możliwe jest także inwestowanie w np. 0,1 lub 0,5 (pół)
lota/kontraktu. Pozwala to na inwestycje rzędu nawet 300
złotych - depozyt dla 0,1 lota kontraktu na USD/PLN - czyli
dostęp do rynku dla praktycznie każdego inwestora.

16.

16.

Załóżmy, że przewidujemy osłabienie się

Załóżmy, że przewidujemy osłabienie się

polskiej waluty w stosunku do waluty europejskiej

polskiej waluty w stosunku do waluty europejskiej

ze względu na prawdopodobne podanie się do

ze względu na prawdopodobne podanie się do

dymisji rządu i prawdopodobieństwo

dymisji rządu i prawdopodobieństwo

przedterminowych wyborów. Na rachunku

przedterminowych wyborów. Na rachunku

inwestycyjnym w inwestor posiada 20.000 PLN, a

inwestycyjnym w inwestor posiada 20.000 PLN, a

aktualny kurs EUR/PLN wynosi 3,9840. Inwestor

aktualny kurs EUR/PLN wynosi 3,9840. Inwestor

jest przekonany o trafności swojej analizy rynku i

jest przekonany o trafności swojej analizy rynku i

postanawia zaryzykować kupując 2 loty EUR/PLN

postanawia zaryzykować kupując 2 loty EUR/PLN

po kursie 3,9840.

po kursie 3,9840.

Zawarcie takiej transakcji oznacza, że inwestor

Zawarcie takiej transakcji oznacza, że inwestor

posiada obecnie otwartą pozycję na wzrost kursu

posiada obecnie otwartą pozycję na wzrost kursu

EUR/PLN o nominale 200.000 EUR. Na

EUR/PLN o nominale 200.000 EUR. Na

zabezpieczenie transakcji zostanie pobrany

zabezpieczenie transakcji zostanie pobrany

depozyt początkowy w wysokości 2*4.000 PLN,

depozyt początkowy w wysokości 2*4.000 PLN,

czyli 8.000 PLN. Inwestor zarobi na tej transakcji,

czyli 8.000 PLN. Inwestor zarobi na tej transakcji,

jeżeli kurs EUR/PLN będzie wyższy niż 3,9840 a

jeżeli kurs EUR/PLN będzie wyższy niż 3,9840 a

straci, jeżeli będzie niższy niż 3,9840. Prześledźmy

straci, jeżeli będzie niższy niż 3,9840. Prześledźmy

zatem stan naszego rachunku inwestycyjnego w

zatem stan naszego rachunku inwestycyjnego w

zależności od hipotetycznych zmian kursu na

zależności od hipotetycznych zmian kursu na

rynku.

rynku.

17.

17.

Dzień pierwszy - na zamknięciu dnia kurs

Dzień pierwszy - na zamknięciu dnia kurs

EUR/PLN wynosił 3,9700.

EUR/PLN wynosił 3,9700.

Strata inwestora z wyceny wynosi: 200.000*(3,97-

Strata inwestora z wyceny wynosi: 200.000*(3,97-

3,9840)= -2.800 PLN. Inwestor decyduje się jednak

3,9840)= -2.800 PLN. Inwestor decyduje się jednak

przetrzymać pozycję i przerolować ją na następny dzień.

przetrzymać pozycję i przerolować ją na następny dzień.

Operacja rolowania przebiega automatycznie. Otwarta

Operacja rolowania przebiega automatycznie. Otwarta

pozycja inwestora zostanie zastąpiona nową, identyczną

pozycja inwestora zostanie zastąpiona nową, identyczną

pozycją tzn. będzie on miał kupione 200.000 EUR/PLN po

pozycją tzn. będzie on miał kupione 200.000 EUR/PLN po

kursie 3,9840, jego rachunek zostanie obciążony kwotą

kursie 3,9840, jego rachunek zostanie obciążony kwotą

punktów swapowych za jeden dzień. Jako że zgodnie z

punktów swapowych za jeden dzień. Jako że zgodnie z

Tabelą Punktów Swapowych np. gdy punkty swapowe za

Tabelą Punktów Swapowych np. gdy punkty swapowe za

jeden lot wynoszą –29 PLN to rachunek inwestora

jeden lot wynoszą –29 PLN to rachunek inwestora

zostanie obciążony kwotą: 2*29 PLN = 58 PLN.

zostanie obciążony kwotą: 2*29 PLN = 58 PLN.

Dzień drugi - na zamknięciu dnia kurs EUR/PLN

Dzień drugi - na zamknięciu dnia kurs EUR/PLN

wynosił 3,9880.

wynosił 3,9880.

Zysk inwestora z wyceny wynosi: 200.000*(3,988-3,9840)

Zysk inwestora z wyceny wynosi: 200.000*(3,988-3,9840)

= 800 PLN. Inwestor stwierdza jednak, że zysk w

= 800 PLN. Inwestor stwierdza jednak, że zysk w

wysokości 800 PLN jest dla niego niewystarczający i

wysokości 800 PLN jest dla niego niewystarczający i

postanawia przetrzymać pozycję do następnego dnia,

postanawia przetrzymać pozycję do następnego dnia,

rolując ją tak jak w dniu poprzednim. Znowu jego konto

rolując ją tak jak w dniu poprzednim. Znowu jego konto

zostaje obciążone kwotą 58 PLN z tytułu ujemnych

zostaje obciążone kwotą 58 PLN z tytułu ujemnych

punktów swapowych.

punktów swapowych.

18

18

.

.

Dzień trzeci - o godzinie 14:00 pojawia

Dzień trzeci - o godzinie 14:00 pojawia

się informacja o dymisji rządu i

się informacja o dymisji rządu i

przedterminowych wyborach, rynek jest

przedterminowych wyborach, rynek jest

niespokojny. O godzinie 15:15 kurs EUR/PLN

niespokojny. O godzinie 15:15 kurs EUR/PLN

wynosi już 4,0190.

wynosi już 4,0190.

Inwestor stwierdza, że taki poziom kursu jest dla

Inwestor stwierdza, że taki poziom kursu jest dla

niego satysfakcjonujący i postanawia zamknąć

niego satysfakcjonujący i postanawia zamknąć

pozycję, sprzedając ją po kursie 4,0190. Zysk

pozycję, sprzedając ją po kursie 4,0190. Zysk

inwestora wynosi: 200 000*(4,0190-3,9840) = 7

inwestora wynosi: 200 000*(4,0190-3,9840) = 7

tys. PLN. Inwestor poniósł jednak koszty punktów

tys. PLN. Inwestor poniósł jednak koszty punktów

swapowych za dwa dni.

swapowych za dwa dni.

Tak więc zysk netto inwestora z przeprowadzonej

Tak więc zysk netto inwestora z przeprowadzonej

operacji wynosi =7 000PLN – 2 * 58 PLN = 6 884

operacji wynosi =7 000PLN – 2 * 58 PLN = 6 884

PLN

PLN

20.

1. Inwestor otrzymuje 1mln zł, lokuje je w Banku

na 6 miesięcy. A więc za 6 miesięcy otrzyma 106
tys. zł z tytułu odsetek (1 mln × 21,20% × 0,5).

2. Lokując tę samą kwotę w lipcu, otrzymałby po 6

miesiącach 117,5 tys. zł. Poniósł zatem
alternatywną stratę (uzyska mniejszy zysk) w
wysokości 10,5 tys. zł.

3. Inwestor zamyka też kontrakty futures

(sprzedaje kontrakty przeciwne) w cenie 78,90.

4. Jego zysk na kontraktach futures wyniósł 220

tików czyli: 4 × 220 × 12,5 =11 tys. zł Jak
zatem widać, jego alternatywna strata została
pokryta z nawiązką.

21.

Jest 20 marca. Bank udziela firmie 6-miesięcznego kredytu na
następujących warunkach:
 kwota kredytu: 1 mln zł
 spłata: w dwóch trzymiesięcznych ratach - pierwsza rata pod
koniec czerwca, druga płatna pod koniec września
oprocentowanie: 3 miesięczna stawka WIBOR +2 punkty
procentowe .
Aktualna stawka 3M WIBOR wynosi 13,2%. Jednak nieznana jest
stawka 3M WIBOR, jaka ukształtuje się na rynku w dniu 20.06

.

Bank narażony jest więc na ryzyko spadku stopy procentowej.
Chciałby jednak uzyskać za okres czerwiec - wrzesień
oprocentowanie w wysokości przynajmniej 15% w stosunku
rocznym (czyli 1 mln × 15%×0,25 = 37,5 tys. zł). Do
zabezpieczenia swojej pozycji, również może wykorzystać rynek
futures.

22.

20 marca, sytuacja na rynku stóp procentowych
przedstawia się następująco:
•3M WIBOR:

13,20

•Futures na 3M WIBOR
 Czerwiec

86,90

Wrzesień 87,20
Na rynku futures Bank może więc zapewnić sobie
czerwcową stopę na poziomie 13,10 % (100-86,90).
W tym celu musi kupić odpowiednią ilość
kontraktów futures:

23.

20 czerwca sytuacja rynkowa przedstawia się następująco:
3M WIBOR:

10,80

Futures na 3M WIBOR
Czerwiec 89,24
Wrzesień

89,35

Bank otrzymał pierwszą ratę w wysokości: 1 mln × (13,20 +
2pkt%) × 0,25=38 tys. zł Ze względu na spadek stóp
procentowych kolejna rata, która będzie płatna we wrześniu,
wyniesie już tylko 1 mln × (10,80 + 2pkt%) × 0,25 = 32 tys. zł.
W stosunku do zakładanych 37,5 tys. stanowi to stratę w
wysokości 5,5 tys. zł.
Jednak na rynku terminowym Bank zanotował zyski. Zamyka
swoją pozycję w cenie 89,24. Zarobił więc po 234 tiki na każdym
kontrakcie (89,24 - 86,90), co stanowi kwotę: 2 × 234 × 12,5 zł
=
5 850 zł. Zatem poniesione straty zostały zrekompensowane na
rynku futures.

Kredyt, leasing

1.

Przedsiębiorstwo SOUL trzy lata

temu zaciągnęła kredyt na kwotę
330 000 zł, który miał być spłacany
w równych (anuitetowych) ratach
kwartalnych ciągu 5 lat.
Oprocentowanie kredytu wynosi 8%.
Jaka kwota kredytu pozostała jeszcze
do spłacenia?

2.

Spółka ENTER zamierza zaciągnąć
kredyt w wysokości 2 mln zł
oprocentowany w wysokości 12%,
który byłby spłacany w równych
(anuitetowych) ratach kwartalnych w
okresie 5 lat. Jaka będzie wysokość
tych rat? Jaką część trzeciej raty
stanowić będą odsetki?

3.

Przedsiębiorstwo UNIA zaciągnęło
kredyt w kwocie 2 500 tys. zł na 16%
rocznie, który zamierza spłacić w
równych ratach kwartalnych w ciągu 4
lat.
Jaka będzie wysokość tych rat?
Ile wyniosą odsetki za pierwszy rok?

4.

Firma MAD musi zapłacić kredytodawcy na
koniec kolejnych lat: 10 000 zł, 8 000 zł, 6
000 zł, 4 000 zł.
Jeśli firma chciałaby zrestrukturyzować swój
zadłużenie i spłacić je w sześciu równych
ratach na koniec każdego z kolejnych lat, to
ile wyniesie rata przy uzgodnionym z
kredytodawcą oprocentowaniu w wysokości
10%? Jaką część trzeciej raty stanowić
będzie spłata odsetek?

5.

 

Zawarto umowę leasingu na 3 lat, w której

określono:

•wartość początkową przedmiotu
leasingu w kwocie 120 000,00 zł,
•sumę wszystkich półrocznych opłat
leasingowych w kwocie 145 000,00 zł.

Stosując metodę szczebelkowo-procentową
określić część odsetkową i umorzeniową w
każdej racie leasingowej.

6.

Proszę sporządzić harmonogram rocznych
płatności leasingowych, z wyodrębnieniem
części odsetkowej i umorzeniowej w każdej
racie, przy następujących parametrach:
wartość początkowa przedmiotu leasingu =200
000, zł;
okres użytkowania n = 5 lat,
stopa dyskontowa r = 11%.
równe raty leasingowe regulowane będą “z
góry„.

 

7.

Przedmiotem leasingu jest samochód o wartości
130 tys. zł. Uzgodniono, że opłata wstępna
wyniesie 20 % wartości przedmiotu leasingu,
natomiast wartość wykupu, płatna po zakończeniu
umowy wyniesie symboliczną złotówkę, można ją
pominąć w kalkulacji. Płatności leasingowe
obejmą 30 rat płatnych na początku kolejnych
okresów miesięcznych w kwocie 5 200 zł. Jaki jest
efektywny roczny koszt kredytu? Jaką nominalną
roczną stopę procentową zastosował finansujący
w ustalaniu rat leasingowych?

8.

Przedmiot leasingu: samochód śmieciarka na
podwoziu Scania, zabudowa Medium 16 m³
produkcji Ekocel, nowy, o wartości ok. 600 tys.
zł netto.

Umowę leasingu zawarto na

okres 3 lat, w której określono:

Opłatę wstępną w wysokości 10%,
Kwartalne raty leasingowe w kwocie
53 000 zł.

Jaką efektywną roczną stopę procentową
zastosował leasingodawca?

9.

Przedmiotem umowy jest leasing serwerów
komputerowych, macierzy i oprogramowania
wartości 300 tys. zł netto przy następujących
parametrach:
•Okres użytkowania n = 3 lata,
•Stopa dyskontowa r = 8%.
•Równe raty leasingowe regulowane na koniec
kolejnych okresów półrocznych.
Proszę sporządzić harmonogram rocznych płatności
leasingowych, z wyodrębnieniem części
odsetkowej i umorzeniowej w każdej racie.

 

Weksel

1.

Należność za dostarczony towar wynosi 36
000 zł i będzie płatna po 75 dniach. Na jaką
sumę należy wystawić weksel, jeśli
uzgodniono oprocentowanie w wysokości
18%? Jeśli po trzech tygodniach weksel
zostanie przedłożony do dyskonta, to jaką
kwotę odsetek potrąci bank, w którym
oprocentowanie kredytu dyskontowego
wynosi 7,2%?

 

2.

Kontrahent za nabywane towary o wartości
35 tys. zł chce zapłacić wekslem przez jego
indos (przeniesienie praw z weksla na
sprzedawcę). Weksel na kwotę 36 tys. zł
wystawiono 38 dni temu z terminem
płatności za 80 dni. Czy warto przyjąć ten
weksel jako zapłatę za sprzedawane towary,
jeśli stopa dyskonta weksla w banku wynosi
12%?

 

3.

Bank komercyjny przyjął do dyskonta weksel
na kwotę 80 000 zł, którego termin płatności
upływa za 45 dni.
Ile otrzyma podawca weksla, jeśli stopa
dyskonta weksli wynosi 11,5%?
Jeśli po 20 dniach weksel zostanie przez
bank komercyjny zredyskontowany w banku
centralnym, to w jakiej wysokości odsetki
potrąci NBP na podstawie stopy redyskonta
weksli w wysokości 4%?

4.

Przedsiębiorstwo Y ma do wyboru dwie oferty:
a) zaciągnięcie kredytu krótkoterminowego na okres 30
dni w kwocie 100 000 z oprocentowaniem 21 % oraz
prowizją przygotowawczą 2,5 %,
b) dyskonto weksla w banku wystawionego na kwotę
100 000 z terminem płatności 30 dni przy stopie
dyskontowej 21 % oraz prowizji od złożonego weksla 2,5
%.
Przyjmując założenie, że prowizja jest płatna w ciężar
kredytu i dyskonta weksla określ jaką kwotą będzie
dysponowało przedsiębiorstwo Y po uruchomieniu
kredytu i po wykupie weksla. Który wariant jest
korzystniejszy?

5.

Przedsiębiorstwo Z przedstawiło bankowi do wykupu dwa
weksle:
a) na kwotę 50 000 z terminem płatności po 60 dniach,
b) na kwotę 130 000 z terminem 180 dni.
Oferta banku została określona na następującym
poziomie:
a) stopa dyskonta dla pierwszego weksla 20 %, prowizja
2 %, wykup 5 dni po wystawieniu,
b) stopa dyskonta dla drugiego weksla 22 %, prowizja 2,5
%, wykup 5 dni po wystawieniu, 20 % kwoty weksla
zostanie zdeponowane jako fundusz gwarancyjny do
czasu wykupu weksla przez kontrahenta firmy Z.
Określ łączną kwotę postawioną do dyspozycji
przedsiębiorstwa Z przez bank.