PODSTAWY

DECYZJI

EKONOMICZNYCH

PRODUCENTA

Przedmiot rachunku ekonomicznego –
produkcja.
Jest ona rozumiana jako przetwarzanie
zasobów, wytwarzanie dóbr zaspokajających
potrzeby konsumentów.
Produkcja to inaczej kombinowanie zasobów.
Produkcję charakteryzujemy przez
współczynniki technologiczne, czyli ilość
zasobów poszczególnych rodzajów, które
należy zużyć na wyprodukowanie jednostki
dobra.

Współczynniki te znajdują swoją identyfikację
w takich kategoriach, jak:

•

materiałochłonności,

•

surowcochłonności,

•

energochłonności,

•

pracochłonności,

•

kapitałochłonności.

Materiałochłonność - ilość materiałów
potrzebna dla wyprodukowania jednostki
dobra.
Pozostałe charakteryzujemy podobnie do
materiałochłonności.

Współczynniki technologiczne charakteryzują
sprawność technologii, a więc posiadają istotny
wpływ na rachunek ekonomiczny.
Głównym kanonem stosowania rachunku
ekonomicznego jest rozpoznanie relacji
osiąganych wyników do nakładów.
Po stronie wyników znajdują się konkretne dobra
i świadczone przez przedsiębiorstwa usługi.
Po stronie wyników są zarówno dobra pośrednie,
których przetwarzanie nie zostało jeszcze
zakończone, jak i dobra finalne.

Mają one dwojaki charakter:

•

dobra inwestycyjne – to środki pracy np. maszyny,

•

dobra konsumpcyjne – to dobra, które zostają

skierowane na rynek dla konsumentów.
Nakłady
Nad względem rzeczowym przedsiębiorstwo ponosi
nakłady przez wykorzystanie surowców, maszyn, a
także nakłady związane z pożyczonym kapitałem.
Znajdują one swoje potwierdzenie w kosztach
świadczenia usług.
Relacje między wynikami i nakładami ściśle zależą
od przebiegu produkcji, a duże znaczenie posiada
sprawność stosowanej technologii.

Produkcja składa się z trzech faz:

•

faza jej przygotowania – następuje tu

pozyskanie zasobów przez przedsiębiorstwo
(kupowanie),

•

połączenie uzyskanych zasobów – faza

właściwej produkcji,

•

sprzedaż wytworzonych dóbr, a więc

następuje zamiana kapitału rzeczowego na
kapitał pieniężny.

Suma pieniędzy, które przedsiębiorstwo
otrzymuje w trzeciej fazie może być większa,
mniejsza lub równa sumie pieniędzy
wydatkowanych pierwszej fazie.
Gdy suma pieniędzy w trzeciej fazie jest
większa niż suma wydatkowana w fazie
pierwszej, to przedsiębiorstwo realizuje zysk.
Kwoty pieniędzy uzyskane ze sprzedaży to
przychód (utarg).
Istnieją trzy kategorie utargu:

•

całkowity,

•

przeciętny,

•

marginalny.

Utarg (przychód) całkowity (UC) – iloczyn
ilości sprzedanych produktów (Q) i ich ceny (P).

UC = Q *P

Utarg (przychód) przeciętny (UP) – utarg
całkowity (UC) przypadający na jednostkę
sprzedanego produktu (Q).

UP = UC / Q

Utarg (przychód) marginalny (krańcowy)
(UM) – przyrost utargu całkowitego związany ze
zwiększeniem sprzedaży o dodatkową
jednostkę.

UM = ΔUC / ΔQ

Te trzy rodzaje utargu pozostają w pewnej
zależności.
Dopóki przychód marginalny jest dodatni
rośnie przychód całkowity.
W analizach ekonomicznych zakłada się, że
przychód marginalny charakteryzuje się stałą
tendencją spadkową.
Wynika to z zachowań uczestników rynku.
Aby sprzedać każdą dodatkową jednostkę
towaru należy obniżyć jej cenę.

Zysk – to nadwyżka, którą realizuje
przedsiębiorstwo.

Zysk brutto – przychód ze sprzedaży
produktów pomniejszony o całość kosztów
produkcji i kosztów sprzedaży.

Zysk brutto = przychód ze sprzedaży –

koszty produkcji i sprzedaży

Zysk brutto nie jest dochodem przedsiębiorstwa,
którym może ono swobodnie dysponować.
Najpierw należy zapłacić podatki nakładane na
dochody przedsiębiorstw przez państwo.
Po opłaceniu podatków w przedsiębiorstwie
pozostaje kwota określana zyskiem netto.

Zysk netto = zysk brutto – podatki

Zazwyczaj zysk netto nie jest w całości
przekazywany właścicielom przedsiębiorstwa
(np. w formie dywidendy dla akcjonariuszy).
Przed podziałem zysku netto należy utworzyć
rezerwy obowiązkowe (określone przepisami
prawa), a następnie można tworzyć rezerwy
dobrowolne przeznaczone np. na inwestycje.

Zysk dla właścicieli = zysk netto – rezerwy

obowiązkowe i dobrowolne

Podstawą rachunku ekonomicznego jest
określanie efektywności.
Efektywność charakteryzuje się dwoma
aspektami:

•

techniczna,

•

ekonomiczna.

Efektywność techniczna oznacza, że
producent maksymalizując efekt produkcji nie
będzie wkładał do produkcji więcej czynników
(nakładów) niż jest to konieczne dla
osiągnięcia danej wielkości efektu.

Stosowane przez producentów zasoby podlegają
substytucji.
Stąd efektywność techniczna nie jest
równoznaczna z efektywnością ekonomiczną.
Efektywność techniczna nie musi iść parze z
efektywnością ekonomiczną.
Efektywność ekonomiczna – polega na takim
wykorzystaniu nakładów czynników produkcji,
aby koszt wytworzenia jednostki produktu był
minimalny.
Efektywność ekonomiczna oznacza wybór w
oparciu o zasadę najmniejszego kosztu produkcji.

Produkcja polega na kombinowaniu (łączeniu)
określonych nakładów (czynników produkcji) w
celu osiągnięcia efektu w postaci
wytworzonych produktów i usług.
Teoria produkcji jest analizą relacji, jakie
występują między nakładem czynników i
osiąganym z tego nakładu produktem.
Zależność między wielkością produkcji a
rozmiarem nakładu czynników można
przedstawić przy pomocy funkcji produkcji.

Q = f (F

, F

, …, F

gdzie: Q – wielkość produkcji

F – czynniki produkcji.

Posługując się zasadą ceteris paribus można
uprościć analizę funkcji produkcji.
Jeżeli uwzględniony zostanie tylko jeden z
czynników produkcji zakładając, że wpływ
pozostałych czynników na rozmiary produkcji
jest niezmienny, to otrzymamy
jednoczynnikową funkcję produkcji.

Q = f (L)

Q = f (K),

gdzie:
L – siła robocza,
K – kapitał.

Jeżeli założymy, że na zmiany wielkości
produkcji wpływają zarówno zmiany czynnika
siły roboczej (L), jak i czynnika kapitału (K), to
otrzymamy wieloczynnikową funkcję
produkcji ( w tym wypadku dwuczynnikową).

Q = f (F

, F

)

Czynniki produkcji dzielimy na:

•

czynniki stałe,

Ich nakład nie ulega zmianie wraz ze zmianami
rozmiarów produkcji.

•

czynniki zmienne.

Ich nakłady zmieniają się wraz ze zmianami
rozmiarów produkcji.
Podział czynników produkcji na stałe i zmienne
związany jest z uwzględnieniem czasu w
analizie procesu produkcyjnego.

Krótki okres to taki, w którym nie zmienia się

technologia produkcji.

W krótkim okresie technologia produkcji jest

dana.

W długim okresie następują zmiany w

technologiach produkcji wynikające z
postępu technicznego.

Funkcja produkcji w krótkim okresie

W funkcji jednoczynnikowej rozpatrujemy

zależność między nakładem jednego czynnika
zmiennego (np. czynnika praca) a wielkością
produkcji zakładając, że pozostałe czynniki
są niezmienne.

Dalsze uproszczenia: uwzględniamy tylko jeden

czynnik zmienny (praca) oraz jeden czynnik
stały (kapitał).

Oznacza to, że rozmiary produkcji zmieniają się

jedynie w wyniku zmian w ilości
zatrudnionych osób.

Podstawowe założenia analizy funkcji

produkcji:

•

istnieje tylko jeden czynnik zmienny,

•

istnieje tylko jeden czynnik zmienny,

•

technologia produkcji jest dana,

•

czynniki produkcji mogą łączyć się z sobą w
różnych proporcjach,

•

produkt jest jednorodny.

Produkt całkowity, przeciętny i marginalny

Zgodnie z przyjętymi założeniami wielkość

produkcji zmienia się w wyniku zmian
nakładów na siłę roboczą.

Produkcja jest tym większa, im więcej, ceteris

paribus, zatrudniamy pracowników.

Produkt przeciętny (PP) – otrzymujemy

dzieląc wielkość produkcji całkowitej przez
nakłady zmiennego czynnika produkcji.

Przeciętny produkt pracy (PPL)–

otrzymujemy dzieląc wielkość produkcji
przez ilość zatrudnionych pracowników.

PPL = PC / L

Produkt marginalny (PM) – stosunek

przyrostu produkcji całkowitej wywołany
zwiększeniem nakładów zmiennego czynnika
produkcji o dodatkową jednostkę.

Marginalny produkt pracy (PML) - stosunek

przyrostu produkcji całkowitej wywołany
zwiększeniem nakładów czynnika praca o
dodatkową jednostkę.

PML = ΔPC / ΔL

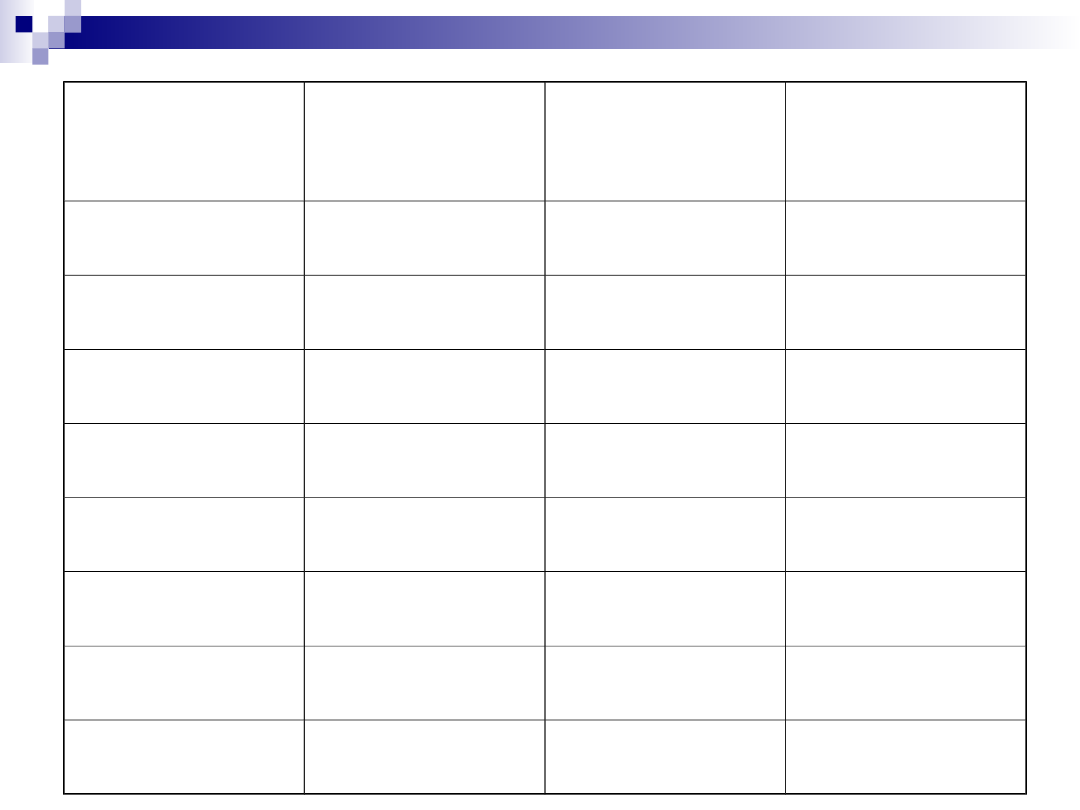
Ilość

pracowników

(L)

Produkcja

całkowita

(PC)

Przeciętny

produkt pracy

(PPL)

Marginalny

produkt pracy

(PML)

-3

Produkcja całkowita dobra X rośnie wraz ze

wzrostem liczby pracowników.

Produkcja wzrasta do pewnego punktu

maksymalnego, po przekroczeniu którego
produkcja zaczyna spadać.

U nas produkcja dobra X rośnie wraz ze

zwiększeniem liczby pracowników od 0 do 6.

Po przekroczeniu tej liczby pracowników produkcja

całkowita zmniejsza się.

Produkt przeciętny i marginalny początkowo

wzrastają, a następnie, po osiągnięciu maksimum,
zmniejszają się.

Równocześnie początkowo produkt marginalny

rośnie szybciej aniżeli produkt przeciętny (PM >
PP).

Następnie, po przekroczeniu punktu zrównania

się obydwu produktów (PM = PP), produkt
marginalny zaczyna spadać szybciej niż
produkt przeciętny (PM < PP).

PM zrównuje się z PP, gdy PP osiąga

maksimum.

PM > PP, gdy PP rośnie
PM < PP, gdy PP spada.
Dlatego krzywa PM znajduje się powyżej

krzywej PP, gdy ta ostatnia rośnie,

Kiedy krzywa PP spada, wtedy krzywa PM

znajduje się poniżej.

Prawo malejących przychodów: zwiększając

nakład zmiennego czynnika produkcji ( przy
założeniu, że pozostałe czynniki są stałe)
osiągamy taki punkt, po przekroczeniu
którego każda dodatkowa jednostka
zmiennego czynnika produkcji daje coraz
mniejsze przyrosty produkcji.
Produktywność kolejnego zmiennego czynnika
produkcji zmniejsza się – PM maleje.

Prawo malejących przychodów odnosi się do

procesów produkcyjnych w krótkim okresie,
tzn. gdy przynajmniej jeden czynnik produkcji
jest stały.

Efekty skali produkcji

Odnoszą się do procesów produkcji, w których

wszystkie czynniki produkcji są zmienne, czyli

dotyczy okresu długiego.

Stałe efekty skali produkcji: występują, gdy

wszystkie czynniki produkcji zmieniają się

proporcjonalnie, wówczas produkcja zmienia

się w tej samej proporcji.

Malejące efekty skali produkcji: występują,

gdy wszystkie czynniki produkcji zmieniają się

proporcjonalnie, a produkcja zmienia się mniej

niż proporcjonalnie.

Rosnące efekty skali produkcji: występują,

gdy wszystkie czynniki produkcji zmieniają się

proporcjonalnie, a produkcja zmienia się mniej

niż proporcjonalnie.

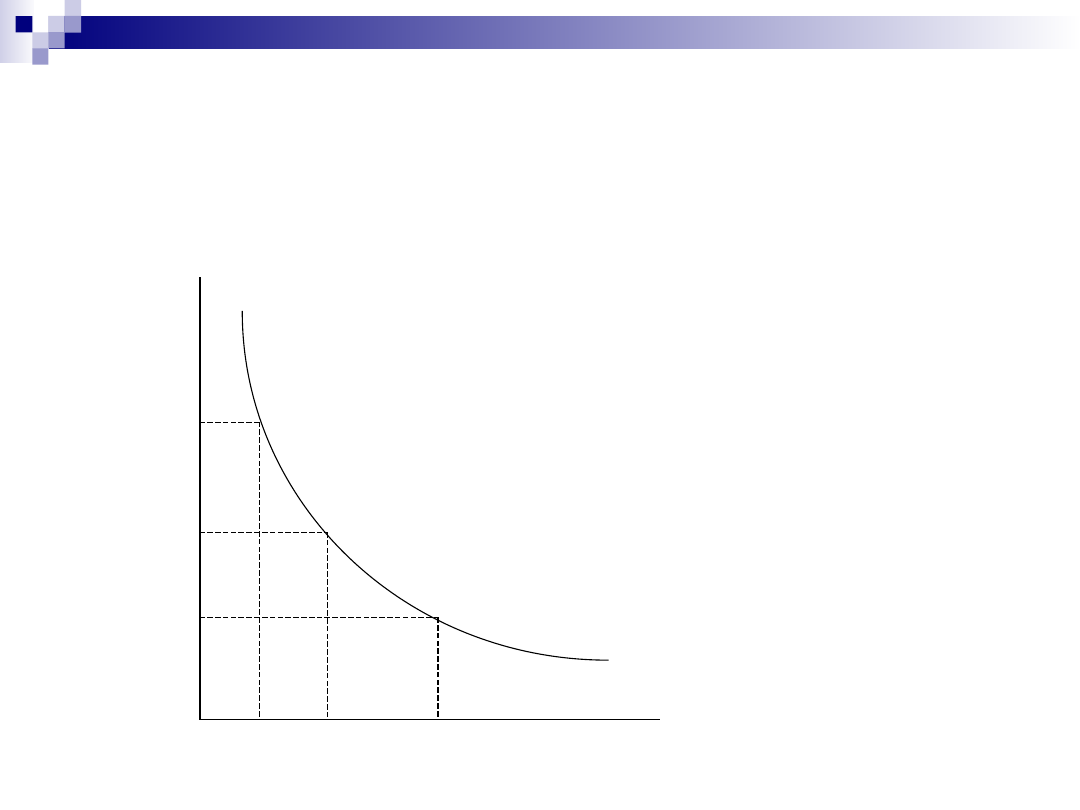
Izokwanta (linia jednakowego produktu) –

zbiór wszystkich kombinacji zasobów, które

umożliwiają osiągnięcie tego samego poziomu

produkcji.

K1 A

K2 B

K3 C

L1 L2 L3 L

Te same rozmiary produkcji można osiągnąć przy
wykorzystaniu różnych technik wytwarzania.
Metoda „A” polega na zaangażowaniu L1 czynnika
pracy i K1 czynnika kapitału, metodę „B”
charakteryzują odpowiednio L2 czynnika pracy i
K2 czynnika kapitału, zaś metodę „C” L3 i K3.
Ruch wzdłuż izokwanty produkcji oznacza, że
zmianie ulegają wielkości nakładów czynników
produkcji oraz proporcje między czynnikami,
natomiast nie zmienia się poziom produkcji.
Przemieszczanie się wzdłuż linii izokwanty
oznacza spadek jednego i wzrost drugiego
czynnika wytwórczego, przy zachowaniu tego
samego poziomu produkcji.

Izokwanta jest wypukła w stosunku do
początku układu współrzędnych i posiada
ujemne nachylenie, ponieważ wzrostowi
zaangażowania jednego czynnika produkcji
towarzyszy zawsze zmniejszenie wykorzystania
drugiego zasobu i odwrotnie.

Marginalna stopa technicznej substytucji
(MSTS) – stosunek, godnie z którym można

zastąpić jeden czynnik produkcji (pracę) drugim
czynnikiem (kapitał) tak, aby wielkość produkcji

nie uległa zmianie.

Wartość MSTS < 0, ponieważ w miarę
przesuwania się w dół izokwanty występują

ujemne przyrosty kapitału, zaś przy przesuwaniu
się w górę – ujemne przyrosty czynnika pracy.
Jest to konsekwencją wypukłości izokwanty

względem początku układu współrzędnych.

MSTS









Malejąca MSTS oznacza, że w miarę
zastępowania czynnika kapitału przez coraz
większą ilość czynnika pracy zmniejsza się
ilość kapitału, którą można zastąpić przez
każdą dodatkową jednostkę pracy.

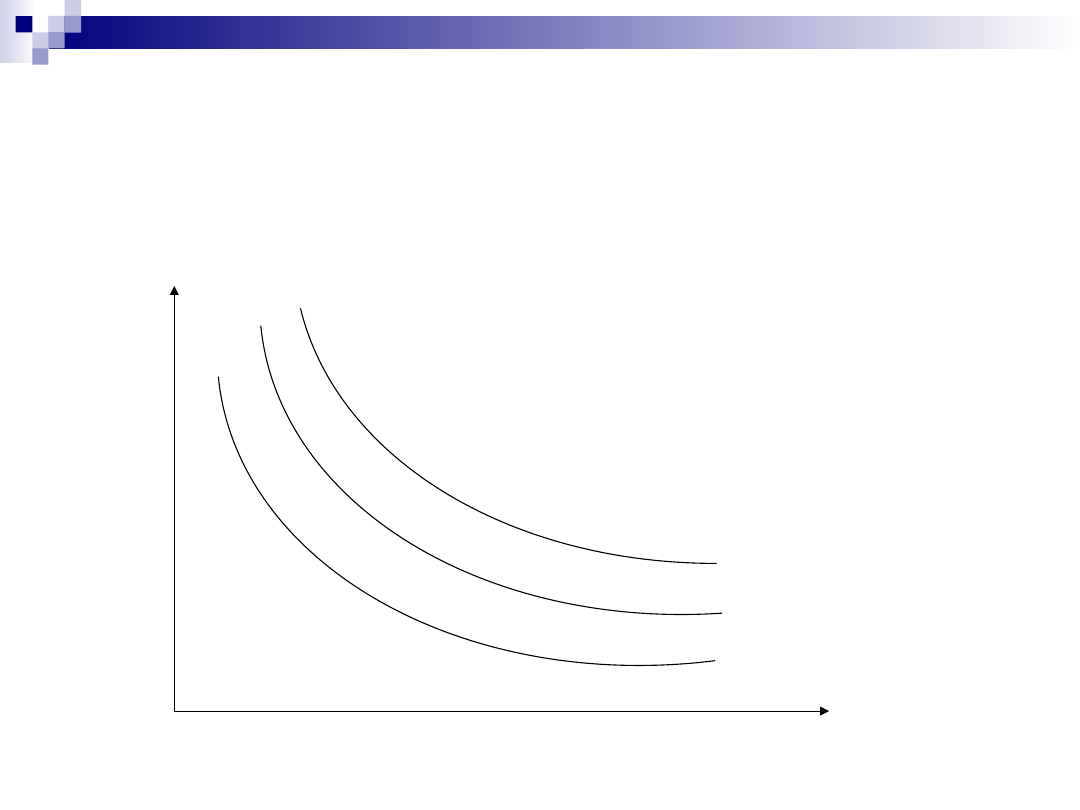
Izokwant produkcji może być nieskończenie
wiele.
Każda z nich prezentuje kombinacje ilościowe
pracy i kapitału, które pozwalają wytworzyć
określone rozmiary produkcji.
K

       Q1
       Q2
       Q3
    L

Izokwanta produkcji Q1 przedstawia wszystkie
efektywne kombinacje ilościowe dwóch czynników
wytwórczych: pracy (L) i kapitału (K), które
pozwalają osiągnąć taki sam poziom produkcji.
Analogiczna sytuacja dotyczy izokwant Q2 i Q3.
Im wyżej położona izokwanta w stosunku do
początku układu współrzędnych, tym większe
rozmiary produkcji można wytworzyć
wykorzystując kombinację zasobów opisanych
przez tę izokwantę (Q1 < Q2 < Q3).
Przemieszczenie się z jednej izokwanty na drugą,
powoduje zmiany wielkości produkcji opisane
przez kombinacje zasobów na izokwancie.

Typowe izokwanty produkcji posiadają cztery

podstawowe własności:

Posiadają nachylenie ujemne,

Nie mogą się przecinać,

Jest ich nieskończenie wiele,

Są wypukłe w stosunku do początku układu
współrzędnych.

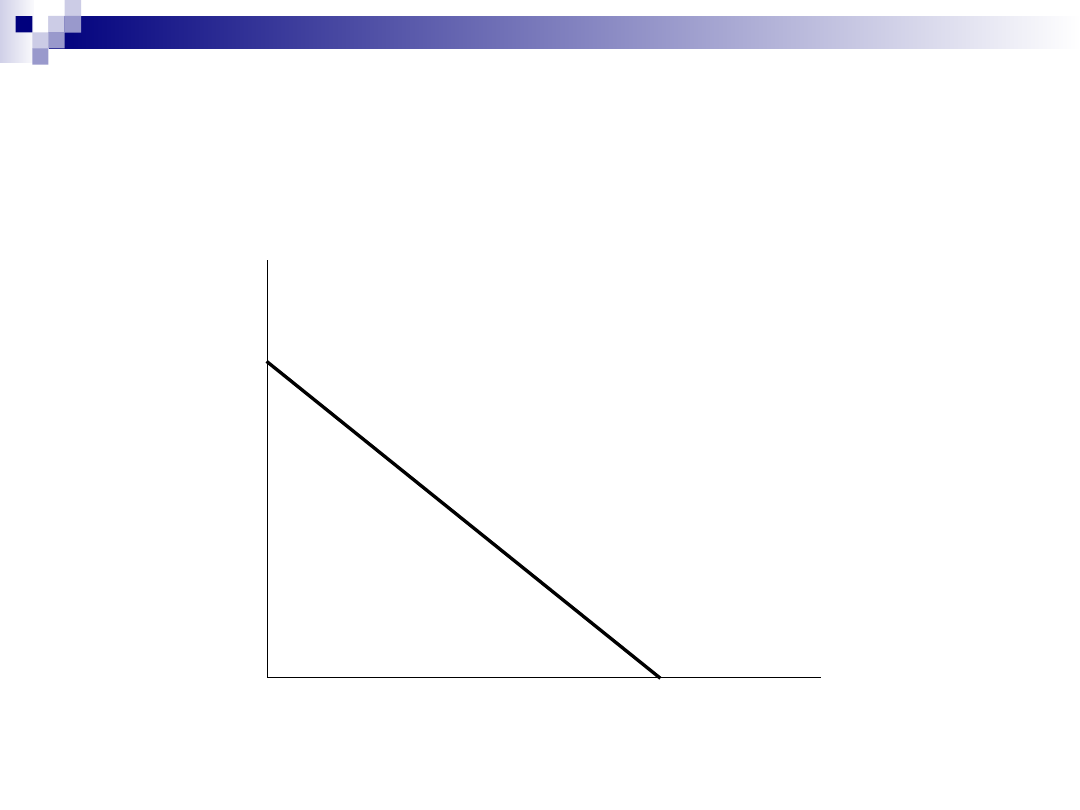
Izokoszta (linia jednakowego kosztu) – zbiór

wszystkich kombinacji nakładów dwóch
czynników produkcji, których koszt całkowity

jest taki sam.

KC/P

0 KC/P

























Jeżeli Q

= 0, wówczas maksymalna ilość czynnika

produkcji L (pracy), którą może nabyć przedsiębiorstwo,
określa relacja kosztu całkowitego do ceny tego
czynnika produkcji, co można zapisać:

Jeżeli Q

= 0, wówczas maksymalna ilość czynnika

produkcji K (kapitału), którą może nabyć
przedsiębiorstwo, określa relacja kosztu całkowitego do
ceny tego czynnika produkcji, co można zapisać:





0





0

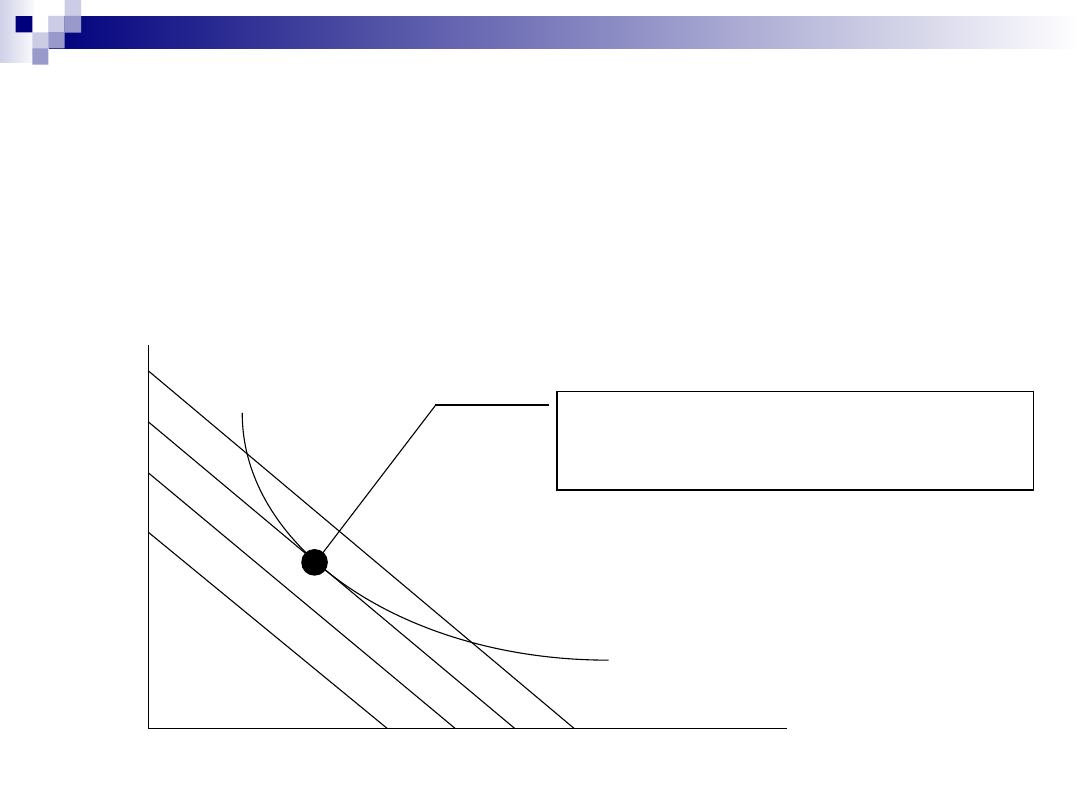
Optymalna kombinacja czynników

produkcji

Kombinacja oszczędna – pozwala wytworzyć dany

poziom produkcji przy jak najniższych kosztach.
Jest to punkt styczności danej izokwanty z możliwie
najniżej położoną izokosztą.

                                          KC1   KC2  KC3  KC4

Optymalna kombinacja

czynników produkcji

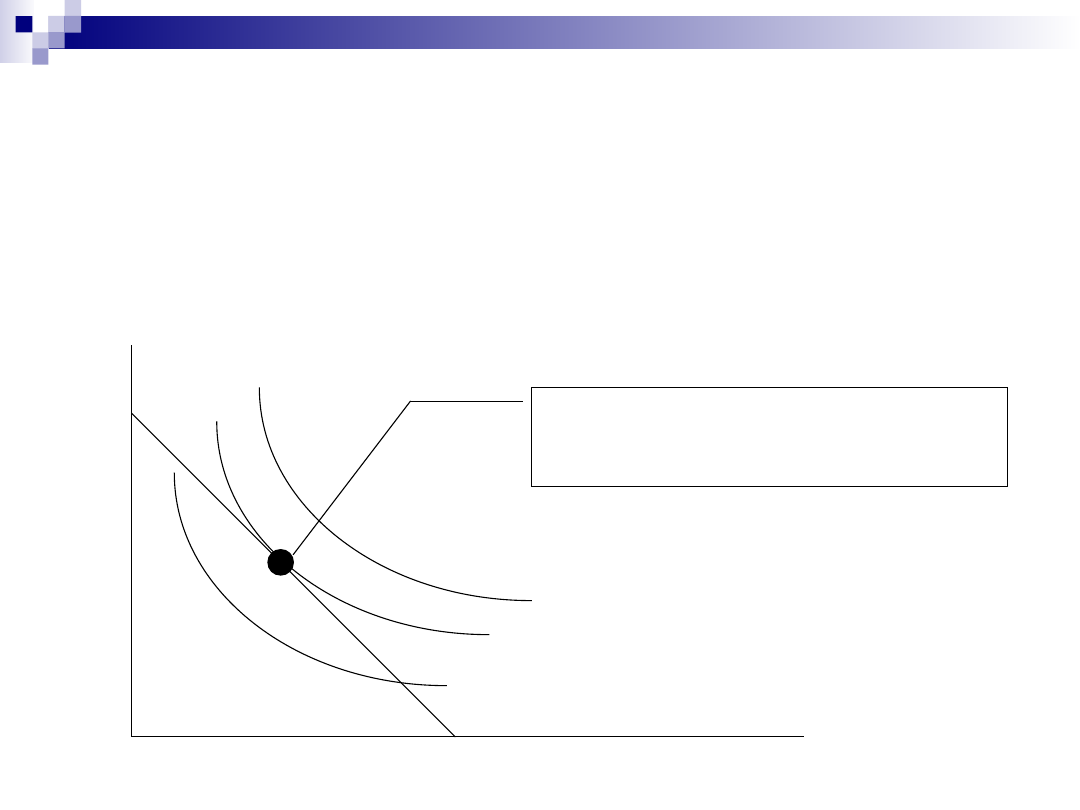
Optymalna kombinacja czynników

produkcji

Kombinacja wydajna – pozwala wytworzyć

maksymalny poziom produkcji przy danych
kosztach.
Jest to punkt styczności danej izokoszty z
możliwie najwyżej położoną izokwantą.

                                                     Q3
                                                    Q2
                                                Q1

Optymalna kombinacja

czynników produkcji

Document Outline

Slide 1
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
Slide 16
Slide 17
Slide 18
Slide 19
Slide 20
Slide 21
Slide 22
Slide 23
Slide 24
Slide 25
Slide 26
Slide 27
Slide 28
Slide 29
Slide 30
Slide 31
Slide 32
Slide 33
Slide 34
Slide 35
Slide 36
Slide 37
Slide 38
Slide 39
Slide 40