Właściwości koligatywne roztworów

Właściwości koligatywne roztworów

Obniżenie prężności par
Rozważamy roztwór złożony z rozpuszczalnika 1 i nielotnej
substancji 2. Ponieważ roztwór jest doskonałym roztworem
rozcieńczonym, rozpuszczalnik spełnia prawo Raoulta:

ponieważ x

1

= 1 – x

2

, czyli:

Stąd

ΔP jest obniżeniem prężności par roztworu w porównaniu z
czystym rozpuszczalnikiem.

1

1 1

*

P

x P

=

(

)

*

1

2

1

1

P

x P

= -

1

1

2 1

*

*

P

PΔP x P

-

=

=

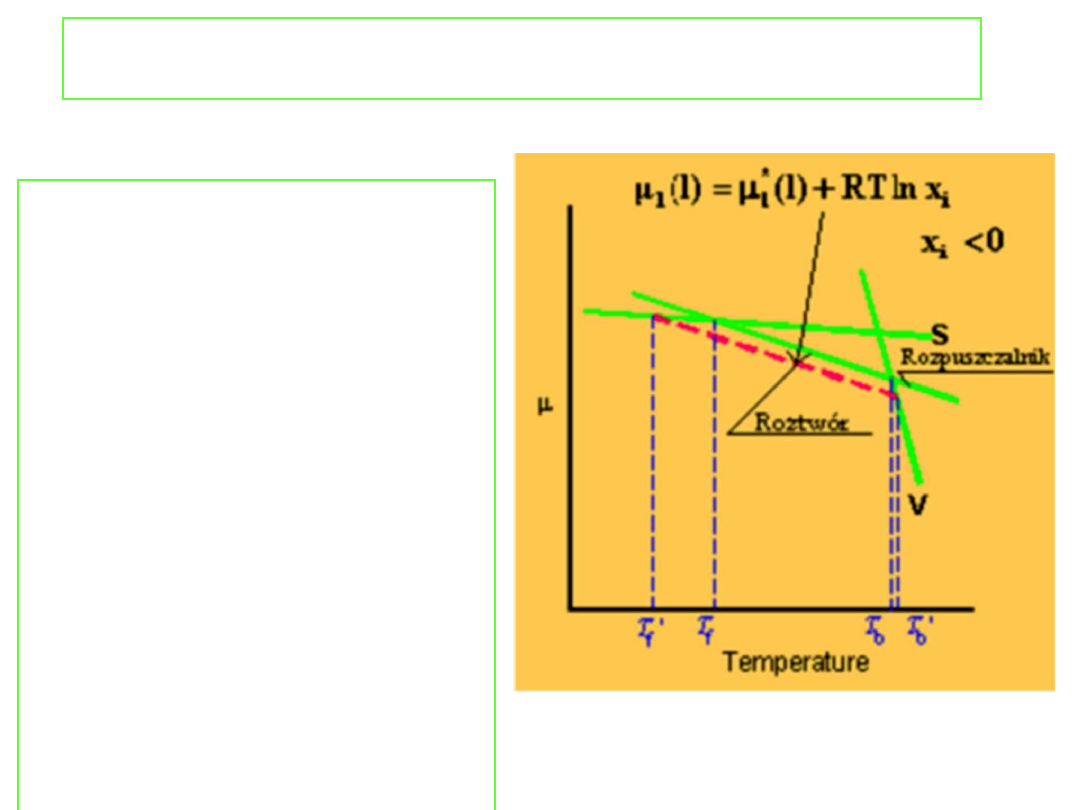
Podwyższenie temperatury
wrzenia

Punkt wrzenia jest
określony przez
temperaturę, w której
prężność par wrzącej
cieczy jest równa ciśnieniu
zewnętrznemu. Można
więc oczekiwać, że skoro
dodatek nielotnej
substancji rozpuszczonej
obniża prężność par
roztworów to również
temperatura wrzenia tego
roztworu musi ulec
podwyższeniu. Jakościowo
efekt ten przedstawia
rysunek:

Właściwości koligatywne roztworów

Właściwości koligatywne roztworów

Właściwości koligatywne roztworów

Dlatego

Na podstawie Gibbsa – Helmholtza

możemy zapisać

gdzie to molowa entalpia parowania
rozpuszczalnika z roztworu. Ponieważ roztwór jest
rozcieńczony możemy przyjąć, że wielkość ta jest równa
molowej entalpii parowania czystego rozpuszczalnika.
Z poprzedniego równania:

*

1

1

1

ln

par

(g)

(c)

Δ G

μ

μ

R x

T

T

-

=

=

2

G

d

H

T

dT

T

D

� �

� �

D

� �=-

1

2

ln

par

par

Δ G

d

T

Δ H

d( x )

R

dt

T

dT

�

�

�

�

�

� -

�

�=

=

par

H

D

1

2

ln

par

Δ H

d x

dT

RT

-

=

Po całkowaniu w granicach między x

1

= 1 czysty rozpuszczalnik,

któremu odpowiada T

w

a x

1

, ułamek molowy rozpuszczalnika w

roztworze, czemu odpowiada temperatura wrzenia roztworu T

w

’:

Właściwości koligatywne roztworów

dT

RT

H

Δ

x

d

x

'

T

T

par

w

w

ln

1

1

ln

ln

2

1









czyli

2

1

1

1

ln

w

par

w

w

w

w

par

w

w

par

T

ΔT

R

H

Δ

' T

T

T

'

T

R

H

Δ

T

'

T

R

H

Δ

x





























przy założeniach, że

(1)

H

Δ

par

jest niezależna od temperatury

(2)

w

w

T

'

T 

czyli

2

w

w

w

T

' T

T



Chcemy znaleźć zależność ΔT od x

2

ułamka molowego substancji rozpuszczonej





2

2

1

1

ln

ln

w

par

T

ΔT

R

H

Δ

x

x









Dla

2

,

0

2



x





...

3

2

1

ln

3

2

2

2

2

x

x

x

x











2

x





(dla x

2

« 1)

Stąd

2

2

x

H

Δ

RT

ΔT

par

w



Zmieniamy ułamek molowy na molalność (m

2

)

1

1

2

1

2

2

1

2

2

M

W

n

n

n

n

n

n

x









W

1

- masa rozpuszczalnika w kg

M

1

– masa molowa rozpuszczalnika

2

1

2

m

W

n



stąd x

2

= m

2

M

1

Właściwości koligatywne roztworów

A w ięc

2

1

2

m

H

Δ

M

RT

ΔT

par

w



Przyjm ując

H

Δ

M

RT

K

par

w

e

1

2



stała ebulioskopow a

otrzym ujem y

2

m

K

ΔT

e





Właściwości koligatywne roztworów

Obniżenie temperatury krzepnięcia
W identyczny, jak poprzednio sposób możemy wyprowadzić wzór na obniżenie
temperatury krzepnięcia roztworu

'

t

T

w stosunku do czystego rozpuszczalnika T

t

2

m

K

T

T

ΔT

k

'

t

t









k

K

stała krioskopowa

gdzie



k

K

stała krioskopowa dana jest wyrażeniem

H

Δ

M

RT

K

top

t

k

1

2



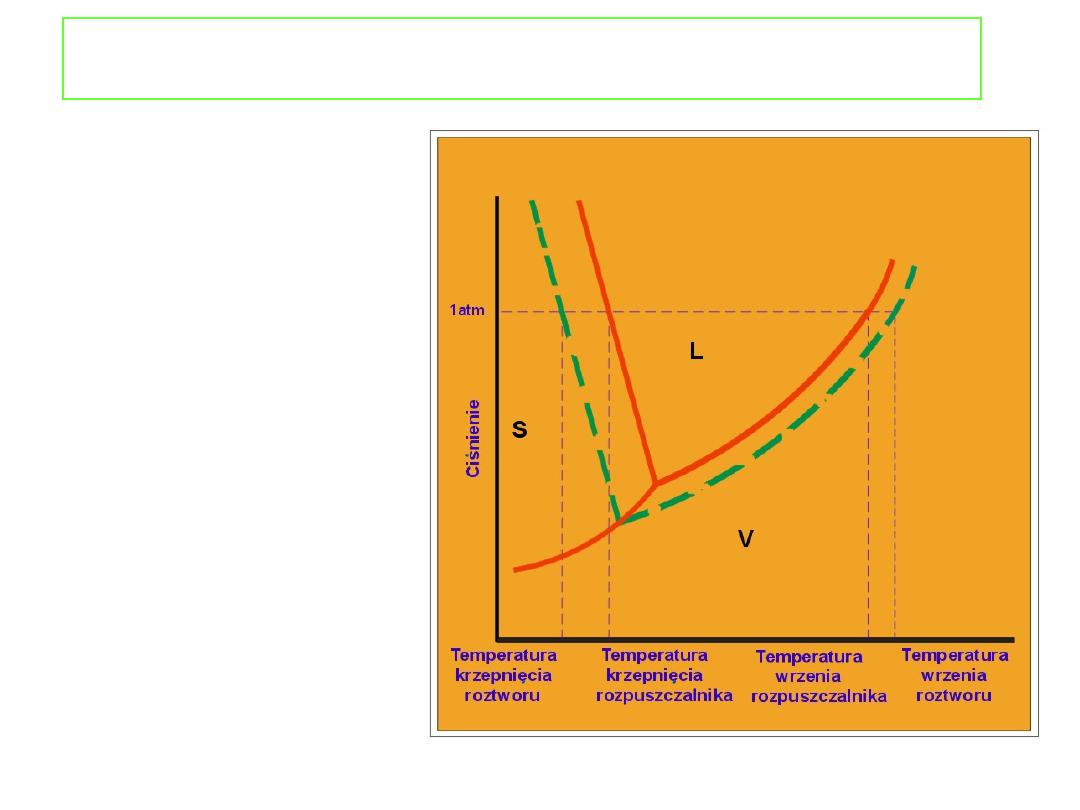
Właściwości koligatywne roztworów

Podwyższenie
temperatury wrzenia i
obniżenie temperatury
krzepnięcia może być
także przedstawione na
wykresie fazowym (np.
wody).

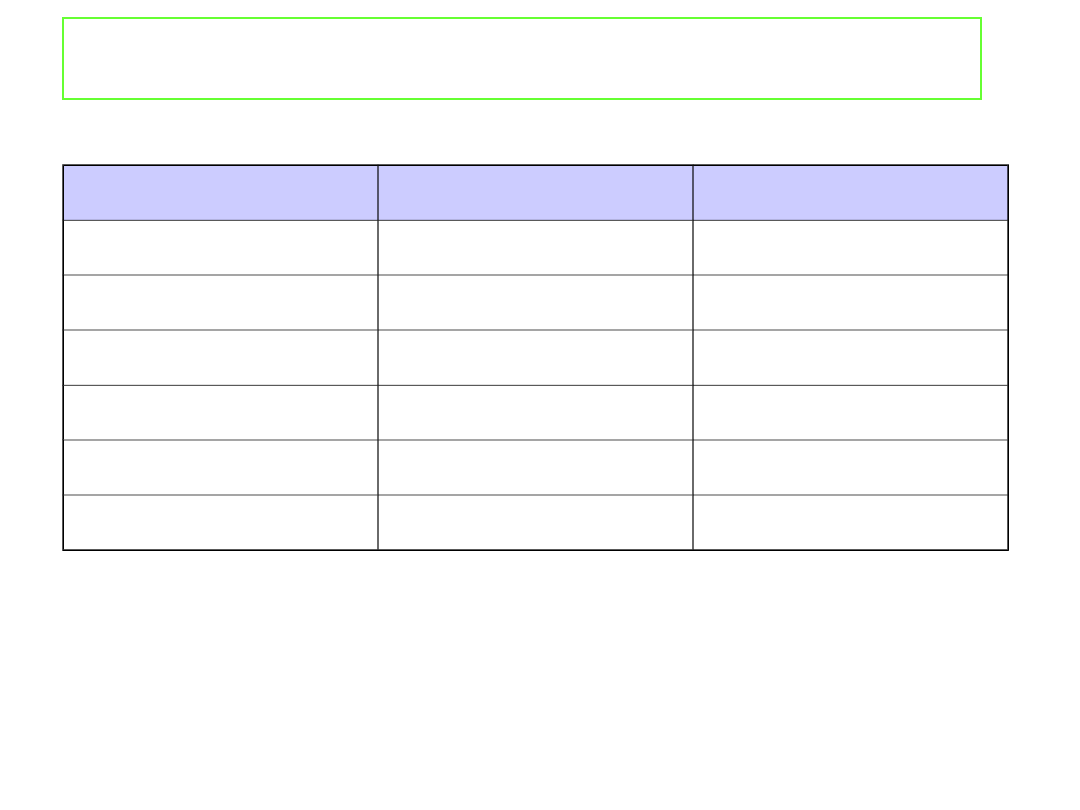
Właściwości koligatywne roztworów

Rozpuszczalnik

K

b

/K mol

-1

·kg

K

f

/K mol

-1

kg

H

2

O

0.51

1.86

C

2

H

5

OH

1.22

-

C

6

H

6

2.53

5.12

CHCl

3

3.63

-

CH

3

COOH

2.93

3.90

CCl

4

5.03

-

Właściwości koligatywne roztworów

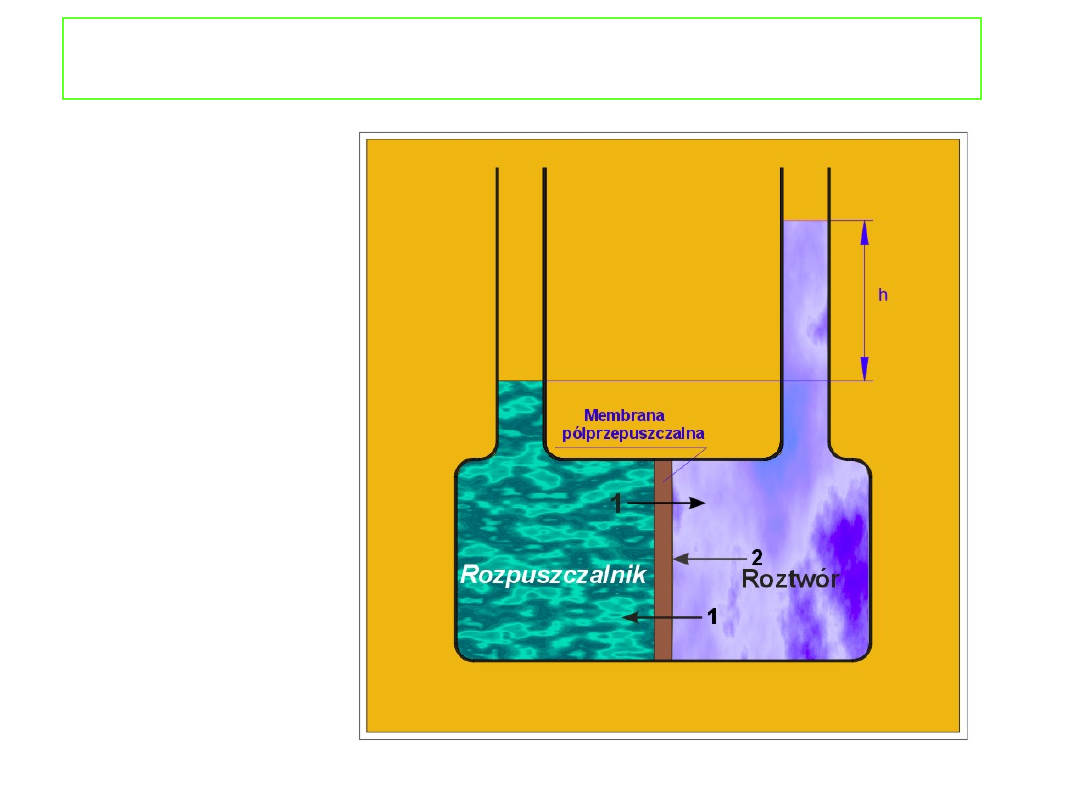
Ciśnienie osmotyczne

Właściwości koligatywne roztworów

O z n a c z a m y

rozp

μ

1

i

R-r

μ

1

- t o p o t e n c j a ł y c h e m i c z n e r o z p u s z c z a l n i k a w c z y s t y m

r o z p u s z c z a l n i k u i w r o z t w o r z e .
P r z e d u s t a l e n i e m s i ę r ó w n o w a g i :

*

rozp

μ

μ

1

1



( x

1

= 1 )

i

1

1

1

ln x

RT

μ

μ

*

R-r





( x

1

< 1 )

S t ą d :

1

1

1

1

1

ln x

RT

μ

μ

μ

μ

*

R-r

*

rozp









N i e r ó w n o ś ć t a w s k a z u j e , ż e w i ę c e j c z ą s t e c z e k p r z e j d z i e z o b s z a r u , w k t ó r y m z n a j d u j e s i ę

c z y s t y r o z p u s z c z a l n i k d o o b s z a r u , g d z i e z n a j d u j e s i ę r o z t w ó r .

Ciśnienie osmotyczne

jest to ciśnienie jakie musi

być przyłożone do roztworu, aby potencjał
chemiczny rozpuszczalnika w roztworze wzrósł do
wartości potencjału chemicznego czystego
rozpuszczalnika pozostającego pod ciśnieniem
atmosferycznym.

W stanie równowagi:

V

π

x

RT

μ

μ

μ

*

R-r

rozp









1

1

1

1

ln

Ponieważ

*

rozp

μ

μ

1

1



więc

1

lnx

RT

V

π





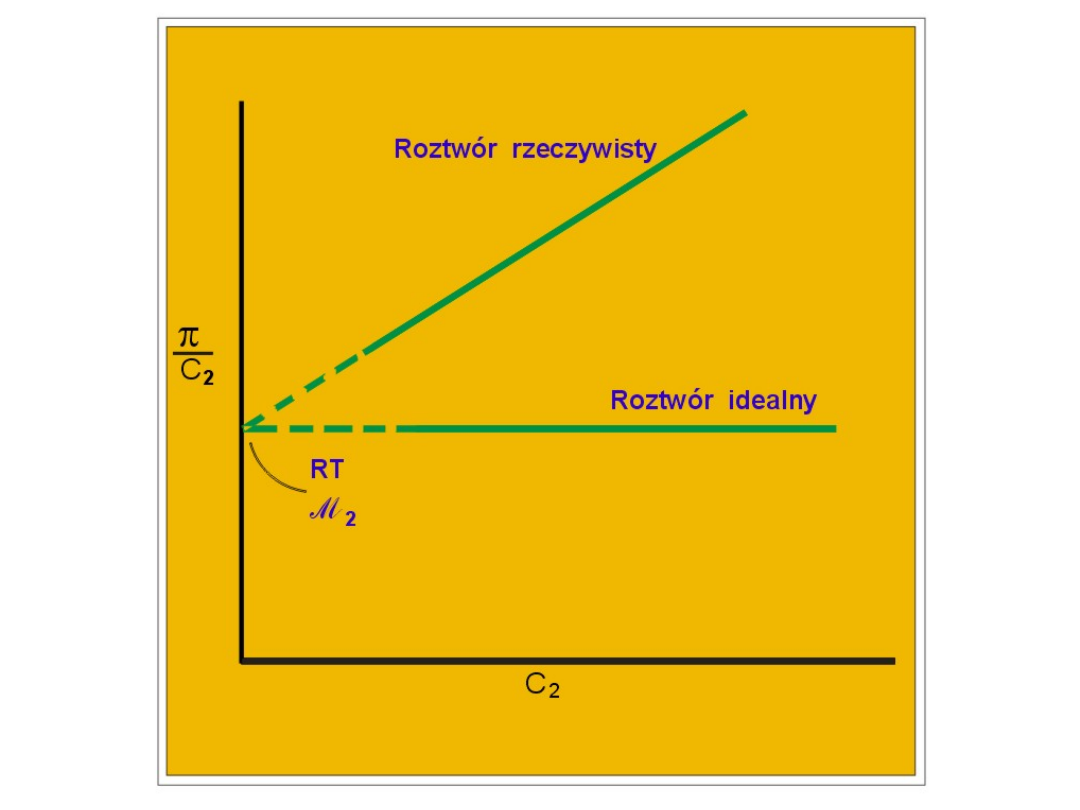
Z a k ł a d a m y , ż e





2

2

1

1

ln

ln

x

x

x















1

2

x 

i ż e

1

2

2

1

2

2

n

n

n

n

n

x











2

1

n

n 

W ó w c z a s

















1

2

2

n

n

RT

RTx

V

π

1

n

V

V 

1

2

1

n

n

RT

n

V

π



c z y l i

RT

n

πV

2



i

RT

c

RT

V

n

π

M





2

g d z i e c

M

to m o l a rn o ś ć ro z tw o ru .

P

rzyjm

u

jąc, że c

2

to stężen

ie roztw

oru

w

g/ dm

-3

, M

2

to m

asa m

olow

a substan

cji

rozpu

szczonej m

ożem

y zapisać:

RT

M

c

π

2

2



i

2

2

M

RT

c

π



R

ów

n

an

ie to pozw

ala n

a w

yzn

aczen

ie m

asy m

olow

ej su

bstan

cji rozpu

szczon

ej.

Równowaga chemiczna w stanie gazowym -

gazy doskonałe

Równowaga chemiczna w stanie gazowym - gazy

doskonałe

Reakcja przebiega w takim kierunku, aby następowało
zmniejszanie entalpii swobodnej, tzn. (∂G/ ∂ζ)

T,P

< 0.

Stąd reakcja A → B jest samorzutna gdy μ

B

> μ

A

, a reakcja B

→A jest samorzutna, gdy μ

B

< μ

A

. W stanie równowagi μ

A

= μ

B

i

(∂G/∂ξ)

T,P

= 0.

Równowaga chemiczna w stanie gazowym - gazy

doskonałe

Δ

r

G < 0 reakcja A → B jest

samorzutna

Δ

r

G > 0 reakcja B → A jest

samorzutna

Δ

r

G = 0 układ jest w równowadze

Równowaga chemiczna w stanie gazowym - gazy

doskonałe

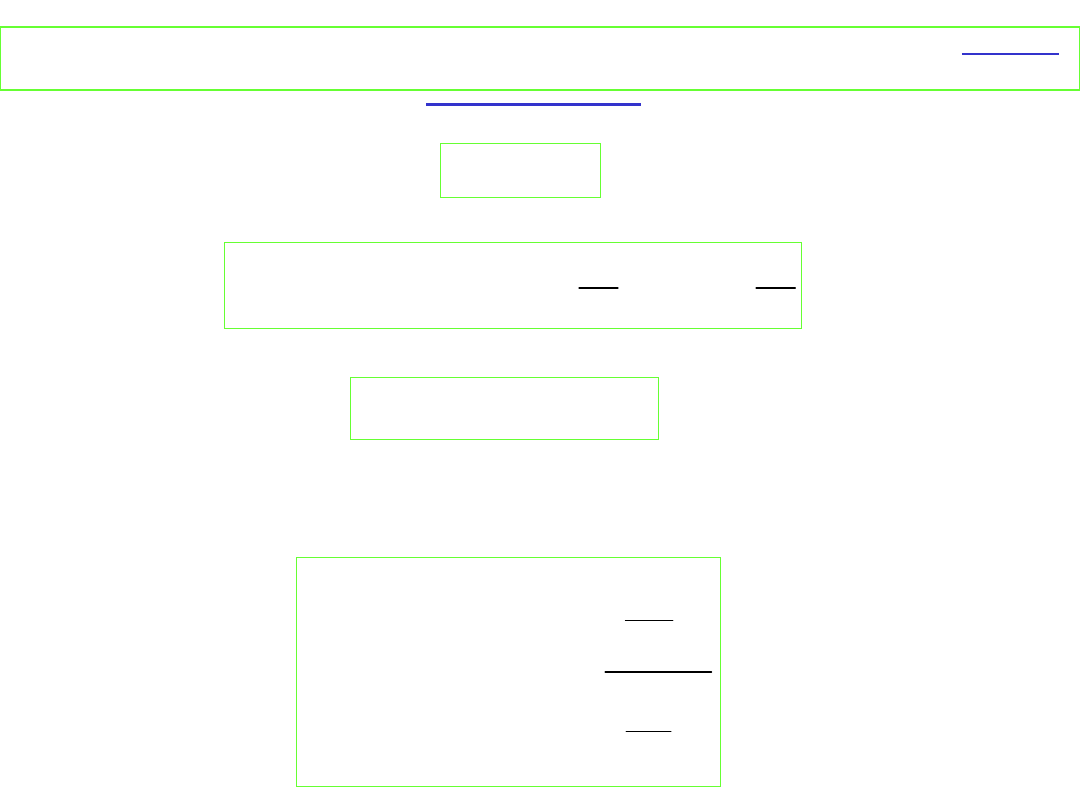
Rozpatrzmy przypadek:

gdzie a i b to współczynniki stechiometryczne.
W roztworach doskonałych potencjał chemiczny i-tego
składnika opisuje równanie:

P

i

– ciśnienie cząstkowe składnika i

- standardowy potencjał chemiczny składnika i

P˚ = 1 bar
Stąd

(g)

(g)

bB

aA









P

P

RT

μ

μ

i

ln

1

1







1

μ





P

P

RT

μ

μ

A

A

A

ln









P

P

RT

μ

μ

rs

B

B

ln





Równowaga chemiczna w stanie gazowym - gazy

doskonałe

Zmiana entalpii swobodnej reakcji A → B jest równa

więc

Ponieważ

- standardowa zmiana entalpii swobodnej reakcji

więc

A

B

aμ

bμ 









P

P

a RT

P

P

b RT lu

aμ

bμ

G

Δ

A

B

A

B

r

ln















A

B

r

aμ

bμ

G

Δ







G

Δ

r

a

A

b

o

B

r

r

P

P

P

P

RT lu

G

Δ

G

Δ

































Równowaga chemiczna w stanie gazowym - gazy

doskonałe

Zdefiniujmy ciśnieniową stałą równowagi:

W stanie równowagi , więc:

i

Równanie to jest jednym z najważniejszych i użytecznych
równań w termodynamice chemicznej. Wiąże ono w bardzo
prosty sposób (ciśnieniową) stałą równowagi i zmianę
standardowej entalpii swobodnej reakcji Δ

r

G

o

. Wartość Δ

r

G

o

zależy od temperatury oraz rodzaju substratów i produktów.

 

b

a

o

a

A

b

B

a

o

A

b

o

B

p

P

P

P

P

P

P

P

K































0



G

Δ

r

p

o

r

K

RT

G

Δ

ln

0





p

o

r

K

RT

G

Δ

ln





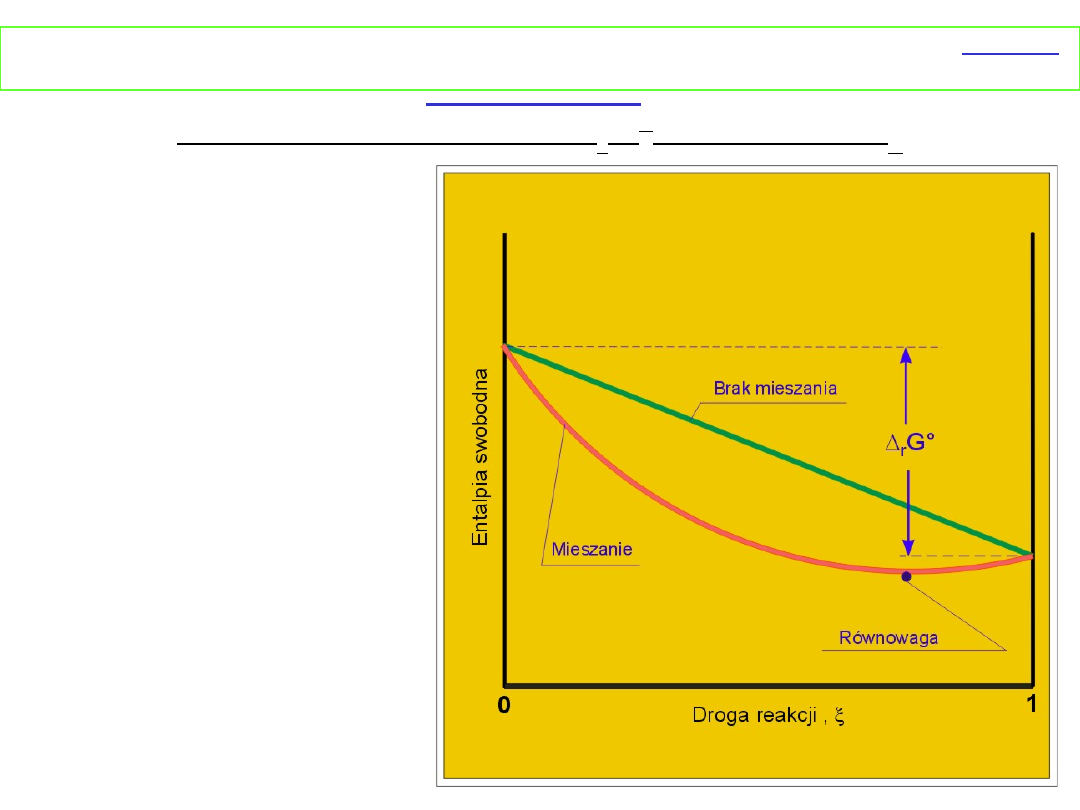
Równowaga chemiczna w stanie gazowym - gazy

doskonałe

Dyskusja równania Δ

r

G

o

= - RT ln K

p

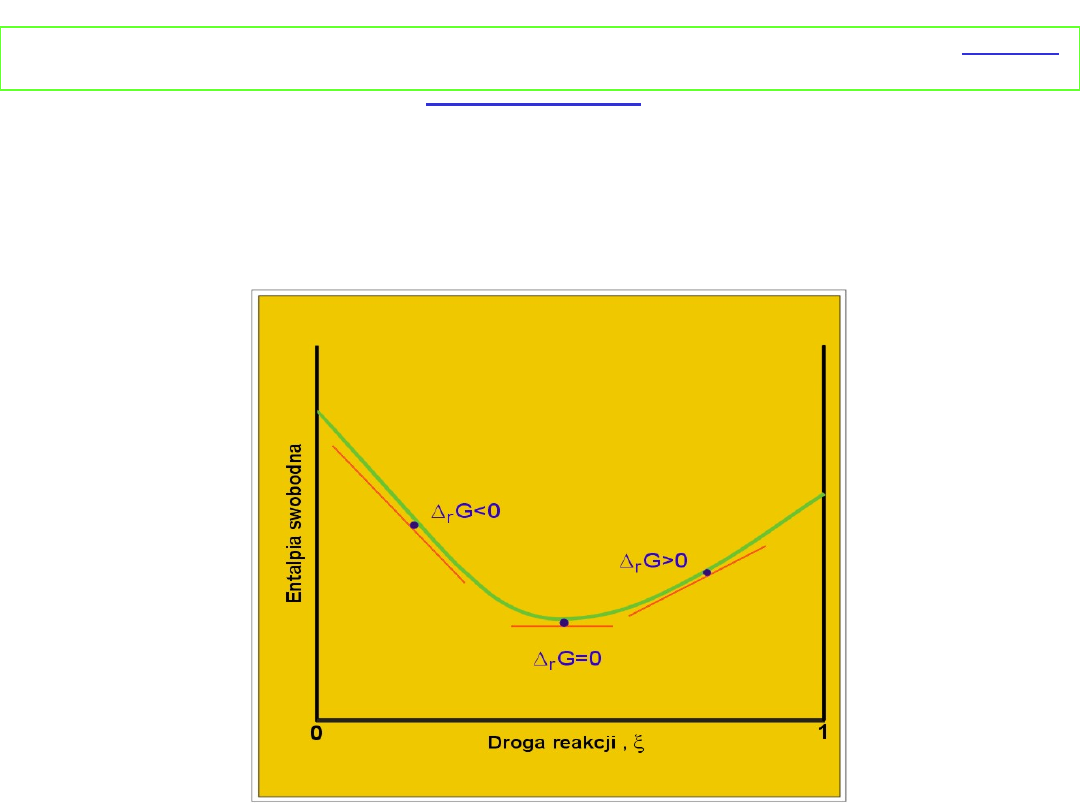
I.      Zmiana

entalpii swobodnej
podczas reakcji

w

zależności od
postępu reakcji przy
założeniu,
że Δ

r

G

o

< 0

przedstawia rysunek
obok.

)

(

)

(

g

g

bB

aA




Równowaga chemiczna w stanie gazowym - gazy

doskonałe

Jeżeli reagenty nie mieszają się z produktami,
entalpia swobodna maleje liniowo
w miarę postępu reakcji i w rezultacie substraty zostaną
zamienione w produkty. Jak wyprowadziliśmy wcześniej
Δ

miesz

G jest zawsze ujemna, dlatego w przypadku mieszania

się substratów i produktów entalpia swobodna będzie
miała mniejsze wartości niż w poprzednim przypadku
(niemieszanie). Dlatego też stan równowagi zostanie
osiągnięty, gdy zrównają się entalpie swobodne dwóch
przeciwstawnych efektów przemiana substratów w produkt
i mieszanie produktów z substratami.

II. Znając Δ

r

G

o

możemy obliczyć K

p

. Ponieważ









sub

o

tw

prod

o

tw

o

r

G

Δ

G

Δ

G

Δ













III. Gdy:
Δ

r

G

o

< 0

K

p

> 1

Δ

r

G

o

> 0

K

p

< 1

Δ

r

G

o

= 0

K

p

= 1

Gdy Δ

r

G

o

> 0 nie oznacza to, że nie zachodzi reakcja. Np. gdy

Δ

r

G

o

= 10 kJ mol

-1

i T = 298 K, K

p

= 0,018 i pewna ilość produktów

powstanie, szczególnie gdy substraty są w dużych ilościach.

Równowaga chemiczna w stanie gazowym - gazy

doskonałe

IV. K

p

zależy wyłącznie od temperatury (ponieważ μ

o

zależy

wyłącznie od temperatury) i jest bezwymiarowa (dzielimy
ciśnienie przez P˚).

V.Dla dowolnego stanu w postępie reakcji możemy

obliczyć Δ

r

G

gdzie Q – iloraz stężeń produktów od substratów.

Pozwala nam to określić w jakim kierunku zachodzi

reakcja samorzutnie jeżeli znamy stężenia reagentów.

Q

RT

G

Δ

G

Δ

o

r

r

ln





Równowaga chemiczna w stanie gazowym - gazy

rzeczywiste

Zachowanie gazów
rzeczywistych opisano
poprzez równania
wirialne i van der Waalsa

(i mogą być inne).

Zastosowanie procedury
podobnej do użycia
aktywności w przypadku
roztworów ciekłych.
Ciśnienie cząstkowe
zastępuje się wielkością
zwaną lotnością (f) i dla
gazów rzeczywistych
otrzymujemy równanie:

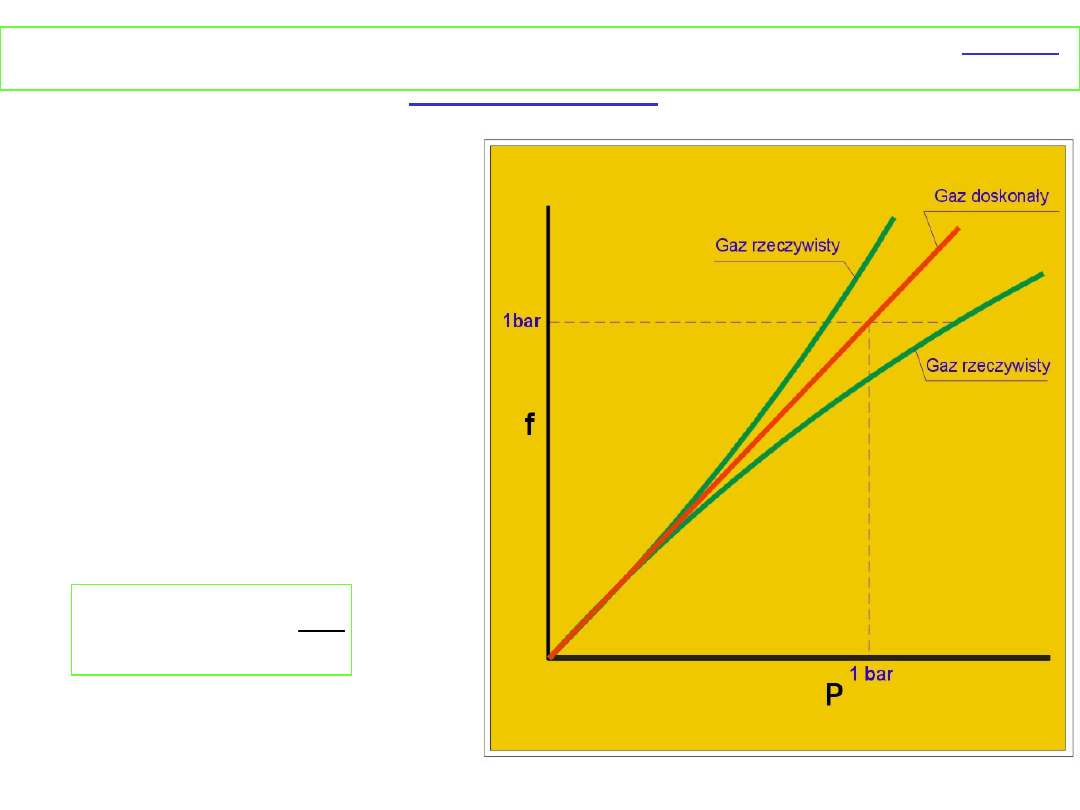
Zależność lotności od
ciśnienia przedstawia
rysunek

o

o

P

f

RT

μ

μ

ln





Równowaga chemiczna w stanie gazowym - gazy

rzeczywiste

Dla małych ciśnień gaz rzeczywisty zachowuje się jak gaz
doskonały i lotność jest równa ciśnieniu cząstkowemu, dla
wyższych ciśnień występują odstępstwa. Stan standardowy
lotności gazu rzeczywistego to stan, w którym lotność byłaby
równa 1 bar gdyby gaz zachował się doskonale
 
Ogólnie:

Współczynnik lotności α jest zdefiniowany jako:

i

Lotności nie można zmierzyć. Można ją jedynie obliczyć na
podstawie pomiarów ciśnienia.

P

f

P



 0

lim

P

f

α

1

lim

0





α

P

Równowaga chemiczna w stanie gazowym - gazy

rzeczywiste

Dla dyskutowanej wcześniej reakcji

możemy zapisać wyrażenie na stałą równowagi K

f

(f-lotność)

gdzie K

f

to termodynamiczna stała równowagi

Ponieważ f = γP powyższe równanie można zapisać jako:

gdzie ,

a K

p

zdefiniowana była poprzednio – nazywana jest pozorną

stałą równowagi, ponieważ jej wartość dla danej temperatury
zależy od ciśnienia.
Dla gazu doskonałego K

f

= K

p

.

)

(

)

(

g

g

bB

aA












a

A

b

B

f

/

f

/

f

K

bar

1

bar

1











p

γ

a

A

b

B

a

A

b

B

f

K

K

/

P

/

P

γ

γ

K







1bar

1bar

a

A

b

B

γ

γ

γ

K 

Równowaga chemiczna w stanie gazowym - gazy

rzeczywiste

Dla reakcji

stałe równowagi w temperaturze 450˚C przedstawia tablica:

(g)

(g)

(g)

NH

H

N

3

2

2

2

2

3

2

1






Ciśnienie
całkowite/bar

3

NH

P

2

N

P

2

N

P

p

K

γ

K





Kγ

K

K

p

f

10,2

0,204

2,30

7,67 0,0064

0,994

0,0064

30,3

1,76

6,68 21,9 0,0066

0,975

0,0064

50,6

4,65 10,7 35,2 0,0068

0,95

0,0065

101,0

16,6 19,4 65,0 0,0072

0,89

0,0064

302,8

108

42,8 152

0,0088

0,70

0,0062

606

326

56,5 223

0,0130

0,50

0,0065

 Reakcje w roztworach ciekłych

Dla reakcji

zakładamy, że A i B są nieelektrolitami. Jeżeli roztwór
jest doskonały i stężenie wyrazimy jako molalność
otrzymujemy:

to stężenie

)

(

)

(

r

r

bB

aA






m

m

RT

μ

μ

A

o
A

A

ln







m

rozp

kg

mol

1

 Reakcje w roztworach ciekłych

Stosując te same przekształcenia jak dla gazów doskonałych
otrzymujemy:

gdzie

Jeżeli stężenie wyrazimy jako molarność (mol dm

-3

) stała

równowagi przybiera postać:

stężeniowa stała
równowagi

Zarówno K

m

jak i K

c

są bezwymiarowe, ponieważ stężenia są

dzielone przez

standardowe (odpowiednio i
).

m

r

K

RT

G

Δ

ln







a

A

b

B

m

m

m

m

m

K































 

 

a

b

c

/

A

/

B

K



























3

3

dm

mol

1

dm

mol

1

(rozp)

kg

mol

1

ru)

(r

dm

mol

1

3



 Reakcje w roztworach ciekłych

W warunkach odbiegających od stanu równowagi entalpia
swobodna reakcji opisana jest równaniem

Q - iloczyn stężeń
W przypadku roztworów niedoskonałych stężenia zastępujemy
poprzez aktywności.
Potencjał chemiczny i-tego składnika wynosi więc

Wychodząc z wyrażenia opisującego potencjał chemiczny i-
tego składnika możemy otrzymać wyrażenie na
termodynamiczną stałą równowagi

a ponieważ

Q

RT

G

Δ

G

Δ

r

r

ln







i

o

i

i

a

RT

μ

μ

ln





a

A

b

B

a

a

a

K 

m

γ

a





 Reakcje w roztworach ciekłych

więc









m

γ

a

A

b

B

a

A

b

B

a

K

K

/m

m

/m

m

x

γ

γ

K









Równowaga w układzie heterogenicznym

Rozważmy rozkład termiczny CaCO

3

w układzie zamkniętym

CaCO

3(s)

CaO

(s)

+ CO

2(g)

 

Zwykle stężeń ciał stałych nie uwzględnia się w opisie stałej
równowagi.
Dlatego zapisując powyższe wyrażenie na stałą równowagi
jako:

i uwzględniając, ze stężenia CaCO

3

i CaO są stałe możemy

zapisać











3

2

CaCO

CO

CaO



'

c

K













2

3

CO

CaO

CaCO



'

c

K





2

CO



c

K

W opisanych warunkach łatwiej zmierzyć ciśnienie CO

2

więc

możemy zapisać

K

c

i K

p

to wielkości bezwymiarowe, bowiem stężenie CO

2

i

ciśnienie CO

2

są

podzielone przez odpowiednie wielkości standardowe (
i 1 bar).

Dla termodynamicznej stałej równowagi

Z definicji
i

Dla niezbyt wysokich ciśnień możemy założyć, że CO

2

zachowuje się jak gaz doskonały

2

CO

P

K

P



3

-

dm

mol

mol

1

3

2

CaCO

CO

CaO

a

a

a

K

a





1

CaO

CaCO

3



a

a

bar

1

2

CO

f

K

a



bar

1

2

CO

P

K

K

p

a





Równowaga w układzie heterogenicznym

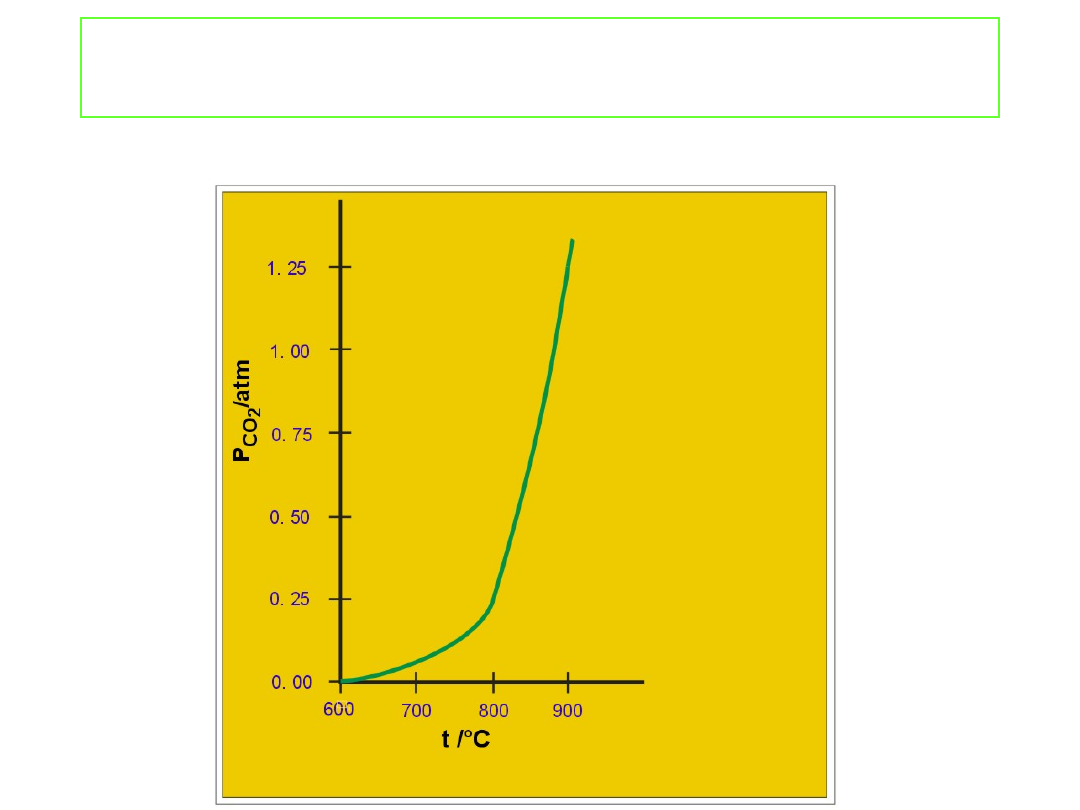
Równowaga w układzie heterogenicznym

Równowagowe ciśnienie CO

2

w kontakcie z CaCO

3

i CaO w

funkcji temperatury.

Wpływ temperatury na stałą równowagi.

Dla reakcji w stanie równowagi

z równania Gibbsa – Helmholtza

K

RT

G

Δ

r

ln







2

T

H

Δ

T

T

G

Δ

r

P

r





















































Otrzymuje

i

Jest to równanie van’t Hoff’a.

2

ln

T

H

Δ

T

T

K

RT

r

P











































 



2

ln

RT

H

Δ

K

K

r

P





















Wpływ temperatury na stałą równowagi.

Wpływ temperatury na stałą równowagi.

Zakładając, że Δ

r

H˚ nie zależy od temperatury można

scałkować powyższe równanie otrzymując:

Ponieważ

i

otrzymujemy

Jest to inna postać równania vant’a Hoffa.

2

1

1

2

2

1

1

2

1

1

ln

T

T

T

T

R

H

Δ

T

T

R

H

Δ

K

K

r

r

























RT

G

Δ

K

r







ln







S

TΔ

H

Δ

G

Δ

r

r

r





R

S

Δ

RT

H

Δ

K

r

r











ln

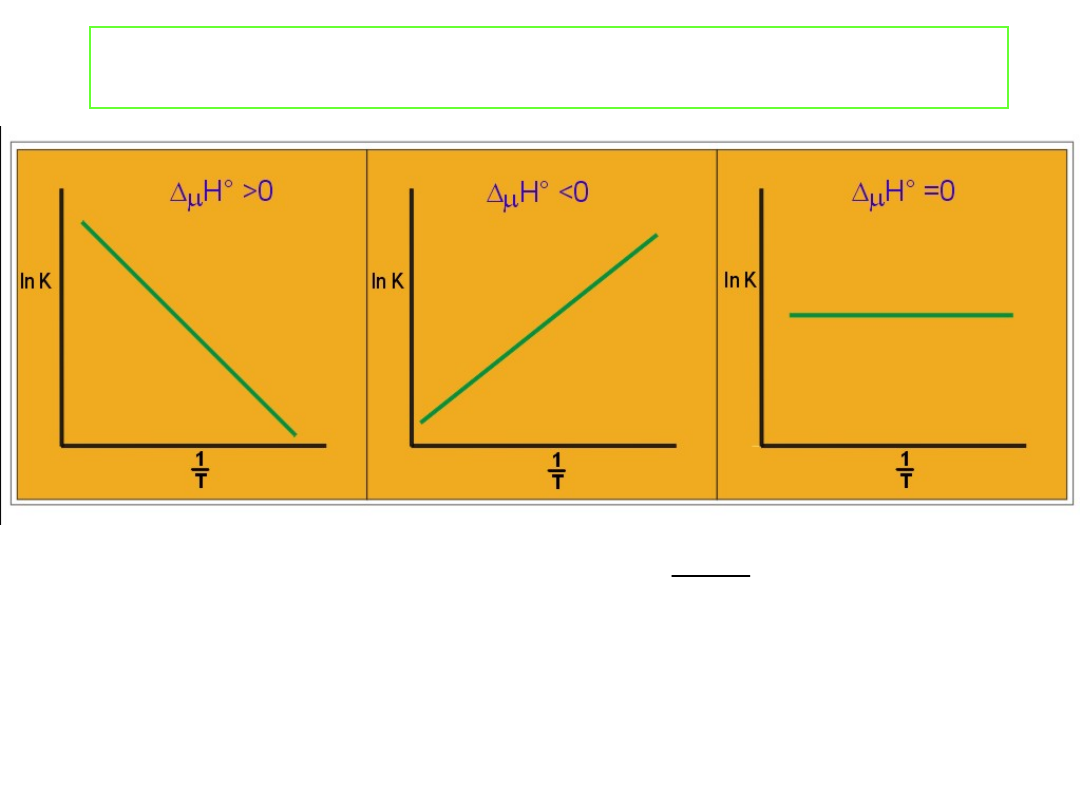
Wpływ temperatury na stałą równowagi.

Współczynnik kierunkowy Δ

r

H˚/R, a wyraz wolny

Linie proste otrzymamy jedynie wówczas gdy Δ

r

H˚ i Δ

r

S˚ są

niezależne od temperatury. Dla małych zakresów temperatur
około 50 K założenie to jest spełnione dość dobrze i metoda ta
pozwala w dogodny sposób wyznaczyć Δ

r

H˚

i Δ

r

S˚ dla danej reakcji.

R

S

Δ

r



Dyskusja równania van’t Hoffa

Jeżeli proces A → B jest endotermiczny, wówczas Δ

r

H˚ jest

dodatnie.
Gdy T

2

> T

1

prawa strona równania

jest dodatnia, a więc

Jeżeli proces A → B jest egzotermiczny Δ

r

H˚ jest ujemne to

lewa strona powyższego równania jest również ujemna i

Wzrost temperatury przesuwa równowagę z lewa na prawo -
dla procesu endotermicznego, a dla procesu egzotermicznego,
równowaga wraz ze wzrostem temperatury przesuwa się z
prawa na lewo. Jest to zgodne z zasadą Le Chatelier’a (regułą
przekory).

Reguła przekory (reguła Le Chateliera i Brauna)

określa

kierunek przesunięcia równowagi chemicznej. Zgodnie z tą
regułą, w przypadku zmiany parametrów reakcji chemicznej
(temperatury, ciśnienia, stężenia) równowaga układu
przesuwa się w takim kierunku, aby przeciwdziałać tej
zmianie.

1

2

1

2

1

2

ln

T

T

T

T

R

H

Δ

K

K

r







1

2

K

K 

1

2

K

K 

Dyskusja równania van’t Hoffa

Reakcja syntezy amoniaku:
N

2(g)

+ 3H

2

(g)

2NH

3

(g)

ΔH˚ = – 46,19 kJ mol

-1

ΔH˚ = „-” reakcja łączenia azotu z wodorem jest
egzotermiczna - przebiega z wydzieleniem ciepła, procesowi
temu będzie sprzyjało obniżenie temperatury. Wzrost
temperatury spowoduje natomiast przesunięcie równowagi w
stronę azotu i wodoru (rozpad amoniaku).

Reakcja zachodzi w fazie gazowej: z wartości współczynników
stechiometrycznych wynika, że w przypadku stałej objętości
układu przebieg reakcji w prawą stronę prowadzi do
zmniejszenia ciśnienia – z 4 objętości (N

2

+ 3H

2

) powstają 2

objętości (2NH

3

). Zatem wzrost ciśnienia zewnętrznego

powoduje przesunięcie równowagi w stronę prawą, a obniżenie
ciśnienia w lewą.

Dodanie do układu będącego w równowadze jakiejkolwiek
substancji biorącej udział
w reakcjach spowoduje przesunięcie równowagi w stronę
przeciwną niż ta, po której znajduje się dana substancja. Tak
więc wzrost stężenia wodoru i azotu przesuwa równowagę
rozpatrywanej reakcji w prawo, a wzrost stężenia amoniaku w
lewo.

Wpływ ciśnienia na stałą równowagi

Δ

r

G˚ = – RT ln K

p

Δ

r

G˚ nie zależy od ciśnienia, ponieważ jako wartość

standardowa jest zdefiniowana dla określonego ciśnienia 1
bar.
Pozorna stała równowagi K

p

jest niezależna od ciśnienia tylko

wówczas, gdy reagują gazy doskonałe. Dla gazów
rzeczywistych K

p

zależy od ciśnienia. Termodynamiczna stała

równowagi K

f

jest niezależna od stężenia zarówno dla gazów

doskonałych jak i rzeczywistych.
Dla reakcji, w których uczestniczą gazy doskonałe K

f

= K

p

i dla

stałej temperatury możemy zapisać

0

P

K

T

p



















Wpływ ciśnienia na stałą równowagi

Reakcja między doskonałymi gazami, będącą w stanie
równowagi:

n - liczba moli substancji A, przed reakcją,
α – ułamek mola substancji A, który przereagował wówczas w
stanie równowagi
liczba moli substancji A n(1-α)
liczba moli substancji B 2nα
Sumaryczna liczba moli w stanie równowagi:
n - nα + 2nα = n + nα = n (1 + 2)
a ułamki molowe substancji A i B wynoszą:

(g)

(g)

2B

A












α

α

α

n

α

n

x

A













1

1

1

1





α

α

α

n

nα

x

B









1

2

1

2

Ciśnienia cząstkowe A i B

P – całkowite ciśnienie panujące w układzie
Stałą równowagi opisuje zależność:

P

α

α

P

A







1

1

P

α

α

P

B





1

2

P

α

α

P

α

α

P

α

α

P

P

K

A

B

p

2

2

2

2

2

1

4

1

1

1

2



























Wpływ ciśnienia na stałą równowagi

Wpływ ciśnienia na stałą równowagi

K

p

jest wielkością stałą, więc wartość α zależy wyłącznie od P.

Jeżeli P jest duże
α jest małe i odwrotnie, jeżeli P jest małe α jest duże. Jest to
zgodna z zasadą
Le Clateliera. Jeżeli zwiększymy ciśnienie, równowaga
przeniesie się w stronę, która daje mniej cząsteczek (od
prawej do lewej w rozpatrywanym przypadku)
i α maleje. Gdy obniżymy ciśnienie, zachodzą przeciwne efekty.

P

K

K

α

p

p

4



