Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

1/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

INTERNAL FORCES

IN BARS

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

2/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

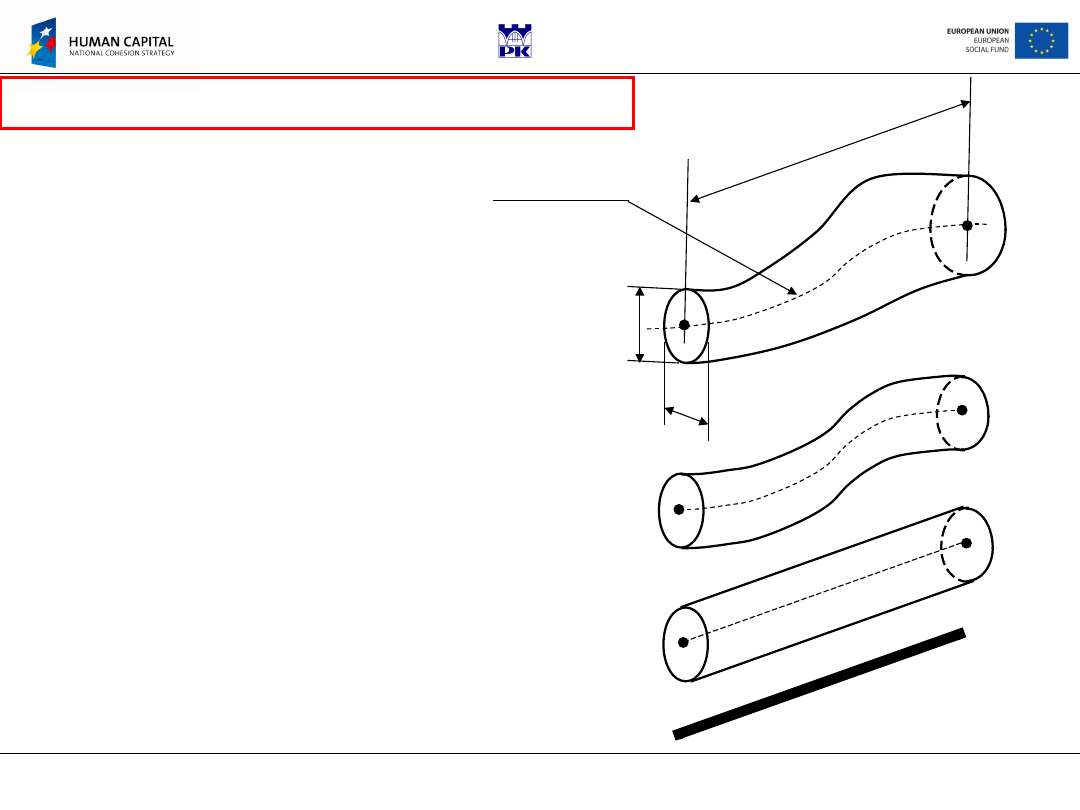
Definitions

L

H

B

•Bar – a body for which L»H,B
•Bar axis - locus of

gravitational centres of bar
sections cutting its surface

•Prismatic bar – when

generator of bar surface is
parallel to the bar axis

•Straight bar – when bar axis

is a straight line

Bar axis

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

3/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

Assumptions

•Bar axis represents the whole

body and loading is applied not
to the bar surface but the bar
axis

•Set of bar and loading will be

considered as

the

plane one if

forces acts in plane of the bar.

P

q

M

.

M

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

4/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

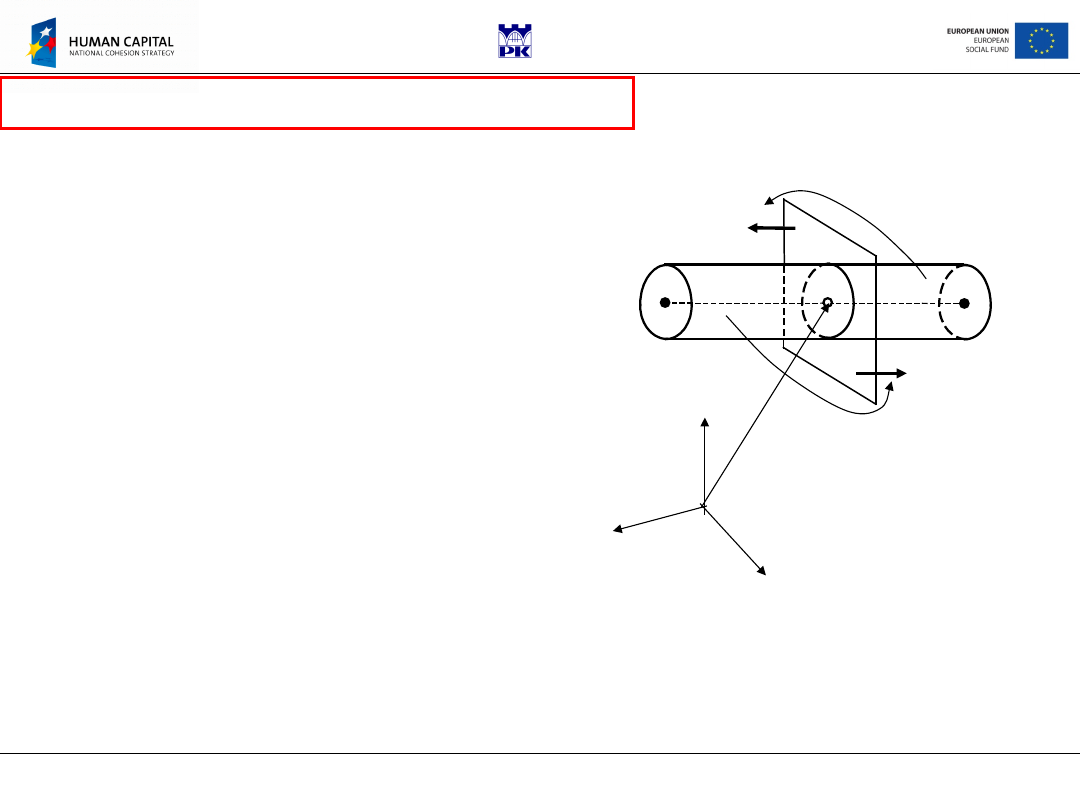
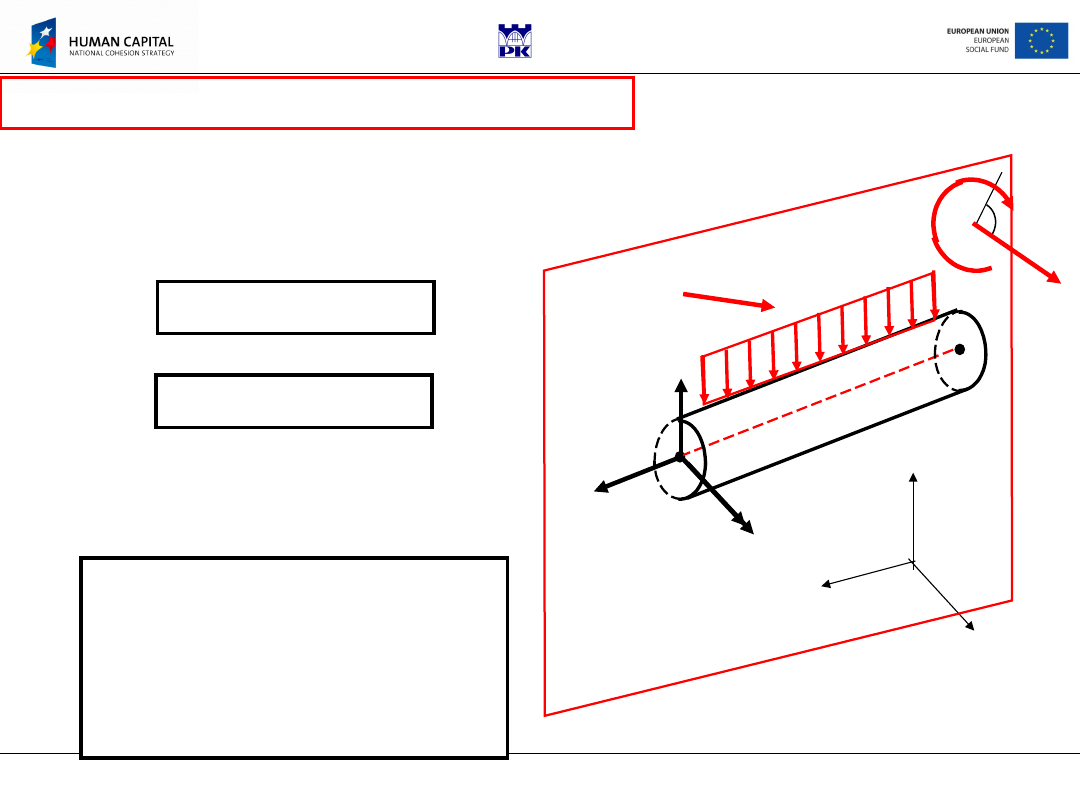
Agreements

•Reduction cent

re

O

is located

on the bar axis by vector

r

0

•Internal forces are determined

on the planes perpendicular
to the bar axis (vector

n

is

parallel to the axis)

•Vector

n

is an outward

normal vector

n

n

O

x

y

z

r

0

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

5/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

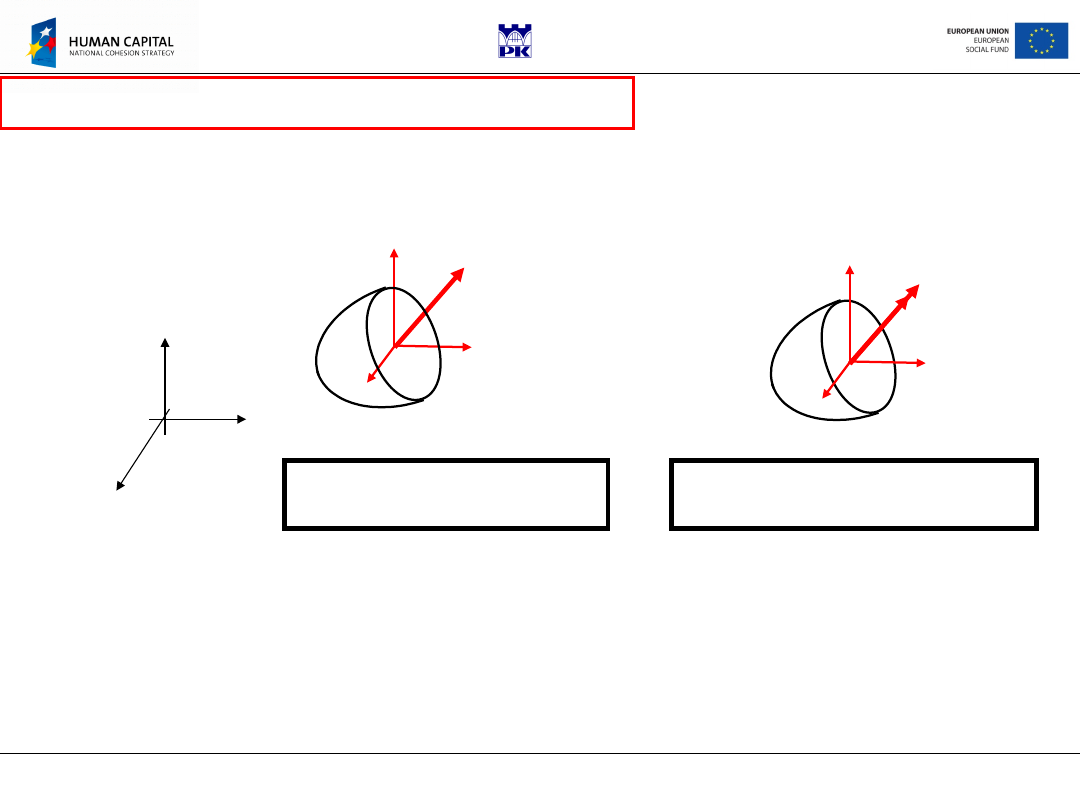
Components of internal forces resultants

S

wx

, S

wy

, S

wz

and

M

wx

, M

wy

, M

wz

are called cross-sectional forces

In 3D vectors of internal forces resultants have three components each

S

w

{ S

wx

, S

wy

, S

wz

}

M

w

{

M

wx

,

M

wy

,

M

wz

}

x

y

z

S

wz

S

ny

S

wx

S

w

M

wz

M

wx

M

w

y

M

w

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

6/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

S

w

= S

w

(r

O

, n)

M

w

= M

w

(r

O

,

n)

S

w

= S

w

(r

O

)

M

w

=

M

w

(r

O

)

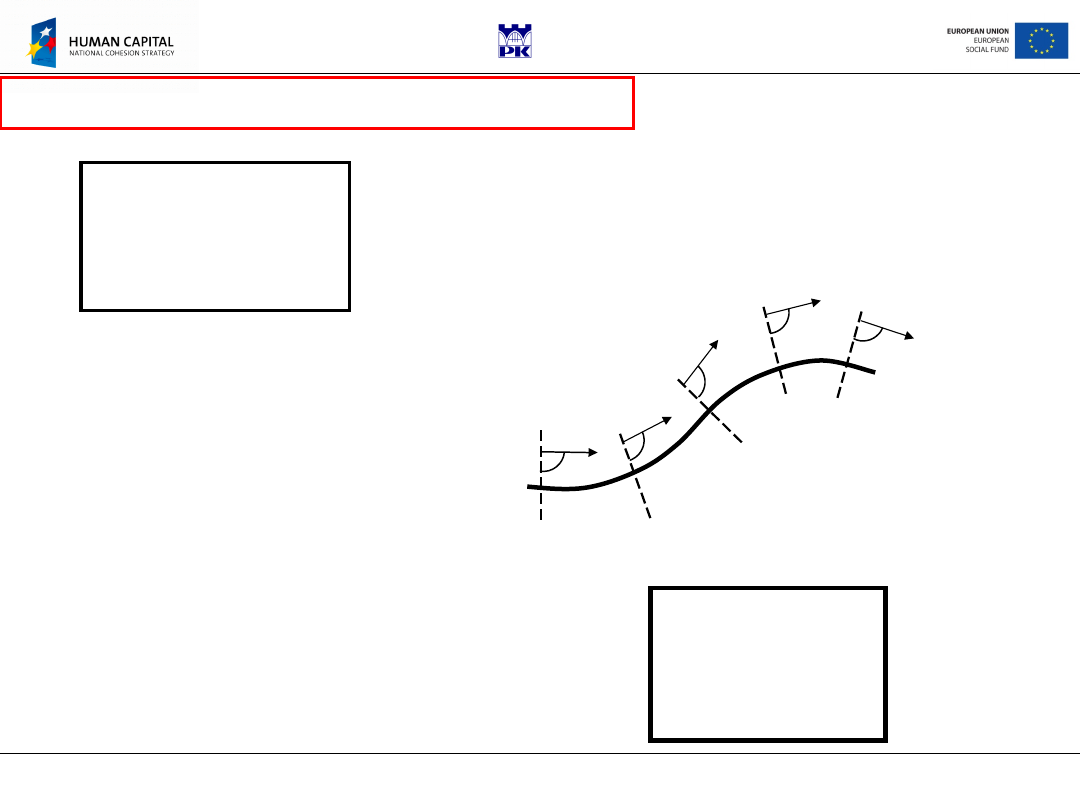
Vector

n

is known if

we know the shape of
bar axis

.

n

.

n

.

n

.

n

.

n

Thus, resultants of internal
forces for known bar structure
are function of only one vector

r

0

Resultants of internal forces are
vector functions of two vectors

r

o

and

n

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

7/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

In 2D number of cross-sectional
forces is reduced, because
loading and bars axes are in the
same plane (x, z):

S

w

{ S

x

, 0, S

z

}

M

w

{ 0, M

y

, 0 }

x

y

z

P

q

.

M

M

S

x

S

z

M

y

We will use following notations
and names for these
components:

S

x

=N

- axial forces

S

z

=Q

- shear force

M

y

= M

- bending

moment

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

8/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars

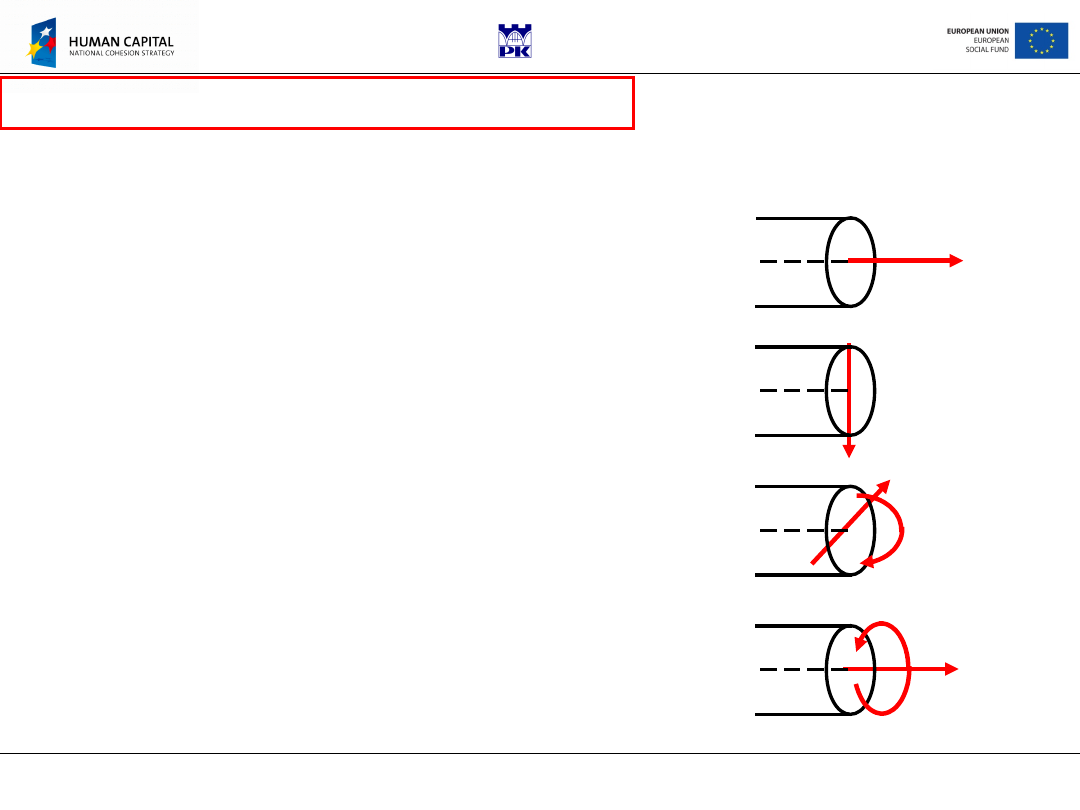
Special cases of internal forces
reductions are called:

TENSION – when internal forces reduce to
the sum vector only, which is parallel to
the bar axis

SHEAR – when internal forces reduce to
the sum vector only, which is
perpendicular to the bar axis

BENDING – when internal forces reduce to
the moment vector only, which is
perpendicular to the bar axis

TORSION – when internal forces reduce to
the moment vector only, which is parallel
to the bar axis

M

M

s

Q

N

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

9/8

M.Chrzanowski: Strength of Materials

SM1-02: Statics 1: Internal forces in bars



stop