Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
1/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
CONTINUUM MECHANICS
(CONSTITUTIVE EQUATIONS -
- HOOKE LAW)
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
2/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
0
j
ij
i
x
P
j
ij
i
q
3
internal equilibrium
equations (Navier eq.)
6
unknown functions (stress
matrix components)
Boundary
conditions (statics)
i
j
j
i
ij
x
u
x
u
2
1
6
kinematics equations (Cauchy
eq.),
9
unknown functions (6 strain
matrix components, 3
displacements)
Boundary
conditions
(kinematics)
u
S
i
u
9
equations
15
unknown functions (6
stresses, 6 strains, 3
displacements)
From the formal point of view
(mathematics) we are lacking 6
equations
From the point of view of physics –
there are no material properties
involved
Summary of stress and strain state
equations
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
3/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
Strain versus stress
An obvious solution is to exploit
already noticed interrelation
between strains and stresses
Material
deformability
properties
General property of majority of
solids is elasticity (instantaneous
shape memory)
P
u
Linear
elasticity
Deformation versus internal
forces
CEIIINOSSSTTUV
UT TENSIO SIC VIS
u
k
P
which reads:
„as much the extension as the
force is”
where
k
is a constant
dependent on a material
and
body shape
This observation was made
already in 1676 by Robert
Hooke:
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
4/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
Physical
quantities
(measurable)
Mathematical
quantities (non-
measurable)
Dynamics
Kinematic
s
P
u
ij
ij
ij
f
Hooke, 1678
Navier, 1822
ij
f
- linear function of all strain matrix
components defining all stress component
matrix
To make Hooke’s law independent of a body shape one has to use state
variables characterizing internal forces and deformations in a material point
i.e. stress and strain.
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
5/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
The coefficients of this equation do depend only on the material
considered,
but not on the body shape
.
As Navier equation is a set of 9 linear algebraic equations then the
number of coefficient in this set is 81 and can be represented as a
matrix of 3
4
=81 components:
kl
ijkl
ij
C
Summation
over
kl
indices reflects linear character of this
constitutive equation.
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
6/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
Nevertheless, the number of assumptions allows for the reduction of
the coefficients number: two of them are already inscribed in the
formula:
Universality of linear elasticity follows observation, that for loading
below a certain limit (elasticity limit) most of materials exhibit this
property.
kl
ijkl
ij
C
1. For zero valued deformations all stresses vanish: the body in a
natural state is free of initial stresses.
2. Coefficients
C
ijkl
do not depend on position in a body – material
properties are uniform (homogeneous).
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
7/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
3. Assumption of the existence of elastic potential yields symmetry of
group of indices
ij - kl
thus reducing the number of independent
coefficients to
36 [=(81-9)/2].
4. Symmetry of material inner structure allows for further reductions.
In a general case of lacking any symmetry (
anisotropy
) the number
of independent coefficients is 21 [=(36-6)/2+6].
5. In the simplest and the most frequent case of structural
materials (
except the composite materials
) – the number of
coefficients is 2 (
isotropy
):
ij
kk
ij
ij
G
2
or in an inverse
form:
ij
kk
ij
ij
v
E
1
1
The pairs of coefficients
G,
i
E, ν
are interdependent so there
are really only two material independent constants.
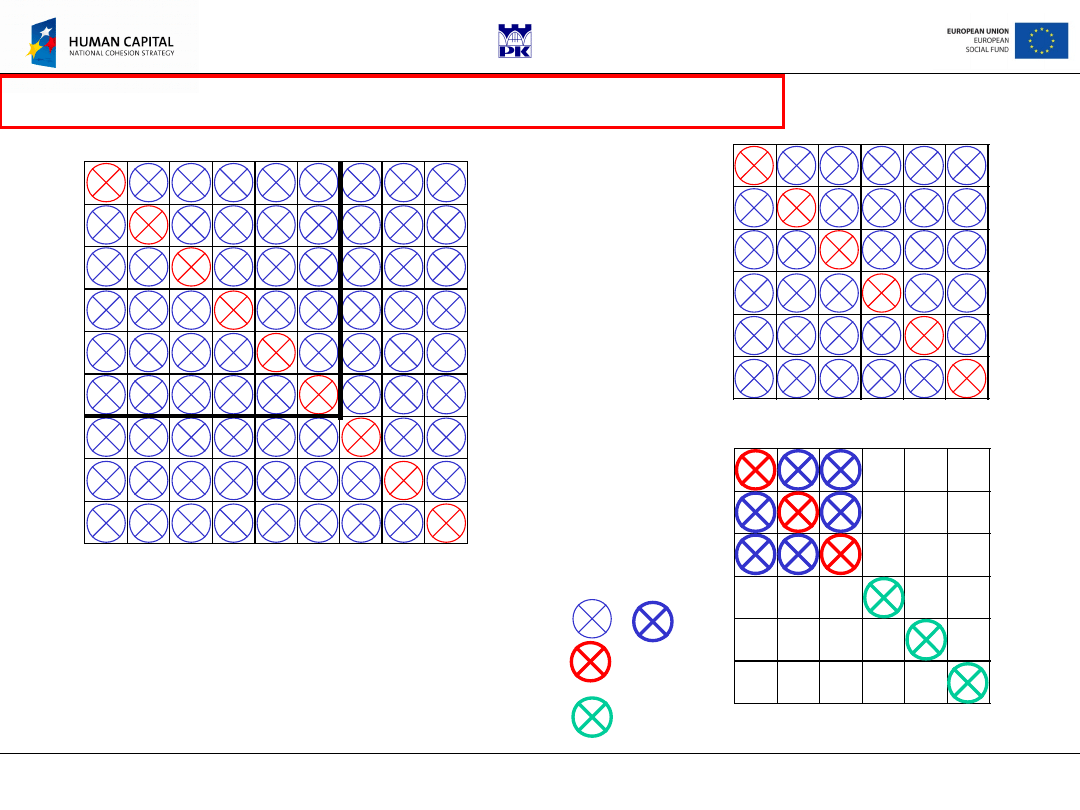
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
8/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
9
9
6
6
81 components of
C
ijkl
General anisotropy: 15+6=21
constants
Isotropy: 2
constants
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0
0 0
0
0
Symmetrical
components
Identical components
Components dependent on
other components
ji
ij
ji
ij
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
9/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
ij
kk
ij
ij
G
2
,
G
Summation obeys !
Kronecker’s delta
Lamé
constants [Pa]
)
(
2
33
22
11
11
11
G
)
(
2
33
22
11
22
22
G
)
(
2
33
22
11
33
33
G
12
12
2
G
23
23
2
G
31
31
2
G
Normal stress and normal
strain dependences
Shear stress and shear
strain dependences
This equation consists of two
groups:
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
10/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
E
Summation
obeys !
Kronecker’s
delta
Poisson modulus [0]
)
(
1
1
33
22
11
11
11
E
E
12
12
1
ij
kk
ij
ij
v
E
1
1
Young modulus [Pa]
E
)
(
33
11
22
22
E
)
(
33
22
11
11
E
)
(
22
11
33
33
E
23
23
1
E
31
31
1
ij
kk
ij
ij
v
E
1
1
31
31
2
G
1
2
E
G
G
2
31
31
Normal stress and normal
strain dependences
Shear stress and shear
strain dependences
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
11/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
ij
kk
ij
ij
G
2
l
j
i
m
ll
3
33
22
11
ll
kk
ll
ll
G
2
3
ll
m
Mean strain
3
kk
m
Mean stress
=3
3
3
3
2
3
m
m
m
G
m
m
K
3
3
2
3
G
K
Prawo zmiany objętości
m
m
G
3
2
m
m
m
m
m
m
K
0
0
0
0
0
0
3
0
0
0
0
0
0
ij
m
ij
m
K
3
Volume change law
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
12/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
t
T
m
m
m
m
m
m
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
0
0
0
0
0
0
33
32
31
23
22
22
13
12
11
33
32
31
23
22
22
13
12
11
ij
t
T
ij
m
ij
m
ij
ij
t
t
t
t
t
D
t
A
=
+
3
/
kk
m
t
t
deviator
axiato
r
ij
m
ij
t
t
t
D
ij
m
t
t
A
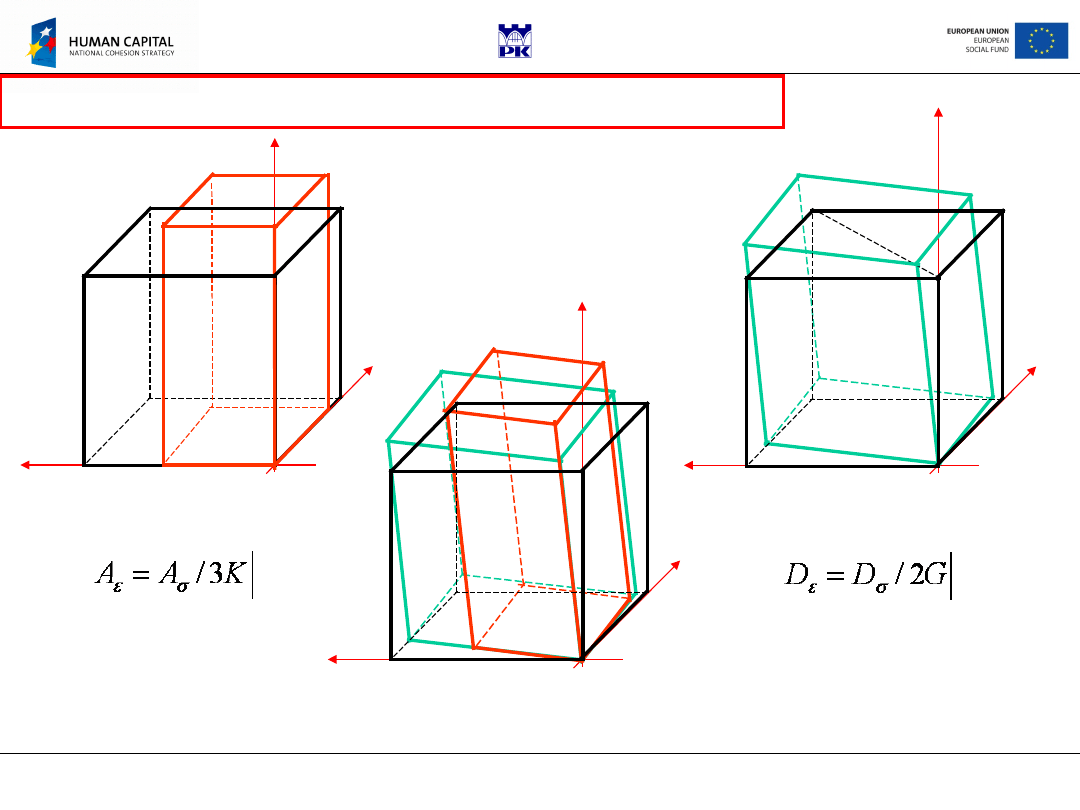
Decomposition of symmetric matrix (tensor) into deviator and
volumetric part (axiator)
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
13/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
m
m
m
m
m
m
K
0
0
0
0
0
0
3
0
0
0
0
0
0
ij
m
ij
m
K
3
KA
A
3
Volume change law
Distortion
law
ij
m
m
ij
K
G
3
3
2
ij
m
ij
kk
ij
ij
m
ij
K
G
3
2
ij
m
m
ij
G
G
3
3
2
2
ij
m
ij
ij
m
ij
G
G
G
2
2
2
GD
D
2
3
2
3
G
K
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
14/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
KA
A
3
2
1
1
E
GD
D
2
GD
KA
T
2
3
K
A
A
3
/
G
D
D
2
/
G
D
K
A
T
2
/
3
/
E
v
ij
kk
ij
ij
1
ij
kk
ij
ij
G
2
1
2
E
G
3
2
3
G
K
-1
ν
1/2
G
E/3
E/9
K
-
2
1
3
E
K
0
No volume change:
incompressible
material
Constants cross-
relations:
0
No shape
change:
stiff material
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
15/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
x
1
x
2
x
3
Volume change
Composed (full)
deformation
x
1
x
2
x
3
Shape change
x
1
x
2
x
3
G
D
K
A
T
2
/
3
/
+
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
16/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
x
1
x
2
x
3
Volume change
Composed (full)
deformation
x
1
x
2
x
3
Shape change
x
1
x
2
x
3
G
D
K
A
T
2
/
3
/
+
FAST
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
17/16
M.Chrzanowski: Strength of Materials
SM1-10: Continuum Mechanics: Constitutive
equations
stop