Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
1/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
CONTINUUM MECHANICS
(TORSION
as BOUNDARY VALUE PROBLEM - BVP)
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
2/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
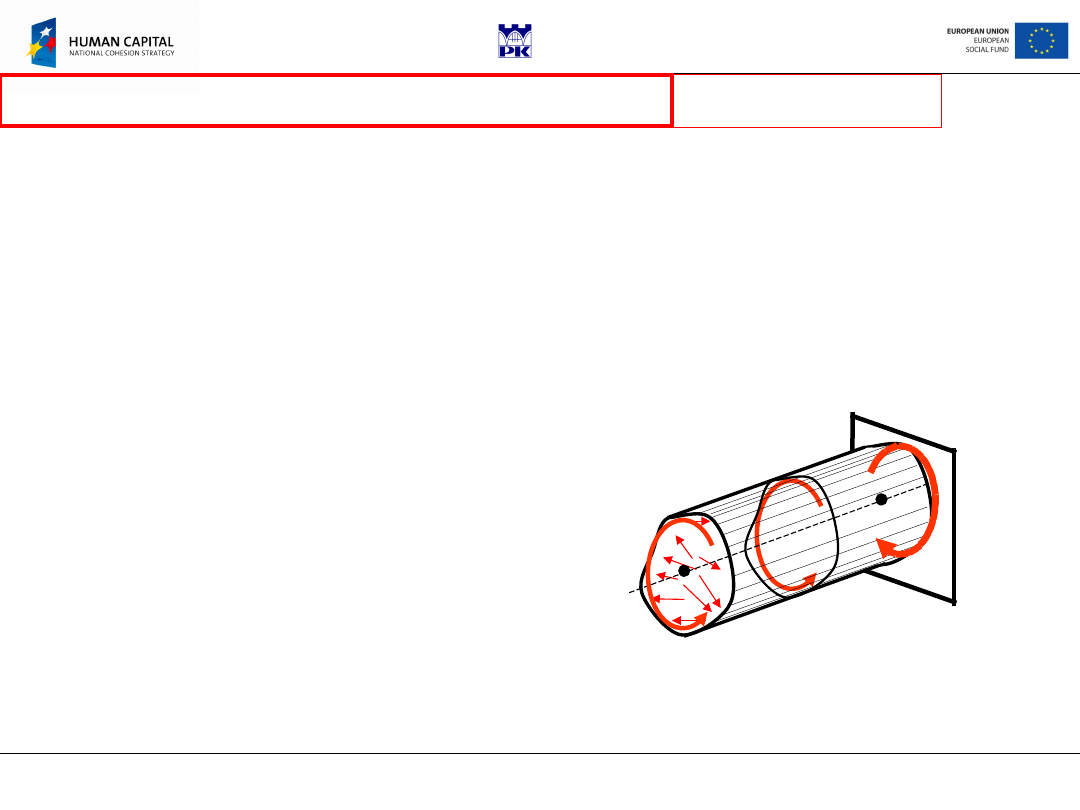
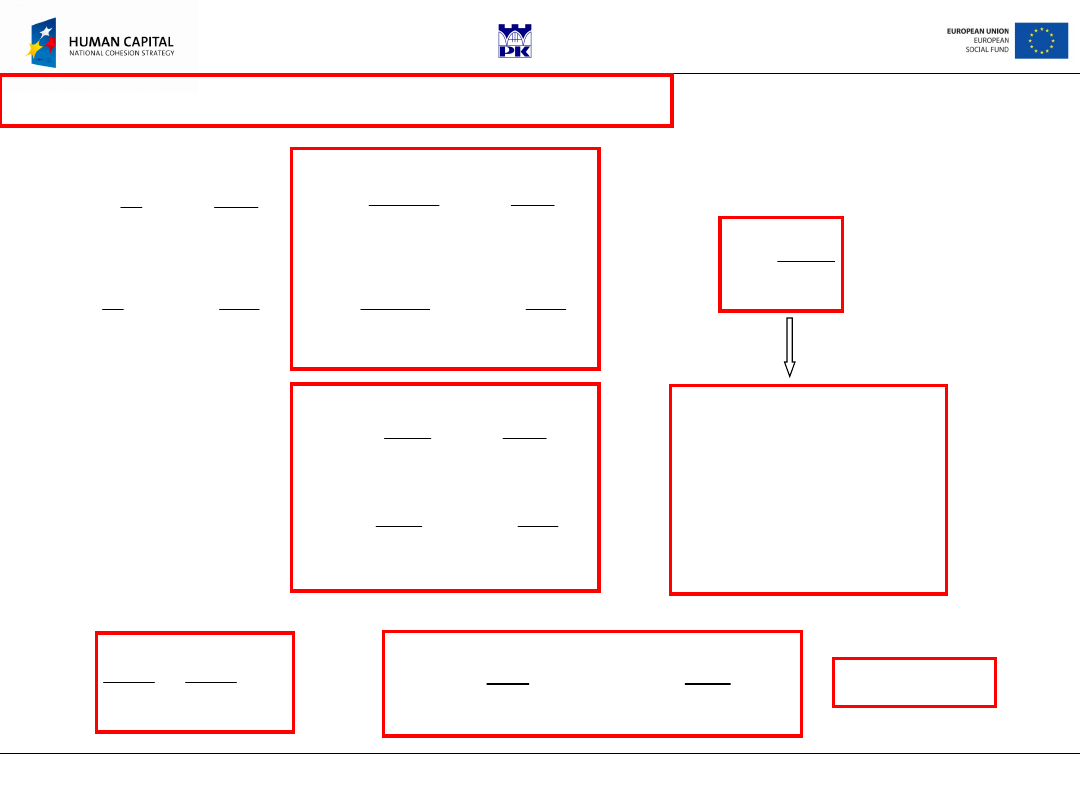
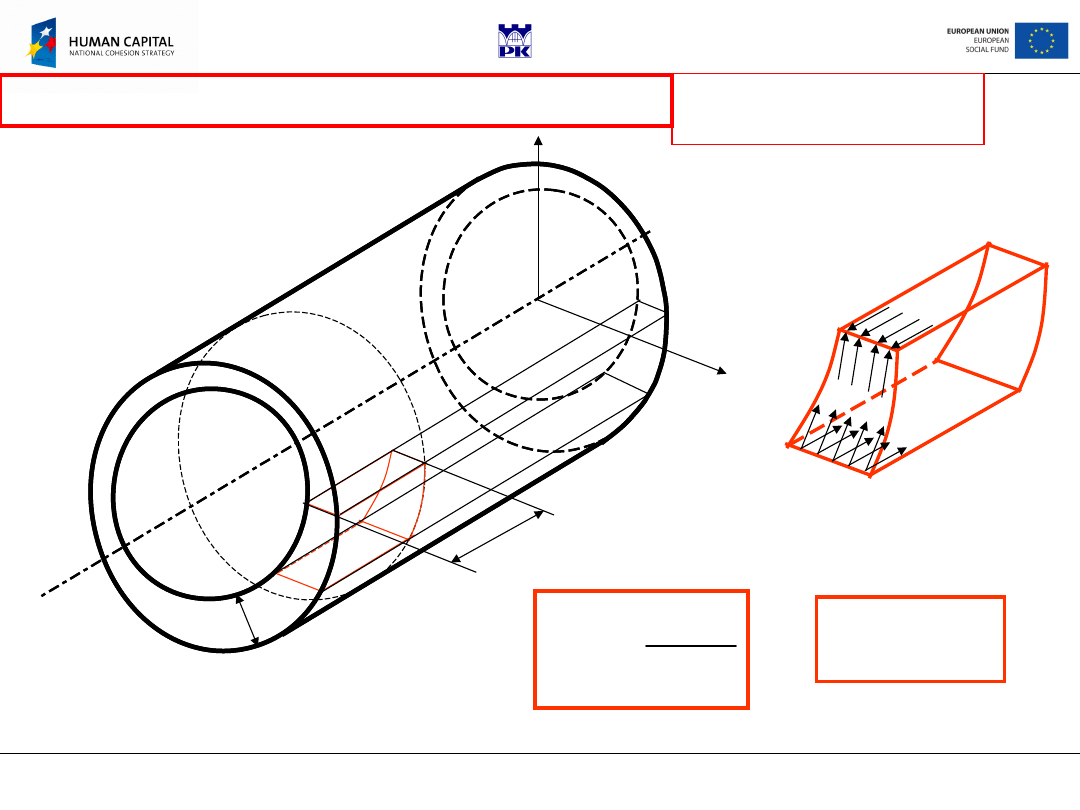
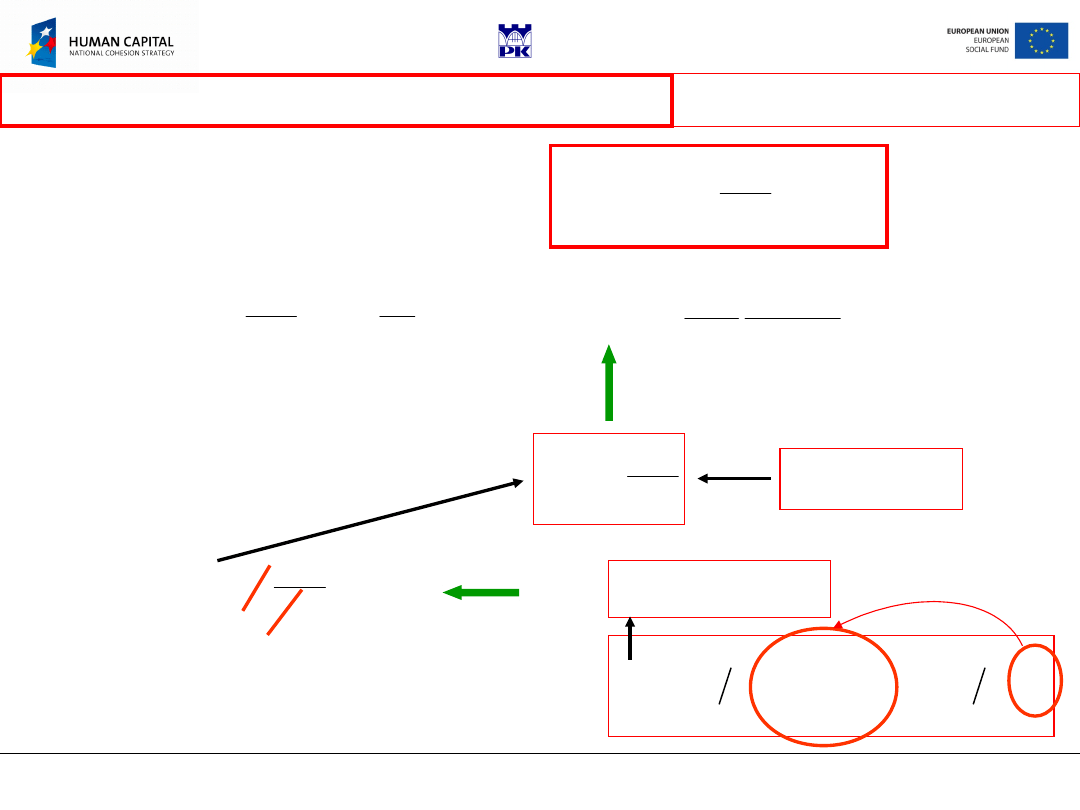
Body shape
:
straight prismatic bar with end surfaces perpendicular to
the bar axis, cross-section of arbitrary shape.
Loading:
distributed loading over end surfaces yielding torque as only
cross-sectional force, side surface free of loading, no volume forces.
Kinematics boundary conditions:
Bar fixed at one end (all
displacements and their derivatives vanish there).
M
S
Problem
formulation
In a further analysis we shall adopt the
assumption of replacing kinematics
conditions by statics ones (reaction
torque); the bar is considered as being
in the equilibrium but free to be
twisted (free torsion).
M
We will make also use of de Sain-Venant principle replacing distributed
loading with a torque
M
S
=
M
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
3/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
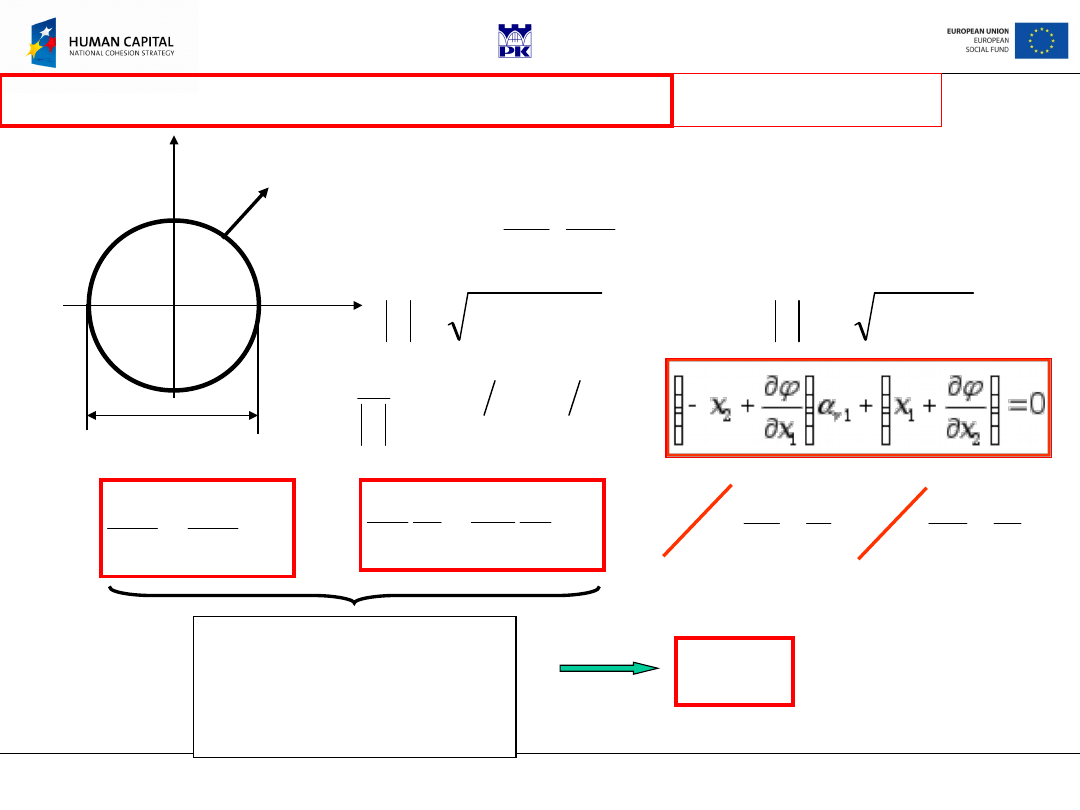
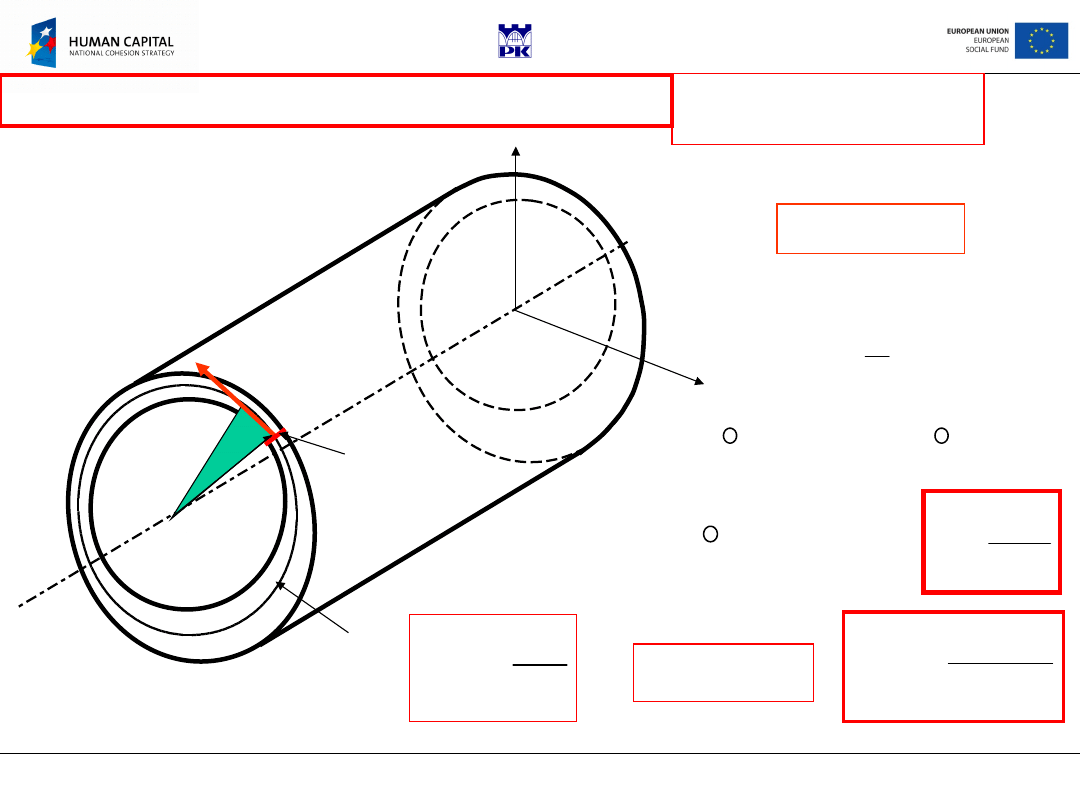
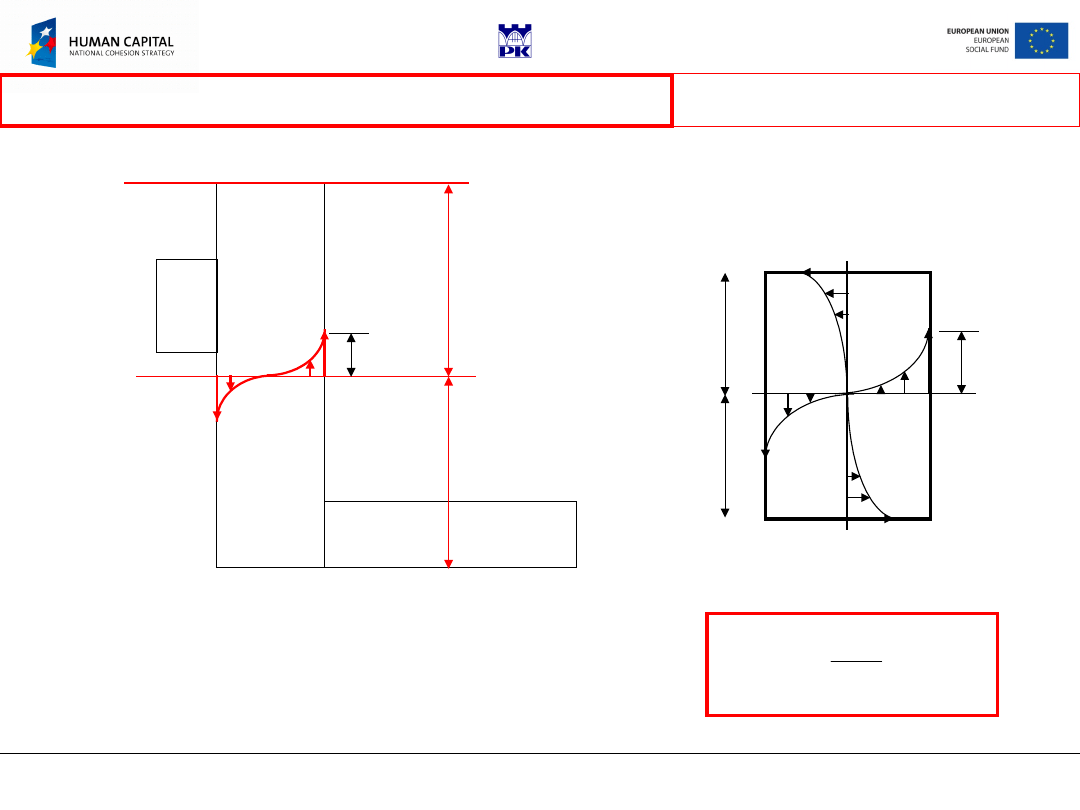
x
3
x
1
x
2
cos
sin
sin
cos
cos
cos
cos
1
r
r
r
u
x
1
x
2
A
A’
r
r’
Assume:
r’ =
r
sin
cos
sin
cos
sin
sin
sin
2
r
r
r
u
Assume:
3
x
0
,
,
2
1
sin
1
cos
2
1
sin
x
r
u
1
2
cos
x
r
u
Twist angle
per
unit length
(unit
angle)
1
,
0
,
0
3
2
1
x
x
u
3
1
2
x
x
u
2
1
3
,x
x
u
?
A
A’
1
1
Total
twist
angle
Distortion
function
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
4/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
i
j
j
i
ij
x
u
x
u
2
1
3
2
1
x
x
u
3
1
2
x
x
u
2
1
3
,x
x
u
2
1
2
3
3
2
23
2
1
2
1
x
x
x
u
x
u
0
2
2
22
x
u
0
3
3
33
x
u
0
1
1
11
x
u
0
2
1
2
1
3
3
1
2
2
1
12
x
x
x
u
x
u
1
2
1
3
3
1
13
2
1
2
1
x
x
x
u
x
u
0
0
0
0
0
T
ij
kk
ij
ij
G
2
0
kk
0
0
0
0
0
2G
T
13
2
1
23
'
x
G
31
1
2
13
'
x
G
- distortion function
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
5/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
0
j
ij
i
x
P
31
1
2
13
'
x
G
0
0
0
3
33
2
32
1
31
3
23
2
22
1
21
3
13
2
12
1
11
x
x
x
x
x
x
x
x
x
0
0
0
0
0
0
0
2
2
2
2
1
2
x
x
0
0
''
0
''
0
2
1
G
G
32
2
1
23
'
x
G
The governing
equation of torsion
boundary value
problem
0
2
or:
Laplacian
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
6/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
Statics boundary conditions
On a bar surface
0
,
0
,
0
q
0
,
,
2
1
0
'
'
2
2
1
1
1
2
x
G
x
G
On bar ends:
1
,
0
,
0
0
,
,
2
1
q
q
q
1
2
1
'
x
G
q
2
1
2
'
x
G
q
x
1
x
2
q
ν1
q
ν2
S
A
M
dA
x
q
x
q
2
1
1
2
S
A
M
dA
x
x
x
x
G
2
1
2
1
2
1
'
'
+
M
S
S
S
GJ
M
J
S
Torsion inertia
moment
This is boundary value condition for distortion function differential
equation
By de Saint Venant
hypothesis
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
7/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
2
1
23
2
x
x
GJ
M
S
S
GT
T
2
dA
x
x
x
x
J
A
S
2
1
2
1
2
1
'
'
S
S
GJ
M
2
1
23
2
x
x
1
2
13
2
x
x
1
2
13
2
x
x
GJ
M
S
S
2
1
23
x
x
J
M
S
S
1
2
13
x
x
J
M
S
S
3
2
1
x
x
u
3
1
2
x
x
u
2
1
3
,x
x
u
0
2
2
2
2
1
2
x
x
0
2
1
1
1
2
x
x
x
x
0
0
,
0
,
0
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
8/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
2
1
,
x
f
x
f
n
0
2
2
2
2
1
2
x
x
2
R
x
1
x
2
n
0
,
2
2
2
2
1
2
1
R
x
x
x
x
f
2
1
2
1
4
4
x
x
n
2
1
2
,
2
x
x
n
R
x
R
x
n
n
2
1
,
0
2
2
1
1
1
2
R
x
x
x
R
x
x
x
0
2
2
1
1
R
x
x
R
x
x
0
Governing equation
and
boundary
condition are
homogeneous
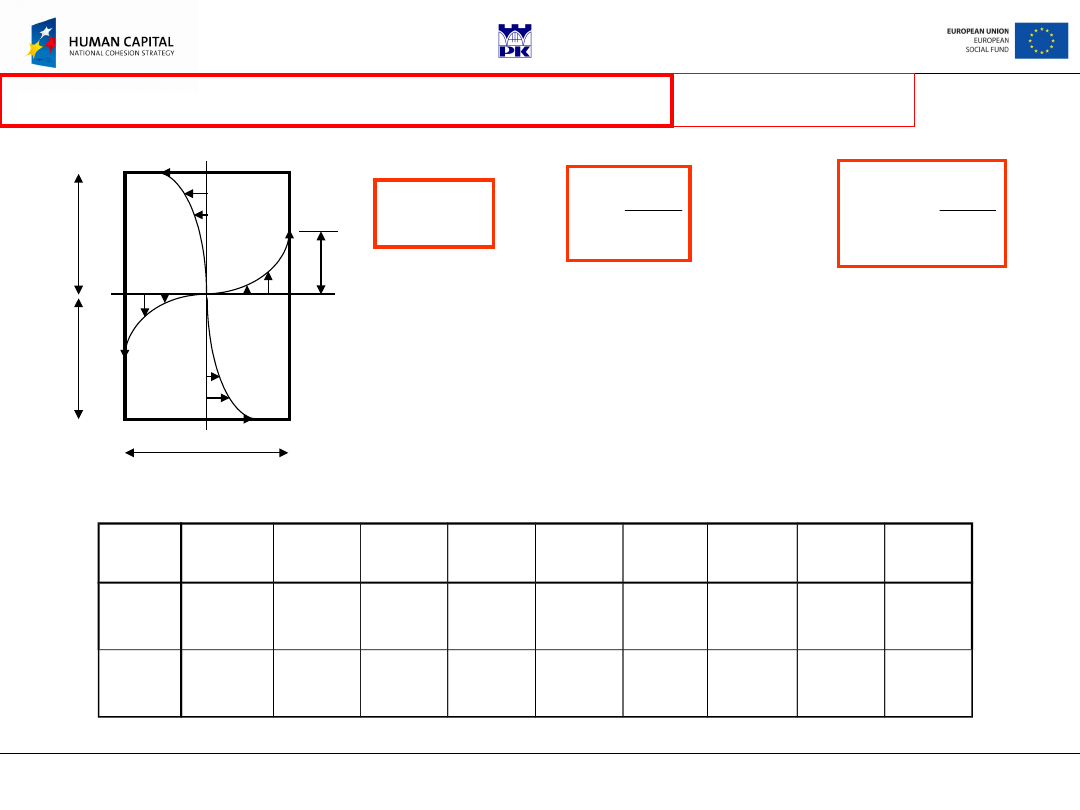
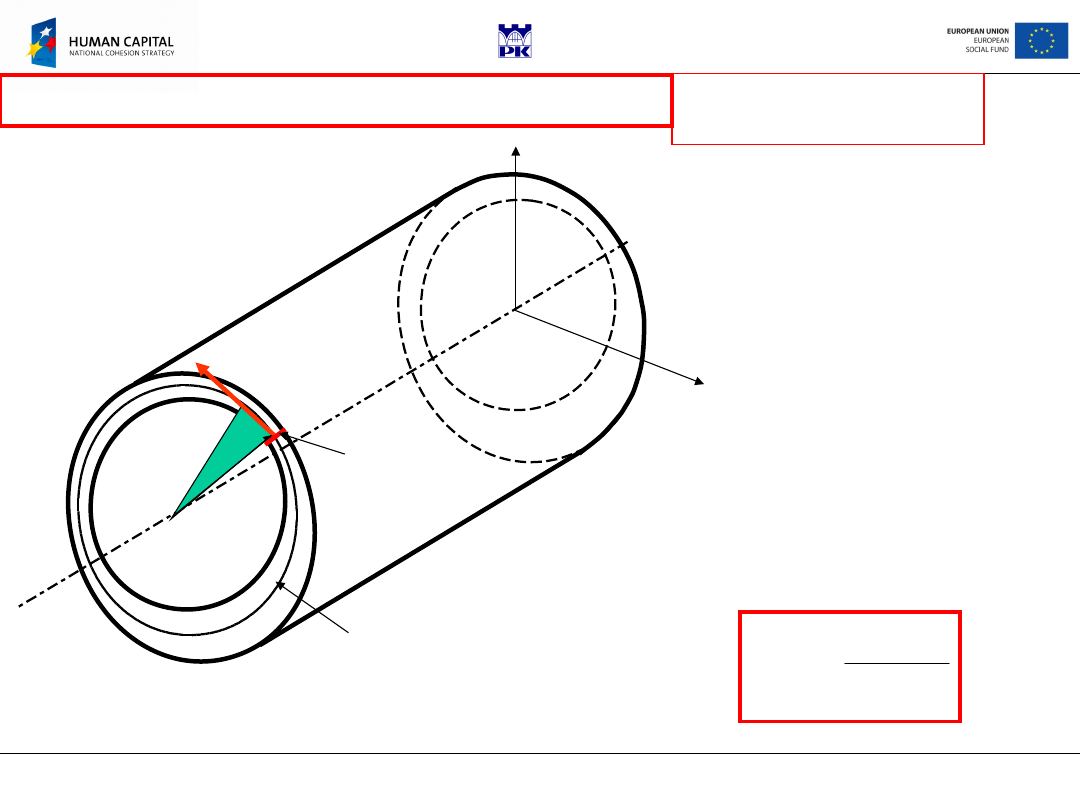
Solid circular
shaft
Contour
equation:
No
distortion!
R
x
x
n
2
2
2
1
2
1
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
9/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
dA
x
x
x
x
J
A
S
2
1
2
1
2
1
'
'
S
S
GJ
M
2
1
23
x
x
J
M
S
S
1
2
13
x
x
J
M
S
S
0
0
2
2
2
2
1
J
dA
r
dA
x
x
J
A
A
S
2
0
13
x
J
M
S
1
0
23
x
J
M
S
r
J
M
x
x
J
M
S
S
0
2
1
2
1
0
2
23
2
13
r
0
0
max
W
M
R
J
M
S
S
3
0
3
x
GJ
M
x
S
Twist angle
Unit twist
angle
Total twist angle for a shaft of
length
l
l
GJ
M
S
0
max
)
(r
Solid circular
shaft
1
x
2
x
Torsion section
modulus
Polar inertia moment
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
10/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
S
S
GJ
M
0
S
S
W
M
max
s
s
J
J
s
s
W
W
For
h
b
b
h/2
max
h
b
J
s
3
h
b
W
s
2
h/b
1
1,5
2
2,5
3
4
6
8
0,208
0,23
1
0,24
6
0,25
8
0,26
7
0,28
2
0.29
9
0,30
7
0,33
3
0,141
0,19
6
0,22
9
0,24
9
0,26
3
0,28
1
0.29
9
0,30
7
0,33
3
Rectangular bar
)
,
( b
h
h/2
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
11/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
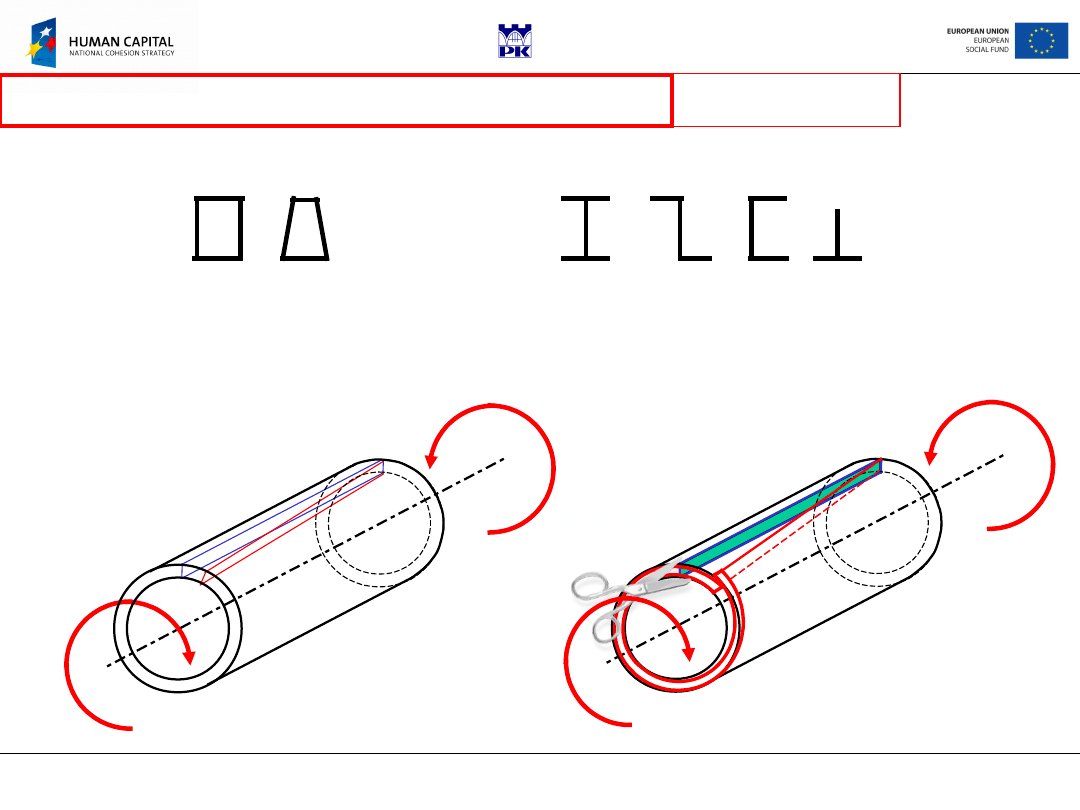
Bars of open cross-
sections
Bars of closed cross-
sections
The behaviour of the above types of bars differs significantly when
subjected to the action of a torque. One can make a simple
experiment cutting a tube:
Thin-walled
bars
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
12/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
1
2
1
Assume: constant
distribution of shear
stress across of tube
thickness
2
Assume: prismatic tube
of varying wall thickness
From equilibrium condition:
const
2
2
1
1
0
2
2
1
1
min
max
const
Closed thin-walled
cross-sections
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
13/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
d
s
dA
r(s)
s
ds
s
r
dA
)
(
2
1
dA
ds
s
r
M
s
s
s
2
)
(
const
S
dA
M
s
s
2
2
S
– area of the figure
embedded within central
curve
s
S
M
s
2
s
s
W
M
max
S
W
s
min
2
min
max
2
S
M
s
Closed thin-walled
cross-sections
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
14/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
b
1
h
1
b
2
h
2
b
3
h
3
n
i
si
s
M
M
1
i
i
i
b
h
Solutions for torsion of rectangular bars
obey:
s
si
GJ
M
si
si
i
W
M
max
i
i
i
si
h
b
J
3
i
i
i
si
h
b
W
2
A2
i
i
i
Si
i
h
b
G
M
3
i
i
i
si
h
b
G
M
3
A3
n
i
i
i
i
s
h
b
G
M
1
3
s
s
n
i
i
i
i
s
J
G
M
h
b
G
M
1
3
Assumptions:
Cross-section
partitioning:
A1
A2
A3
A1
Open thin-walled cross-
sections
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
15/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
si
si
i
W
M
max
i
i
i
si
h
b
W
2
i
i
i
si
h
b
G
M
3
s
s
n
i
i
i
i
s
J
G
M
h
b
G
M
1
3
i
i
i
s
s
si
h
b
GJ
M
G
M
3
i
i
i
s
s
i
i
i
i
i
i
s
s
i
b
J
M
h
b
h
b
J
M
2
3
max
i
s
s
i
b
J
M
max
max
max
i
i
i
s
s
i
b
J
M
max
max
max
For h
i
/b
i
>6
i
=
i
Open thin-walled cross-
sections
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
16/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
i
s
s
b
J
M
max
max
max
h/2
h/2
max
Open thin-walled cross-
sections
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
17/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
d
s
dA
r(s)
s
S
– area of the figure
embedded within central
curve
s
min
max
2
S
M
s
Closed thin-walled
cross-sections
Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union
within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education
18/17
M.Chrzanowski: Strength of Materials
SM1-12: Continuum Mechanics: Torsion as
BVP
stop