Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

1/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem

CONTINUUM MECHANICS

(BOUNDARY VALUE PROBLEM -

BVP)

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

2/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem



























i

j

j

i

ij

x

u

x

u

2

1



...



u

S

i

u

...







u

S

j

i

x

u

0























j

ij

i

x

P



j

ij

i

q











ij

kk

ij

ij

G











2

NE

CE

HE

SBC

KBC

The set of NE+CE+ HE equations consists of 15 linear differential-
algebraic equations – and is always the same for any static problem
(except of material constants in HE).

Individual problems are different only due to different

boundary

conditions

, which define

body shape



i

, loading

q

i

and

displacements

u

i

on the body surface (

supports). Here is where name

Boundary Value Problem of Elasticity

comes from.

,

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

3/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem



























i

j

j

i

ij

x

u

x

u

2

1



0























j

ij

i

x

P



ij

kk

ij

ij

G











2

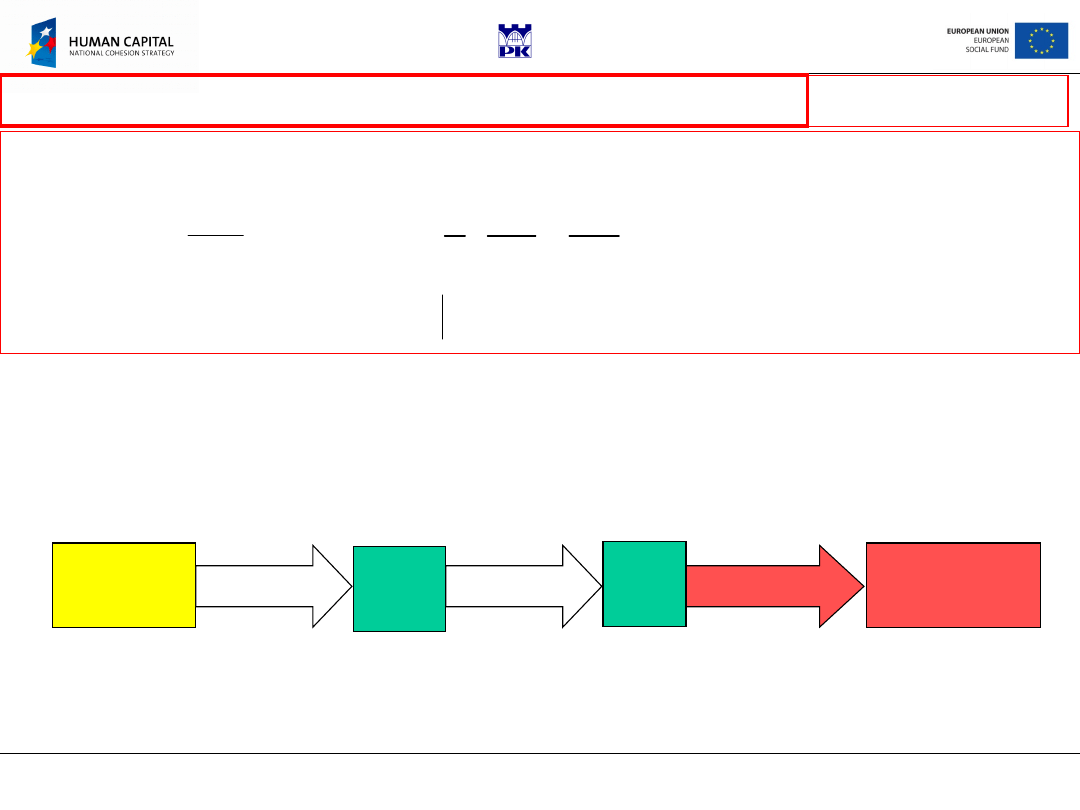
1. Reduction of unknown functions number in exchange for upgrading

the differential equations order

a/ Substitution of CE to HE and next to NE; this yields the set of 3
differential equations of the second order for displacements as
unknowns

(Lamé equations

):

b/ Elimination of displacements by transforming CE into compatibility
equations and substitution HE; this yields the set of 6 differential
equations of the second order for stress components (

Beltrami-Michell

equations

):



























i

j

j

i

ij

x

u

x

u

2

1











E

v

ij

kk

ij

ij













 1

0

,

,

,

,









ik

jl

jl

ik

ij

kl

kl

ij









Analytical

methods

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

4/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem

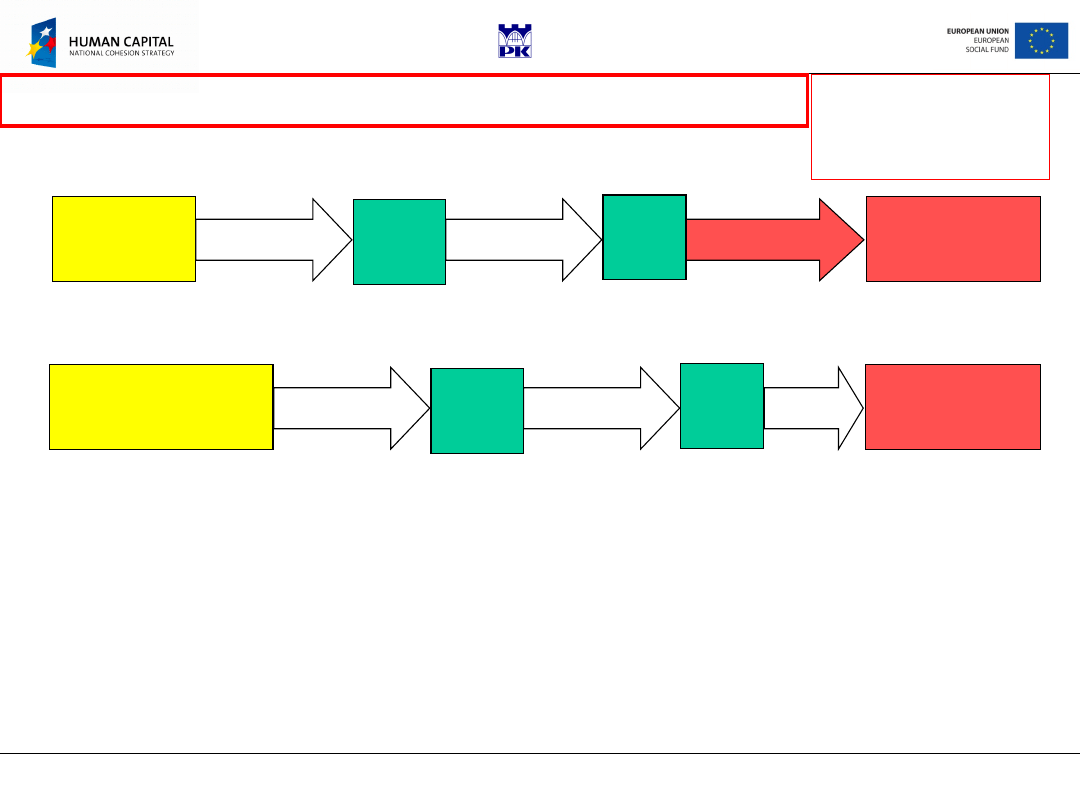
2. Inverse

method

In this method the full solution compaltible with NE, CE and HE is guessed,
then SBC and KBC are checked to comply with a given problem.

3. Semi-inversed
methods

a/ Displacement approach:

3 functions

u

i

satisfying KBC are guessed,

and then the strains are found by differentiation according to CE, and
inserted into algebraic HE to obtain stresses which have to satisfy NE
and SBC

u

i

+

KBC



ij

σ

ij

SWB?

Substitutio
n

Differentiati
on

Differentiatio
n

CE

HE

NE?

Analytical

methods

Substitutio
n



























i

j

j

i

ij

x

u

x

u

2

1



0























j

ij

i

x

P



ij

kk

ij

ij

G











2

CE

(Cauchy)

NE

(Navier)

HE (Hooke)

...



u

S

i

u

j

ij

i

q











SBC

KBC

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

5/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem

σ

ij

+ NE + SBC



ij

u

i

KBC?

Substitutio
n

Substitutio
n

Integratio
n

HE

CE

b/ Stress approach:

6 functions



ij

satisfying NE and SBC are guessed,

and the strains are found by inserting them into HE; then set of Cauchy
Equations CE has to be integrated to find displacements

u

i

. The only

remaining action left is to check KBC by inserting displacements

3. Semi-inversed
methods



























i

j

j

i

ij

x

u

x

u

2

1



0























j

ij

i

x

P



ij

kk

ij

ij

G











2

CE

(Cauchy)

NE

(Navier)

HE (Hooke)

...



u

S

i

u

j

ij

i

q











SBC

KBC

Analytical

methods

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

6/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem

σ

ij

+ NE + SBC



ij

u

i

KBC?

Substitutio
n

Substitutio
n

Integratio
n

HE

CE

b/ Stress
approach:

Out of these two semi-inverse methods, the displacement approach seems

to be superior as it requires only three displacements to be guessed which

are physical quantities and can be measured experimentally. Moreover,

only two operations to be performed are insertion and differentiation, the

latter being much easier than integration required by stress approach.

The price to be paid in displacement approach is a necessity of checking

Navier Equation of equilibrium and Static Boundary Condition.

u

i

+

KBC



ij

σ

ij

SWB?

Substitutio
n

Differentiati
on

Differentiatio
n

CE

HE

NE?

Substituiti
on

a/ Displacement approach

Comparison of

semi-inverse

methods

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

7/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem

Numerical Methods

features space discretisation and application of

one of numerous methods: development in power series, finite
differences, finite elements, boundary integrals, meshless methods
etc.

Numerical methods are discussed in detail as a separate subject of
curriculum and will not be dealt with here. However, it is worthwhile
to emphasise that numerical methods allow for overcoming of the
fundamental problem of theory of elasticity which is solving problems
with singular boundary conditions (sharp edges of structures,
concentrated loadings etc.)

Numerical

methods

Project “The development of the didactic potential of Cracow University of Technology in the range of modern construction” is co-financed by the European Union

within the confines of the European Social Fund and realized under surveillance of Ministry of Science and Higher Education

8/7

M.Chrzanowski: Strength of Materials

SM1-11: Continuum Mechanics: Boundary Value

Problem



stop