Metodologia ze

Metodologia ze

statystyką

statystyką

(

(

kurs zaawansowany)

kurs zaawansowany)

Prof. dr Jerzy Karylowski
Dr A. Fila-Jankowska

Quasi-eksperymenty: Schematy z

Quasi-eksperymenty: Schematy z

nie-losową grupą kontrolną (non-

nie-losową grupą kontrolną (non-

equivalent control group design)

equivalent control group design)



Podobne do eksperymentu z dwiema

Podobne do eksperymentu z dwiema

grupami ale bez losowego doboru do grup

grupami ale bez losowego doboru do grup



Nie w pełni rozwiązany problem selekcji.

Nie w pełni rozwiązany problem selekcji.

Nierozwiązane problemy regresji,

Nierozwiązane problemy regresji,

śmiertelności i interakcji miedzy selekcją a

śmiertelności i interakcji miedzy selekcją a

dojrzewaniem.

dojrzewaniem.



Przykład: badanie nad wpływem

Przykład: badanie nad wpływem

uczestnictwie w programie Head Start na

uczestnictwie w programie Head Start na

inteligencje i osiągnięcia szkolne.

inteligencje i osiągnięcia szkolne.

Schemat nieciągłości regresji

Schemat nieciągłości regresji

(regression-discontinuity

(regression-discontinuity

design)

design)



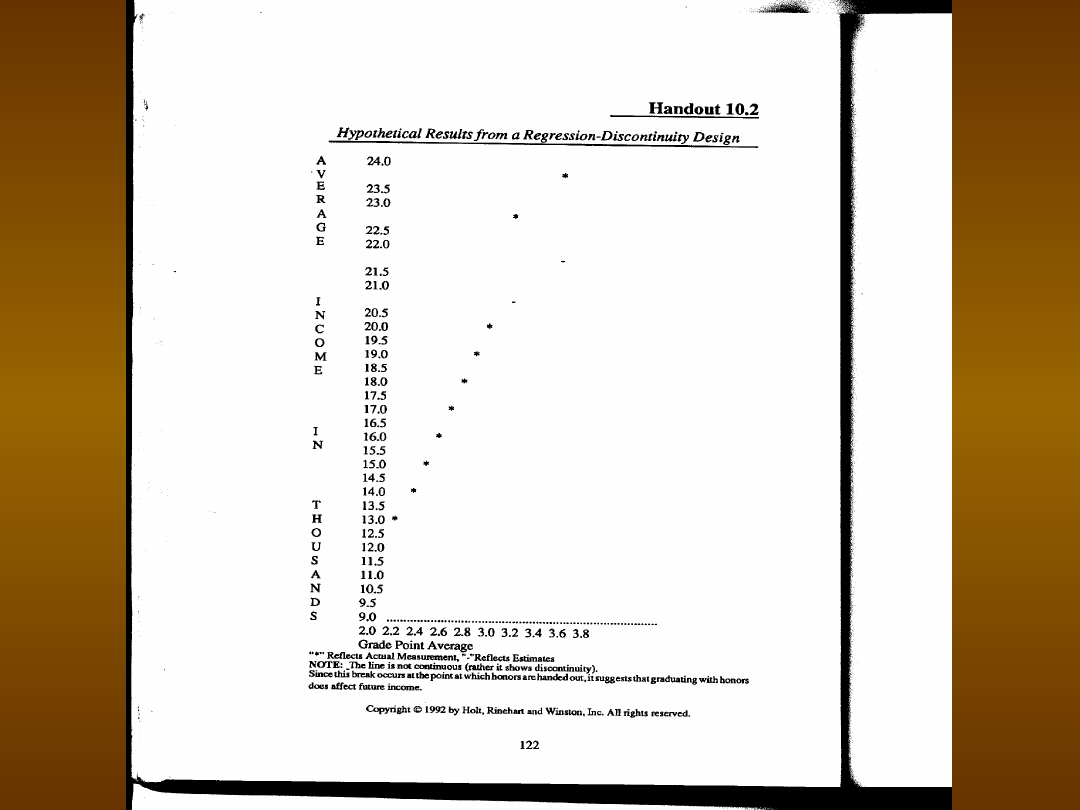
Czy uzyskanie dyplomu z wyróżnieniem ma

Czy uzyskanie dyplomu z wyróżnieniem ma

związek z przyszłymi zarobkami?

związek z przyszłymi zarobkami?



Porównując osoby które otrzymały dyplom

Porównując osoby które otrzymały dyplom

z wyróżnieniem i takie, które nie otrzymały

z wyróżnieniem i takie, które nie otrzymały

dyplomu z wyróżnieniem spotykamy się z

dyplomu z wyróżnieniem spotykamy się z

problemem selekcji (osoby te różnią się

problemem selekcji (osoby te różnią się

także pod innymi względami np pod

także pod innymi względami np pod

względem średniej ocen)

względem średniej ocen)



Czy związek ten da się sprowadzić do

Czy związek ten da się sprowadzić do

związku miedzy średnią ocen a przyszłymi

związku miedzy średnią ocen a przyszłymi

zarobkami?

zarobkami?

Korelacje z opóżnieniem

Korelacje z opóżnieniem

czasowym (time-lag

czasowym (time-lag

correlations)

correlations)

Test Chi-kwadrat dla tablic 2x2:

Test Chi-kwadrat dla tablic 2x2:

przypomnienie przykładu z

przypomnienie przykładu z

poprzedniego semestru

poprzedniego semestru

Czy istnieje zależność między

Czy istnieje zależność między

płcią a wyborem miejsca w

płcią a wyborem miejsca w

klasie

klasie

Tabela krzyżowa PLEC * MIEJSCE

26

20

46

12

35

47

38

55

93

Liczebność
Liczebność
Liczebność

kobieta
mezczyzna

PLEC

Ogółem

przod

tyl

MIEJSCE

Ogółem



Aby sprawdzić czy uzyskany patern

Aby sprawdzić czy uzyskany patern

wyników nie powstał przez przypadek (czy

wyników nie powstał przez przypadek (czy

jest statystycznie istotny) stosujemy test

jest statystycznie istotny) stosujemy test

Chi-kwadrat

Chi-kwadrat

Informacje konieczne do

Informacje konieczne do

obliczenia wartości Chi-

obliczenia wartości Chi-

kwadrat

kwadrat



fo

fo

- liczebności zaobserwowane

- liczebności zaobserwowane

(dla każdej kratki tabeli)

(dla każdej kratki tabeli)

Liczebności zaobserwowane a

Liczebności zaobserwowane a

liczebności oczekiwane

liczebności oczekiwane



fo

fo

- liczebności zaobserwowane:

- liczebności zaobserwowane:

ile obserwacji (ile osób) znalazło

ile obserwacji (ile osób) znalazło

się w każdej z czterech kratek

się w każdej z czterech kratek

tabeli

tabeli



fe -

fe -

liczebności oczekiwane: ile

liczebności oczekiwane: ile

obserwacji (ile osób) powinno się

obserwacji (ile osób) powinno się

było znaleźć w każdej z czterech

było znaleźć w każdej z czterech

kratek tabeli gdyby zmienne płeć i

kratek tabeli gdyby zmienne płeć i

wybór miejsca były od siebie

wybór miejsca były od siebie

niezależne

niezależne

Obliczanie liczebności

Obliczanie liczebności

oczekiwanych

oczekiwanych

f

f

e

e



Liczebność wiersza / Całkowita

Liczebność wiersza / Całkowita

liczebność x Liczebność kolumny

liczebność x Liczebność kolumny



Np. Oczekiwana liczebność kobiet

Np. Oczekiwana liczebność kobiet

siedzących z przodu to

siedzących z przodu to



ilość kobiet / ilość studentów x ilość

ilość kobiet / ilość studentów x ilość

studentów siedzących z przodu

studentów siedzących z przodu

Liczebności zaobserwowane i

Liczebności zaobserwowane i

liczebności oczekiwane

liczebności oczekiwane

Tabela krzyżowa PLEC * MIEJSCE

26

20

46

18,8

27,2

46,0

12

35

47

19,2

27,8

47,0

38

55

93

38,0

55,0

93,0

Liczebność
Liczebność
oczekiwana
Liczebność
Liczebność
oczekiwana
Liczebność
Liczebność
oczekiwana

kobieta

mezczyzna

PLEC

Ogółem

przod

tyl

MIEJSCE

Ogółem

Płeć a wybór miejsca w klasie: Wyniki

Płeć a wybór miejsca w klasie: Wyniki

obliczeń

obliczeń

Testy Chi-kwadrat

9,239

b

1

,002

8,001

1

,005

9,414

1

,002

,003

,002

9,140

1

,003

93

Chi-kwadrat
Pearsona
Poprawka na
ciągłość

a

Iloraz wiarygodności
Dokładny t est
Fishera
Test związku
liniowego
N Ważnych
obserwacji

Wart ość

df

Ist ot ność

asympt ot ycz

na

(dwust ronn

a)

Ist ot ność

dokładna

(dwust ronn

a)

Ist ot ność

dokładna

(jednost r

onna)

Obliczone wyłącznie dla t abeli 2x2.

a.

,0% komórek (0) ma liczebność oczekiwaną mniejszą niż 5. Minimalna liczebność
oczekiwana wynosi 18,80.

b.



Sprawdzić czy ilość ważnych obserwacji jest co najmniej

Sprawdzić czy ilość ważnych obserwacji jest co najmniej

20, jeśli tak można użyć testu Chi-kwadrat

20, jeśli tak można użyć testu Chi-kwadrat



Gdyby ilość obserwacji była niższa niż 20, należałoby

Gdyby ilość obserwacji była niższa niż 20, należałoby

użyć dokładnego testu Fishera

użyć dokładnego testu Fishera



Uwaga: Podejście tradycyjne zezwala na użycie test Chi-

Uwaga: Podejście tradycyjne zezwala na użycie test Chi-

kwadrat jedynie gdy żadna z liczebności oczekiwanych

kwadrat jedynie gdy żadna z liczebności oczekiwanych

nie jest niższa niż 5, nawet gdy całkowita ilość ważnych

nie jest niższa niż 5, nawet gdy całkowita ilość ważnych

obserwacji jest wyższa niż 20

obserwacji jest wyższa niż 20

Ważne elementy poprzedniej

Ważne elementy poprzedniej

tabeli

tabeli

Testy Chi-kwadrat

9,239

1

,002

93

Chi-kwadrat
Pearsona
N Ważnych
obserwacji

Wartość

df

Istotność

asymptotyczna

(dwustronna)

Odczytać poziom istotności dla testu Chi-kwadrat

Odczytać poziom istotności dla testu Chi-kwadrat



Jeśli istotność niższa niż 0,05 to znaczy, że

Jeśli istotność niższa niż 0,05 to znaczy, że

zależność między płcią studenta w wyborem

zależność między płcią studenta w wyborem

miejsca w klasie jest istotna (mało

miejsca w klasie jest istotna (mało

prawdopodobne by pojawiła się przez

prawdopodobne by pojawiła się przez

przypadek)

przypadek)

Chi - kwadrat:

Chi - kwadrat:

Informacje dodatkowe

Informacje dodatkowe



Jest tzw. testem nieparametrycznym,

Jest tzw. testem nieparametrycznym,

nie opiera się na założeniu o

nie opiera się na założeniu o

normalności rozkładu

normalności rozkładu



Może być używany do tabel większych

Może być używany do tabel większych

niż 2 x 2 (więcej niż dwa poziomy

niż 2 x 2 (więcej niż dwa poziomy

zmiennej lub / i więcej niż dwie

zmiennej lub / i więcej niż dwie

zmienne)

zmienne)



Dane w poszczególnych kratkach tabeli

Dane w poszczególnych kratkach tabeli

muszą być od siebie niezależne!

muszą być od siebie niezależne!

Test Chi-kwadrat dla tablic

Test Chi-kwadrat dla tablic

większych niż 2x2:

większych niż 2x2:

dwie zmienne, więcej niż cztery

dwie zmienne, więcej niż cztery

kratki

kratki



Przykład w klasie: (5x3) stan cywilny

Przykład w klasie: (5x3) stan cywilny

a poziom satysfakcji z życia

a poziom satysfakcji z życia

.

.

Czy jest istotny związek w

Czy jest istotny związek w

populacji?

populacji?

Obliczanie Chi-kwadrat

Obliczanie Chi-kwadrat







2 - wartość statystyki Chi-kwadrat

2 - wartość statystyki Chi-kwadrat



fo

fo

- liczebność zaobserwowana

- liczebność zaobserwowana



f

f

e

e

- liczebność oczekiwana

- liczebność oczekiwana



2 może się wahać od 0 do

nieskończoności



Poziom istotności odczytać można z tabeli

istotności lub z wydruku SPSS



2

=  (f

o

– f

e

)

2

/ f

e

Stopnie swobody dla testu Chi-

Stopnie swobody dla testu Chi-

kwadrat

kwadrat



Przy odczytywaniu z tabeli

istotności potrzebna informacja o

ilości stopni swobody (df)



Df to iloczyn ilości wierszy – 1 oraz

ilości kolumn – 1 w tabeli danych

dla których obliczono Chi-kwadrat



W naszym przypadku df = (5-1) x

(3-1) = 8

Test Chi-kwadrat dla tablicy

Test Chi-kwadrat dla tablicy

5x3

5x3



Przykład w klasie z użyciem SPSS:

Przykład w klasie z użyciem SPSS:

stan cywilny a poziom satysfakcji z

stan cywilny a poziom satysfakcji z

życia

życia

.

.

Tabela krzy¿owa Stan cywilny * ¯ycie jest pasjonuj¹ce/zwyczajne/nudne

21

241

251

513

33,5

236,4

243,1

513,0

17

54

40

111

7,2

51,2

52,6

111,0

10

74

65

149

9,7

68,7

70,6

149,0

6

11

8

25

1,6

11,5

11,8

25,0

11

79

108

198

12,9

91,2

93,8

198,0

65

459

472

996

65,0

459,0

472,0

996,0

LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana
LiczebnoϾ
LiczebnoϾ oczekiwana

¯onaty/zamê¿na/KONK

Wdowiec/wdowa

Rozwiedziona/y

Separacja

Kawaler/panna

Stan
cywilny

Ogó³em

Nudne

Zwyczajne Pasjonuj¹ce

¯ycie jest

pasjonuj¹ce/zwyczajne/nudne

Ogó³em

Testy Chi-kwadrat

39,220

a

8

,000

31,911

8

,000

,034

1

,854

996

Chi-kwadrat Pearsona
Iloraz wiarygodnoœci
Test zwi¹zku liniowego
N Wa¿nych obserwacji

WartoϾ

df

IstotnoϾ

asymptotyczn

a

(dwustronna)

6,7% komórek (1) ma liczebnoœæ oczekiwan¹ mniejsz¹ ni¿
5. Minimalna liczebnoϾ oczekiwana wynosi 1,63.

a.

Uwaga: Ponieważ zmienna stan cywilny nie jest porządkowa, test związku
liniowego nie ma sensu

Problemy interpretacji

Problemy interpretacji

wyników

wyników



Liczebności oczekiwane niższe niż 5

Liczebności oczekiwane niższe niż 5



Trudność ustalenia, które kombinacje

Trudność ustalenia, które kombinacje

poziomów dwóch zmiennych

poziomów dwóch zmiennych

odpowiedzialne są za istotną

odpowiedzialne są za istotną

zależność

zależność

Problem: Liczebności

Problem: Liczebności

oczekiwane niższe niż 5

oczekiwane niższe niż 5



Zwiększyć próbę

Zwiększyć próbę



Pominąć w analizie szczególnie nieliczne

Pominąć w analizie szczególnie nieliczne

kategorie (np separacja)

kategorie (np separacja)



Połączyć kategorie (np połączyć separacje

Połączyć kategorie (np połączyć separacje

i rozwód lub separacje, rozwód, stan wolny

i rozwód lub separacje, rozwód, stan wolny

i wdowieństwo)

i wdowieństwo)

Problem: Trudność ustalenia,

Problem: Trudność ustalenia,

które kombinacje poziomów

które kombinacje poziomów

dwóch zmiennych

dwóch zmiennych

odpowiedzialne są za istotną

odpowiedzialne są za istotną

zależność

zależność



Połączyć kategorie tak by otrzymać tabele 2x2 (np

Połączyć kategorie tak by otrzymać tabele 2x2 (np

połączyć separacje, rozwód, stan wolny i

połączyć separacje, rozwód, stan wolny i

wdowieństwo a także dwie kategorie satysfakcji)

wdowieństwo a także dwie kategorie satysfakcji)



Skoncentrować się w analizie na kategoriach, które

Skoncentrować się w analizie na kategoriach, które

są dla badacza szczególnie interesujące (np żonaci

są dla badacza szczególnie interesujące (np żonaci

vs kawalerowie/panny, życie nudne vs ekscytujące)

vs kawalerowie/panny, życie nudne vs ekscytujące)



Zrobić analizę dla wszystkich możliwych kombinacji

Zrobić analizę dla wszystkich możliwych kombinacji

2x2 (dopuszczalne tylko jeśli wynik analizy

2x2 (dopuszczalne tylko jeśli wynik analizy

globalnej był istotny!)

globalnej był istotny!)