
1
Automatyka
Wykład 11
Stabilność liniowych układów
automatycznej regulacji
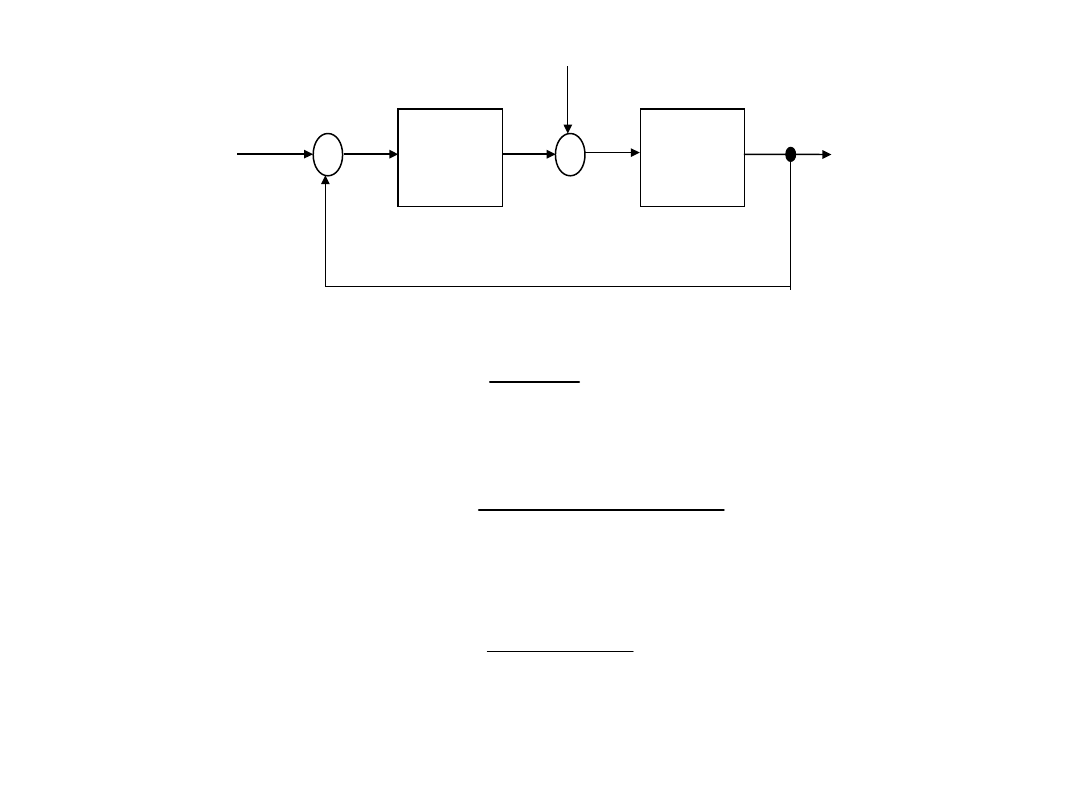
2
G
r
(s)
G
ob
(s)
z(t)
w(t)
y(t)
u(t)
e(t)
_
+
)
(
)
(
)
(
s
W
s
Y
s
G
def
(1)
)
s
(
G
)
s
(
G
)
s
(
G
)
s
(
G
)
s
(
G
r
r
ob
ob
1
)
(
1
)
(
)
(
0
0
s
G
s
G
s
G
(2)
(3)

3
0
1
1
1
0
1
1
1
)
(
a
s
a
s
a
s
a
b
s
b
s
b
s
b
s
G
n
n
n
n
m
m
m
m
(2)
)
)(
(
)
)(
(
)
)(
(
)
)(
(
)
(
1
2
1
1
2
1
n
n
n
m
m
m
s
s
s
s
s
s
s
s
a
z
s
z
s
z
s
z
s
b
s
G
(3)
n
i
t
s
i
i
e
A
s
G
L
t
g
1
1
)
(
)
(
(4)
0
0
1
1
1
a
s
a
s
a
s
a
n
n
n
n
(5)
0
Re
i
s
(6)
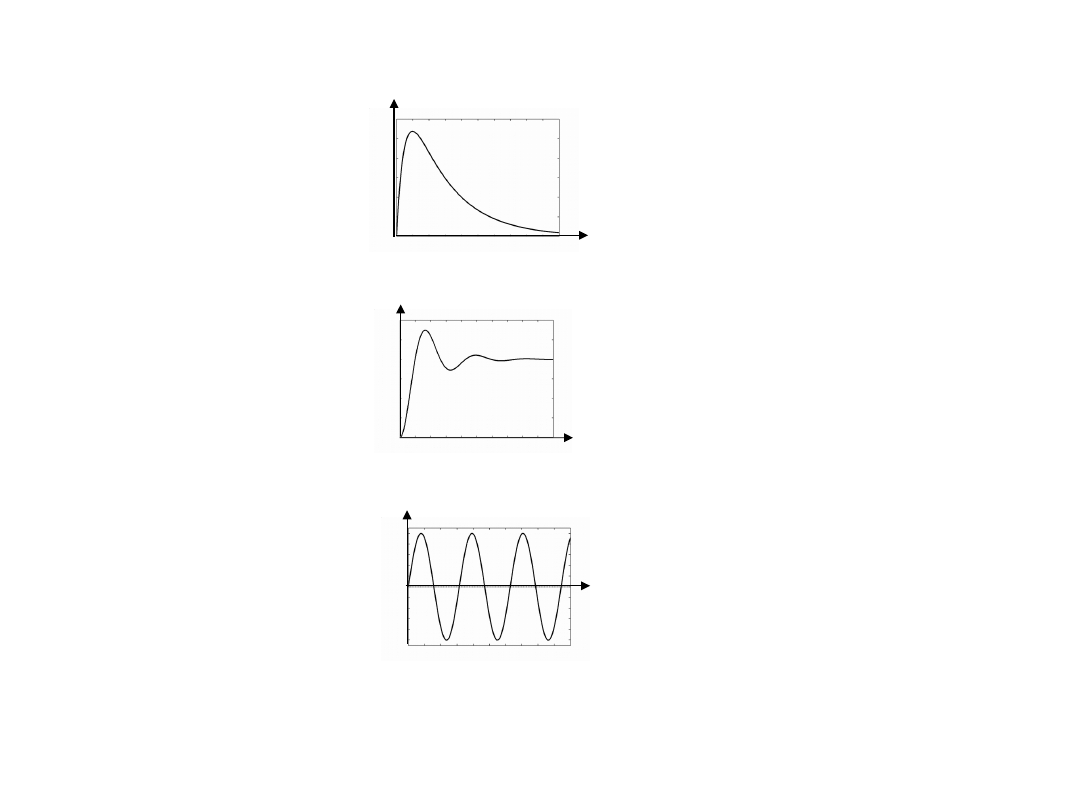
4
g
t
0
g
t
0
g
t
0

5
0
0
1
1
1
a
s
a
s
a
s
a
n
n
n
n
(7)
0
2
1
4
3
1
2
3
4
5
6
7
1
2
3
4
5
1
2
3
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
Kryteria stabilności
Kryterium Hurwitza

6
1
1
n
a
2
3
1
2
n
n
n
n
a
a
a
a
3
4
5
1
2
3
1
3
0
n
n
n
n
n
n
n
n
a
a
a
a
a
a
a
a
1
0
3
2
4
5
6
7
2
3
4
5
1
2
3
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n

7
0
0
1
2
2
3
3
a
s
a
s
a
s
a
Przykład 1. Znaleźć na podstawie kryterium
Hurwitza warunki stabilności dla układu trzeciego
rzędu
Rozwiązanie:
Równanie charakterystyczne układu ma postać
0
0
0
,
0
0
1
2
3
a
a
a
a
.
przy
czym
Wyznacznik Hurwitza
3
musi być dodatni czyli
0
0
0
0
0
2
1
0
3
2
a
a
a
a
a
a

8
0
2
0
3
0
1
2
a
a
a
a
a
0
)
(
0
3
1
2
0
a
a
a
a
a
0
0
3
1
2
a
a
a
a
Z wyznacznika
3
wynikają następujące
nierówności:
0
2
1
a
Podwyznaczni
k
0
1
0
3
2
2
a
a
a
a
0
0
3
1
2
a
a
a
a
0
3
1
2
a
a
a
a
Podwyznaczni
k
9
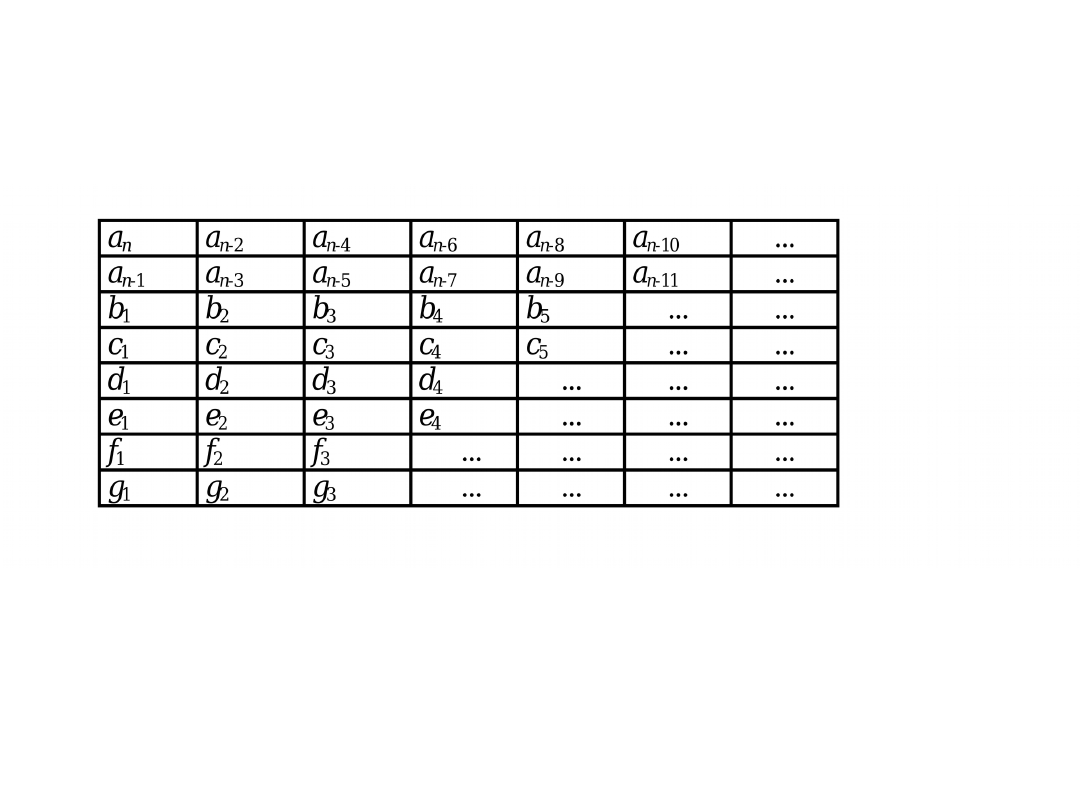
Kryterium Routha
Tablica Routha

10
,
,
,
1
7
1
6
3
1
5
1
4
2
1
3
1
2
1
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a
a
a
a
a
b
a
a
a
a
a
b
a
a
a
a
a
b
,
,
,
1
4
1
7
1
3
1
3
1
5
1
2
1
2
1
3
1
1
b
b
b
a
a
c
b
b
b
a
a
c
b
b
b
a
a
c
n
n
n
n
n
n
,
,
,
1
4
1
4
1
3
1
3
1
3
1
2
1
2
1
2
1
1
c
c
c
b
b
d
c
c
c
b
b
d
c
c
c
b
b
d
1
4
1
4
1
3
1
3
1
3
1
2
1
2
1
2
1
1
,
,
d
d
d
c
c
e
d
d
d
c
c
e
d
d
d
c
c
e
itd.
(8
)

11
0
1
2
2
3
3
4
4
a
s
a
s
a
s
a
s
a
Przykład 2. Określić na podstawie kryterium
Routha ogólny warunek stabilności dla układu
czwartego rzędu.
Rozwiązanie:
Wielomian charakterystyczny układu ma postać
a
0
0, a
1
0, a
2
0, a
3
0,
a
4
0.
Warunek konieczny stabilności jest
następujący:
Warunkiem dostatecznym stabilności jest taki sam znak
wyrazów pierwszej kolumny tablicy Routha.
Wyrazy pierwszej kolumny tablicy Routha obliczamy
na podstawie wzorów (8).

12
0
3
3
0
4
2
3
1
4
2
3
3
1
3
2
4
1
0
a
a
a
a
a
b
a
a
a
a
a
a
a
a
a
a
b
0
0
0
1
1
3
2
1
4
2
3
0
2
3
1
1
2
3
1
1
2
3
1
1
1
2
1
1
3
1
b
b
a
c
a
a
a
a
a
a
a
b
b
a
a
b
b
a
b
a
b
b
b
a
a
c
0
0
2
0
2
1
1
2
1
1
d
a
b
c
c
b
b
d

13
Warunki stabilności:
0
1
b
i
.
0
1
c
1
4
2
3
a
a
a
a
1
4
2
3
0
2
3
1
a
a
a
a
a
a
a
i
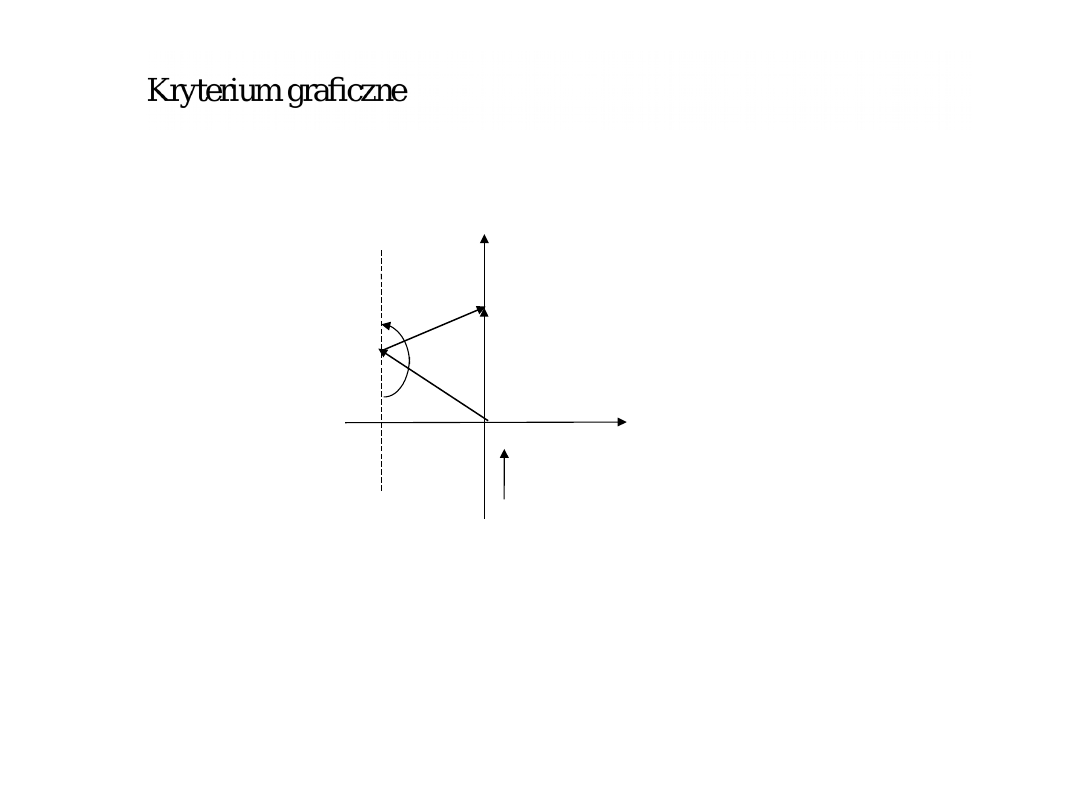
14
)
)...(
)(
(
)
(
2
1
n
n
s
j
s
j
s
j
a
j
M
π
)
(
arg
0
)
Re(
i
i
s
j
s
π
)
(
arg
0
)
Re(
n
j
M
s
i
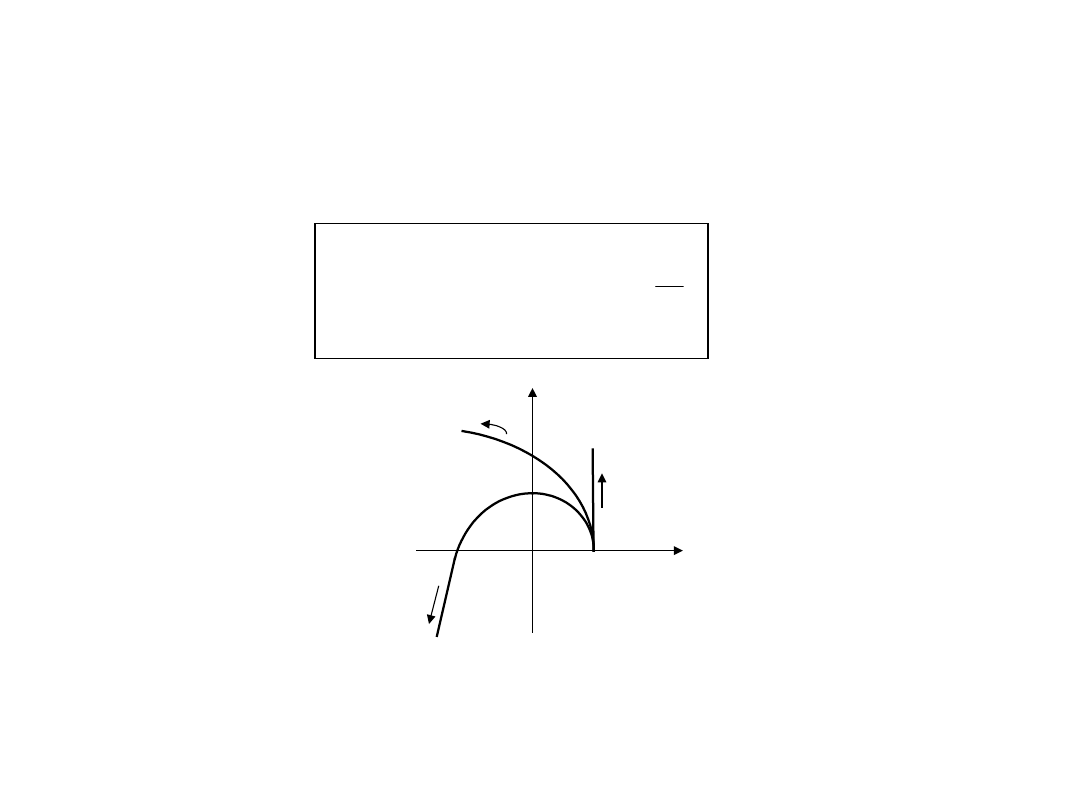
Re[s]
j
(j
– s
i
)
+
Im[s]
0
s
i
15
)
(
Im
)
(
Im
)
(
Re
)
(
Re
j
M
j
M
j
M
j
M
2
π
)
(
arg
0
n
j
M
n=1
n=2
n=3
= 0
0
(9
)
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
Wyszukiwarka
Podobne podstrony:
Automamaty 1 11
AutomatykaII 11
Saba Schwarzwald Automatic 11 Schematic
AUTOMATY 11 Te dobre kurna
Automatyka (wyk 11 12) ppt [try Nieznany
003HISTORIA SZTUKI WCZESNOCHRZEŚCIJAŃSKIEJ I BIZANTYJASKIEJ WYKŁAD III 3 11 09 (Automatycznie zapisa
Automaty ściąga do ćw 11
sprawko automatyka no 11
26-11, Automatyka i Robotyka, Semestr I, Fizyka, Semestr 2, Laboratoria, Instrukcje, Zadanie 11, Pom
wstęp ćw 11, PWr W9 Energetyka stopień inż, IV Semestr, Podstawy automatyki - laboratorium, Podsatwy
automatyka i sterowanie wyklad 11
26-5, Automatyka i Robotyka, Semestr I, Fizyka, Semestr 2, Laboratoria, Instrukcje, Zadanie 11, Pomo
har ST Ii AIR AMU 6 l 11 12, Automatyka i robotyka air pwr, VI SEMESTR
26-6, Automatyka i Robotyka, Semestr I, Fizyka, Semestr 2, Laboratoria, Instrukcje, Zadanie 11, Pomo
11 Podstawy automatyki - Transformata Z, PWr W9 Energetyka stopień inż, III Semestr, Podstawy automa
CLAB 11 2010-2011, Automatyka i Robotyka, Język programowania
11 automaty gotowe
11, wojtek studia, Automatyka, studia 2010, obrona inz, Pytania na obrone, brak tematu , dyplomowka
więcej podobnych podstron