Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z metodami wyznaczania charakterystyk dynamicznych obiektów i znajdowaniem transmitancji zastępczych.

Zadania do wykonania:

1. Na podstawie doświadczalnej odpowiedzi skokowej na wymuszenie prostokątnym impulsem - wyznaczyć graficznie odpowiedź skokową obiektu inercyjnego 3-go rzędu (k=1 ; T=20).

2. Wyznaczyć doświadczalnie odpowiedź skokową obiektu inercyjnego 3-go rzędu (k=1 ; T=20) i porównać z otrzymaną graficzną.

3. Z otrzymanej w punkcie 2 odpowiedzi skokowej obiektu wyznaczyć parametry zastępcze transmitancji i przyporządkować danemu obiektowi odpowiadającą mu transmitancję zastępczą według Rotacza.

4. Wyznaczyć doświadczalnie odpowiedź skokową obiekty bez wyrównania, opracować graficznie i przyporządkować obiektowi transmitancję zastępczą.

5. Wyznaczyć odpowiedzi skokowe układu regulacji z obiektem z wyrównaniem (k=1 ; T=5) i regulatorem typu: a) P (k_p=1)

b) PI (k_p=1 ; T_i=0,5)

6. Wyznaczyć odpowiedzi skokowe układu regulacji z obiektem bez wyrównania (całkującym) i regulatorem typu: a) P (k_p=1)

• b) I (T_i=30)

c) PI (k_p=1,2 ; T_i=1)

7. Skomentować otrzymane wyniki.

Zadania wykonane: ćwiczenie 1.11

Ad 1.

Układ blokowy dla programu TUTSIM.

gdzie:

PLS: A=1 ; t_o=0s ; t_k=200s

FIO₁ ÷ FIO₃: k=1 ; T=20s

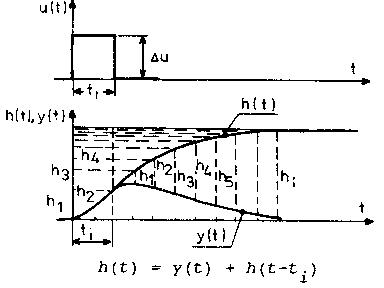
Z otrzymanej charakterystyki - (dołączona do sprawozdania jako charakterystyka nr 1) uzyskaliśmy charakterystykę odpowiedzi skokowej obiektu inercyjnego 3-go rzędu - narysowane ołówkiem (na podstawie zamieszczonego sposobu).

Ad 2.

Wyznaczona doświadczalnie odpowiedź skokowa obiektu inercyjnego 3-go rzędu (k=1 ; T=20), zamieszczona jest na dołączonym do sprawozdania jako charakterystyka nr 2.

Otrzymana doświadczalnie charakterystyka w momencie, gdy przechodzi przez tzw. punkt przegięcia P- zaczyna dążyć do wartości ΔY. Charakterystyka otrzymana graficznie - rysowana na podstawie wyżej zamieszczonego rysunku posiada zbliżony charakter.

h(t) = y(t) +h( t - t_i )

Ad 3.

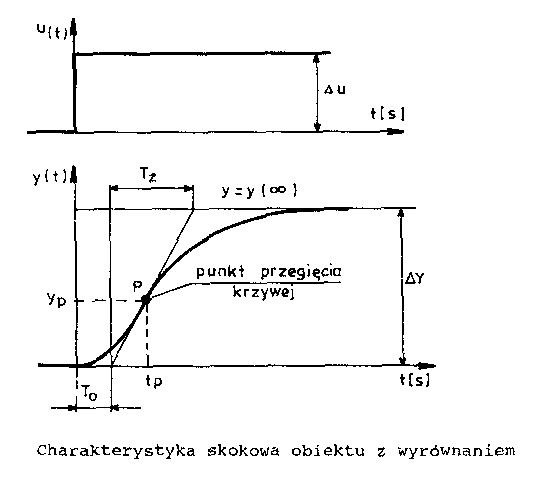
Wyznaczmy parametry zastępcze transmitancji do otrzymanej w punkcie 2 odpowiedzi skokowej obiektu. Następnie przyporządkowywujemy danemu obiektowi odpowiadającą mu transmitancję zastępczą według Rotacza.

Parametry zastępcze:

- h_p = 0,334

- T₀ = 15,79s

- T_z = 75s

- T_zr = T_z(1-h_p) = 75(1-0,334) = 49,95s

- T_0r = T­₀+ T_zh_p - T_zrln(1/(1-h_p) = 15,79 + 75*0,334 -75*ln(1/(1-0,334)) = 10,35s

Transmitancja zastępcza według Rotacza wynosi:

Ad 4.

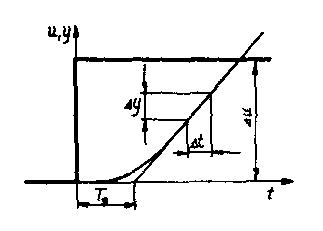
Wyznaczona doświadczalnie odpowiedź skokowa obiektu bez wyrównania - opracowana graficznie (według podanej niżej metody), zamieszczona jest w sprawozdaniu jako charakterystyka nr 3.

Układ blokowy dla programu TUTSIM.

gdzie:

PLS: A=1 ; t_o=0s ; t_k=200s

FIO₃ ÷ FIO₅: k=0,2 ; T=10s

Δt = 14,47s Δy = 13,16 Δu = 1

T_c = 14,47/13,16 = 1,1s T₀ = 30,92s

Transmitancja zastępczą przyporządkowana danemu obiektowi:

lub

Ad 5.

Ćwiczenie 2.1

Układ blokowy dla programu TUTSIM.

Odpowiedź skokowa układu regulacji z obiektem z wyrównaniem i regulatorem typu P:

k_p=1 ; T =3,07s ; Δz₀ =0,5

Transformata sygnału wejściowego:

Natomiast przebieg czasowy:

Odpowiedź skokowa układu regulacji z obiektem z wyrównaniem i regulatorem typu PI:

k_p=1 ; T_i=0,5s

Transformata sygnału wejściowego:

Charakter przebiegu zależy od współczynnika tłumienia ξ. Jest on równy:

co oznacza, iż mamy charakter oscylacyjny, gdyż 0<ξ<1.

Natomiast przebieg czasowy:

Porównując obydwie charakterystyki, można jednoznacznie stwierdzić, iż uzyskanie stabilności w układzie regulacji z obiektem z wyrównaniem jest lepsze, gdy zastosujemy regulator PI.

Ad 6.

Układ blokowy dla programu TUTSIM.

Odpowiedź skokowa układu regulacji z obiektem bez wyrównania i regulatorem typu P:

k_p=1 ; T =1,18s ; Δz₀ =1

Transformata sygnału wejściowego:

Natomiast przebieg czasowy:

Odpowiedź skokowa układu regulacji z obiektem bez wyrównania i regulatorem typu I:

T_i=30s ; k_p=0,001

Odpowiedź skokowa układu regulacji z obiektem bez wyrównania i regulatorem typu PI:

k_p=1,2 ; T_i=1s

Transformata sygnału wejściowego:

Charakter przebiegu zależy od współczynnika tłumienia ξ. Jest on równy:

co oznacza, iż mamy charakter oscylacyjny, gdyż 0<ξ<1.

Natomiast przebieg czasowy:

Porównując obydwie charakterystyki, można jednoznacznie stwierdzić, iż uzyskanie stabilności w układzie regulacji z obiektem bez wyrównania jest lepsze, gdy zastosujemy regulator PI. Natomiast gdy stosujemy regulator I w tymże układzie - otrzymujemy układ strukturalnie niestabilny. Uzyskanie stabilności w takim układzie jest możliwe po zmianie struktury układu regulacji.

Wnioski:

Do ćwiczenia 1.11

Charakterystyka odpowiedzi skokowej obiektu inercyjnego 3-go rzędu - narysowana ołówkiem jest mniej dokładna aniżeli charakterystyka otrzymana za pomocą programu TUTSIM wynika to z jej krzywoliniowości (brak odpowiedniej ilości punktów naniesionych ołówkiem).

Każdemu obiektowi przyporządkowaliśmy transmitancje zastępczą według Rotacza. Są jeszcze dwie możliwości przyporządkowania charakterystyk - dopiero porównanie tych trzech mogło by nam bardziej przybliżyć właściwości tych obiektów.

Do ćwiczenia 2.1

Porównując obydwie charakterystyki w punkcie 5, można jednoznacznie stwierdzić, iż uzyskanie stabilności w układzie regulacji z obiektem z wyrównaniem jest lepsze, gdy zastosujemy regulator PI.

Porównując obydwie charakterystyki zestawione w punkcie 6, można także stwierdzić, iż uzyskanie stabilności w układzie regulacji z obiektem bez wyrównania jest lepsze, gdy zastosujemy regulator PI. Natomiast gdy stosujemy regulator I w tymże układzie - otrzymujemy układ strukturalnie niestabilny. Uzyskanie stabilności w takim układzie jest możliwe po zmianie struktury układu regulacji.

---