
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
1
Rzut środkowy – część 2
Rzut środkowy – część 2
Plan wykładu
•
Równoległość i prostopadłość
•
Konstrukcje miarowe –
kład płaszczyzny i punkt mierzenia prostej
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
2
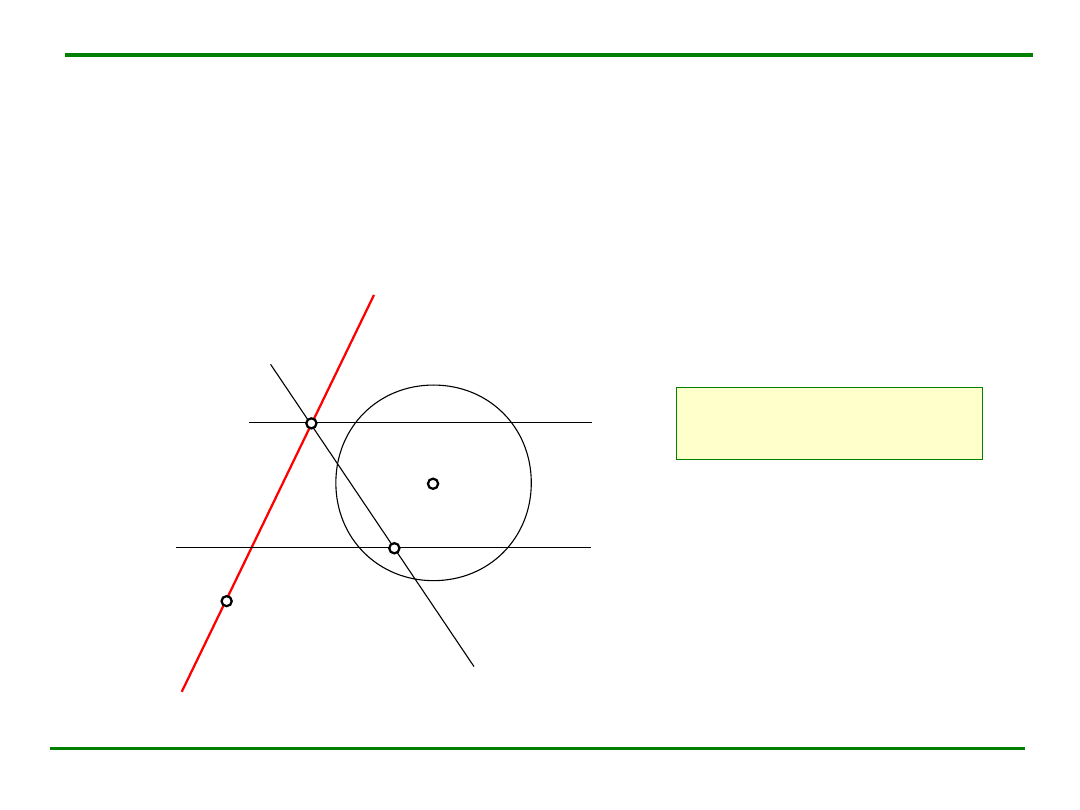
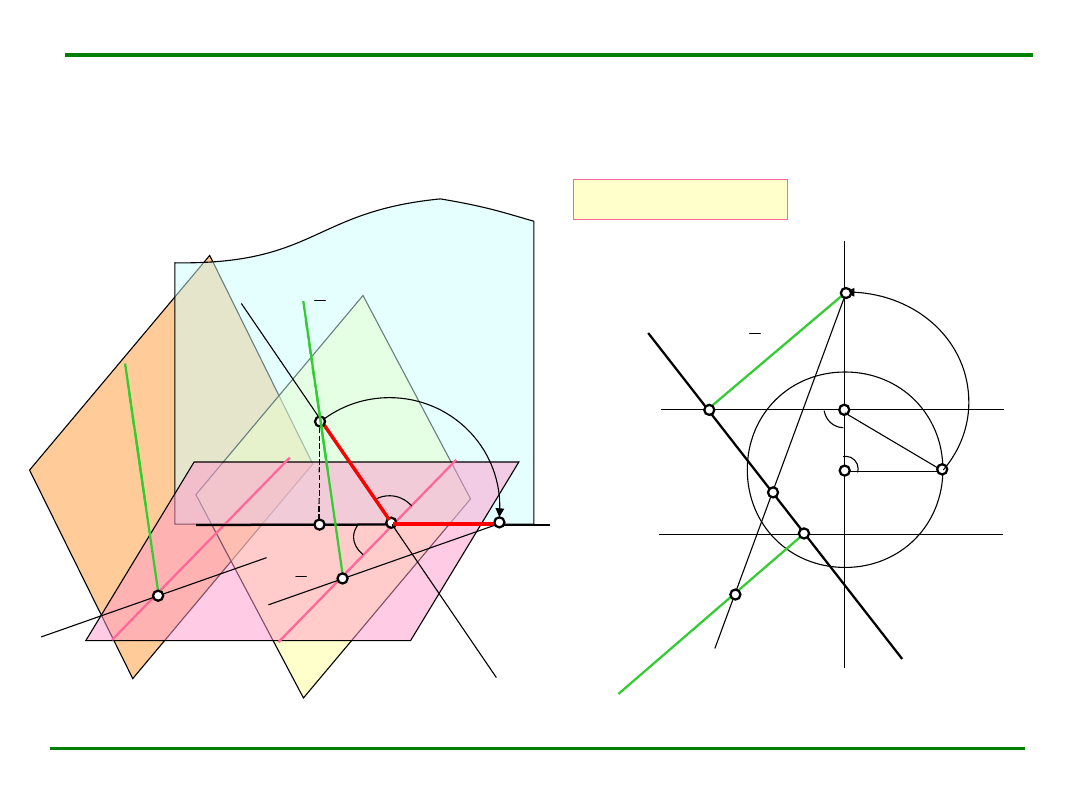
Prosta równoległa do płaszczyzny
Prosta równoległa do płaszczyzny
t
z
S
b’
Twierdzenie.
Prosta jest równoległa do danej płaszczyzny, jeśli jest równoległa do jakiejś
prostej leżącej w tej płaszczyźnie.
T
b
Warunek równoległości:
Z
prostej
z
płaszczyzny
Z
b
=
a’
Z
a
T
a
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
3
z
t
b’
Z
b
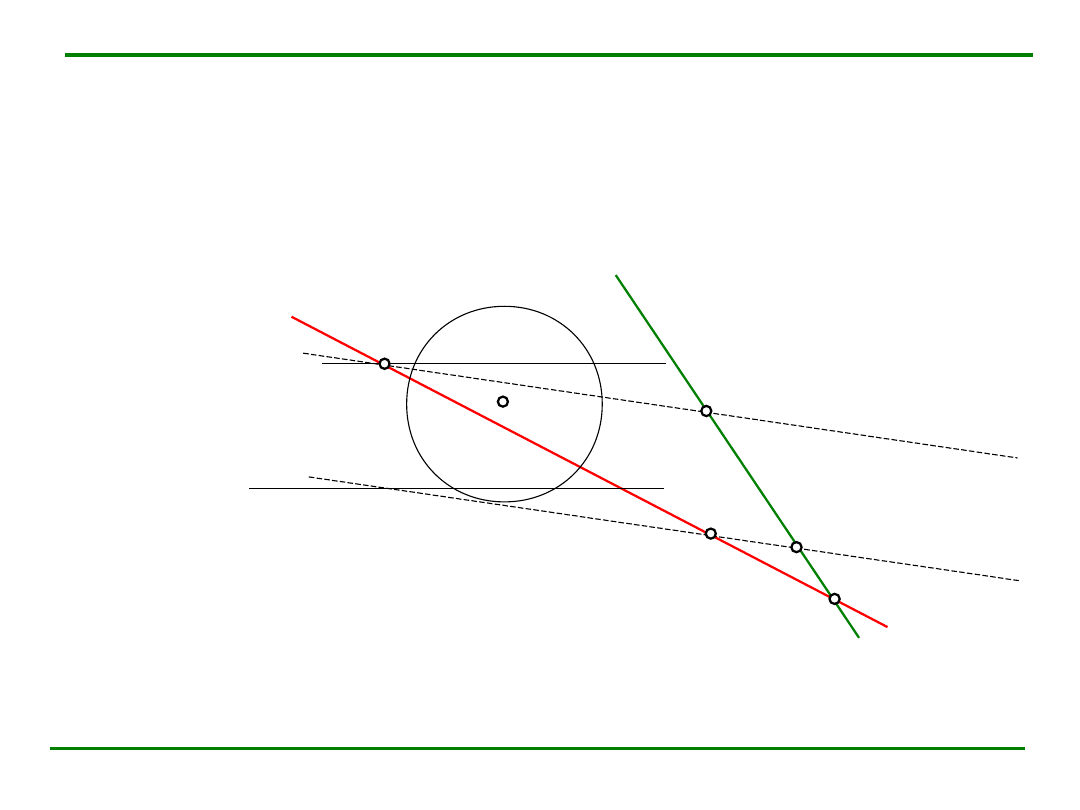
Zadanie
Zadanie
Przez dany punkt A poprowadź prostą b równoległą do danej płaszczyzny
t
z
S
a’
Z
a
T
a
T
b
A’
Plan zadania:
1.
Przez punkt A rysujemy dowolną prostą b ||
2.
Rysujemy ślady płaszczyzny(a,b).
3.
Punkt przecięcia śladu t
z
rzutem prostej b jest jej śladem tłowym T
b
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
4
t
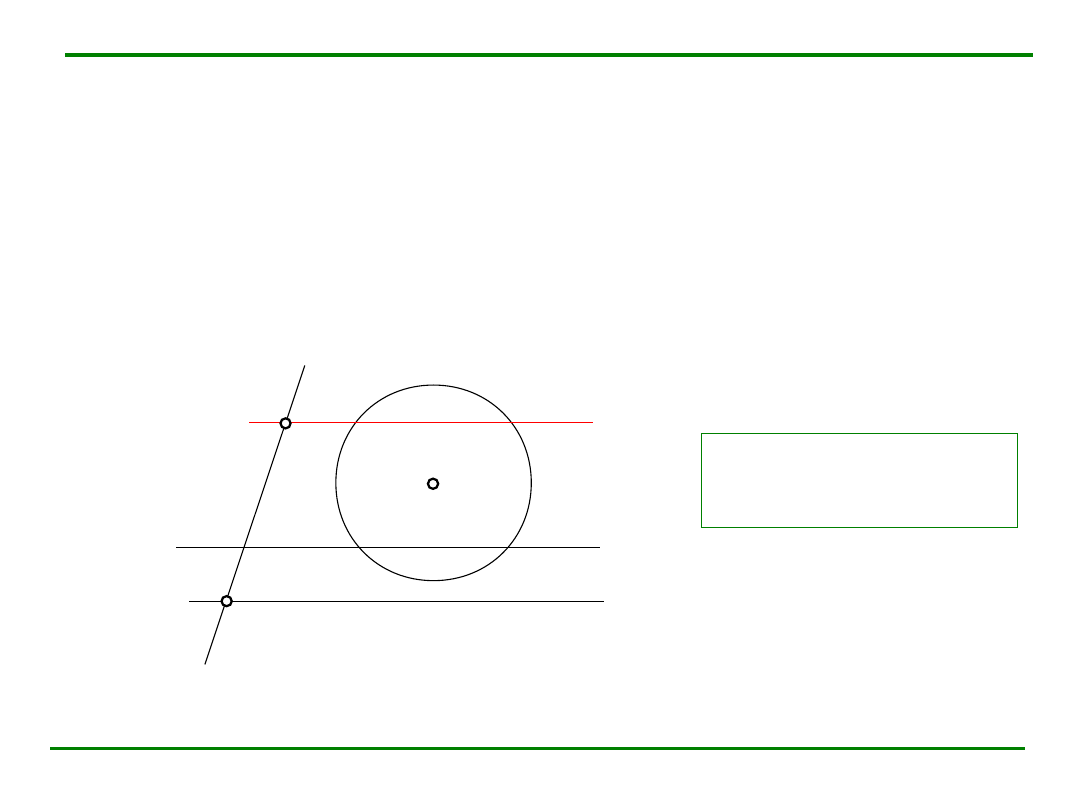
Płaszczyzny równoległe.
Płaszczyzny równoległe.
t
z
S
Twierdzenie.
Płaszczyzna jest równoległa do drugiej płaszczyzny, jeśli zawiera dwie proste
przecinające się równoległe do tej płaszczyzny.
Warunek równoległości:
z
z
t
t
=z
a’
Z
a
T
a
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
5
Prosta prostopadła do płaszczyzny
Prosta prostopadła do płaszczyzny
S
S
t
z
p
p
Z
p
.
.
.
L
’
W rzucie mamy:
t
z
S
p’
T
p
’
L
.
Z
p
.
S
x
.
– płaszczyzna
zawierająca prostą p oraz punkt S
T
p

UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
6
Zdjęcia fotogrametryczne
Zdjęcia fotogrametryczne
Stereogram – para zdjęć z 60% pokryciem
Prostopadłe do tła
Wspólny punkt zbiegu
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
7
o
a
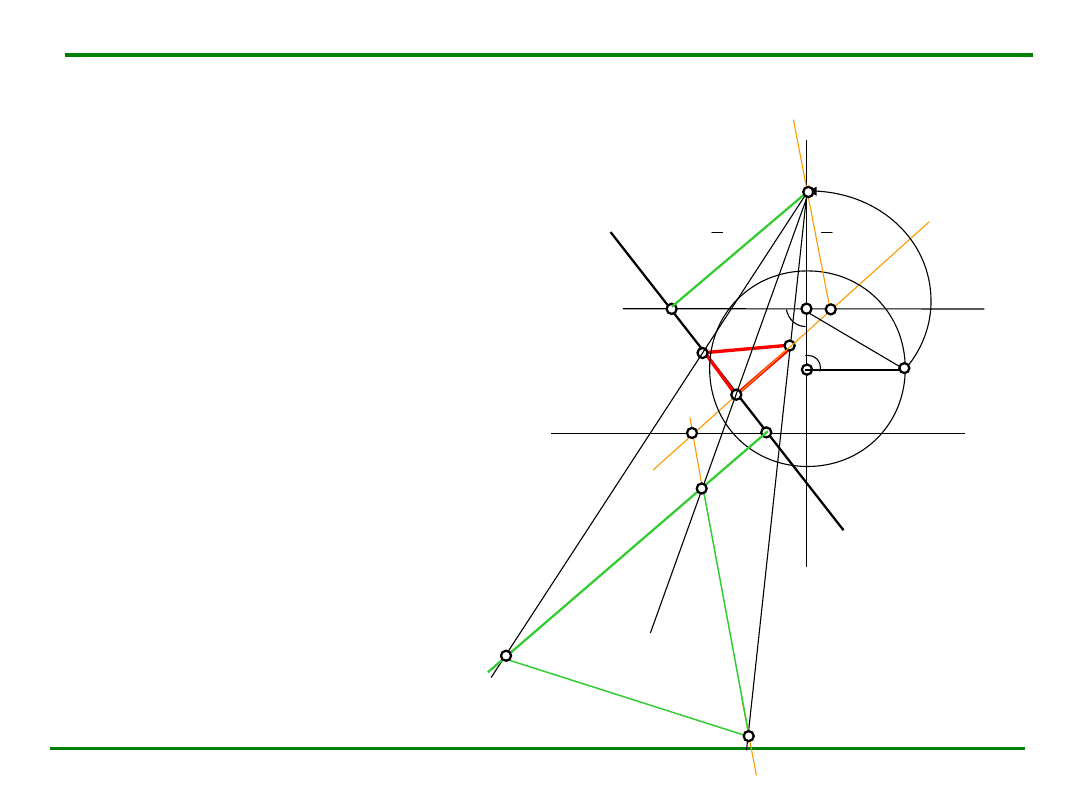
Kład płaszczyzny
Kład płaszczyzny
S
S
t
z
L
.
.
’
S
o
o
a
a
o
a
Z
a
a
T
a
W rzucie mamy:
t
z
S
a’
T
a
’
L
.
Z
a
.
S
x
S
o
a
o
A’
A
o
Punkty: A’, S
o
i A
o
leżą na jednej prostej
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
8
C’
t
z
b’
T
b
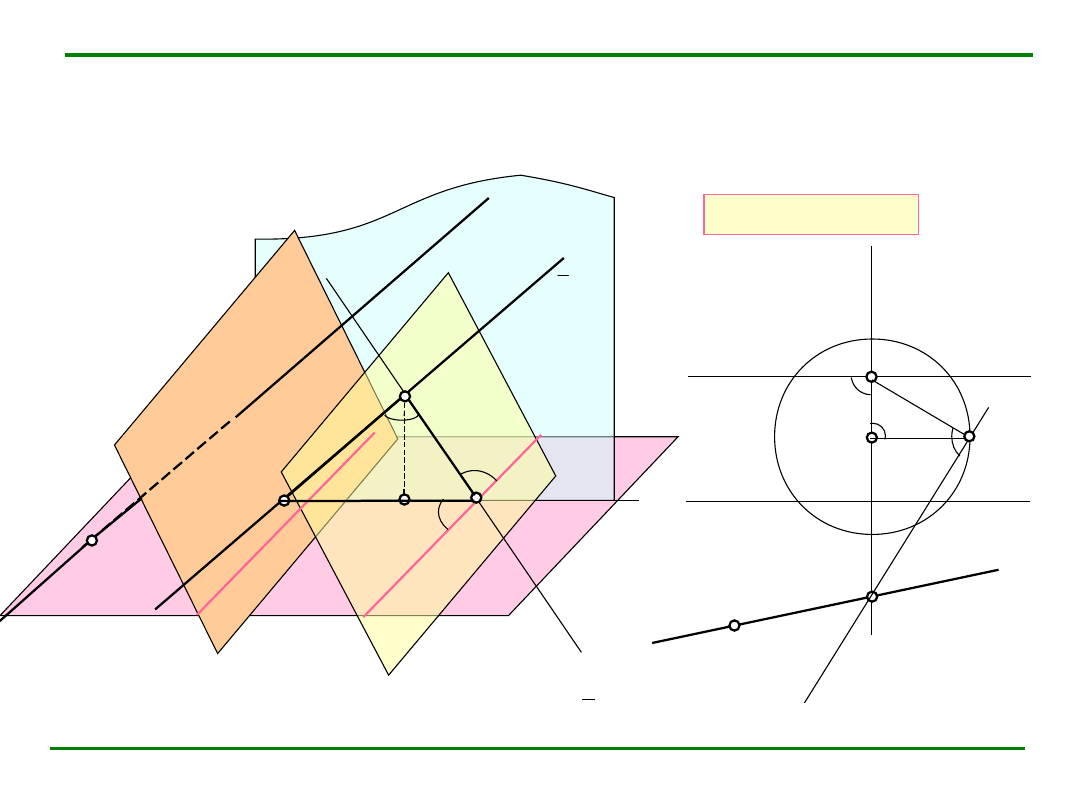
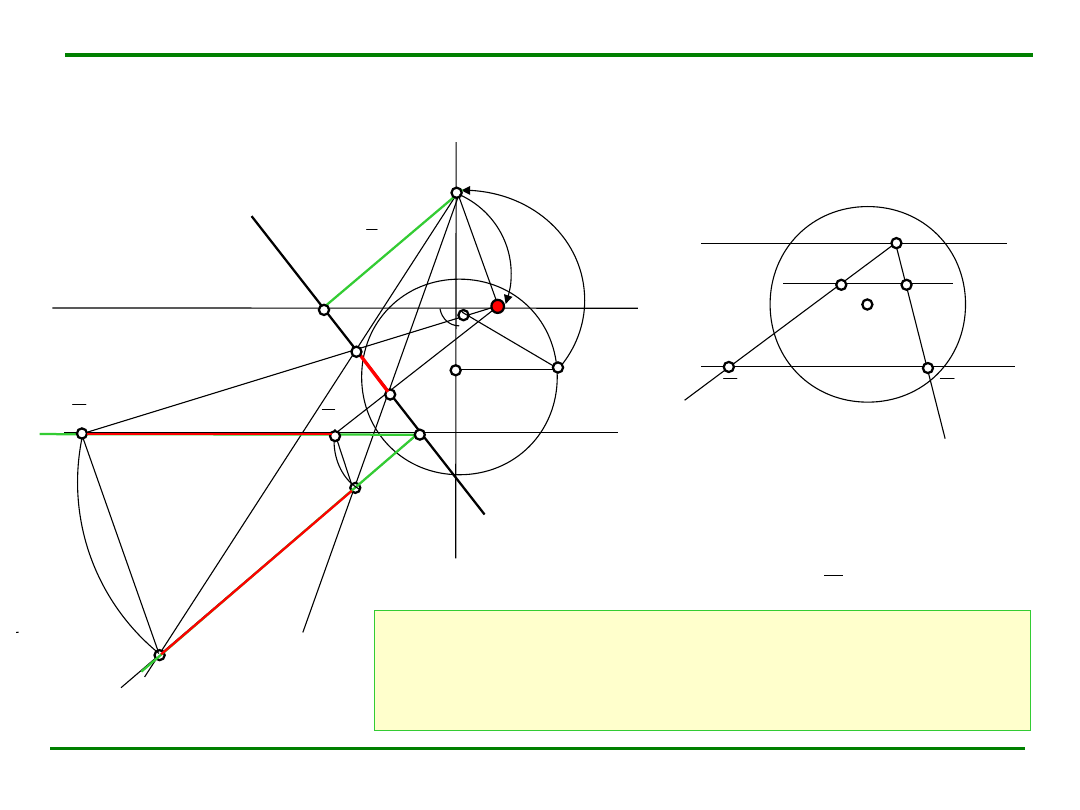
Podniesienie z kładu
Podniesienie z kładu
Zadanie:
Narysuj rzut środkowy trójkąta
równobocznego ABC, którego bok
AB jest dany.
S
a’
T
a
’
Z
a
.
A’
B’
C
o
Z
b
o
b
b
o
Plan zadania:
1. przez prostą a prowadzimy
płaszczyznę
2. wykonujemy kład płaszczyzny i
kład odcinka AB
3. konstruujemy trójkąt A
o
B
o
C
o
w
kładzie
4. podnosimy punkt C z kładu (za
pomocą prostej b zawierającej bok
BC)
o
a
L
S
x
S
o
a
o
A
o
B
o
.
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
9
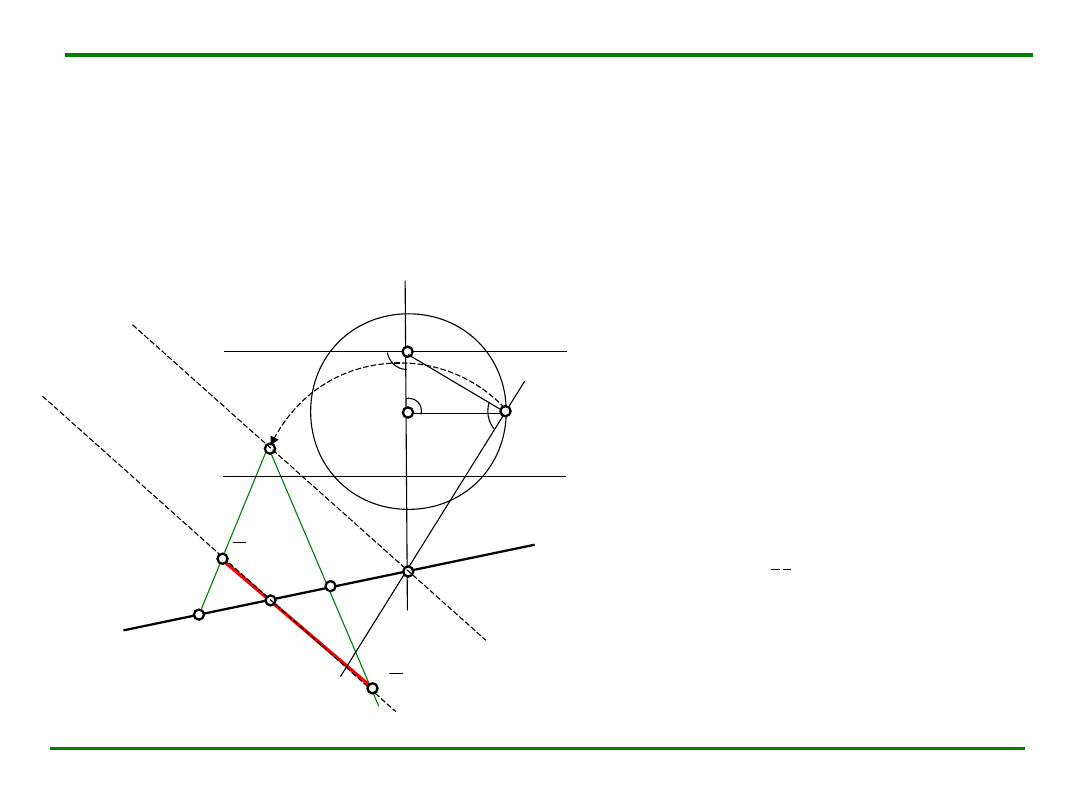
Punkt mierzenia prostej
Punkt mierzenia prostej
t
z
o
a
L
S
x
S
o
a
o
A
o
B
o
.
S
’
T
a
a’
Z
a
A’
B
’
A
B
M
a
M
A’
B
’
A
B
S
t
z
Jeśli odcinek AB jest równoległy do rzutni,
punktem mierzenia może być dowolny
punkt M z
Z podobieństwa trójkątów S
o
Z
a
M
a
oraz A
o
T
a
A
mamy:
Z
a
S
o
=Z
a
M
a
Punkt
M
a
z
(płaszczyzny, w której leży prosta)
nazywamy
punktem mierzenia
prostej b.
Służy on do wyznaczania rzeczywistych wymiarów odcinków leżących
na danej prostej.
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
10
Punkt mierzenia dla prostej prostopadłej.
t
z
S
p’
T
p
’
L
.
Z
p
.
S
x
.
Wyznacz rzeczywistą długość odcinka AB p
A’
B’
M
p
t
z
A
B
Punkt mierzenia prostej p leży na śladzie zbiegu płaszczyzny
zawierającej tę prostą.
Odległość punktu mierzenia M
p
od środka
rzutów jest w tym przypadku równa długości
odcinka Z
p
S
x
.
Długość odcinka AB tjest rzeczywistą
długością odcinka AB.

UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
11
Zadania
Zadania
1.
Narysuj odcinek, którego odległość jest równa rzeczywistej odległości
danego punktu od danej:
a)
prostej,
b)
płaszczyzny.
2.
Narysuj odcinek, którego odległość jest równa rzeczywistej odległości
danych:
a)
prostych równoległych,
b)
płaszczyzn równoległych.
UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
12
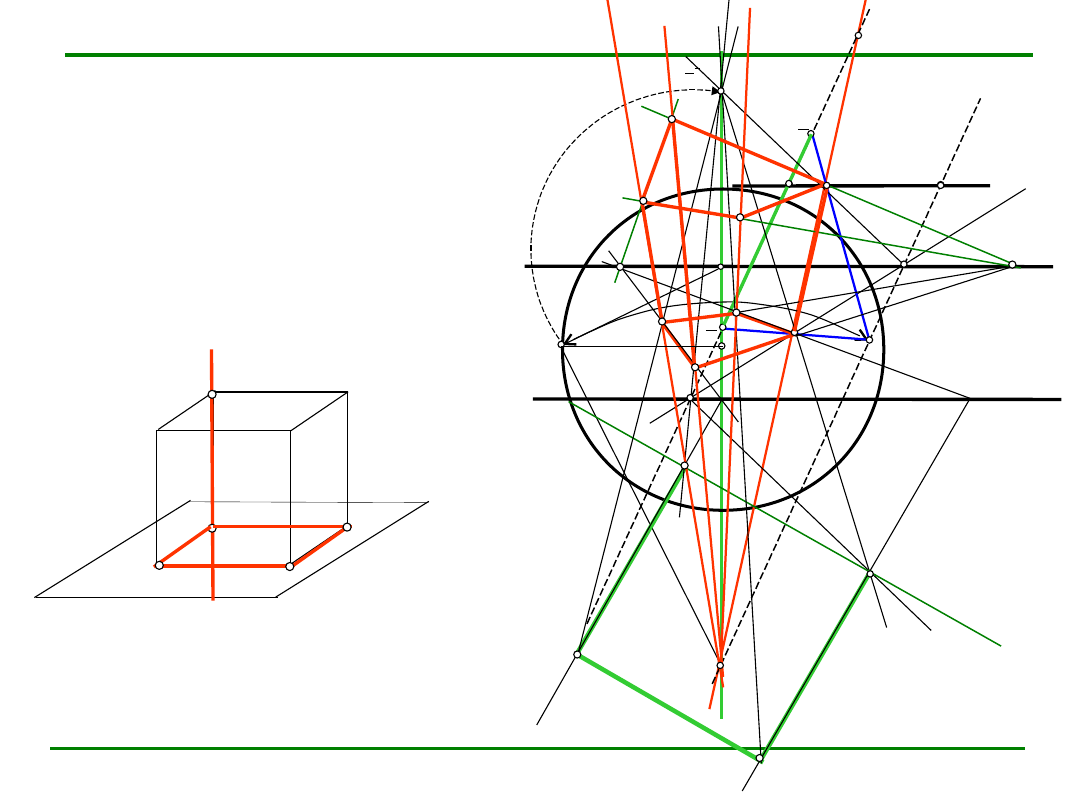
Konstrukcja sześcianu
S
T
m
H’
z
t
’
L
Z
p
S
x
Z
m
t
z
T
p
k’
D’
M
p
D
H
S
o
k
o
Z
k
T
k
k
o
D
o
A
o
B
o
C
o
C’
B’
A’
Z
2
Z
1
G’
E’
F’
Dane:
•
płaszczyzna podstawy ABCD
•
wierzchołek H ma prostej m
Narysuj rzut sześcianu ABCDEFGH wiedząc, że
krawędź AD podstawy tworzy kąt 30
0
ze śladem tłowym płaszczyzny .
A
H
G
F
E
D
C
B

UWM - Geodezja i Szacowanie Nieruchomości rok I – Olsztyn 2008/9
28.10.21
dr Renata Jędryczka
13
Literatura
1.
Otto, E., F., 1975, Podręcznik geometrii wykreślnej, PWN
2.
http://matwbn.icm.edu
Wykład na stronie przedmiotu:
http://www.kfit.uwm.edu.pl/geometria/
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
Wyszukiwarka
Podobne podstrony:
Wykład 5 rzut środkowy
Rzut środkowy
w12 rzut środkowy 3
19 rzut środkowyid 18360
Rzut środkowy zadania, Geodezja i Kartografia, I rok, Grafika Inżynierska
25 rzut srodkowy
Wykład 5 rzut środkowy
w12 rzut środkowy 3
Rzut środkowy zadania[1]
Rzut cechowany i srodkow zadania, Studia, grafika
EŚT 07 Użytkowanie środków transportu
spoleczna w10
W10
Nowotwory łagodne i złośliwe gardła środkowego
W10 Przetw A Cmin
W10
System platnosci srodkow europejskich
więcej podobnych podstron