NARZĘDZIA

ANALIZY

DECYZYJNEJ

NARZĘDZIA

ANALIZY

DECYZYJNEJ

EKONOMIA

MENEDŻERSKA

10.01.2014

Plan prezentacji

1. Wstęp
2. Racjonalne decyzje a proces

decyzyjny

3. Teoria decyzji
4. Procedury decydowania
5. Drzewa decyzyjne
6. Model Markova
7. Programowanie liniowe
8. Programowanie wielokryterialne

1) WSTĘP

Podejmowanie decyzji

wybór jednej z co najmniej dwóch

możliwości, dwóch rozwiązań

(wariantów), dróg czy kierunków

postępowania, pożądanych z punktu

widzenia interesu (potrzeb) systemu, w

ramach którego wybór ten jest

dokonywany.

Istota decydowania polega na tym, że

menedżer mając świadomość wyboru

działania powinien postanowić co i

dlaczego wybiera i jakie mogą być

tego przewidywane skutki.

2) RACJONALNE DECYZJE A
PROCES DECYZYJNY

Racjonalne decyzje powinny być rezultatem
PROCESU DECYZYJNEGO, obejmującego:

Logicznie powiązaną grupę
operacji myślowych

Określenie warunków
rozwiązania
problemu

Wybór najkorzystniejszego
wariantu

Racjonaln

e

rozwiązan

ie

problemu

Rzetelna

ocena

sytuacji

DECYZJ

A

PROCES

DECYZYJN

Y

AKT

PODJĘCIA

DECYZJI

3) TEORIA DECYZJI

Podejście Normatywne

Matematyka, Statystyka,

Ekonomia

• Wyznaczenie decyzji

optymalnej, tzn.

przynoszącej największe

korzyści, lub

minimalizujące stratę.

Podejście

Deskryptywne

Psychologia,

Kognitywistyka, Socjologia

• Zwrócenie szczególnej

uwagi na przebieg

procesów decyzyjnych w

umyśle człowieka,

badanie wpływu cech

osobowościowych na

podejmowane decyzje.

Metody

klasycznej teorii

decyzji

4) PROCEDURY
DECYDOWANIA

Diagnoza problemu

Formułowanie problemu

Konstrukcja modelu

Wdrożenie wyników

5) DRZEWA DECYZYJNE

•

Graficzne wsparcie procesu decyzyjnego.

• Schemat ten zdolny jest pomieścić wszystkie

informacje potrzebne do rozwiązania procesu
decyzyjnego.

•

Naszkicowanie uproszczonej wersji drzewa decyzyjnego
pomaga ustrukturyzować istniejący problem i
uporządkować istniejące warianty wyboru.

• Struktura drzewa wskazuje najistotniejsze elementy

procesu decyzyjnego niezbędne do podjęcia
prawidłowej decyzji takie jak: dostępne opcje, wyniki
ich wyboru czy też rozkład prawdopodobieństwa.

•

Drzewo decyzyjne pozwala w sposób wizualny
prześledzić drogę rozumowania i dostarczyć
argumentacji uzasadniającej wybór określonego
wariantu decyzyjnego.

• Umożliwia także dokonanie wielokrotnej analizy

wrażliwości, zmodyfikowanie podstawowych
parametrów i założeń oraz zbadanie wpływu tych zmian
na zalecany kierunek przyszłych działań.

Graf – drzewo

budowa:

Korzeń
Węzły
Krawędzie
Liście

EV

A

EV

B

D

A

D

B

P(O

A1

,D

A

)

P(O

A2

,D

A

)

P(O

B1

,D

B

)

P(O

B2

,D

B

)

O

A1

O

A2

O

B1

O

B2

Punkt podjęcia decyzji / Węzeł
decyzyjny

Niepewne zdarzenie – wartość oczekiwana

D

A ,

D

B

Warianty decyzji

O

A1,A2 ,

O

B1,B2

PRZYKŁADOWY SCHEMAT DRZEWA

DECYZYJNEGO

Wyniki podjętych decyzji

P(O,D)

Prawdopodobieństwo wystąpienia zdarzenia (wyniku)

EV

AB

Wartość
oczekiwana

PRZYKŁAD (1)

Pewien poszukiwacz ropy musi podjąć decyzję o
rozpoczęciu odwiertów pod szyb naftowy w
Pewnej lokalizacji. Koszt wiercenia wynosi 600 tys. zł.

Jeśli

ropa nie zostanie odnaleziona a zatem odwiert okaże

się

„suchy” kwota ta zostanie bezpowrotnie stracona.

Jeżeli

odwiert okaże się „mokry” a zatem ropa zostanie
odnaleziona, to (według oceny poszukiwacza)

całkowity

zysk (bez uwzględnienia kosztów wierceń) z

eksploatacji

szybu wyniesie 2 miliony 400 tys. zł, co oznacza że w

razie

sukcesu poszukiwacz osiągnie zysk w wysokości 1

milion

800 tys. zł.

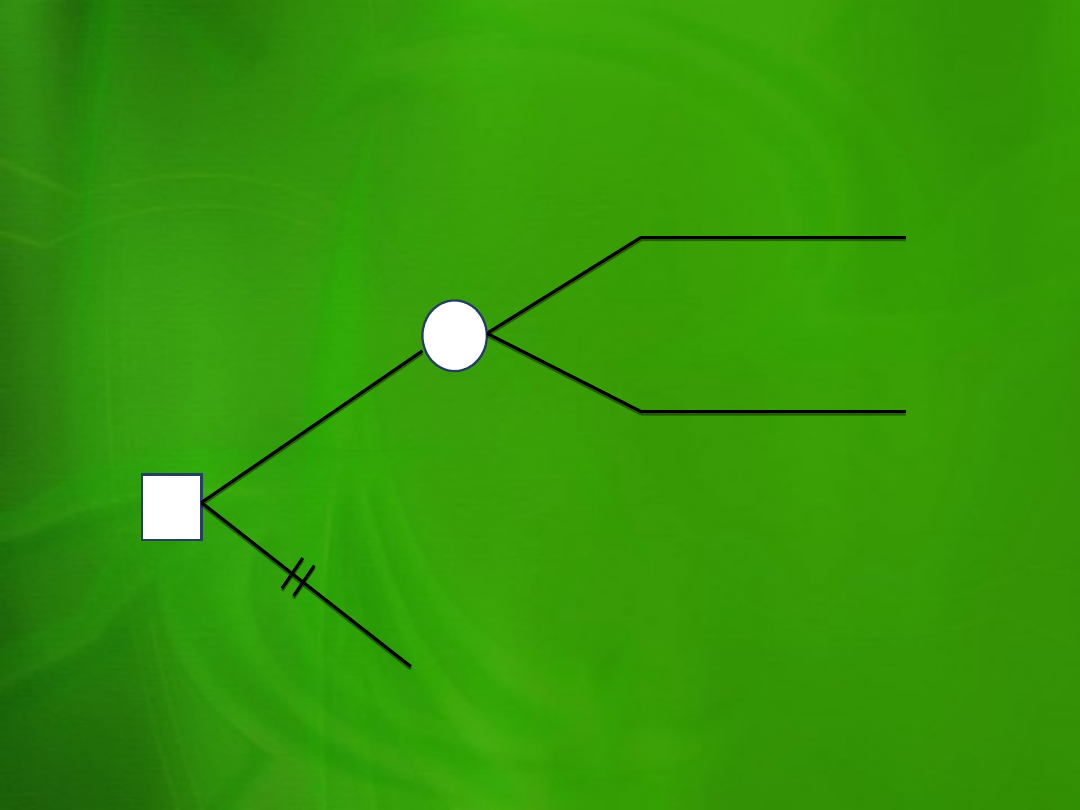
ROZWIĄZANIE

0,6

0,4

Nie wiercić

360

0

Mokro

Sucho

1 800

- 600

6) MODEL MARKOVA

• Modele Markova należą do matematycznych technik

modelowania opartych na rachunku macierzowym

• Charakteryzuje się pewną liczbą dopuszczalnych

stanów i regułami przechodzenia między nimi

Konstruując modele Markova określamy:
• Możliwe stany
• Długość cyklu
• Perspektywę czasową
• Prawdopodobieństwa przejść

RODZAJE MODELI

MARKOVA

Modele Kohortowe

Modele Monte Carlo

• Polegają na przepuszczeniu przez

model grupy jednostek jako całości

• Dopuszczają możliwość

wprowadzenia zmiennych

prawdopodobieństw w czasie oraz

zmiennych miar użyteczności

• Nie pozwalają na określenie

rozkładu oraz zmienności

oczekiwanych wyników

• Polegają na przepuszczeniu przez

model pojedynczej jednostki przy

użyciu generatora liczb losowych,

powtórzenie tej tej operacji

odpowiednią ilość razy powinno dać

wyniki zbliżone do wyników symulacji

kohortowej

• Pozwalają na zdobycie informacji

nie tylko o średniej, ale także

wariancji otrzymanych wyników

• Wymagają dłuższego czasu obliczeń

ŁAŃCUCH MARKOVA

• Łańcuch Markowa jest ciągiem X

1

, X

2

,

X

3

, ... zmiennych losowych

• Dziedzinę tych zmiennych nazywamy przestrzenią

stanów

• Realizacja X

n

 to stany w czasie n

ZALETY ŁAŃCUCHÓW

MARKOVA

• Możliwość predykcji w momencie gdy nie są znane

przyczyny występowania danego zjawiska lub gdy
jest ich za dużo by móc uwzględnić je w analizie.

•

Możliwość konstruowania prognoz dla zjawisk
mierzalnych i niemierzalnych (jakościowych).

• Możliwość budowy prognoz krótko, średnio oraz

długoterminowych

•

Możliwość prognozowanie strukturalnych zjawisk
ekonomicznych wzajemnie zależnych w czasie
elementach składowych

• Możliwość użycia otrzymanych prognoz do

przekształcenia przyszłości zgodnie z
zaplanowanymi potrzebami

PROBLEM DECYZYJNY

MARKOVA

Obliczanie polityki w postaci kompletnego

odwzorowania

stanów do zbioru akcji nazywane jest problemem
Decyzyjnym Markowa (MDP). Model ten zapewnia
matematyczne ramy dla podejmowania decyzji w

sytuacjach,

gdy modelowanie wyniki są częściowo losowe, a

częściowo

pod kontrolą decydenta. Jeśli prawdopodobieństwa

przejść

wynikające z podejmowanych akcji jest zależne tylko

od

bieżącego stanu, a nie np. od historii. Mówimy wtedy,

że

problem posiada własność Markowa.

PROBLEM DECYZYJNY

MARKOVA

Formalnie problem decyzyjny Markowa jest określany

jako:

• Zbiór stanów ze stanem początkowym s

0

• A to skończony zbiór działań A

s

(to skończony zbiór

działań dla stanu s)

• Model przejść P

a

(s,s) = P

r

(s

t+1 =

s|s

t =

s, a

t

= a) to

prawdopodobieństwo, że akcja w stanie w czasie
przejdzie w stan s w czasie t+1

• Funkcje nagrody R

a

(

s,s

) to natychmiastowa nagroda

(lub oczekiwana natychmiastowa nagroda) po
przejściu ze stanu s do stanu s.

7) PROGRAMOWANIE

LINIOWE

•

Programowanie liniowe jest to model, w
którym zarówno warunki ograniczające
jak i funkcja celu mają postać liniową.

• Ma szerokie zastosowanie w teorii

decyzji np. optymalizacja planu
produkcyjnego.

•

Uniwersalną metodą rozwiązywania
zadań programowania liniowego jest
algorytm_simpleks.

ALGORYTM SIMPLEKS

Istota tego algorytmu polega na badaniu

kolejnych

rozwiązań bazowych (dopuszczalnych)

programu

liniowego w postaci kanonicznej w taki

sposób, że:



Znajdujemy dowolne rozwiązanie
bazowe programu



Sprawdzamy czy jest ono optymalne



Jeżeli nie jest optymalne to
konstruujemy następne rozwiązania
bazowe lepsze (lub nie gorsze od
poprzedniego)

Postępowanie kończy się w momencie

stwierdzenia,

że aktualne rozwiązanie bazowe jest

optymalne.

Algorytm simpleks jest procedurą etapową a wyniki
poszczególnych etapów, zestawia się w kolejnych
tablicach simpleks. Każdy program liniowy np.

Można zestawić w postaci macierzowej:

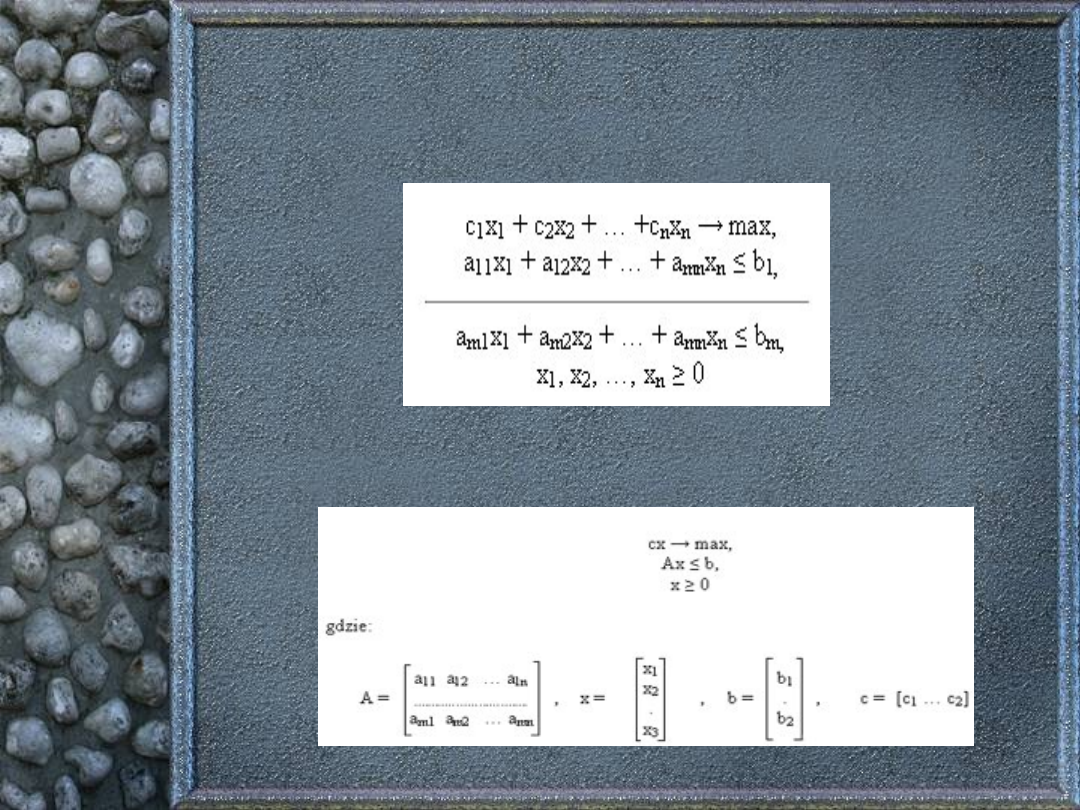
MACIERZOWA POSTAĆ 1

TABLICY MACIERZOWEJ

A – macierz współczynników warunków ograniczających
b – wektor wyrazów wolnych warunków ograniczających
c – wektor wierszowy współczynników funkcji celu
xb – wektor zmiennych bazowych
cb – wektor kolumnowy współczynników funkcji celu przy
zmiennych bazowych
I – macierz jednostkowa o wymiarach mxm
0 – wektor zerowy
cj – zj – kryterium simpleks

PRZYKŁAD (2)

Przedsiębiorstwo produkuje dwa wyroby:

W1 i W2

. W procesie

produkcji tych wyrobów zużywa się wiele środków, spośród

których

dwa są limitowane. Limity te wynoszą:

środek I - 96 000

jedn.,

Natomiast

środek II - 80 000 jedn

. Nakłady limitowanych

środków na

jednostkę wyrobów

W1 i W2

podano w poniższej tabeli:

Wiadomo także, że zdolności produkcyjne jednego z

wydziałów, nie

pozwalają produkować więcej niż

3000 szt

. wyrobów

W1

oraz

4000

szt.

wyrobów

W2

. Ponadto, działająca w ramach

przedsiębiorstwa

komórka analizy rynku ustaliła optymalne proporcje produkcji,

które

kształtują się odpowiednio jak

3:2

.Cena sprzedaży (w zł)

jednostki

wyrobu

W1

wynosi

30

, a wyrobu

W2

-

40

.Ustalić rozmiary

produkcji

przy założeniu, że uzyskany przychód ze sprzedaży będzie

maksymalny.

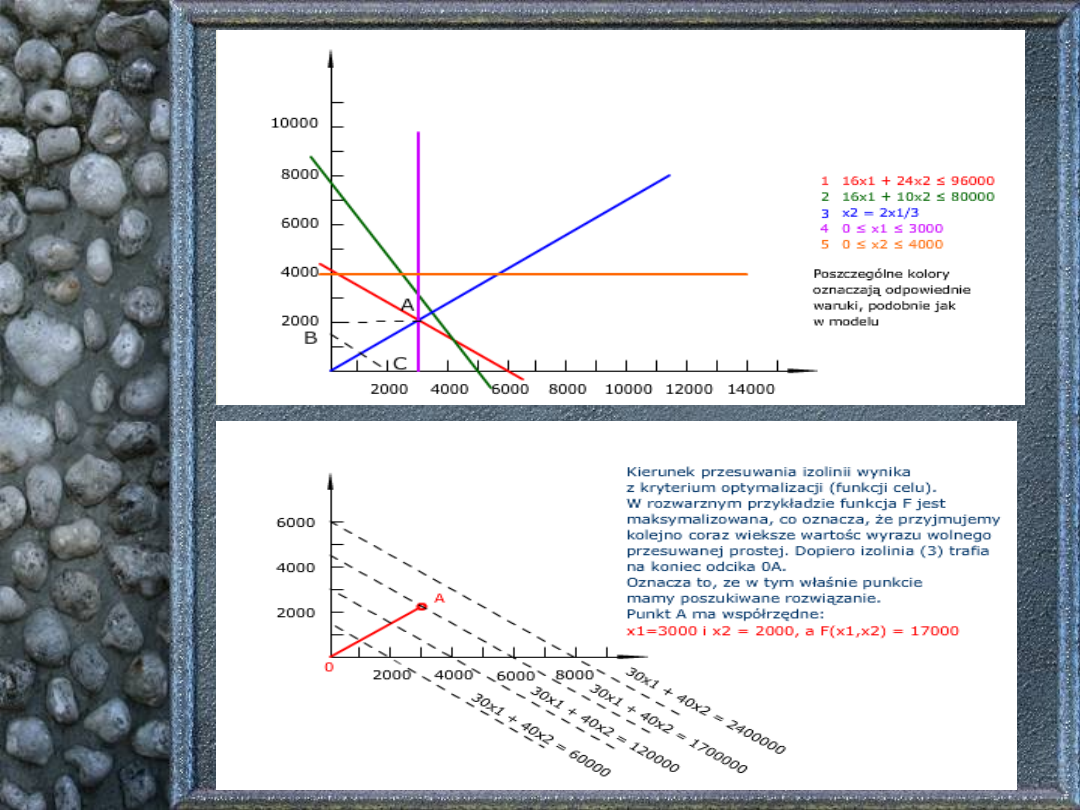
ROZWIĄZANIE

(1)16x1 + 24x2 ≤ 96 000
(2)16x1 + 10x2 ≤ 80 000

(3)x2 = 2/3 x1

(4)0 ≤ x1 ≤ 3 000
(5)0 ≤ x2 ≤ 4 000

(6)F(x1,x2) = 30x1 + 40x2

max.

8) PROGRAMOWANIE

WIELOKRYTERIALNE

Programowanie liniowe operuje jednym kryterium oceny
porównywalnych wariantów decyzji. W rzeczywistości

większość

problemów jest oceniana ze względu na wiele kryteriów, zatem
powstaje pytanie, czy można zbudować model, który łączyłby
zalety programowania liniowego i zarazem mógł służyć
rozwiązywaniu problemów wielokryterialnych.Okazuje się, że

z

formalnego punktu widzenia odpowiedź jest

negatywna,

gdyż

w

większości problemów wielokryterialnych nie istnieje bowiem
rozwiązanie w takim sensie jak w programowaniu liniowym.
Wśród rozważanych decyzji zwykle nie istnieje taka, której

ocena

ze względu na każde kryterium przewyższa odpowiednie oceny
pozostałych decyzji. Fakt ten zaprezentujemy na dwóch
przykładach graficznych przedstawiających przypadki, gdy nie

istnieje

najlepsza decyzja i gdy takiej decyzji brak.

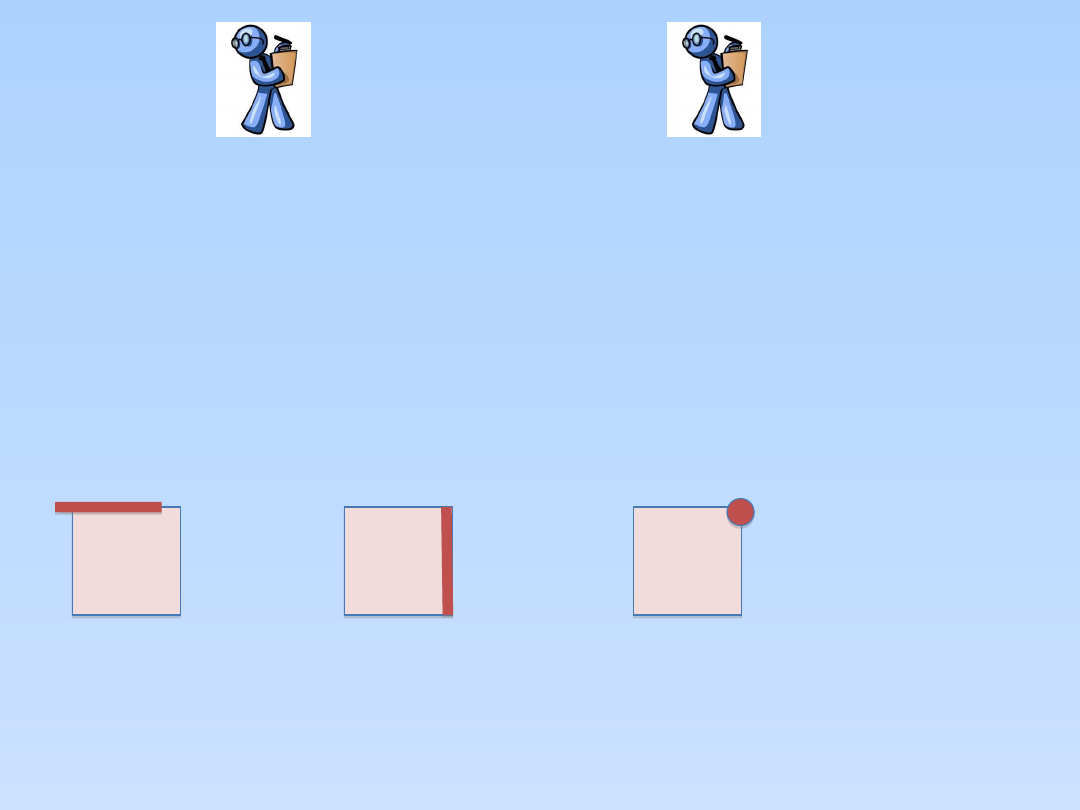
PRZYKŁAD (3)

Na poniższym rysunku przedstawiono 3 kwadraty. Jeśli zadanie

sprowadza się

do wyznaczenia punktu najbardziej wysuniętego na północ, to istnieje

wiele

rozwiązań - ich zbiór przedstawia pogrubiony górny bok pierwszego

kwadratu.

Podobnie punkty najbardziej wysunięte na wschód przedstawia

pogrubiony bok

drugiego kwadratu. Jeśli zaś poszukujemy punktów, które są

najbardziej

wysunięte jednocześnie na północ i na wschód, to rozwiązaniem jest

prawy

górny róg, co zaprezentowane jest na trzecim kwadracie.

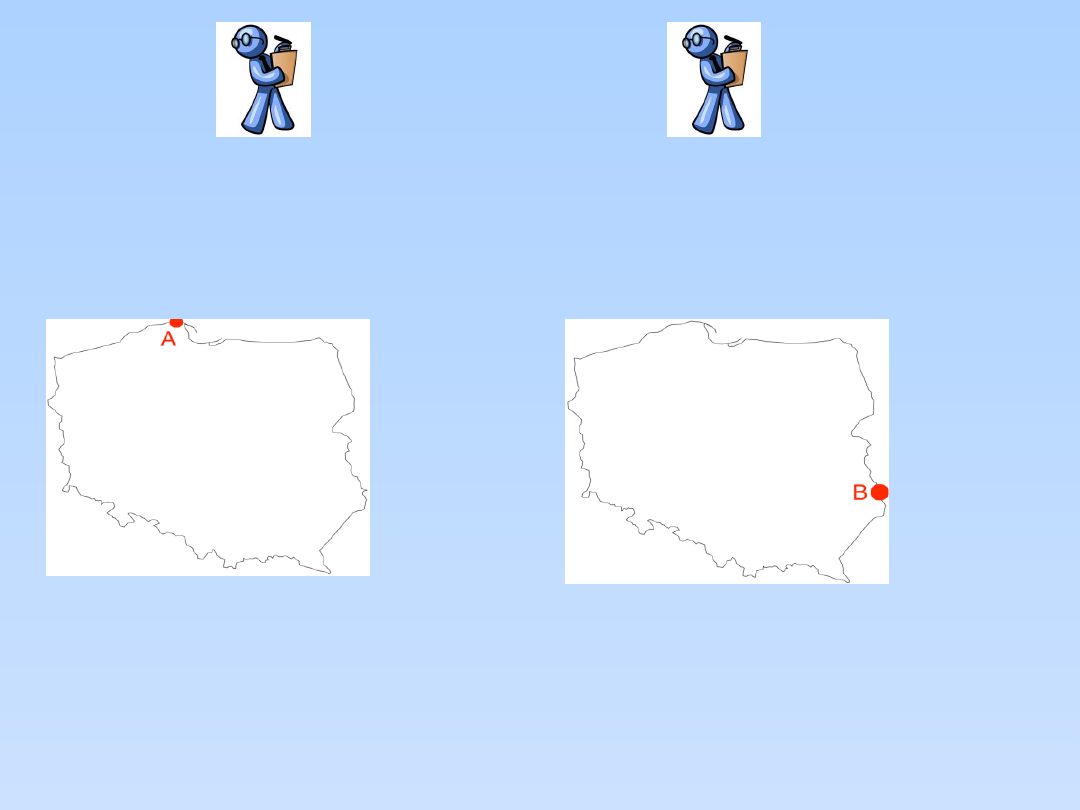
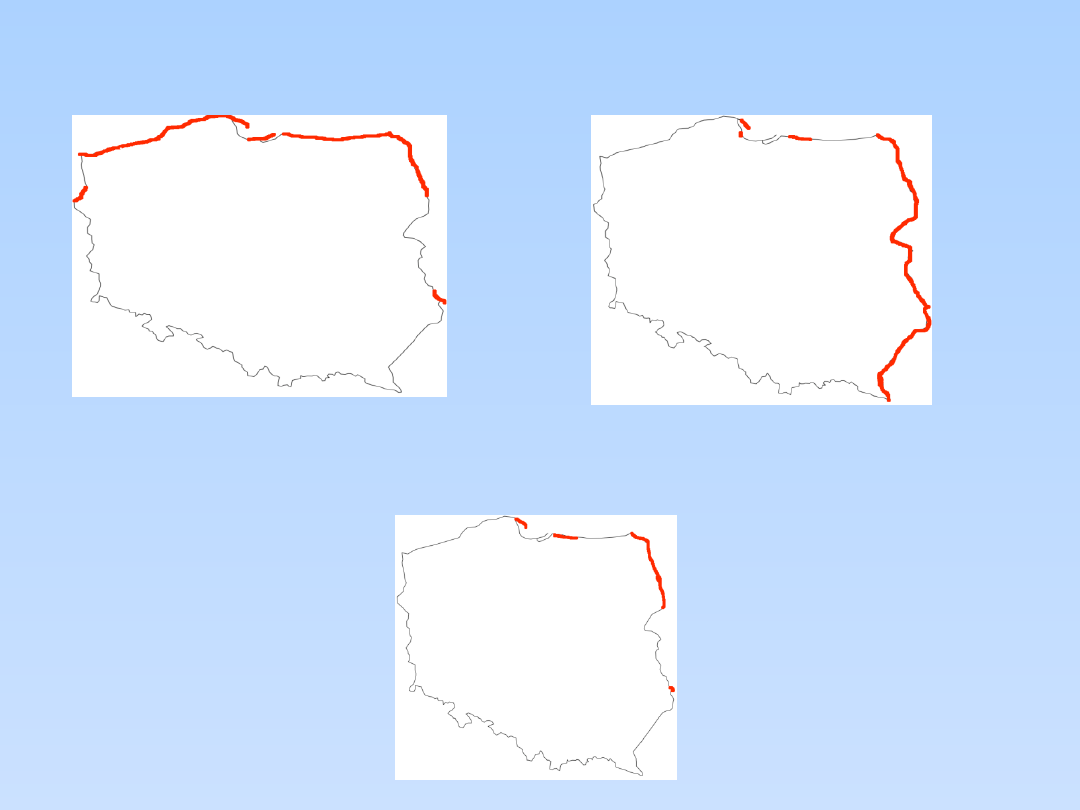
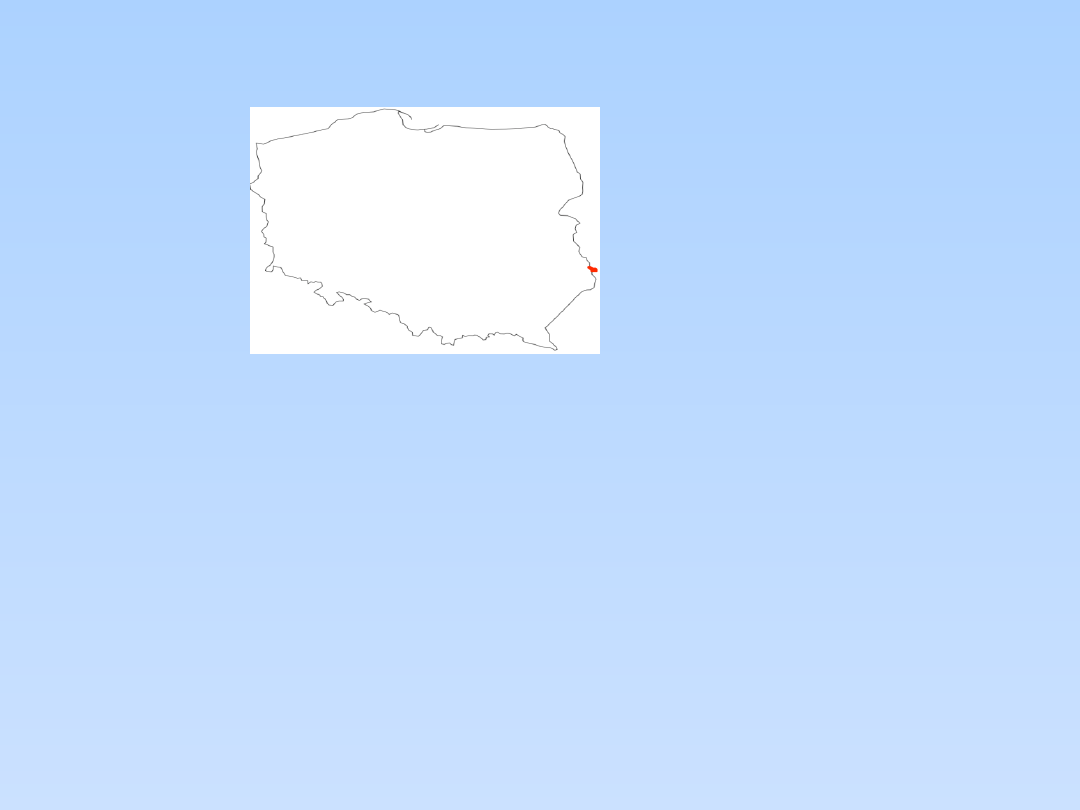
PRZYKŁAD (4)

Rozważmy to samo zadanie: wyznaczyć punkt najbardziej wysunięty
jednocześnie na wschód i na północ, ale nie w kwadracie, lecz na

mapie Polski.

Poniższe dwa rozwiązania przedstawiają rozwiązania cząstkowe.

Podejście leksykograficzne – podejmujący decyzję jest w stanie ściśle
uporządkować kryteria według ich ważności, następnie maksymalizuje
kolejno funkcje celu.

Budowa funkcji pomocniczej (superkryterium) – operuje różnymi
receptami na przejście od wielu kryteriów ocen do pojedynczego.

Programowanie matematyczne – w tej metodzie korzysta się z
Paretowskiej definicji rozwiązania.

Programowanie interaktywne – pozwala rozważać warunki elastyczne i
odrzuca automatyczne reguły wyboru, dopuszczając by wyborem sterował
użytkownik zgodnie ze swymi zmieniającymi się poziomami aspiracji.

KONIEC

DZIĘKUJEMY ZA UWAGĘ !!!

•

Błażej Bereta 50266

•

Katarzyna Brzozowska 51201

•

Katarzyna Dąbek 61572

•

Tomasz Górka 61688

•

Dominik Jurczyński 51230

•

Katarzyna Łojewska 51256

•

Grzegorz Morawski 51262

•

Michał Zadrożny 51315