Podstawowe elementy

liniowe

Własności statyczne i

dynamiczne

Elementy liniowe klasyfikuje się najczęściej ze względu na
ich własności dynamiczne. Wyróżniamy sześć grup
elementów podstawowych:
1. Bezinercyjne (proporcjonalne)
2. Inercyjne
3. Całkujące
4. Różniczkujące
5. Oscylacyjne
6. Opóźniające.

Własności statyczne określa charakterystyka statyczna, a
własności

dynamiczne

równanie

różniczkowe,

transmitancja

operatorowa

i

widmowa

a

także

charakterystyki czasowe i częstotliwościowe.

Człon bezinercyjny (proporcjonalny)

Ogólna postać równania elementu bezinercyjnego jest
następująca:

y = k x ,

gdzie y – wielkość wyjściowa, x – wielkość wejściowa, k –
współczynnik proporcjonalności (wzmocnienia).

Transmitancja elementu bezinercyjnego jest równa
współczynnikowi wzmocnienia:

k

s

X

s

Y

s

G





)

(

)

(

)

(

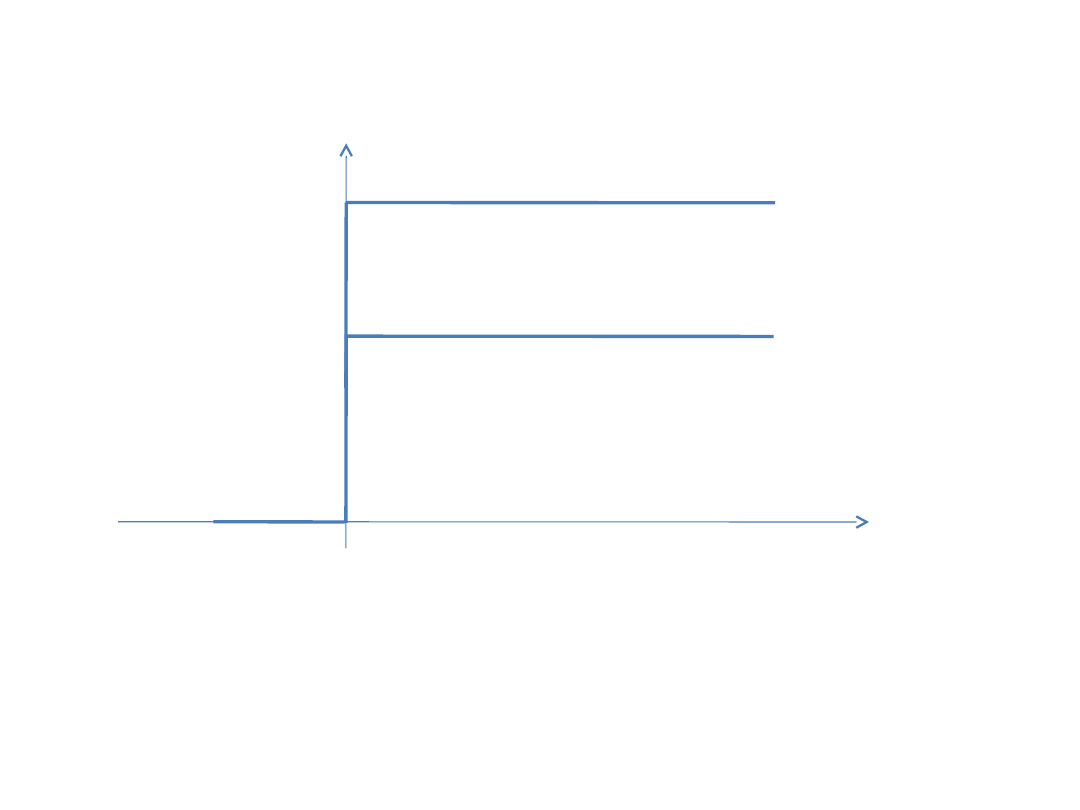
Odpowiedzią na skok jednostkowy członu
proporcjonalnego jest skok o wartości k.

0

t

h(t)

1

k

Charakterystyki częstotliwościowe są linią prostą o stałym
wzmocnieniu z przesunięciem fazowym równym 0.

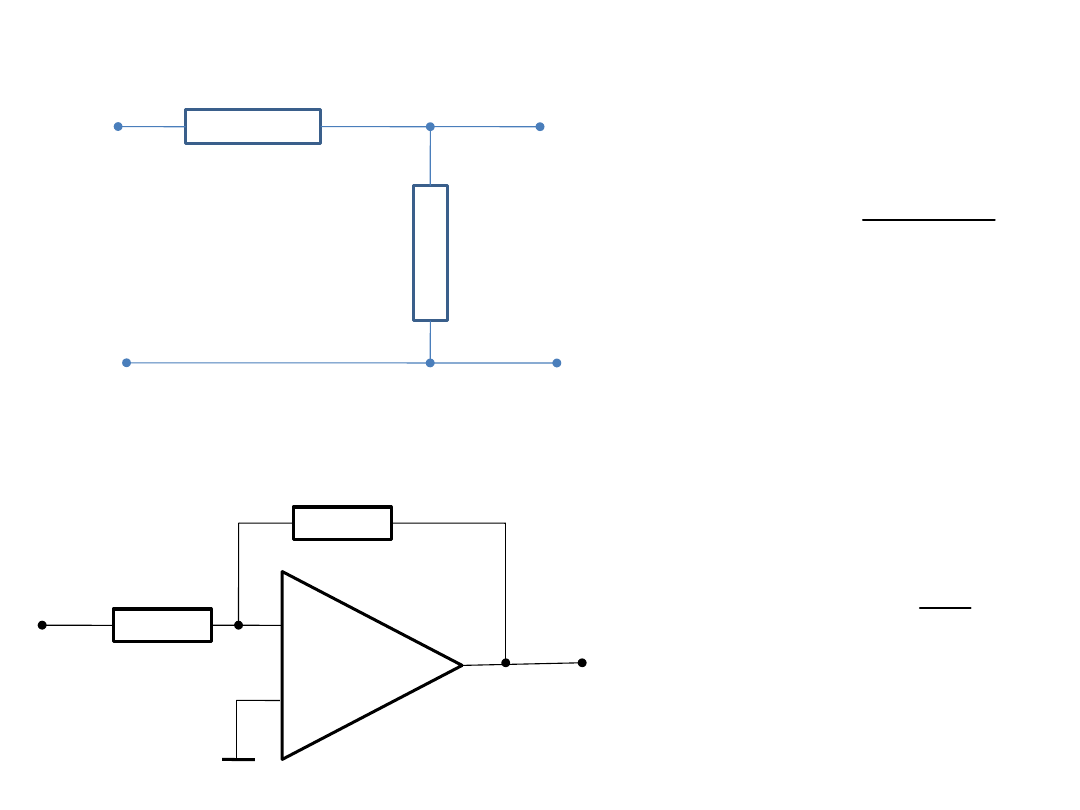
Przykłady realizacji członu proporcjonalnego:
a) dzielnik napięciowy

b) mnożenie przez stałą (wzmacniacz operacyjny)

2

1

2

)

(

R

R

R

k

s

G







1

2

)

(

R

R

k

s

G







R

1

R

2

-
+

R

1

R

2

Człon inercyjny I rzędu

Ogólna postać równania różniczkowego elementu
inercyjnego pierwszego rzędu jest następująca:

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia, T – stała czasowa
[s]

kx

y

dt

dy

T





1

)

(





Ts

k

s

G

)

1

(

)

1

(

)

(

)

1

(

1

)

1

(

1

1

)

(

)

(

)

(

T

t

T

t

e

k

e

T

T

k

t

y

T

s

s

T

k

Ts

s

k

s

Ts

k

s

X

s

G

s

Y



























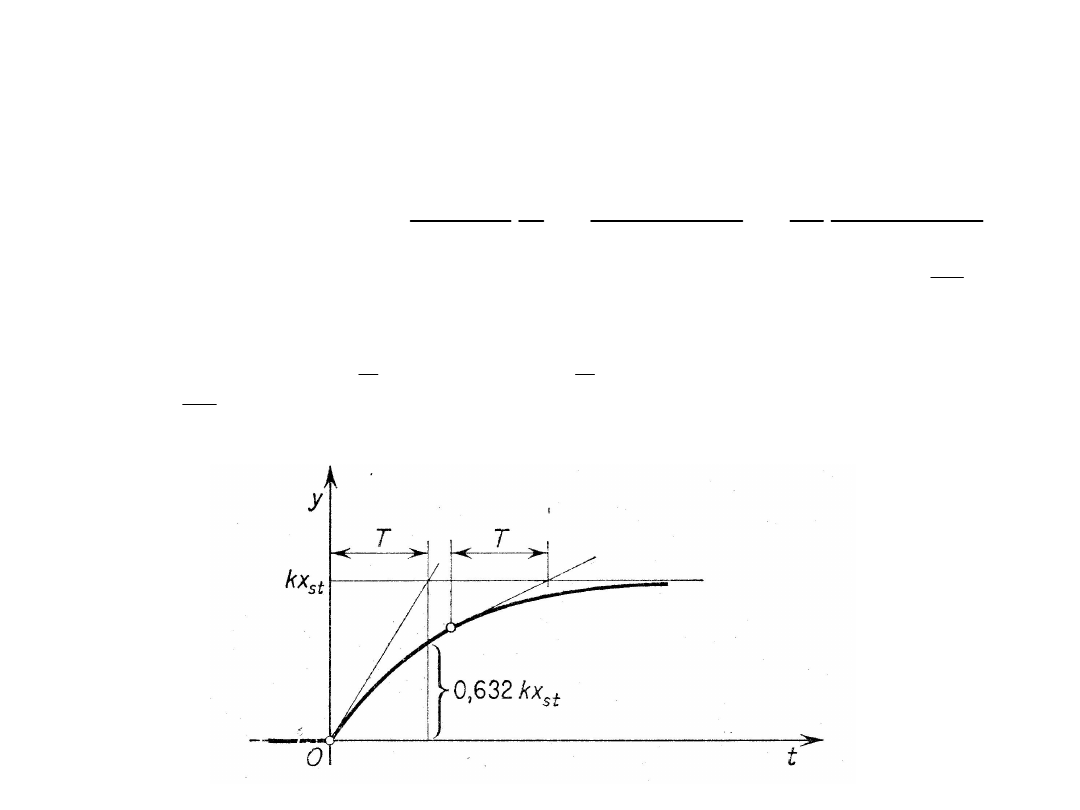
Odpowiedź na skok jednostkowy obliczamy na podstawie
własności przekształcenia Laplace’a, otrzymując:

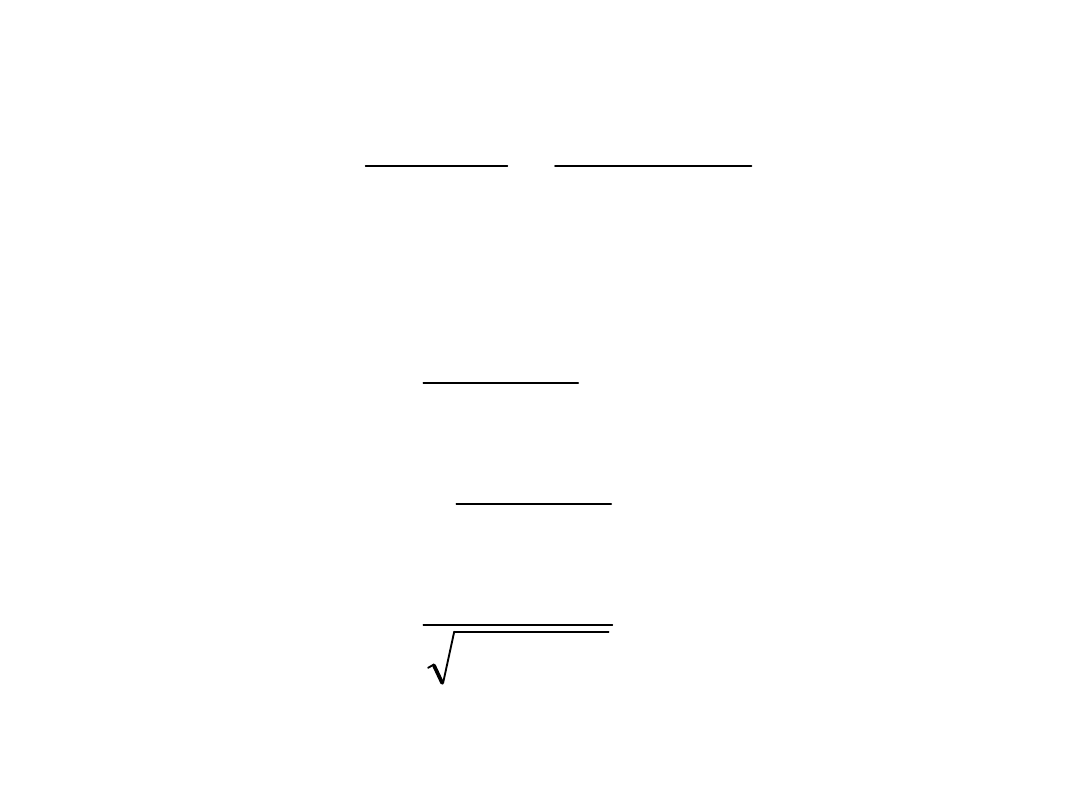
Transmitancja widmowa jest następująca:

2

2

1

)

1

(

1

)

(

T

T

j

k

T

j

k

j

G



















Stąd

T

T

k

A

T

T

k

Q

T

k

P





















arctg

)

(

1

)

(

1

)

(

1

)

(

2

2

2

2

2

2



















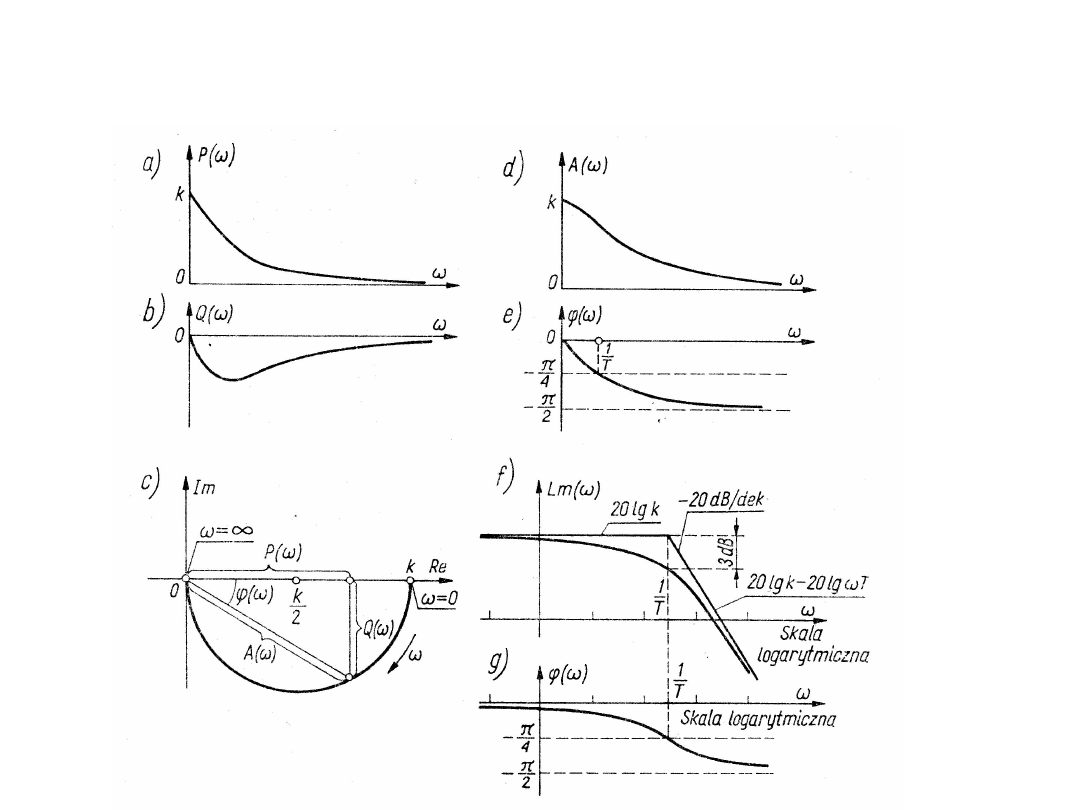
Charakterystyki częstotliwościowe członu inercyjnego I
rzędu wyglądają następująco:

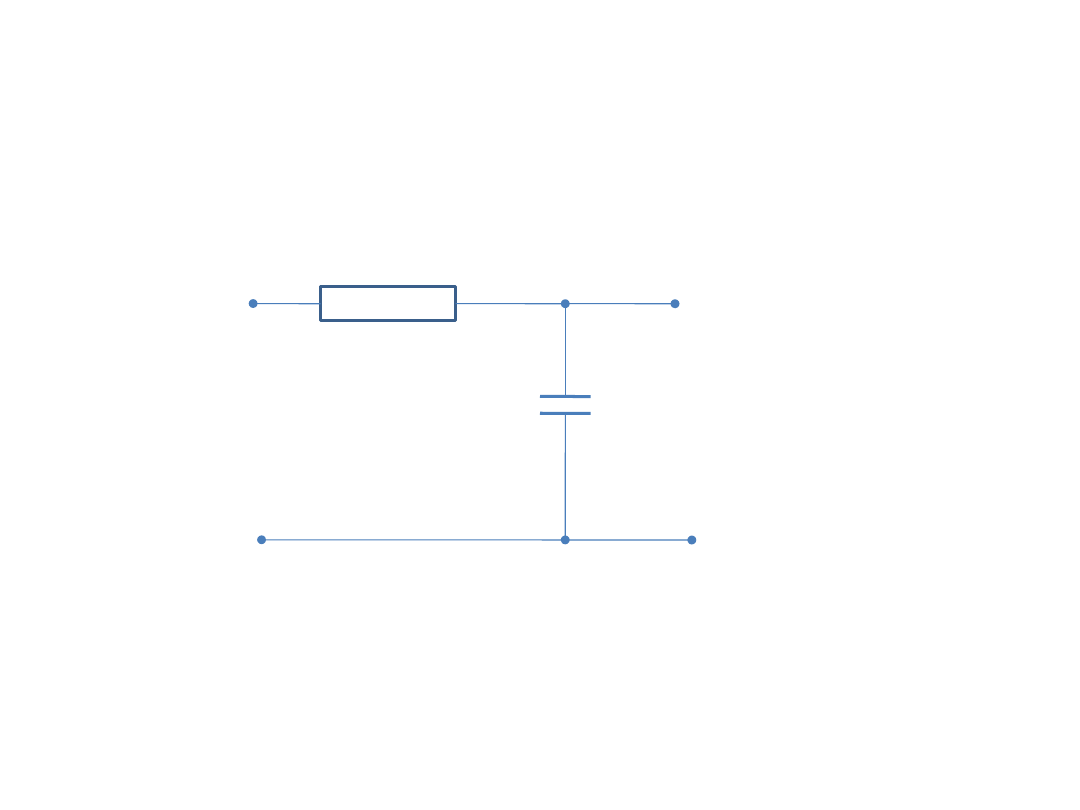
Przykładem układu inercyjnego I rzędu jest filtr
dolnoprzepustowy RC, w którym sygnałem wejściowym i
wyjściowym jest napięcie, lub silnik prądu stałego (lub
indukcyjny 3-fazowy), w którym skokowe włączenie
zasilania jest sygnałem wymuszającym a wyjściem jest
prędkość kątowa wału silnika.

R

C

Człon całkujący idealny

Ogólna postać równania różniczkowego elementu
całkującego idealnego jest następująca:

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia
W przypadku szczególnym (k ma wymiar odwrotności
czasu), może zajść:

kx

dt

dy



s

k

s

G



)

(

Ts

s

G

1

)

( 

kt

t

y

s

k

s

s

k

s

X

s

G

s

Y









)

(

1

)

(

)

(

)

(

2

Odpowiedź na skok jednostkowy obliczamy na podstawie
własności przekształcenia Laplace’a, otrzymując:

Transmitancja widmowa jest następująca:







k

j

j

k

j

G







)

(

Stąd

2

)

(

)

(

)

(

0

)

(





























k

A

k

Q

P

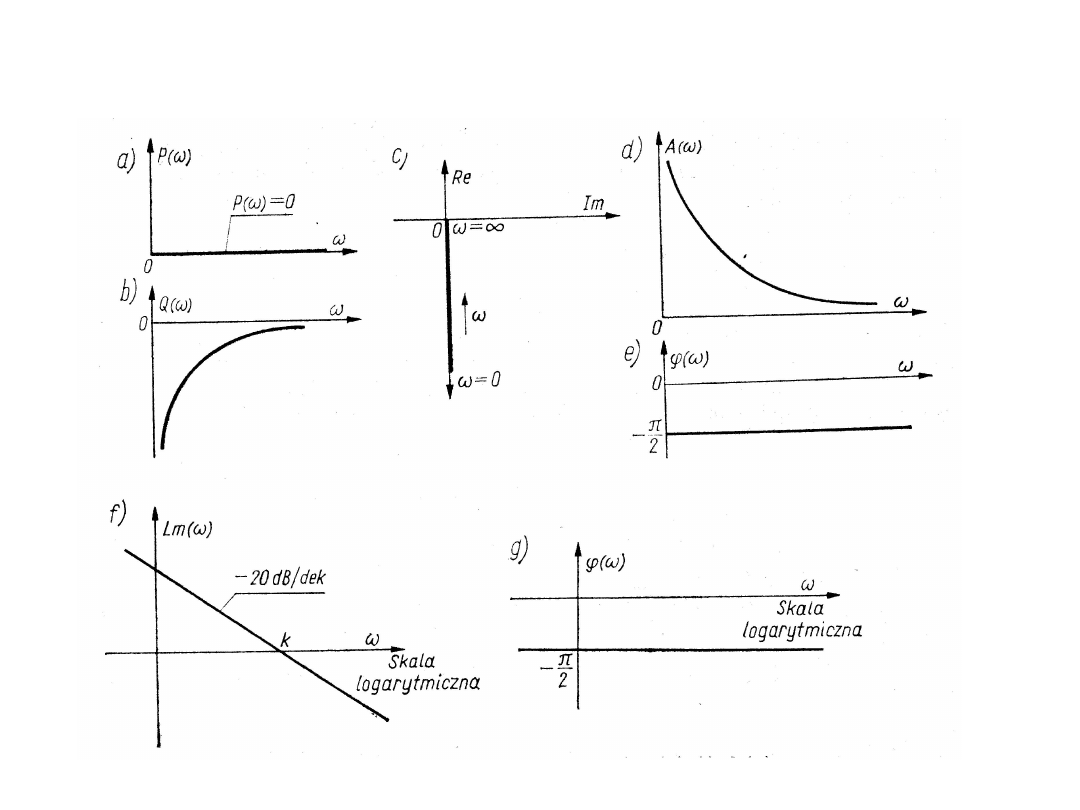
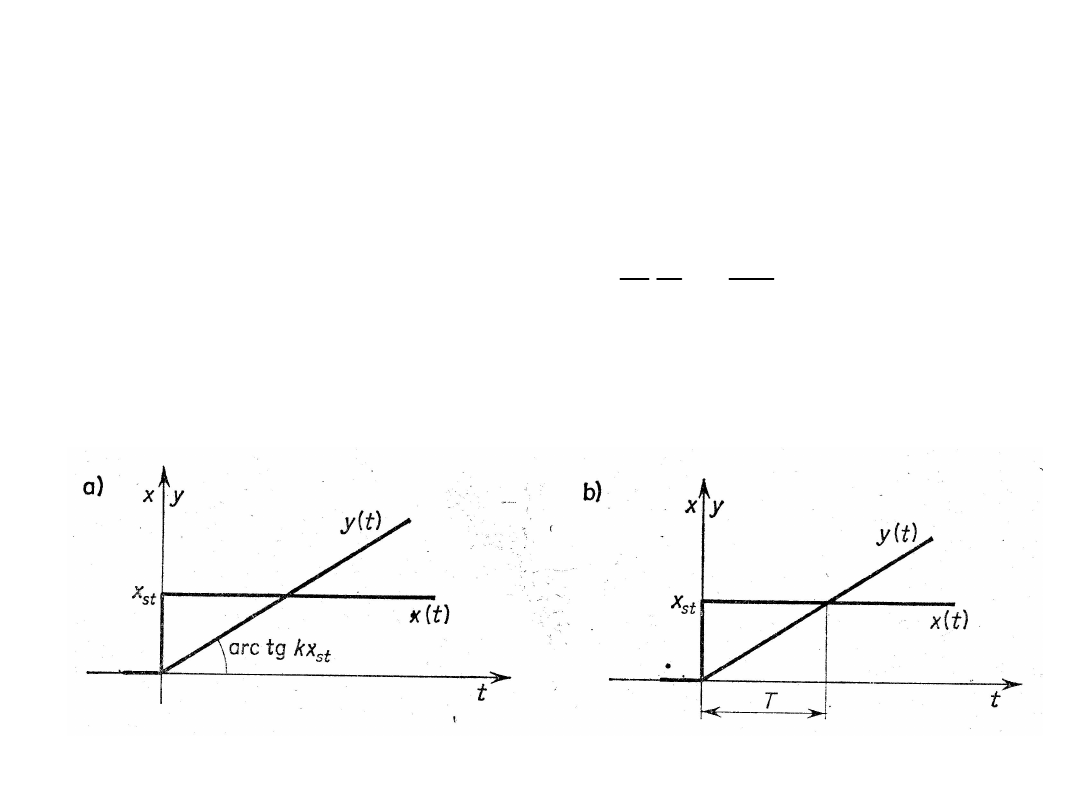
Charakterystyki częstotliwościowe członu całkującego
idealnego wyglądają następująco:

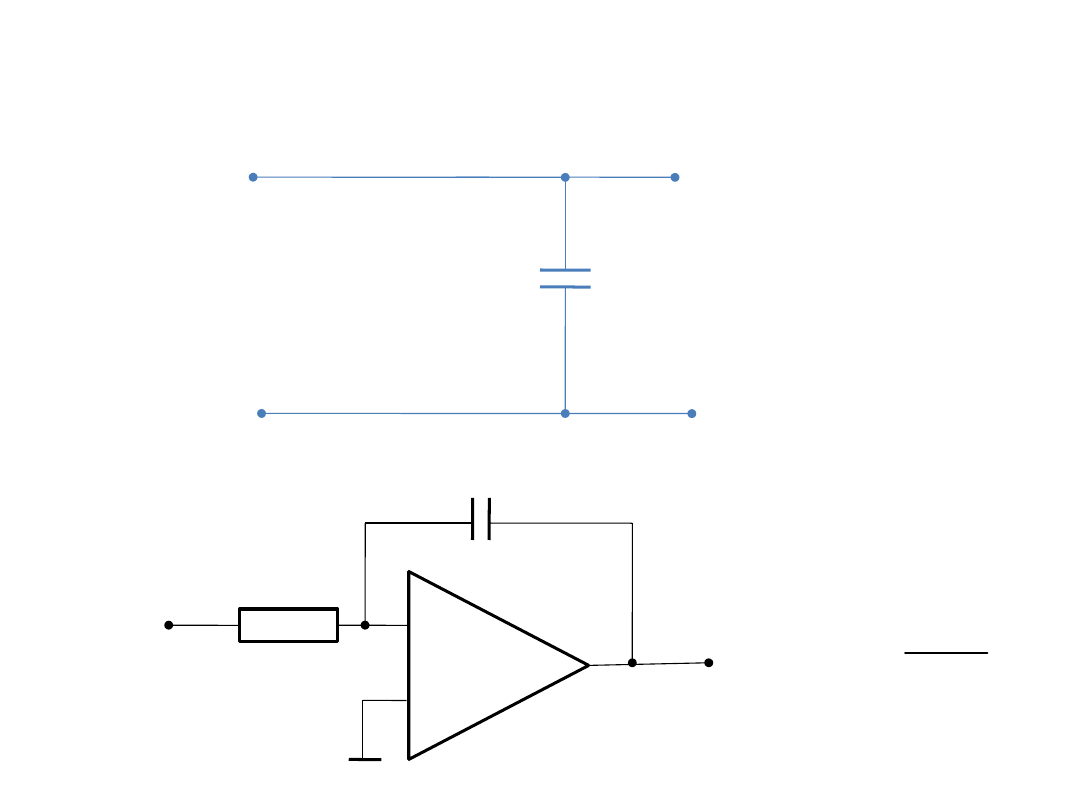
Przykładem układu całkującego jest układ zawierający
idealny kondensator C, przy czym sygnałem wejściowym
jest prąd a wyjściowym napięcie na kondensatorze.

C

-
+

R

C

RCs

s

G

1

)

(





Człon całkujący rzeczywisty

Ogólna postać równania różniczkowego elementu
całkującego rzeczywistego (z inercją) jest następująca:

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia, T – stała czasowa.

kx

dt

dy

dt

y

d

T





2

2

)

1

(

)

(





Ts

s

k

s

G

)

1

(

)

(

)

1

(

1

)

1

(

)

(

)

(

)

(

2

T

t

e

kT

kt

t

y

Ts

s

k

s

Ts

s

k

s

X

s

G

s

Y



















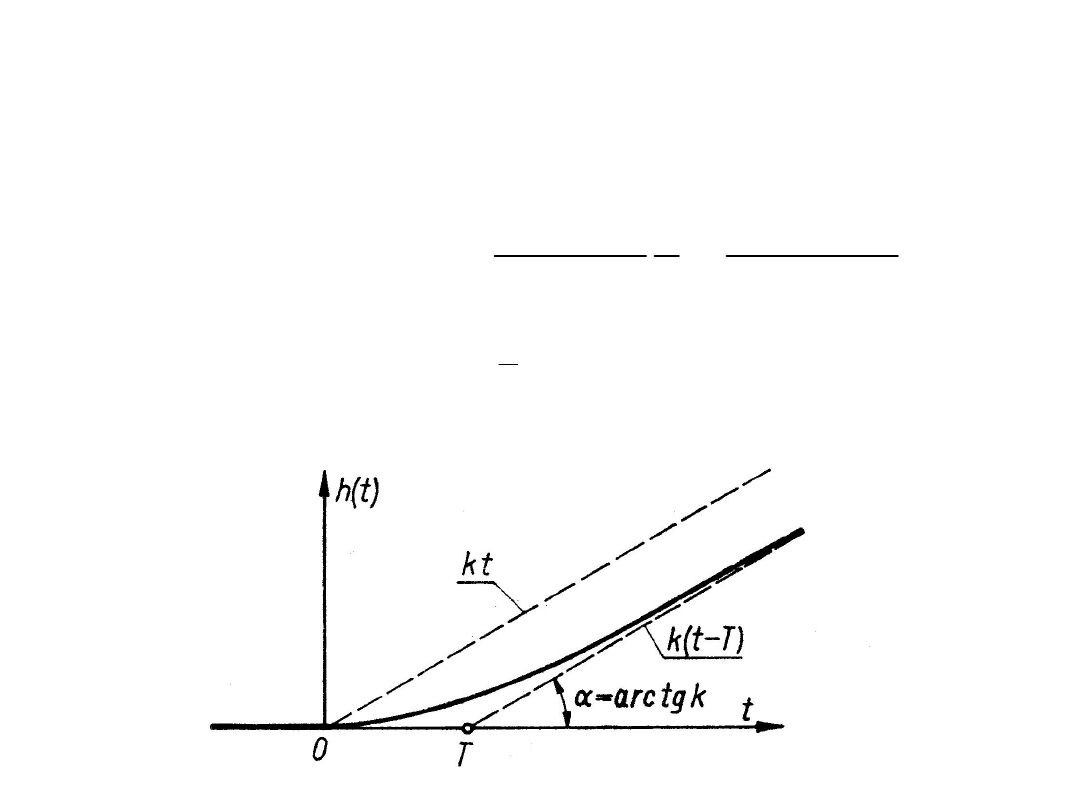
Odpowiedź na skok jednostkowy obliczamy na podstawie
własności przekształcenia Laplace’a, otrzymując:

Transmitancja widmowa jest następująca:

)

1

(

1

)

1

(

)

(

2

2

2

2

T

k

j

T

kT

T

j

j

k

j

G



























Stąd

2

arctg

1

arctg

)

(

1

)

(

)

1

(

)

(

1

)

(

2

2

2

2

2

2



















































T

T

T

k

A

T

k

Q

T

kT

P

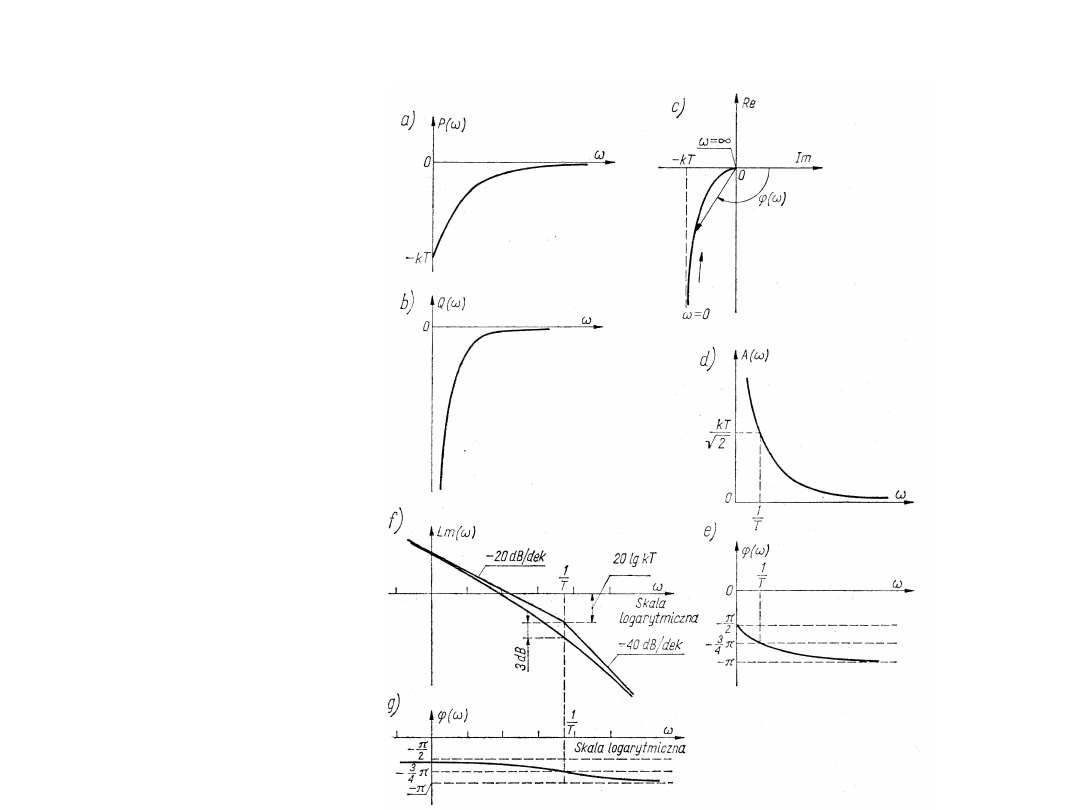
Charakterystyki częstotliwościowe członu całkującego
rzeczywistego wyglądają następująco:

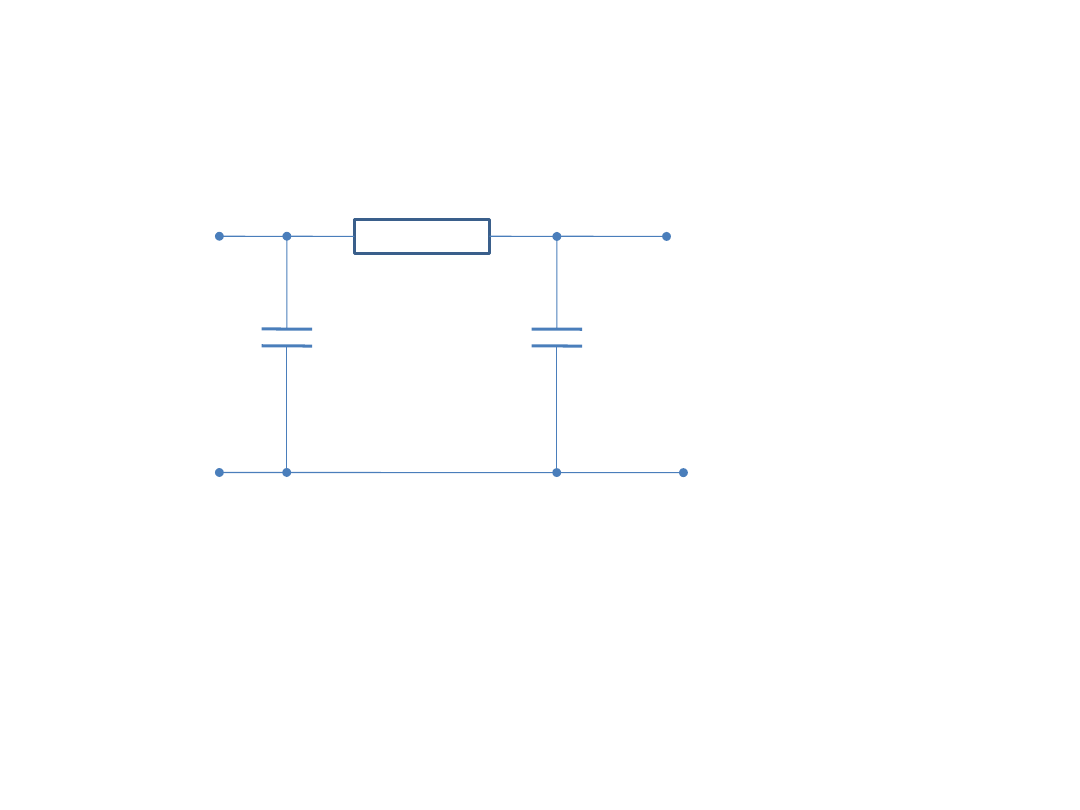
Przykładem układu całkującego rzeczywistego jest układ
filtru RC w układzie , lub silnik obcowzbudny prądu
stałego, w którym wymuszeniem jest skok napięcia
wirnika a wyjściem kąt obrotu wirnika.

R

C

Człon różniczkujący idealny

Ogólna postać równania różniczkowego elementu
różniczkującego idealnego jest następująca:

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia.

dt

dx

k

y 

ks

s

G



)

(

)

(

)

(

1

1

)

(

)

(

)

(

t

t

y

k

s

ks

s

ks

s

X

s

G

s

Y















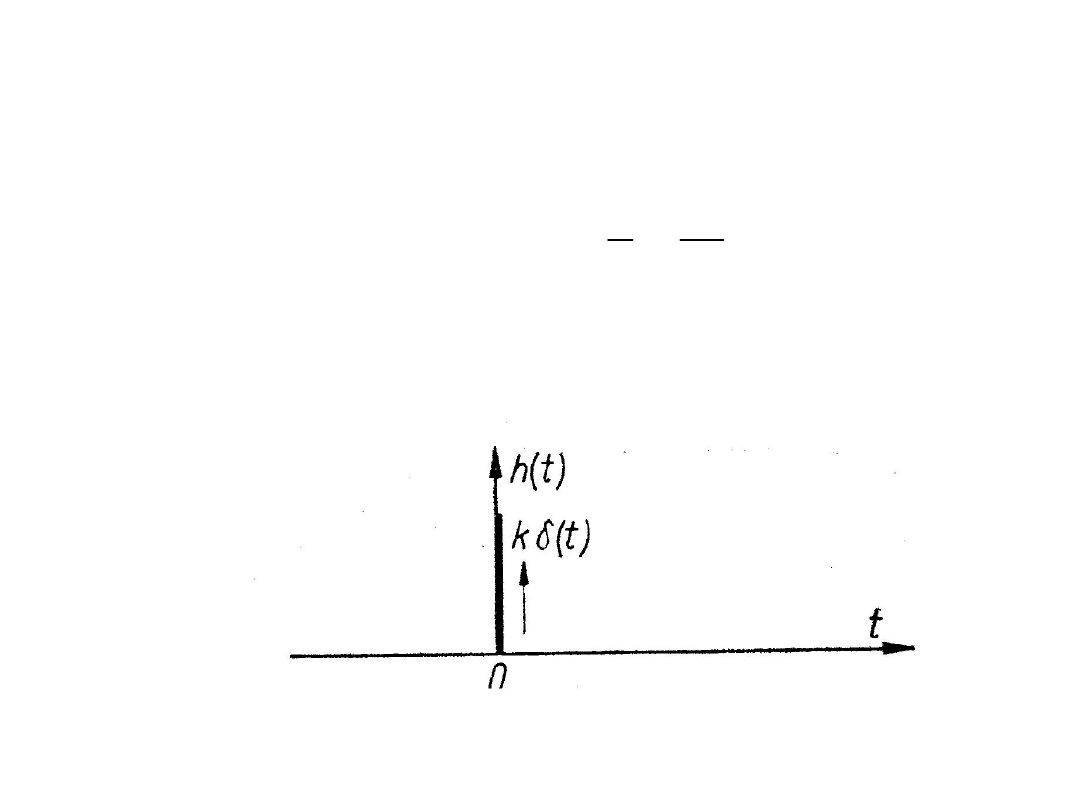
Odpowiedź na skok jednostkowy obliczamy na podstawie
własności przekształcenia Laplace’a, otrzymując:

Transmitancja widmowa jest następująca:

k

j

kj

j

G











)

(

Stąd

2

)

(

)

(

)

(

0

)

(

























k

A

k

Q

P

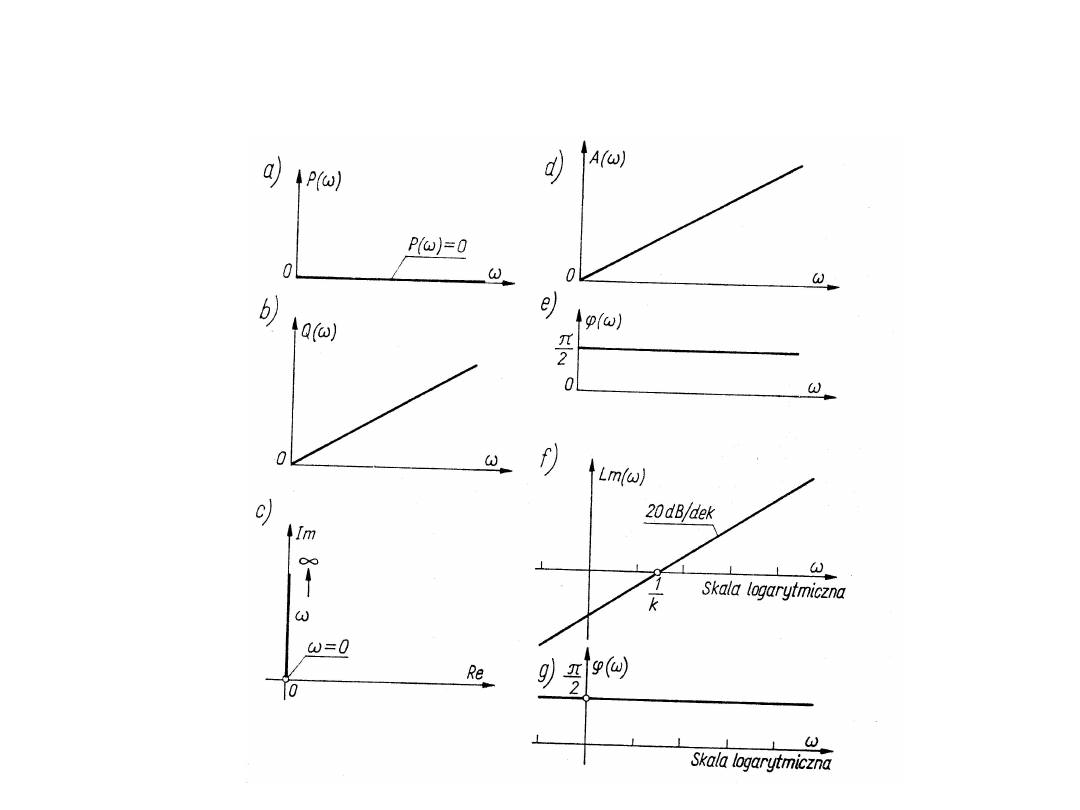
Charakterystyki częstotliwościowe członu różniczkującego
idealnego wyglądają następująco:

Przykładem układu różniczkującego idealnego jest
kondensator idealny C , przy czym sygnałem wejściowym
jest napięcie a wyjściowym prąd.

C

-
+

R

C

sCR

s

G





)

(

Człon różniczkujący rzeczywisty

Ogólna postać równania różniczkowego elementu
różniczkującego

rzeczywistego

(z

inercją)

jest

następująca:

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia, T – stała czasowa.

dt

dx

k

y

dt

dy

T





)

1

(

)

(





Ts

ks

s

G

T

t

e

T

k

t

y

Ts

k

s

Ts

ks

s

X

s

G

s

Y















)

(

)

1

(

1

)

1

(

)

(

)

(

)

(

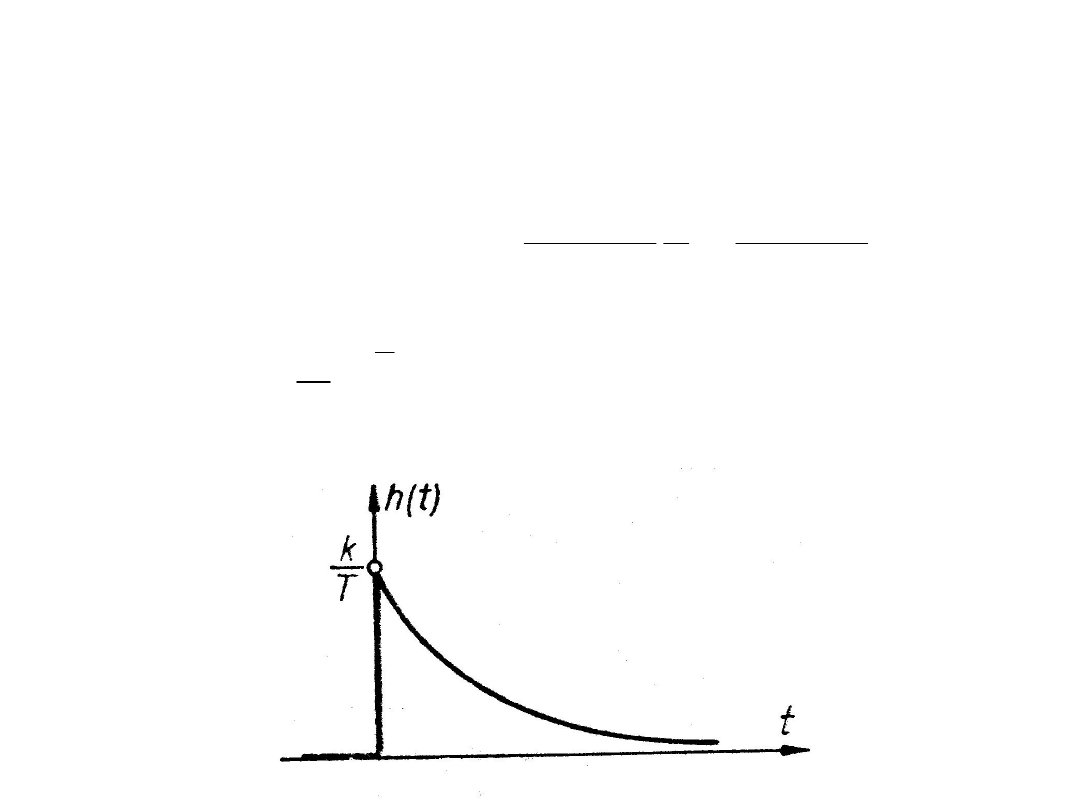
Odpowiedź na skok jednostkowy obliczamy na podstawie
własności przekształcenia Laplace’a, otrzymując:

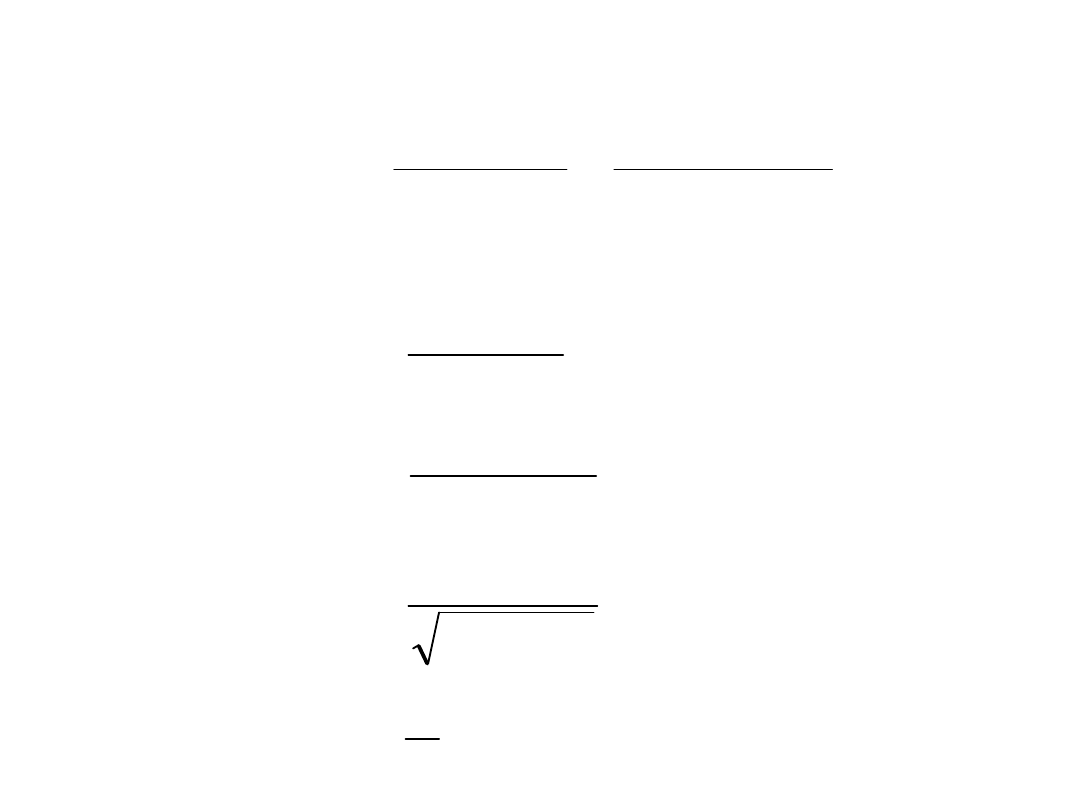
Transmitancja widmowa jest następująca:

2

2

2

1

)

1

(

)

(

T

jk

T

k

T

j

kj

j

G























Stąd

T

T

k

A

T

k

Q

T

T

k

P



























arctg

2

)

(

1

)

(

)

1

(

)

(

1

)

(

2

2

2

2

2

2

2

















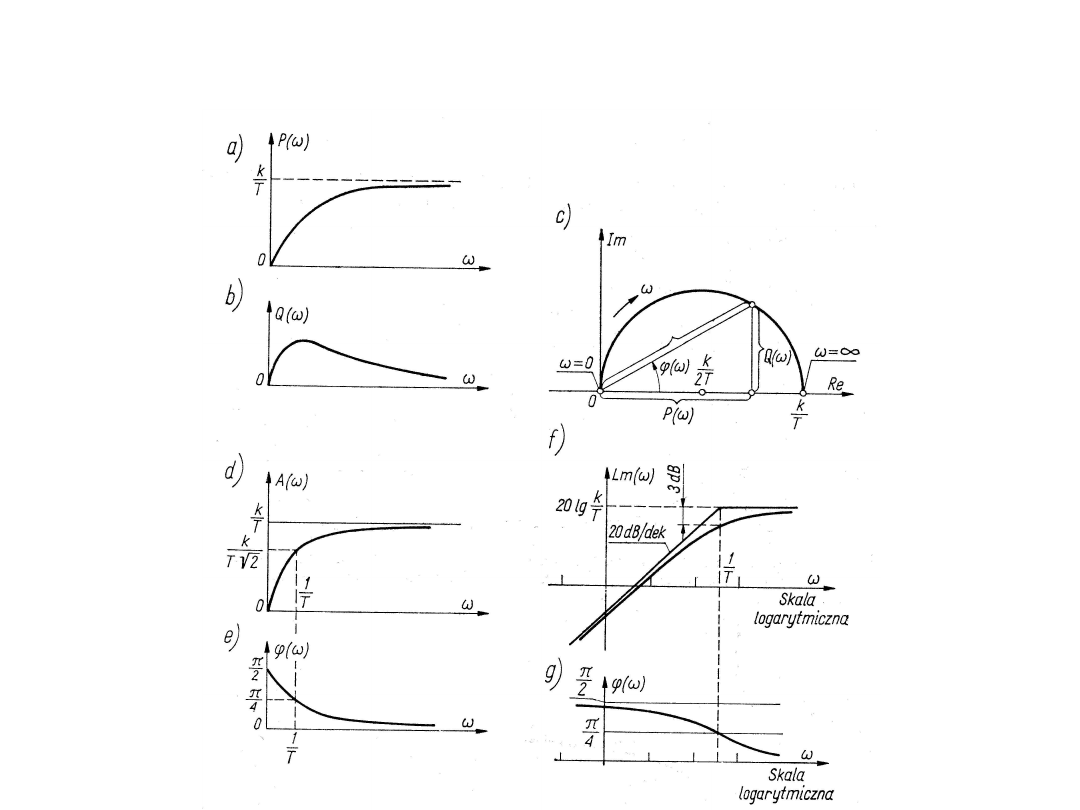
Charakterystyki częstotliwościowe członu różniczkującego
rzeczywistego wyglądają następująco:

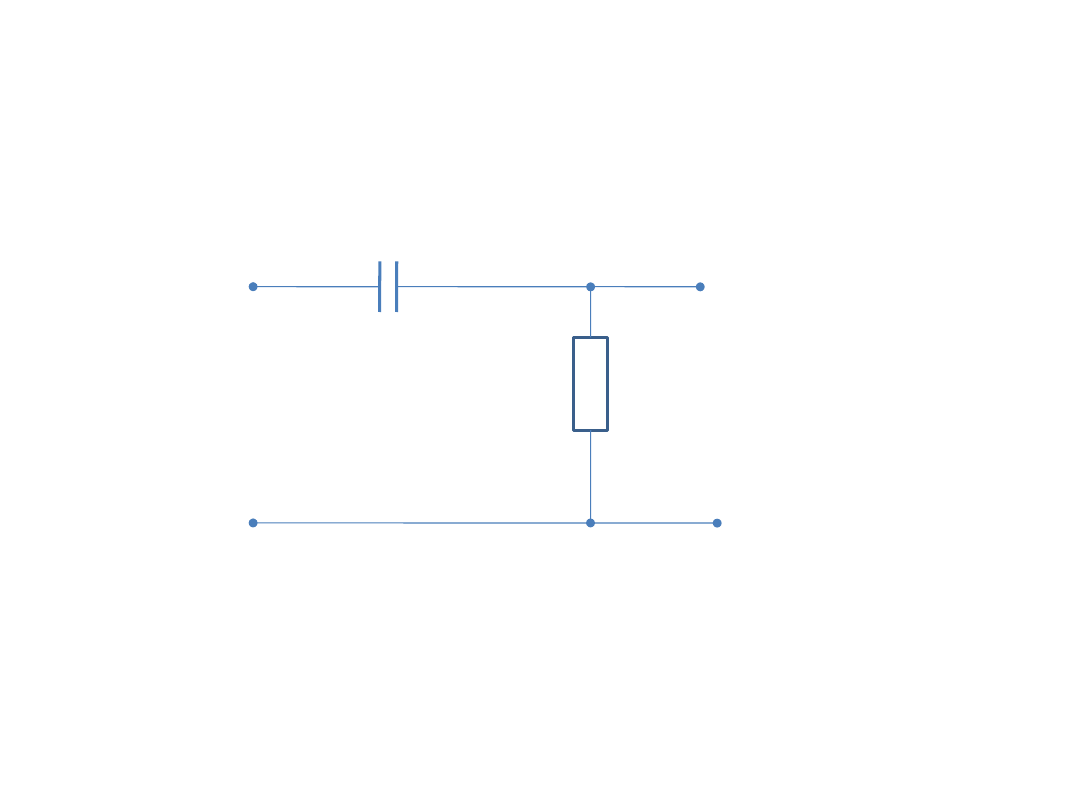
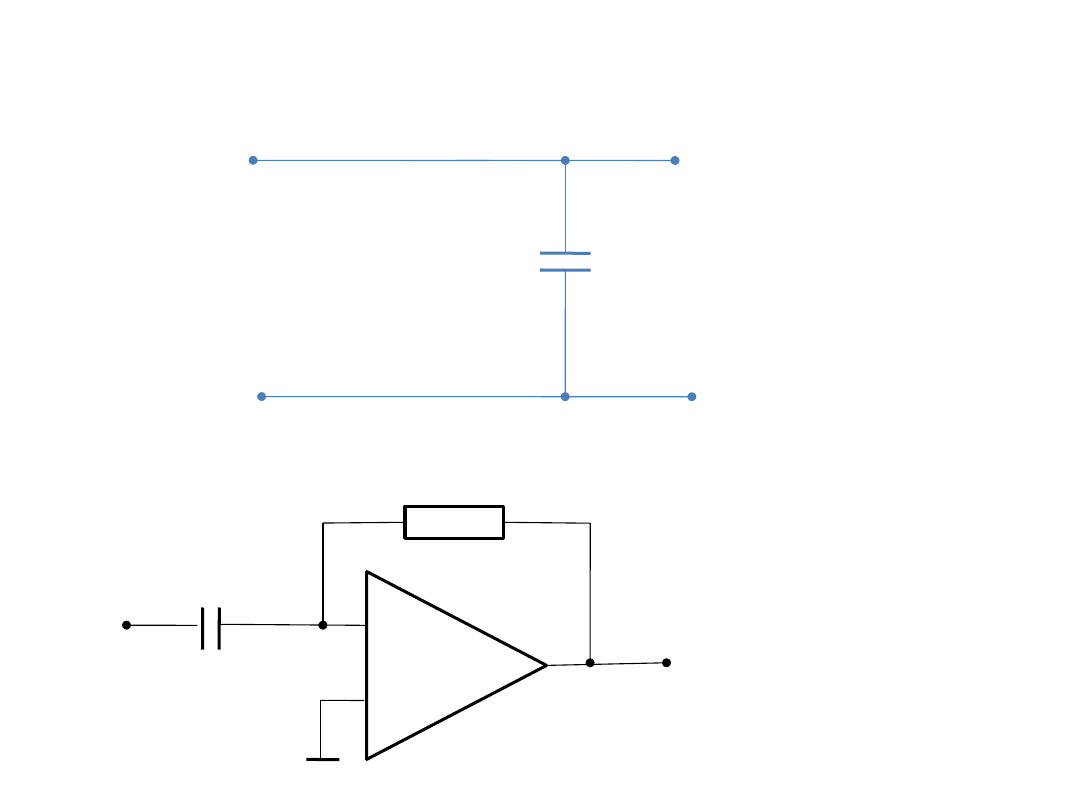
Przykładem układu różniczkującego rzeczywistego jest
układ filtru górnoprzepustowego RC.

R

C

Człon oscylacyjny

Ogólna postać równania różniczkowego elementu
oscylacyjnego jest następująca:

przy czym

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia, T

1

, T

2

– stałe

czasowe.

2

1

2

2

2

2

2

2

1

4T

T

kx

y

dt

dy

T

dt

y

d

T









)

1

(

)

(

2

2

2

1







s

T

s

T

k

s

G

Inna

postać

równania

różniczkowego

elementu

oscylacyjnego jest następująca:

przy czym

Stąd wynika transmitancja:

gdzie: k – współczynnik wzmocnienia, T – stała czasowa,

 – współczynnik tłumienia.

1

2

2

2

0

2

0

0

2

2

2

















x

k

y

dt

dy

dt

y

d

T

)

1

2

(

)

(

2

2







Ts

s

T

k

s

G



























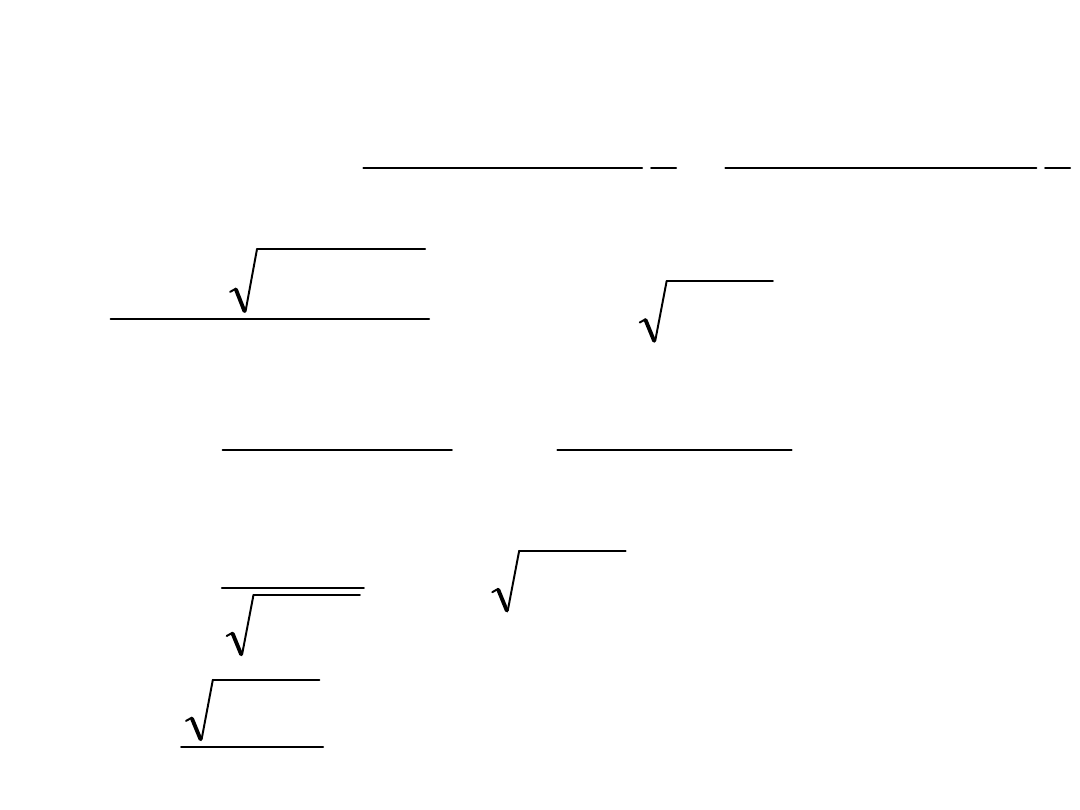
2

2

0

2

1

2

2

2

1

2

1

1

2

1

2

0

2

1

2

1

2

2

2

2

,

1

2

2

2

2

2

1

1

arctg

)]

1

sin(

1

1

[

)

(

]

)

(

1

)

(

1

1

[

)

(

)

1

(

2

4

1

)

1

2

(

1

)

1

(

)

(

)

(

)

(

0

2

1























































t

e

k

t

y

e

s

s

s

T

e

s

s

s

T

k

t

y

T

T

T

T

s

s

Ts

s

T

k

s

s

T

s

T

k

s

X

s

G

s

Y

t

t

s

t

s



Odpowiedź na skok jednostkowy obliczamy na podstawie
własności przekształcenia Laplace’a, otrzymując:

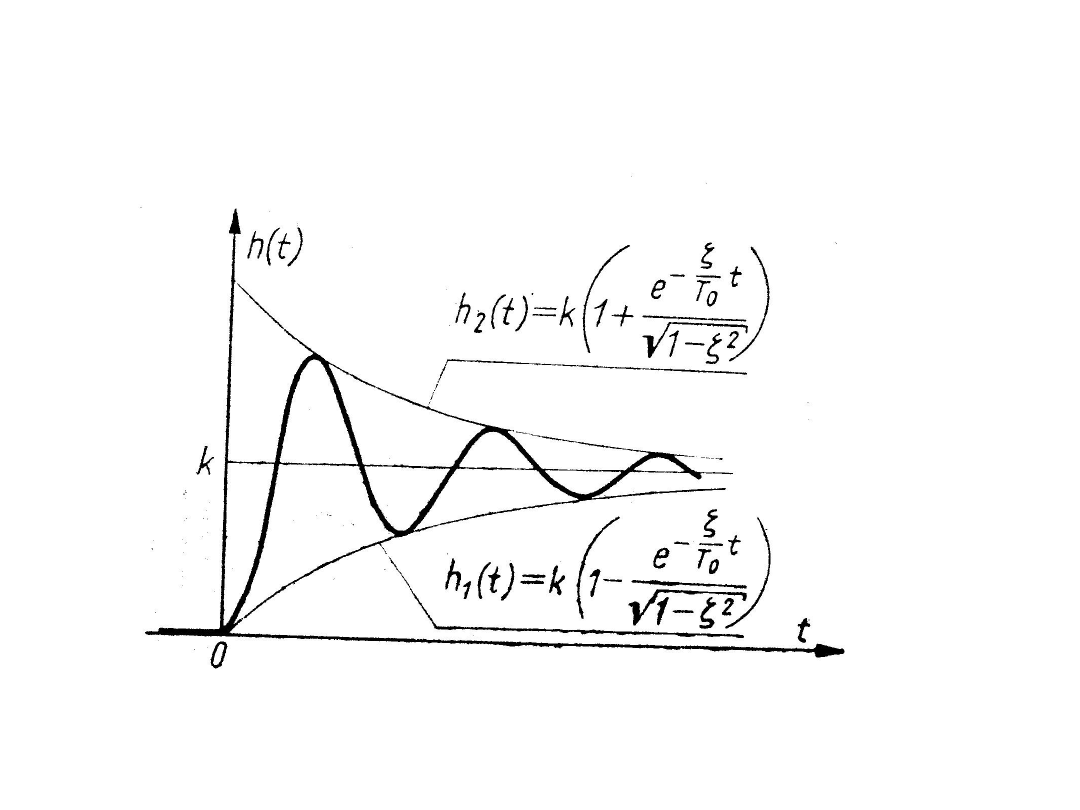
Odpowiedź członu oscylacyjnego na skok jednostkowy
wygląda następująco:

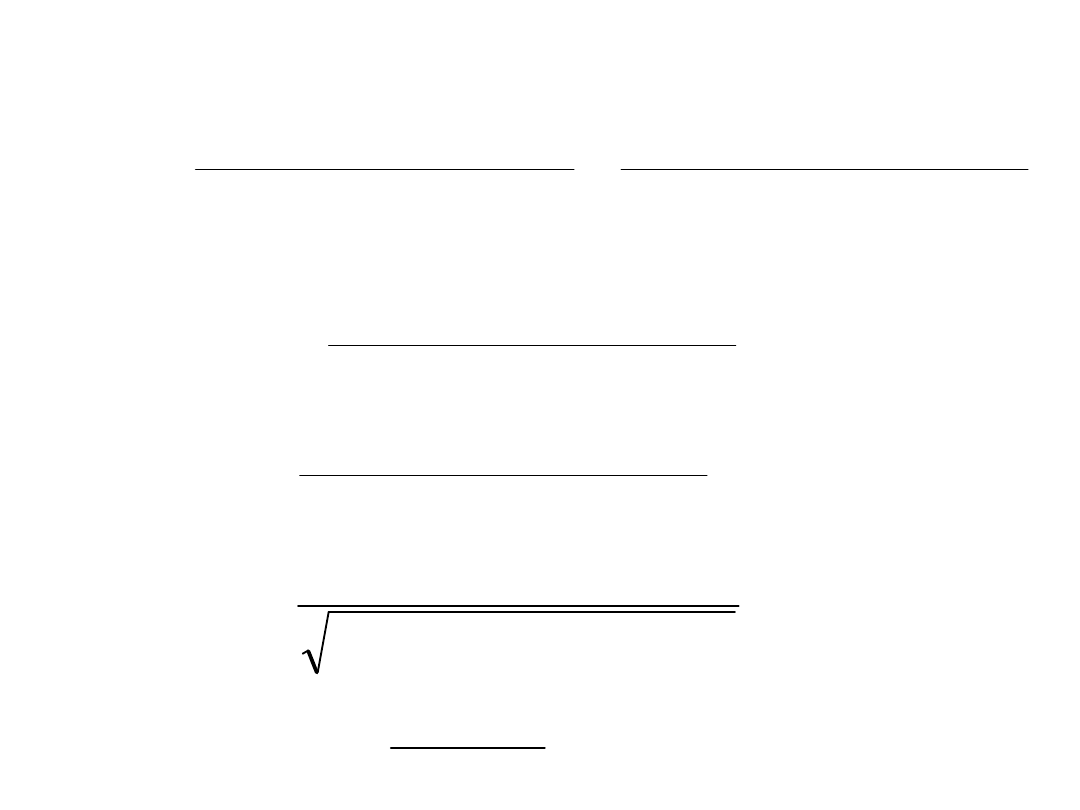
Transmitancja widmowa jest następująca:

2

2

2

2

2

2

2

2

2

2

4

)

1

(

]

2

)

1

[(

1

2

)

(

)

(

T

T

T

j

T

k

T

j

j

T

k

j

G



































Stąd

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

1

2

arctg

)

(

4

)

1

(

)

(

4

)

1

(

2

)

(

4

)

1

(

)

1

(

)

(

T

T

T

T

k

A

T

T

T

k

Q

T

T

T

k

P



































































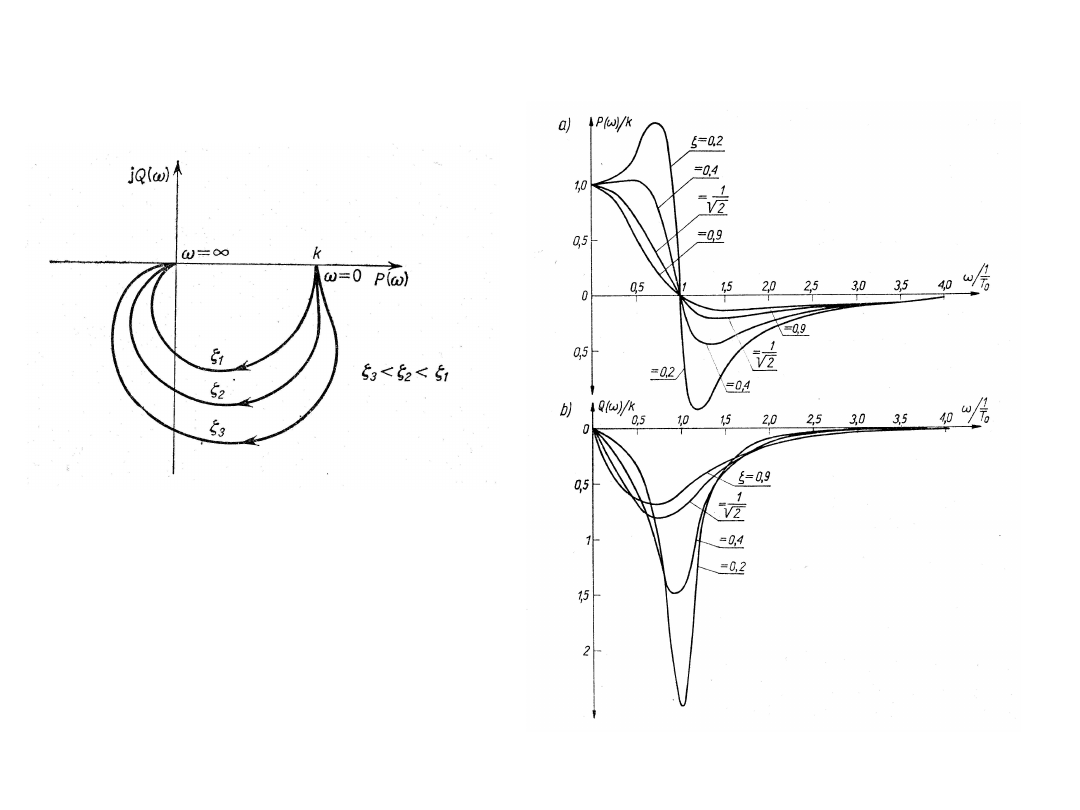
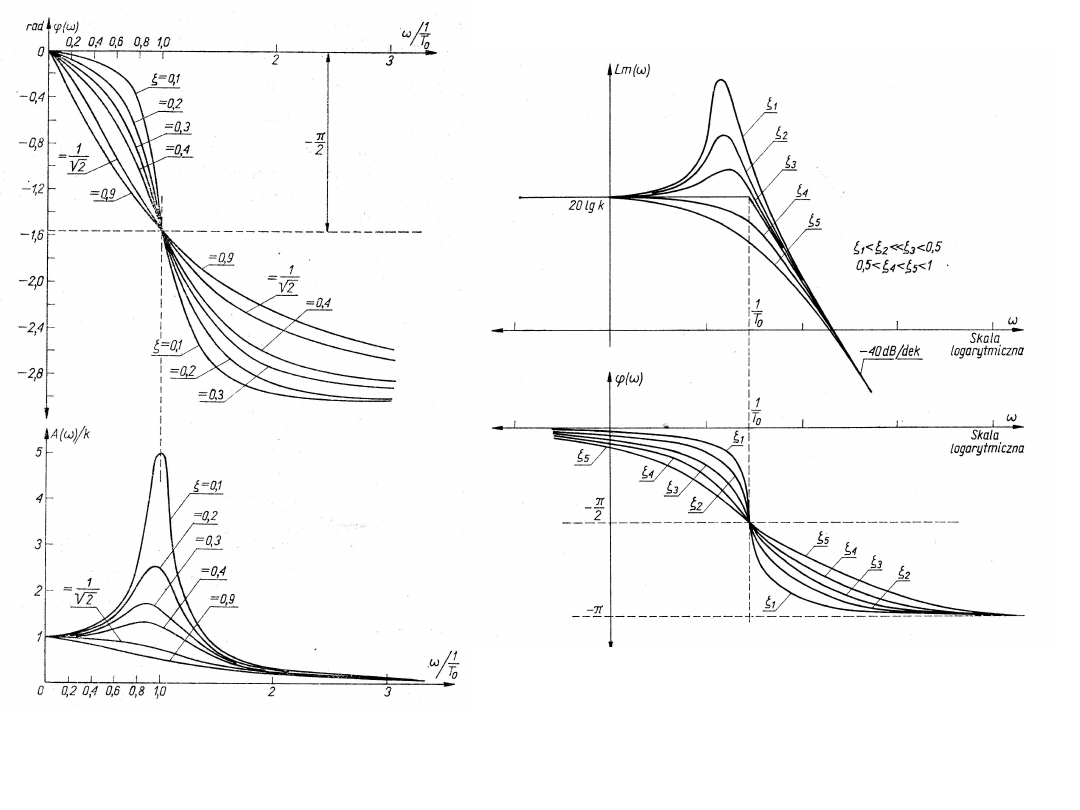
Charakterystyki częstotliwościowe członu oscylacyjnego
wyglądają następująco:

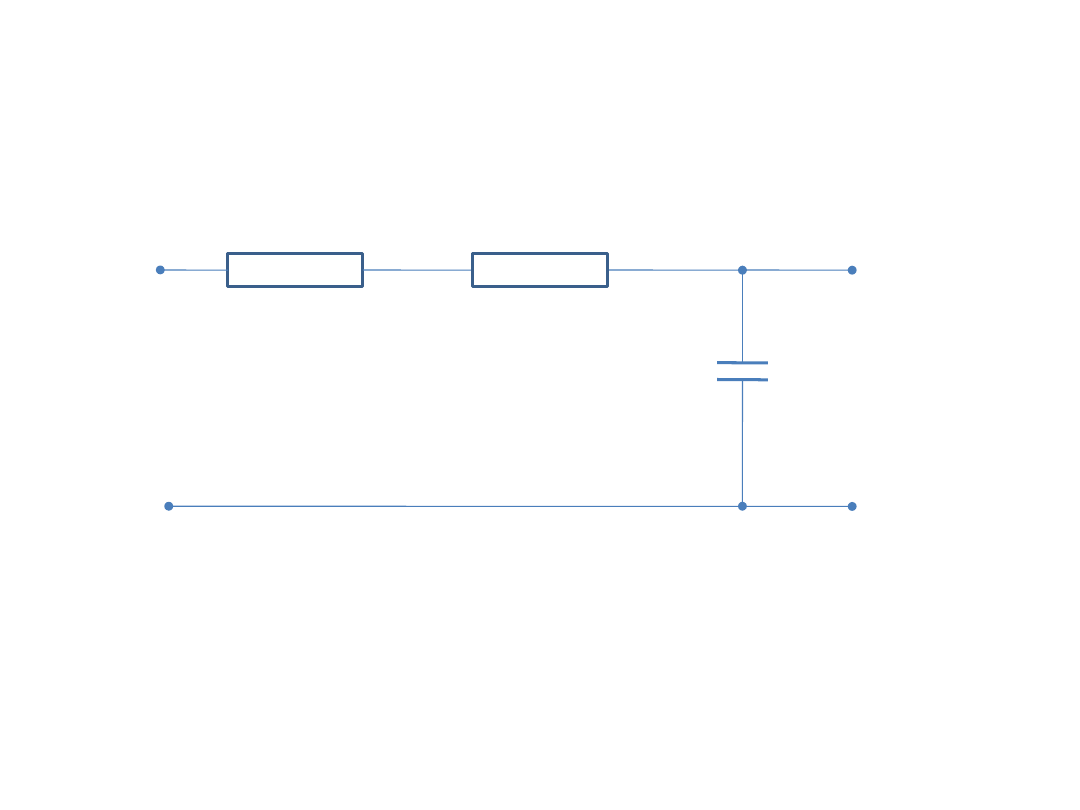
Przykładem układu oscylacyjnego jest układ RLC.

R

C

L

)

(

)

(





 t

x

t

y

s

e

s

X

s

Y

s

G









)

(

)

(

)

(

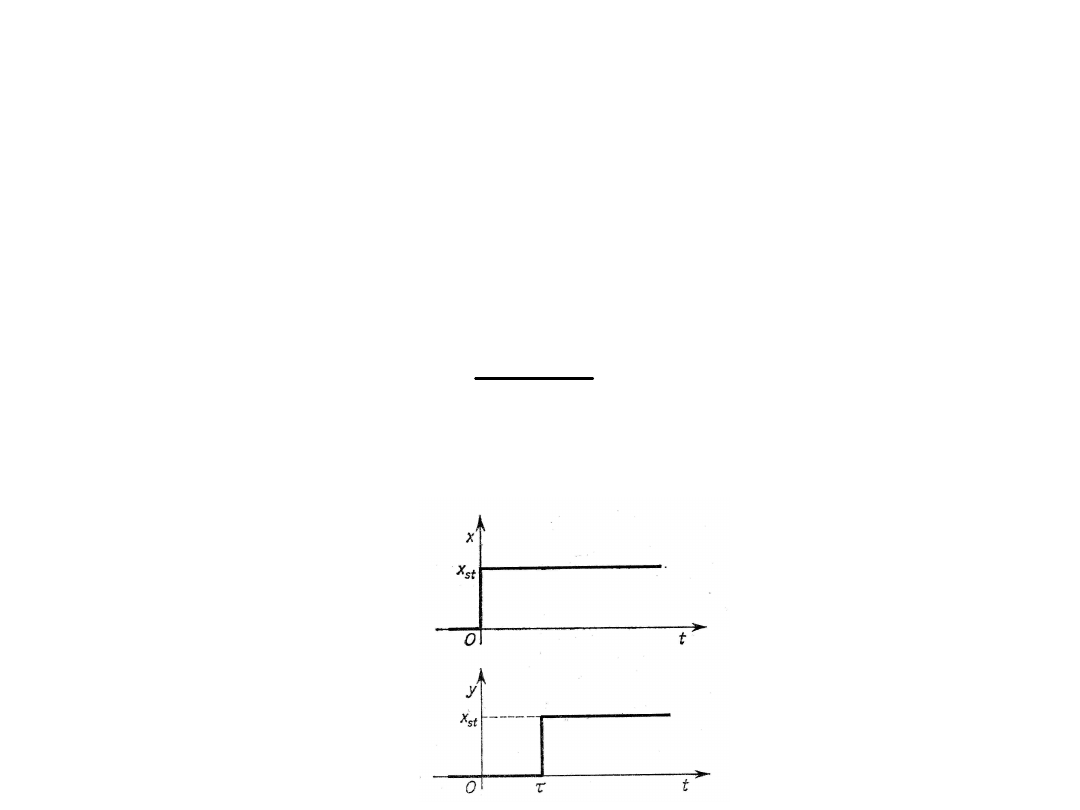
Człon opóźniający

Równanie elementu opóźniającego ma postać:

skąd na podstawie twierdzenia o przesunięciu
rzeczywistym wynika transmitancja:

Element opóźniający nie zniekształca sygnału
wejściowego lecz jedynie przesuwa go w czasie.

Dziękuję za

uwagę!