W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność BIBO – kryterium algebraiczne Routha-Hurwitza
144
Inżynieria systemów dynamicznych
Ważne informacje:
•Liczba zmian znaków współczynników w pierwszej kolumnie oznacza liczbę
pierwiastków równania charakterystycznego znajdujących się w prawej
półpłaszczyźnie
•W przypadku gdy w trakcie obliczeń wystąpi cały rząd zer, równanie
charakterystyczne ma pierwiastki urojone, sprzężone
•Postępowanie w przypadku, gdy w pierwszej kolumnie wystąpi zero zostanie
pokazane na ćwiczeniach
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
2
0
5
1
5
3
3
0
5
6
0
5
5
1
6
2
5
5
3
6
4
5
4
1
3
5
5
0
2
4
6
6
a
F
E
Fa
s
F
E
Ca
ED
s
a
C
A
Ca
E
C
AD
BC
s
D
A
a
a
Aa
C
A
B
a
Aa
s
a
a
a
a
a
B
a
a
a
a
a
A
a
a
a
a
a
s
a
a
a
s
a
a
a
a
s
=
×
-
=
-
=
×
-
=
-
=
-
=
-
=
×
-
=
-
=
-
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność BIBO – kryterium algebraiczne Routha-Hurwitza - przykład
145
Inżynieria systemów dynamicznych
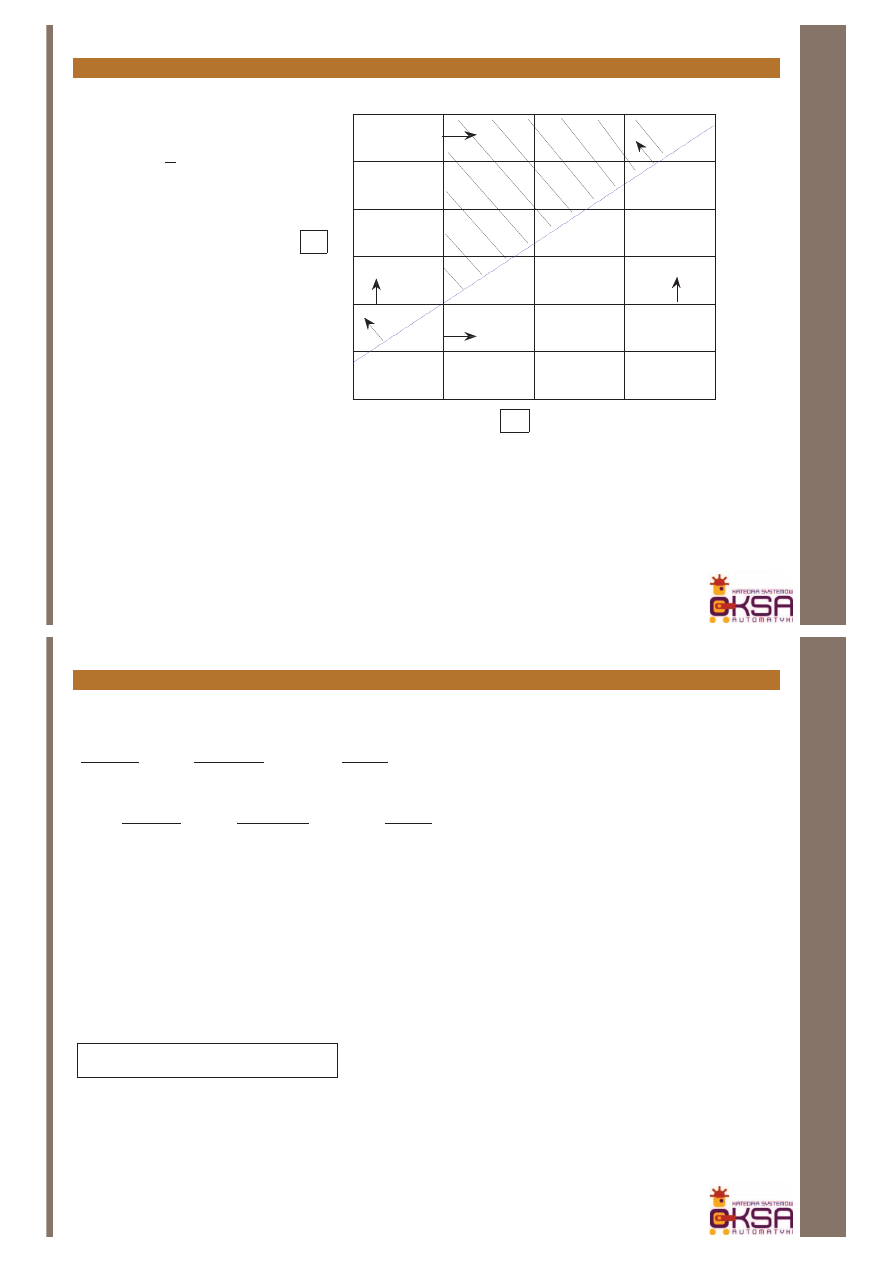
Wyznacz, jakie powinny być wartości parametrów regulatora, aby poniższy
układ był BIBO stabilny
R(s)
Y(s)
_
2
)
2
(
1
+
s
s
k
as +
0
)
4
(
2
2
3
=
+
+
+
+
k
s
a
s
s
k
s
a
k
s
k
s
a
s
0
1
2
3
0
2
8
2
2
4
1
+
+
-
+
0
)
4
(
>
+ a
0
>
k
Równanie charakterystyczne
Warunek konieczny
0
0
2
8
2
>
>
+
+
-
k
a
k
Warunek z tablicy
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność BIBO – kryterium algebraiczne Routha-Hurwitza - przykład
146
Inżynieria systemów dynamicznych
4
0
4
2
1
-
>
>
-
>
a
k
k
a
-5
0
5
10
15
-8
-6
-4
-2
0
2
4
k
a
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Równanie charakterystyczne z równania różniczkowego
Dla modelu danego równaniem różniczkowym
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
1
1
1
1
0
1
1
1
1
t
u
b
dt
t
du
b
dt
t
u
d
b
dt
t
u
d
b
t
y
a
dt
t
dy
a
dt
t
y
d
a
dt
t
y
d
m
m
m
m
m
m
n
n
n
n
n
+
+
+
+
=
+
+
+
+
-
-
-
-
-
-
L
L
0
0
1
1
1
=
+
+
+
+
-
-
a
s
a
s
a
s
n
n
n
L
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
1
1
1
0
1
1
1
s
U
b
s
sU
b
s
U
s
b
s
U
s
b
s
Y
a
s
sY
a
s
Y
s
a
s
Y
s
m
m
m
m
n
n
n
+
+
+
+
=
+
+
+
+
-
-
-
-
L
L
Równanie charakterystyczne
147
Inżynieria systemów dynamicznych

W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Równanie charakterystyczne z modelu stanowego
Dla modelu danego modelem stanowym
Równanie charakterystyczne
)
(
)
(
)
(
t
t
t
Bu
Ax
x
+
=
·
)
(
)
(
)
(
t
t
t
Du
Cx
y
+
=
[
]
0
det
=
- A
I
s
148
Inżynieria systemów dynamicznych
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Wartości własne macierzy
Wartościami własnymi macierzy A nazywamy pierwiastki równania
charakterystycznego
[
]
0
det
=
- A
I
s
Ważne informacje:
•jeśli wszystkie elementy macierzy A są liczbami rzeczywistymi, to jej wartości własne
są liczbami rzeczywistymi bądź parami liczb zespolonych sprzężonych
•wartości własne macierzy A są jednocześnie miejscami zerowymi wielomianu
mianownika transmitancji, czyli biegunami systemu (UWAGA: tylko wtedy, gdy nie
zachodzi kompensacja czynników licznika i mianownika przy wyznaczaniu transmitancji
na podstawie modelu stanowego)
•systemy o tej samej transmitancji ale o różnych modelach stanowych mają to samo
równanie charakterystyczne, czyli ich macierze procesu mają te same wartości własne
149
Inżynieria systemów dynamicznych
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) układu sterowania
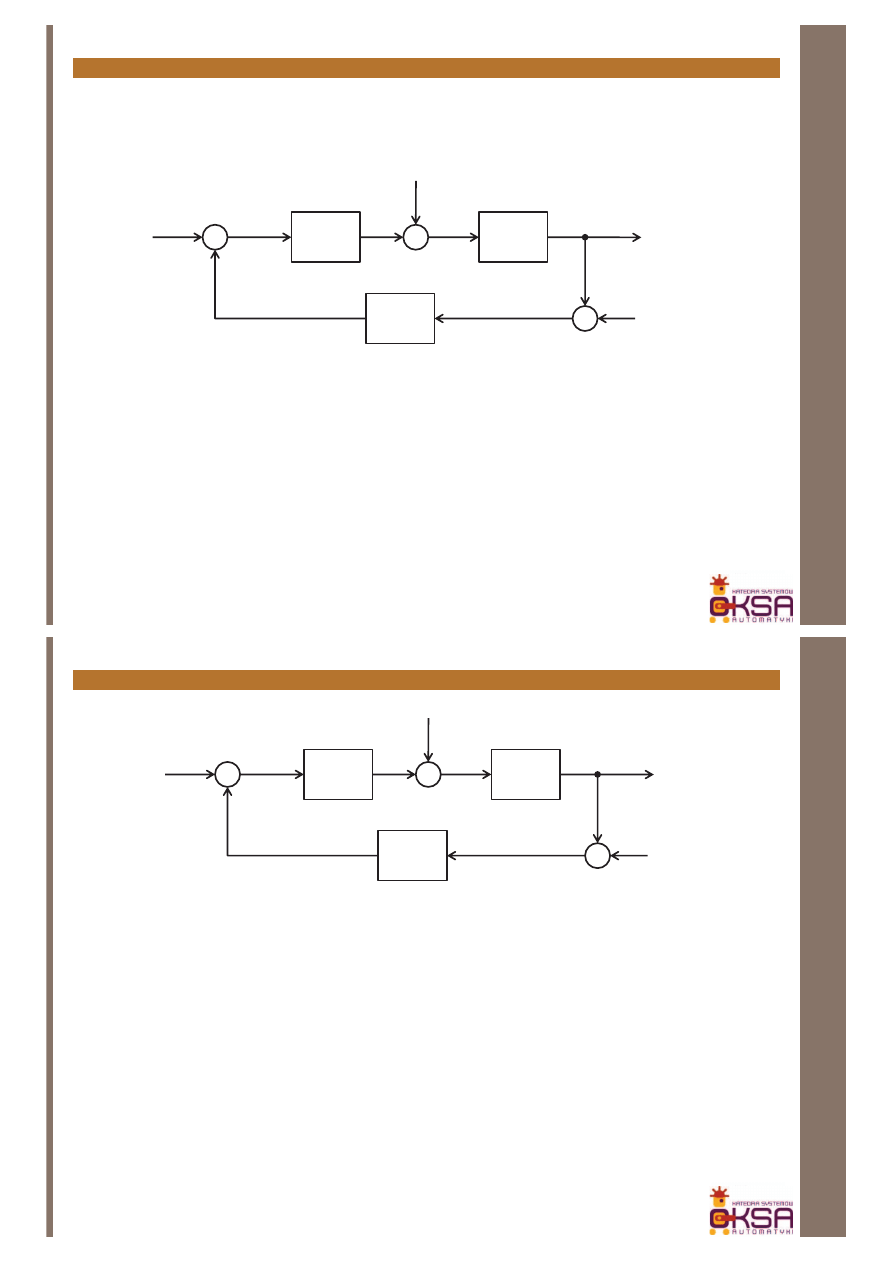
Rozważmy typowy schemat układu sterowania ze sprzężeniem zwrotnym:
150
Inżynieria systemów dynamicznych
C(s)
G(s)
H(s)
R(s)
Y(s)
_
D
1
(s)
D
2
(s)
W(s)
U(s)
Totalna (wewnętrzna) stabilność tego układu wymaga, aby wszystkie
występujące w nim sygnały były ograniczone, jeśli sygnały wejściowe są
ograniczone.
Wszystkie występujące w układzie transmitancje muszą więc być stabilne w
sensie BIBO.
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) test wewnętrznej stabilności
151
Inżynieria systemów dynamicznych
C(s)
G(s)
H(s)
R(s)
Y(s)
_
D
1
(s)
D
2
(s)
W(s)
U(s)
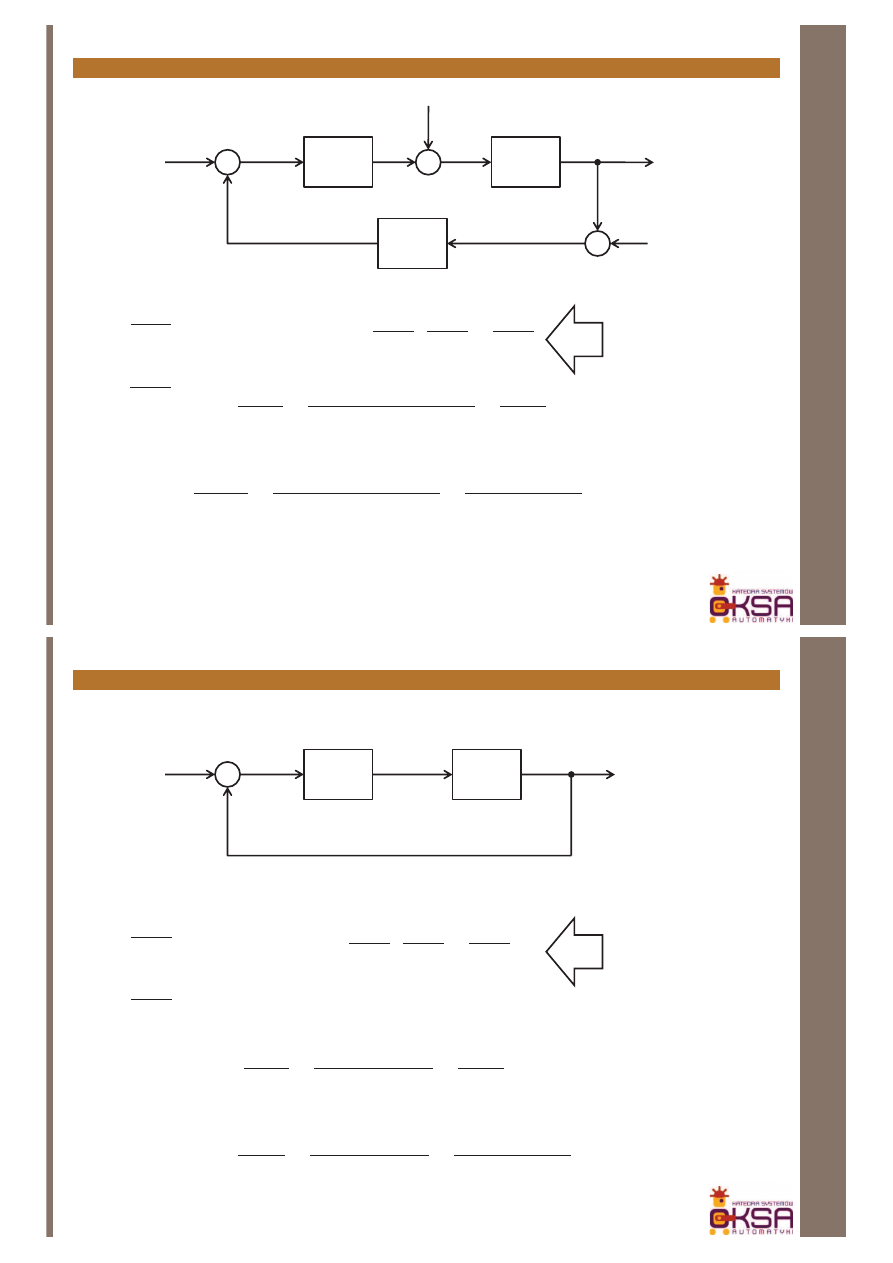
Układ ze sprzężeniem zwrotnym jak na rysunku będzie wewnętrznie stabilny
wtedy i tylko wtedy, gdy transmitancja operatorowa 1+H(s)C(s)G(s) nie ma
zer w p.p. z włączeniem osi urojonej, zaś w iloczynie H(s)C(s)G(s) nie
występują uproszczenia zer z biegunami leżącymi w p.p. i na osi urojonej.
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) test wewnętrznej stabilności - przykład
152
Inżynieria systemów dynamicznych
C(s)
G(s)
H(s)
R(s)
Y(s)
_
D
1
(s)
D
2
(s)
W(s)
U(s)
1
1
)
(
-
=
s
s
G
1
1
)
(
+
-
=
s
s
s
C
1
)
(
=
s
H
1
1
1
1
1
1
)
(
)
(
)
(
+
=
-
×
+
-
=
s
s
s
s
s
G
s
C
s
H
Nastąpiło uproszczenie
bieguna w p. s=1 – układ
nie jest wewnętrznie
stabilny
2
1
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
+
=
+
=
s
s
G
s
C
s
H
s
G
s
C
s
R
s
Y
)
2
)(
1
(
1
)
(
)
(
)
(
1
)
(
)
(
)
(
1
+
-
+
=
+
=
s
s
s
s
G
s
C
s
H
s
G
s
D
s
Y
Układ jest stabilny z punktu widzenia wejścia zadającego r(t), ale jakiekolwiek zakłócenie
pojawiające się na wejściu d1(t) spowoduje jego destabilizację
Przykład:
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) test wewnętrznej stabilności - przykład
153
Inżynieria systemów dynamicznych
C(s)
G(s)
R(s)
Y(s)
_
U(s)
1
1
)
(
+
-
=
s
s
s
G
1
1
)
(
-
=
s
s
C
1
1
1
1
1
1
)
(
)
(
+
=
+
-
×
-
=
s
s
s
s
s
G
s
C
Nastąpiło uproszczenie
bieguna w p. s=1 – układ
nie jest wewnętrznie
stabilny
2
1
)
(
)
(
1
)
(
)
(
)
(
)
(
+
=
+
=
s
s
G
s
C
s
G
s
C
s
R
s
Y
)
2
)(
1
(
1
)
(
)
(
1
)
(
)
(
)
(
+
-
=
+
=
s
s
s
G
s
C
s
C
s
R
s
U
Przykład:
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) test wewnętrznej stabilności - przykład
154
Inżynieria systemów dynamicznych
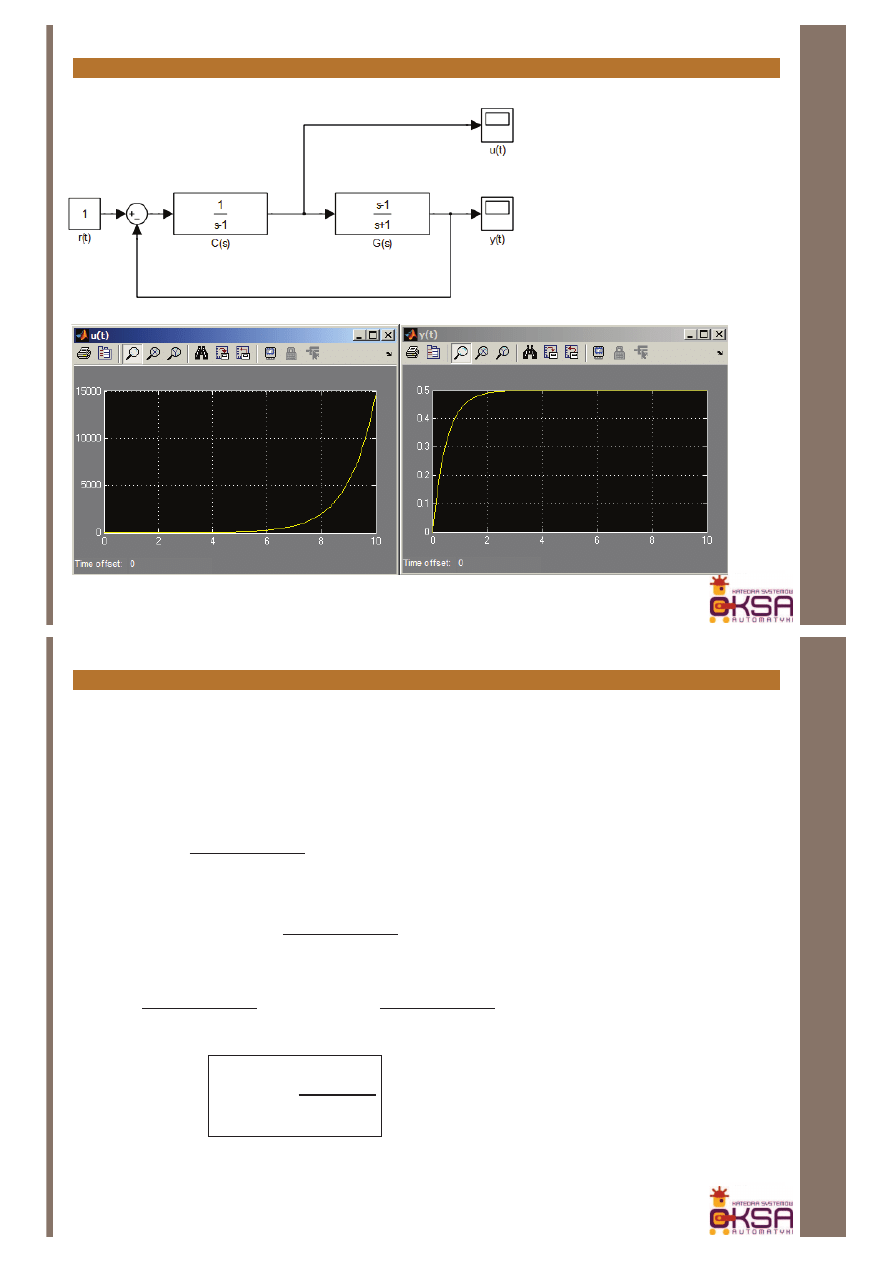
Układ jest stabilny z punktu
widzenia wyjścia, ale wewnątrz
układu sygnał sterujący u(t) będzie
nieograniczony
Model układu w Simulinku
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) model stanowy - przykład
Wyznaczmy transmitancję systemu danego równaniami stanu:
[
]
[ ]
0
,
1
1
,
0
1
,
0
1
2
1
=
-
=
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é-
=
D
C
B
A
[
]
ú
û
ù
ê
ë
é
+
+
-
=
-
-
1
1
2
)
2
)(
1
(
1
1
s
s
s
s
s
A
I
[
]
[
]
[
]
)
2
)(
1
(
1
1
1
1
)
2
)(
1
(
1
)
(
0
1
1
1
2
1
1
)
2
)(
1
(
1
)
(
1
+
-
-
=
ú
û
ù
ê
ë
é
-
+
-
=
ú
û
ù
ê
ë
é
ú
û
ù
ê
ë
é
+
-
+
-
=
-
=
-
s
s
s
s
s
s
s
G
s
s
s
s
s
s
G
B
A
I
C
)
2
(
1
)
(
+
=
s
s
G
Zauważmy: model transmitancyjny w tym przypadku ma rząd niższy niż
model stanowy! Dlaczego? Jakie są tego konsekwencje?
155
Inżynieria systemów dynamicznych
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność totalna (wewnętrzna) test wewnętrznej stabilności - przykład
156
Inżynieria systemów dynamicznych
0
2
4
6
8
10
12
0
0.5
1
y
(t
)
0
2
4
6
8
10
12
0
1
2
x 10
4
x
1
(t
)
0
2
4
6
8
10
12
0
1
2
x 10
4
x
2
(t
)
t
clear
all
; close
all
; clc;
T=0:0.05:11;
A = [-1 2; 1 0];
B = [1; 0];
C = [1 -1];
D = [0];
[Y,T,X] = step(ss(A,B,C,D),T)
subplot(3,1,1);
plot(T,Y);
ylabel(
'y(t)'
)
subplot(3,1,2);
plot(T,X(:,1));
ylabel(
'x_1(t)'
)
subplot(3,1,3);
plot(T,X(:,2));
ylabel(
'x_2(t)'
)
xlabel(
't'
)
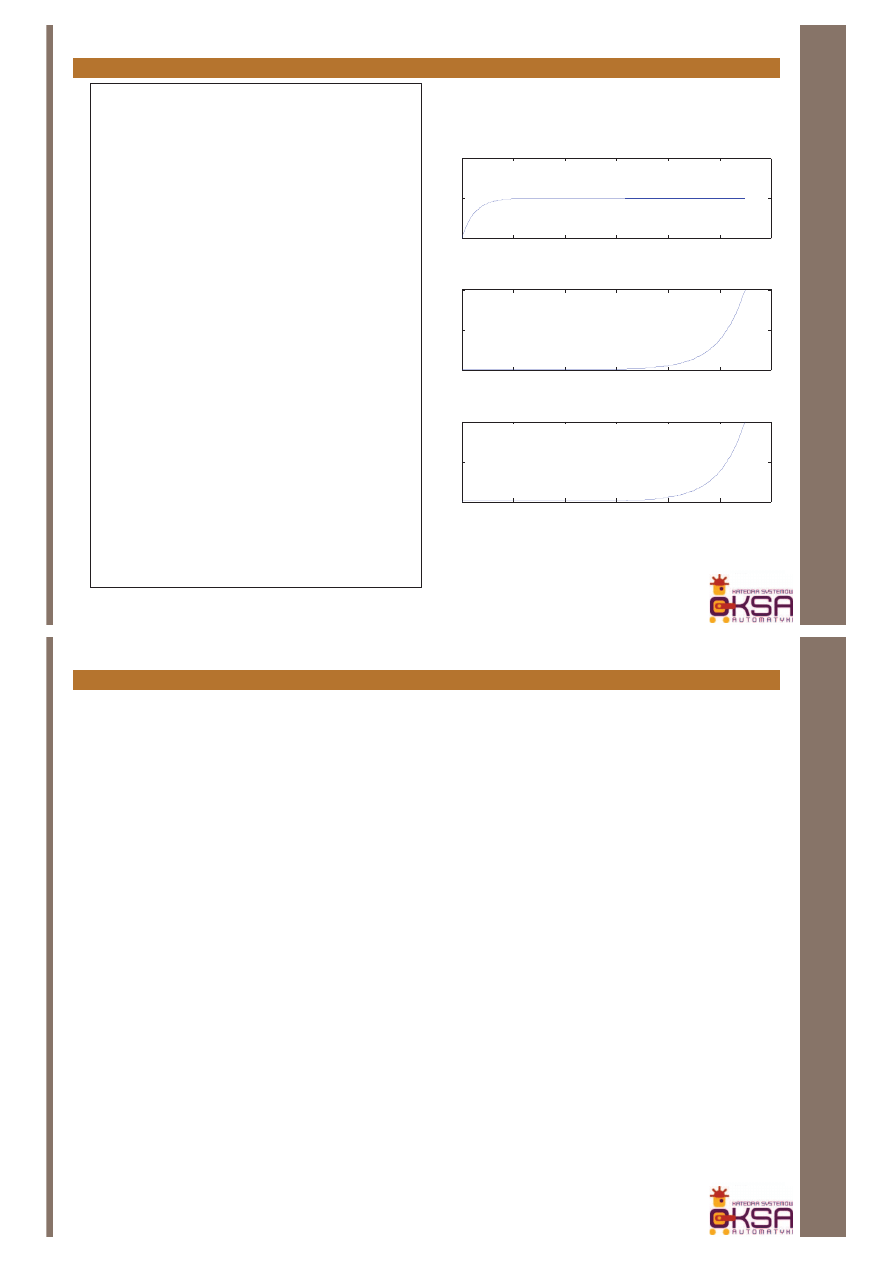
Odpowiedź skokowa układu wygenerowana
w Matlabie
W
Y
M
A
G
A
N
IA
S
T
A
W
IA
N
E
U
K
Ł
A
D
O
M
RE
G
U
L
A
C
JI
Stabilność asymptotyczna
157
Inżynieria systemów dynamicznych
Niech dany będzie pewien układ:
0
0
,
x
)
x(
Ax(t)
(t)
x
=
=
·
Mówimy, że układ ten jest asymptotycznie stabilny, gdy dla dowolnego
warunku początkowego zachodzi:
0
)
x( ®
Þ
¥
®
t
t
,
Warunkiem asymptotycznej stabilności jest to, aby wszystkie wartości
własne macierzy A leżały w lewej półpłaszczyźnie
UWAGA:
Warunkiem wystarczającym BIBO stabilności jest stabilność asymptotyczna
Wyszukiwarka
Podobne podstrony:
WYK6 BazyDanych
INSTRUKCJA OBSŁUGI DEKODER SAGEM ISD 4285 PL
ub-wyk6, FIR UE Katowice, SEMESTR IV, Ubezpieczenia, ubezpieczenia
isd wyk3
isd cwiczenia
klimat polarny wyk6
Iinstrukcja Sagem ISD 83
socwsi wyk6, Socjologia wsi
et-wyk6, Logistyka, rok2, ekonomika transportu, ek
io wyk6
wyk6
isd wyk4
isd wyk7
ISD test
PrawoPRACY wyk6 OK
mb-wyk6, UE Katowice FiR, marketing bankowy
rfin-wyk6, STUDIA UE Katowice, Rynki finansowe, RYNKI FINANSOWE
więcej podobnych podstron