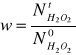Grzegorz Piechota
ĆWICZENIE NUMER 6
Wyznaczanie stałej szybkości reakcji rozkładu nadtlenku wodoru na katalizatorze węglowym.
1. Wstęp teoretyczny.
Adsorpcja - gromadzenie się cząstek jednej substancji, zwanej adsorbatem, na powierzchni drugiej substancji, zwanej adsorbentem, na skutek występowania sił międzycząsteczkowych albo tworzenia się wiązań chemicznych; wykorzystywana do wydzielania określonych składników z mieszaniny gazowej lub ciekłej.
Katalizator niejednorodny tworzy najczęściej odrębną fazę stałą nazywaną kontaktem. Proces katalityczny zachodzi na powierzchnie tej fazy. Z tego względu powierzchnia katalizatora powinna być jak największa. Osiąga się to przez stosowanie katalizatorów silnie rozdrobnionych (sproszkowanych) albo porowatych. Katalizator może być również nanoszony na inną substancję o rozwiniętej powierzchni nazywaną nośnikiem.
Mechanizm działania katalizatora jest złożony i nawet w tej samej reakcji jest dla różnych katalizatorów odmienny.
Na aktywność katalizatora wpływają czynniki decydujące o stanie jego powierzchni, takie jak: wielkość powierzchni, skład chemiczny warstwy powierzchniowej, obecność domieszek substancji obcej itp.
Warunkiem koniecznym działania katalizatora jest chemisorpcja co najmniej jednego substratu na centrach aktywnych katalizatora. Chemisorpcja jest z reguły związana z wymianą elektronów pomiędzy adsorbentem i adsorbatem z wytworzeniem wiązań typu kowalencyjnego lub jonowego. Cząsteczka zaadsorbowana różni się więc istotnie od cząsteczki swobodnej i wchodzi w reakcję ze znacznie niższą energią aktywacji.
Cały proces katalityczny na katalizatorze stałym składa się z kilku etapów:
- „dopływ” substratów do katalizatora i „odpływ” produktów,
- adsorpcja substratów i desorpcja produktów,
- właściwa reakcja z udziałem chemisorbowanych reagentów.
O szybkości całego procesu może decydować każdy z wymienionych etapów.
Zależność ![]()
od stężenia opisuje równanie izotermy adsorpcji Langmuira o następującej postaci:
![]()
(1.1), gdzie:
![]()
- oznacza ułamek miejsc zajętych,
c - stężenie,
b - stałą wartość liczbową.
Zgodnie z powyższym równaniem, ![]()
reprezentuje stężenie substratu reakcji i równanie kinetyczne procesu katalitycznego ma postać:
![]()
(1.2).
Można przewidywać dwa przypadki skrajne:
a) Gdy adsorpcja jest niewielka, tzn. przy bardzo małym c, wtedy bc << 1 i ![]()
= bc. Podstawienie takiej wartości ![]()
do równania (1.2) prowadzi do równania kinetycznego I rzędu (względem substratu):
![]()
(1.3), gdzie:
K = kb jest wielkością stałą.
b) Gdy obsadzenie centrów aktywnych jest całkowite, tzn. ![]()
= 1 i bc>>1. W tym przypadku równanie (1.2) przyjmuje postać równania reakcji zerowego rzędu:
![]()
(1.4).
Reakcja rozkładu H2O2 jest podana równaniem:
H2O2
H2O + ![]()
O2.
Reakcja rozkładu prowadzona w warunkach zapewniających niewielki stopień pokrycia katalizatora przebiega według równania kinetycznego I-go rzędu, więc możemy zapisać, że:
![]()
(1.5)
albo
![]()
(1.6), gdzie:
c - oznacza stężenie substratu (w danej chwili),
x - stężenie produktu (w danej chwili),
a - początkowe stężenie substratu.
Z równań tych otrzymamy wyrażenia pozwalające na obliczenie stałej szybkości reakcji. W tym celu rozdzielamy zmienne z równania z (1.5) i całkujemy je w granicach stężeń od c = a przy t = 0 do c przy t = t:
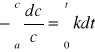
(1.7)
otrzymując:
![]()
(1.8).
Objętość mieszaniny reakcyjnej w czasie reakcji jest praktycznie stała, stąd stężenie początkowe H2O2 (a) oraz stężenie H2O2 w czasie reakcji (c) możemy zastąpić odpowiednimi liczbami moli: ![]()
oraz ![]()
(gdyż 1 mol H2O2 tworzy w reakcji 0,5 mola tlenu).
Po podstawieniu tych liczb do wyrażenia na stałą szybkości otrzymamy:
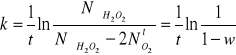
(1.9), gdzie:
![]()
.
Schemat układu pomiarowego do oznaczania stałej szybkości katalitycznego rozkładu H2O2.
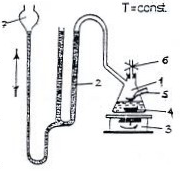
Części układu:
1 - naczynie reakcyjne,
2 - biureta gazowa,
3 - mieszadło magnetyczne,
4 - łopatka,
5 - kran.
Całość w termostacie powietrznym.
2. Literatura.
Ceynowa J., Litowska M., Nowakowski R., Ostrowska-Czubenko J., Podręcznik do ćwiczeń laboratoryjnych z chemii fizycznej, UMK, Toruń, 1999, str.81-86.
Sobczyk L., Kisza A., Gatner K., Koll A, Eksperymentalna chemia fizyczna, PWN Warszawa, 1982, str. 489-491.
Atkins P.W „Chemia fizyczna” PWN Warszawa 2001 str. 738-763
3. Oświadczenie.
Oświadczam, że zapoznałem się z kartami charakterystyk w/w substancjami i znane mi są właściwości tych substancji, sposoby bezpiecznego postępowania z nimi oraz zasady udzielania pierwszej pomocy w nagłych wypadkach.
…………………..
4. Cel wykonana ćwiczenia:
Celem ćwiczenia jest wyznaczenie wartości stabelaryzowanej - stałej szybkości reakcji rozkładu nadtlenku wodoru na katalizatorze węglowym. Zapoznanie się z aparatura, oraz typem reakcji rozkładu.
5. Opis wykonania ćwiczenia.
Włączyłem regulator temperatury do sieci, ustawiłem termometr kontaktowy na temperaturę 22,7 ˚C, otworzyłem obieg wody do chłodnicy, uruchomiłem wentylator. W kolbie miarowej o objętości 100 cm3 odmierzyłem 5 cm3 roztworu nadtlenku wodoru o stężeniu 6%, następnie uzupełniłem kolbę wodą destylowaną do kreski. Na wadze analitycznej odważyłem 0,0845 g węgla aktywowanego bezpośrednio na łopatce naczynia reakcyjnego. Do naczynia reakcyjnego wprowadziłem za pomocą pipety 50 cm3 mego roztworu nadtlenku wodoru, otworzyłem kranik, umieściłem mieszadełko, umieściłem łopatkę z węglem aktywnym, wyrównałem poziom wody w biurecie gazowej z podziałką, a następnie termostatowałem układ przez 15 minut. W międzyczasie oznaczałem stężenie molowe przygotowanego roztworu H2O2, przez miareczkowanie roztworem KMnO4 w obecności H2SO4. W tym celu pobrałem 2 cm 3 sporządzonego przeze mnie roztworu H2O2, dodałem 1 cm3 4 M H2SO4, następnie miareczkowałem roztworem KMnO4. Miareczkowanie wykonałem 3- krotnie. Po wytermostatowaniu układu, zamknąłem kranik (odczytałem poziom wody w biurecie gazowej), włączyłem mieszanie roztworu, przez obrót łopatki wprowadziłem węgiel do roztworu, włączyłem stoper. Odczytywałem poziom wody w biurecie gazowej w następujących odstępach czasu od włączenia stopera: 2, 4, 6, 8, 10, 12, 14, 16, 20, a dalej co 5 minut aż do osiągnięcia całkowitego czasu 60 minut. Przy każdej zmianie poziomu cieczy w obu ramionach biurety wyrównywałem go poprzez obniżanie poziomu naczynia wyrównawczego. Zanotowałem ciśnienie atmosferyczne panujące na pracowni: 759,3 mmHg.
6. Obliczenia.
W tabeli 1 zestawiam wyniki ważeń oraz informacje o temperaturze i ciśnieniu.
Tabela 1.
masa łopatki pustej [g] |
masa łopatki pełnej [g] |
masa węgla aktywnego [g] |
temeratura [K] |
ciśnienie [mmHg] |
|
|
|
|
|
15,5738 |
15,6583 |
0,0845 |
295,85 |
759,3 |
W tabeli 2 przedstawiam wyniki miareczkowań manganometrycznych.
Tabela 2.
Nr miareczkowania |
|
|
|
Objętość KMnO4 [cm3] |
|
1 |
3,70 |
|
2 |
3,70 |
|
3 |
3,70 |
|
śr. objętość [cm3] |
3,70 |
|
Wykorzystując wyniki miareczkowania manganometrycznego oraz reakcję nadtlenku wodoru z nadmanganianem w środowisku kwaśnym:
2KMnO4- + 5H2O2 + 6H+→ 2Mn2+ + 5O2 + 8H2O
obliczam stężenie H2O2 ze wzoru:
c = 5*((stężenie KMnO4*objętość miareczkowania)/4)
5*0,00176*0,0037/4=0,00814
Tabela 3.
c KMnO4 [mol/dm3]: |
0,00176 |
|
V H2O2 [dm3]: |
|
0,002 |
c H2O2 [mol/dm3] |
0,00814 |
|
Obliczam początkową liczbę moli H2O2 w naczyniu reakcyjnym (![]()
) uwzględniając objętość roztworu H2O2 jaką użyto do reakcji ze wzoru c=n/V
Tabela 4.
c H2O2 [mol/dm3] |
0,00814 |
V H2O2 [dm3]: |
0,050 |
n H2O2 [mol] |
0,000407 |
Tabela 5.
temp. [oC] |
20 |
25 |
30 |
35 |
40 |
p [mmHg] |
17,53 |
23,76 |
31,84 |
42,17 |
55,322 |
Wykres powyższej zależności :
Wykres który opisuję wielomianem 3 stopnia mającym postać: y = 0,0006x3 - 0,0123x2 + 0,8154x + 0,9698 Rozwiązaniem równania będzie szukana prężność pary. Po czym obliczam ciśnienie wewnątrz naczynia ze wzoru: p = patm - ppara wodna, gdzie:
patm - oznacza ciśnienie atmosferyczne [Pa],
ppara wodna - oznacza prężność par wody nad roztworem nadtlenku wodoru [Pa].
Tabela 6.
Prężność pary nasyconej wody w temperaturze 25 oC [mmHg]: |
23,042 z moich danych |
R [J/mol K]: |
8,314 |
T [K]: |
295,85 |
p [Pa] |
98063,935 |
Następnie obliczam liczbę moli tlenu powstającego wyniku reakcji rozkładu wody utlenionej w czasie t {korzystam przy tym z równania stanu gazu doskonałego Clapeyrona: pV = nRT , gdzie: V - objętość powstającego tlenu odczyta za pomocą biurety gazowej [m3],
p - ciśnienie tlenu wewnątrz naczynia [Pa], T - temperatura [K],
n -liczba moli tlenu [mol],
R - stała gazowa (R = 8,314 J/mol K)}, liczbę moli H2O2, rozłożonego w czasie t (![]()
) zgodnie z równaniem reakcji: H2O2 → H2O + 1/2O2 . wg wzoru:
N02= (p*V02*0,000001/T*R). Później liczę wielkość charakteryzującą postęp reakcji 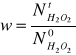
, a dalej ln(1/1-w). N =N /N .Wszystkie wyniki obliczeń zestawiam w tabeli 7.
Tabela 7.
Czas [s] |
[cm3]
|
[mol]
|
[mol]
|
|
ln(1/1-w) |
|
|
|
|
|
|
|
|
|
|
|
|
120 |
0,20 |
7,920E-06 |
1,584E-05 |
3,892E-02 |
3,970E-02 |
240 |
0,35 |
1,386E-05 |
2,772E-05 |
6,811E-02 |
7,054E-02 |
360 |
0,45 |
1,782E-05 |
3,564E-05 |
8,757E-02 |
9,164E-02 |
480 |
0,55 |
2,178E-05 |
4,356E-05 |
1,070E-01 |
1,132E-01 |
600 |
0,60 |
2,376E-05 |
4,752E-05 |
1,168E-01 |
1,242E-01 |
720 |
0,70 |
2,772E-05 |
5,544E-05 |
1,362E-01 |
1,464E-01 |
840 |
0,80 |
3,168E-05 |
6,336E-05 |
1,557E-01 |
1,692E-01 |
960 |
0,85 |
3,366E-05 |
6,732E-05 |
1,654E-01 |
1,808E-01 |
1200 |
0,90 |
3,564E-05 |
7,128E-05 |
1,751E-01 |
1,925E-01 |
1500 |
1,00 |
3,960E-05 |
7,920E-05 |
1,946E-01 |
2,164E-01 |
1800 |
1,15 |
4,554E-05 |
9,108E-05 |
2,238E-01 |
2,533E-01 |
2100 |
1,30 |
5,148E-05 |
1,030E-04 |
2,530E-01 |
2,916E-01 |
2400 |
1,40 |
5,544E-05 |
1,109E-04 |
2,724E-01 |
3,180E-01 |
2700 |
1,45 |
5,742E-05 |
1,148E-04 |
2,822E-01 |
3,315E-01 |
3000 |
1,55 |
6,138E-05 |
1,228E-04 |
3,016E-01 |
3,590E-01 |
3300 |
1,65 |
6,534E-05 |
1,307E-04 |
3,211E-01 |
3,872E-01 |
3600 |
1,70 |
6,732E-05 |
1,346E-04 |
3,308E-01 |
4,017E-01 |
Sporządzam wykres ln(1/1-w) = f(t) dla powyższych pomiarów.
Metodą najmniejszych kwadratów wyznaczam równanie prostej.
Współczynnik b obliczam ze wzoru:
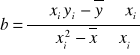
= 0,0714
gdzie: x- czas[t] , y-ln(1/1-w)
Natomiast współczynnik a ze wzoru:
![]()
= 0,0001
Czyli równanie mojej prostej ma postać: y=0,0001x + 0,0714
Współczynnik korelacji obliczam ze wzoru:
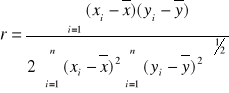
= 0,9868
Z równania y = 0,0001x +0,0714 wyznaczam stałą szybkości rozkładu, która ma wartość: k=0,0001![]()
.
8. Wnioski.
Z wykresu zależności ln(1/(1-w)) = f(t) pomiaru widać, liniową zależność ln(1/(1-w)) od t. Stała szybkości reakcji wyznaczona za pomocą metody najmniejszych kwadratów wyniosła k= 0,0001 ![]()
. Podczas wykonania ćwiczenia niezbędne jest utrzymanie stałej temperatury i taka została zachowana, gdyż stała szybkości reakcji zależy od temperatury, a wszelkie wahania temperatury mogą spowodować jej zmianę. Podczas wykonywania ćwiczenia popełniony został błąd: zamiast naważyć 0,1g węgla zostało naważone 0,01g węgla .. czyli 10 krotnie mniej .. ale wyniki są opracowane dla danej naważki i w pełni odzwierciedlają poprawność przeprowadzonego ćwiczenia >> o czym świadczy wysoka korelacja. W opracowaniu powyższych wyników pominąłem pierwszy pomiar gdyż odbiegał on najbardziej od linii trendu, a tym samym był błędnie odczytany.
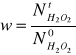
![]()
![]()
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE NUMER 3 Grzesiu doc
Ćwiczenie nr 2 Grzesiu doc
Ćwiczenie nr 5 grzesiu doc
ĆWICZENIE NUMER 15 Grzesiu doc
Ćwiczenie nr 19 Grzesiu doc
Ćwiczenie nr 30 Grzesiu doc
Ćwiczenie nr 16 Grzesiu doc
Protokół zawiera opracowanie ćwiczenia numer 1
Metodologia cwiczenie numer
Ćwiczenia na pośladki[ doc]
fizyka moje, cw3, Ćwiczenie numer: 3
Ćwiczenia laboratoryjne GiK doc
instrukcja do ćwiczeń nr 11 doc
Cwiczenia 1, Gotowosc szkolna doc
Cwiczenie numer 7
Protokół zawiera opracowanie ćwiczenia numer 9
Warystory i termistory, Cwiczenie numer 1.
Ćwiczenie numer 7, Polibuda
Wstęp teoretyczny do ćwiczeń laboratoryjnych numerW doc
więcej podobnych podstron