4. PRÓG RENTOWNOŚCI

Przy niskiej produkcji suma utargów nie pokrywa sumy kosztów i przedsiębiorstwo ponosi straty. Dzieje się tak dlatego, że przeciętny koszt produkcji, obciążony wysokimi kosztami stałymi, jest wyższy od ceny, po której sprzedawany jest produkt. W miarę zwiększania produkcji koszt jednost-kowy maleje, poprawia się relacja między ceną a kosztem i przedsiębiorstwo zaczyna osiągać zyski. Przy zbyt wysokim poziomie produkcji znów mogą pojawić się straty na skutek wzrostu kosztów jednostkowych.

Próg rentowności (opłacalności) wielkość produkcji, przy której przedsiębiorstwo przechodzi od strat do zysków.

Ilustruje to rys. 6.9. Zakładamy, że przedsiębiorstwo sprze-daje swój produkt po ustalonej cenie, niezależnej od wielkości produkcji, co odpowiada warunkom konkurencji doskonałej. Wariant (a) dotyczy liniowej funkcji kosztów, wariant (b) - nieliniowej funkcji kosztów. Progiem rentowności w obu przy-padkach jest wielkość produkcji OA.

OA - próg rentowności

OA - próg rentowności

Rys. 6.9

Próg rentowności

Gdy funkcja kosztów całkowitych jest linią prostą, tzn. gdy przeciętny koszt zmienny
= const., i gdy cena p = const., do wyznaczenia progu rentowności stosujemy formułę:

próg rentowności =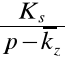
,

tzn. szukamy wielkości produkcji, przy której nadwyżka utargu nad sumą kosztów zmiennych zwraca poniesione koszty stałe.

Przykład

K_s = 2000 zł,
= 6 zł/szt., p = 10zł/szt.

próg rentowności =
= 500 szt.

5. CENA OPTYMALNA

W warunkach doskonałej konkurencji przedsiębiorstwo musi akceptować aktualną cenę rynkową - jest biorcą ceny. W warunkach niedoskonałej konkurencji przedsiębiorstwo samo ustala ceny swoich wyrobów lub usług. Musi brać jednak pod uwagę ten fakt, że po wyższej cenie sprzeda mniej niż po cenie niższej. Przed taką firmą stoi zagadnienie optymalnego po-ziomu ceny, który pozwoli zmaksymalizować sumę zysku. Zagadnienie to jest odpowiednikiem wyboru optymalnej wiel-kości produkcji.

Cena optymalna wynika z formuły:

.

gdzie:  - elastyczność cenowa popytu.

Oznacza to, że wysokość narzutu (marży zysku) ponad koszt krańcowy, wyrażona w procentach ceny, powinna być odwrot-nie proporcjonalna do cenowej elastyczności popytu na dane dobro lub usługę. Im bardziej elastyczny jest popyt, tzn. im mocniej nabywcy reagują na podwyżkę ceny, tym niższy musi być narzut.

Powyższą formułę można również przekształcić do postaci:

.

Ten zapis wskazuje, że cena powinna zależeć zarówno od kosztów, jak i od popytu. Podstawą do wyznaczenia prawid-łowej ceny jest koszt krańcowy z uwzględnieniem elastyczności popytu. Towary o wysokiej elastyczności popytu należy ofero-wać po możliwie niskich cenach.

Przykład

Przy  = -3 narzut zysku na koszt krańcowy może wynieść nawet 50%, ale przy  = -5 marża zysku musi być zmniejszona do 25%. Za pomocą reklamy przedsiębiorstwa starają się obniżyć elastyczność cenową popytu, co pozwala uzyskać wyższe ceny.

Omówiona zasada dotyczy jedynie popytu o elastyczności większej od 1, gdyż w przypadku popytu o elastyczności niż-szej od 1 żadna cena nie zapewni maksymalnego zysku. Jak się dowiemy z rozdziału 7, w warunkach niedoskonałej konku-rencji przedsiębiorstwo poszukuje optymalnej wielkości pro-dukcji (i optymalnego poziomu ceny) na elastycznej części krzywej popytu na swój produkt, tzn. na odcinku, gdzie || > 1.

W praktyce przedsiębiorstwa ustalają swe ceny według innej metody, przyjmując za podstawę łatwy do obliczenia koszt przeciętny (a nie koszt krańcowy) i określony narzut, tzn. według formuły:

,

gdzie: m - narzut (marża) zysku.

Ta formuła zapewnia pokrycie pełnych kosztów produkcji i osiągnięcie założonego zysku - niekoniecznie jednak maksy-malnego.

Między teoretycznie poprawną formułą ceny (opartą na koszcie krańcowym) a formułą stosowaną w rzeczywistości (opartą na koszcie przeciętnym) nie ma zasadniczej sprzecz-ności, o ile przy ustalaniu wysokości narzutu firma bierze pod uwagę elastyczność popytu. Z obserwacji praktyk cenowych różnych firm wynika, że przy ustalaniu ceny uwzględniają one elastyczność popytu.

6. WYBÓR TECHNIKI PRODUKCJI

Technika produkcji

Technikę (metodę) produkcji opisuje ilościowa kombinacja nakładów czynników produkcji (pracy i kapitału) zużywanych do wytworzenia jednostki wyrobu.

Technikę angażującą stosunkowo dużo kapitału rzeczowego nazywamy techniką kapitałochłonną, zaś technikę zużywającą stosunkowo dużo pracy - techniką pracochłonną.

W sensie ekonomicznym efektywną metodą produkcji jest taka kombinacja czynników, która minimalizuje koszty (nie pogarszając jakości wyrobu).

Jednostkowy koszt produkcji (tzn. koszt przeciętny) zależy od wielkości zużycia poszczególnych czynników produkcji na jednostkę wyrobu oraz od cen tych czynników. Wielkość zużycia czynnika produkcji na jednostkę wyrobu jest odwrotnością produkcyjności tego czynnika. Koszty produkcji można obniżyć przez lepsze wykorzystanie czynników produkcji (zwiększenie ich produkcyjności) lub przez zastępowanie czynników drogich (w stosunku do ich produk-cyjności) czynnikami relatywnie tańszymi. Zmiany relacji cen czynników oraz ich produkcyjności skłaniają przedsiębiorców do zmian metod wytwarzania.

Postępem technicznym nazywamy takie zmiany techniki produkcji, które zapewniają poprawę jakości wyrobów lub obniżkę kosztów produkcji.

Zagadnienie wyboru technik produkcji angażujących różne ilości pracy i kapitału można przeanalizować na wykresach przedstawiających różne nakłady pracy i kapitału oraz uzyskiwaną wielkość produkcji.

Izokwanta i linia jednakowego kosztu

Technikę produkcji opisują krzywe nazywane izokwantami. Każda izokwanta (I) przedstawia różne kombinacje ilościowe pracy (L) i kapitału (K), tzn. różne techniki produkcji, za pomocą których można wytworzyć produkcję o określonej wielkości. Wyżej położone izokwanty odpowiadają większym rozmiarom produkcji.

Koszty produkcji są przedstawiane jako linie jednakowego kosztu, łączące takie kombinacje pracy i kapitału, które charakteryzują się jednakowym kosztem. Na rys. 6.10 są to linie K₀L₀ i K₁L₁.

Rys. 6.10

Wybór techniki produkcji

Dla każdej wielkości produkcji, tzn. dla każdej izokwanty, najtańsza jest taka technika, którą wyznacza punkt styczności danej izokwanty z najniżej położoną linią kosztu. Na rys. 6.10 na izokwancie I₁ jest to punkt A, a na izokwancie I₂ punkt B.

Technika optymalna

Nachylenie izokwanty wyraża stosunek krańcowej produkcyj-ności dwóch rozważanych czynników, a nachylenie linii jedna-kowego kosztu - relację cen tych czynników.

Oznaczmy:

q_L', q_K' - krańcowa produkcyjność pracy i kapitału;

w - cena pracy (płaca);

r - cena kapitału (stawka opłaty kapitału).

Produkcyjność krańcowa przyrost produkcji uzyskiwany dzięki zwiększeniu o jednostkę nakładów danego czynnika.

Optymalna technika:

czyli

Optymalna jest zatem taka technika, przy której relacje pro-dukcyjności krańcowej wykorzystywanych czynników pro-dukcji są równe relacjom ich cen. Inaczej mówiąc, należy zatrudnić oba czynniki w takich ilościach, aby ostatnia jednostka nakładu ponoszonego na zatrudnienie dowolnego czynnika dawała producentowi jednakową korzyść, mierzoną uzyskiwanym przyrostem produkcji.

Uwaga: Symbole r i w oznaczają realne stawki wynagrodzenia pracy i kapitału. W tym znaczeniu stosujemy także określenie „cena czynnika”. Pojęcie stawki opłaty kapitału, inaczej stawki najmu, będzie dokładniej wyjaśnione w rozdz. 9.

Ciekawa dygresja

Jak widzimy, rozwiązanie problemu optymalnej techniki produkcji jest pod względem analitycznym podobne do rozwiązania problemu wyboru optymalnej ilości dwóch dóbr przez konsumenta. Linia jednakowego kosztu to linia budże-towa producenta, a izokwantę, która wyraża różne kombina-cje pracy i kapitału zapewniające taką samą wielkość pro-dukcji, można porównać z krzywą obojętności konsumenta, opisującą różne kombinacje ilościowe dwóch dóbr dające taką samą całkowitą użyteczność.

Zmiany cen czynników

Rys. 6.11 pokazuje wpływ wzrostu płac na wybór techniki produkcji w przedsiębiorstwie.

Rys. 6.11

Skutki wzrostu płaC

Wzrost płac sprawia, że linia kosztu K₁L₁ odchyla się do położenia K₁L₂. Bezpośrednim skutkiem podwyżki płac jest zmniejszenie zatrudnienia z L_B do L_C.

Ilość zaangażowanego kapitału może wzrosnąć lub zmaleć w zależności od tego, czy przeważy efekt substytucyjny (zastę-powanie pracy kapitałem), czy efekt podażowy (zmniejszenie zapotrzebowania na obydwa czynniki w związku z ograni-czeniem produkcji, spowodowanym przez wzrost kosztów). Na rysunku przeważył ten pierwszy efekt: przedsiębiorstwo zwiększyło zasób kapitału z K_B do K_C.

Powyższe ustalenia nie biorą pod uwagę efektów pośrednich, związanych z ewentualnym wpływem podwyżki płac na wy-dajność pracy. Jeżeli w rezultacie podwyżki płac nastąpi wzrost wydajności pracy, to w dłuższym okresie może to skłonić przedsiębiorstwo do zwiększenia rozmiarów produkcji i zatrudnienia.

Rozwiązanie ogólne

Dla techniki obejmującej n czynników rozwiązanie można zapisać:

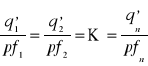
czyli
= const dla i = 1, 2,…, n.

Symbolem pf_i oznaczyliśmy tu jednostkową cenę czynnika i. Optymalna jest taka kombinacja czynników produkcji, która wyrównuje produkcyjność krańcową każdego czynnika w przeliczeniu na złotówkę nakładu.

Technika i skala produkcji

Powyższe rozwiązania dotyczą wyboru techniki przy okreś-lonej z góry skali produkcji. Formułując pytanie szerzej, warto zastanowić się, jaka skala produkcji umożliwia wybór techniki optymalnej. Będzie to taka technika i skala produkcji, przy której produkcyjności krańcowe czynników zostaną zrównane z ich cenami:

= w i
= r,

a ogólniej:

q_i' = pf_i dla i = 1, 2,..., n.

Takie rozwiązanie zminimalizuje koszty i zmaksymalizuje zyski w przypadku, gdy możemy wybierać nie tylko technikę produkcji, lecz także skalę produkcji.

K

U

Q

O

A

strata

zysk

U

Q

O

A

K

zysk

strata

U

B

L

L₁

I₂

I₁

L₀

L_B

L_A

K₁

K

K₀

K_B

K_A

O

A

I₂

I₁

K

K_C

K_B

B

C

L

L₁

L₂

K₁

O

L_B

L_C

pf_i

---