Sprawozdanie z laboratorium 7

Algorytmy przetwarzania sygnałów.

Temat: „Średnia i wariancja sygnału”

Data wykonania:

Prowadzący zajęcia:

1. Sygnał sinusoidalny.

N = 100;

t = linspace (1, N, N);

x = sin (2*pi*0.15*t + pi/5);

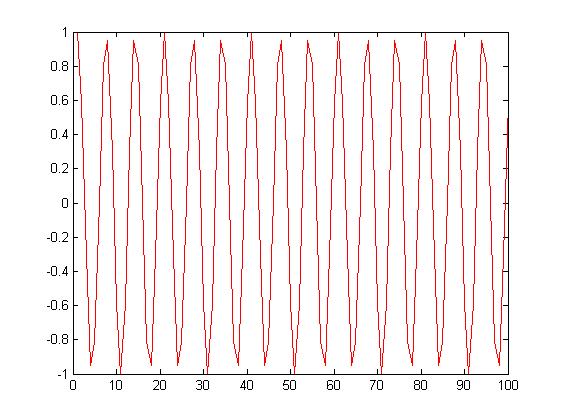
1. Wartośćśredniasygnałusinusoidalnego

Kod:

function m = wart_srednia(x,N,Skip,Len)

m = 0;

for k = 1:Len

m = m+x(k+Skip);

end

m = m / Len;

>>m = wart_srednia (x, N, 10, 20);

Wartość średnia =1.8874e-016

Wartość średnia dla fp=50.

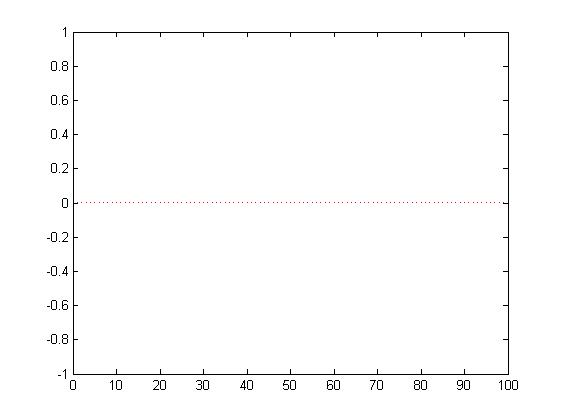
Wartośćśredniadlafp=300.

2. Wartośćchwilowasygnałusinusoidalnego.

Kod:

function [m] = chwilowa_w_srednia(x,N,Len)

for i = 1:Len-1

a = 0;

for k = 1:i-1

a = a + x(k);

end;

m(i) = a / i;

end;

for i = Len:N

a = 0;

for k = i-Len+1:i

a = a + x(k);

end

m(i) = a / Len;

end;

dla k=5

Dla k=15

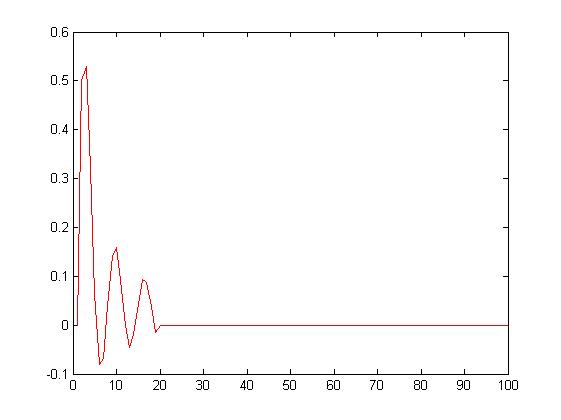
3. Bieżąca wartość średnia sygnału sinusoidalnego.

Kod:

function [m] = biezaca_w_srednia (x, N, alfa)

if (alfa< 0.0 || alfa> 1.0)

error('nieprawidłowaalfa')

end

m(1) = x(1);

for i = 2:N

m(i) = alfa * m(i-1) + (1-alfa) * x(i);

end;

dla alfa= 0,0

d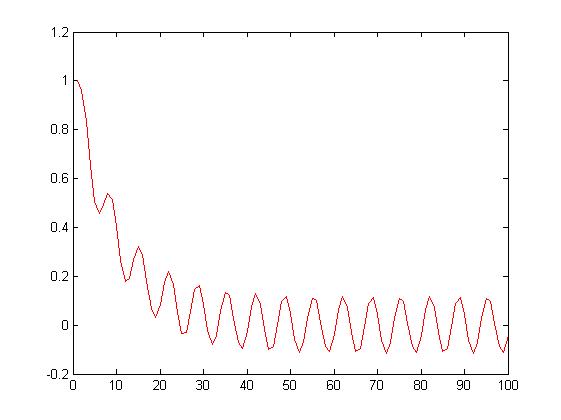
la alfa= 0,5

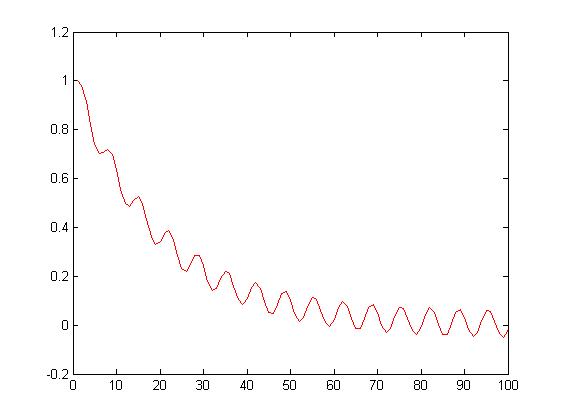
dla alfa= 0,95

4. Wariancja sygnału sinusoidalnego.

Kod:

function v = war (x,N,Skip,Len)

if (Skip+Len> N)

error('Skip+Lenwieksze od dlugoscisygnalu')

end

m = 0;

for k = 1:N

m = m + x(k);

end

m = m / N;

v = 0;

for k = 1:Len

v = v + (x(k+Skip)-m)^2;

end

v = v / Len;

disp(['wariancja wynosi ', num2str(v)])

wariancja = 0.5 ; fp=100

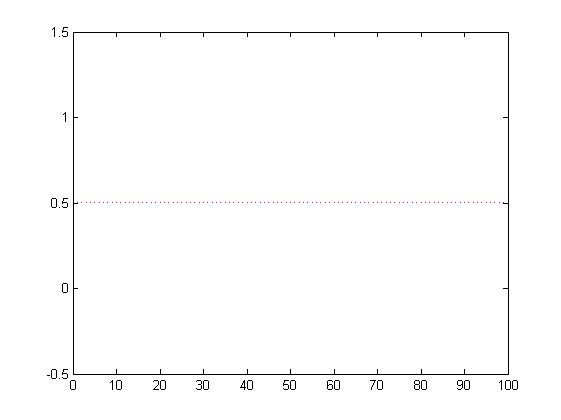
wariancja = 0.5 ; fp=300

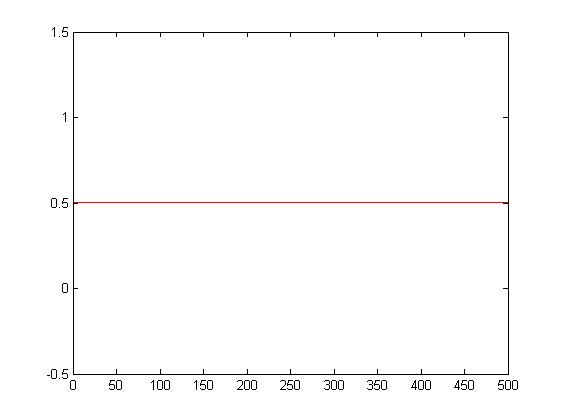
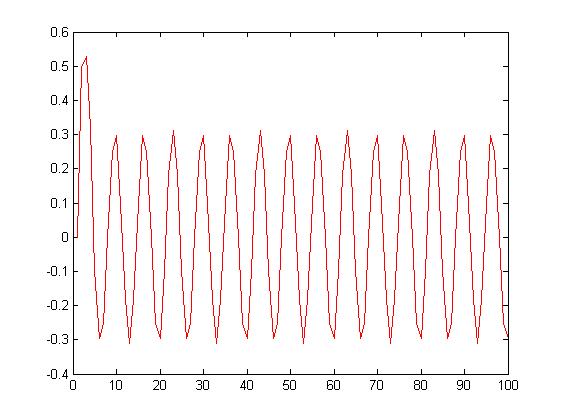
5. Wariancja chwilowa sygnału sinusoidalnego.

Kod:

function [v] = chwilowa_wariancja (x, N, Len)

if (Len > N)

error('Len wieksze od dł. sygnalu')

end

m = 0;

for k = 1:i-1

m = m + x(k);

end

m = m / i;

a = 0;

for k = 1:i-1

a = a + (x(k)-m)^2;

end;

v(i) = a / i;

end;

m = 0;

for k = i-Len+1:i

m = m + x(k);

end

m = m / Len;

a = 0;

for k = i-Len+1:i

a = a + (x(k)-m)^2;

end

v(i) = a / Len;

end;

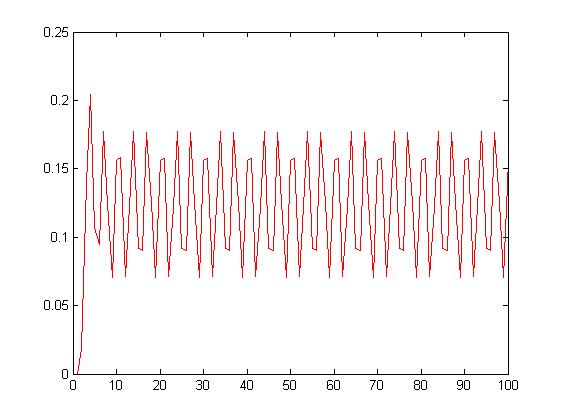
dla Len = 5

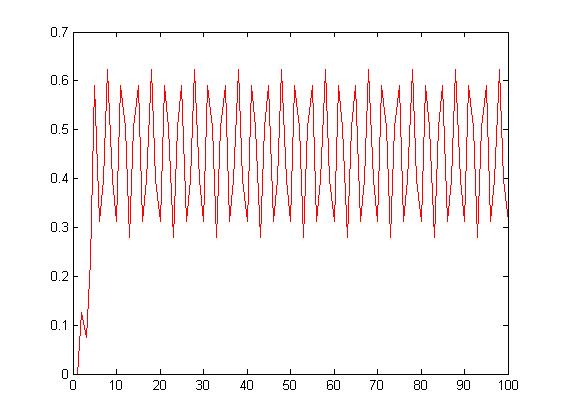
dla Len = 15

6. Bieżąca wariancja sygnału sinusoidalnego.

Kod:

function [v] = biezaca_wariancja (x, N, alfa)

if (alfa < 0.0 || alfa > 1.0)

error('Nieprawidłowa alfa')

end

m = x(1);

v(1) = (x(1)-m)^2;

for i = 2:N

m = alfa * m + (1-alfa) * x(i);

v(i) = alfa * v(i-1) + (1-alfa) * (x(i)-m)^2;

end;

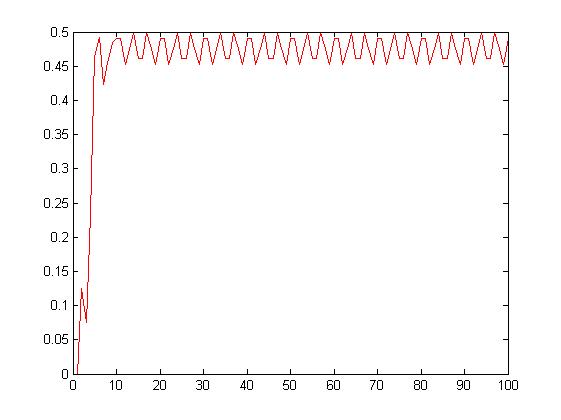
dla alfa = 0,5

dla alfa = 1

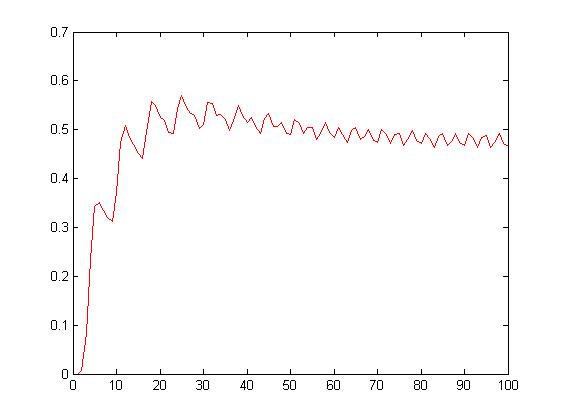
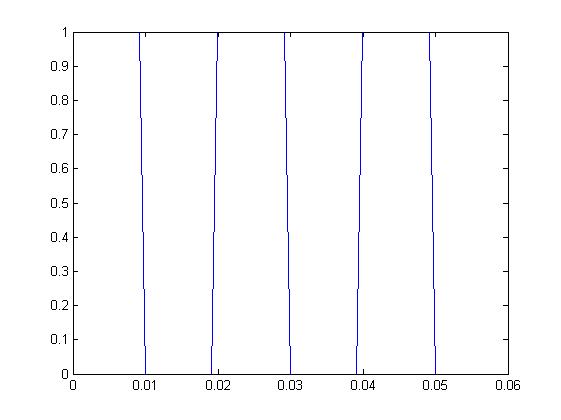
2. Sygnał prostokątny.

1. Wartośćśredniasygnałuprostokątnego

Kod:

>> length(x);

ans =72

>> N=1000

N =1000

>> m = wart_srednia (x, N, 0, 72);

wartoscsrednia = 0.5

2. Chwilowa wartość średnia sygnału prostokątnego.

dla N=50, Len=20

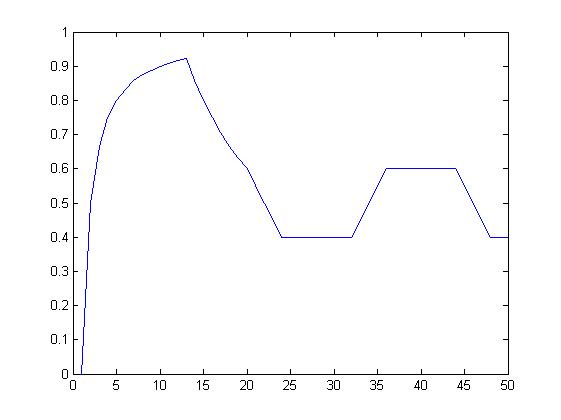
dla N= 40, Len= 10

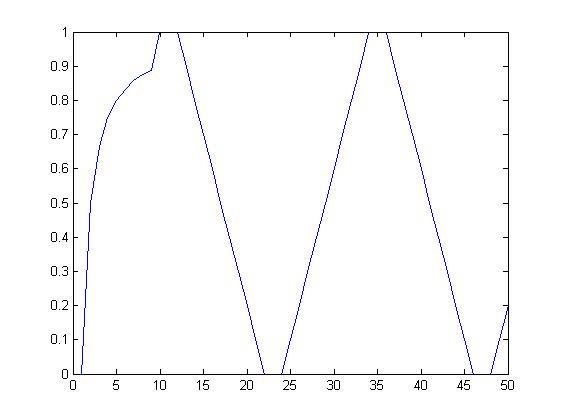
3. Bieżąca wartość średnia sygnału prostokątnego.

dla alfa= 0,5 dla alfa= 0,90

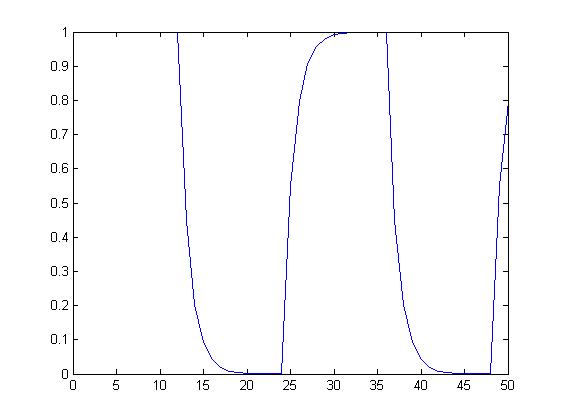
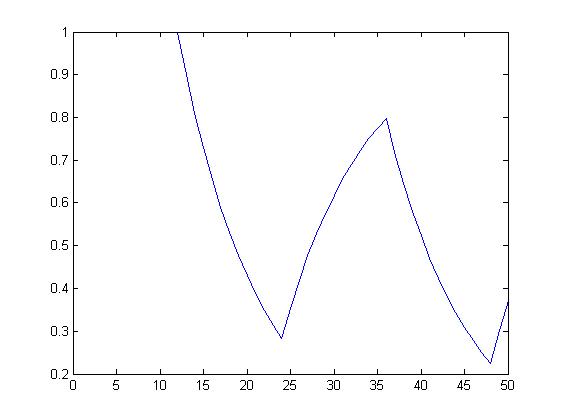
4. Wariancja sygnału prostokątnego.

Kod:

Dla N=50;

>> v = wariancja (x, N, 10, 10);

wariancja wynosi 0.2624

Dla N=25;

>> v = wariancja (x, N, 10, 10);

wariancja wynosi 0.2624

5. Wariancja chwilowa sygnału prostokątnego.

dla Len= 5 dla Len= 10

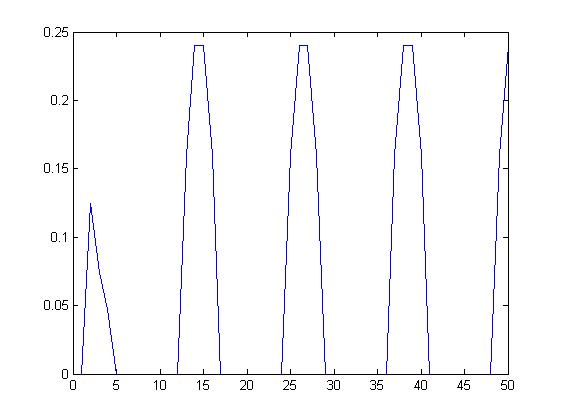
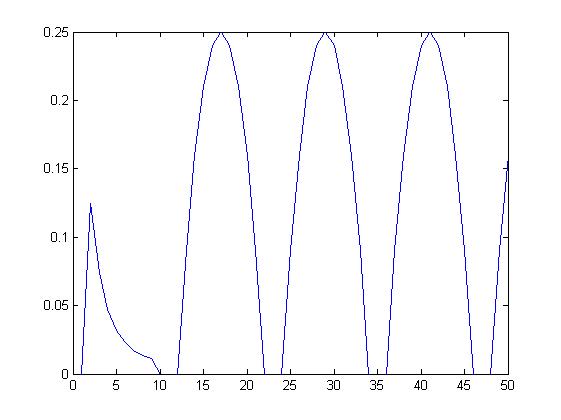
6. Bieżąca wariancja sygnału prostokątnego.

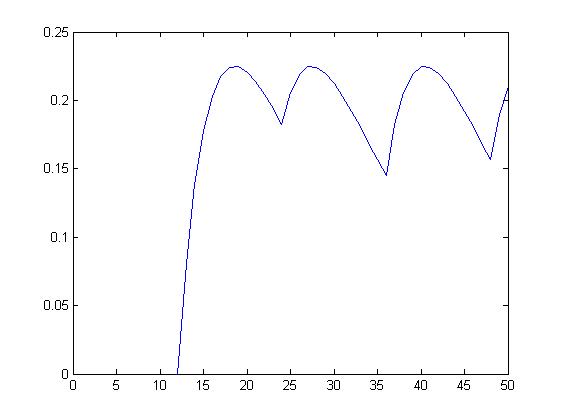
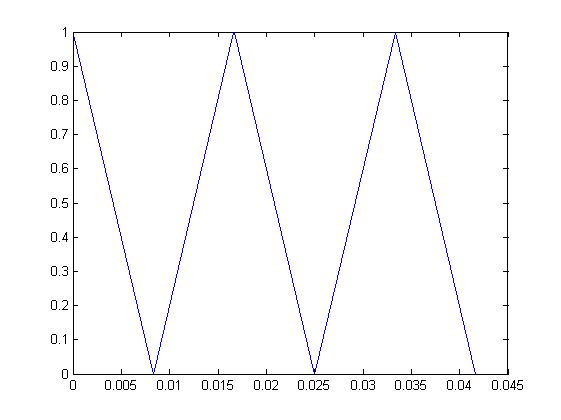
3. Sygnał trójkątny.

1. Wartość średnia sygnału trójkątnego.

>> N=120

>> m = wart_srednia (x, N, 0, 61);

wartoscsrednia wynosi 0.4918

2. Chwilowa wartość średnia sygnału trójkątnego.

dla Len= 15 dla Len= 20

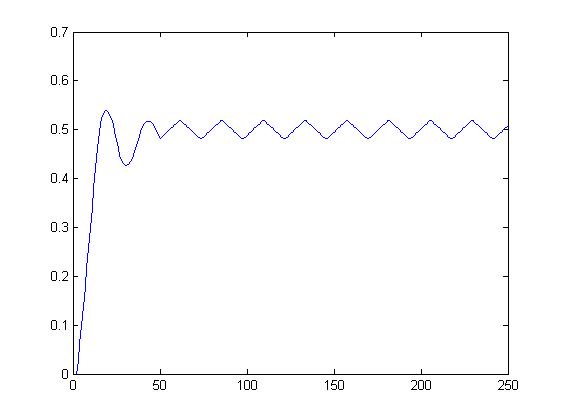
3. Bieżąca wartość średnia sygnału trójkątnego: N=100

dla alfa= 0,45 dla alfa= 1

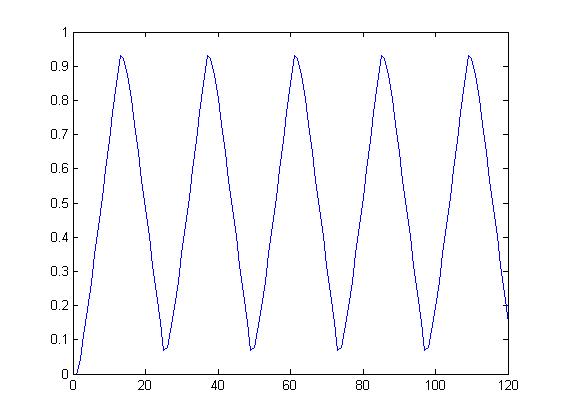
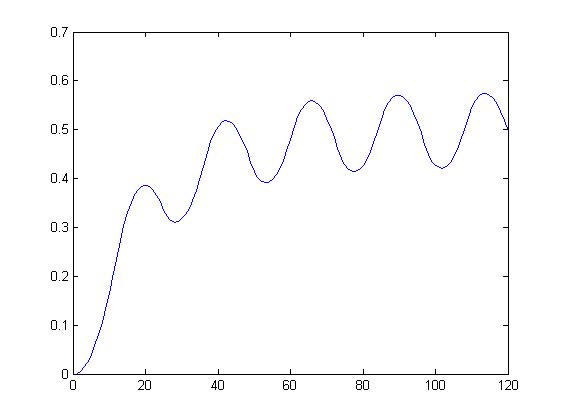
>> N=100;

>> v = wariancja (x, N, 10, 20);

wariancja wynosi 0.096528

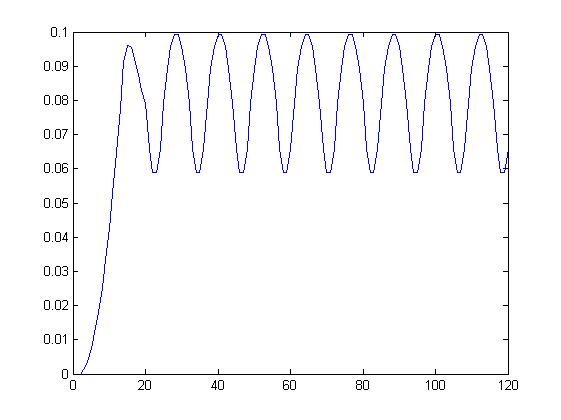
4. Wariancja chwilowa sygnału trójkątnego.

dla Len = 20

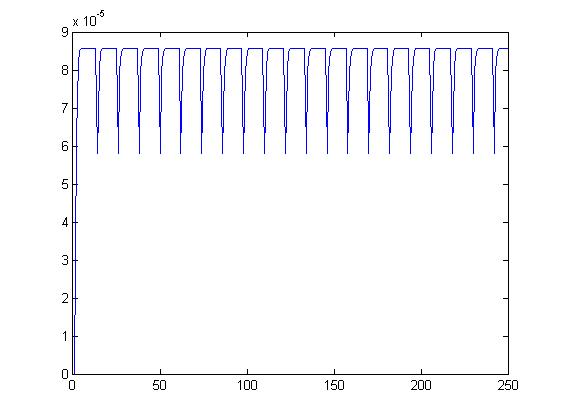
5. Wariancja bieżąca sygnału trójkątnego.

dla alfa= 0,1 dla alfa= 1

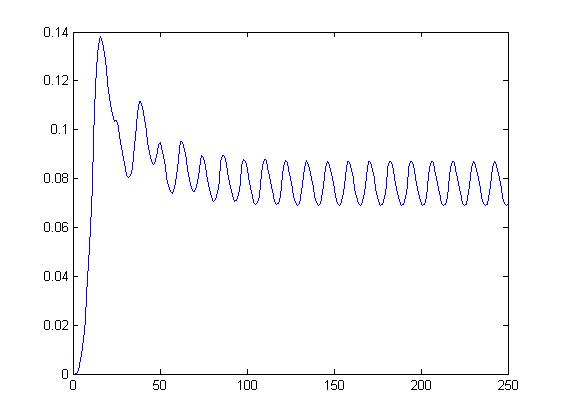
dla alfa= 0 dla alfa= 0,5

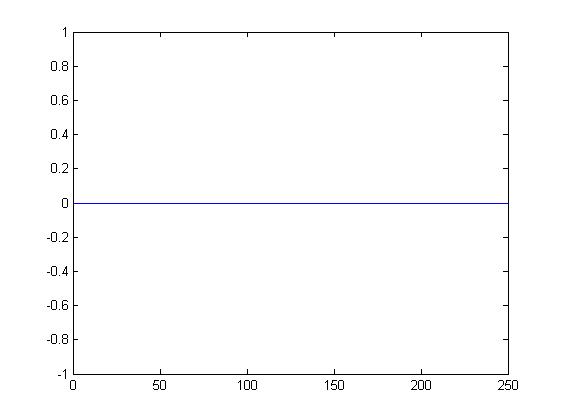
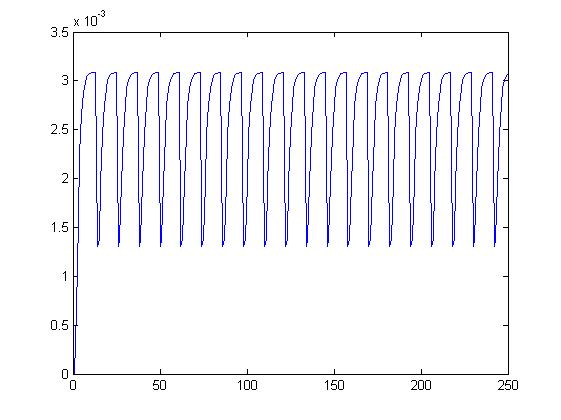
4. Wnioski.

• W przypadku wpływu alfa na wariancję można zauważyć, iż wykres przechodził z prostej linii poprzez mocne oscylacje (np. alfa=0.4) aż do dosyć spokojnych (np. alfa 0.9 ) przez co można dostrzec iż wykres się wygładził.

• Wpływ skoku miał znaczenia iż w przypadku zmniejszania go sygnał wykazywał tendencję do wygładzania- im mniejszy skok tym wykres był bardziej wygładzony.

• Długość sygnału nie miała żadnego znaczenia na wynik średniej ponieważ był on zwracany taki sam.

• Wpływ alfa na sygnał w przypadku średniej był już dosyć znaczący i łatwo go zauważyć – w przypadku zwiększania alfa od 0 do 0.9 można zaobserwować jak sygnał z dosyć mocno usianego oscylacjami przechodzi w bardzo rzadkie, w porównaniu do stanu wejściowego niemal bardzo łagodne.

• W przypadku wariancji zwiększanie długości sygnału również nie miało znaczenia ponieważ zwracana wariancja była taka sama. Wpływ skoku w przypadku wariancji – zwiększanie go skutkowało wygładzeniem oscylacji.

Strona 13 z 13