54 Â

WIAT

N

AUKI

Kwiecieƒ 1998

W

czasach, kiedy niektórzy eks-
perci przepowiadajà koniec
nauki, poniewa˝ dokonano

ju˝ wszystkich wa˝nych odkryç, war-
to podkreÊliç, ˝e wcià˝ jeszcze nie uda-
∏o si´ pogodziç ze sobà dwóch filarów
XX-wiecznej fizyki, czyli mechaniki
kwantowej i ogólnej teorii wzgl´dnoÊci
Einsteina. Ogólna teoria wzgl´dnoÊci jest
sprzeczna z regu∏ami mechaniki kwan-
towej, które rzàdzà zachowaniem czà-
stek elementarnych, natomiast zacho-
wanie czarnych dziur podwa˝a fun-
damenty mechaniki kwantowej. Musi
z tego wyniknàç coÊ wielkiego. Ta sytu-
acja sprawia, ˝e przysz∏oÊç rysuje si´
mniej ponuro, ni˝ by to wynika∏o z prze-
powiedni milenijnych Jeremiaszy; w rze-
czywistoÊci stoimy w obliczu kolejnej re-
wolucji naukowej.

Jeszcze do niedawna fizycy dà˝àcy do

po∏àczenia mechaniki kwantowej z teo-
rià grawitacji i opisania wszystkich od-
dzia∏ywaƒ elementarnych najwi´ksze
nadzieje pok∏adali w teorii strun – jedno-
wymiarowych obiektów, których ró˝ne
typy drgaƒ reprezentujà czàstki elemen-
tarne. W ciàgu ostatnich dwóch lat teo-
ria strun zosta∏a w∏àczona do tzw. M-teo-
rii. Jak powiedzia∏ guru teorii strun
(a wed∏ug tygodnika Life szósty najbar-
dziej wp∏ywowy Amerykanin pokolenia
wy˝u demograficznego) Edward Witten
z Institute for Advanced Study w Prin-
ceton (New Jersey): „M oznacza magi´,
misterium lub membran´, wedle gustu.”

1

Ostatnio ka˝dy dzieƒ przynosi kolejne
dowody przemawiajàce za tà teorià. Ma-
my obecnie do czynienia z najbardziej
podniecajàcym okresem w rozwoju teo-
rii strun od czasów, kiedy po raz pierw-
szy pojawi∏y si´ one na fizycznej scenie.

M-teoria, podobnie jak teoria strun,

opiera si´ na idei supersymetrii. Fizycy
dzielà czàstki na dwie klasy, zale˝nie
od ich w∏asnego momentu p´du, czyli
spinu. Supersymetria wymaga, aby ka˝-
dej znanej czàstce o spinie ca∏kowitym
– 0, 1, 2 itd. (w jednostkach kwantowych)
– odpowiada∏a czàstka majàca takà sa-
mà mas´ oraz spin po∏ówkowy (

1

/

2

,

3

/

2

,

5

/

2

itd.) i vice versa.

Niestety, dotychczas nie uda∏o si´ wy-

kryç takich superpartnerów znanych czà-
stek. Supersymetria, jeÊli w ogóle istnie-
je, musi byç z∏amana, co powoduje, ˝e
postulowane czàstki nie majà takiej sa-
mej masy jak czàstki znane – sà zbyt ma-
sywne, aby mo˝na je by∏o zaobserwowaç
w doÊwiadczeniach prowadzonych za
pomocà istniejàcych obecnie akcelerato-
rów. Mimo to teoretycy zachowali wia-
r´ w supersymetri´ z jednego powodu:
dostarcza ona teoretycznego schematu,
który byç mo˝e pozwoli na po∏àczenie
oddzia∏ywaƒ s∏abych, elektromagnetycz-
nych i silnych z najbardziej nieuchwyt-
nà ze wszystkich si∏ – grawitacjà.

Operacje supersymetrii przekszta∏cajà

wspó∏rz´dne przestrzeni i czasu w ten
sposób, ˝e prawa fizyki majà takà samà
postaç dla wszystkich obserwatorów.
Z warunku tego wynika ogólna teoria
wzgl´dnoÊci, a zatem supersymetria wià-
˝e si´ z istnieniem grawitacji. W rzeczy-
wistoÊci supersymetria prowadzi do „su-
pergrawitacji”, w której czàstka o spinie
2, czyli grawiton, przenosi oddzia∏ywa-
nia grawitacyjne. Superpartnerem gra-
witonu jest grawitino, majàce spin

3

/

2

.

Z konwencjonalnej grawitacji nie wy-

nikajà ˝adne ograniczenia na liczb´
wymiarów czasoprzestrzeni – odpo-
wiednie równania mo˝na w zasadzie
sformu∏owaç w czasoprzestrzeni o do-
wolnej liczbie wymiarów. Inaczej jest

w przypadku supergrawitacji – maksy-
malna dopuszczalna liczba wymiarów
czasoprzestrzeni wynosi 11. Znany nam
WszechÊwiat ma, rzecz jasna, trzy wy-
miary przestrzenne: d∏ugoÊç, szerokoÊç
i wysokoÊç, czas zaÊ stanowi czwarty
wymiar czasoprzestrzeni. Jednak w po-
czàtkach lat dwudziestych niemiecki fi-
zyk Theodore Kaluza i Szwed Oskar
Klein zasugerowali, ˝e czasoprzestrzeƒ
mo˝e mieç piàty ukryty wymiar. Zgod-
nie z ich koncepcjà w dodatkowym wy-
miarze przestrzeƒ nie jest p∏aska, lecz
zwija si´ w okràg, dooko∏a którego mo-
gà krà˝yç fale kwantowe. Poniewa˝ wo-
kó∏ okr´gu musi si´ zmieÊciç ca∏kowita
liczba d∏ugoÊci fal, to ka˝da taka fala od-
powiada czàstce o innej energii. Energia
czàstek jest „skwantowana”, czyli przy-
biera dyskretne wartoÊci.

Obserwator ˝yjàcy w pozosta∏ych

czterech wymiarach widzi jednak zbiór
czàstek majàcych dyskretne ∏adunki,
a nie energie. W teorii Kaluzy i Kleina
kwant, czyli jednostka ∏adunku, zale˝y
od promienia okr´gu w piàtym wymia-
rze. W rzeczywistym Êwiecie ∏adunek
elektryczny jest skwantowany, przy
czym jego jednostkà jest ∏adunek elek-

Powrót teorii strun

W nowej Teorii Wszystkiego istotnà rol´ odgrywajà nie tylko struny,
ale równie˝ membrany i czarne dziury

Michael J. Duff

Â

WIAT

N

AUKI

Kwiecieƒ 1998 55

tronu e. Aby otrzymaç poprawnà war-
toÊç e, nale˝y przyjàç, ˝e promieƒ okr´-
gu jest bardzo ma∏y i wynosi 10

–33

cm.

To z powodu niezwykle ma∏ych roz-

miarów ludzie, a nawet atomy go nie po-
strzegajà. Jednak przyj´cie tej hipotezy
pozwala w jednolity sposób opisaç elek-
tromagnetyzm i grawitacj´ dzia∏ajàce
w czasoprzestrzeni czterowymiarowej.

W 1978 roku Eugene Cremmer, Ber-

nard Julia i Joel Scherk z Ècole Normale
Supérieure w Pary˝u zauwa˝yli, ˝e su-
pergrawitacja dopuszcza nie tylko sie-
dem dodatkowych wymiarów czaso-
przestrzeni, ale przyjmuje najbardziej
eleganckà postaç w 11-wymiarowej
czasoprzestrzeni (10 wymiarów prze-
strzennych i czas). Prawa obowiàzujà-
ce w znanym nam czterowymiarowym
wszechÊwiecie zale˝à wtedy od tego,
w jaki sposób sà zwini´te dodatkowe
wymiary ˆ la Kaluza i Klein. Dysponu-
jàc kilkoma dodatkowymi wymiarami,
fizycy mogli próbowaç wyprowadziç
nie tylko elektromagnetyzm, ale rów-
nie˝ silne i s∏abe oddzia∏ywania jàdrowe.
Z tego powodu wielu fizyków zaj´∏o si´
badaniem supergrawitacji w 11 wymia-
rach w nadziei, ˝e b´dzie to zunifiko-
wana teoria wszystkich oddzia∏ywaƒ.

W 1984 roku supergrawitacja zosta∏a

jednak brutalnie stràcona z piedesta∏u.
Wa˝nà cechà rzeczywistego Êwiata jest
brak symetrii mi´dzy prawà i lewà stro-
nà: prawa rzàdzàce s∏abymi oddzia∏y-
waniami wyglàdajà inaczej, gdy oglàda-
my dany proces w lustrze. (Na przyk∏ad
neutrino jest zawsze lewoskr´tne.) Jed-
nak jak podkreÊla∏ Witten i inni fizycy,
nie ma ˝adnego prostego sposobu, by
uzyskaç takà „skr´tnoÊç”, gdy nast´-

puje redukcja liczby wymiarów czaso-
przestrzeni z 11 do 4.

Miejsce supergrawitacji zaj´∏a teoria

superstrun w dziesi´ciu wymiarach.
Dominujàcà pozycj´ zdoby∏o pi´ç kon-
kurujàcych teorii nazwanych przez od-
wo∏anie si´ do ich matematycznej struk-
tury odpowiednio: teorià heterotycznà
E

8

3 E

8

, teorià heterotycznà SO(32) i

SO(32) typu I, typu IIA i IIB. (Struny ty-
pu I sà otwarte, czyli majà postaç seg-
mentu, natomiast pozosta∏e sà zamkni´-
te – tworzà p´tle.) Szczególnie obiecujàca
wydawa∏a si´ teoria heterotycznych strun
E

8

3 E

8

, poniewa˝ budzi∏a nadzieje na

wyjaÊnienie w∏aÊciwoÊci wszystkich czà-
stek i oddzia∏ywaƒ elementarnych,
w tym równie˝ ich skr´tnoÊci. Ponadto
w przeciwieƒstwie do supergrawitacji
superstruny wydawa∏y si´ prowadziç do
teorii grawitacji zgodnej z mechanikà
kwantowà. Te wszystkie zalety sprawi-
∏y, ˝e struny urzek∏y fizyków, a 11-wy-
miarowa supergrawitacja popad∏a w nie-
∏ask´. Ówczesny nastrój najlapidarniej
wyrazi∏ Murray Gell-Mann z California
Institute of Technology, mówiàc na pew-
nej konferencji: „Supergrawitacja w je-
denastu wymiarach. Eee!”

P-brany

Gdy jednak min´∏a poczàtkowa eu-

foria, pojawi∏y si´ wàtpliwoÊci. Po
pierwsze, wydaje si´, ˝e na gruncie tej
teorii, pos∏ugujàc si´ tradycyjnymi me-
todami matematycznymi, nie mo˝na
udzieliç odpowiedzi na wiele wa˝nych
pytaƒ, a zw∏aszcza dokonaç porównaƒ
teorii z doÊwiadczeniami. Rozstrzygni´-
cie tych problemów wymaga∏o zupe∏-

nie nowych metod obliczeniowych. Po
drugie, dlaczego istnieje pi´ç ró˝nych
teorii strun? JeÊli ktoÊ poszukuje Teorii
Wszystkiego, to niewàtpliwie nadmier-
ne bogactwo jest k∏opotliwe. Po trzecie,
jeÊli supersymetria dopuszcza istnienie
11 wymiarów, to dlaczego superstruny
zatrzymujà si´ na 10? Po czwarte i ostat-
nie, jeÊli wyobra˝amy sobie punktowe
czàstki jako ma∏e struny, to dlaczego nie
jako membrany, a mówiàc ogólniej, ja-
ko pewne p-wymiarowe obiekty nie-
uchronnie nazwane p-brany?

2

Podczas gdy wi´kszoÊç teoretyków m´-

czy∏a si´ z superspaghetti, niewielka gru-
pa entuzjastów nabra∏a apetytu na super-
ravioli. Czàstka punktowa majàca zero
wymiarów zakreÊla lini´ Êwiata w czaso-
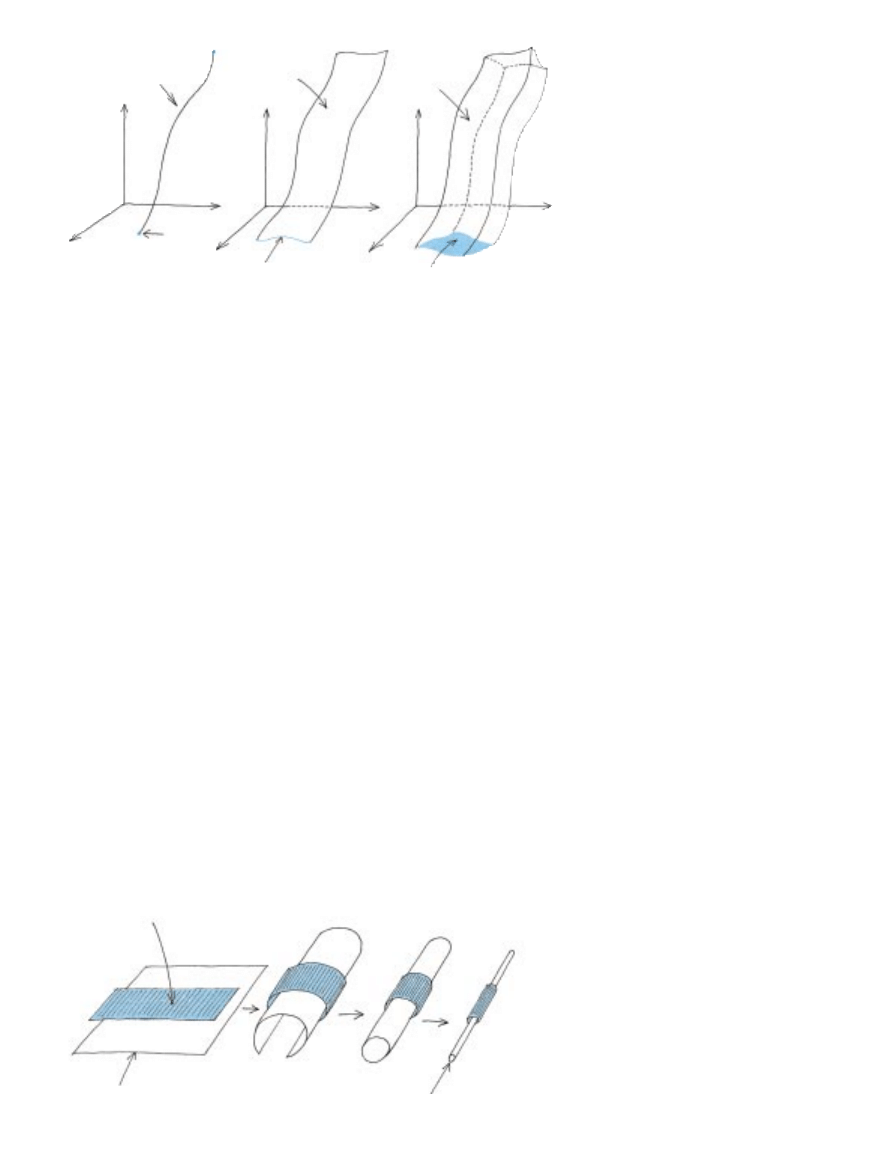
przestrzeni [ilustracja na nast´pnej stronie].
Struna majàca jeden wymiar (d∏ugoÊç) za-
kreÊla dwuwymiarowà powierzchni´
Êwiata, a membrana z dwoma wymiara-
mi (d∏ugoÊcià i szerokoÊcià) wytycza trój-
wymiarowà „obj´toÊç Êwiata”.

3

Ogólnie

mówiàc, p-brana zakreÊla p + 1 wymia-
rowà obj´toÊç Êwiata. (Rzecz jasna, musi
istnieç miejsce, w którym p-brana mog∏a-
by si´ poruszaç w czasoprzestrzeni, a za-
tem p + 1 nie mo˝e przekroczyç liczby
wymiarów czasoprzestrzeni.)

Ju˝ w 1962 roku Paul A. M. Dirac, je-

den z twórców mechaniki kwantowej,
skonstruowa∏ model wykorzystujàcy
membran´. Wysunà∏ mianowicie suge-
sti´, ˝e elektron nie jest czàstkà punkto-
wà, lecz maleƒkim bàblem, zamkni´tà
membranà. Oscylacje membrany mia∏y
jego zdaniem t∏umaczyç istnienie takiej
czàstki jak mion, bardziej masywnej od-
miany elektronu. Choç jego koncepcja si´
nie przyj´∏a, w istocie do dziÊ pos∏uguje-
my si´ podanym przez niego równaniem
membrany. Membrana mo˝e przyjàç po-
staç bàbla lub rozciàgaç si´ w dwóch wy-
miarach niczym pow∏oka z gumy.

Z supersymetrii wynikajà bardzo suro-

we ograniczenia na mo˝liwà liczb´ wy-
miarów p-bran. Eric Bergshoeff, tak˝e
z Rijksuniversitet Groningen, Ergin Se-
zgin obecnie pracujàcy w Texas A & M
University oraz Paul K.Townsend z Uni-
versity of Cambridge odkryli matema-
tycznie membran´ w przestrzeni 11-wy-
miarowej. Ma ona tylko dwa wymiary
i wyglàda jak pow∏oka. Paul S. Howe
z King’s College London, Takeo Inami
z Uniwersytetu w Kioto, Kellogg Stelle
z Imperial College w Londynie i ja zdo-
∏aliÊmy wykazaç, ˝e gdy jeden z 11 wy-
miarów czasoprzestrzeni jest zwini´ty
w okràg, to mo˝na raz owinàç membra-

WSZECHÂWIAT, ˚YCIE i wszystkie obiek-
ty mog∏y powstaç wskutek oddzia∏ywaƒ
mi´dzy strunami, bàblami i pow∏okami
w 11-wymiarowej czasoprzestrzeni.

DUSAN PETRICIC

n´ wokó∏ tego okr´gu, skleiç brzegi
i utworzyç rurk´. JeÊli promieƒ okr´gu
jest dostateczne ma∏y, to zwini´ta mem-
brana wyglàda jak struna w 10-wymia-
rowej czasoprzestrzeni; w ten sposób
otrzymujemy superstrun´ typu IIA.

Mimo tych rezultatów ortodoksyjni

zwolennicy strun ignorowali analiz´
membran. Na szcz´Êcie sytuacja uleg∏a
zmianie dzi´ki post´powi w dziedzinie
fizyki z pozoru zupe∏nie nie zwiàzanej
z membranami.

W 1917 roku niemiecka matematycz-

ka Amalie Emmy Noether wykaza∏a, ˝e
masa, ∏adunek i inne cechy czàstek ele-
mentarnych na ogó∏ podlegajà zasadom
zachowania z powodu istnienia pew-
nych symetrii. Na przyk∏ad zasada za-
chowania energii wynika z niezmienno-
Êci praw fizyki, czyli jest skutkiem
symetrii ze wzgl´du na przesuni´cia
w czasie. Z kolei zasada zachowania ∏a-
dunku bierze si´ z symetrii funkcji falo-
wej czàstek ze wzgl´du na zmian´ fazy.

Zdarza si´ jednak, ˝e pewne cechy

podlegajà zasadzie zachowania z powo-
du deformacji pól. W takich przypad-
kach mówimy o topologicznych zasa-
dach zachowania, poniewa˝ topologia
to dziedzina matematyki zajmujàca si´
kszta∏tem obiektów. Mo˝e si´ na przy-
k∏ad zdarzyç, ˝e linie pola tworzà w´-
ze∏, tzw. soliton, którego nie mo˝na wy-
g∏adziç. Z tego powodu soliton nie ulega
dysypacji i zachowuje si´ podobnie jak
czàstki. Klasycznym przyk∏adem takie-
go obiektu jest monopol magnetyczny

– pojedynczy biegun magnesu – które-
go wprawdzie nie zaobserwowano
w przyrodzie, ale który pojawia si´ nie-
kiedy w teoriach jako pewna splàtana
konfiguracja pól.

Zgodnie z tradycyjnym poglàdem

czàstki takie jak elektrony i kwarki (ma-
jàce ∏adunki wynikajàce z twierdzenia
Noether) uwa˝ane sà za elementarne,
a czàstki takie jak monopole (majàce ∏a-
dunki topologiczne) – za wtórne. Jed-
nak w 1977 roku Claus Montonen, obec-
nie pracujàcy w Helsiƒskim Instytucie
Fizyki, i David I. Olive z University of
Wales w Swansea wysun´li Êmia∏à hi-
potez´, ˝e istnieje alternatywne sformu-
∏owanie teorii fizycznych, w którym ro-
le ∏adunków Noether (takich jak ∏a-
dunek elektryczny) i ∏adunków topolo-
gicznych (takich jak ∏adunek magne-
tyczny) sà odwrócone. W takiej „dual-
nej” teorii monopole magnetyczne
by∏yby obiektami elementarnymi, a do-
brze znane kwarki, elektrony i inne
czàstki – solitonami.

Mówiàc ÊciÊlej, czàstka elementarna

z ∏adunkiem e by∏aby równowa˝na czà-
stce solitonowej z ∏adunkiem

1

/e. A po-

niewa˝ ∏adunek jest miarà si∏y oddzia-
∏ywaƒ, jeÊli zatem oryginalna czàstka
oddzia∏uje silnie (tzn. gdy e ma du˝à
wartoÊç), to monopol oddzia∏uje s∏abo,
i na odwrót.

Gdyby to przypuszczenie okaza∏o si´

trafne, pozwoli∏oby na ogromne mate-
matyczne uproszczenia. Na przyk∏ad
w teorii kwarków fizycy niewiele mo-

gà obliczyç, poniewa˝ kwarki oddzia-
∏ujà silnie. Wobec tego monopole w tej
teorii muszà oddzia∏ywaç s∏abo. Mo˝-
na sobie wyobraziç, ˝e wykonujemy
wszystkie rachunki w teorii dualnej
z elementarnymi monopolami i auto-
matycznie dostajemy odpowiednie wy-
niki dla kwarków, poniewa˝ teoria du-
alna daje takie same wyniki koƒcowe.

Niestety ta idea nie wzbudzi∏a wi´k-

szego zainteresowania. By∏ to klasycz-
ny problem jajka i kury. Dowiedzenie
hipotezy Montonena i Olive’a pozwo-
li∏oby wyjÊç daleko poza konwencjonal-
ne metody rachunkowe, ale dowód wy-
maga∏by innych metod obliczeniowych.

Jak si´ okaza∏o, p-brany równie˝ mo˝-

na uwa˝aç za solitony. W 1990 roku An-
drew Strominger z Institute for Theore-
tical Physics w Santa Barbara wykaza∏,
˝e soliton w teorii strun w dziesi´ciu
wymiarach to 5-brana. Opierajàc si´ na
moich wczeÊnejszych hipotezach, Stro-
minger zasugerowa∏, ˝e silnie oddzia-
∏ujàca struna jest dualnym odpowied-
nikiem s∏abo oddzia∏ujàcej 5-brany.

Dalszy rozwój koncepcji dualnoÊci

wymaga∏ pokonania dwóch powa˝nych
przeszkód. Po pierwsze, oryginalna hi-
poteza Montonena i Olive’a, zgodnie
z którà dualnoÊç mia∏a dotyczyç elek-
trycznoÊci i magnetyzmu w zwyk∏ej
czterowymiarowej czasoprzestrzeni, nie
zosta∏a wówczas jeszcze udowodniona,
a zatem dualnoÊç mi´dzy strunami i 5-
branami w dziesi´ciowymiarowej czaso-
przestrzeni opiera∏a si´ na jeszcze wà-
tlejszych podstawach. Po drugie, do
rozwiàzania pozosta∏y liczne problemy
kwantowej teorii 5-bran, a tym samym
równie˝ nowej dualnoÊci.

Pierwsza z tych przeszkód zosta∏a po-

konana, gdy Ashoke Sen z Instytutu Ba-
daƒ Podstawowych Tata w Bombaju wy-
kaza∏, ˝e w supersymetrycznych teoriach
muszà istnieç pewne solitony majàce
równoczeÊnie oba ∏adunki – elektryczny
i magnetyczny. O takich w∏aÊnie obiek-
tach mówi hipoteza Montonena i Olive’a.
Ten na pozór skromny wynik przekona∏

56 Â

WIAT

N

AUKI

Kwiecieƒ 1998

TRAJEKTORIA CZÑSTKI punktowej w
czasoprzestrzeni to tzw. linia Êwiata. Po-
dobnie struna lub membrana zakreÊla-
jà w czasoprzestrzeni odpowiednio po-
wierzchni´ lub obj´toÊç Êwiata.

JEDNOCZESNE KURCZENIE SI¢ membrany i wy-
miarów czasoprzestrzeni mo˝e spowodowaç po-
wstanie struny. Gdy przestrzeƒ, ukazana tutaj w po-
staci dwuwymiarowej powierzchni, zwija si´
i tworzy cylinder, membrana owija si´ wokó∏ cy-
lindra. Zwini´ty wymiar staje si´ tak ma∏ym okr´-
giem, ˝e dwuwymiarowa przestrzeƒ ostatecznie
wyglàda jak jednowymiarowa linia. Ciasno zwi-
ni´ta membrana przypomina wtedy strun´.

DUSAN PETRICIC

DUSAN PETRICIC

Czasoprzestrzeƒ

CZAS

CZAS

CZAS

PRZESTRZE¡

PRZESTRZE¡

PRZESTRZE¡

PRZESTRZE¡

PRZESTRZE¡

PRZESTRZE¡

LINIA ÂWIATA

Czàstka

POWIERZCHNIA ÂWIATA

Struna

OBJ¢TOÂå ÂWIATA

Membrana

Membrana

Czasoprzestrzeƒ

wielu sceptyków i spowodowa∏ lawin´
prac. W szczególnoÊci zainspirowa∏ Na-
thana Seiberga z Rutgers University
i Wittena, którzy rozpocz´li poszukiwa-
nia dualnoÊci w bardziej prawdopodob-
nych (choç nadal supersymetrycznych)
teoriach kwarków. Uzyskali oni liczne
nowe wyniki dotyczàce pól kwanto-
wych, o jakich jeszcze kilka lat temu trud-
no by∏o marzyç.

DualnoÊç dualnoÊci

W 1990 roku kilku teoretyków uogól-

ni∏o ide´ dualnoÊci Montonena i Oli-
ve’a na przypadek strun w czterowy-
miarowej czasoprzestrzeni. W takiej
teorii idea ta wydaje si´ jeszcze bardziej
naturalna. DualnoÊç t´, która pozostaje
jednak spekulatywnà koncepcjà, przyj´-
to okreÊlaç jako S-dualnoÊç.

W rzeczywistoÊci teoretycy strun ju˝

wczeÊniej przywykli do dualnoÊci zu-
pe∏nie innego rodzaju, tzw. T-dualno-
Êci. T-dualnoÊç to zwiàzek mi´dzy dwo-
ma rodzajami czàstek, które powstajà,
gdy struna tworzy p´tle w zwartych
wymiarach czasoprzestrzeni. Czàstki
pierwszego rodzaju (odpowiadajàce po-
ziomom energii strun zwiàzanym
z drganiami, czyli poziomom oscylacyj-
nym) sà analogiczne do czàstek przewi-
dzianych przez Kaluz´ i Kleina, to zna-
czy powstajà wskutek drgaƒ p´tli ze
struny [ilustracja na nast´pnej stronie]. Ta-
kie czàstki majà tym wi´kszà energi´,
im mniejsza jest p´tla. Struna mo˝e rów-
nie˝ utworzyç wiele zwojów wokó∏
okr´gu, podobnie jak gumka receptur-
ka wokó∏ nadgarstka; jej energia jest
wówczas tym wi´ksza, im wi´ksza licz-
ba zwojów i wi´kszy promieƒ okr´gu.
Ka˝dy poziom energii odpowiada wów-
czas nowej czàstce (takie poziomy na-
zwiemy poziomami nawini´cia).

Zgodnie z koncepcjà T-dualnoÊci

czàstki odpowiadajàce ró˝nej liczbie
zwojów struny wokó∏ okr´gu o promie-

niu R sà iden-

tyczne z czàstkami

powstajàcymi wskutek

drgaƒ struny tworzàcej okr´g

o promieniu

1

/

R

i vice versa. Z punktu

widzenia fizyka te dwa zbiory czàstek sà
nieodró˝nialne: gruby zwarty wymiar
czasoprzestrzeni daje takie same czàst-
ki jak cienki.

T-dualnoÊç pociàga za sobà wiele da-

leko idàcych konsekwencji. Przez dzie-
siàtki lat fizycy usi∏owali zrozumieç za-
chowanie natury w bardzo ma∏ych
skalach odleg∏oÊci zbli˝onych do d∏u-
goÊci Plancka, która wynosi 10

-33

cm. Za-

wsze przypuszczaliÊmy, ˝e znane nam
prawa fizyki za∏amià si´, gdy dotrzemy
do jeszcze mniejszych odleg∏oÊci. T-du-
alnoÊç sugeruje jednak, ˝e w takiej ska-
li wszechÊwiat wyglàda tak samo jak
w du˝ej. Mo˝na nawet wyobraziç so-
bie, ˝e gdyby wszechÊwiat skurczy∏ si´
do rozmiarów mniejszych od d∏ugoÊci
Plancka, to przekszta∏ci∏by si´ we
wszechÊwiat dualny, ten zaÊ powi´k-
sza∏by si´ w miar´ kurczenia si´ wszech-
Êwiata oryginalnego.

DualnoÊç mi´dzy strunami i 5-brana-

mi nadal by∏a tylko hipotezà, poniewa˝
do rozwiàzania pozosta∏ problem kwan-
tyzacji 5-bran. W 1991 roku zespó∏ z Te-
xas A & M w sk∏adzie Jianxin Lu, Ruben
Minasian, Ramzi Khuri i ja rozpoczà∏
prac´ nad tym zagadnieniem; uda∏o
nam si´ rozwiàzaç problem, po prostu
go omijajàc. JeÊli cztery z dziesi´ciu wy-
miarów ulegajà zwini´ciu i 5-brana owi-
ja si´ wokó∏ tych wymiarów, to powsta-
je jednowymiarowy obiekt – solitonowa
struna w szeÊciowymiarowej czasoprze-
strzeni. Ponadto elementarna struna
z 10-wymiarowej czasoprzestrzeni po-
zostaje taka równie˝ w czasoprzestrze-
ni szeÊciowymiarowej. Wobec tego kon-
cepcja dualnoÊci mi´dzy strunami i
5-branami ust´puje miejsca hipotezie

o dualnoÊci mi´dzy strunami solitono-
wymi i elementarnymi.

Przewaga takiego podejÊcia do pro-

blemu polega na tym, ˝e wiemy, jak
kwantowaç struny. Pozwala sprawdziç
hipotez´ dualnoÊci mi´dzy dwoma ro-
dzajami strun. Mo˝na na przyk∏ad wy-
kazaç w pe∏nej zgodnoÊci z pierwotnym
za∏o˝eniem, ˝e sta∏a sprz´˝enia oddzia-
∏ywaƒ strun solitonowych jest odwrot-
noÊcià sta∏ej sprz´˝enia oddzia∏ywaƒ
strun elementarnych.

W 1994 roku Christopher M. Hull

z Queen Mary and Westfield College
wraz z Townsendem wysun´li przy-
puszczenie, ˝e w szeÊciowymiarowej
czasoprzestrzeni s∏abo oddzia∏ujàce he-
terotyczne struny sà dualne w stosun-
ku do silnie oddzia∏ujàcych strun typu
IIA. W ten sposób zacz´∏y si´ kruszyç
bariery mi´dzy ró˝nymi teoriami strun.
Nast´pnie ja sam wpad∏em na to, ˝e du-
alnoÊç mi´dzy strunami przynosi jesz-
cze dodatkowe nieoczekiwane korzyÊci.
JeÊli zredukujemy czasoprzestrzeƒ sze-
Êciowymiarowà do czterowymiarowej,
zwijajàc jeszcze dwa wymiary, to ele-
mentarne i solitonowe struny zyskujà T-
dualnoÊç. I tu mamy do czynienia z cu-
dem: T-dualnoÊç struny solitonowej to
S-dualnoÊç struny elementarnej, i na od-
wrót. To zjawisko, w którym wymiana
∏adunków w jednym obrazie jest rów-
nowa˝na wymianie wymiarów w obra-
zie dualnym, zosta∏o nazwane dualno-
Êcià dualnoÊci. Dzi´ki niej poprzednia
spekulatywna koncepcja S-dualnoÊci zy-
ska∏a równie solidne podstawy jak do-
brze znana T-dualnoÊç. Na dodatek du-
alnoÊç dualnoÊci pozwala przewidzieç
si∏´ oddzia∏ywaƒ – ∏adunki sà teraz po-
wiàzane z rozmiarami niewidocznych
wymiarów. ¸adunek w jednym Êwiecie
mo˝e byç wymiarem w innym.

W niezwykle wa˝nym wyk∏adzie wy-

g∏oszonym w University of Southern Ca-
lifornia w 1995 roku Witten nieoczeki-
wanie zebra∏ wszystkie rezultaty uzyska-
ne w pracach na temat T-dualnoÊci, S-
dualnoÊci i dualnoÊci mi´dzy strunami
na gruncie jednej M-teorii w 11-wymia-
rowej czasoprzestrzeni. W ciàgu kilku

Â

WIAT

N

AUKI

Kwiecieƒ 1998 57

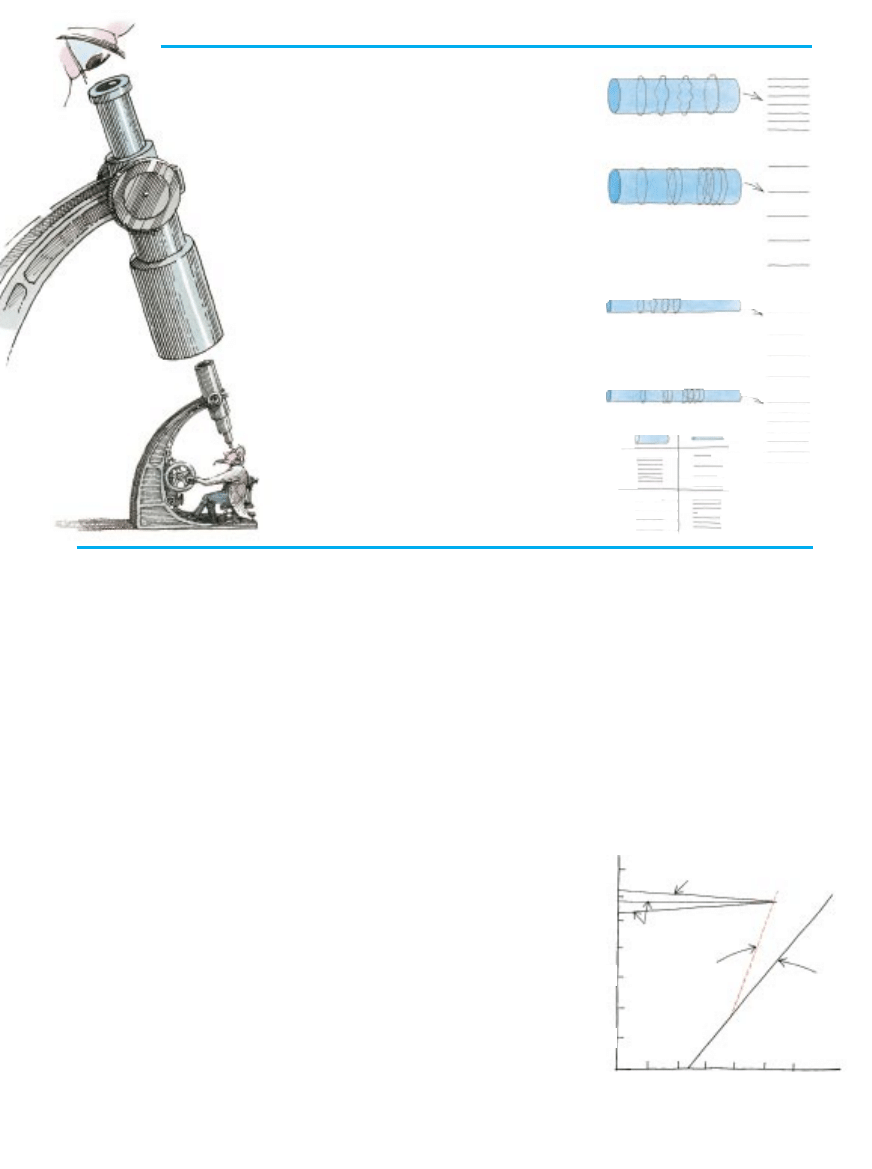
DODATKOWY WYMIAR zwini´-
ty w rurk´ daje mo˝liwoÊç wejrze-
nia w struktur´ czasoprzestrzeni.

LISTA BRAN wyst´pujàcych w czasoprze-
strzeniach o ró˝nej liczbie wymiarów. Mem-
brana zerowymiarowa to czàstka punkto-
wa; jednowymiarowa – to struna; dwu-
wymiarowa – pow∏oka lub bàbel. Niektóre
brany nie majà spinu (czerwony), ale brany
Dirichleta majà spin 1 (niebieski).

DUSAN PETRICIC

DUSAN PETRICIC

LICZBA WYMIARÓW MEMBRANY

LICZBA WYMIARÓ

W

CZASO

PRZESTRZENI

0

10

0

10

nast´pnych miesi´cy w Internecie poja-
wi∏y si´ dos∏ownie setki prac, które po-
twierdza∏y, ˝e niezale˝nie od tego, czym
w∏aÊciwie jest M-teoria, z pewnoÊcià
wa˝nà rol´ odgrywajà w niej membrany.

Nawet obiecujàca z fizycznego punk-

tu widzenia teoria strun E

8

3 E

8

, o któ-

rej sàdzono, ˝e jej skr´tnoÊci nie da si´
wyprowadziç z 11 wymiarów, ma swe
êród∏o w M-teorii. Witten wraz z Pe-
trem Horavà z Princeton University po-
kazali, w jaki sposób mo˝na zmniejszyç
dodatkowe wymiary w M-teorii, tak aby
otrzymaç odcinek. Zgodnie z ich teorià
mamy dwa 10-wymiarowe wszech-
Êwiaty (na obu koƒcach odcinka) po∏à-
czone 11-wymiarowà czasoprzestrze-
nià. Czàstki (i struny) istniejà tylko
w równoleg∏ych wszechÊwiatach na ich
koƒcach, które mogà si´ kontaktowaç
tylko za poÊrednictwem grawitacji.
(Mo˝na spekulowaç, ˝e ca∏a widzialna
materia le˝y na jednym koƒcu, „ciem-
na materia” zaÊ, która jak si´ przypusz-
cza, odpowiedzialna jest za istnienie nie-
widzialnej masy wszechÊwiata, znajduje
si´ na przeciwnym koƒcu.)

Z tego scenariusza wynikajà konse-

kwencje majàce du˝e znaczenie dla em-
pirycznej weryfikacji M-teorii. Na przy-
k∏ad fizycy wiedzà, ˝e sta∏e sprz´˝enia
okreÊlajàce si∏´ oddzia∏ywaƒ mi´dzy
czàstkami zale˝à od ich energii. W teo-

riach supersymetrycznych sta∏e sprz´-
˝enia oddzia∏ywaƒ silnych, s∏abych
i elektromagnetycznych przybierajà ta-
kà samà wartoÊç, gdy energia czàstek
wynosi oko∏o 10

16

GeV. Ponadto sta∏e

sprz´˝enia sà wtedy prawie (ale nie do-
k∏adnie) równe bezwymiarowej liczbie
GE

2

, gdzie G to sta∏a grawitacji Newto-

na. Ta niemal ca∏kowita zgodnoÊç
dwóch niezale˝nych od siebie wielko-
Êci, która zapewne nie jest przypadkiem,
wymaga wyjaÊnienia; dla wielu fizyków
jest ona êród∏em frustracji.

W dziwacznej czasoprzestrzeni opi-

sanej przez Horav´ i Wittena mo˝na wy-
braç wielkoÊç jedenastego wymiaru
w taki sposób, by wszystkie cztery si∏y
spotka∏y si´ przy tej energii. Jest ona
znacznie mniejsza ni˝ energia Plancka
wynoszàca 10

19

GeV. WczeÊniej fizycy

przypuszczali, ˝e kwantowe efekty gra-
witacyjne stajà si´ znaczàce dopiero dla
czàstek o energiach Plancka. (Wed∏ug

mechaniki kwantowej du˝a energia
zwiàzana jest z niewielkimi odleg∏oÊcia-
mi. Energia Plancka to po prostu d∏u-
goÊç Plancka wyra˝ona w jednostkach
energii.) Wynika z tego, ˝e kwantowe
efekty grawitacyjne mogà pojawiaç si´
przy energiach czàstek znacznie bli˝-
szych energiom wyst´pujàcym w co-
dziennych procesach. Ten rezultat, któ-
rego wczeÊniej si´ nie spodziewano,
móg∏by mieç wiele istotnych konse-
kwencji kosmologicznych.

Niedawno Joseph Polchinsky z Insti-

tute for Theoretical Physics w Santa Bar-
bara zauwa˝y∏, ˝e niektóre p-brany sà
identyczne z pewnymi powierzchnia-
mi odkrytymi przez XIX-wiecznego nie-

58 Â

WIAT

N

AUKI

Kwiecieƒ 1998

DualnoÊç ma∏ych i du˝ych skal odleg∏oÊci

T

-dualnoÊç pozwala powiàzaç prawa fizyczne obowiàzujàce w du-
˝ych czasoprzestrzeniach z prawami rzàdzàcymi ma∏ymi czasoprze-

strzeniami. Wyobraêmy sobie zwini´tà czasoprzestrzeƒ jako cylinder.

Struna tworzàca p´tl´ wokó∏ cylindra ma dwa rodzaje poziomów ener-

gii. Pierwszy zbiór zwiàzany jest z falami na strunie, takimi, dla któ-

rych obwód cylindra stanowi ca∏kowità wielokrotnoÊç d∏ugoÊci fali;

poziomy te nazywamy poziomami oscylacyjnymi. JeÊli cylinder jest

gruby, d∏ugoÊç fal jest du˝a, a energia odpowiednio ma∏a. Dlatego

odleg∏oÊç mi´dzy poziomami energii ró˝niàcymi si´ o jednà d∏u-

goÊç fali jest niewielka – poziomy sà ciasno upakowane.

Struna mo˝e owinàç si´ wokó∏ cylindra niczym rozciàgni´ta

gumka, tworzàc wiele zwojów. JeÊli cylinder jest gruby, rozcià-

gni´cie struny wymaga du˝ej energii, a zatem energie stanów

odpowiadajàcych ró˝nej liczbie zwojów (poziomy nawini´cia)

sà od siebie oddalone.

Teraz przyjrzyjmy si´ poziomom energii dla cienkiego cy-

lindra. Fale, które pasujà do obwodu cylindra, majà ma∏à

d∏ugoÊç, a zatem odpowiednio du˝à energi´. Wobec tego

odleg∏oÊci mi´dzy poziomami drgaƒ sà du˝e. Natomiast

nawini´cie kolejnego zwoju nie wymaga du˝ej energii, tak

wi´c poziomy nawini´cia sà g´sto upakowane.

Obserwator z zewnàtrz nie mo˝e jednak zauwa˝yç

ró˝nic fizycznych mi´dzy stanami drgaƒ i nawini´cia.

Zarówno cienki, jak i gruby cylinder ostatecznie da-

jà taki sam uk∏ad poziomów energii, które interpre-

tujemy jako czàstki. Wobec tego ma∏a skala cien-

kiej czasoprzestrzeni mo˝e prowadziç do takich

samych praw fizycznych jak du˝a.

STA¸E SPRZ¢˚ENIA trzech oddzia∏ywaƒ
majà takà samà wartoÊç, gdy energia czà-
stek wynosi 10

16

GeV. Dotychczas uwa˝a-

no, ˝e grawitacja nie trafia w punkt prze-
ci´cia. Jednak obliczenia uwzgl´dniajàce
11-wymiarowà M-teori´ Êwiadczà, ˝e si∏a
grawitacji równie˝ dà˝y do tego samego
punktu. Wobec tego znalezienie jednolitej
teorii grawitacji i pozosta∏ych oddzia∏ywaƒ
mo˝e byç ∏atwiejsze ni˝ wczeÊniej sàdzono.

DUSAN PETRICIC

DUSAN PETRICIC

GRUBA RURKA

Poziomy

energii

Stany oscylacyjne

Stany nawini´cia

Drgania

Nawini´cia

Nawini´cia

CIENKA RURKA

Poziomy

energii

Poziomy energii

Drgania

Stany

oscylacyjne

Stany

nawini´cia

Grawitacja

(stara)

ST

A¸A SPRZ¢˚ENIA

ENERGIA

Silne

S∏abe

i elektromagnetyczne

Grawitacja (nowa)

10

0

10

–2

10

–4

10

–6

10

12

10

15

10

18

mieckiego matematyka Petera G. L. Di-
richleta. Czasami takie brany mo˝na
uwa˝aç za czarne dziury, a raczej czar-
ne brany – obiekty, z których nic, nawet
Êwiat∏o, nie mo˝e uciec.

Otwarte struny mo˝na zatem uwa˝aç

za kawa∏ki zamkni´tych strun, których
reszta pozostaje schowana za czarnymi
branami. To odkrycie pozwoli∏o na nowà
interpretacj´ czarnych dziur, zgodnie
z którà sà to przecinajàce si´ czarne bra-
ny owini´te wokó∏ siedmiu zwartych
wymiarów. Dzi´ki temu mo˝na mieç na-
dziej´, ˝e M-teoria wyjaÊni nawet para-
doksy czarnych dziur, które pojawi∏y si´
w wyniku badaƒ Stephena W. Hawkin-
ga z University of Cambridge.

W 1974 roku Hawking udowodni∏, ˝e

czarne dziury w rzeczywistoÊci nie sà
doskonale czarne, ale emitujà energi´.
W takim razie muszà mieç równie˝
entropi´, która mierzy nieuporzàdko-
wanie uk∏adu, zliczajàc jego stany kwan-
towe. Jednak mikroskopowe pochodze-
nie stanów kwantowych czarnej dziury
pozostawa∏o tajemnicà. Stosujàc techni-
k´ bran Dirichleta, Strominger i Cum-
run Vafa z Harvard University zdo∏ali
policzyç stany kwantowe czarnych bran.
Ich entropia zgadza si´ doskonale
z przewidywaniami Hawkinga, co mo˝-
na uznaç za kolejny sukces M-teorii.

Czarne brany stwarzajà równie˝ na-

dziej´ na rozwiàzanie jednego z najwi´k-
szych problemów teorii strun: wydaje
si´, ˝e istniejà miliardy ró˝nych sposo-
bów zgniecenia dziesi´ciu wymiarów
czasoprzestrzeni do czterech. To powo-
duje, ˝e istnieje wiele ró˝nych przewi-
dywaƒ, jak powinien zachowywaç si´
obserwowany Êwiat; inaczej mówiàc, nie
potrafimy przewidzieç jego zachowa-
nia. Okazuje si´ jednak, ˝e masa czarnej
brany mo˝e zniknàç, gdy kurczy si´
czarna dziura, wokó∏ której jest owini´-
ta brana. Zdumiewajàce, ˝e efekt ten ma
wp∏yw na czasoprzestrzeƒ – dzi´ki nie-
mu jedna czasoprzestrzeƒ z pewnà licz-
bà dziur (przypominajàca ser szwajcar-
ski) zmienia si´ w czasoprzestrzeƒ z innà
liczbà dziur, co jest sprzeczne z prawa-
mi klasycznej topologii.

JeÊli wszystkie czasoprzestrzenie sà

w ten sposób powiàzane, to znalezienie

w∏aÊciwej staje si´ ∏atwiejsze. Struna mo-
˝e ostatecznie wybraç czasoprzestrzeƒ
majàcà, powiedzmy, najmniejszà ener-
gi´. Jej oscylacje powodujà nast´pnie
powstanie znanych czàstek i oddzia∏y-
waƒ elementarnych, tzn. znanego nam
Êwiata.

10 do 11 – jeszcze nie za póêno

Mimo tych osiàgni´ç fizycy poznali

dopiero ma∏e fragmenty M-teorii i wcià˝
brakuje im jej ca∏oÊciowego obrazu.
Ostatnio Thomas Banks i Stephen H.
Shenker z Rutgers University wspólnie
z Willy Fischlerem z University of Texas
i Leonardem Susskindem ze Stanford
University zaproponowali Êcis∏à defini-
cj´ M-teorii. Ich teoria „macierzowa”
opiera si´ na nieskoƒczonej liczbie 0-
bran (tzn. czàstek punktowych). Wspó∏-
rz´dne tych czàstek nie sà zwyk∏ymi
liczbami, lecz nieprzemiennymi macie-
rzami (nieprzemiennoÊç oznacza, ˝e xy
nie jest równe yx). W tej teorii czaso-
przestrzeƒ jest obiektem rozmytym,
a wspó∏rz´dne nie sà zwyk∏ymi liczba-
mi, lecz macierzami.

Fizycy od dawna podejrzewali, ˝e po-

∏àczenie grawitacji, czyli geometrii cza-
soprzestrzeni, z mechanikà kwantowà
sprawi, i˝ poj´cie czasoprzestrzeni prze-
stanie byç dobrze okreÊlone, przynaj-
mniej dopóty, dopóki nie znajdziemy
nowej definicji. PodejÊcie macierzowe
wywo∏a∏o wielkie poruszenie, ale wy-

daje si´, ˝e nie powiedziano jeszcze
ostatniego s∏owa. Mamy nadziej´, ˝e
w ciàgu kilku lat dowiemy si´, czym jest
naprawd´ M-teoria.

Witten lubi sobie wyobra˝aç, jak mo-

g∏aby si´ rozwinàç fizyka na innej plane-
cie, gdzie wielkich odkryç, takich jak
ogólna teoria wzgl´dnoÊci, mechanika
kwantowa i supersymetria, dokonano
by w innej kolejnoÊci ni˝ na Ziemi. W
podobnym duchu chcia∏bym tu zasuge-
rowaç, ˝e na innych planetach, zamiesz-
kanych przez bardziej logicznych uczo-
nych, punktem wyjÊcia by∏aby teoria
w 11 wymiarach, z której nast´pnie wy-
prowadzono by teori´ strun w 10 wy-
miarach. Przyszli ziemscy historycy po-
wiedzà zapewne, ˝e w ciàgu ostatniego
dwudziestolecia XX wieku teoretycy by-
li niczym dzieci bawiàce si´ na pla˝y
i radujàce si´ z co g∏adszych kamyków
i ∏adniejszych muszelek, podczas gdy
wielki ocean M-teorii rozciàga∏ si´ przed
nimi niezbadany.

T∏umaczy∏

Piotr Amsterdamski

Przypisy t∏umacza:

1

W oryginale: Magic, Mystery or Membrane, co

nale˝a∏oby przet∏umaczyç: magia, tajemnica lub

membrana, gubiàc przy tym gr´ s∏ów.

2

„P-brane” fonetycznie trudno odró˝niç od okreÊle-

nia „pea-brain” oznaczajàcego mózg wielkoÊci ziar-

na grochu, co pozwala na cz´ste, a czasem ˝enujà-

ce ˝arty i kalambury nieprzet∏umaczalne na j´zyk

polski.

3

Ta terminologia jest nieuchronnà konsekwencjà

tradycyjnego terminu „linia Êwiata”. Chodzi oczy-

wiÊcie nie o lini´ Êwiata, lecz lini´ czàstki w Êwie-

cie, w czasoprzestrzeni. Podobnie z powierzchnià

Êwiata i obj´toÊcià Êwiata.

Â

WIAT

N

AUKI

Kwiecieƒ 1998 59

Informacje o autorze

MICHAEL J. DUFF prowadzi badania w dziedzinie zunifikowanych teo-

rii czàstek elementarnych, kwantowej grawitacji, supergrawitacji, super-

strun, supermembran i M-teorii. Otrzyma∏ stopieƒ doktora fizyki teore-

tycznej w Imperial College w Londynie w 1972 i objà∏ tam stanowisko

profesora w 1980 roku. W 1988 przeprowadzi∏ si´ do Stanów Zjednoczo-

nych, gdzie od 1992 roku pracuje w Texas A & M University. Jest rzecz-

nikiem British Scientist Abroad, grupy angielskich naukowców emigran-

tów, którzy wyst´pujà przeciw niedostatecznemu finansowaniu nauki

brytyjskiej i wynikajàcemu z tego drena˝owi mózgów. Jest cz∏onkiem

American Physical Society.

Literatura uzupe∏niajàca

THE MEMBRANE AT THE END OF THE UNIVERSE

. Michael Duff i Christine

Sutton, New Scientist, vol. 118, nr 1619, ss. 67–71, 30 VI 1988.

UNITY FROM DUALITY

. Paul Townsend, Physics World, vol. 8, nr 9,

ss.1–6, IX/1995.

TEORA WSZYSTKIEGO

. Madhusree Mukerjee, Âwiat Nauki, nr 3(55),

ss. 74–80, III/1996.

REFLECTIONS ON THE FATE OF SPACETIME

. Edward Witten, Physics To-

day, vol. 49, nr 4, ss. 24–30, IV/1996.

DUALITY, SPACETIME AND QUANTUM MECHANICS

. Edward Witten, Phy-

sics Today, vol. 50, nr 5, ss. 28–33, V/1997.

M-TEORIA w 11-wymiarowej czasoprzestrzeni prowadzi do pi´ciu teorii strun w 10 wy-
miarach. Gdy dodatkowy wymiar zwija si´ w okr´g, M-teoria daje superstrun´ typu IIA,
która jest zwiàzana ze strunà typu IIB przez T-dualnoÊç. JeÊli natomiast dodatkowy wymiar
kurczy si´ do odcinka, M-teoria redukuje si´ do obiecujàcej fizycznie teorii heterotycz-
nych strun E

8

3

E

8

. Taka struna jest zwiàzana z heterotycznà strunà SO(32) przez T-dual-

noÊç. Heterotyczne struny sà zwiàzane ze strunà SO(32) I typu relacjà dualnoÊci.

DUSAN PETRICIC

M

-TEORIA

TEORIE

STRUN

11-wymiarowa czasoprzestrzeƒ

10-wymiarowa czasoprzestrzeƒ

Typ

IIB

Typ
IIA

dualnoÊç

dualnoÊç

dualnoÊç

E

8

3

E

8

SO(32)

SO(32)

Typ I

HETEROTYCZNA

HETEROTYCZNA