KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Ćwiczenie 12
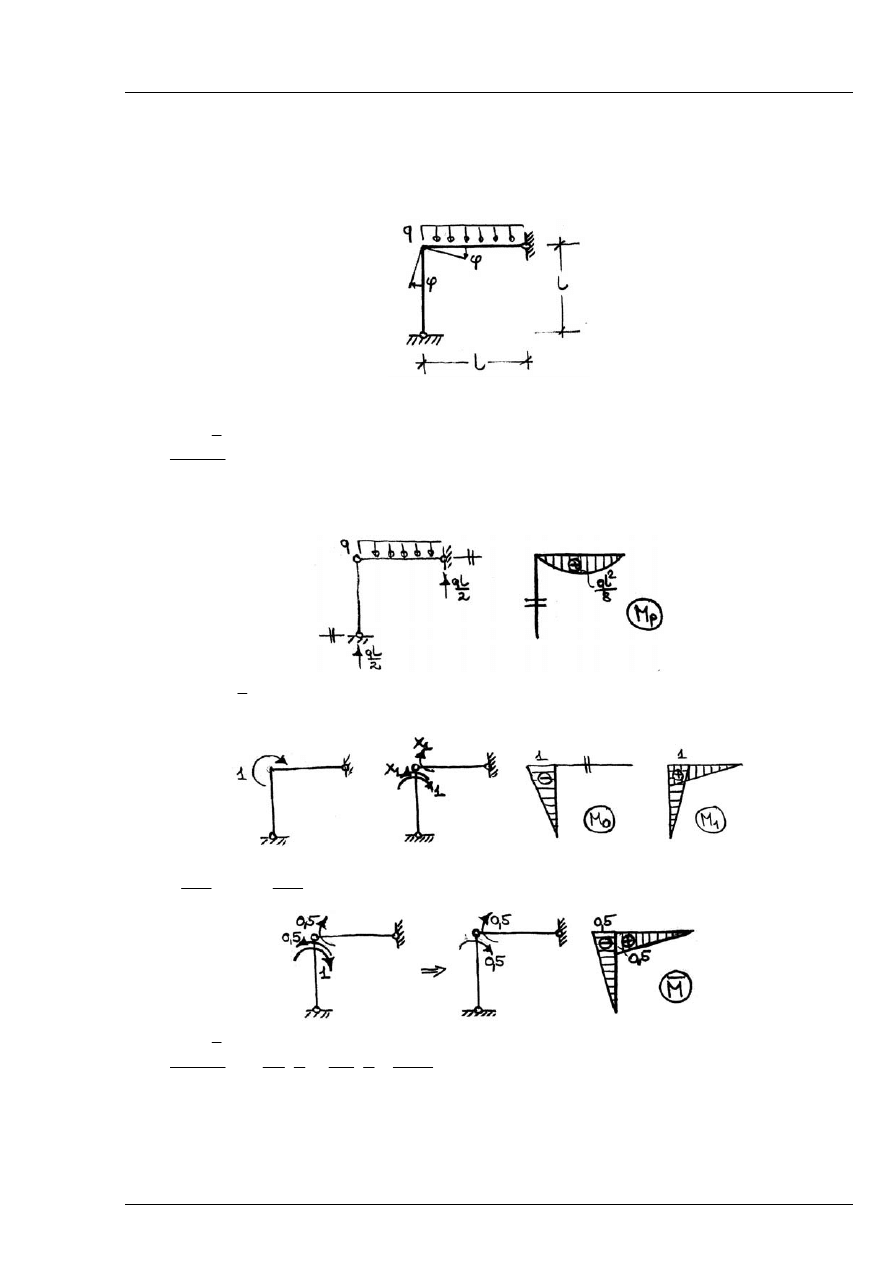
Zad. 12.1
Obliczyć kąt obrotu
ϕ
Rys. 12.1.1
Korzystamy z II twierdzenia redukcyjnego
p
L
M
M
ds
EI
ϕ
⋅
=
∫
(12.1)
Rozwiązanie
p
M - stan obciążenia zewnętrznego w układzie podstawowym metody sił:
Rys. 12.1.2
Rozwiązanie M - jednostkowe obciążenie wirtualne w układzie niewyznaczalnym – stosujemy
metodę sił
Rys. 12.1.3
10
11
1
2
,
0
3
3
l
l
X
EI
EI
δ
δ
= −
=
⇒
=
−
,5 [ ]
Rys. 12.1.4
2
3
1 2
3
8 4
48
p
L
M
M
ql
l
ql
ds
l
EI
EI
EI
ϕ
⋅
=
=
⋅ ⋅ ⋅
⋅ =
∫
C16-2005-cw12
94
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
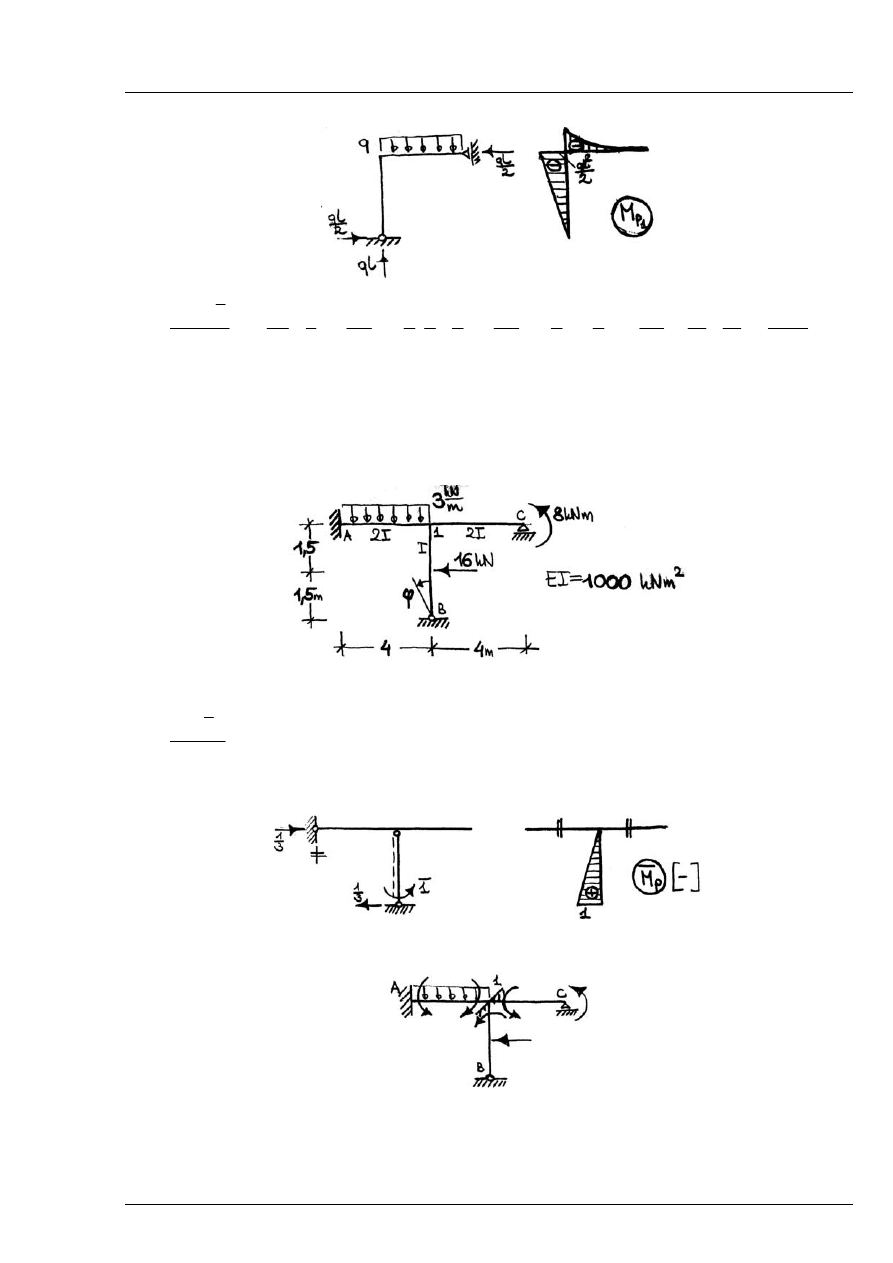
Inny układ podstawowy (ze stanem obciążenia zewnętrznego):
Rys. 12.1.5
2
2
3
1
1
1
3 1 1
2
1
1
1
3
2
4 2 2
2
3
2
16 12
48
p
L
M
M
ql
ql
ql
ql
ds
l
l
EI
EI
EI
EI
ϕ
⋅
⎡
⎤
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
=
=
⋅
⋅ −
⋅ ⋅ ⋅ + ⋅ −
⋅ ⋅ ⋅ −
=
−
+
=
⎢
⎥
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎣
⎦
∫
3
Zad. 12.2
Obliczyć kąt obrotu
ϕ
Rys. 12.2.1
Korzystamy z II twierdzenia redukcyjnego
p
L
M M
ds
EI
ϕ
⋅
=
∫
(12.2)
Jednostkowe obciążenie wirtualne w układzie podstawowym metody sił – wg rysunku:
Rys. 12.2.2
Obciążenie zewnętrzne w układzie niewyznaczalnym – rozwiązanie metodą przemieszczeń
(
1
g
n
)
=
Rys. 12.2.3
C16-2005-cw12
95
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
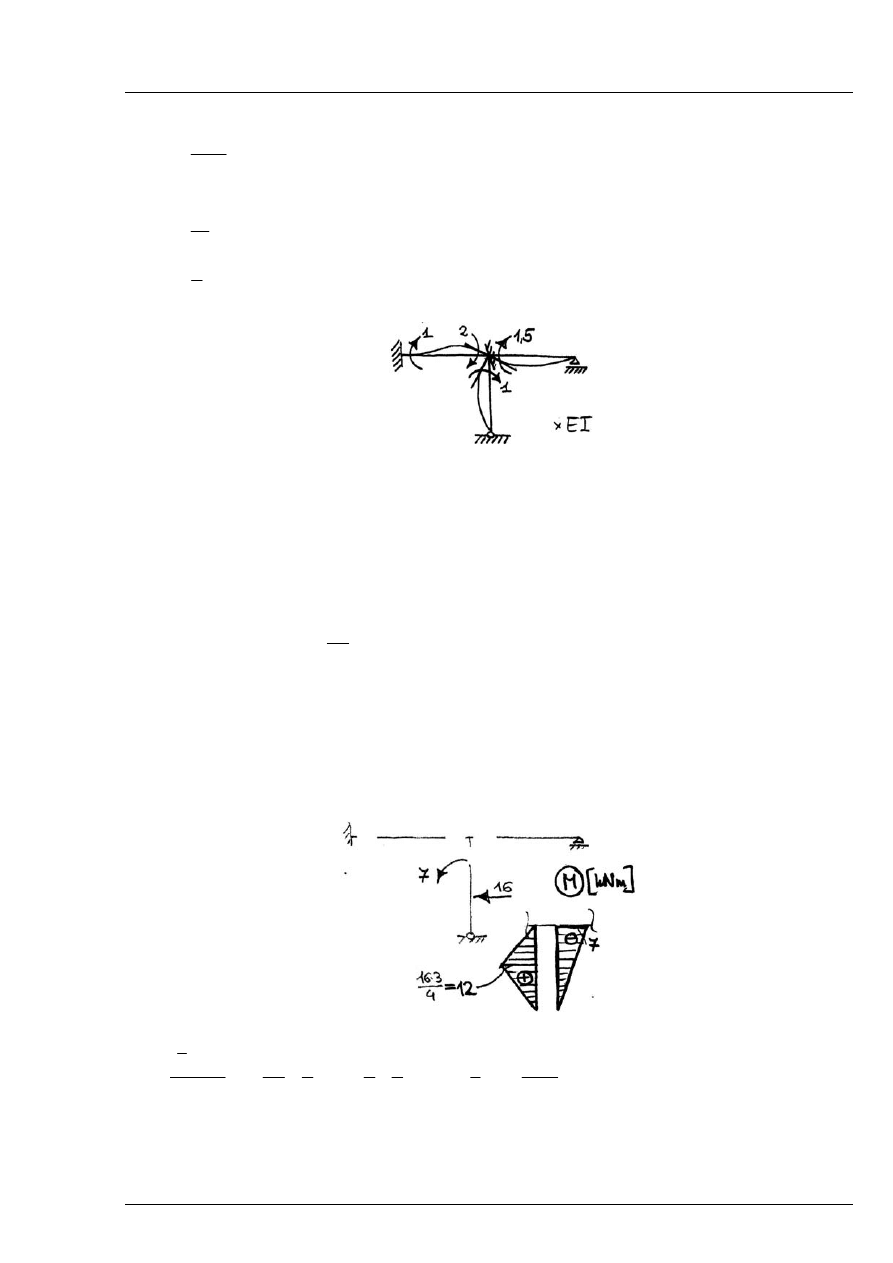
Momenty wyjściowe:
2
0
1
0
1
0
1
0
1
3 4
4 [
]
12
4 [
]
3
16 3
9 [
]
16
1
8
4 [
]
2
A
A
B
C
M
k
M
kNm
Nm
M
kNm
M
kN
⋅
= −
= −
=
= −
⋅ ⋅ = −
= − ⋅ = −
m
Sumaryczne momenty przywęzłowe:
Rys. 12.2.4
1
1
1
1
4
4 2
9
4 1,5
A
A
B
C
M
EI
M
EI
M
EI
M
EI
ϕ
ϕ
ϕ
ϕ
= − +
= +
= − +
= − +
Równanie równowagi:
1
1
1
1
0
2
9 4,5
0
A
B
C
M
M
M
M
EI
EI
ϕ
ϕ
Σ
=
+
+
=
− +
=
⇒
=
Wartości momentów przywęzłowych
1
1
1
1
4 2
2 [
]
4 4 8 [
]
9 2
7 [
]
4 3
1[
]
A
A
B
C
M
kNm
M
kNm
M
kNm
M
kNm
= − + = −
= + =
= − + = −
= − + = −
Potrzebny jest jedynie fragment wykresu M na odcinku 1 B
−
Rys. 12.2.4
( )
1
1
1 1
1
5,5
3 12
3
7
1
0,0055 [
] 18'55"
2
2 2
3
1000
p
L
M
M
ds
rad
EI
EI
ϕ
⋅
⎡
⎤
=
=
⋅
⋅ ⋅ ⋅ + ⋅ ⋅ − ⋅ ⋅ =
=
=
⎢
⎥
⎣
⎦
∫
C16-2005-cw12
96
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
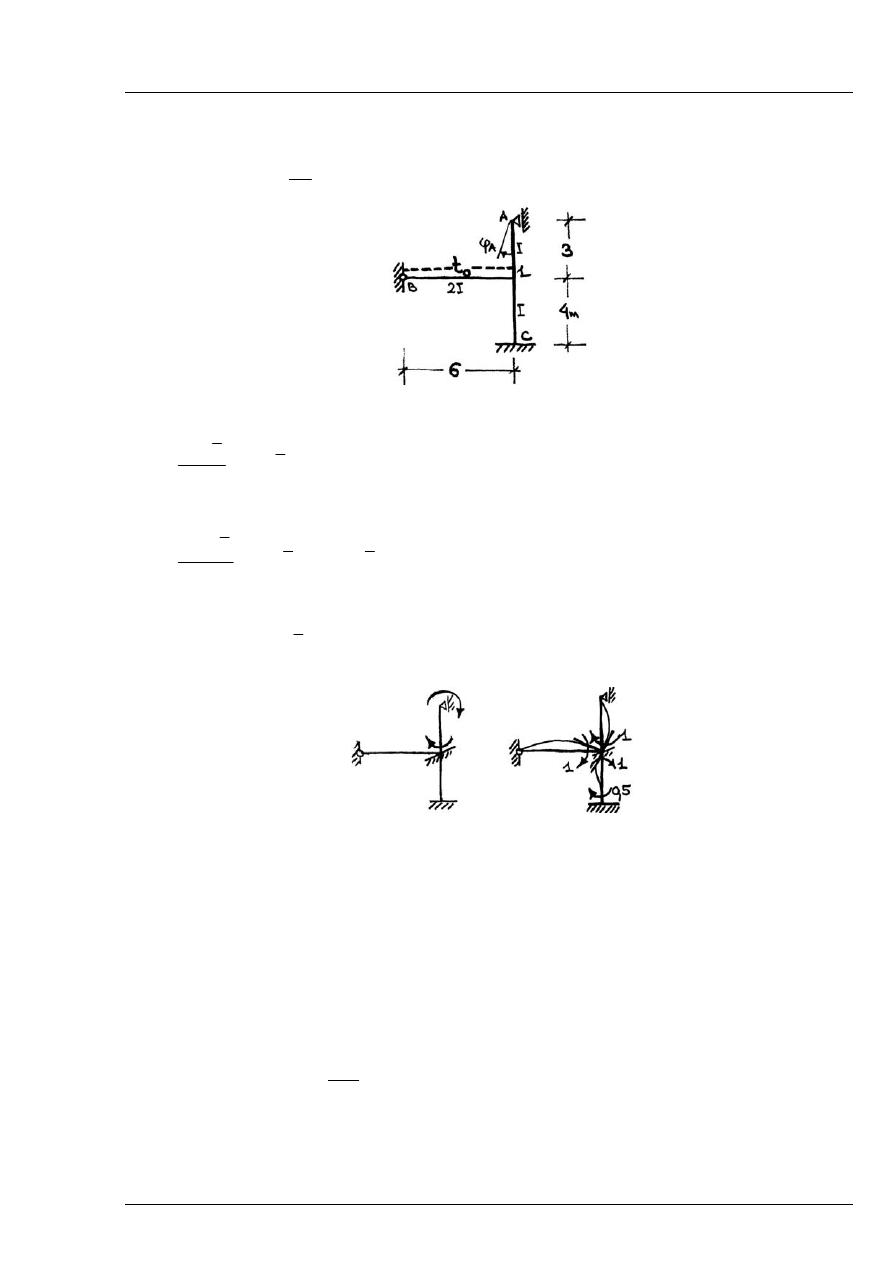
Zad. 12.3 (*zadanie dodatkowe)
Obliczyć kąt obrotu
A
ϕ
wywołany równomiernym ogrzaniem elementu B-1 o wielkość
5
0
1
24
,
10
o
t
o
t
C
C
α
−
=
=
Rys. 12.3.1
Z zasady prac wirtualnych wynika wzór:
0
A
L
L
M M
ds
N
t ds
EI
ϕ
⋅
=
+
∫
∫
t
α
(12.3)
Przy zastosowaniu I twierdzenia redukcyjnego dostajemy
0
0
(
p
A
t
t
L
L
L
M
M
ds
N t ds
N
t ds
M
EI
ϕ
α
α
⋅
=
+
=
∫
∫
∫
0)
p
= (12.4)
Należy rozwiązać układ wyjściowy (niewyznaczalny) z obciążeniem wirtualnym – potrzebna jest
jedynie siła normalna
1B
N
Metoda przemieszczeń (
1)
g
n
=
Rys. 12.3.2
Momenty wyjściowe:
0
1
0,5 [ ]
A
M
=
−
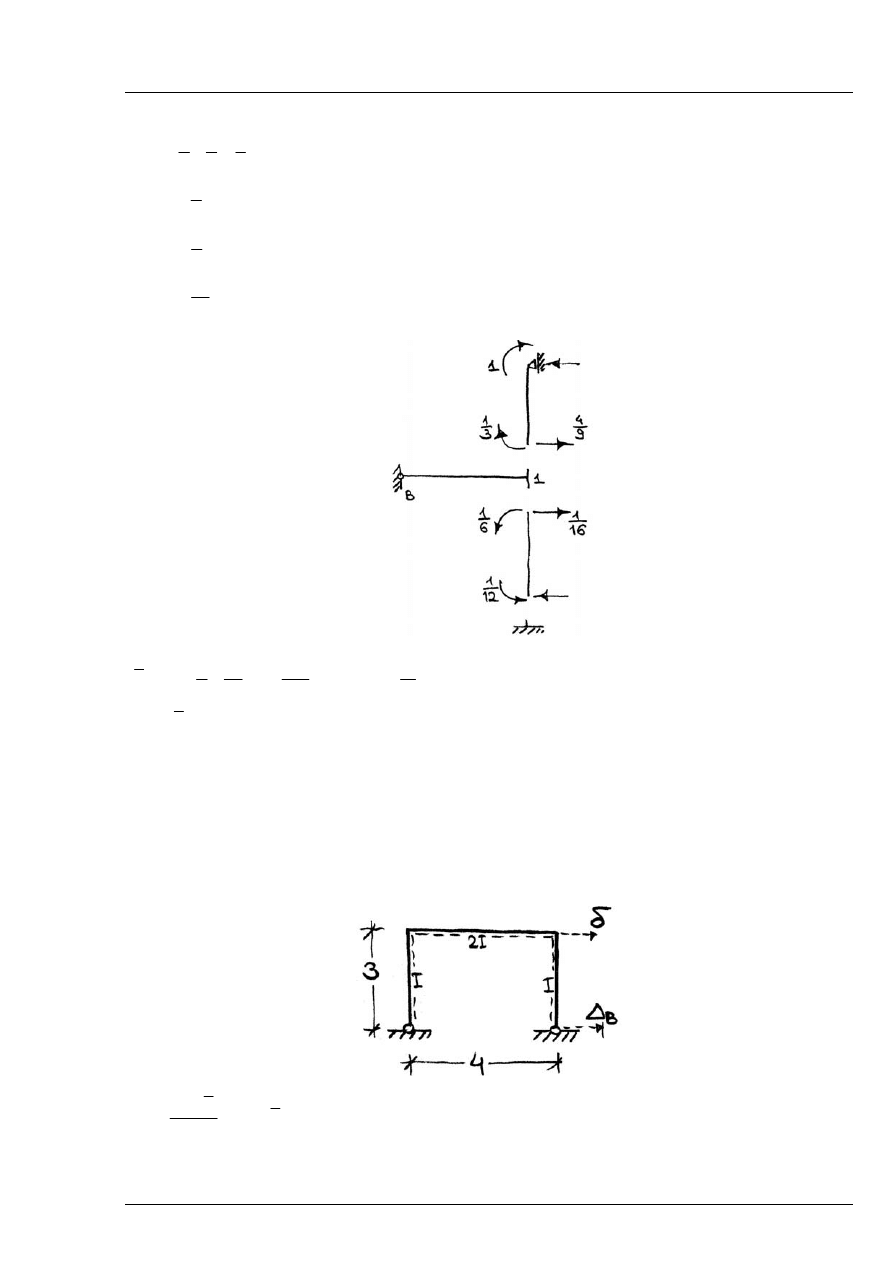
Sumaryczne momenty przywęzłowe:
1
1
1
1
0,5
0,5
A
B
C
C
M
EI
M
EI
M
EI
M
EI
ϕ
ϕ
ϕ
ϕ
=
+
=
=
=
Równanie równowagi:
1
1
1
1
0
1
0,5 3
0
6
A
B
C
M
M
M
M
EI
EI
ϕ
ϕ
Σ
=
+
+
=
+
=
⇒
= −
C16-2005-cw12
97
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Wartości momentów przywęzłowych
1
1
1
1
1 1
1
[ ]
2 6
3
1
[ ]
6
1
[ ]
6
1
[ ]
12
A
B
C
C
M
M
M
M
= − =
−
= −
−
= −
−
= −
−
Rozwiązanie:
Rys. 12.3.3
1
4
1
73
1
0,5069
9 16
144
B
N
m
⎛
⎞
⎡
= −
+
= −
= −
⎜
⎟
⎤
⎢ ⎥
⎝
⎠
⎣ ⎦
5
3
0
10
24 ( 0,5069) 6
7,3 10 [
]
25'05"
t
L
N t ds
rad
ϕ
α
−
−
=
=
⋅
⋅ −
⋅ = −
⋅
= −
∫
Zad. 12.4
Obliczyć przemieszczenie
δ układu ramowego wywołane wymuszeniem kinematycznym -
przemieszczeniem podpory
5 [
]
B
cm
∆ =
Rys. 12.4.1
i
L
M M
ds
R
EI
δ
⋅
=
− ∑
∫
i
⋅ ∆
(12.5)
C16-2005-cw12
98
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Stosując II twierdzenie redukcyjne – obciążenie zewnętrzne w układzie podstawowym metody sił,
obciążenie wirtualne w układzie niewyznaczalnym
Wzór zapisujemy w postaci:
(
i
i
p
R
M
M
δ
∆
= − ∑ ⋅ ∆
=
= 0)
(12.6)
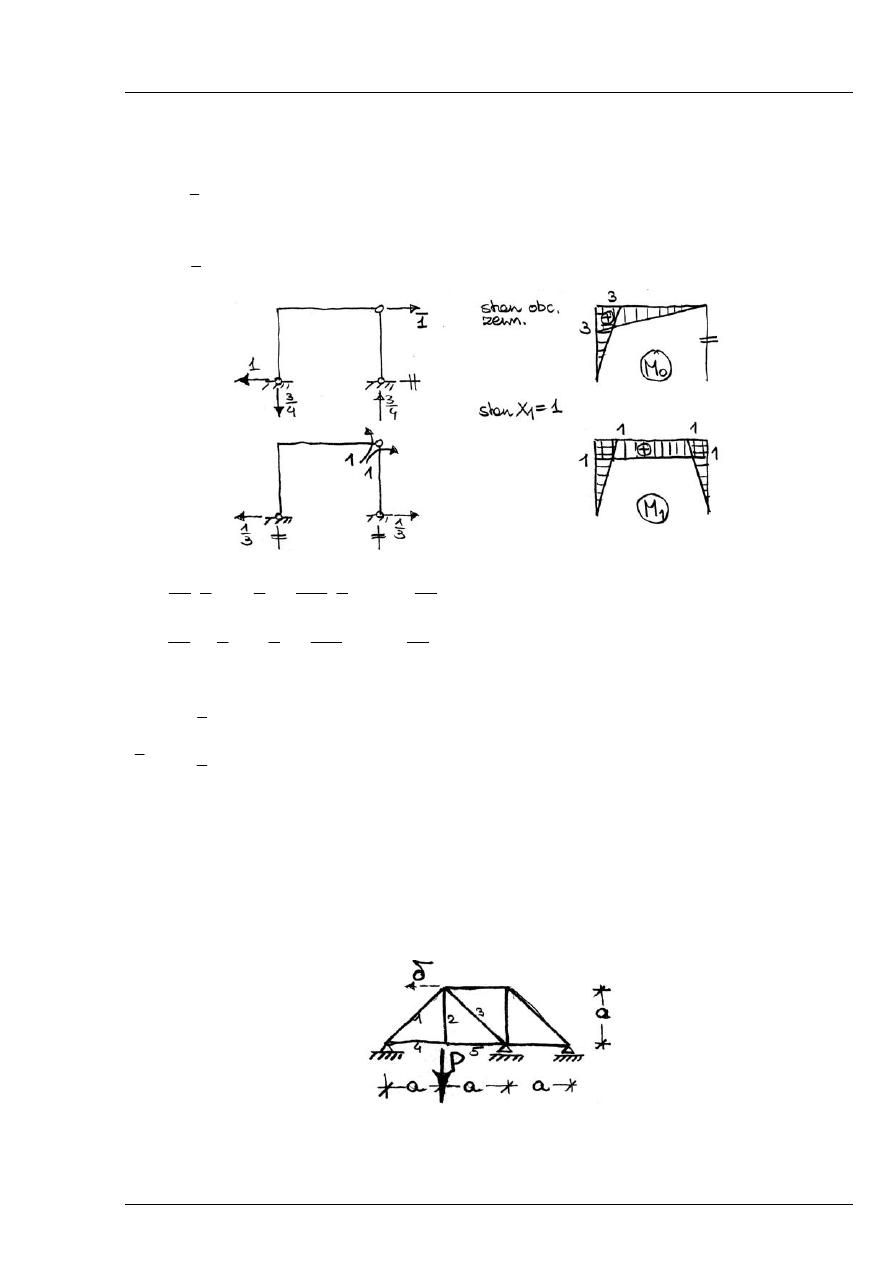
Rozwiązanie dla obciążenia wirtualnego w układzie niewyznaczalnym (należy obliczyć jedynie
reakcję
B
H ).
Rys. 12.4.2
10
11
1
1 1
2
1
1
6
3 3
1
3 4 1
2
3
2
2
1
1
2
1
4
2
3 1
1
1 4 1
2
3
2
1,5 [ ]
EI
EI
EI
EI
EI
EI
X
m
δ
δ
=
⋅ ⋅ ⋅ ⋅ ⋅ +
⋅ ⋅ ⋅ ⋅ =
=
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ +
⋅ ⋅ ⋅ =
= −
Reakcja
B
H (z superpozycji)
1
0
( 1,5)
0,5 [ ]
3
B
H
= + ⋅ −
= −
−
Przemieszczenie:
5 ( 0,5) 2,5 [
]
cm
δ
= − ⋅ −
=
Zad. 12.5
Dla kratownicy jak na rys. obliczyć przemieszczenie .
.
EA
const
δ
=
Rys. 12.5.1
C16-2005-cw12
99
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Wykorzystując II twierdzenie redukcyjne można zapisać
( )
i
i
p
i
i
S
S
l
EA
δ
= ∑
(12.7)
( )
i
p
S
− siły w prętach w układzie podstawowym metody sił, obciążenie zewnętrzne
i
S
− siły w prętach w układzie niewyznaczalny, obciążenie wirtualne
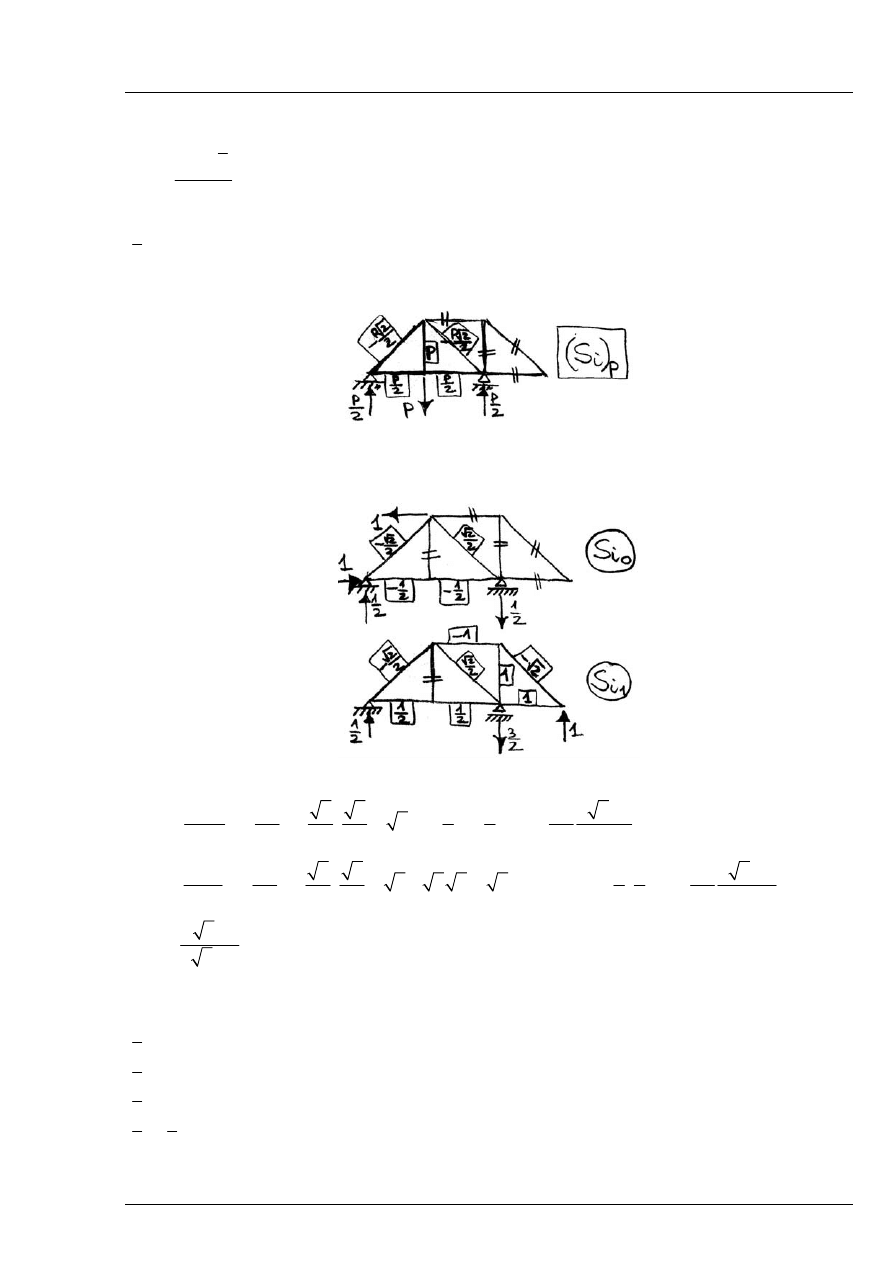
Obciążenie zewnętrzne w układzie podstawowym metody sił:
Rys. 12.5.2
Niezerowe są jedynie pręty 1, 3, 4 i 5
Obciążenia wirtualne w układzie niewyznaczalnym:
Rys. 12.5.3
0
1
10
1
1
11
1
1
2
2
1
1
2 2 1
2
2 2
2
2
2
2
2
1
2
2
1 1
6 2
2
2
2 2
2 3 1 1
2
2
2
2 2
2
2 2 1
0,1181
6 2 7
i
i
i
i
i
i
i
i
S S
a
l
a
a
EA
EA
EA
S S
a
l
a
a
a
a
EA
EA
EA
X
δ
δ
⎡
⎤
−
⎛
⎞
= ∑
=
⋅
⋅
⋅
+ ⋅ ⋅ −
⋅
=
⎢
⎥
⎜
⎟
⎝
⎠
⎣
⎦
⎡
⎤
7
+
= ∑
=
⋅
⋅
⋅
+
⋅
+ ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅
=
⎢
⎥
⎣
⎦
−
= −
≈ −
+
Rozwiązanie uzyskujemy z superpozycji:
0
1
1
1
2
3
4
5
0,6236
0
0,6236
0,5591
i
i
i
S
S
S
X
S
S
S
S
S
=
+
⋅
= −
=
=
=
= −
C16-2005-cw12
100
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Szukane przemieszczenie:
( )
(
)
1
2
0,5591
0,5591
2
i
i
p
i
i
S
S
P
P
l
a
EA
EA
EA
δ
= ∑
=
⋅ ⋅ ⋅ −
⋅ = −
a
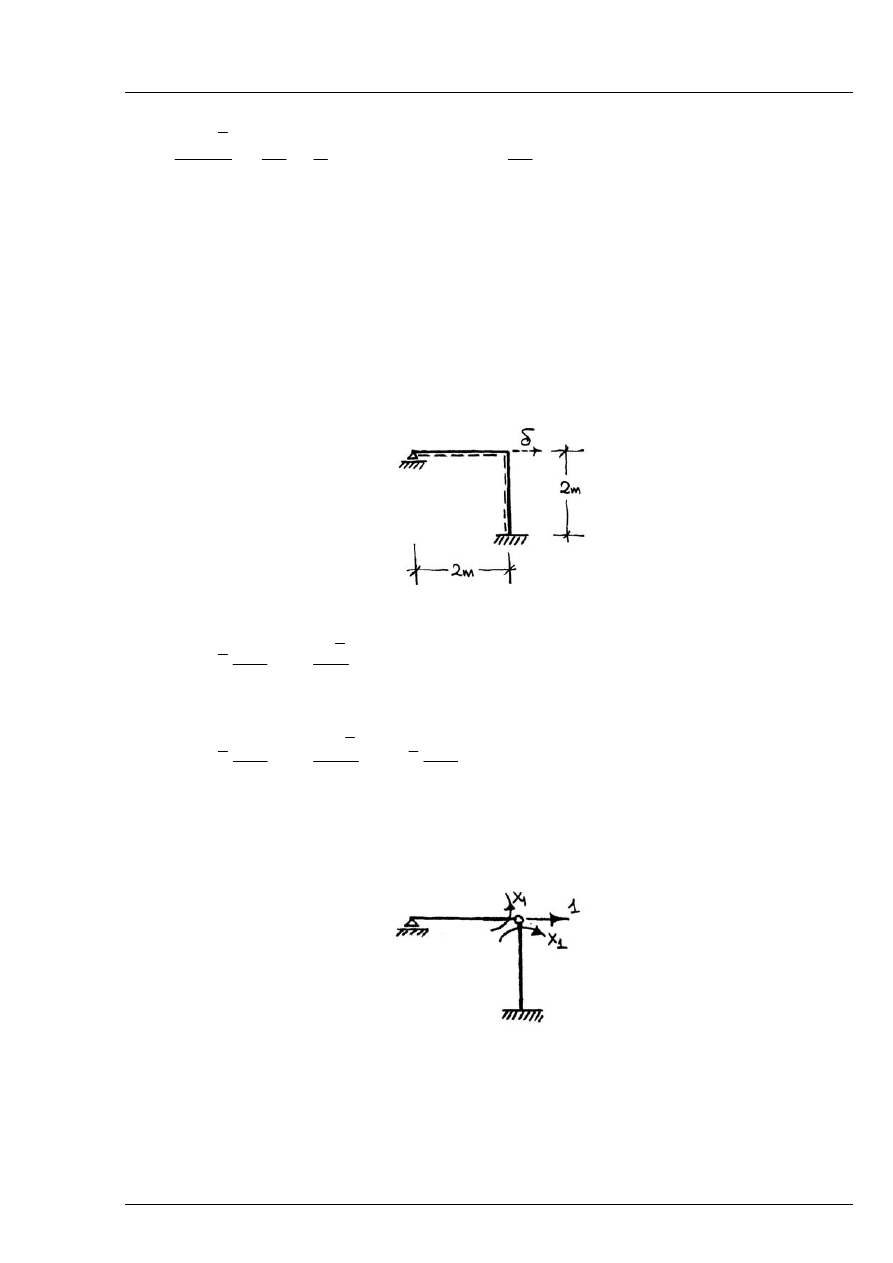
Zad. 12.6
Obliczyć przemieszczenie
δ
powstałe pod wpływem nierównomiernego ogrzania całego układu
5
1
32
0, 4 [ ]
10
deg
o
d
g
t
t
t
t
C
h
m
const
EI
const
α
−
−
∆ = − =
=
=
⎡
⎤
=
⎣
⎦
=
Rys. 12.6.1
Z zasady prac wirtualnych wynika wzór:
t
L
L
t
MM
M
ds
ds
h
EI
α
δ
∆
=
+
∫
∫
(12.8)
Stosując I twierdzenie redukcyjne mamy:
p
t
L
L
L
M M
t
t
t
M
ds
ds
M
ds
h
EI
h
α
δ
∆
=
+
=
∫
∫
∫
α
∆
)
(12.9)
gdyż
0 (wpływ temperatury w układzie podstawowym metody sił)
p
M
=
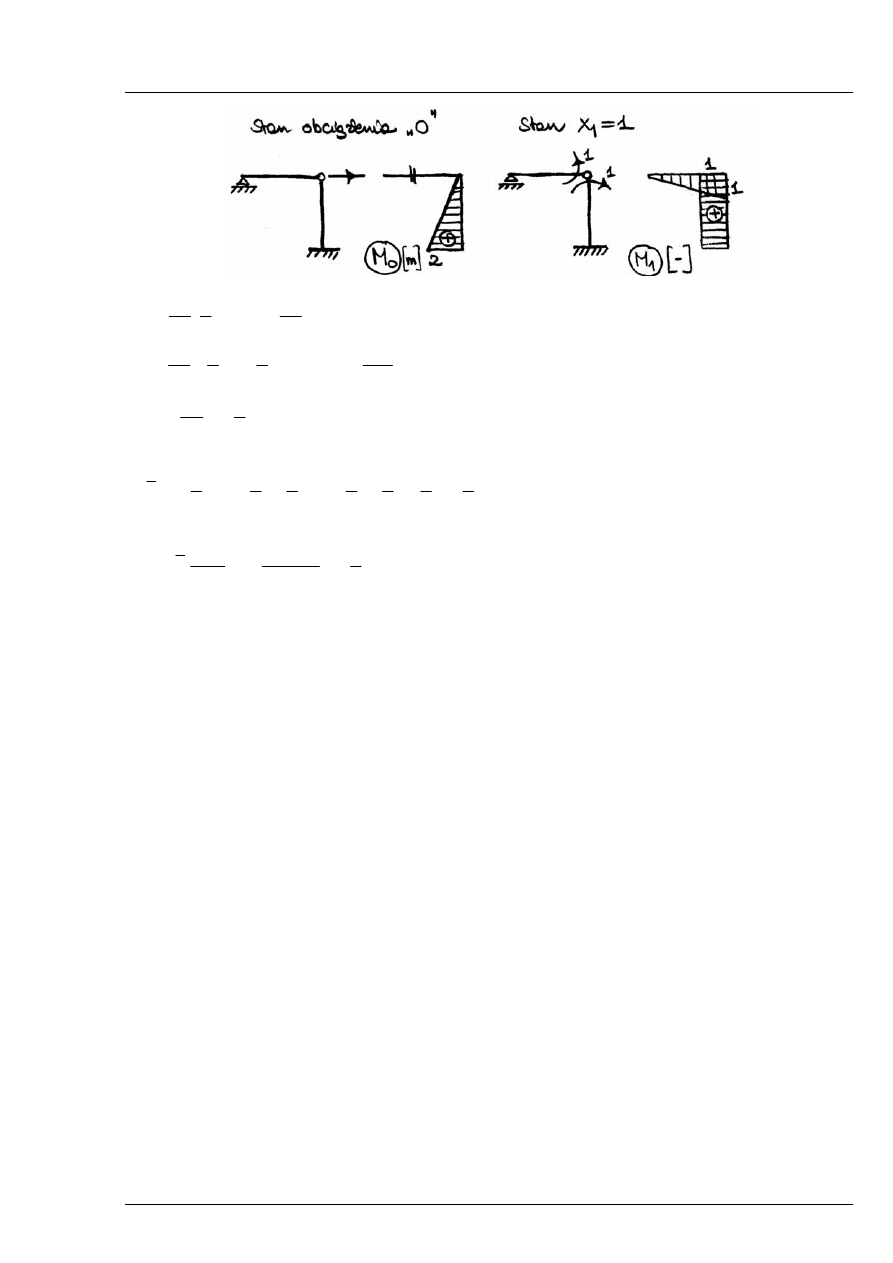
Obciążenia wirtualne w układzie niewyznaczalnym
Metoda sił (
1
s
n
=
Rys. 12.6.2
C16-2005-cw12
101
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Rys. 12.6.3
10
11
10
1
11
1 1
2
2 2 1
2
1
1
2
8
1 1
1 2 1 1
2
3
3
3
4
EI
EI
EI
EI
X
δ
δ
δ
δ
=
⋅ ⋅ ⋅ ⋅ =
⎡
⎤
=
⋅
⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ =
⎢
⎥
⎣
⎦
= −
= −
1
3
1
3
1
5
2
2
2
2
4
2
4
2
4
L
Mds
⎛
⎞
⎛
⎞
= ⋅ ⋅ −
+ ⋅ ⋅ −
+ ⋅ ⋅ = −
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
∫
1
4
Szukane przemieszczenie:
5
4
10
32
1
2 10 [ ]
0,02 [
]
0, 4
4
t
L
t
M
ds
m
cm
h
α
δ
−
−
∆
⋅
⎛
⎞
=
=
⋅ −
= − ⋅
= −
⎜
⎟
⎝
⎠
∫
C16-2005-cw12
102
Document Outline
Wyszukiwarka
Podobne podstrony:
C16 2005 cw12 id 96896 Nieznany
C16 2005 cw01 repet
C16 2005 cw14
C16 2005 cw02
C16 2005 cw06
C16 2005 cw02
C16 2005 cw15 id 96900 Nieznany
C16 2005 cw08
C16 2005 cw01
C16 2005 cw13
C16 2005 cw05
C16 2005 cw10 id 96894 Nieznany
C16 2005 cw09
C16 2005 cw07
C16 2005 cw04
C16 2005 cw15
C16 2005 cw04
więcej podobnych podstron