KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Ćwiczenie 15
Repetytorium
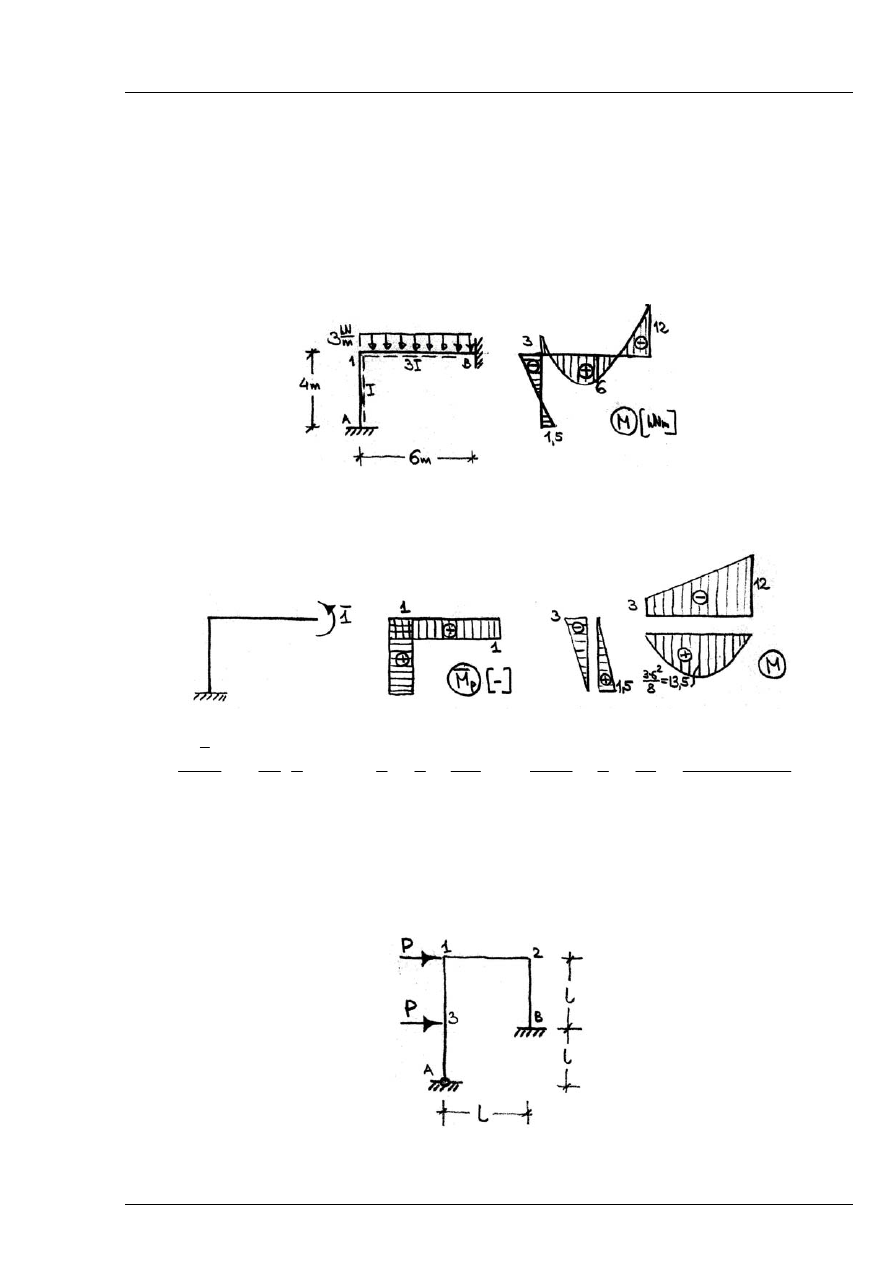
Zad. 15.1
Sprawdzić poprawność wykonania wykresu M poprzez obliczenie przemieszczenia zerowego
(zastosowanie twierdzenia redukcyjnego)
Rys. 15.1.1
Stosujemy II tw. redukcyjne – przyjmując układ podstawowy wg rys. obliczamy kąt obrotu
B
ϕ
Rys. 15.1.2
1 1
1
3
1
3 12
2
27
6 3 15 18
4 ( 3)
4
6
6
0
2
2
2
3
2
3
2
p
B
L
MM
ds
EI
EI
EI
EI
ϕ
⎡
+
⎤ − + − +
⎡
⎤
⎛
⎞
=
=
⋅ ⋅ − + ⋅ ⋅
+
⋅ −
+ ⋅ ⋅
=
=
⎜
⎟
⎢
⎥
⎢
⎥
⎣
⎦
⎝
⎠
⎣
⎦
∫
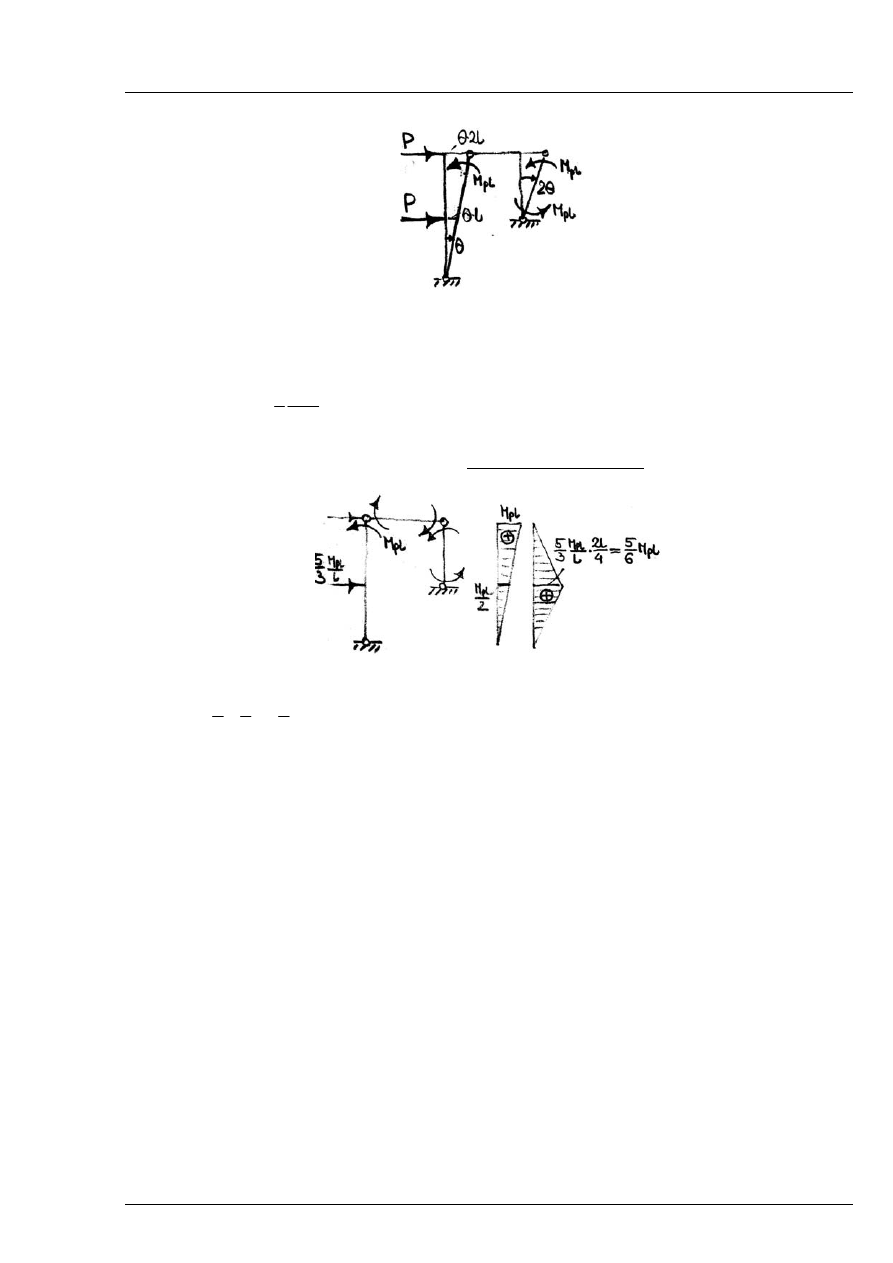
Zad. 15.2
W układzie wg rys. określono mechanizm zniszczenia przez wprowadzenie przegubów
plastycznych w punktach 1, 2 i B. Obliczyć graniczną wartość obciążenia
gr
P oraz narysować
wykres M w stanie granicznym. Sprawdzić, czy założony mechanizm jest poprawny.
pl
M
const
=
Rys. 15.2.1
C16-2005-cw15
116
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Przyjęty mechanizm zniszczenia:
Rys. 15.2.2
2
2
5
w
pl
pl
pl
pl
L
M
M
M
M
θ
θ
θ
=
⋅ +
⋅
+
⋅
=
⋅
θ
l
2
3
z
L
P
l
P
l
P
θ
θ
θ
= ⋅ ⋅ + ⋅ ⋅ =
⋅ ⋅
5
3
pl
w
z
gr
M
L
L
P
l
=
⇒
=
Należy sprawdzić, czy dany mechanizm jest statycznie dopuszczalny – w żadnym przekroju nie
może być przekroczona odpowiednia wartość momentu granicznego.
Rys. 15.2.3
3
1 5
4
2 6
3
pl
pl
pl
M
M
M
⎛
⎞
=
+
=
>
⎜
⎟
⎝
⎠
M
Zatem założony mechanizm zniszczenia jest statycznie niedopuszczalny.
C16-2005-cw15
117
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
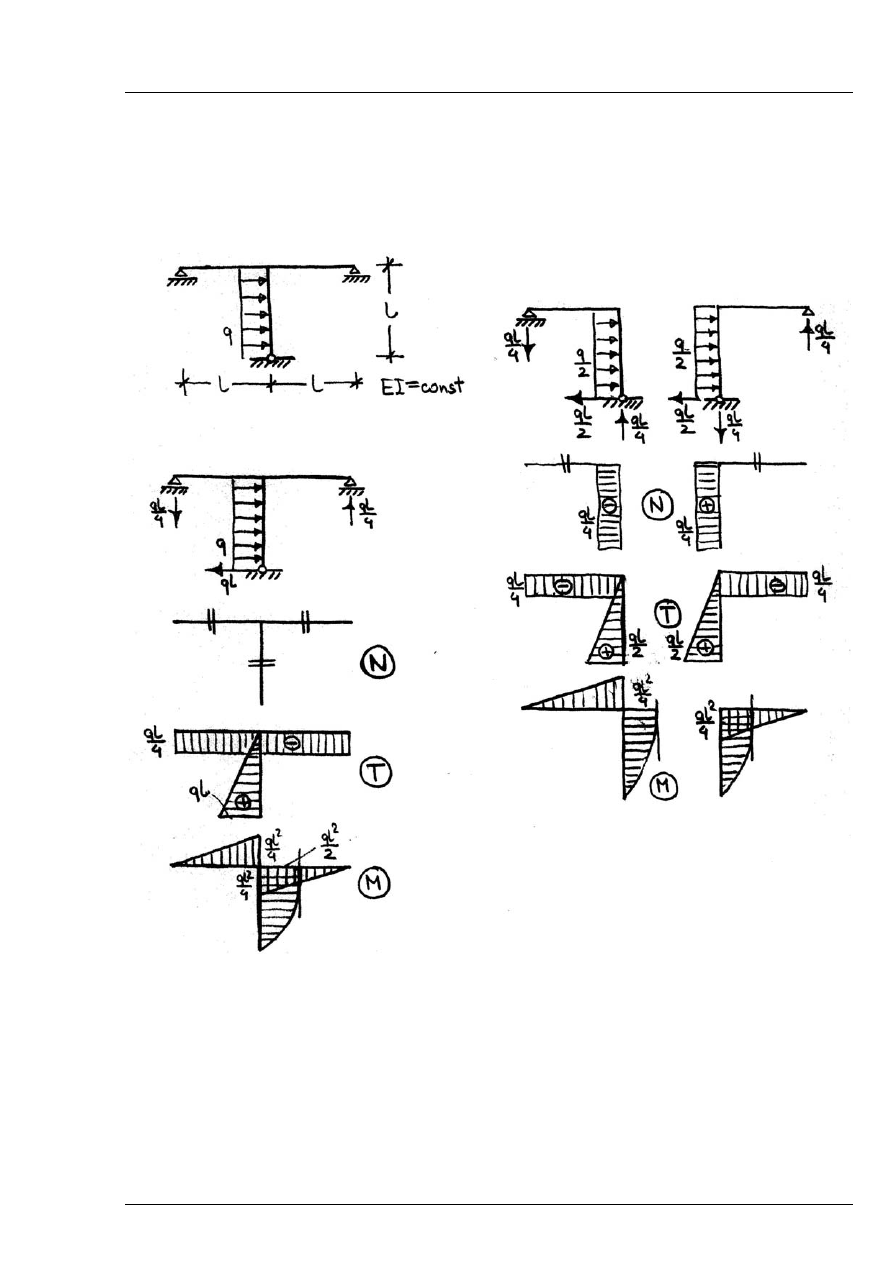
Zad. 15.3
Sporządzić wykresy sił wewnętrznych.
Antysymetria – schemat zredukowany to układ statycznie wyznaczalny.
Rys. 15.3.1
C16-2005-cw15
118
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
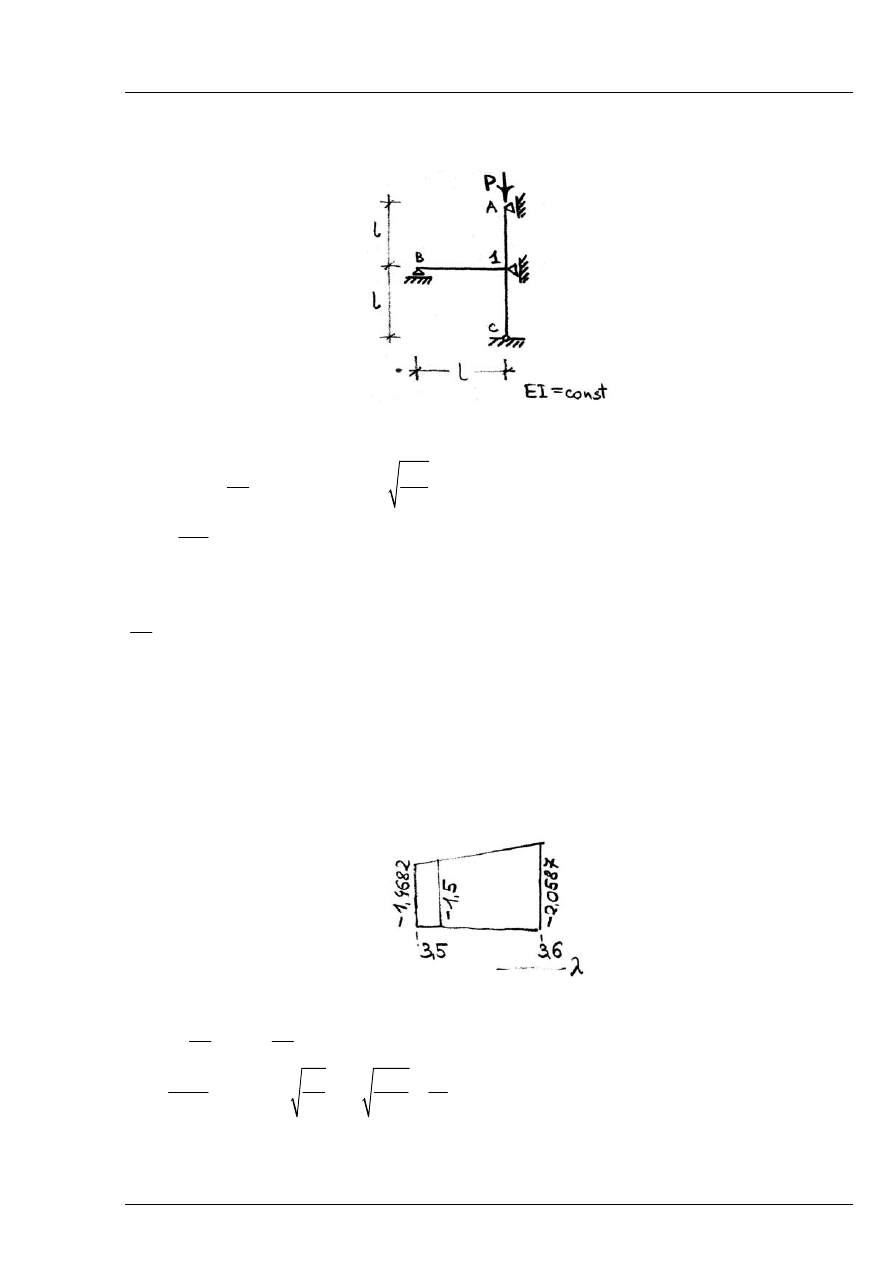
Zad. 15.4
Obliczyć krytyczną wartość obciążenia P oraz długości wyboczeniowe elementów ściskanych.
EI
const
=
Rys. 15.4.1
2
1
1
1
`( ) ,
3
A
C
B
EI
Pl
M
M
gdzie
l
E
EI
M
l
α λ ϕ
λ
ϕ
=
=
=
=
I
Równanie równowagi:
[
]
1
0
2 `( ) 3
0
M
EI
l
α λ
ϕ
Σ
=
+
=
Niezerowe rozwiązanie
(
0)
`( )
1,
dla
5
ϕ
α λ
≠
= −
Przybliżone rozwiązanie – z zastosowaniem tablicy funkcji
'
α
3,5
`( )
1, 4682
3,6
`( )
2,0587
λ
α λ
λ
α λ
=
⇒
= −
=
⇒
= −
Interpolacja liniowa:
3,51
λ
=
Rys. 15.4.2
Obciążenie krytyczne
2
2
2
12,32
kr
EI
EI
P
l
l
λ
=
=
2
2
2
0,895
kr
w
w
kr
kr
EI
EI
EI
l
P
l
l
l
P
P l
π
π
π
π
λ
=
⇒
=
=
=
=
l
C16-2005-cw15
119
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Zad.15.5
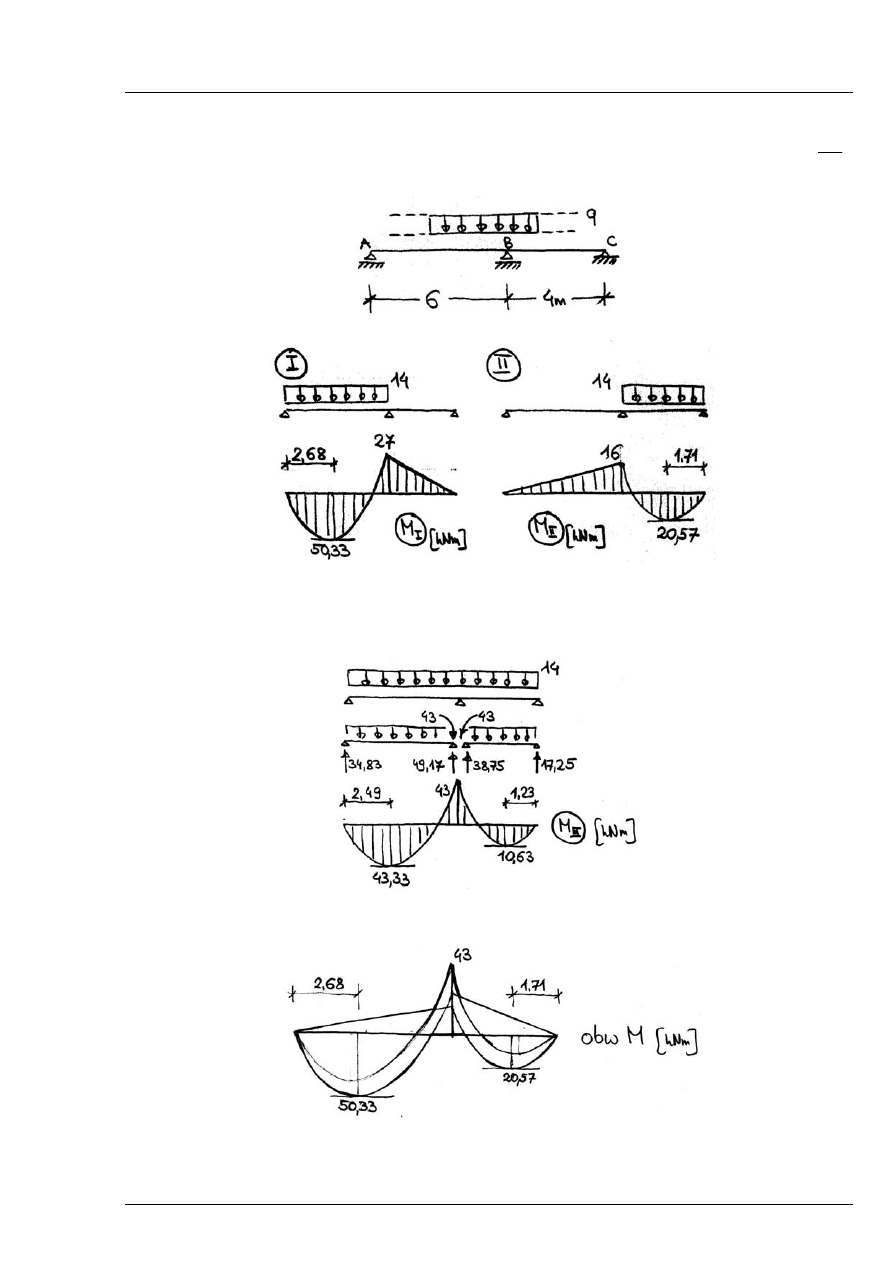
Narysować obwiednie momentów zginających dla belki ciągłej z obciążeniem zmiennym
7
kN
q
m
=
o dowolnej długości (dane są rozwiązania I i II)
Rys. 15.5.1
Rys. 15.5.2
Obciążenie I przyjęte jest tak, aby dawało max
AB
M
, obciążenie II daje max
BC
M
. Potrzebny jest
schemat obciążenia dający min
B
M - jest to przypadek obciążenia ciągłego na obu przęsłach,
uzyskujemy go jako (I + II)
Rys. 15.5.3
Obwiednie momentów zginających:
Rys. 15.5.4
C16-2005-cw15
120