Krzysztof Wójtowicz
Strona 1
Politechnika Poznańska Projekt wykonał: Krzysztof Wójtowicz
Instytut Konstrukcji Budowlanych Konsultacje: dr inż. Przemysław Litewka
Zakład Mechaniki Budowli
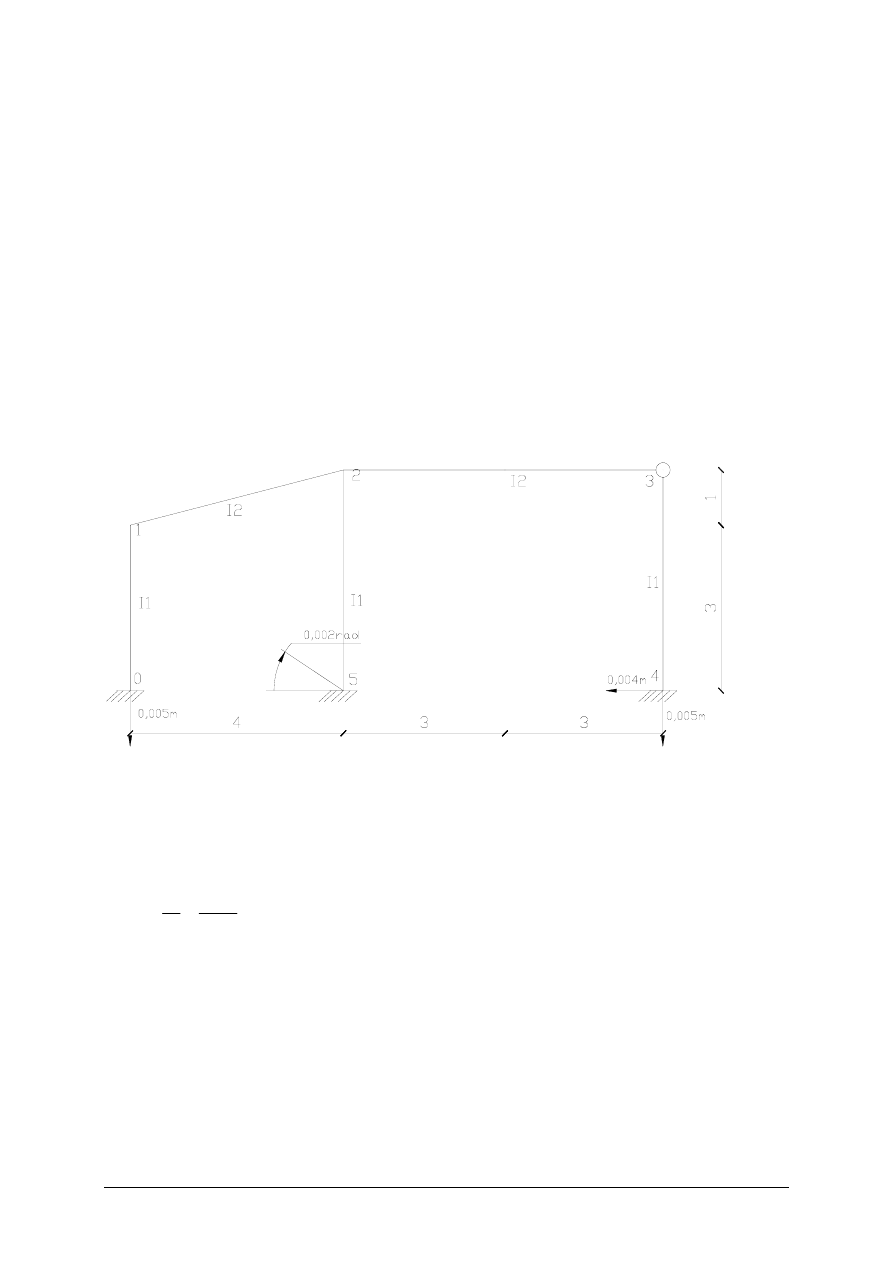
Obliczenie Ramy Metodą Przemieszczeń
Zakładamy przekroje dwuteowe:
I1- I220 -I1=3060 cm
4
I2- I240 -I2=4250 cm
4
1,389I1
I2
1,389
3060
4250
I1
I2
=
⇒
=
=
Krzysztof Wójtowicz
Strona 2
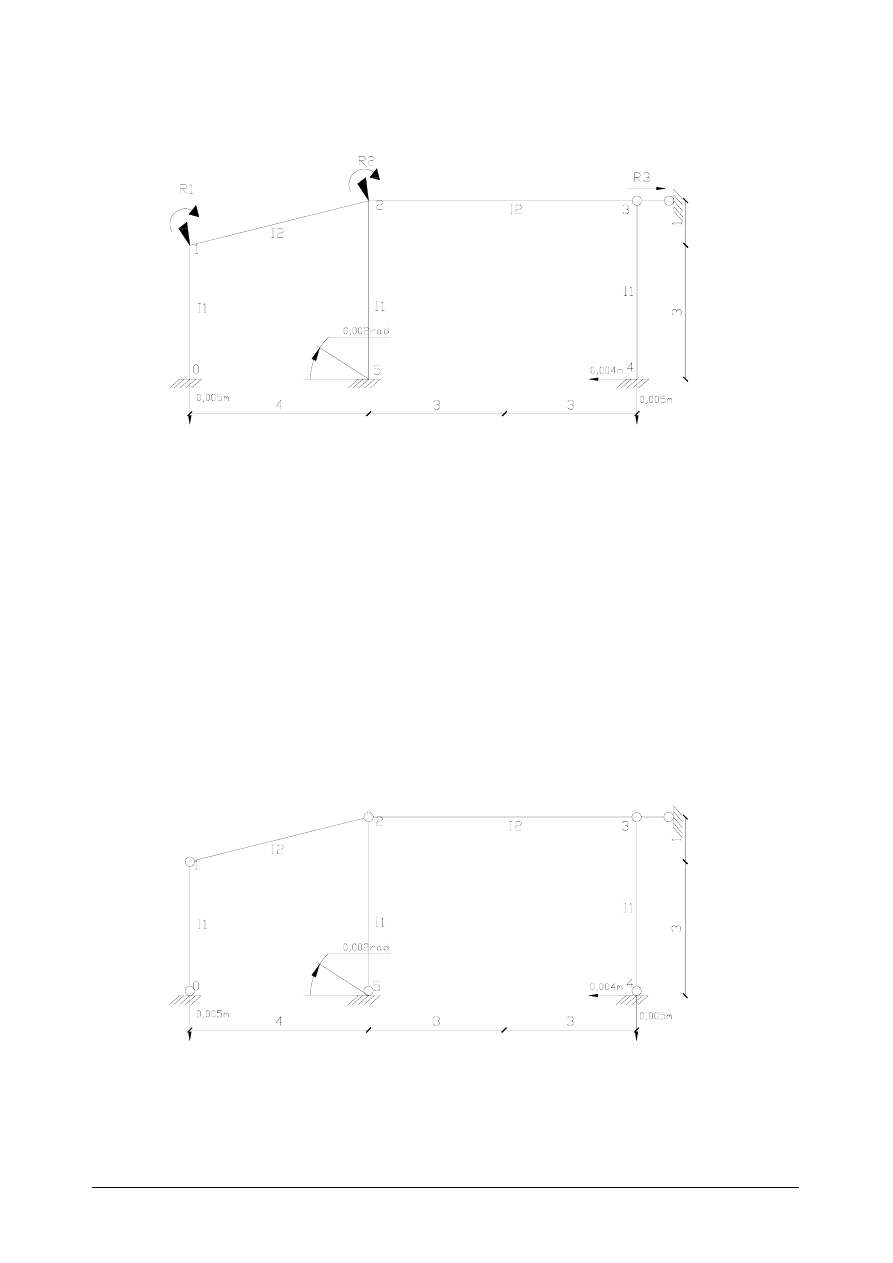
Układ podstawowy
SGN=3
Ponieważ układ podstawowy jest identyczny jak dla ramy obliczonej dla sił zewnętrznych
reakcje r
ik
pozostają takie same. Pozostaje tylko obliczyć r
i
∆
.
Łańcuch kinematyczny
=
+
+
+
=
+
+
+
=
+
+
+
⇒
=
=
=
∆
∆
∆
0
r
z3
r
z2
r
z1
r
0
r
z3
r
z2
r
z1
r
0
r
z3
r
z2
r
z1
r
0
R3
0
R2
0
R1
3
33
32
31
2
23
22
21
1
13
12
11
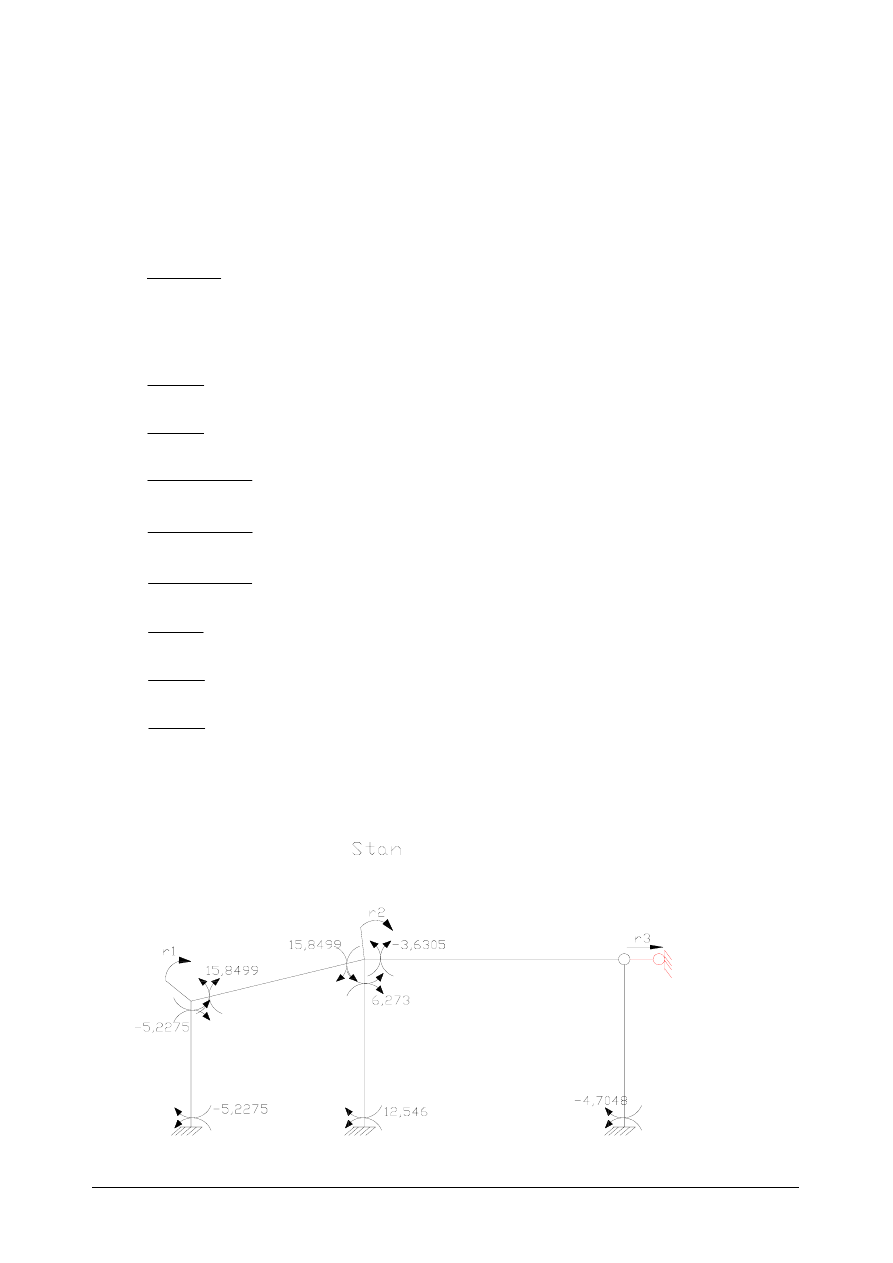
Krzysztof Wójtowicz
Strona 3
Kąty obrotu prętów powstałe od osiadania podpór w układzie podstawowym
43
→
523
→
5234
↓
0125
→
-0,004+
Ψ
43
·4=0 0+
Ψ
52
·
4+0=0 0+
Ψ
52
·
0+
Ψ
23
·
6=0,005 0,005+
Ψ
01
·
0+
Ψ
12
·
4+
Ψ
25
·0=0
Ψ
43
=0,001rad
Ψ
52
=0
Ψ
23
=0,00083333rad
Ψ
12
= -0,00125rad
0123
→
Ψ
01
·
3+
Ψ
12
·
1+
Ψ
23
·
0=0
Ψ
01
·
3= -
Ψ
12
Ψ
01
=
rad
0,00041667
3
0,00125
=
−
−
Podstawiając do wzorów transformacyjnych otrzymujemy momenty(EI
1
=6273kNm
2
):
kNm
kNm
2275
,
5
)
0041667
,
0
3
0
0
(2
3
6273
2
M
2275
,
5
)
00041667
,
0
3
0
0
(2
3
6273
2
M
10
01
−
=
⋅
−
+
⋅
⋅
=
−
=
⋅
−
+
⋅
⋅
=
∆
∆
kNm
kNm
kNm
kNm
kNm
kNm
273
,
6
0)
3
0,002
0
(2
4
6273
2
M
546
,
12
)
0
3
0
0,002
(2
4
6273
2
M
7048
,
4
)
001
,
0
(0
4
6273
3
M
6305
,
3
)
00083333
,
0
(0
6
6273
1,389
3
M
8499
,
15
)
)
00125
,
0
(
3
0
0
(2
4,123
6273
1,389
2
M
8499
,
15
)
)
00125
,
0
(
3
0
0
(2
4,123
6273
1,389
2
M
25
52
43
23
21
12
=
⋅
−
+
⋅
⋅
=
=
⋅
−
+
⋅
⋅
=
−
=
−
⋅
=
−
=
−
⋅
⋅
=
=
−
⋅
−
+
⋅
⋅
⋅
=
=
−
⋅
−
+
⋅
⋅
⋅
=
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆

Krzysztof Wójtowicz
Strona 4
Z równowagi węzłów otrzymujemy
18,4924kNm
r
0
15,8499
6,273
3,6305
r
2∆
2∆
=
=
−
−
+
r
3
∆
obliczymy z pracy wirtualnej
Ψ=0,3333
Ψ=0,25
Ψ=0,25
_
_
_
_
− −
0,043899kN
r
0
0,25
4,7048
0,25
6,273
0,25
12,546
0,3333
5,2275)
(
2
1
r
3∆
____
_____
____
_______
_
3∆
=
=
⋅
−
⋅
+
⋅
+
⋅
−
⋅
+
⋅
Podstawiając do równań kanonicznych otrzymujemy
=
−
⋅
+
⋅
−
⋅
−
=
+
⋅
−
⋅
+
⋅
=
+
⋅
−
⋅
+
⋅
0
043899
,
0
6787
,
0
375
,
0
6666
,
0
0
4924
,
18
375
,
0
0425
,
3
6738
,
0
0
6224
,
10
6666
,
0
6738
,
0
681
,
2
3
1
2
1
1
1
3
1
2
1
1
1
3
1
2
1
1
1
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
−
=
−
=
−
=
50995
,
7
0494
,
6
3090
,
4
1
3
1
2
1
1
EI
z
EI
z
EI
z
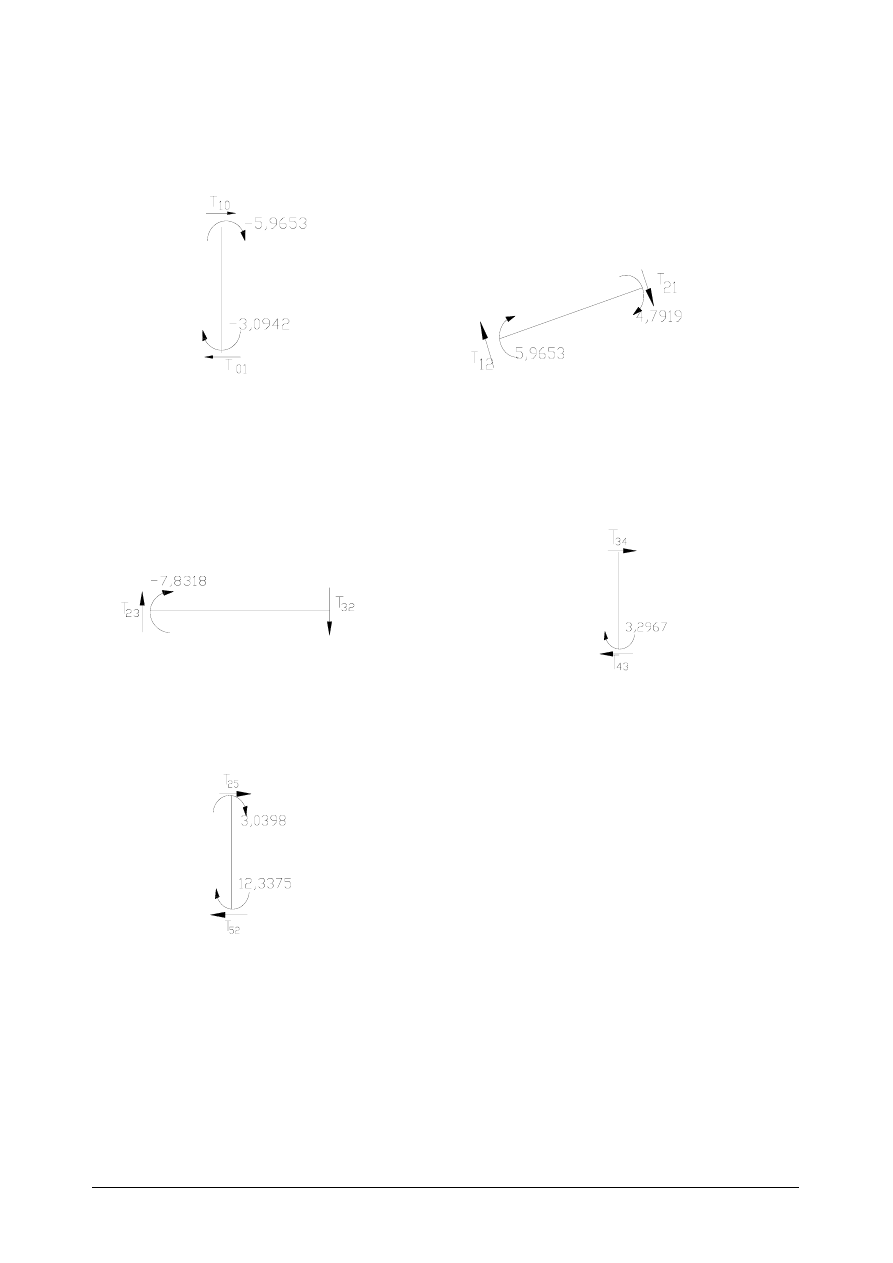
Podstawiając wartości do równań momentowych(wzory redukcyjne) z poprzedniej części
projektu, uwzględniając momenty od osiadań otrzymujemy:
-5,9653kNm
2275
,
5
)
50995
,
7
(
0,6666
)
3090
,
4
(
1,333
M
0942
,
3
2275
,
5
)
50995
,
7
(
0,6666
)
3090
,
4
(
0,6667
M
10
01
=
−
−
⋅
−
−
⋅
=
−
=
−
−
⋅
−
−
⋅
=
kNm
3,0398kNm
273
,
6
)
50995
,
7
(
0,3750
)
0494
,
6
(
1
M
3375
,
12
546
,
12
)
50995
,
7
(
0,3750
)
0494
,
6
(
0,5
M
2967
,
3
7048
,
4
)
50995
,
7
(
0,1875
M
8318
,
7
6305
,
3
)
0494
,
6
(
0,6945
M
7919
,
4
8499
,
5
1
)
3090
,
4
(
0,6738
)
0494
,
6
(
1,348
M
9653
,
5
8499
,
15
)
0494
,
6
(
0,6738
)
3090
,
4
(
1,348
M
25
52
43
23
21
12
=
+
−
⋅
−
−
⋅
=
=
+
−
⋅
−
−
⋅
=
−
=
−
−
⋅
−
=
−
=
−
−
⋅
=
=
+
−
⋅
+
−
⋅
=
=
+
−
⋅
+
−
⋅
=
kNm
kNm
kNm
kNm
kNm
10,6224kNm
r
0
5,2275
15,8499
r
1∆
1∆
=
=
+
−
Krzysztof Wójtowicz
Strona 5
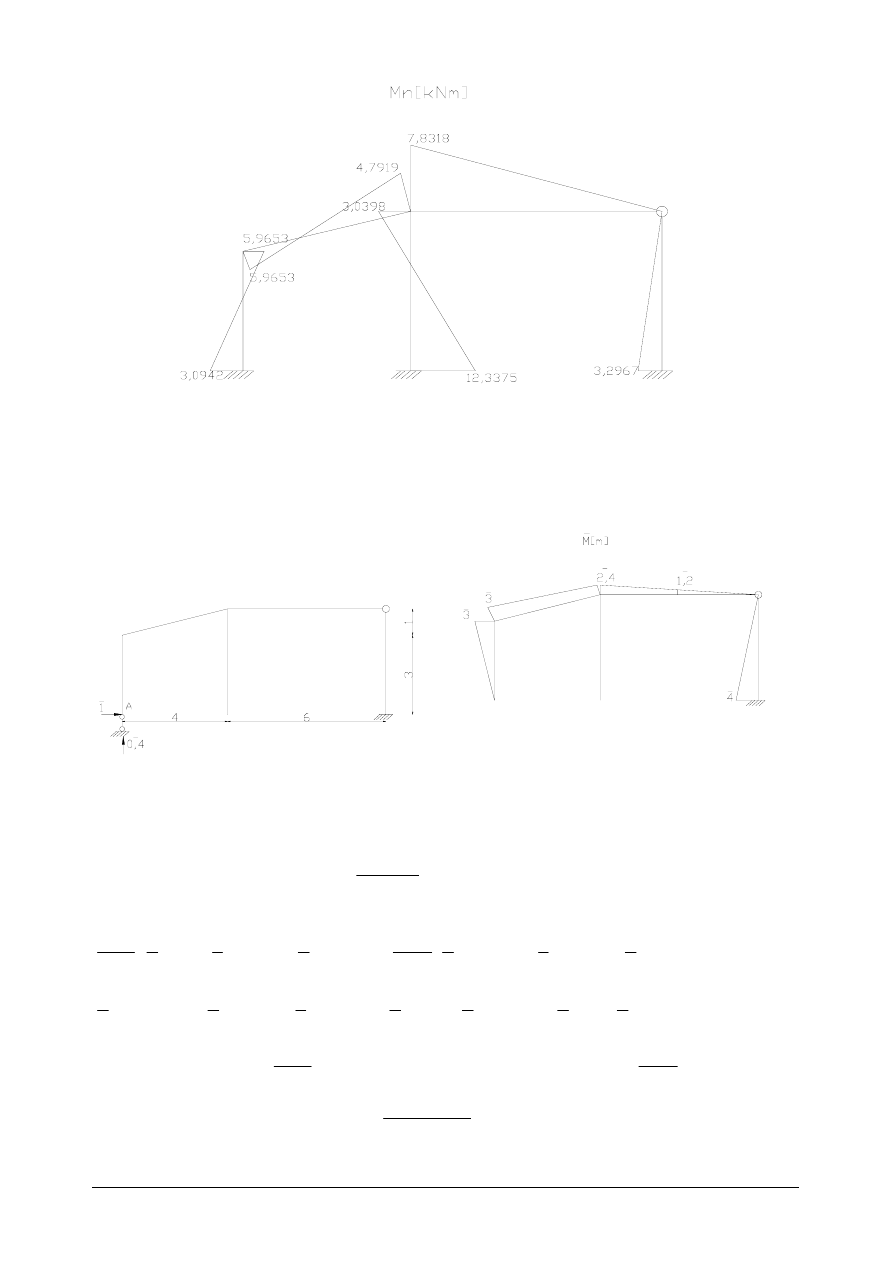
Kontrola kinematyczna
H
A
= 0
⇒
0
_
1
_
=
∆
⋅
−
⋅
∑∫
R
dx
EI
M
M
N
EI
1
=6273kNcm
2
H
A
=
(
)
%
006
,
0
%
100
00400024
,
0
0,00000024
0
00000024
,
0
004
,
0
00400024
,
0
004
,
0
5824
,
17
389
,
1
1
5926
,
37
9674
,
5
7164
,
14
2546
,
13
6273
1
1
004
,
0
4
,
0
005
,
0
4
,
0
005
,
0
2967
,
3
3
2
4
4
2
1
8318
,
7
3
2
6
4
,
2
2
1
9653
,
5
3
1
7919
,
4
3
2
123
,
4
4
,
2
2
1
9653
,
5
3
2
7919
,
4
3
1
123
,
4
3
2
1
389
,
1
1
9653
,
5
3
2
0942
,
3
3
1
3
3
2
1
6273
1
=
⋅
≈
=
−
=
−
+
⋅
+
+
−
+
−
=
⋅
−
⋅
−
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
Krzysztof Wójtowicz
Strona 6
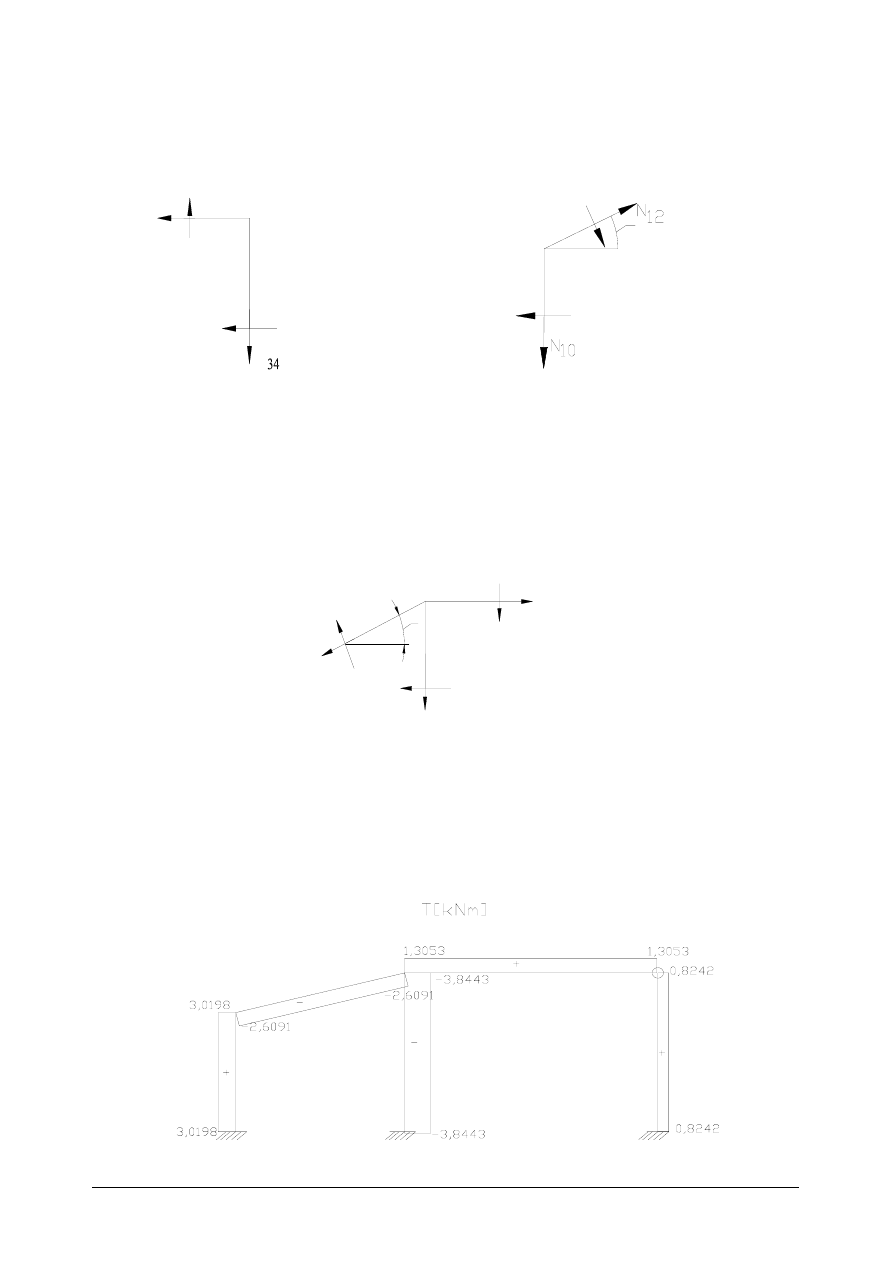
Obliczenie sił tnących
(
siły tnące obliczamy z sumy momentów, dlatego siły normalne pomijamy na rysunkach
gdyż nie wchodzą one do równań momentowych)
kN
T
T
T
M
0198
,
3
0
0942
,
3
9653
,
5
3
:
01
10
10
0
=
=
=
−
−
⋅
∑
kN
T
T
T
M
6091
,
2
0
7919
,
4
9653
,
5
123
,
4
:
12
21
21
1
−
=
=
=
−
+
⋅
∑
kN
T
T
T
M
3053
,
1
0
8318
,
7
0
,
6
:
23
32
32
2
=
=
=
−
⋅
∑
kN
T
T
T
M
8242
,
0
0
2967
,
3
0
,
4
:
43
34
42
3
=
=
=
−
⋅
∑
kN
T
T
T
M
8843
,
3
0
0398
,
3
3375
,
12
4
:
52
25
25
5
−
=
=
=
+
+
⋅
∑
Krzysztof Wójtowicz
Strona 7
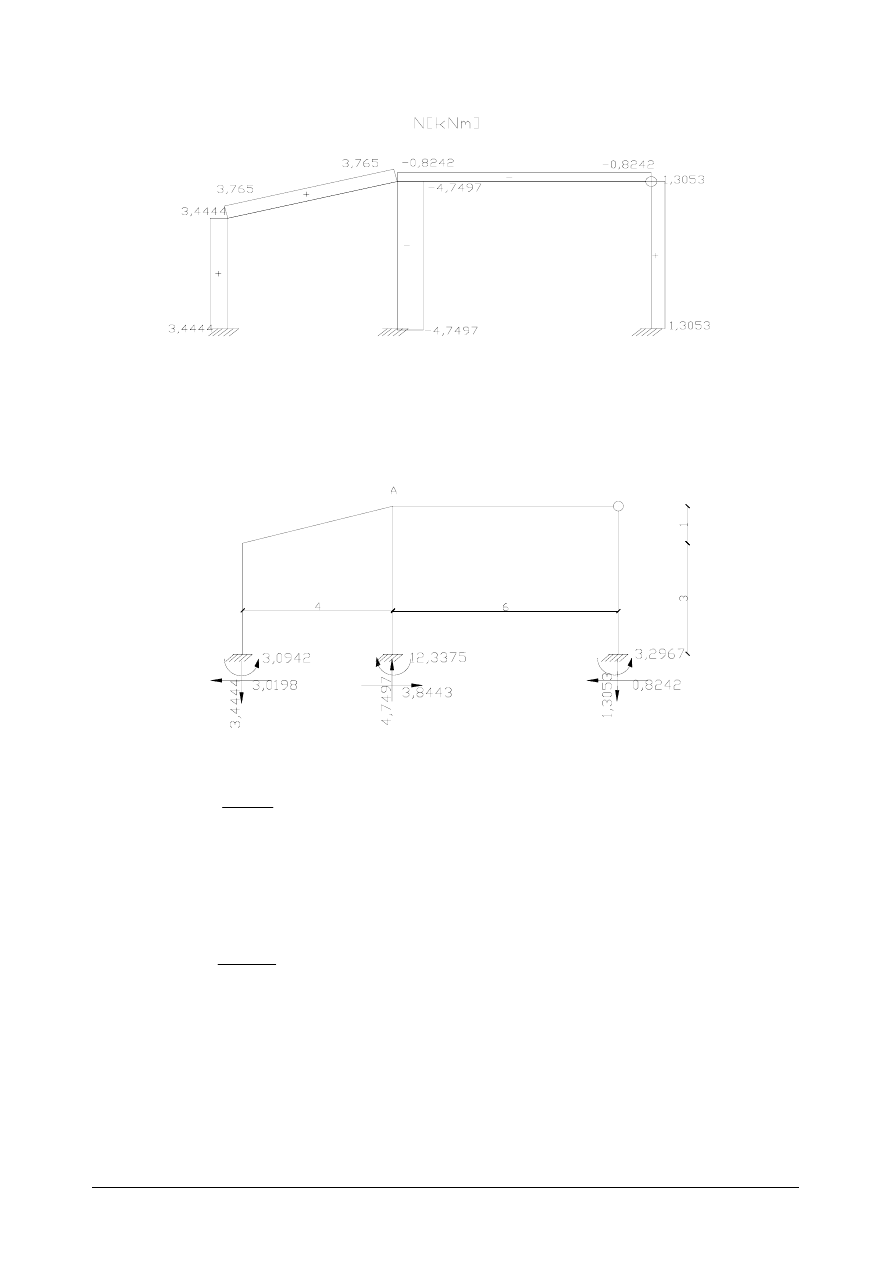
Obliczenie sił normalnych
(siły normalne obliczamy z sumy na poszczególne osie dlatego momenty pomijamy na rysunkach
gdyż nie wchodzą one w skład równań)
sin
α
=0,24254 cos
α
=0,97014
N
23
=N
32
= -0,8242kN
Σ
X: -3,0198-2,6091·0,24254+N
12
·
0,97014=0
N
43
=N
34
=1,3053kN N
12
=N
21
=3,765kN
Σ
Y: -N
10
+3,765·0,24254+2,6091·0,97014=0
N
10
=N
01
=3,4444kN
Σ
Y: -N
25
-1,3053-2,691·0,97014-3,765·0,24254=0
N
25
=N
52
= -4,7497kN
Ν
32
Ν
1,3053
0,8242
α
−2,6091
3,0198
α
25
Ν
−2,6091
1,3053
−0,8242
−3,8443
3,765
Krzysztof Wójtowicz
Strona 8
Kontrola
statyczna
Σ
X: -3,0198+3,8443-0,8242=0,0003 kN
≈
0
%
008
,
0
%
100
8443
,
3
0003
,
0
=
⋅
Σ
Y: -3,4444+4,7497-1,3053=0
Σ
M
A
: 3,0198·4-3,4444·4-3,8443·4+0,8242·4+1,3053·6-3,0942+12,3375-3,2967=
=12,0792-13,7776-15,3772+3,2968+7,8319-3,0942+12,3375-3,2967=0,0012 kNm
≈
0
%
01
,
0
%
100
3375
,
12
0012
,
0
=
⋅
Wyszukiwarka
Podobne podstrony:
Metoda przemieszczen osiadanie podpor7
Metoda przemieszczen osiadanie podpor5
Metoda przemieszczen osiadanie podpor1
Metoda przemieszczen osiadanie podpor7
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ OD OSIADANIA PODPÓR projekt42
cwicz mechanika budowli metoda przemieszczen rama osiadanie
Mechanika projekt metoda przemieszczeń (temperatura, przesuw podpór)
belka obroty i przesuwy metoda przemieszczeń
Linie wpływu Metoda przemieszczeń mmp belka lw
Metoda przemieszczeń
cwicz mechanika budowli metoda przemieszczen rama ugiecie
Metoda przemieszczen projekt4
Obliczanie ram metodą przemieszczeń wersja komputerowa
metoda przemieszczen0002
metoda przemieszczen0001
więcej podobnych podstron